Bijective function

Example of bi-yective function of two finite sets, where you can see that 日本語X日本語=日本語And日本語{displaystyle LICKXS ==.

In mathematics, a function is bijective if it is both injective and surjective; that is, if all the elements of the output set have a different image in the arrival set, and each element of the arrival set corresponds to an element of the output set.

Formally, given a function f{displaystyle f}:

f:XΔ Δ Andx and=f(x){displaystyle {begin{array}{rccl}f: strangerX fakelongrightarrow &Y hypo age-longmapsto &y=f(x)end{array}}}}}}}}}

The function is bijective if the following condition is met:

Русский Русский and한 한 And:consuming consuming !x한 한 X/f(x)=and{displaystyle forall yin Y;:quad exists ! xin X;/quad f(x)=y}

I mean, for everything. and{displaystyle and} of And{displaystyle Y} it is fulfilled that there is only one x{displaystyle x} of X{displaystyle X}such that the function evaluated in x{displaystyle x} equals and{displaystyle and}.

Given two finite sets X{displaystyle X} e And{displaystyle Y}, then there will be a bijection between both if and only X{displaystyle X} e And{displaystyle Y} They have the same number of elements.

Proposition

Yeah. f{displaystyle f,} is a real bi-yective function, then its reverse function f− − 1{displaystyle f^{-1},} exists and is also bi-ective.

Example

The function:

f(x)=α α x+β β ,{displaystyle f(x)=alpha x+beta ,} with α α ,β β 한 한 R{displaystyle alphabeta in mathbb {R} } and α α I was. I was. 0{displaystyle alpha neq 0}

is bijective.

Then its inverse:

f− − 1(x)=x− − β β α α {displaystyle f^{-1}(x)={frac {x-beta }{alpha }}}{,}

so is.

The following bipartite graph diagram shows that the function is bijective if it is injective and surjective:

Function	Injective	Not injecting
Over and over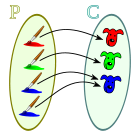
Not overyect

Examples

Seats and students in a classroom

In a class there are a certain number of seats. A group of students enter the class and the teacher asks everyone to sit down. After taking a quick look around the classroom, the teacher confidently states that there is a bijectivity between the group of students and the number of seats, where each student is paired with their corresponding seat. What the teacher had to observe in order to make this statement is:

1. All the students were sitting (no one was standing),
2. No student was sitting in more than one seat,
3. Each seat was occupied (there were no empty seats)
4. No seat was occupied by more than one student.

The teacher, thanks to that observation, was able to conclude that there were the same number of seats as there were students, without having to count the number of seats.

Cardinality and Bijectivity

Given two sets A{displaystyle scriptstyle A} and B{displaystyle scriptstyle B}among which there is a bi-ective function f:A→ → B{displaystyle scriptstyle f:Ato B} have cardinals who fulfill

card(A)=card(B){displaystyle {mbox{card}}(A)={mbox{card}}(B),}

Homeomorphism

A homeomorphism (not to be confused with homomorphism) is defined as an application between two topological spaces verifying to be a bijective and bicontinuous transformation.