AVL tree

ImprimirCitar

Animation that shows the construction of an AVL tree and includes all its rotations.

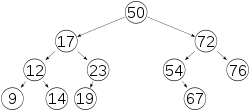
An AVL tree is a special type of binary tree devised by the Soviet mathematicians Adelson-Velskii and Landis. It was the first self-balancing binary search tree ever devised.

Description

An example of unbalanced binary tree (not AVL)

A balanced binary tree example (yes AVL)

The AVL tree takes its name from the last initials of its inventors, Georgii Adelson-Velskii and Yevgeniy Landis. They made it known in the publication of an article in 1962, "An algorithm for the organization of information" ("An algorithm for the organization of information").

AVL trees are always balanced in such a way that for all nodes, the height of the left branch does not differ by more than one unit from the height of the right branch or vice versa. Thanks to this form of balancing (or balancing), the complexity of a search in one of these trees is always maintained in order of complexity O(log n). The balance factor can be stored directly in each node or be computed from the heights of the subtrees.

To achieve this balancing property, the insertion and deletion of nodes must be done in a special way. If performing an insert or delete operation breaks the equilibrium condition, a series of node rotations must be performed.

The deepest AVL trees are Fibonacci trees.

Formal definition

Definition of the height of a tree

Sea $T$ a binary search tree and be $T_i$ and ${displaystyle T_{d}}$ his subtrees, his height ${displaystyle H(T)}$ It's:

${displaystyle 0}$ If the tree $T$ contains only the root
${displaystyle 1+max(H(T_{i}),H(T_{d}))}$ if it contains more nodes

AVL Tree Definition

An empty tree is an AVL tree
Yeah. $T$ It's an unempty tree. $T_i$ and ${displaystyle T_{d}}$ their subtrees, then $T$ It's AVL if and only if:

$T_i$ It's AVL.
${displaystyle T_{d}}$ It's AVL.
$<math alttext="{displaystyle |H(T_{i})-H(T_{d})|日本語H(Ti)− − H(Td)日本語♫1{displaystyle ΔH(T_{i})-H(T_{d}) implied=1}<img alt="{displaystyle |H(T_{i})-H(T_{d})|$

Balance factor

Each node, in addition to the information it is intended to store, must have both pointers to the left and right trees, just like the binary search trees (ABB), and also the data that controls the balance factor.

The balance factor is the difference between the heights of the left and right tree:

FE = right subtree height - left subtree height

By definition, for an AVL tree, this value should be -1, 0 or 1.

If the balance factor of a node is:

0 - PHP the node is balanced and its subtrees have exactly the same height.

1 - the node is balanced and its right subtree is a higher level.

-1 - the node is balanced and its left subtree is a higher level.

If the balance factor $=2}" xmlns="http://www.w3.org/1998/Math/MathML">日本語Fe日本語▪2{displaystyle 日本語=2}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/c433bbf07d466906bd70f5e0c37e6f18974a6a46" style="vertical-align: -0.838ex; width:10.187ex; height:2.843ex;"/>$ it is necessary to rebalance.

Operations

The basic operations of an AVL tree generally involve performing the same algorithms that would be performed on an unbalanced binary search tree, but preceded or followed by one or more so-called "AVL rotations".

Rotations

Internal rotations in binary trees are common internal operations used to maintain the perfect (or almost perfect) balance of the binary tree. A balanced tree allows for logarithmic time operations

Rebalancing occurs from the bottom up on the nodes where the imbalance occurs. Two cases can occur: simple rotation or double rotation; in turn, both cases can be to the right or to the left.

Simple rotation to the right

From a tree with root (r) and left (i) and right (d) children, what we will do is form a new tree whose root is the root of the left child, as left child we place the left child of i (our i') and as the right child we build a new tree that will have as its root, the root of the tree (r), the right child of i (d') will be the left child and the right child will be the right child of the tree (d).

op rotDer: AVL{X! - 2005 [chuckles]AVL{X!] .eq rotDer(treeBin(R1, treeBin(R2, I2, D2), D1) ♪treeBin(R2, I2, treeBin(R1, D2, D) .

Simple rotation to the left

From a root tree (r) and left (i) and right (d) children, it consists of forming a new tree whose root is the root of the right child, as the right child we place the right child of d (our d') and as the left child we build a new tree that will have the root of the tree (r) as its root, the left child of d will be the right child (i') of r and the left child will be the left child of the tree (i).

Precondition: It must have a non-empty right child.

op rotIzq: AVL{X! - 2005 [chuckles]AVL{X!] .eq rotIzq(treeBin(R1, I, treeBin(R2, I2, D2()))) ♪treeBin(R2, treeBin(R1, I, I2), D2) .

If the insertion occurs in the right child of the left child of the unbalanced node (or vice versa) a double rotation must be performed.

Double rotation to the right

Double Right Rotation is two single rotations, first single left rotation and then single right rotation.

Double rotation to the left

Double Left Rotation is two single rotations, first single right rotation and then single left rotation.

Insert

Insertion into an AVL tree can be performed by inserting the given value into the tree as if it were an unbalanced binary search tree and then backtracking towards the root, rotating over any nodes that may have become unbalanced during the insertion.

Insertion process:

1 Search until you find the insertion or modification position (process identical to insertion into binary search tree)

2 Insert the new node with “balanced” balance factor

3 Unravel the search path, verify the balance of the nodes, and re-balance if necessary

Because rotations are an operation having constant complexity and because the height is limited to O(log(n)), the execution time for insertion is of the order O(log(n)).

op insert: X$Elt AVL{X! - 2005 AVLNV{X! .eq insert(R, create) ♪ treeBin(R, create, create) .ceq insert(R1, treeBin(R2, I, D) ♪if (R1♪R2) thentreeBin(R2, I, D)elseif (R1.R2) thenif ( (height(insert(R1,I) - height(D) . 2) thentreeBin(R2, insert(R1, I), D)else ***There. that rebalanceif (R1 . root(I) thenrotateDer(treeBin(R2, insert(R1, I), D)elserotateDer(treeBin(R2, rotateIzq(insert(R1, I)), D)fi .fi .elseif ( (height(insert(R1,I) - height(D) . 2) thentreeBin(R2, insert(R1, I), D)else *** There. that rebalanceif (R1 ▪ root(D) thenrotateIzq(treeBin(R, I, insert(R1, D())))elserotatIzq(treeBin(R, I, rotateDer(insert(R1, D())))fi .fi .fi .

Extraction

The deletion procedure is the same as in the binary search tree case. The difference is in the post rebalancing process. The extraction problem can be solved in O(log(n)) steps. An extraction brings with it a decrease in the height of the branch where it was extracted and will have the effect of a change in the balance factor of the parent node of the branch in question, which may require a rotation.

This decrease in height and correction of balance factors with their possible associated rotations can be propagated to the root.

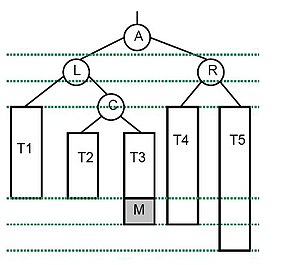Delete A, and the new root will be M.

Bored A, the new root is M. We apply rotation to the left.

The resulting tree has lost height.

In erasing, multiple rebalancing operations may be necessary, and you have to keep checking until you get to the root.

op eliminate: X$Elt AVL{X! - 2005 AVL{X! .eq eliminate(R, create) ♪ create .ceq eliminate(R1, treeBin(R2, I, D) ♪if (R1 ♪ R2) thenif It's empty.(I) thenDelseif It's empty.(D) thenIelsefor (i=0; i♫2 i+)if (height(I) - height(eliminate(min(D),D) . 2) thentreeBin(min(D), I, eliminate(min(D), D)***We've got that rebalanceelseif (height(sonIzq(I) ▪ height(SonDer(I()))) thenrotDer(treeBin(min(D), I, eliminate(min(D),D())))else rotDer(treeBin(min(D), rotIzq(I), eliminate(min(D),D())))

Search

Example in Java

public class No. { int numMat; No. izqda, drcha; public No.(int mat♪ numMat = mat; izqda = drcha = null; ! public void re_enorden(){ if(izqda = null) izqda.re_enorden(); System.out.println("Matricula: " +numMat); if(drcha = null) drcha.re_enorden(); ! ! public class AVL { private No. root; public AVL (){ root = null; ! public void insert(int newM♪ if(root♪null♪ root = new No.(newM); ! else{ insert(root,newM); ! ! private void insert(No. rz, int nm♪ if (rz ♪ null) rz = new No.(nm); else if(nm . rz.numMat) insert(rz.izqda,nm); else if(nm ▪ rz.numMat) insert(rz.drcha,nm); else System.out.println("Numero Duplicados"); ! public void visualization(){ if(root=null) root.re_enorden(); ! !public class Run { public static void main(String []args♪ AVL tree = new AVL (); tree.insert(6); tree.insert(3); tree.insert(7); tree.visualization(); ! !

Example of TAD AVL in C++

# Include ≤3struct AVL{int data, FB; // FB is the height of the left subtree less the height of the right subtreeAVL ♪izq, ♪der;Bool deleted;};void rotateLL(AVL♪ "A♪ //precond: the tree needs a LL rotationAVL♪ aux = A- 2005izq- 2005der;A- 2005izq- 2005der = A;A- 2005izq- 2005FB = 0; AVL♪ aux2 = A- 2005izq;A- 2005izq = aux;A- 2005FB = 0;A = aux2;!void rotary(AVL♪ "A♪ //precond: the tree needs a rotation RRAVL♪ aux = A- 2005der- 2005izq;A- 2005der- 2005izq = A;A- 2005der- 2005FB = 0; AVL♪ aux2 = A- 2005der;A- 2005der = aux;A- 2005FB = 0;A = aux2;!void rotateLRalter(AVL♪ "A♪ //precond: The tree needs a LR rotationrotary(A- 2005izq);rotateLL(A);!void rotateRLalter(AVL♪ "A♪ //precond: the tree needs a RL rotationrotateLL(A- 2005der);rotary(A);!AVL♪ Create(){return NULL;!void Insert(int n, Bool "increase, AVL♪ "A♪if (A ♪ NULL♪A = new AVL;A- 2005data = n;A- 2005FB = 0;A- 2005izq = NULL;A- 2005der = NULL;increase = bar;A- 2005deleted = false;!else{if (n . A- 2005data♪Insert(n, increase, A- 2005izq);if (increase♪switch (A- 2005FB♪case -1:{A- 2005FB = 0;increase = false;break;!case 0:{ A- 2005FB = 1;increase = bar;break;!case 1:{if (A- 2005izq- 2005FB ♪ 1♪ // If it is 1 you need a LL rotation if it is -1 you need a LR rotationrotateLL(A);!else{rotateLRalter(A);!increase = false;break;!!!!else{Insert(n, increase, A- 2005der);if (increase♪switch (A- 2005FB♪case -1:{if (A- 2005der- 2005FB ♪ 1♪ // If it is 1 you need an RL rotation if it is -1 you need a RR rotationrotateRLalter(A);!else{rotary(A);!increase = false;break;!case 0:{A- 2005FB = -1;increase = bar;break;!case 1:{A- 2005FB = 0;increase = false;break;!!!!!!void Insert(AVL♪ "A, int n♪Bool increase;Insert(n, increase, A);!Bool It's empty.(AVL♪ A♪return A ♪ NULL;!Bool It belongs(AVL♪ A, int n♪if (A ♪ NULL♪return false;!else{if (A- 2005data ♪ n♪if (A- 2005deleted♪return false;!else{return bar;!!else if (n . A- 2005data♪return It belongs(A- 2005izq, n);!else{return It belongs(A- 2005der, n);!!!void Delete(AVL♪ "A, int n♪if (A- 2005data ♪ n♪A- 2005deleted = bar;!else if (n . A- 2005data♪Delete(A- 2005izq, n);!else{Delete(A- 2005der, n);!!

Contenido relacionado

Más resultados...