Atomic orbital

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

3D representations of atomic orbitals (up to the right) and molecular (down to the right). On the left is shown the Moeller Diagram, a mnemotechnic graph that helps to follow the Madelung rule in order to build the electronic configuration (filling order and orbital occupation, shown at the bottom of the figure) from the knowledge of the atomic number Z, following the Principle of Aufbau. Note: It should be taken into account that atomic orbitals

{displaystyle phi ({vec {r}})=phi (r,thetaphi)}

are functions of three variables (the distance to the core, r, and the two angles,

{displaystyle thetaphi }

). The images shown represent only the angular component of each orbital that defines its form. The color change in the gray scale indicates a change of sign in the OA and, according to the case, evidences the presence of nodal surfaces, where the wave function is canceled.

A atomic orbit (OA) is a monoelectronic wave function $phi$ which, therefore, describes the behavior of a single electron in the context of an atom. It is obtained in the framework of the Quantum Mechanics applied to the treatment of atoms (along with atomic theory, it constitutes one of the bases of Quantum Chemistry) and corresponds to a particular spatial solution of the Schrödinger equation independent of the time for an electron subject to the coulombian potential generated by the atomic nucleus (and the remaining electrons in poly-electronic atoms). Schrödinger's equation describing the behavior of an electron in an atom has an exact solution only for the case of the hydrogen atom (extensible to atomic ions to which all the less one electrons are extracted, identified as "hydrogenoid atoms"). The concept of atomic orbital applied to an electron in a poly-electronic atom is an approximation, which is obtained after disconnecting the movement of each pair of electrons and treating them as if each one moves in an average electrostatic field (approximation of Hartree-Fock).

In all cases the space orbital orbit is defined by three quantum numbers, which naturally appear in the general solution of the atomic Schrödinger equation ${displaystyle {mathcal {H}}phi _{n,l,m}=E_{n}phi _{n,l,m}}$ and point to a specific electronic state. Those three quantum numbers refer to the total energy of the electron ( $n$ , main quantum number), to the orbital angular moment module ${displaystyle {vec {L}}}$ ( ${displaystyle {mathcal {l}}}$ , quantum orbital angular moment number) and the module of its projection ${displaystyle {vec {L_{z}}}}$ ( ${displaystyle m_{l}}$ , magnetic quantum number) on the z axis of the external reference system (laboratory).

Like any wave function in quantum mechanics, the atomic orbit $phi$ It lacks for itself physical meaning, but according to Born's interpretation, its square module ( ${displaystyle mid {displaystyle phi }mid ^{2}={displaystyle phi }^{*}.{displaystyle phi }}$ ) represents the probability density of finding that electron at each point of space (or more briefly, an electronic density) and allows to calculate the probability of finding it in a certain volume of the atom.

The superposition of all the electronic densities associated with each of the different atomic orbitals, with spherical symmetry centered on the atomic nucleus, gives rise to the electronic shell, represented by the shell model, which is adjusted to each element chemical according to the corresponding electron configuration.

Introduction

The atomic orbit $phi$ contains all available information about the spatial behavior of an electron within the atom, in the state defined by the three quantum numbers $n$ , ${displaystyle {mathcal {l}}}$ and ${displaystyle m_{l}}$ . Through the undulating description of quantum mechanics and associated probability density, the size, shape and orientation of a space region available for an electron is defined. Each orbital with different values n presents a specific energy for the state of the electron in hydrogenoid atoms.

The probability of finding an electron at a point of space is defined through its spatial coordinates. In Cartesian coordinates such probability density is denoted as ${displaystyle mid {displaystyle phi ({vec {r}})}mid ^{2}=mid phi (x,y,z)mid ^{2}}$ . As spherical symmetry is assumed in the atoms, it is usually worked alternatively with the wave function ${displaystyle phi ({vec {r}})}$ expressed in terms of spherical coordinates, where ${displaystyle phi ({vec {r}})=phi (r,thetaphi)}$ and electronic density ${displaystyle mid {displaystyle phi ({vec {r}})}mid ^{2}=mid phi (r,thetaphi)mid ^{2}}$ .

Physical Fundamentals

The wave function solution of the atomic Schrödinger Equation

Main articles: Wave function and Stationary State (quantum mechanics).

In the atomic model that emerged after applying quantum mechanics to the description of the internal movement of electrons in atoms (model after the atomic model of Bohr and other derivatives such as the atomic model of Sommerfeld), it is called atomic orbital to each of the mono-electronic wave functions that describe the spatial stationary states of an electron in the hydrogen atom and atom ions. That is, they are the physical stationary states represented as function of the spatial position ${displaystyle {vec {r}}}$ , ${displaystyle phi _{nlm}({vec {r}})=langle {vec {r}}|nlmrangle }$ which are obtained by solving the equation of Schrödinger independent of the time for the atom ${displaystyle {mathcal {H}}phi _{n,l,m}=E_{n}phi _{n,l,m}}$ , that is, the functions of the Haitian operator, $mathcal{H}$ . They do not represent the concrete position of an electron in the atomic space, which cannot be known precisely given its mechanical-quantum nature, but from them is defined a region of space around the atomic nucleus in which the probability of finding the electron is high.

The quantum numbers that define the state of an electron in an atom

Main article: Quantum number

In the case of hydrogen atom and hydrogenoid ions, the electronic Schrödinger (ES) equation can be resolved in an exact way, finding that the wave functions $phi$ solution of the ES are determined by the values that can assume the three quantum numbers $n$ , ${displaystyle {mathcal {l}}}$ and ${displaystyle m_{l}}$ . These quantification conditions arise from the restrictions imposed by the contour conditions on the electronic movement within the atom; not all the state pairs (described by the wave function) and associated energy value are physically possible. Let's see what values these three quantum numbers can assume and what quantities of the electron are associated with.

The value of the quantum number n (main quantum number, takes values 1.2.3...) defines the total energy level and the size of the atomic orbital. The higher the n, greater will be the volume associated with the corresponding atomic orbital and also the energy of the electron. Stop. $n=1$ the electron is in its basal or fundamental state, which corresponds the lowest possible energy and is therefore the most stable state of the electron.
The value of the quantum number l (azimutal quantum number, associated with the total angular moment, takes values 0, 1, 2,... to n-1) defines the shape of the orbital and the angular moment of the electron ${displaystyle {vec {L}}}$ whose module ${displaystyle mid {vec {L}}mid }$ is given by:

{displaystyle |L|=hbar {sqrt {l(l+1)}}}

the notation for atomic orbitals (from atomic spectroscopy) is as follows:

Stop. ${displaystyle {mathcal {l}}}$ = 0, orbital s
Stop. ${displaystyle {mathcal {l}}}$ = 1, orbital p
Stop. ${displaystyle {mathcal {l}}}$ = 2, orbital d
Stop. ${displaystyle {mathcal {l}}}$ = 3, orbital f
Stop. ${displaystyle {mathcal {l}}}$ = 4, orbital g;

and arises in relation to the lines of the spectrum of an atomic element (in English, s for sharp, p for Principal, d for diffuse and f for fundamental) until ${displaystyle {mathcal {l}}}$ = 3 and then continue to assign the orbital type by alphabetical order (g, hetc.).

3. The value of ${displaystyle m_{l}}$ (quantum magnetic number, takes values 0, ± 1, ± 2,... ± ${displaystyle {mathcal {l}}}$ ) defines the orientation of the atomic orbital in front of an external magnetic field. For the projection ${displaystyle L_{z}}$ the total angular moment on the z axis of the external field, is verified:

${displaystyle L_{z}=hbar m_{l}}$

Subsequently the need to include ad hoc a quarter quantum number ${displaystyle m_{s}}$ (increasing in the solutions of the atomic Schrödinger equation) to completely determine the status of an electron. In the relativistic quantum mechanics the sphin arises naturally in the solutions of the Dirac equation. by hand. The angular moment of thorn ${displaystyle {vec {s}}}$ , adopts for the electron a unique value s = 1/2 that determines that ${displaystyle mid {vec {s}}mid =hbar {sqrt {s(s+1)}}={sqrt {0.75}}hbar }$ and defines the existence of 2 different electronic states through quantum number ${displaystyle m_{s}}$ (which takes the values +1/2 or -1/2) where ${displaystyle s_{z}=hbar {displaystyle m_{s}}}$ . When the electronic spin is not taken into account, it is said that the atomic orbital is a spatial orbital, while if considered the state of spine, it is called the atomic orbital spine.

An atomic orbital can be decomposed into a radial and an angular part, using the following as a spherical coordinate system:

${displaystyle Psi _{n,l,m_{l}}({vec {r}})=R_{n,l}(r)Theta _{l,m_{l}}(theta)Phi _{m_{l}}(varphi)}$

where ${displaystyle R_{n,l}(r)}$ represents the radial part of the atomic orbital, which depends on the r distance of the electron to the nucleus, e ${displaystyle Y_{ell }^{m_{l}}(thetavarphi)=}$ ${displaystyle Theta _{l,m_{l}}(theta)Phi _{m_{l}}(varphi)}$ represents its angular component, corresponding to spherical harmonics of the form

${displaystyle Y_{ell }^{m_{l}}(thetavarphi)=NP_{ell }^{m_{l}}(cos {theta })e^{im_{l}varphi }}$

Where N is a normalization factor and ${displaystyle P_{ell }^{m_{l}}}$ an associate polynomial of Legendre. For the graphic representation of the angular variation of an atomic orbital the square module of this complex function is used ${displaystyle leftvert {Y_{ell }^{m_{l}}(thetavarphi)}rightvert ^{2}}$ which is proportional to electronic probability density or electronic density and defines a volume that contains most of the probability of finding the electron or, if preferred, the volume or region of the space where the electron passes most of the time.

Beyond the hydrogen atom: atoms with more than one electron

Main article: Polyelectronic atom

In the strict sense, atomic orbitals are wave functions that try to describe -in a manner consistent with the description of quantum mechanics- the stationary states of a single electron subjected to an electric field of central symmetry (or eventually two electrons, when the space atomic orbital is combined with each of the two states of e-spin incorporating ${displaystyle m_{s}}$ and gives rise to the atomic orbital spine). It should be noted that since the core is not explicitly described as a reference point for the electronic internal movement, the OAs do not even fully describe the hydrogen atom. In atomic systems of more than one electron, the coupling between the movement of electron pairs that repel each other and is reflected in the term of inter-electronic repulsion of Hamiltonian $mathcal{H}$ corresponding poly-electronic, it prevents the exact analytical resolution of the atomic Schrödinger equation. These mathematical constructions are not adequate, because of their mono-electronic origin, to take into account the instant correlation between electrons (and thus, when an orbital approach is used in systems of more than one electron, the error of electronic correlation is introduced) or the antisymetry that must have the function that describes the whole of electrons to the exchange between them, required by the statistics of Fermi (note that electrons are ferns). Thus, approximate descriptions of the behavior of a single electron immersed in the electrostatic field of Coulomb generated by the nucleus and the remaining electrons, which come out of their strict sense, have shown to be of enormous utility in the field of quantum chemistry, so that they are used not only to describe poly-electronic atomic systems, but also for poly-electronic systems (s like molecules).

Also, beyond its strict sense, chemists refer to them as physical entities rather than as mathematical constructions, with expressions such as "two electrons fit in one orbital".^{[citation needed]}

Shape of atomic orbitals and associated electron density

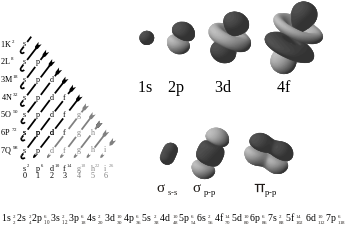
There are different ways to represent in 3D the shape of spatial atomic orbitals and the electron density associated with them. For simplicity, in some images only its angular component is represented, omitting to show the radial behavior that can present nodes (points or planes where the OA is canceled and the electron density as well, which is an always positive function, associated as mentioned to the square module of the OA function).

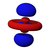
S-orbitals

The "s" They have spherical symmetry around the atomic nucleus. The following figure shows different alternative ways to represent the electron cloud associated with an s orbital: in the first, the probability of finding the electron (represented by the density of points) decreases as we move away from the center; in the second, the spherical volume in which the electron spends most of the time is represented and lastly the electron is observed.

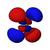
P orbitals

The geometric shape of the p orbitals is that of two spheres flattened towards the point of contact (the atomic nucleus) and oriented according to the coordinate axes. Depending on the values that the third quantum number m_l (-1, 0 and 1) can take, the three symmetric p orbitals are obtained with respect to the X, Z and y. Analogously to the previous case, the p orbitals present n-2 radial nodes in the electron density, so that as the value of the principal quantum number increases, the probability of finding the electron moves away from the atomic nucleus. The "p" It also represents the energy that an electron possesses and increases as the distance between the nucleus and the orbital moves away.

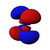
D-orbitals

The d orbitals have more diverse orientations. Four of them are in the form of 4 lobes of alternate signs (two nodal planes, in different orientations in space), and the last one is a double lobe surrounded by a ring (a double nodal cone). Following the same trend, they present n-3 radial nodes. This has 5 orbitals and corresponds to the quantum number l (azimuthal)

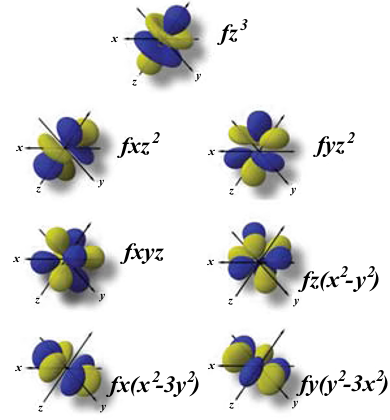
F-orbitals

The f orbitals have even more exotic orientations, which can be derived by adding a nodal plane to the shapes of the d orbitals. They present n-4 radial nodes.

G orbitals

According to the orbital approximation in quantum mechanical descriptions of atomic structure, elements with partially filled g orbitals lie in the hypothetical g block. However, spin–orbit coupling effects substantially reduce the validity of the orbital approximation for elements of high atomic number. Thus, an element in the column labeled g¹ could have exactly one g (as the name suggests), but it is also possible that it has more or none. They would present n-5 radial nodes.

Orbital Table

The table below shows all the orbital configurations for hydrogen, as wave functions, from 1s to 7s. The polyelectronic atoms would be lodging their electrons in said groups of orbitals.

	s (l=0)	p (l=1)			d (l=2)					f (l=3)
	m=0	m=0	m=±1		m=0	m=±1		m=±2		m=0	m=±1		m=±2		m=±3
	s	p_z	p_x	p_and	d_z²	d_xz	d_yz	d_xy	d_{x²- and²}	f_z³	f_xz²	f_yz²	f_xyz	f_{z(x²- and²)}	f_x²-3y²)	f_{and(3x)²- and²)}
n=1
n=2
n=3
n=4
n=5										...	...	...	...	...	...	...
n=6					...	...	...	...	...	...	...	...	...	...	...	...
#7		...	...	...	...	...	...	...	...	...	...	...	...	...	...	...