Atomic nucleus

Approximate representation of Helio atom: in the nucleus the protons are represented in red and the neutrons in blue. In reality the core is also symmetrically spherical.

The atomic nucleus is the central part of an atom, has a positive charge, and concentrates more than 99.9% of the total mass of the atom.

It is made up of protons and neutrons (called nucleons) that are held together by the strong, detailed nuclear interaction that allows the nucleus to be stable, even though the protons repel each other (like the poles). equal of two magnets). The number of protons in the nucleus (atomic number) determines the chemical element to which it belongs. Atomic nuclei do not necessarily have the same number of neutrons, since atoms of the same element can have different masses, that is, they are isotopes of the element.

The existence of the atomic nucleus was deduced from the Rutherford experiment, where a thin sheet of gold was bombarded with alpha particles, which are helium atomic nuclei emitted by radioactive rocks. Most of these particles passed through the sheet, but some bounced off, proving the existence of a tiny atomic nucleus.

History

The discovery of electrons was the first indication of the internal structure of atoms. At the beginning of the 20th century the accepted model of the atom was J.J Thomson's 'raisin pudding', model in which the atom was a large ball of positive charge with the small negatively charged electrons embedded within it. By then, physicists had also discovered three types of radiation from atoms: alpha, beta, and gamma radiation. Experiments in 1911 by Lise Meitner and Otto Hahn, and by James Chadwick in 1914 showed that the beta decay spectrum is continuous and not discrete. That is, electrons are ejected from the atom with a range of energies, rather than the discrete amounts of energy seen in gamma rays and alpha decay. This seemed to indicate that energy was not conserved in these decays. Later it was discovered that energy is conserved, with the discovery of neutrinos.

In 1906 Ernest Rutherford published "The Lag of the Sphere alpha of radius when it passes through matter", in Philosophical Magazine (12, p. 134-46). Hans Geiger expanded on this work in a communication to the Royal Society (Proc. Roy. Soc. 17 Jul 1908) with experiments and Rutherford had passed air through the α-particles, aluminum foil, and gold foil. Geiger and Marsden published additional work in 1909 (Proc. Roy. Soc. A82 p. 495-500) and further expanded the work in Geiger's 1910 publication (Proc. Roy. Soc. Feb. 1, 1910). In 1911-2 Rutherford explained the experiments to the Royal Society and proposed the new theory of the atomic nucleus. Therefore, it is considered that Rutherford demonstrated in 1911 the existence of the atomic nucleus.

Around the same time (1909) Ernest Rutherford conducted an experiment in which Hans Geiger and Ernest Marsden, under his supervision, shot alpha particles (helium nuclei) into a thin sheet of gold. Thomson's atomic model predicted that alpha particles should exit the sheet with small deviations from their trajectories. However, he discovered that some particles are scattered at large angles, and even completely backwards in some cases. This discovery in 1911 led to Rutherford's atomic model, in which the atom is made up of protons and electrons. Thus, the nitrogen-14 atom would be made up of 14 protons and 7 electrons.

Rutherford's model worked quite well for many years. It was thought that the repulsion of the positive charges between protons was solved by the electrons (with a negative charge) interposed orderly in the middle, for which reason the electron was considered a "nuclear cement". This was until studies carried out by Franco Rasetti at the California Institute of Technology in 1929. In 1925 it was known that protons and electrons have a spin of 1 / 2, and in the Rutherford model nitrogen - 14 the 14 protons and six of the electrons should cancel their contributions to the total spin, estimating a total spin of 1 / 2. Rasetti discovered, however, that nitrogen - 14 has unit total spin.

In 1930 Wolfgang Pauli was unable to attend a meeting in Tübingen, instead sending a famous letter with the classic introduction "Dear Radioactive Ladies and Gentlemen ". In his letter, Pauli suggested that perhaps there was a third particle in the nucleus, which he named "neutrons". He suggested that it was lighter than an electron and without an electrical charge, and that it did not easily interact with matter (and thus had not yet been detected). This hypothesis made it possible to solve both the problem of conservation of energy in beta decay and the spin of nitrogen - 14, the first because the neutrons carried undetected energy and the second because an extra electron coupled with the surplus electron in the nitrogen nucleus - 14 to provide a spin of 1. Enrico Fermi renamed Pauli neutrons in 1931 as neutrinos (Italian for small neutral) and some thirty years later it was finally shown that a neutrino is indeed emitted in beta decay.

In 1932 James Chadwick realized that the radiation that had been observed by Walther Bothe, Herbert L. Becker, Irène and Jean Frédéric Joliot-Curie was actually due to a particle he called the neutron. In the same year Dimitri Ivanenko suggested that neutrons were, in fact, spin 1/2 particles, existing in the nucleus and no electrons in the nucleus, and Francis Perrin suggested that neutrinos are nuclear particles, created during beta decay. Fermi published in 1934 a theory of neutrinos with a solid theoretical basis. In the same year Hideki Yukawa proposed the first major theory of force to explain the way the nucleus holds together.

After the discovery of the neutron, by James Chadwick, Werner Heisenberg (who enunciated years before the uncertainty principle), indicated that neutrons can be part of the nucleus, and not electrons. This theory completely solved the spin mismatch problem, as well as explaining all aspects of nuclear behavior.

However, the new theory brought with it another severe problem: with the previous model, which included electrons as "nuclear cement", it was explained that the protons, all with the same positive charge, remained totally together, without being thrown out by the repulsion of equal charges. However, with the model that includes the neutron, there was no explanation for how the nucleus holds together and does not immediately explode (ie, no element should exist, with the sole exception of hydrogen). To illustrate, the force with which two protons repel each other at a distance (one ten billionth of a centimeter) is approximately 240 newtons, enough force to lift an object weighing just over 24 kilograms into the air (note the unimaginable enormity of that force since we are talking about two protons, whose mass is a little more than 10^-27 kilograms)

The enormous difficulty suffered by the theory was gradually resolved. In 1927, Heisenberg proposed the uncertainty principle, which states that the more precisely we know the velocity of a particle, the less precisely we can know its position.

In 1930 Einstein deduced from this principle, by mathematical means, that if the principle is correct, another type of indeterminacy about the measurement of the energy existing in a closed system is also correct. The shorter the period of time in which you want to know the amount of energy in the system, the less accurately you can measure it.

At the time of suggesting the proton-neutron model of the nucleus, in 1932, Heisenberg also suggested the existence of a force field that united the protons, through the ephemeral existence of a particle. The existence of this particle would be possible only because of the uncertainty principle, in the version enunciated by Einstein.

The Japanese physicist, Hideki Yukawa, then began to analyze the properties of the particle proposed by Heisenberg, and in 1935 he described those properties precisely. The particle could only exist for an instant of about 5 × 10^-24 seconds, long enough for it to go from one proton to another, but no further than the nucleus of the atom. The energy required for the existence of this particle in that brief period conforms to the uncertainty principle in Einstein's version. Using these equations, the energy available in that period would be 20 pJ (pico joules, 2 × 10 ^-11 J or 1.25 × 10⁸ eV), which is equivalent to a particle with a mass 250 times that of an electron.

Since then there have been several attempts to detect that particle experimentally. Of course, being a particle that only exists for a brief moment, and using unavailable energy, only thanks to the uncertainty principle, it would be impossible to detect, except if that energy were provided. Cosmic rays—particles arriving from space at enormous speeds—can provide that energy. In 1948, while experimenting with cosmic rays in Bolivia, the particle was detected by Cecil Frank Powell. The particle was named Pion.

Kernel Description

Nucleus shape and size

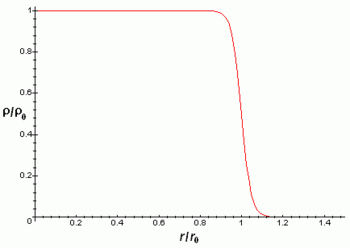
Atomic nuclei are much smaller than the typical size of an atom (10,000 to 100,000 times smaller). They also contain more than 99% of the mass, with which the mass density of the nucleus is very high. Atomic nuclei have some kind of internal structure, for example neutrons and protons seem to be orbiting around each other, a fact that manifests itself in the existence of the nuclear magnetic moment. However, experiments reveal that the nucleus closely resembles a compact 10^-15 m (= 1 fm) sphere or ellipsoid, in which the density appears almost constant. Naturally the radius varies according to the number of protons and neutrons, being the heavier nuclei and with more particles somewhat larger. The following formula gives the radius of the nucleus as a function of the number of nucleons A:

Rn=r0A13{displaystyle R_{n}=r_{0}A^{frac {1}{3}{3}}}{3}}}}

Where r0≈ ≈ 10− − 15m{displaystyle r_{0}approx 10^{-15}{mbox{ m}}

Electric charge density in the atomic nucleus.

The electrical load density of the core is approximately constant to the distance Rn{displaystyle scriptstyle R_{n}} and then decay quickly up to 0 in a distance a{displaystyle scriptstyle a} according to the formula:

ρ ρ (r)=ρ ρ 01+Exp (r− − Rn0,228a){displaystyle rho (r)={frac {rho _{0}}}{1+exp left({frac {r-R_{n}}{0,228a}}}}}}}}}}}

Where r is the radial distance from the center of the atomic nucleus.

The above approximations are better for spherical nuclei, although most nuclei do not appear to be spherical as it reveals that they possess non-zero quadrupole moment. This quadrupole moment manifests itself in the hyperfine structure of atomic spectra and makes the electric field of the nucleus not a spherically symmetric Coulomb field.

Kernel stability

Segrè diagram, in red stable nuclei, in other colors unstable nuclei colored according to the disintegration period. Note that a slight excess of neutrons favors stability in heavy atoms.

Atomic nuclei behave like composite particles at sufficiently low energies. In addition, most atomic nuclei below a certain atomic weight and which also present a balance between the number of neutrons and the number of protons (atomic number) are stable. However, we know that isolated neutrons and nuclei with too many neutrons (or too many protons) are either unstable or radioactive.

The explanation of this stability of the nuclei resides in the existence of pions. In isolation, neutrons can undergo the following disintegration via a weak interaction:

(1)n0→ → p++e− − +.. ! ! e{displaystyle n^{0}to p^{+}+e^{-}+{bar {nu }}{e}}

However, within the atomic nucleus the proximity between neutrons and protons makes the reactions much faster, via strong interaction:

(2){n0▪ ▪ p++π π − − p+▪ ▪ n0+π π +{displaystyle {begin{cases}n^{0}rightleftarrows p^{+}pi ^{-}p^{+}rightleftarrows n^{0}+pi ^{+}end{cases}}}}

This continuously causes the neutrons in the nucleus to transform into protons, and some protons into neutrons, this causes the reaction (1) to barely take time of occurrence, which explains why the neutrons of atomic nuclei are much more stable than isolated neutrons. If the number of protons and neutrons becomes unbalanced, the possibility opens that at each moment there are more neutrons and the reaction is easier to occur (1).

Structure models of the atomic nucleus

Internal structure of the atom.

In 1808 the English chemist John Dalton proposed a new theory on the constitution of matter. According to Dalton all matter is made up of indivisible and invisible atoms, these in turn unite to form compounds in fixed and constant integer proportions. In fact, Dalton proposed the existence of atoms as a hypothesis to explain why atoms only combined in certain specific combinations. The study of these combinations led him to be able to calculate atomic weights. For Dalton the existence of the atomic nucleus was unknown and it was considered that there were no smaller parts.

In 1897 Joseph John Thomson was the first to propose an internal structural model of the atom. Thomson was the first to identify the electron as a negatively charged subatomic particle and concluded that "if atoms contain negative particles and matter occurs as charge neutral, then positive particles must exist." This is how Thomson postulated that the atom It must be a positive compact sphere in which the electrons would be embedded in different places, so that the amount of negative charge is equal to the positive charge.

Thus neither Dalton's nor Thomson's atomic model included any description of the atomic nucleus. The notion of the atomic nucleus arose in 1911 when Ernest Rutherford and his collaborators Hans Geiger and Ernest Marsden, using a beam of alpha radiation, bombarded very thin laminated metal sheets, placing a zinc sulfide screen around them, a substance that had the quality to produce sparkles with the collision of the incident alpha particles. The metal foil was traversed by most of the incident alpha particles; some of them followed in a straight line, others were diverted from their path, and most surprisingly, very few bounced against the sheet.

In light of the dispersion formula used by Rutherford:

(1)χ χ =2π π − − 2#− − 1 (2K/(E0b)1+(2K/(E0b))2){displaystyle chi =2pi -2cos ^{-1}left({frac {2K/(E_{0}b)}{sqrt {1+(2K/(E_{0}b)}^{2}}}}}{right)}

Where:

K=(qN/4π π ε ε 0){displaystyle K=(q_{N}/4pi varepsilon _{0}),}, being ε ε 0{displaystyle varepsilon} the dielectric constant of void and qN{displaystyle q_{N},}It's the electric charge of the dispersed center.

E0{displaystyle E_{0},}, is the initial kinetic energy of the alpha particle incident.

b{displaystyle b,} is the impact parameter.

The results of the experiment required very small impact parameters, and therefore that the nucleus be concentrated in the central part, the positively charged nucleus, where the mass of the atom would be concentrated. with this he explained the deviation of alpha particles (positively charged particles). The electrons would be found in an external structure rotating in circular orbits very far from the nucleus, which would explain the majority of alpha particles passing through the gold foil.

In 1913 Niels Bohr postulated that electrons revolve at high speeds around the atomic nucleus. The electrons are arranged in various circular orbits, which determine different energy levels. The electron can access a higher energy level, for which it needs to "absorb" Energy. To return to its original energy level it is necessary for the electron to emit the absorbed energy (for example in the form of radiation).

There are commonly two different models to describe the atomic nucleus:

• The model of the drop of water
• The layer model

Although these models are mutually exclusive in their basic hypotheses as originally formulated, A. Bohr and Mottelson built a mixed model that phenomenologically combined features of both models.

Liquid drop model

Link energy by nucleon (=B/A) for known isotopes.

This model is not intended to describe the complex internal structure of the nucleus but only the binding energies between neutrons and protons as well as some aspects of the excited states of an atomic nucleus that are reflected in nuclear spectra. It was initially proposed by Bohr (1935) and the nucleus in analogy with a mass of classical fluid composed of neutrons and protons and a central repulsive Coulomb force proportional to the number of protons Z and originating from the center of the drop.

From the quantitative point of view it is observed that the mass of an atomic nucleus is inferior to the mass of the individual components (protons and neutrons) that form it. This non-maintenance of the mass is connected to the equation E=mc2{displaystyle E=mc^{2}} of Einstein, by which part of the mass is in the form of ligation energy between these components. Quantitatively you have the following equation:

mN=Zmp+(A− − Z)mn− − Bc2{displaystyle m_{N}=Zm_{p}+(A-Z)m_{n}-{frac {B}{c^{2}}}}}}}

Where:

mN,mp,mn{displaystyle m_{N},m_{p},m_{n}, are respectively the mass of the core, the mass of a proton and the mass of a neutron.

Z,A,A− − Z{displaystyle Z,A,A-Z,} are respectively the atomic number (which matches the number of protons), the masic number (which matches the number of nucleons) and A-Z therefore it coincides with the number of neturones.

B{displaystyle B,} is the energy of linking all nucleons.

The water drop model aims to describe the binding energy B from geometric considerations and interprets the energy of the excited states of the nuclei as rotations or semiclassical vibrations of the "drop of water" which represents the nucleus. Specifically, in this model the binding energy is represented as B:

B=Bv+Bs+Bc+Ba+Bp{displaystyle B=B_{v}+B_{s}+B_{c}+B_{a+}B_{p},}

Where:

Bv=avA{displaystyle B_{v}=a_{v}a,} this term represents the favorable effect of volume.

Bs=− − asA2/3{displaystyle B_{s}=-a_{s}A^{2/3},} this term represents the unfavorable effect of the surface.

Bc=− − acZ2A− − 1/3{displaystyle B_{c}=-a_{c}Z^{2}A^{-1/3},} represents the effect of the coulombian repulsion between protons.

Ba=− − aa(A2Z)2/A{displaystyle B_{a}=-a_{a}(A_{2}Z)^{2}/A,} represents the fact that the "balanced" cores with a similar number of protons and neutrons are more stable.

Bp{displaystyle B_{p},} represents the fact that the nuclei with a pair of protons and neutrons are more stable than those with an odd number of both species. Mathematically the term is given by:

Bp={+apA− − 1/2(parking)0(impar-par)− − apA− − 1/2(cleaning){displaystyle B_{p}={begin{cases}+a_{p}A^{-1/2}{mbox{(par-par)}}} fake{mbox{mbox{(impar-par)}}}}}{-a_{p}{{{mbox{mbox{(impar-impar}}}}}}}{end{cases}}}}}}}}}}}}

Layered model

This is a model that tries to capture part of the internal structure reflected in both the angular momentum of the nucleus and its angular momentum. In addition, the model tries to explain why the nuclei with a "magic number" of nucleons (neutrons and protons) are more stable (the magic numbers are 2, 8, 20, 28, 50, 82 and 126).

The explanation of the model is that nucleons are grouped in "shells". Each shell is made up of a set of quantum states with similar energies, the energy difference between two layers is large compared to the energy variations within each shell. Thus, since nucleons are fermions, an atomic nucleus will have the lower energy shells filled, so the nucleons cannot fall to lower, already filled shells. The layers here must be understood in an abstract sense and not as physical layers like the layers of an onion, in fact the geometric shape of the space occupied by a nucleon in a certain state of a layer interpenetrates with the space occupied by nucleons of other layers., analogous to how the electronic shells interpenetrate in an atom.