Asymptote

Graphics of two hyperboles and their asymptotes on the Cartesian plane.

In integral calculus, the asymptote of the graph of a function is a line to which the graph of that function continually approaches; that is, the distance between the two tends to be zero (0), as they extend indefinitely.
Or that both exhibit asymptotic behavior. Generally, rational functions have asymptotic behavior.

Treaty on conicals, s. XVIII

History and significance

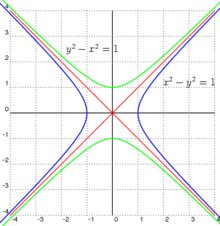
The word asymptote derives from the Greek: ἀσύμπτωτος asýmptōtos, «that which does not fall»; where a- has a privative value (= not), while sym-ptōtos connotes that which "falls" or "falls together (with something)". The definition of an asymptote is usually given to a curve that "never meets". which does not intersect a branch of a hyperbola.

In geometry, asymptotic behavior refers to an eventual property between curves, and more precisely, between functions or parts of functions: line segments, leaves of hyperbolas or parabolas, etc. It is in this sense that one speaks of an “asymptotic line” as tangent to infinity of a parabolic branch, or of asymptotic curves.

His deepest study goes beyond the mere field of application of elementary geometry and the drawing of plane curves; With the development of algebra and infinitesimal calculus, the intuitive notions "tends to infinity" and "tends to zero" are formalized with the concept of mathematical limit, and with it also the calculus of asymptotes.

Graph of asymptotes

They help to represent curves, provide structural support and indicate their long-term behavior. As straight lines, the equation of an asymptote is simply that of a straight line, and its analytical expression will depend on the choice of the reference system (y = m•x + b in Cartesian coordinates).

Although they are usually represented in the same coordinate system, the asymptotes are not part of the analytical expression of the function, so -in numerous examples- they are not explicitly included within the graph, or they are indicated by a dotted line.
In many cases, the asymptotes coincide with the coordinate axes, that is, their equations in Cartesian coordinates will be: x = 0, y = 0.

There are three types:

• Vertical symptoms: straights perpendicular to the axis of abscises, of equation x = constant.
• Horizontal symptoms: straights perpendicular to the axis of the orders, of equation y = constant.
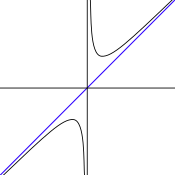
• Oblical symptoms: if they are not parallel or perpendicular to the axes, of equation y = m•x + b.

The branches of the function have asymptotes.

The axles are asymptotes.

The branches of the function have asymptotes.

Asymptotic behavior between a curve and a straight.

Analytic determination of asymptotes

In analysis, calculus, and analytic geometry, the behavior of non-trivial functions in the vicinity of "undefined" points (such as division by zero or indeterminate forms) provides valuable information about their graph, and in this context the asymptotes arise naturally as "solutions" (or directions) at these points. In this sense, a function can have a "right asymptote" but not a left one (or vice versa); or a line can intersect a curve at a finite (or infinite) number of points, and still behave asymptotically.

Calculation of asymptotes by means of limits

Asymptotes of rational functions

In the graphical representation of a rational function, asymptotes play an essential role, when they exist. Although it is possible to apply the limit method described above, in the case of rational functions, algorithmic techniques that do not require mathematical analysis are often used.
A rational function can have more than one vertical asymptote, but only one that is horizontal or oblique (ie if it has a horizontal asymptote then it cannot have an oblique asymptote, and vice versa).

• The function domain determines vertical asymptotes.
• The polynomial division provides horizontal or oblique asymptotes.

For clarity, let:

A(x)B(x)=amxm+am− − 1xm− − 1+...+a1x+a0bnxn+bn− − 1xn− − 1+...+b1x+b0{displaystyle {frac {A(x)}{B(x)}}}}={frac {a_{m}x^{m}+a_{m-1}x^{m-1}+a_{1}{1}x+a_{0}{b_{n}x^{n}+b_{n-1}x^{n-1}

Yeah. <math alttext="{displaystyle mm.n{displaystyle m visn,}<img alt="m, there is a horizontal equation asymptote: y = 0.
Yeah. m=n{displaystyle m=n,}, there is a horizontal equation asymptote: y = A_m/b_n (the ratio of the main coefficients).
Yeah. n,}" xmlns="http://www.w3.org/1998/Math/MathML">m▪n{displaystyle mpurn,}n,}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/6b42eb5c04a75b4188062739beb7a28fa2950623" style="vertical-align: -0.338ex; width:6.921ex; height:1.843ex;"/>, there is no horizontal asymptote; if the numberer's degree is exactly one more than the denominator, there is an oblique asymptote, and its equation is given by the quotient of the polynomial division.

Vertical asymptotes occur at values that cancel out the denominator but not the numerator. If there is a root in common, the multiplicity of the roots is compared.
Examples:

1. The homographic function f(x)=ax+bcx+d{displaystyle f(x)={frac {ax+b}{cx+d}}}} He's got two ass, xv=− − dc{displaystyle x_{v}={frac {-d}{c}}}}}and andv=ac{displaystyle y_{v}={frac {a}{c}}}}
2. In the particular case and=1x{displaystyle and}{frac {1}{x}}} the asymptotes are the Cartesian axis themselves.

Rational function with Oblique asymptote and two Vertical Symptoms

and=1x{displaystyle and}{frac {1}{x}}}

Rational function with Horizontal asymptota and two Vertical Symptoms

Examples

The most varied functions show asymptotic behavior: from the simple graph of a flat curve in two dimensions, to more complex three-dimensional surfaces; both in algebraic (polynomial, rational) and transcendental (trigonometric, logarithmic, exponential) functions, either in Cartesian or polar coordinates, etc.
The asymptotes act as guide curves for graphing other curves, or functions.

Transcendent functions

so(x)
Vertical symptoms each π.

ln(x)
Vertical midwife down.

ex(x)
Horizontal sign to the left.

Polar curves

Converse Spiral of Archimedes

rθ θ =a{displaystyle rtheta =a }

Sontota en and=a{displaystyle and}.

Curva kappa

Folium de Descartes
r(θ θ )=3awithout θ θ # θ θ without3 θ θ +#3 θ θ {displaystyle r(theta)={frac {3asin theta cos theta }{sin ^{3}theta +cos ^{3}theta }}}}}}{theta }}}}

Sontota en x+and+a=0{displaystyle x+y+a=0 }.

Asymptotic curves

Newton Trident:
xand=ax3+bx2+cx+d{displaystyle xy=ax^{3}+bx^{2}+cx+d,}.

Soon: the parable of equation and=ax2+bx+c{displaystyle ,y=ax^{2}+bx+c},
and the hyperbola of equation and=dx{displaystyle and}{frac {d}{x}}}

Function: and=x3+2x2+3x+4x{displaystyle y={frac {x^{3}+2x^{2}+3x+4}{x}}}}}},

Sontota curviline: and=x2+2x+3{displaystyle y=x^{2}+2x+3 }

Surfaces and structures

Torricelli trumpet
The surface is asymptotic to a straight that passes through its center.

In this example, obtained by rotating the curve y=1/x on the axis x.

Hyperboloid

Soon
The close relationship between asymptotes and hyperboles extends, in three dimensions, to hyperboloids, approaching a asymptotic cone. [1]

While straight supports, asymptotic lines provide stability, as seen in hyperboloid structures