Astrodynamics

A satellite in orbit around the Earth has a tangential speed and an acceleration in.

Astrodynamics or orbital mechanics is the application of ballistics and celestial mechanics to practical problems relating to the motion of rockets and other spacecraft. The motion of these objects is generally calculated from Newton's laws of motion and universal gravitation. It is a core discipline within the design and control of space missions.

Celestial mechanics deals more broadly with the orbital dynamics of systems under the influence of gravity, including both spacecraft and natural astronomical bodies such as star systems, planets, moons, and comets. Orbital mechanics focuses on spacecraft trajectories, including orbital maneuvers, orbit plane changes, and interplanetary transfers, and is used by mission planners to predict the outcomes of propulsive maneuvers. General relativity is a more exact theory than Newton's laws for calculating orbits, and is sometimes needed for greater precision or in high-gravity situations (such as orbits close to the Sun). It is the part of astronomy that studies the orbits, especially of artificial satellites and space probes.

The movement of planets and other natural bodies is the domain of celestial mechanics, a discipline that consists of the application of Newton's laws of movement and the law of universal gravitation.

Laws of Astrodynamics

The fundamental laws of astrodynamics are Newton's law of universal gravitation and Newton's laws of motion, while the fundamental mathematical tool is its differential calculus.

Each orbit and trajectory outside the atmospheres is in principle reversible, that is, in the space-time function, time is inverted. The velocities are reversed and the accelerations are the same, including those due to rocket explosions. Therefore, if a rocket burst is in the direction of velocity, in the reversed case it is opposite to velocity. Of course, in the case of rocket explosions there is no total reversal of events, the same delta-v is used both ways and the same mass ratio is applied.

Standard assumptions in astrodynamics include no interference from external bodies, negligible mass for one of the bodies, and other negligible forces (such as from the solar wind, atmospheric drag, etc.). More accurate calculations can be made without these simplifying assumptions, but they are more complicated. The increased accuracy often does not make enough of a difference to the calculation to be worthwhile.

Kepler's laws of planetary motion can be derived from Newton's laws, when it is assumed that the orbiting body is subject only to the gravitational force of the central attractor. When an engine thrust or propelling force is present, Newton's laws still apply, but Kepler's laws are superseded. When the thrust stops, the resulting orbit will be different, but once again it will be described by Kepler's laws. The three laws are:

1. The orbit of each planet is an ellipse with the sun in one of the foci.
2. A line that unites a planet and the sun sweeps equal areas for equal time intervals.
3. The squares of the orbital periods of the planets are directly proportional to the cubes of the semi-major axis of the orbits.

Orbital Maneuver

In spaceflight, an orbital maneuver is the use of propulsion systems to change a spacecraft's orbit. For spacecraft far from Earth—such as those in orbit around the Sun—an orbital maneuver is called a deep space maneuver (DSM).

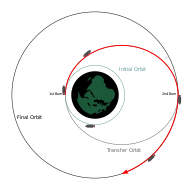
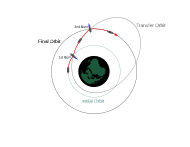
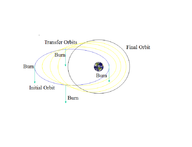
Orbital Transfer

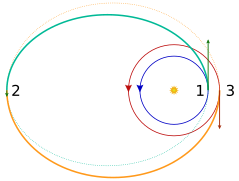
Transfer orbits are usually elliptical orbits that allow spacecraft to move from one (usually circular) orbit to another. They usually require a boost at the beginning, a boost at the end, and sometimes one or more boosts in between.

• The transfer orbit of Hohmann requires a minimum of delta-v.
• A bieliptic transfer may require less energy than the transfer of Hohmann, if the orbit ratio is 11,94 or greater, but it occurs at the expense of an increase in the shooting time during the transfer of Hohmann.
• The fastest transfers can use any orbit that crosses the original and destination orbits, at the expense of a greater delta-v.
• Using low push engines (such as electrical propulsion), if the initial orbit is supersynchronous to the final desired circular orbit then the optimal transfer orbit is achieved by continually pushing in the direction of speed in the apogee. This method, however, takes much longer due to the low thrust.

For the case of orbital transfer between non-coplanar orbits, the plane shift thrust must be done at the point where the orbital planes intersect (the "node").

A transfer of Hohmann from a circular orbit down to a higher circular orbit.

A bi-eliptic transfer from a low circular orbit (dark blue), to a higher circular orbit (red).

Generic transfer of two elliptical impulses between two circular orbits.

A general transfer from a circular orbit down to a higher circular orbit.

An optimal sequence to transfer a satellite from a supersynchronous orbit to a geosynchronous orbit using electrical propulsion.

Gravity assist and Oberth effect

In a gravity assist, a spacecraft swings past a planet and departs in a different direction, at a different speed. This is useful for speeding up or slowing down a spacecraft instead of carrying more fuel.

This maneuver can be approximated by elastic collision at great distances, although the flyby does not involve any physical contact. Due to Newton's third law (equal and opposite reaction), any momentum gained by a spacecraft must be lost by the planet, or vice versa. However, because the planet is so much more massive than the spacecraft, the effect on the planet's orbit is negligible.

The Oberth effect can be used, particularly during a gravity assist operation. This effect is that the use of a propulsion system works better at high speeds, and therefore course changes are better done when close to a gravitational body; This can multiply the effective delta-v.

Interplanetary Transport Network and diffuse orbits

It is now possible to use computers to find routes using the nonlinearities in the gravity of the planets and moons of the Solar System. For example, it is possible to trace an orbit from high Earth orbit to Mars, passing close to one of Earth's Trojan points. Collectively called the Interplanetary Transportation Network, these highly disturbing, even chaotic orbital paths require no more fuel than is necessary to reach the Lagrange point (in practice, maintaining the path requires some course corrections). The biggest problem with them is that they can be very slow, taking many years. Also, the release windows can be far apart.

However, they have been used in projects like Genesis. This spacecraft visited the Earth-Sun point L1 and returned using very little propellant.