Associativity (algebra)

ImprimirCitar

Transformation rules
Propositional logic
Inference rules
Modus tollendo tollens / puts Modus laying papers / tollens Introduction of the biconditional / elimination Introduction of conjunction / elimination Introduction of disjunction / elimination Disjunctive / hypothetical siloge Constructive / destructive dilemma Absorption
Replacement rules
Association Conmutativity Distribution Double denial Laws of De Morgan Transposition Material involvement Export Tautology Introduction of denial
Preaching logic
Generalization/universal instance Generalization / existential instance
Logical modal
v t e

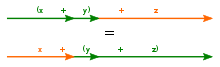
La association is a property in algebra and the propositional logic that is fulfilled if given three or more elements any of a particular set, it is verified that there is a operation: ${displaystyle circledcirc }$ to fulfil equality:

{displaystyle acircledcirc (bcircledcirc c)=(acircledcirc b)circledcirc c}

That is, in an associative expression with two or more successive occurrences of the same associative operator, the order in which the operations are executed does not alter the result, as long as and when the sequence of the operands is kept intact. In other words, rearranging the parentheses in an associative expression does not change its final value.

The sum and the product of real numbers fulfill the associative property, being valid the equalities:

{displaystyle a+(b+c)=(a+b)+c}

for addition and multiplication:

{displaystyle acdot (bcdot c)=(acdot b)cdot c}

In both, the placement of the brackets does not alter the result. Notice that the operands have been kept in their original position within the expression. Many important operations are non-associative, for example subtraction and exponentiation. Expressions that contain both associative operations and non-associative operations result in expressions non-associative.

Do not confuse associativity with commutativity, which states that you can change the order of the operands without affecting the final result.

Formal notation

Sea A a set in which an internal binary operation has been defined ${displaystyle circledcirc }$ such as

{displaystyle {begin{array}{rccl}circledcirc:&Atimes A&longrightarrow &A\&(a,b)&longmapsto &c=acircledcirc bend{array}}}

It is said that the operation ${displaystyle circledcirc }$ That's it. associative Yes:

{displaystyle forall a,b,cin A;:quad acircledcirc (bcircledcirc c)=(acircledcirc b)circledcirc c}

The associative law can also be expressed in functional notation like this:

{displaystyle f(f(x,y),z)=f(x,f(y,z)),}

Addition and subtraction

Starting from the set of natural numbers

{displaystyle mathbb {N} ={1,2,3,4,dots }}

for the addition operation, defined as:

{displaystyle {begin{array}{rccl}+:&mathbb {N} times mathbb {N} &longrightarrow &mathbb {N} \&(a,b)&longmapsto &c=a+bend{array}}}

${displaystyle (mathbb {N}+),}$ has the associative property, since:

{displaystyle forall a,b,cin mathbb {N} ;:quad a+(b+c)=(a+b)+c}

For example:

{displaystyle 5+(3+2)=(5+3)+2}

However, for the subtraction operation, defined as:

{displaystyle {begin{array}{rccl}-:&mathbb {N} times mathbb {N} &longrightarrow &mathbb {N} \&(a,b)&longmapsto &c=a-bend{array}}}

${displaystyle (mathbb {N}-),}$ No. has the associative property, since:

{displaystyle forall a,b,cin mathbb {N} ;:quad a-(b-c)neq (a-b)-c}

For example:

{displaystyle 5-(3-2)neq (5-3)-2}

Examples

The addition of real numbers is associative.

Concatenation of character strings "hola", " ", "mundo" can be computed by concatenating the first two character strings (resulting in "hola ") and then the third string of characters ("mundo"), or alternatively, joining the second and third string of characters (resulting in " mundo") and concatenating the first string of characters ("hola") with that result. The two methods produce the same final result. Concatenation of character strings is associative (but No. is switching).
In arithmetic, the addition and multiplication of real numbers are associative. Because of its associativeness, the grouping by parenthesis can be omitted without ambiguity. This is,

{displaystyle left.{begin{matrix}(x+y)+z=x+(y+z)=x+y+zquad \(x,y)z=x(y,z)=x,y,zqquad qquad qquad quad ,end{matrix}}right}{mbox{para todo }}x,y,zin mathbb {R}.}

An example of the association of the sum is:

{displaystyle (2+3)+7=5+7=12quad =quad 2+(3+7)=2+10=12}

and of the association of multiplication

{displaystyle (2cdot 3)cdot 7=6cdot 7=42quad =quad 2cdot (3cdot 7)=2cdot 21=42}

However, the subtraction No. is associative,

{displaystyle 2-(3-1)=0quad neq quad (2-3)-1=-2}

And neither is division,

{displaystyle (4:2):2=1quad neq quad 4:(2:2)=4}

nor the exposure, which is equally non-associative

{displaystyle 2^{(2^{3})}=2^{8}=256quad neq quad (2^{2})^{3}=4^{3}=64}

The addition and multiplication of complex numbers and quaternions are associative. The addition of octonions is also associative, but the multiplication of octonions is non-associative.
The maximum common dividing functions and minimum common multiple functions act associative.

{displaystyle left.{begin{matrix}operatorname {mcd} (operatorname {mcd} (x,y),z)=operatorname {mcd} (x,operatorname {mcd} (y,z))=operatorname {mcd} (x,y,z) quad \operatorname {mcm} (operatorname {mcm} (x,y),z)=operatorname {mcm} (x,operatorname {mcm} (y,z))=operatorname {mcm} (x,y,z)quad end{matrix}}right}{mbox{ para todo }}x,y,zin mathbb {Z}.}

The intersection or union of assemblies are associative.

{displaystyle left.{begin{matrix}(Acap B)cap C=Acap (Bcap C)=Acap Bcap Cquad \(Acup B)cup C=Acup (Bcup C)=Acup Bcup Cquad end{matrix}}right}{mbox{para todos los conjuntos }}A,B,C.}

Yes M It's some outfit. S denotes the set of all M a M, then the functional composition operation on S It's associative.

{displaystyle (fcirc g)circ h=fcirc (gcirc h)=fcirc gcirc hqquad {mbox{para todo }}f,g,hin S.}

More generally, given four sets M, N, P and Q, with h: M a N, g: N a Pand f: P a Q, then

{displaystyle (fcirc g)circ h=fcirc (gcirc h)=fcirc gcirc h}

as in the previous example. In short, the composition of applications is always associative.

For a set with three elements A, B, and C, the following operation is associative.

×	A	B	C
A	A	A	A
B	A	B	C
C	A	A	A

This way, for example, A(BC)=(AB)C = A. This operation No. It's commutative.

Since the matrices represent linear transformation functions, with matrix multiplication representing functional composition, it can be concluded immediately that the matrix multiplication is associative.

In propositional logic

Replacement Rule

In standard propositional logic, association, or associativity are two valid replacement rules. These rules allow you to move parentheses in logical expressions used in logical tests. The rules are:

{displaystyle (Plor (Qlor R))Leftrightarrow ((Plor Q)lor R)}

{displaystyle (Pland (Qland R))Leftrightarrow ((Pland Q)land R),local2000}

where $Leftrightarrow$ "is a metalogical symbol that represents "can be replaced in a test by".

Truth function connectives

Associativity is a property of some logical connectives in the truth functions of propositional logic. The following logical equivalences show that associativity is a property of particular logical connectives. They are also tautologies of truth functions.

Associativity of disjunction: