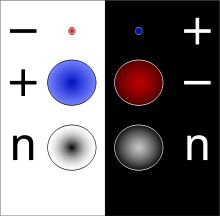Antiparticle

Division of the universe in matter and antimatter.

In particle physics, each type of particle is associated with an antiparticle with the same mass, but opposite physical charges (such as electric charge). Some particles are identical to their antiparticle, such as the photon, which has no charge. But not all charged neutral particles are identical to their antiparticle. We have always had the impression that the laws of nature seemed to have been designed so that everything was symmetric between particles and antiparticles until experiments called CP violation (charge-parity violation) found that time symmetry was violated in certain events. of the nature. The observed excess of baryons relative to anti-baryons in the universe is one of the major unanswered problems in cosmology.

Particle-antiparticle pairs can annihilate each other if they are in the appropriate quantum state. These states can occur in various processes. These processes are used in particle accelerators to create new particles and test the theories of particle physics. High energy processes in nature can create antiparticles, and these are visible due to cosmic rays and in certain nuclear reactions. The word antimatter refers to elementary antiparticles, the antiparticle compounds made from them (such as antihydrogen), and larger formations that can be made from them.

Illustration of the electrical load of particles (left) and anti-particles (right). From top to bottom; electron/positron, proton/antiproton, neutron/antineutron.

History

Experiment

In 1932, shortly after Dirac's prediction of the positron, Carl D. Anderson found that cosmic ray collisions produced these particles within a cloud chamber—a particle detector where electrons or positrons moving through it leave paths behind them, marking their movement through the gas. The relationship between the electric charge and the mass of a particle can be measured by observing the curves that mark their path through the cloud chamber within a magnetic field. Originally positrons, because their paths also curved, were mistaken for electrons traveling in the opposite direction.

The antiproton and the antineutron were found by Emilio Segrè and Owen Chamberlain in 1955, at the University of California. Since then, the antiparticles of many other subatomic particles have been created in particle accelerator experiments. In recent years, it has been possible to generate complete atoms of antimatter composed of antiprotons and positrons, collected in electromagnetic traps.

Dirac's Theory

...the development of quantum field theory made the interpretation of antiparticles unnecessary as hollows, even though unfortunately still persists in many textbooks.

The solutions of Dirac's equation contained quantum states of negative energy. As a result, an electron could always radiate energy by falling into a state of negative energy. Even worse than that, you could be radiating an infinite amount of energy because infinitely many states of negative energy would be available. To resolve this situation that went against physics, Dirac postulated that a "sea" Negative energy electrons filled the universe, already occupying all negative energy states in such a way that, due to the Pauli exclusion principle, no other electrons could fall into them. However, sometimes one of these negative energy particles could be lifted from this Dirac sea to a higher energy level to become a positive energy particle. But, when lifted, this particle would leave a hole behind in the sea, which would act exactly like an electron of positive energy but with an opposite charge. Dirac interpreted these inverse electrons as protons, thus calling his 1930 paper A Theory of Electrons and Protons.

Dirac was already aware of the problem that this representation implied an infinite negative charge for the universe, and tried to argue that we would perceive this state as the normal state of zero charge. Another difficulty that this theory encountered was the difference between the masses of the electron and the proton. Here Dirac tried to solve it by arguing that this was due to electromagnetic interactions with that 'sea', until Hermann Weyl proved that the hole theory was completely symmetric between negative and positive charges. Dirac also predicted an e^- + p⁺ → γ + γ reaction (in which the electron and proton annihilate to give two photons).). Robert Oppenheimer and Igor Tam proved that this would cause ordinary matter to disappear too quickly. A year later, in 1931, Dirac modified his theory and postulated the positron, a new particle with the same mass as the electron. The discovery of that particle the following year removed the last two objections to his theory.

However, the problem of the infinite charge of the universe remained. Also, as we now know, bosons (particles with integer spin) also have antiparticles, but these do not obey the Pauli exclusion principle, so the hole theory does not work for them. Quantum field theory provides a unified interpretation of antiparticles, which solves both problems.

Particle-Antiparticle Annihilation

An example of a couple of virtual pions that influence the spread of a kaon, making a neutral kaon mezcle with the antikaon. This is an example of renormalization in quantum field theory, field theory being necessary because of the change in the number of particles.

If a particle and its antiparticle are in the appropriate quantum states, then they can annihilate each other and produce other particles. Reactions like:

e⁺ + e^- → γ + γ

(annihilation of an electron-positron pair into two photons) are an example of the process.

The annihilation of an electron-positron pair in a single photon: e⁺ + e^- → γ it cannot occur because it is impossible for both energy and momentum to be conserved in this process. The reverse reaction is also impossible for this reason. However, this phenomenon is observed in nature; an electron-positron pair can be created from a single photon with an energy of at least the mass of both particles: 1.022 MeV. What is certain is that, according to quantum field theory, this process is allowed as an intermediate quantum state for sufficiently short times in which the violation of the conservation of energy can accommodate the Heisenberg uncertainty principle. This opens the way for the production of virtual pairs or their annihilation where the single-particle quantum state can fluctuate in a two-particle quantum state and back to its initial state.. These processes are important in the quantum vacuum and the renormalization of a quantum field theory. It also opens the way for a mixture of neutral particles through processes like the one shown here, which is a complicated example of mass renormalization.

Properties of Antiparticles

The quantum states of a particle and its antiparticle can be interchanged by applying charge symmetry (C), parity (P), and time symmetry (T). If |p,σ,n> is the quantum state of a particle (n), with momentum p, spin J whose component in the z-direction is σ, then we have

CPT Δp,σ,n HCFC = (-1)^J-σ _^c▪

where n^c is the conjugate charge state, that is, the antiparticle. This behavior under CPT is the same that establishes that a particle and its antiparticle are in the same irreducible representation of the Poincaré group. The properties of antiparticles can thus be related to those of particles. If T is a good symmetry of the dynamics, then

T Δp,σ,n expectations α Δ-p,-σ,n

CP Δp,σ,n α Δ-p,σ,n^c▪

C Δp,σ,n α Δp,σ,n^c▪

where the proportionality sign indicates that there could be a phase term on the right hand side of the equation. In other words, the particle and its antiparticle must have:

• Same mass m,
• the same state of thorn J,
• opposite electric charges q and - Okay..

Quantum Field Theory

This section uses the ideas, language, and notation used in canonical quantization of quantum field theory.

One can try to quantize the field of an electron without mixing the creation and annihilation operators by writing:

φ(x) = φ_k u_k(x) a_k e^{-i E(k)t},

where the symbol k is being used to denote the quantum numbers p and σ from the previous sections, the sign of the energy E(k) and a_k denote the corresponding annihilation operators. Of course, since we are dealing with fermions, the operators will have to satisfy the canonical anticommutative relations. However, if we write the Hamiltonian

H = φ_k E(k) a⁺_k a_k,

we see immediately that the expectation value of H need not be positive. This is because E(k) can have any possible sign, and the combination of creation and annihilation operators has an expected value of 1 or 0.

So we must introduce the conjugate charge antiparticle field with its own creation and annihilation operators that satisfy the following relations:

b_k' =⁺_k and b⁺_k' =_k

where k' has the same p, opposite σ and energy sign. So we can rewrite the field in the form:

φ(x) = φ_k(+) u_k(x) a_k e^{-i E(k)t} + ␡_k(-) u_k(x) b⁺_k e^{-i E(k)t},

where the first summation is performed on the positive energy states and the second on those of negative energy. The energy is then transformed into

H = φ_k(+) E(k) a⁺_k a_k + ␡_k(-) 日本語⁺_k b_k + E₀,

where E₀ is a negative infinite constant. The empty state is defined as the state that does not contain any particles or antiparticles, that is, a_k |0> = 0 and b_k |0> = 0. In this way the energy of the vacuum will be exactly E₀. Since all energies are measured with respect to a vacuum, H will definitely be positive. An analysis of the properties of a_k and b_k shows that one is the annihilation operator for the particles and the other for antiparticles. This is the case of a fermion.

We owe this approximation to Vladimir Fok, Wendell Furry and Robert Oppenheimer. If a real scalar field is quantized, then it is found that there is only one kind of annihilation operator, so scalar fields describe neutral bosons. Since complex scalar fields admit two different classes of annihilation operators, which are related by conjugation, these fields describe charged bosons.

Feynman and Stueckelberg interpretation

Considering the propagation back in time of the half of the electron field having positive energies, Richard Feynman showed that causality was violated unless some particles were allowed to travel faster than light. But if particles could travel faster than light then from the point of view of another inertial observer it would appear as if it were traveling backwards in time and oppositely charged.

In this way Feynman came to understand graphically the fact that the particle and its antiparticle had the same mass m and spin J but opposite charges. This allowed him to rewrite the theory of perturbations precisely in the form of diagrams, called Feynman diagrams, with particles traveling back and forth in time. This technique is now the most widespread for calculating amplitudes in quantum field theory.

This graph was developed independently by Ernest Stueckelberg, and has therefore been called the Feynman and Stueckelberg interpretation of antiparticles.

Further reading

• Feynman, R. P. (1987). «The reason for antiparticles». In R. P. Feynman; S. Weinberg, eds. The 1986 Dirac memorial lectures (in English). Cambridge University Press. ISBN 0-521-34000-4. (requires registration).
• Weinberg, S. (1995). The Quantum Theory of Fields, Volume 1: Foundations (in English). Cambridge University Press. ISBN 0-521-55001-7. (requires registration).