Annex: Mathematical constants
The following is an addendum about mathematical constants.
Mathematical constants and functions
The structure of the table is as follows:
- Value numerical of the constant and link to MathWorld or OEIS Wiki.
- LaTeX: Formula or series in the TeX format.
- Formula: To use in Wolfram Alpha. If in the calculations, ∞ takes a long time, it can be changed by 20000, to obtain an approximate result.
- OEIS: On-Line Encyclopedia of Integer Sequences.
- Continuous fracture: In the simple format [Full part; frac1, frac2, frac3,...] suprarayed if it's periodic.
- Year: From the discovery of the constant, or data of the author.
- Web format: Constant value, in format suitable for web search engines.
- N.o: Number Type
- R - Rational
- I - Irrational
- A - Algebraic
- T - Transcendental
- C - Complex
- (The table can be ordered ascendant or descendant, by any of the fields, but press in the heading titles.)
| Valor | Nombre | Gráfico | Símbolo | LaTeX | Fórmula | N.º | OEIS | Fracción continua | Año | Formato web |
|---|---|---|---|---|---|---|---|---|---|---|
| 0,88622 69254 52758 01364 | Factorial de un medio |
.5 ! {displaystyle {.5},!} | Γ ( 3 2 ) = 1 2 π = ∫ 0 ∞ x 1 / 2 e − x d x {displaystyle Gamma left({tfrac {3}{2}}right),={tfrac {1}{2}}{sqrt {pi }},=int _{0}^{infty }x^{1/2}e^{-x}dx} | sqrt(Pi)/2 | A019704 | [0;1,7,1,3,1,2,1,57,6,1,3,1,37,3,41,1,10,2,1,1,...] | 0.88622692545275801364908374167057259 | |||
| 0,74048 04896 93061 04116 | Constante de Hermite Empaquetamiento óptimo de esferas 3D Conjetura de Kepler | 
|
μ K {displaystyle {mu _{_{K}}}} | π 3 2 . . . . {displaystyle {frac {pi }{3{sqrt {2}}}}{color {white}....color {black}}} Después de 400 años, Thomas Hales demostró en 2014 con El Proyecto Flyspeck, que la Conjetura de Kepler era cierta. | pi/(3 sqrt(2)) | A093825 | [0;1,2,1,5,1,4,2,2,1,1,2,2,2,6,1,1,1,5,2,1,1,1,...] | 1611 | 0.74048048969306104116931349834344894 | |
| 1,60669 51524 15291 76378 | Constante de Erdős–Borwein | E B {displaystyle {E}_{,B}} | ∑ m = 1 ∞ ∑ n = 1 ∞ 1 2 m n = ∑ n = 1 ∞ 1 2 n − 1 = 1 1 + 1 3 + 1 7 + 1 15 + . . . {displaystyle sum _{m=1}^{infty }sum _{n=1}^{infty }{frac {1}{2^{mn}}}=sum _{n=1}^{infty }{frac {1}{2^{n}-1}}={frac {1}{1}}!+!{frac {1}{3}}!+!{frac {1}{7}}!+!{frac {1}{15}}!+!...} | sum[n=1 to ∞] {1/(2^n-1)} |
I | A065442 | [1;1,1,1,1,5,2,1,2,29,4,1,2,2,2,2,6,1,7,1,6,1,2,...] | 1949 | 1.60669515241529176378330152319092458 | |
| 0,07077 60393 11528 80353 -0,68400 03894 37932 129 i |
Constante MKB · · |
M I {displaystyle M_{I}} | lim n → ∞ ∫ 1 2 n ( − 1 ) x x x d x = ∫ 1 2 n e i π x x 1 / x d x {displaystyle lim _{nrightarrow infty }int _{1}^{2n}(-1)^{x}~{sqrt[{x}]{x}}~dx=int _{1}^{2n}e^{ipi x}~x^{1/x}~dx} | lim_(2n->∞) int[1 to 2n] {exp(i*Pi*x)*x^(1/x) dx} |
C | A255727 A255728 |
[0;14,7,1,2,1,23,2,1,8,16,1,1,3,1,26,1,6,1,1,...] - [0;1,2,6,13,41,112,1,25,1,1,1,1,3,13,2,1,...] i |
2009 | 0.07077603931152880353952802183028200 -0.68400038943793212918274445999266 i | |
| 3,05940 74053 42576 14453 | Constante Doble factorial |
|
C n ! ! {displaystyle {C_{_{n!!}}}} | ∑ n = 0 ∞ 1 n ! ! = e [ 1 2 + γ ( 1 2 , 1 2 ) ] {displaystyle sum _{n=0}^{infty }{frac {1}{n!!}}={sqrt {e}}left[{frac {1}{sqrt {2}}}+gamma ({tfrac {1}{2}},{tfrac {1}{2}})right]} | Sum[n=0 to ∞]{1/n!!} | A143280 | [3;16,1,4,1,66,10,1,1,1,1,2,5,1,2,1,1,1,1,1,2,...] | 3.05940740534257614453947549923327861 | ||
| 0,62481 05338 43826 58687 + 1,30024 25902 20120 419 i |
Fracción continua generalizada de i | F C G ( i ) {displaystyle {{F}_{CG}}_{(i)}} | i + i i + i i + i i + i i + i i + i i + i / . . . = 17 − 1 8 + i ( 1 2 + 2 17 − 1 ) {displaystyle textstyle i{+}{frac {i}{i+{frac {i}{i+{frac {i}{i+{frac {i}{i+{frac {i}{i+{frac {i}{i+i{/...}}}}}}}}}}}}}={sqrt {frac {{sqrt {17}}-1}{8}}}+ileft({tfrac {1}{2}}{+}{sqrt {frac {2}{{sqrt {17}}-1}}}right)} | i+i/(i+i/(i+i/(i+i/(i+i/(i+i/(i+i/( i+i/(i+i/(i+i/(i+i/(i+i/(i+i/(i+i/( i+i/(i+i/(i+i/(i+i/(i+i/(i+i/(i+i/( ...))))))))))))))))))))) |
C A | A156590 A156548 |
[i;1,i,1,i,1,i,1,i,1,i,1,i,1,i,1,i,1,i,1,i,1,i,1,..] = [0;1,i] |
0.62481053384382658687960444744285144 + 1.30024259022012041915890982074952 i | ||
| 0,91893 85332 04672 74178 | Fórmula de Raabe | ζ ′ ( 0 ) {displaystyle {zeta '(0)}} | ∫ a a + 1 log Γ ( t ) d t = 1 2 log 2 π + a log a − a , a ≥ 0 {displaystyle int limits _{a}^{a+1}log Gamma (t),mathrm {d} t={tfrac {1}{2}}log 2pi +alog a-a,quad ageq 0} | integral_a^(a+1) {log(Gamma(x))+a-a log(a)} dx | A075700 | [0;1,11,2,1,36,1,1,3,3,5,3,1,18,2,1,1,2,2,1,1,...] | 0.91893853320467274178032973640561763 | |||
| 0,42215 77331 15826 62702 | Volumen del Tetraedro de Reuleaux | 
|
V R {displaystyle {V_{_{R}}}} | s 3 12 ( 3 2 − 49 π + 162 arctan 2 ) {displaystyle {frac {s^{3}}{12}}(3{sqrt {2}}-49,pi +162,arctan {sqrt {2}})} | (3*Sqrt[2] - 49*Pi + 162*ArcTan[Sqrt[2]])/12 | A102888 | [0;2,2,1,2,2,7,4,4,287,1,6,1,2,1,8,5,1,1,1,1,...] | 0.42215773311582662702336591662385075 | ||
| 1,17628 08182 59917 50654 | Constante de Salem, conjetura de Lehmer | σ 10 {displaystyle {sigma _{_{10}}}} | x 10 + x 9 − x 7 − x 6 − x 5 − x 4 − x 3 + x + 1 {displaystyle x^{10}+x^{9}-x^{7}-x^{6}-x^{5}-x^{4}-x^{3}+x+1} | x^10+x^9-x^7-x^6-x^5-x^4-x^3+x+1 | A | A073011 | [1;5,1,2,17,1,7,2,1,1,2,4,7,2,2,1,1,15,1,1,... | 1983? | 1.17628081825991750654407033847403505 | |
| 2,39996 32297 28653 32223 Radianes |
Ángulo áureo |  
|
b {displaystyle {b}} | ( 4 − 2 Φ ) π = ( 3 − 5 ) π {displaystyle (4-2,Phi),pi =(3-{sqrt {5}}),pi } = 137.507764050037854646...° | (4-2*Phi)*Pi | T | A131988 | [2;2,1,1,1087,4,4,120,2,1,1,2,1,1,7,7,2,11,...] | 1907 | 2.39996322972865332223155550663361385 |
| 1,26408 47353 05301 11307 | Constante de Vardi | V c {displaystyle {V_{c}}} | 3 2 ∏ n ≥ 1 ( 1 + 1 ( 2 e n − 1 ) 2 ) 1 / 2 n + 1 {displaystyle {frac {sqrt {3}}{sqrt {2}}}prod _{ngeq 1}left(1+{1 over (2e_{n}-1)^{2}}right)^{!1/2^{n+1}}} | A076393 | [1;3,1,3,1,2,5,54,7,1,2,1,2,3,15,1,2,1,1,2,1,...] | 1991 | 1.26408473530530111307959958416466949 | |||
| 1,5065918849 ± 0,0000000028 | Área del fractal de Mandelbrot | 
|
γ {displaystyle gamma } | Se conjetura que el valor exacto es: 6 π − 1 − e {displaystyle {sqrt {6pi -1}}-e} = 1,506591651... | A098403 | [1;1,1,37,2,2,1,10,1,1,2,2,4,1,1,1,1,5,4,...] | 1912 | 1.50659177 +/- 0.00000008 | ||
1,61111 49258 08376 736 111•••111 27224 36828 183213 unos |
Constante Factorial exponencial |
S E f {displaystyle {S_{Ef}}} | ∑ n = 1 ∞ 1 n ( n − 1 ) ⋅ ⋅ ⋅ 2 1 = 1 + 1 2 1 + 1 3 2 1 + 1 4 3 2 1 + 1 5 4 3 2 1 + ⋯ {displaystyle sum _{n=1}^{infty }{frac {1}{n^{(n{-}1)^{cdot ^{cdot ^{cdot ^{2^{1}}}}}}}}=1{+}{frac {1}{2^{1}}}{+}{frac {1}{3^{2^{1}}}}+{frac {1}{4^{3^{2^{1}}}}}+{frac {1}{5^{4^{3^{2^{1}}}}}}{+}cdots } | T | A080219 | [1; 1, 1, 1, 1, 2, 1, 808, 2, 1, 2, 1, 14,...] | 1.61111492580837673611111111111111111 | |||
| 0,31813 15052 04764 13531 ±1,33723 57014 30689 40 i |
Punto fijo Super-logaritmo · |
|
− W ( − 1 ) {displaystyle {-W(-1)}} |
lim
n
→
∞
{displaystyle lim _{nrightarrow infty }}
f
(
x
)
=
log
(
log
(
log
(
log
(
⋯
log
(
log
(
x
)
)
)
)
)
)
⏟
log
s
anidados n veces
{displaystyle f(x)=underbrace {log(log(log(log(cdots log(log(x)))))),!} atop {log _{s}{text{ anidados n veces}}}}
Para un valor inicial de x distinto a 0, 1, e, e^e, e^(e^e), etc. |
-W(-1) Donde W=ProductLog Lambert W function |
C | A059526 A059527 |
[-i;1 +2i,1+i,6-i,1+2i,-7+3i,2i,2,1-2i,-1+i,-,...] | 0.31813150520476413531265425158766451 -1.33723570143068940890116214319371 i | |
| 1,09317 04591 95490 89396 | Constante de Smarandache 1.ª | S 1 {displaystyle {S_{1}}} |
∑
n
=
2
∞
1
μ
(
n
)
!
.
.
.
.
{displaystyle sum _{n=2}^{infty }{frac {1}{mu (n)!}}{color {white}....color {black}}}
La función Kempner μ(n) se define como sigue:
μ(n) es el número más pequeño por el que μ(n)! es divisible por n |
A048799 | [1;10,1,2,1,2,1,13,3,1,6,1,2,11,4,6,2,15,1,1,...] | 1.09317045919549089396820137014520832 | ||||
| 1,64218 84352 22121 13687 | Constante de Lebesgue L2 | L 2 {displaystyle {L2}} | 1 5 + 25 − 2 5 π = 1 π ∫ 0 π | sin ( 5 t 2 ) | sin ( t 2 ) d t {displaystyle {frac {1}{5}}+{frac {sqrt {25-2{sqrt {5}}}}{pi }}={frac {1}{pi }}int _{0}^{pi }{frac {left|sin({frac {5t}{2}})right|}{sin({frac {t}{2}})}},dt} | 1/5 + sqrt(25 - 2*sqrt(5))/Pi |
T | A226655 | [1;1,1,1,3,1,6,1,5,2,2,3,1,2,7,1,3,5,2,2,1,1,...] | 1910 | 1.64218843522212113687362798892294034 | |
| 0,82699 33431 32688 07426 | Disk Covering | 
|
C 5 {displaystyle {C_{5}}} | 1 ∑ n = 0 ∞ 1 ( 3 n + 2 2 ) = 3 3 2 π {displaystyle {frac {1}{sum _{n=0}^{infty }{frac {1}{binom {3n+2}{2}}}}}={frac {3{sqrt {3}}}{2pi }}} | 3 Sqrt[3]/(2 Pi) | T | A086089 | [0;1,4,1,3,1,1,4,1,2,2,1,1,7,1,4,4,2,1,1,1,1,...] | 1939 1949 |
0.82699334313268807426698974746945416 |
| 1,78723 16501 82965 93301 | Constante de Komornik–Loreti | q {displaystyle {q}} |
1
=
∑
n
=
1
∞
t
k
q
k
Raiz real de
∏
n
=
0
∞
(
1
−
1
q
2
n
)
+
q
−
2
q
−
1
=
0
{displaystyle 1=!sum _{n=1}^{infty }{frac {t_{k}}{q^{k}}}qquad scriptstyle {text{Raiz real de}}displaystyle prod _{n=0}^{infty }!left(!1{-}{frac {1}{q^{2^{n}}}}!right)!{+}{frac {q{-}2}{q{-}1}}=0}
t k = Sucesión de Thue-Morse |
FindRoot[(prod[n=0 to ∞] {1-1/(x^2^n)}+ (x-2)/(x-1))= 0, {x, 1.7}, WorkingPrecision->30] |
T | A055060 | [1;1,3,1,2,3,188,1,12,1,1,22,33,1,10,1,1,7,...] | 1998 | 1.78723165018296593301327489033700839 | |
| 0,59017 02995 08048 11302 | Constante de Chebyshev · | λ C h {displaystyle {lambda _{Ch}}} | Γ ( 1 4 ) 2 4 π 3 / 2 = 4 ( 1 4 ! ) 2 π 3 / 2 {displaystyle {frac {Gamma ({tfrac {1}{4}})^{2}}{4pi ^{3/2}}}={frac {4({tfrac {1}{4}}!)^{2}}{pi ^{3/2}}}} | (Gamma(1/4)^2) /(4 pi^(3/2)) |
A249205 | [0;1,1,2,3,1,2,41,1,6,5,124,5,2,2,1,1,6,1,2,...] | 0.59017029950804811302266897027924429 | |||
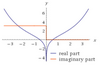
| 0,52382 25713 89864 40645 | Función Chi Coseno hiperbólico integral |
|
C h i ( ) {displaystyle {operatorname {Chi()} }} | γ + ∫ 0 x cosh t − 1 t d t {displaystyle gamma +int _{0}^{x}{frac {cosh t-1}{t}},dt} γ = Constante de Euler–Mascheroni = 0,5772156649... {displaystyle scriptstyle gamma ,{text{= Constante de Euler–Mascheroni = 0,5772156649...}}} |
Chi(x) | A133746 | [0;1,1,9,1,172,1,7,1,11,1,1,2,1,8,1,1,1,1,1,...] | 0.52382257138986440645095829438325566 | ||
| 0,62432 99885 43550 87099 | Constante de Golomb–Dickman | λ {displaystyle {lambda }} | ∫ 0 ∞ f ( x ) x 2 d x P a r a x > 2 = ∫ 0 1 e L i ( n ) d n Li = Integral logarítmica {displaystyle int limits _{0}^{infty }{underset {Para;x>2}{{frac {f(x)}{x^{2}}}dx}}=int limits _{0}^{1}e^{Li(n)}dnquad scriptstyle {text{Li = Integral logarítmica}}} | N[Int{n,0,1}[e^Li(n)],34] | A084945 | [0;1,1,1,1,1,22,1,2,3,1,1,11,1,1,2,22,2,6,1,...] | 1930 y 1964 |
0.62432998854355087099293638310083724 | ||
| 0,98770 03907 36053 46013 | Área delimitada por la rotación excéntrica del Triángulo de Reuleaux |
|
T R {displaystyle {mathcal {T}}_{R}} | a 2 ⋅ ( 2 3 + π 6 − 3 ) {displaystyle a^{2}cdot left(2{sqrt {3}}+{frac {pi }{6}}-3right)} donde a= lado del cuadrado | 2 sqrt(3)+pi/6-3 | T | A066666 | [0;1,80,3,3,2,1,1,1,4,2,2,1,1,1,8,1,2,10,1,2,...] | 1914 | 0.98770039073605346013199991355832854 |
| 0,70444 22009 99165 59273 | Constante Carefree2 | C 2 {displaystyle {mathcal {C}}_{2}} | ∏ n = 1 ∞ ( 1 − 1 p n ( p n + 1 ) ) p n : p r i m o {displaystyle {underset {p_{n}:,{primo}}{prod _{n=1}^{infty }left(1-{frac {1}{p_{n}(p_{n}+1)}}right)}}} | N[prod[n=1 to ∞] {1 - 1/(prime(n)* (prime(n)+1))}] |
A065463 | [0;1,2,2,1,1,1,1,4,2,1,1,3,703,2,1,1,1,3,5,1,...] | 0.70444220099916559273660335032663721 | |||
| 1,84775 90650 22573 51225 | Constante camino auto-evitante en red hexagonal · | 
|
μ {displaystyle {mu }} |
2
+
2
=
lim
n
→
∞
c
n
1
/
n
{displaystyle {sqrt {2+{sqrt {2}}}};=lim _{nrightarrow infty }c_{n}^{1/n}}
La menor raíz real de : x 4 − 4 x 2 + 2 = 0 {displaystyle:;x^{4}-4x^{2}+2=0} |
sqrt(2+sqrt(2)) | A | A179260 | [1;1,5,1,1,3,6,1,3,3,10,10,1,1,1,5,2,3,1,1,3,...] | 1.84775906502257351225636637879357657 | |
| 0,19452 80494 65325 11361 | 2ª Constante Du Bois Reymond | C 2 {displaystyle {C_{2}}} | e 2 − 7 2 = ∫ 0 ∞ | d d t ( sin t t ) n | d t − 1 {displaystyle {frac {e^{2}-7}{2}}=int _{0}^{infty }left|{{frac {d}{dt}}left({frac {sin t}{t}}right)^{n}}right|,dt-1} | (e^2-7)/2 | T | A062546 | [0;5,7,9,11,13,15,17,19,21,23,25,27,29,31,...] = [0;2p+3], p∈ℕ |
0.19452804946532511361521373028750390 | ||
| 2,59807 62113 53315 94029 | Área de un hexágono de lado unitario |
|
A 6 {displaystyle {mathcal {A}}_{6}} | 3 3 2 l 2 {displaystyle {frac {3{sqrt {3}}}{2}},l^{2}} | 3 sqrt(3)/2 | A | A104956 | [2;1,1,2,20,2,1,1,4,1,1,2,20,2,1,1,4,1,1,2,20,...] [2;1,1,2,20,2,1,1,4] |
2.59807621135331594029116951225880855 | |
| 1,78657 64593 65922 46345 | Constante de Silverman |
S m {displaystyle {{mathcal {S}}_{_{m}}}} |
∑
n
=
1
∞
1
ϕ
(
n
)
σ
1
(
n
)
=
∏
n
=
1
∞
(
1
+
∑
k
=
1
∞
1
p
n
2
k
−
p
n
k
−
1
)
p
n
:
p
r
i
m
o
{displaystyle sum _{n=1}^{infty }{frac {1}{phi (n)sigma _{1}(n)}}={underset {p_{n}:,{primo}}{prod _{n=1}^{infty }left(1+sum _{k=1}^{infty }{frac {1}{p_{n}^{2k}-p_{n}^{k-1}}}right)}}}
ø() = Función totien de Euler, σ1() = Función divisor. |
Sum[n=1 to ∞] {1/[EulerPhi(n) DivisorSigma(1,n)]} |
A093827 | [1;1,3,1,2,5,1,65,11,2,1,2,13,1,4,1,1,1,2,5,4,...] | 1.78657645936592246345859047554131575 | |||
| 1,46099 84862 06318 35815 | Constante cuatro-colores de Baxter |
Mapamundi  Coloreado 4C
|
C 2 {displaystyle {mathcal {C}}^{2}} | ∏ n = 1 ∞ ( 3 n − 1 ) 2 ( 3 n − 2 ) ( 3 n ) = 3 4 π 2 Γ ( 1 3 ) 3 {displaystyle prod _{n=1}^{infty }{frac {(3n-1)^{2}}{(3n-2)(3n)}}={frac {3}{4pi ^{2}}},Gamma left({frac {1}{3}}right)^{3}} Γ() = Función Gamma | 3×Gamma(1/3) ^3/(4 pi^2) |
A224273 | [1;2,5,1,10,8,1,12,3,1,5,3,5,8,2,1,23,1,2,161,...] | 1970 | 1.46099848620631835815887311784605969 | |
| 0,66131 70494 69622 33528 | Constante de Feller-Tornier |
C F T {displaystyle {{mathcal {C}}_{_{FT}}}} | 1 2 ∏ n = 1 ∞ ( 1 − 2 p n 2 ) + 1 2 p n : p r i m o = 3 π 2 ∏ n = 1 ∞ ( 1 − 1 p n 2 − 1 ) + 1 2 {displaystyle {underset {p_{n}:,{primo}}{{frac {1}{2}}prod _{n=1}^{infty }left(1-{frac {2}{p_{n}^{2}}}right){+}{frac {1}{2}}}}={frac {3}{pi ^{2}}}prod _{n=1}^{infty }left(1-{frac {1}{p_{n}^{2}-1}}right){+}{frac {1}{2}}} | [prod[n=1 to ∞] {1-2/prime(n)^2}] /2 + 1/2 |
T ? | A065493 | [0;1,1,1,20,9,1,2,5,1,2,3,2,3,38,8,1,16,2,2,...] | 1932 | 0.66131704946962233528976584627411853 | |
| 1,92756 19754 82925 30426 | Constante Tetranacci | T {displaystyle {mathcal {T}}} | La mayor raíz real de : x 4 − x 3 − x 2 − x − 1 = 0 {displaystyle:;;x^{4}-x^{3}-x^{2}-x-1=0} | Root[x+x^-4-2=0] | A | A086088 | [1;1,12,1,4,7,1,21,1,2,1,4,6,1,10,1,2,2,1,7,1,...] | 1.92756197548292530426190586173662216 | ||
| 1,00743 47568 84279 37609 | Constante DeVicci's Teseracto | 
|
f ( 3 , 4 ) {displaystyle {f_{(3,4)}}} | Arista del mayor cubo, dentro de un hipercubo unitario 4D.
La menor raíz real de : 4 x 4 − 28 x 3 − 7 x 2 + 16 x + 16 = 0 {displaystyle:;;4x^{4}{-}28x^{3}{-}7x^{2}{+}16x{+}16=0} |
Root[4*x^8-28*x^6 -7*x^4+16*x^2+16 =0] |
A | A243309 | [1;134,1,1,73,3,1,5,2,1,6,3,11,4,1,5,5,1,1,48,...] | 1.00743475688427937609825359523109914 | |
| 0,15915 49430 91895 33576 | Constante A de Plouffe | A {displaystyle {A}} | 1 2 π {displaystyle {frac {1}{2pi }}} | 1/(2 pi) | T | A086201 | [0;6,3,1,1,7,2,146,3,6,1,1,2,7,5,5,1,4,1,2,42,...] | 0.15915494309189533576888376337251436 | ||
| 0,41245 40336 40107 59778 | Constante de Thue-Morse | 
|
τ {displaystyle tau } |
∑
n
=
0
∞
t
n
2
n
+
1
{displaystyle sum _{n=0}^{infty }{frac {t_{n}}{2^{n+1}}}}
donde
t
n
{displaystyle {t_{n}}}
es la secuencia Thue–Morse y donde τ ( x ) = ∑ n = 0 ∞ ( − 1 ) t n x n = ∏ n = 0 ∞ ( 1 − x 2 n ) {displaystyle tau (x)=sum _{n=0}^{infty }(-1)^{t_{n}},x^{n}=prod _{n=0}^{infty }(1-x^{2^{n}})} |
T | A014571 | [0;2,2,2,1,4,3,5,2,1,4,2,1,5,44,1,4,1,2,4,1,1,...] | 0.41245403364010759778336136825845528 | ||
| 0,58057 75582 04892 40229 | Constante de Pell | P P e l l {displaystyle {{mathcal {P}}_{_{Pell}}}} | 1 − ∏ n = 0 ∞ ( 1 − 1 2 2 n + 1 ) {displaystyle 1-prod _{n=0}^{infty }left(1-{frac {1}{2^{2n+1}}}right)} | N[1-prod[n=0 to ∞] {1-1/(2^(2n+1)}] |
T ? | A141848 | [0;1,1,2,1,1,1,1,14,1,3,1,1,6,9,18,7,1,27,1,1,...] | 0.58057755820489240229004389229702574 | ||
| 2,20741 60991 62477 96230 | Problema moviendo el sofá de Hammersley | 
|
S H {displaystyle {S_{_{H}}}} | π 2 + 2 π {displaystyle {frac {pi }{2}}+{frac {2}{pi }},} ¿Cuál es el área más grande de una forma, que pueda ser maniobrada en un pasillo en forma de L y tenga de ancho la unidad ? | pi/2 + 2/pi | T | A086118 | [2;4,1,4,1,1,2,5,1,11,1,1,5,1,6,1,3,1,1,1,1,7,...] | 1967 | 2.20741609916247796230685674512980889 |
| 1,15470 05383 79251 52901 | Constante de Hermite | γ 2 {displaystyle gamma _{_{2}}} | 2 3 = 1 cos ( π 6 ) {displaystyle {frac {2}{sqrt {3}}}={frac {1}{cos ,({frac {pi }{6}})}}} | 2/sqrt(3) | A | 1+ A246724 |
[1;6,2,6,2,6,2,6,2,6,2,6,2,6,2,6,2,6,2,6,2,6,2,...] [1;6,2] |
1.15470053837925152901829756100391491 | ||
| 0,63092 97535 71457 43709 | Dimensión fractal del Conjunto de Cantor | 
|
d f ( k ) {displaystyle d_{f}(k)} | lim ε → 0 log N ( ε ) log ( 1 / ε ) = log 2 log 3 {displaystyle lim _{varepsilon to 0}{frac {log N(varepsilon)}{log(1/varepsilon)}}={frac {log 2}{log 3}}} | log(2)/log(3) N[3^x=2] |
T | A102525 | [0;1,1,1,2,2,3,1,5,2,23,2,2,1,1,55,1,4,3,1,1,...] | 0.63092975357145743709952711434276085 | |
| 0,17150 04931 41536 06586 | Constante Hall-Montgomery |
δ 0 {displaystyle {{delta }_{_{0}}}} | 1 + π 2 6 + 2 L i 2 ( − e ) L i 2 = Integral dilogarítmica {displaystyle 1+{frac {pi ^{2}}{6}}+2;mathrm {Li} _{2}left(-{sqrt {e}};right)quad mathrm {Li} _{2},scriptstyle {text{= Integral dilogarítmica}}} | 1 + Pi^2/6 + 2*PolyLog[2, -Sqrt[E]] | A143301 | [0;5,1,4,1,10,1,1,11,18,1,2,19,14,1,51,1,2,1,...] | 0.17150049314153606586043997155521210 | |||
| 1,55138 75245 48320 39226 | Constante Triángulo Calabi |
|
C C R {displaystyle {C_{_{CR}}}} | 1 3 + ( − 23 + 3 i 237 ) 1 3 3 ⋅ 2 2 3 + 11 3 ( 2 ( − 23 + 3 i 237 ) ) 1 3 {displaystyle {1 over 3}+{(-23+3i{sqrt {237}})^{tfrac {1}{3}} over 3cdot 2^{tfrac {2}{3}}}+{11 over 3(2(-23+3i{sqrt {237}}))^{tfrac {1}{3}}}} | FindRoot[ 2x^3-2x^2-3x+2 ==0, {x, 1.5}, WorkingPrecision->40] |
A | A046095 | [1;1,1,4,2,1,2,1,5,2,1,3,1,1,390,1,1,2,11,6,2,...] | 1946 ~ | 1.55138752454832039226195251026462381 |
| 0,97027 01143 92033 92574 | Constante de Lochs | £ L o {displaystyle {{text{£}}_{_{Lo}}}} | 6 ln 2 ln 10 π 2 {displaystyle {frac {6ln 2ln 10}{pi ^{2}}}} | 6*ln(2)*ln(10)/Pi^2 | A086819 | [0;1,32,1,1,1,2,1,46,7,2,7,10,8,1,71,1,37,1,1,...] | 1964 | 0.97027011439203392574025601921001083 | ||
| 1,30568 67 ≈ | Dimensión fractal del círculo de Apolonio | 
|
ε {displaystyle varepsilon } |
A052483 | [0;3,2,3,16,8,10,3,1,1,2,1,3,1,2,13,1,1,4,1,5,...] | 1.3056867 ≈ | ||||
| 0,00131 76411 54853 17810 | Constante de Heath-Brown–Moroz | C H B M {displaystyle {C_{_{HBM}}}} | ∏ n = 1 ∞ ( 1 − 1 p n ) 7 ( 1 + 7 p n + 1 p n 2 ) p n : p r i m o {displaystyle {underset {p_{n}:,{primo}}{prod _{n=1}^{infty }left(1-{frac {1}{p_{n}}}right)^{7}left(1+{frac {7p_{n}+1}{p_{n}^{2}}}right)}}} | N[prod[n=1 to ∞] {((1-1/prime(n))^7) *(1+(7*prime(n)+1) /(prime(n)^2))}] |
T ? | A118228 | [0;758,1,13,1,2,3,56,8,1,1,1,1,1,143,1,1,1,2,...] | 0.00131764115485317810981735232251358 | ||
| 0,14758 36176 50433 27417 | Constante gamma de Plouffe | 
|
C {displaystyle {C}} |
1
π
arctan
1
2
=
1
π
∑
n
=
0
∞
(
−
1
)
n
(
2
2
n
+
1
)
(
2
n
+
1
)
{displaystyle {frac {1}{pi }}arctan {frac {1}{2}}={frac {1}{pi }}sum _{n=0}^{infty }{frac {(-1)^{n}}{(2^{2n+1})(2n+1)}}}
= 1 π ( 1 2 − 1 3 ⋅ 2 3 + 1 5 ⋅ 2 5 − 1 7 ⋅ 2 7 + ⋯ ) {displaystyle ={frac {1}{pi }}left({frac {1}{2}}-{frac {1}{3cdot 2^{3}}}+{frac {1}{5cdot 2^{5}}}-{frac {1}{7cdot 2^{7}}}+cdots right)} |
Arctan(1/2)/Pi | T | A086203 | [0;6,1,3,2,5,1,6,5,3,1,1,2,1,1,2,3,1,2,3,2,2,...] | 0.14758361765043327417540107622474052 | |
| 0,70523 01717 91800 96514 | Constante Primorial Suma de productos de inverso de primos |
P # {displaystyle {P_{#}}} | ∑ n = 1 ∞ 1 p n # = 1 2 + 1 6 + 1 30 + 1 210 + . . . = ∑ k = 1 ∞ ∏ n = 1 k 1 p n p n : p r i m o {displaystyle {underset {p_{n}:,{primo}}{sum _{n=1}^{infty }{frac {1}{p_{n}#}}={frac {1}{2}}+{frac {1}{6}}+{frac {1}{30}}+{frac {1}{210}}+...=sum _{k=1}^{infty }prod _{n=1}^{k}{frac {1}{p_{n}}}}}} | Sum[k=1 to ∞](prod[n=1 to k]{1/prime(n)}) | I | A064648 | [0;1,2,2,1,1,4,1,2,1,1,6,13,1,4,1,16,6,1,1,4,...] | 0.70523017179180096514743168288824851 | ||
| 0,29156 09040 30818 78013 | Constante dimer 2D, recubrimiento con dominós · |
|
C π {displaystyle {frac {C}{pi }}} C=catalan |
∫ − π π cosh − 1 ( cos ( t ) + 3 2 ) 4 π d t {displaystyle int limits _{-pi }^{pi }{frac {cosh ^{-1}left({frac {sqrt {cos(t)+3}}{sqrt {2}}}right)}{4pi }}dt} | N[int[-pi to pi] {arccosh(sqrt( cos(t)+3)/sqrt(2)) /(4*Pi) /, dt}] |
A143233 | [0;3,2,3,16,8,10,3,1,1,2,1,3,1,2,13,1,1,4,1,5,...] | 0.29156090403081878013838445646839491 | ||
| 0,72364 84022 98200 00940 | Constante de Sarnak | C s a {displaystyle {C_{sa}}} | ∏ p > 2 ( 1 − p + 2 p 3 ) {displaystyle prod _{p>2}{Big (}1-{frac {p+2}{p^{3}}}{Big)}} | N[prod[k=2 to ∞] {1-(prime(k)+2) /(prime(k)^3)}] |
T ? | A065476 | [0;1,2,1,1,1,1,1,1,1,4,4,1,1,1,1,1,1,1,8,2,1,1,...] | 0.72364840229820000940884914980912759 | ||
| 0,63212 05588 28557 67840 | Constante de tiempo | 
|
τ {displaystyle {tau }} |
lim
n
→
∞
1
−
!
n
n
!
=
lim
n
→
∞
P
(
n
)
=
∫
0
1
e
−
x
d
x
=
1
−
1
e
=
{displaystyle lim _{nto infty }1-{frac {!n}{n!}}=lim _{nto infty }P(n)=int _{0}^{1}e^{-x}dx=1-{frac {1}{e}}=}
∑ n = 0 ∞ ( − 1 ) n n ! = 1 1 ! − 1 2 ! + 1 3 ! − 1 4 ! + 1 5 ! − 1 6 ! + ⋯ {displaystyle sum limits _{n=0}^{infty }{frac {(-1)^{n}}{n!}}={frac {1}{1!}}-{frac {1}{2!}}+{frac {1}{3!}}-{frac {1}{4!}}+{frac {1}{5!}}-{frac {1}{6!}}+cdots } |
lim_(n->∞) (1- !n/n!) !n=subfactorial |
T | A068996 | [0;1,1,1,2,1,1,4,1,1,6,1,1,8,1,1,10,1,1,12,1,...] = [0;1,1,1,2n], n∈ℕ |
0.63212055882855767840447622983853913 | |
| 0.30366 30028 98732 65859 | Constante de Gauss-Kuzmin-Wirsing | λ 2 {displaystyle {lambda }_{2}} |
lim
n
→
∞
F
n
(
x
)
−
ln
(
1
−
x
)
(
−
λ
)
n
=
Ψ
(
x
)
,
{displaystyle lim _{nto infty }{frac {F_{n}(x)-ln(1-x)}{(-lambda)^{n}}}=Psi (x),}
donde Ψ ( x ) {displaystyle Psi (x)} es una función analítica tal que Ψ ( 0 ) = Ψ ( 1 ) = 0 {displaystyle Psi (0)!=!Psi (1)!=!0} . |
A038517 | [0;3,3,2,2,3,13,1,174,1,1,1,2,2,2,1,1,1,2,2,1,...] | 1973 | 0.30366300289873265859744812190155623 | |||
| 1,30357 72690 34296 39125 | Constante de Conway | 
|
λ {displaystyle {lambda }} | x 71 − x 69 − 2 x 68 − x 67 + 2 x 66 + 2 x 65 + x 64 − x 63 − x 62 − x 61 − x 60 − x 59 + 2 x 58 + 5 x 57 + 3 x 56 − 2 x 55 − 10 x 54 − 3 x 53 − 2 x 52 + 6 x 51 + 6 x 50 + x 49 + 9 x 48 − 3 x 47 − 7 x 46 − 8 x 45 − 8 x 44 + 10 x 43 + 6 x 42 + 8 x 41 − 5 x 40 − 12 x 39 + 7 x 38 − 7 x 37 + 7 x 36 + x 35 − 3 x 34 + 10 x 33 + x 32 − 6 x 31 − 2 x 30 − 10 x 29 − 3 x 28 + 2 x 27 + 9 x 26 − 3 x 25 + 14 x 24 − 8 x 23 − 7 x 21 + 9 x 20 + 3 x 19 − 4 x 18 − 10 x 17 − 7 x 16 + 12 x 15 + 7 x 14 + 2 x 13 − 12 x 12 − 4 x 11 − 2 x 10 + 5 x 9 + x 7 − 7 x 6 + 7 x 5 − 4 x 4 + 12 x 3 − 6 x 2 + 3 x − 6 = 0 {displaystyle {begin{smallmatrix}x^{71}quad -x^{69}-2x^{68}-x^{67}+2x^{66}+2x^{65}+x^{64}-x^{63}-x^{62}-x^{61}-x^{60}\-x^{59}+2x^{58}+5x^{57}+3x^{56}-2x^{55}-10x^{54}-3x^{53}-2x^{52}+6x^{51}+6x^{50}\+x^{49}+9x^{48}-3x^{47}-7x^{46}-8x^{45}-8x^{44}+10x^{43}+6x^{42}+8x^{41}-5x^{40}\-12x^{39}+7x^{38}-7x^{37}+7x^{36}+x^{35}-3x^{34}+10x^{33}+x^{32}-6x^{31}-2x^{30}\-10x^{29}-3x^{28}+2x^{27}+9x^{26}-3x^{25}+14x^{24}-8x^{23}quad -7x^{21}+9x^{20}\+3x^{19}!-4x^{18}!-10x^{17}!-7x^{16}!+12x^{15}!+7x^{14}!+2x^{13}!-12x^{12}!-4x^{11}!-2x^{10}\+5x^{9}+x^{7}quad -7x^{6}+7x^{5}-4x^{4}+12x^{3}-6x^{2}+3x-6 = 0quad quad quad end{smallmatrix}}} | A | A014715 | [1;3,3,2,2,54,5,2,1,16,1,30,1,1,1,2,2,1,14,1,...] | 1987 | 1.30357726903429639125709911215255189 | |
| 1,18656 91104 15625 45282 | Constante de Lévy | β {displaystyle {beta }} | π 2 12 ln 2 {displaystyle {frac {pi ^{2}}{12,ln 2}}} | pi^2 /(12 ln 2) | A100199 | [1;5,2,1,3,1,1,28,18,16,3,2,6,2,6,1,1,5,5,9,...] | 1935 | 1.18656911041562545282172297594723712 | ||
| 0,83564 88482 64721 05333 | Constante de Baker | 
|
β 3 {displaystyle beta _{3}} | ∫ 0 1 d t 1 + t 3 = ∑ n = 0 ∞ ( − 1 ) n 3 n + 1 = 1 3 ( ln 2 + π 3 ) {displaystyle int _{0}^{1}{frac {mathrm {d} t}{1+t^{3}}}=sum _{n=0}^{infty }{frac {(-1)^{n}}{3n+1}}={frac {1}{3}}left(ln 2+{frac {pi }{sqrt {3}}}right)} | Sum[n=0 to ∞] {((-1)^(n))/(3n+1)} |
A113476 | [0;1,5,11,1,4,1,6,1,4,1,1,1,2,1,3,2,2,2,2,1,3,...] | 0.83564884826472105333710345970011076 | ||
| 23,10344 79094 20541 6160 | Serie de Kempner(0) | K 0 {displaystyle {K_{0}}} |
1
+
1
2
+
1
3
+
⋯
+
1
9
+
1
11
+
⋯
+
1
19
+
1
21
+
⋯
+
etc.
{displaystyle 1{+}{frac {1}{2}}{+}{frac {1}{3}}{+}cdots {+}{frac {1}{9}}{+}{frac {1}{11}}{+}cdots {+}{frac {1}{19}}{+}{frac {1}{21}}{+}cdots {+},{text{etc.}}}
+ 1 99 + 1 111 + ⋯ + 1 119 + 1 121 + ⋯ d e n o m i n a d o r e s q u e c o n t i e n e n c e r o s . E x c l u i d o s l o s {displaystyle {+}{frac {1}{99}}{+}{frac {1}{111}}{+}cdots {+}{frac {1}{119}}{+}{frac {1}{121}}{+}cdots ;;{overset {Excluidos;los}{underset {contienen;ceros.}{scriptstyle denominadores;que}}}} |
1+1/2+1/3+1/4+1/5 +1/6+1/7+1/8+1/9 +1/11+1/12+1/13 +1/14+1/15+... |
A082839 | [23;9,1,2,3244,1,1,5,1,2,2,8,3,1,1,6,1,84,1,...] | 23.1034479094205416160340540433255981 | |||
| 0,98943 12738 31146 95174 | Constante de Lebesgue | 
|
C 1 {displaystyle {C_{1}}} | lim n → ∞ ( L n − 4 π 2 ln ( 2 n + 1 ) ) = 4 π 2 ( ∑ k = 1 ∞ 2 ln k 4 k 2 − 1 − Γ ′ ( 1 2 ) Γ ( 1 2 ) ) {displaystyle lim _{nto infty }!!left(!{L_{n}{-}{frac {4}{pi ^{2}}}ln(2n{+}1)}!!right)!{=}{frac {4}{pi ^{2}}}!left({sum _{k=1}^{infty }!{frac {2ln k}{4k^{2}{-}1}}}{-}{frac {Gamma '({tfrac {1}{2}})}{Gamma ({tfrac {1}{2}})}}!!right)} | 4/pi^2*[(2 Sum[k=1 to ∞] {ln(k)/(4*k^2-1)}) -poligamma(1/2)] |
A243277 | [0;1,93,1,1,1,1,1,1,1,7,1,12,2,15,1,2,7,2,1,5,...] | 0.98943127383114695174164880901886671 | ||
| 1,38135 64445 18497 79337 | Constante Beta Kneser-Mahler | β {displaystyle beta } | e 2 π ∫ 0 π 3 t tan t d t = e ∫ − 1 3 1 3 ln ⌊ 1 + e 2 π i t ⌋ d t {displaystyle e^{^{textstyle {frac {2}{pi }}displaystyle {int _{0}^{frac {pi }{3}}}textstyle {ttan t dt}}}=e^{^{displaystyle {,int _{frac {-1}{3}}^{frac {1}{3}}}textstyle {,ln lfloor 1+e^{2pi it}}rfloor dt}}} | e^((PolyGamma(1,4/3) - PolyGamma(1,2/3) +9)/(4*sqrt(3)*Pi)) |
A242710 | [1;2,1,1,1,1,1,4,1,139,2,1,3,5,16,2,1,1,7,2,1,...] | 1963 | 1.38135644451849779337146695685062412 | ||
| 1,18745 23511 26501 05459 | Constante de Foias α | F α {displaystyle F_{alpha }} |
x
n
+
1
=
(
1
+
1
x
n
)
n
para
n
=
1
,
2
,
3
,
…
{displaystyle x_{n+1}=left(1+{frac {1}{x_{n}}}right)^{n}{text{ para }}n=1,2,3,ldots }
La constante de Foias es el único número real tal que si x1 = α, entonces la secuencia diverge a ∞. Cuando x1 = α, lim n → ∞ x n log n n = 1 {displaystyle ,lim _{nto infty }x_{n}{tfrac {log n}{n}}=1} |
A085848 | [1;5,2,1,81,3,2,2,1,1,1,1,1,6,1,1,3,1,1,4,3,2,...] | 1970 | 1.18745235112650105459548015839651935 | |||
| 2,29316 62874 11861 03150 | Constante de Foias β | 
|
F β {displaystyle F_{beta }} | x x + 1 = ( x + 1 ) x {displaystyle x^{x+1}=(x+1)^{x}} | x^(x+1) = (x+1)^x |
A085846 | [2;3,2,2,3,4,2,3,2,130,1,1,1,1,1,6,3,2,1,15,1,...] | 2000 | 2.29316628741186103150802829125080586 | |
| 0,66170 71822 67176 23515 | Constante de Robbins | Δ ( 3 ) {displaystyle Delta (3)} | 4 + 17 2 − 6 3 − 7 π 105 + ln ( 1 + 2 ) 5 + 2 ln ( 2 + 3 ) 5 {displaystyle {frac {4!+!17{sqrt {2}}!-6{sqrt {3}}!-7pi }{105}}!+!{frac {ln(1!+!{sqrt {2}})}{5}}!+!{frac {2ln(2!+!{sqrt {3}})}{5}}} | (4+17*2^(1/2)-6 *3^(1/2)+21*ln(1+ 2^(1/2))+42*ln(2+ 3^(1/2))-7*Pi)/105 |
A073012 | [0;1,1,1,21,1,2,1,4,10,1,2,2,1,3,11,1,331,1,4,...] | 1978 | 0.66170718226717623515583113324841358 | ||
| 0,78853 05659 11508 96106 | Constante de Lüroth | 
|
C L {displaystyle C_{L}} | ∑ n = 2 ∞ ln ( n n − 1 ) n {displaystyle sum _{n=2}^{infty }{frac {ln left({frac {n}{n-1}}right)}{n}}} | Sum[n=2 to ∞] log(n/(n-1))/n |
A085361 | [0;1,3,1,2,1,2,4,1,127,1,2,2,1,3,8,1,1,2,1,16,...] | 0.78853056591150896106027632216944432 | ||
| 0,92883 58271 | Constante entre primos gemelos de JJGJJG | B 1 {displaystyle B_{1}} | 1 4 + 1 6 + 1 12 + 1 18 + 1 30 + 1 42 + 1 60 + 1 72 + ⋯ {displaystyle {frac {1}{4}}+{frac {1}{6}}+{frac {1}{12}}+{frac {1}{18}}+{frac {1}{30}}+{frac {1}{42}}+{frac {1}{60}}+{frac {1}{72}}+cdots } | 1/4 + 1/6 + 1/12 + 1/18 + 1/30 + 1/42 + 1/60 + 1/72 +... | A241560 | [0; 1, 13, 19, 4, 2, 3, 1, 1] | 2014 | 0.928835827131 | ||
| 5,24411 51085 84239 62092 | Constante 2 Lemniscata |
|
2 ϖ {displaystyle 2varpi } | [ Γ ( 1 4 ) ] 2 2 π = 4 ∫ 0 1 d x ( 1 − x 2 ) ( 2 − x 2 ) {displaystyle {frac {[Gamma ({tfrac {1}{4}})]^{2}}{sqrt {2pi }}}=4int _{0}^{1}{frac {dx}{sqrt {(1-x^{2})(2-x^{2})}}}} | Gamma[ 1/4 ]^2 /Sqrt[ 2 Pi ] |
A064853 | [5;4,10,2,1,2,3,29,4,1,2,1,2,1,2,1,4,9,1,4,1,2,...] | 1718 | 5.24411510858423962092967917978223883 | |
| 0,57595 99688 92945 43964 | Constante Stephens | C S {displaystyle C_{S}} | ∏ n = 1 ∞ ( 1 − p p 3 − 1 ) {displaystyle prod _{n=1}^{infty }left(1-{frac {p}{p^{3}-1}}right)} | Prod[n=1 to ∞] {1-prime(n) /(prime(n)^3-1)} |
T ? | A065478 | [0;1,1,2,1,3,1,3,1,2,1,77,2,1,1,10,2,1,1,1,7,...] | ? | 0.57595996889294543964316337549249669 | |
| 0,73908 51332 15160 64165 | Número de Dottie | 
|
d {displaystyle d} | lim x → ∞ cos x ( c ) = cos ( cos ( cos ( cos ( ⋯ ( cos ( c ) ) ) ) ) ) ⏟ x {displaystyle lim _{xto infty }cos ^{x}(c)=underbrace {cos(cos(cos(cos(cdots (cos(c))))))} _{x}} | cos(c)=c | T | A003957 | [0;1,2,1,4,1,40,1,9,4,2,1,15,2,12,1,21,1,17,...] | 0.73908513321516064165531208767387340 | |
| 0,67823 44919 17391 97803 | Constante Taniguchi | C T {displaystyle C_{T}} | ∏ n = 1 ∞ ( 1 − 3 p n 3 + 2 p n 4 + 1 p n 5 − 1 p n 6 ) {displaystyle prod _{n=1}^{infty }left(1-{frac {3}{{p_{n}}^{3}}}+{frac {2}{{p_{n}}^{4}}}+{frac {1}{{p_{n}}^{5}}}-{frac {1}{{p_{n}}^{6}}}right)} p n = primo {displaystyle scriptstyle p_{n}=,{text{primo}}} | Prod[n=1 to ∞] {1 -3/prime(n)^3 +2/prime(n)^4 +1/prime(n)^5 -1/prime(n)^6} |
T ? | A175639 | [0;1,2,9,3,1,2,9,11,1,13,2,15,1,1,1,2,4,1,1,1,...] | ? | 0.67823449191739197803553827948289481 | |
| 1,35845 62741 82988 43520 | Constante espiral áurea | 
|
c {displaystyle c} | φ 2 π = ( 1 + 5 2 ) 2 π {displaystyle varphi ^{frac {2}{pi }}=left({frac {1+{sqrt {5}}}{2}}right)^{frac {2}{pi }}} | GoldenRatio^(2/Pi) | A212224 | [1;2,1,3,1,3,10,8,1,1,8,1,15,6,1,3,1,1,2,3,1,1,...] | 1.35845627418298843520618060050187945 | ||
| 2,79128 78474 77920 00329 | Raíces anidadas S5 | S 5 {displaystyle S_{5}} |
21
+
1
2
=
5
+
5
+
5
+
5
+
5
+
⋯
{displaystyle displaystyle {frac {{sqrt {21}}+1}{2}}=scriptstyle ,{sqrt {5+{sqrt {5+{sqrt {5+{sqrt {5+{sqrt {5+cdots }}}}}}}}}};}
= 1 + 5 − 5 − 5 − 5 − 5 − ⋯ {displaystyle =1+,scriptstyle {sqrt {5-{sqrt {5-{sqrt {5-{sqrt {5-{sqrt {5-cdots }}}}}}}}}};} |
(sqrt(21)+1)/2 | A | A222134 | [2;1,3,1,3,1,3,1,3,1,3,1,3,1,3,1,3,1,3,1,3,1,3,...] [2;1,3] |
2.79128784747792000329402359686400424 | ||
| 1,85407 46773 01371 91843 | Constante Lemniscata de Gauss | 
|
L / 2 {displaystyle L{text{/}}{sqrt {2}}} | ∫ 0 ∞ d x 1 + x 4 = 1 4 π Γ ( 1 4 ) 2 = 4 ( 1 4 ! ) 2 π {displaystyle int limits _{0}^{infty }{frac {mathrm {d} x}{sqrt {1+x^{4}}}}={frac {1}{4{sqrt {pi }}}},Gamma left({frac {1}{4}}right)^{2}={frac {4left({frac {1}{4}}!right)^{2}}{sqrt {pi }}}} Γ() = Función Gamma | pi^(3/2)/(2 Gamma(3/4)^2) | A093341 | [1;1,5,1,5,1,3,1,6,2,1,4,16,3,112,2,1,1,18,1,...] | ? | 1.85407467730137191843385034719526005 | |
| 1,75874 36279 51184 82469 | Constante Producto infinito, con Alladi-Grinstead | P r 1 {displaystyle Pr_{1}} | ∏ n = 2 ∞ ( 1 + 1 n ) 1 n {displaystyle prod _{n=2}^{infty }{Big (}1+{frac {1}{n}}{Big)}^{frac {1}{n}}} | Prod[n=2 to ∞] {(1+1/n)^(1/n)} |
A242623 | [1;1,3,6,1,8,1,4,3,1,4,1,1,1,6,5,2,40,1,387,2,...] | 1977 | 1.75874362795118482469989684865589317 | ||
| 1,73245 47146 00633 47358 | Constante inversa de Euler-Mascheroni | 1 γ {displaystyle {frac {1}{gamma }}} | ( ∫ 0 1 − log ( log 1 x ) d x ) − 1 = ∑ n = 1 ∞ ( − 1 ) n ( − 1 + γ ) n {displaystyle left(int _{0}^{1}-log left(log {frac {1}{x}}right),dxright)^{-1}=sum _{n=1}^{infty }(-1)^{n}(-1+gamma)^{n}} | 1/Integrate_ (x=0 to 1) {-log(log(1/x))} |
A098907 | [1;1,2,1,2,1,4,3,13,5,1,1,8,1,2,4,1,1,40,1,11,...] | 1.73245471460063347358302531586082968 | |||
| 1,94359 64368 20759 20505 | Constante Euler Totient | 
|
E T {displaystyle ET} | ∏ p ( 1 + 1 p ( p − 1 ) ) p = Nros. primos = ζ ( 2 ) ζ ( 3 ) ζ ( 6 ) = 315 ζ ( 3 ) 2 π 4 {displaystyle {underset {p{text{= Nros. primos}}}{prod _{p}{Big (}1+{frac {1}{p(p-1)}}{Big)}}}={frac {zeta (2);zeta (3)}{zeta (6)}}={frac {315;zeta (3)}{2pi ^{4}}}} | zeta(2)*zeta(3) /zeta(6) |
A082695 | [1;1,16,1,2,1,2,3,1,1,3,2,1,8,1,1,1,1,1,1,1,32,...] | 1750 | 1.94359643682075920505707036257476343 | |
| 1,49534 87812 21220 54191 | Raíz cuarta de cinco | 5 4 {displaystyle {sqrt[{4}]{5}}} | 5 5 5 5 5 ⋯ 5 5 5 5 5 {displaystyle {sqrt[{5}]{5,{sqrt[{5}]{5,{sqrt[{5}]{5,{sqrt[{5}]{5,{sqrt[{5}]{5,cdots }}}}}}}}}}} | (5(5(5(5(5(5(5) ^1/5)^1/5)^1/5) ^1/5)^1/5)^1/5) ^1/5... |
A | A011003 | [1;2,53,4,96,2,1,6,2,2,2,6,1,4,1,49,17,2,3,2,...] | 1.49534878122122054191189899414091339 | ||
| 0,87228 40410 65627 97617 | Área Círculo de Ford | 
|
A C F {displaystyle A_{CF}} | ∑ q ≥ 1 ∑ ( p , q ) = 1 1 ≤ p < q π ( 1 2 q 2 ) 2 = π 4 ζ ( 3 ) ζ ( 4 ) = 45 2 ζ ( 3 ) π 3 {displaystyle sum _{qgeq 1}sum _{(p,q)=1 atop 1leq p<q}pi left({frac {1}{2q^{2}}}right)^{2}={frac {pi }{4}}{frac {zeta (3)}{zeta (4)}}={frac {45}{2}}{frac {zeta (3)}{pi ^{3}}}} ς() = Función zeta | pi Zeta(3) /(4 Zeta(4)) | [0;1,6,1,4,1,7,5,36,3,29,1,1,10,3,2,8,1,1,1,3,...] | ? | 0.87228404106562797617519753217122587 | ||
| 1,08232 32337 11138 19151 | Constante Zeta(4) | ζ ( 4 ) {displaystyle zeta (4)} | π 4 90 = ∑ n = 1 ∞ 1 n 4 = 1 1 4 + 1 2 4 + 1 3 4 + 1 4 4 + 1 5 4 + . . . {displaystyle {frac {pi ^{4}}{90}}=sum _{n=1}^{infty }{frac {1}{n^{4}}}={frac {1}{1^{4}}}+{frac {1}{2^{4}}}+{frac {1}{3^{4}}}+{frac {1}{4^{4}}}+{frac {1}{5^{4}}}+...} | Sum[n=1 to ∞] {1/n^4} |
T | A013662 | [1;12,6,1,3,1,4,183,1,1,2,1,3,1,1,5,4,2,7,...] | 1.08232323371113819151600369654116790 | ||
| 1,56155 28128 08830 27491 | Raíz Triangular de 2. | 
|
R 2 {displaystyle {R_{2}}} |
17
−
1
2
=
4
+
4
+
4
+
4
+
4
+
4
+
⋯
−
1
{displaystyle {frac {{sqrt {17}}-1}{2}}=,scriptstyle {sqrt {4+{sqrt {4+{sqrt {4+{sqrt {4+{sqrt {4+{sqrt {4+cdots }}}}}}}}}}}},,-1}
= 4 − 4 − 4 − 4 − 4 − 4 − ⋯ {displaystyle =,scriptstyle {sqrt {4-{sqrt {4-{sqrt {4-{sqrt {4-{sqrt {4-{sqrt {4-cdots }}}}}}}}}}}}textstyle } |
(sqrt(17)-1)/2 | A | A222133 | [1;1,1,3,1,1,3,1,1,3,1,1,3,1,1,3,1,1,3,1,1,3,1,...] [1;1,1,3] |
1.56155281280883027491070492798703851 | |
| 1,45607 49485 82689 67139 | Constante de Backhouse | B {displaystyle {B}} |
lim
k
→
∞
|
q
k
+
1
q
k
|
donde:
Q
(
x
)
=
1
P
(
x
)
=
∑
k
=
1
∞
q
k
x
k
{displaystyle lim _{kto infty }left|{frac {q_{k+1}}{q_{k}}}rightvert quad scriptstyle {text{donde:}}displaystyle ;;Q(x)={frac {1}{P(x)}}=!sum _{k=1}^{infty }q_{k}x^{k}}
P ( x ) = ∑ k = 1 ∞ p k x k p k : p r i m o = 1 + 2 x + 3 x 2 + 5 x 3 + 7 x 4 + . . . {displaystyle P(x)=!sum _{k=1}^{infty }{underset {p_{k}:,{primo}}{p_{k}x^{k}}}!!=1{+}2x{+}3x^{2}{+}5x^{3}{+}7x^{4}{+}...} |
1/(FindRoot[0 == 1 + Sum[x^n Prime[n], {n, 10000}], {x, {1}}) |
A072508 | [1;2,5,5,4,1,1,18,1,1,1,1,1,2,13,3,1,2,4,16,4,...] | 1995 | 1.45607494858268967139959535111654355 | ||
| 1,43599 11241 76917 43235 | Constante interpolación de Lebesgue · | 
|
L 1 {displaystyle {L_{1}}} | ∏ i = 0 j ≠ i n x − x i x j − x i = 1 π ∫ 0 π ⌊ sin 3 t 2 ⌋ sin t 2 d t = 1 3 + 2 3 π {displaystyle prod _{begin{smallmatrix}i=0\jneq iend{smallmatrix}}^{n}{frac {x-x_{i}}{x_{j}-x_{i}}}={frac {1}{pi }}int _{0}^{pi }{frac {lfloor sin {frac {3t}{2}}rfloor }{sin {frac {t}{2}}}},dt={frac {1}{3}}+{frac {2{sqrt {3}}}{pi }}} | 1/3 + 2*sqrt(3)/Pi | T | A226654 | [1;2,3,2,2,6,1,1,1,1,4,1,7,1,1,1,2,1,3,1,2,1,1,...] | 1902 ~ | 1.43599112417691743235598632995927221 |
| 1,04633 50667 70503 18098 | Constante mass Minkowski-Siegel | F 1 {displaystyle F_{1}} | ∏ n = 1 ∞ n ! 2 π n ( n e ) n 1 + 1 n 12 {displaystyle prod _{n=1}^{infty }{frac {n!}{{sqrt {2pi n}}left({frac {n}{e}}right)^{n}{sqrt[{12}]{1+{tfrac {1}{n}}}}}}} | N[prod[n=1 to ∞] n! /(sqrt(2*Pi*n) *(n/e)^n *(1+1/n) ^(1/12))] |
A213080 | [1;21,1,1,2,1,1,4,2,1,5,7,2,1,20,1,1,1134,3,..] | 1867 1885 1935 |
1.04633506677050318098095065697776037 | ||
| 1,86002 50792 21190 30718 | Constante espiral de Theodorus | 
|
∂ {displaystyle partial } | ∑ n = 1 ∞ 1 n 3 + n = ∑ n = 1 ∞ 1 n ( n + 1 ) {displaystyle sum _{n=1}^{infty }{frac {1}{{sqrt {n^{3}}}+{sqrt {n}}}}=sum _{n=1}^{infty }{frac {1}{{sqrt {n}}(n+1)}}} | Sum[n=1 to ∞] {1/(n^(3/2) +n^(1/2))} |
A226317 | [1;1,6,6,1,15,11,5,1,1,1,1,5,3,3,3,2,1,1,2,19,...] | -460 a -399 |
1.86002507922119030718069591571714332 | |
| 0,80939 40205 40639 13071 | Constante de Alladi-Grinstead | A A G {displaystyle {{mathcal {A}}_{AG}}} | e − 1 + ∑ k = 2 ∞ ∑ n = 1 ∞ 1 n k n + 1 = e − 1 − ∑ k = 2 ∞ 1 k ln ( 1 − 1 k ) {displaystyle e^{-1+sum limits _{k=2}^{infty }sum limits _{n=1}^{infty }{frac {1}{nk^{n+1}}}}=e^{-1-sum limits _{k=2}^{infty }{frac {1}{k}}ln left(1-{frac {1}{k}}right)}} | e^{(sum[k=2 to ∞] |sum[n=1 to ∞] {1/(n k^(n+1))})-1} |
A085291 | [0;1,4,4,17,4,3,2,5,3,1,1,1,1,6,1,1,2,1,22,...] | 1977 | 0.80939402054063913071793188059409131 | ||
| 1,26185 95071 42914 87419 | Dimensión fractal del Copo de nieve de Koch | C k {displaystyle {C_{k}}} | log 4 log 3 {displaystyle {frac {log 4}{log 3}}} | log(4)/log(3) | T | A100831 | [1;3,1,4,1,1,11,1,46,1,5,112,1,1,1,1,1,3,1,7,...] | 1.26185950714291487419905422868552171 | ||
| 1,22674 20107 20353 24441 | Constante Factorial de Fibonacci | F {displaystyle F} | ∏ n = 1 ∞ ( 1 − ( − 1 φ 2 ) n ) = ∏ n = 1 ∞ ( 1 − ( 5 − 3 2 ) n ) {displaystyle prod _{n=1}^{infty }left(1-left(-{frac {1}{{varphi }^{2}}}right)^{n}right)=prod _{n=1}^{infty }left(1-left({frac {{sqrt {5}}-3}{2}}right)^{n}right)} | prod[n=1 to ∞] {1-((sqrt(5) -3)/2)^n} |
A062073 | [1;4,2,2,3,2,15,9,1,2,1,2,15,7,6,21,3,5,1,23,...] | 1.22674201072035324441763023045536165 | |||
| 0,85073 61882 01867 26036 | Constante de plegado de papel · | 
|
P f {displaystyle {P_{f}}} | ∑ n = 0 ∞ 8 2 n 2 2 n + 2 − 1 = ∑ n = 0 ∞ 1 2 2 n 1 − 1 2 2 n + 2 {displaystyle sum _{n=0}^{infty }{frac {8^{2^{n}}}{2^{2^{n+2}}-1}}=sum _{n=0}^{infty }{cfrac {tfrac {1}{2^{2^{n}}}}{1-{tfrac {1}{2^{2^{n+2}}}}}}} | N[Sum[n=0 to ∞] {8^2^n/(2^2^ (n+2)-1)},37] |
A143347 | [0;1,5,1,2,3,21,1,4,107,7,5,2,1,2,1,1,2,1,6,...] | ? | 0.85073618820186726036779776053206660 | |
| 6,58088 59910 17920 97085 | Constante de Froda | 2 e {displaystyle 2^{,e}} | 2 e {displaystyle 2^{e}} | 2^e | [6;1,1,2,1,1,2,3,1,14,11,4,3,1,1,7,5,5,2,7,...] | 6.58088599101792097085154240388648649 | ||||
| – 0,5 ± 0,86602 54037 84438 64676 i |
Raíz cúbica de 1 | 
|
1 3 {displaystyle {sqrt[{3}]{1}}} | { 1 − 1 2 + 3 2 i − 1 2 − 3 2 i . {displaystyle {begin{cases} 1\-{frac {1}{2}}+{frac {sqrt {3}}{2}}i\-{frac {1}{2}}-{frac {sqrt {3}}{2}}i.end{cases}}} | 1, E^(2i pi/3) E^(-2i pi/3) |
CA | A010527 | - [0,5] ± [0;1,6,2,6,2,6,2,6,2,6,2,6,2,6,2,6,2,6,2,...] i - [0,5] ± [0; 1, 6, 2] i |
- 0,5 ± 0.8660254037844386467637231707529 i | |
| 1,11786 41511 89944 97314 | Constante de Goh-Schmutz | C G S {displaystyle C_{GS}} | ∫ 0 ∞ log ( s + 1 ) e s − 1 d s = − ∑ n = 1 ∞ e n n E i ( − n ) I n t e g r a l E x p o n e n c i a l E i : {displaystyle int _{0}^{infty }{frac {log(s+1)}{e^{s}-1}} ds=!-!sum _{n=1}^{infty }{frac {e^{n}}{n}}Ei(-n){overset {Ei:}{underset {Exponencial}{scriptstyle Integral}}}} | Integrate{ log(s+1) /(E^s-1)} |
A143300 | [1;8,2,15,2,7,2,1,1,1,1,2,3,5,3,5,1,1,4,13,1,...] | 1.11786415118994497314040996202656544 | |||
| 1,11072 07345 39591 56175 | Razón entre un cuadrado y la circunferencia circunscrita | 
|
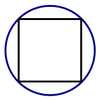
π 2 2 {displaystyle {frac {pi }{2{sqrt {2}}}}} | ∑ n = 1 ∞ ( − 1 ) ⌊ n − 1 2 ⌋ 2 n + 1 = 1 1 + 1 3 − 1 5 − 1 7 + 1 9 + 1 11 − . . . {displaystyle sum _{n=1}^{infty }{frac {(-1)^{lfloor {frac {n-1}{2}}rfloor }}{2n+1}}={frac {1}{1}}+{frac {1}{3}}-{frac {1}{5}}-{frac {1}{7}}+{frac {1}{9}}+{frac {1}{11}}-...} | Sum[n=1 to ∞] {(-1)^(floor((n-1)/2)) /(2n-1)} |
T | A093954 | [1;9,31,1,1,17,2,3,3,2,3,1,1,2,2,1,4,9,1,3,...] | 1.11072073453959156175397024751517342 | |
| 2,82641 99970 67591 57554 | Constante de Murata | C m {displaystyle {C_{m}}} | ∏ n = 1 ∞ ( 1 + 1 ( p n − 1 ) 2 ) p n : p r i m o {displaystyle prod _{n=1}^{infty }{underset {p_{n}:,{primo}}{{Big (}1+{frac {1}{(p_{n}-1)^{2}}}{Big)}}}} | Prod[n=1 to ∞] {1+1/(prime(n) -1)^2} |
T ? | A065485 | [2;1,4,1,3,5,2,2,2,4,3,2,1,3,2,1,1,1,8,2,2,28,...] | 2.82641999706759157554639174723695374 | ||
| 1,52362 70862 02492 10627 | Dimensión fractal de la frontera de la Curva del dragón | 
|
C d {displaystyle {C_{d}}} | log ( 1 + 73 − 6 87 3 + 73 + 6 87 3 3 ) log ( 2 ) {displaystyle {frac {log left({frac {1+{sqrt[{3}]{73-6{sqrt {87}}}}+{sqrt[{3}]{73+6{sqrt {87}}}}}{3}}right)}{log(2)}}} | (log((1+(73-6 sqrt(87))^1/3+ (73+6 sqrt(87))^1/3) /3))/ log(2))) |
T | [1;1,1,10,12,2,1,149,1,1,1,3,11,1,3,17,4,1,...] | 1.52362708620249210627768393595421662 | ||
| 1,30637 78838 63080 69046 | Constante de Mills | θ {displaystyle {theta }} Es primo | ⌊ θ 3 n ⌋ {displaystyle lfloor theta ^{3^{n}}rfloor } | Nest[ NextPrime[#^3] &, 2, 7]^(1/3^8) | A051021 | [1;3,3,1,3,1,2,1,2,1,4,2,35,21,1,4,4,1,1,3,2,...] | 1947 | 1.30637788386308069046861449260260571 | ||
| 2,02988 32128 19307 25004 | Volumen hiperbólico del Complemento del Nudo en Forma de Ocho | 
|
V 8 {displaystyle {V_{8}}} |
2
3
∑
n
=
1
∞
1
n
(
2
n
n
)
∑
k
=
n
2
n
−
1
1
k
=
6
∫
0
π
/
3
log
(
1
2
sin
t
)
d
t
=
{displaystyle 2{sqrt {3}},sum _{n=1}^{infty }{frac {1}{n{2n choose n}}}sum _{k=n}^{2n-1}{frac {1}{k}}=6int limits _{0}^{pi /3}log left({frac {1}{2sin t}}right),dt=}
3 9 ∑ n = 0 ∞ ( − 1 ) n 27 n { 18 ( 6 n + 1 ) 2 − 18 ( 6 n + 2 ) 2 − 24 ( 6 n + 3 ) 2 − 6 ( 6 n + 4 ) 2 + 2 ( 6 n + 5 ) 2 } {displaystyle scriptstyle {frac {sqrt {3}}{9}},sum limits _{n=0}^{infty }{frac {(-1)^{n}}{27^{n}}},left{!{frac {18}{(6n+1)^{2}}}-{frac {18}{(6n+2)^{2}}}-{frac {24}{(6n+3)^{2}}}-{frac {6}{(6n+4)^{2}}}+{frac {2}{(6n+5)^{2}}}!right}} |
6 integral[0 to pi/3] {log(1/(2 sin (n)))} |
A091518 | [2;33,2,6,2,1,2,2,5,1,1,7,1,1,1,113,1,4,5,1,...] | 2.02988321281930725004240510854904057 | ||
| 1,46707 80794 33975 47289 | Constante de Porter | C {displaystyle {C}} |
6
ln
2
π
2
(
3
ln
2
+
4
γ
−
24
π
2
ζ
′
(
2
)
−
2
)
−
1
2
{displaystyle {frac {6ln 2}{pi ^{2}}}left(3ln 2+4,gamma -{frac {24}{pi ^{2}}},zeta '(2)-2right)-{frac {1}{2}}}
γ = Constante de Euler–Mascheroni = 0,5772156649... {displaystyle scriptstyle gamma ,{text{= Constante de Euler–Mascheroni = 0,5772156649...}}} ζ ′ ( 2 ) = Derivada de ζ ( 2 ) = − ∑ n = 2 ∞ ln n n 2 = −0,9375482543... {displaystyle scriptstyle zeta '(2),{text{= Derivada de }}zeta (2),=,-!!sum limits _{n=2}^{infty }{frac {ln n}{n^{2}}},{text{= −0,9375482543...}}} |
6*ln2/Pi^2(3*ln2+ 4 EulerGamma- WeierstrassZeta'(2) *24/Pi^2-2)-1/2 | A086237 | [1;2,7,10,1,2,38,5,4,1,4,12,5,1,5,1,2,3,1,...] | 1974 | 1.46707807943397547289779848470722995 | ||
| 1,85193 70519 82466 17036 | Constante de Gibbs | .PNG)
|
S
i
(
π
)
{displaystyle {Si(pi)}}
Integralsenoidal |
∫
0
π
sin
t
t
d
t
=
∑
n
=
1
∞
(
−
1
)
n
−
1
π
2
n
−
1
(
2
n
−
1
)
(
2
n
−
1
)
!
{displaystyle int _{0}^{pi }{frac {sin t}{t}},dt=sum limits _{n=1}^{infty }(-1)^{n-1}{frac {pi ^{2n-1}}{(2n-1)(2n-1)!}}}
= π − π 3 3 ∗ 3 ! + π 5 5 ∗ 5 ! − π 7 7 ∗ 7 ! + . . . {displaystyle =pi -{frac {pi ^{3}}{3*3!}}+{frac {pi ^{5}}{5*5!}}-{frac {pi ^{7}}{7*7!}}+...} |
SinIntegral[Pi] | A036792 | [1;1,5,1,3,15,1,5,3,2,7,2,1,62,1,3,110,1,39,...] | 1.85193705198246617036105337015799136 | ||
| 1,78221 39781 91369 11177 | Constante de Grothendieck | K R {displaystyle {K_{R}}} | π 2 log ( 1 + 2 ) = π 2 arsinh 1 {displaystyle {frac {pi }{2log(1+{sqrt {2}})}}={frac {pi }{2operatorname {arsinh} 1}}} | pi/(2 log(1+sqrt(2))) | A088367 | [1;1,3,1,1,2,4,2,1,1,17,1,12,4,3,5,10,1,1,3,...] | 1.78221397819136911177441345297254934 | |||
| 1,74540 56624 07346 86349 | Constante media armónica de Khinchin | 
|
K − 1 {displaystyle {K_{-1}}} |
log
2
∑
n
=
1
∞
1
n
log
(
1
+
1
n
(
n
+
2
)
)
=
lim
n
→
∞
n
1
a
1
+
1
a
2
+
.
.
.
+
1
a
n
{displaystyle {frac {log 2}{sum limits _{n=1}^{infty }{frac {1}{n}}log {bigl (}1+{frac {1}{n(n+2)}}{bigr)}}}=lim _{nto infty }{frac {n}{{frac {1}{a_{1}}}+{frac {1}{a_{2}}}+...+{frac {1}{a_{n}}}}}}
a1...an son elementos de una fracción continua [a0;a1,a2,...,an] |
(log 2)/ (sum[n=1 to ∞] {1/n log(1+ 1/(n(n+2))} |
A087491 | [1;1,2,1,12,1,5,1,5,13,2,13,2,1,9,1,6,1,3,1,...] | 1.74540566240734686349459630968366106 | ||
| 0,10841 01512 23111 36151 | Constante de Trott
|
T 1 {displaystyle mathrm {T} _{1}} |
[
1
,
0
,
8
,
4
,
1
,
0
,
1
,
5
,
1
,
2
,
2
,
3
,
1
,
1
,
1
,
3
,
6
,
.
.
.
]
{displaystyle textstyle [1,0,8,4,1,0,1,5,1,2,2,3,1,1,1,3,6,...]}
1 1 + 1 0 + 1 8 + 1 4 + 1 1 + 1 0 + 1 / . . . {displaystyle {frac {1}{1+{frac {1}{0+{frac {1}{8+{frac {1}{4+{frac {1}{1+{frac {1}{0+1{/...}}}}}}}}}}}}}} |
Trott Constant | A039662 | [0;9,4,2,5,1,2,2,3,1,1,1,3,6,1,5,1,1,2,...] | 0.10841015122311136151129081140641509 | |||
| 1,45136 92348 83381 05028 | Constante de Ramanujan–Soldner · | 
|
μ {displaystyle {mu }} |
L
i
(
x
)
=
∫
0
x
d
t
ln
t
=
0
L
i
= Integral logarítmica
{displaystyle mathrm {Li} (x)=int _{0}^{x}{frac {dt}{ln t}}=0qquad mathrm {Li} ,scriptstyle {text{= Integral logarítmica}}}
L i ( x ) = E i ( ln x ) E i = Integral exponencial {displaystyle mathrm {Li} (x);=;mathrm {Ei} (ln {x});;qquad mathrm {Ei} ,scriptstyle {text{= Integral exponencial}}} |
FindRoot[li(x) = 0] | I | A070769 | [1;2,4,1,1,1,3,1,1,1,2,47,2,4,1,12,1,1,2,2,1,...] | 1792 a 1809 |
1.45136923488338105028396848589202744 |
| 0,64341 05462 88338 02618 | Constante de Cahen | ξ 2 {displaystyle xi _{2}} |
∑
k
=
1
∞
(
−
1
)
k
s
k
−
1
=
1
1
−
1
2
+
1
6
−
1
42
+
1
1806
±
⋯
{displaystyle sum _{k=1}^{infty }{frac {(-1)^{k}}{s_{k}-1}}={frac {1}{1}}-{frac {1}{2}}+{frac {1}{6}}-{frac {1}{42}}+{frac {1}{1806}}{,pm cdots }}
sk son términos de la Sucesión de Sylvester 2, 3, 7, 43, 1807...
|
T | A118227 | [0; 1, 1, 1, 4, 9, 196, 16641, 639988804,...] | 1891 | 0.64341054628833802618225430775756476 | ||
| -4,22745 35333 76265 408 | Digamma (¼) | 
|
ψ ( 1 4 ) {displaystyle psi ({tfrac {1}{4}})} | − γ − π 2 − 3 ln 2 = − γ + ∑ n = 0 ∞ ( 1 n + 1 − 1 n + 1 4 ) {displaystyle -gamma -{frac {pi }{2}}-3ln {2}=-gamma +sum _{n=0}^{infty }left({frac {1}{n+1}}-{frac {1}{n+{tfrac {1}{4}}}}right)} | -EulerGamma -pi/2 -3 log 2 |
A020777 | -[4;4,2,1,1,10,1,5,9,11,1,22,1,1,14,1,2,1,4,...] | -4,2274535333762654080895301460966835 | ||
| 1,77245 38509 05516 02729 | Constante de Carlson-Levin | Γ ( 1 2 ) {displaystyle {Gamma }({tfrac {1}{2}})} | π = ( − 1 2 ) ! = ∫ − ∞ ∞ 1 e x 2 d x = ∫ 0 1 1 − ln x d x {displaystyle {sqrt {pi }}=left(-{frac {1}{2}}right)!=int _{-infty }^{infty }{frac {1}{e^{x^{2}}}},dx=int _{0}^{1}{frac {1}{sqrt {-ln x}}},dx} | sqrt (pi) | T | A002161 | [1;1,3,2,1,1,6,1,28,13,1,1,2,18,1,1,1,83,1,...] | 1.77245385090551602729816748334114518 | ||
| 0,23571 11317 19232 93137 | Constante de Copeland-Erdős | C C E {displaystyle {{mathcal {C}}_{CE}}} | ∑ n = 1 ∞ p n 10 n + ∑ k = 1 n ⌊ log 10 p k ⌋ {displaystyle sum _{n=1}^{infty }{frac {p_{n}}{10^{n+sum limits _{k=1}^{n}lfloor log _{10}{p_{k}}rfloor }}}} | sum[n=1 to ∞] {prime(n) /(n+(10^ sum[k=1 to n]{floor (log_10 prime(k))}))} |
I | A033308 | [0;4,4,8,16,18,5,1,1,1,1,7,1,1,6,2,9,58,1,3,...] | 0.23571113171923293137414347535961677 | ||
| 2,09455 14815 42326 59148 | Constante de Wallis | 
|
W {displaystyle W} | 45 − 1929 18 3 + 45 + 1929 18 3 {displaystyle {sqrt[{3}]{frac {45-{sqrt {1929}}}{18}}}+{sqrt[{3}]{frac {45+{sqrt {1929}}}{18}}}} | (((45-sqrt(1929)) /18))^(1/3)+ (((45+sqrt(1929)) /18))^(1/3) |
A | A007493 | [2;10,1,1,2,1,3,1,1,12,3,5,1,1,2,1,6,1,11,4,...] | 1616 a 1703 |
2.09455148154232659148238654057930296 |
| 0,28674 74284 34478 73410 | Constante Strongly Carefree | K 2 {displaystyle K_{2}} | ∏ n = 1 ∞ ( 1 − 3 p n − 2 p n 3 ) p n : p r i m o = 6 π 2 ∏ n = 1 ∞ ( 1 − 1 p n ( p n + 1 ) ) p n : p r i m o {displaystyle prod _{n=1}^{infty }{underset {p_{n}:,{primo}}{left(1-{frac {3p_{n}-2}{{p_{n}}^{3}}}right)}}={frac {6}{pi ^{2}}}prod _{n=1}^{infty }{underset {p_{n}:,{primo}}{left(1-{frac {1}{p_{n}(p_{n}+1)}}right)}}} | N[ prod[k=1 to ∞] {1 - (3*prime(k)-2) /(prime(k)^3)}] |
A065473 | [0;3,2,19,3,12,1,5,1,5,1,5,2,1,1,1,1,1,3,7,...] | 0.28674742843447873410789271278983845 | |||
| 0,56714 32904 09783 87299 | Constante Omega, función W(1) de Lambert | 
|
Ω {displaystyle {Omega }} | ∑ n = 1 ∞ ( − n ) n − 1 n ! = ( 1 e ) ( 1 e ) ⋅ ⋅ ( 1 e ) = e − Ω = e − e − e ⋅ ⋅ − e {displaystyle sum _{n=1}^{infty }{frac {(-n)^{n-1}}{n!}}=,left({frac {1}{e}}right)^{left({frac {1}{e}}right)^{cdot ^{cdot ^{left({frac {1}{e}}right)}}}}=e^{-Omega }={e}^{-e^{-e^{cdot ^{cdot ^{-e}}}}}} | Sum[n=1 to ∞] {(-n)^(n-1)/n!} |
T | A030178 | [0;1,1,3,4,2,10,4,1,1,1,1,2,7,306,1,5,1,2,1,...] | 1728 a 1777 |
0.56714329040978387299996866221035555 |
| 0,54325 89653 42976 70695 | Constante de Bloch-Landau | L {displaystyle {L}} | Γ ( 1 3 ) Γ ( 5 6 ) Γ ( 1 6 ) = ( − 2 3 ) ! ( − 1 + 5 6 ) ! ( − 1 + 1 6 ) ! {displaystyle {frac {Gamma ({tfrac {1}{3}});Gamma ({tfrac {5}{6}})}{Gamma ({tfrac {1}{6}})}}={frac {(-{tfrac {2}{3}})!;(-1+{tfrac {5}{6}})!}{(-1+{tfrac {1}{6}})!}}} | gamma(1/3) *gamma(5/6) /gamma(1/6) |
A081760 | [0;1,1,5,3,1,1,2,1,1,6,3,1,8,11,2,1,1,27,4,...] | 1929 | 0.54325896534297670695272829530061323 | ||
| 0,34053 73295 50999 14282 | Constante de Pólya Random Walk | 
|
p ( 3 ) {displaystyle {p(3)}} |
1
−
(
3
(
2
π
)
3
∫
−
π
π
∫
−
π
π
∫
−
π
π
d
x
d
y
d
z
3
−
cos
x
−
cos
y
−
cos
z
)
−
1
{displaystyle 1-!!left({3 over (2pi)^{3}}int limits _{-pi }^{pi }int limits _{-pi }^{pi }int limits _{-pi }^{pi }{dx,dy,dz over 3-!cos x-!cos y-!cos z}right)^{!-1}}
= 1 − 16 2 3 π 3 ( Γ ( 1 24 ) Γ ( 5 24 ) Γ ( 7 24 ) Γ ( 11 24 ) ) − 1 {displaystyle =1-16{sqrt {tfrac {2}{3}}};pi ^{3}left(Gamma ({tfrac {1}{24}})Gamma ({tfrac {5}{24}})Gamma ({tfrac {7}{24}})Gamma ({tfrac {11}{24}})right)^{-1}} |
1-16*Sqrt[2/3]*Pi^3 /((Gamma[1/24] *Gamma[5/24] *Gamma[7/24] *Gamma[11/24]) |
A086230 | [0;2,1,14,1,3,8,1,5,2,7,1,12,1,5,59,1,1,1,3,...] | 0.34053732955099914282627318443290289 | ||
| 0,35323 63718 54995 98454 | Constante de Hafner-Sarnak-McCurley (1) | σ {displaystyle {sigma }} | ∏ k = 1 ∞ { 1 − [ 1 − ∏ j = 1 n ( 1 − p k − j ) ] 2 } {displaystyle prod _{k=1}^{infty }left{1-left[1-prod _{j=1}^{n}(1-p_{k}^{-j})right]^{2}right}} | prod[k=1 to ∞] {1-(1-prod[j=1 to n] {1-prime(k)^-j})^2} | A085849 | [0;2,1,4,1,10,1,8,1,4,1,2,1,2,1,2,6,1,1,1,3,...] | 1993 | 0.35323637185499598454351655043268201 | ||
| 0,74759 79202 53411 43517 | Constante Parking de Rényi |  
|
m {displaystyle {m}} | ∫ 0 ∞ e ( − 2 ∫ 0 x 1 − e − y y d y ) d x = e − 2 γ ∫ 0 ∞ e − 2 Γ ( 0 , n ) n 2 {displaystyle int limits _{0}^{infty }e^{left(!-2int limits _{0}^{x}{frac {1-e^{-y}}{y}}dyright)}!dx={e^{-2gamma }}int limits _{0}^{infty }{frac {e^{-2Gamma (0,n)}}{n^{2}}}} | [e^(-2*Gamma)] * Int{n,0,∞}[ e^(- 2*Gamma(0,n)) /n^2] | A050996 | [0;1,2,1,25,3,1,2,1,1,12,1,2,1,1,3,1,2,1,43,...] | 1958 | 0.74759792025341143517873094383017817 | |
| 0,60792 71018 54026 62866 | Constante de Hafner-Sarnak-McCurley (2) | 1 ζ ( 2 ) {displaystyle {frac {1}{zeta (2)}}} | 6 π 2 = ∏ n = 0 ∞ ( 1 − 1 p n 2 ) p n : p r i m o = ( 1 − 1 2 2 ) ( 1 − 1 3 2 ) ( 1 − 1 5 2 ) . . . {displaystyle {frac {6}{pi ^{2}}}{=}prod _{n=0}^{infty }{underset {p_{n}:,{primo}}{left(1-{frac {1}{{p_{n}}^{2}}}right)}}{=}textstyle left(1{-}{frac {1}{2^{2}}}right)left(1{-}{frac {1}{3^{2}}}right)left(1{-}{frac {1}{5^{2}}}right)...} | Prod{n=1 to ∞} (1-1/prime(n)^2) |
T | A059956 | [0;1,1,1,1,4,2,4,7,1,4,2,3,4,10,1,2,1,1,1,...] | 0.60792710185402662866327677925836583 | ||
| 0,12345 67891 01112 13141 | Constante de Champernowne | 
|
C 10 {displaystyle C_{10}} | ∑ n = 1 ∞ ∑ k = 10 n − 1 10 n − 1 k 10 k n − 9 ∑ j = 0 n − 1 10 j ( n − j − 1 ) {displaystyle sum _{n=1}^{infty }sum _{k=10^{n-1}}^{10^{n}-1}{frac {k}{10^{kn-9sum _{j=0}^{n-1}10^{j}(n-j-1)}}}} | T | A033307 | [0;8,9,1,149083,1,1,1,4,1,1,1,3,4,1,1,1,15,...] | 1933 | 0.12345678910111213141516171819202123 | |
| 0,76422 36535 89220 66299 | Constante de Landau-Ramanujan | K {displaystyle K} | 1 2 ∏ p ≡ 3 mod 4 ( 1 − 1 p 2 ) − 1 2 p : p r i m o = π 4 ∏ p ≡ 1 mod 4 ( 1 − 1 p 2 ) 1 2 p : p r i m o {displaystyle {frac {1}{sqrt {2}}}prod _{pequiv 3!!!!!mod !4}!!{underset {!!!!!!!!p:,{primo}}{left(1-{frac {1}{p^{2}}}right)^{-{frac {1}{2}}}}}!!={frac {pi }{4}}prod _{pequiv 1!!!!!mod !4}!!{underset {!!!!p:,{primo}}{left(1-{frac {1}{p^{2}}}right)^{frac {1}{2}}}}} | T ? | A064533 | [0;1,3,4,6,1,15,1,2,2,3,1,23,3,1,1,3,1,1,6,4,...] | 1908 | 0.76422365358922066299069873125009232 | ||
| 1,58496 25007 21156 18145 | Dimensión Hausdorf del triángulo de Sierpinski | 
|
l o g 2 3 {displaystyle {log_{2}3}} | l o g 3 l o g 2 = ∑ n = 0 ∞ 1 2 2 n + 1 ( 2 n + 1 ) ∑ n = 0 ∞ 1 3 2 n + 1 ( 2 n + 1 ) = 1 2 + 1 24 + 1 160 + . . . 1 3 + 1 81 + 1 1215 + . . . {displaystyle {frac {log3}{log2}}={frac {sum _{n=0}^{infty }{frac {1}{2^{2n+1}(2n+1)}}}{sum _{n=0}^{infty }{frac {1}{3^{2n+1}(2n+1)}}}}={frac {{frac {1}{2}}+{frac {1}{24}}+{frac {1}{160}}+...}{{frac {1}{3}}+{frac {1}{81}}+{frac {1}{1215}}+...}}} | (Sum[n=0 to ∞] {1/(2^(2n+1)(2n+1))})/ (Sum[n=0 to ∞] {1/(3^(2n+1)(2n+1))}) |
T | A020857 | [1;1,1,2,2,3,1,5,2,23,2,2,1,1,55,1,4,3,1,1,...] | 1.58496250072115618145373894394781651 | |
| 0,11000 10000 00000 00000 0001 | Número de Liouville | £ L i {displaystyle {text{£}}_{Li}} | ∑ n = 1 ∞ 1 10 n ! = 1 10 1 ! + 1 10 2 ! + 1 10 3 ! + 1 10 4 ! + . . . {displaystyle sum _{n=1}^{infty }{frac {1}{10^{n!}}}={frac {1}{10^{1!}}}+{frac {1}{10^{2!}}}+{frac {1}{10^{3!}}}+{frac {1}{10^{4!}}}+...} | Sum[n=1 to ∞] {10^(-n!)} |
T | A012245 | [1;9,1,999,10,9999999999999,1,9,999,1,9] | 0.11000100000000000000000100... | ||
| 0,46364 76090 00806 11621 | Serie de Machin-Gregory | 
|
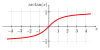
arctan 1 2 {displaystyle arctan {frac {1}{2}}} | ∑ n = 0 ∞ ( − 1 ) n x 2 n + 1 2 n + 1 = 1 2 − 1 3 ⋅ 2 3 + 1 5 ⋅ 2 5 − 1 7 ⋅ 2 7 + . . . P a r a x = 1 / 2 {displaystyle {underset {Para;x=1/2qquad qquad }{sum _{n=0}^{infty }{frac {!!(-1)^{n}x^{2n+1}}{2n+1}}={frac {1}{2}}-!{frac {1}{3cdot 2^{3}}}{+}{frac {1}{5cdot 2^{5}}}-!{frac {1}{7cdot 2^{7}}}{+}{...}}}} | Sum[n=0 to ∞] {(-1)^n (1/2) ^(2n+1)/(2n+1)} |
I | A073000 | [0;2,6,2,1,1,1,6,1,2,1,1,2,10,1,2,1,2,1,1,1,...] | 0.46364760900080611621425623146121440 | |
| 1,27323 95447 35162 68615 | Serie de Ramanujan-Forsyth | 4 π {displaystyle {frac {4}{pi }}} | ∑ n = 0 ∞ ( ( 2 n − 3 ) ! ! ( 2 n ) ! ! ) 2 = 1 + ( 1 2 ) 2 + ( 1 2 ⋅ 4 ) 2 + ( 1 ⋅ 3 2 ⋅ 4 ⋅ 6 ) 2 + . . . {displaystyle displaystyle sum limits _{n=0}^{infty }textstyle left({frac {(2n-3)!!}{(2n)!!}}right)^{2}={1!+!left({frac {1}{2}}right)^{2}!{+}left({frac {1}{2cdot 4}}right)^{2}!{+}left({frac {1cdot 3}{2cdot 4cdot 6}}right)^{2}{+}...}} | Sum[n=0 to ∞] {[(2n-3)!! /(2n)!!]^2} |
I | A088538 | [1;3,1,1,1,15,2,72,1,9,1,17,1,2,1,5,1,1,10,...] | 1.27323954473516268615107010698011489 | ||
| 15,15426 22414 79264 1897 | Constante exponencial reiterado | 
|
e e {displaystyle e^{e}} | ∑ n = 0 ∞ e n n ! = lim n → ∞ ( 1 + n n ) n − n ( 1 + n ) 1 + n {displaystyle sum _{n=0}^{infty }{frac {e^{n}}{n!}}=lim _{nto infty }left({frac {1+n}{n}}right)^{n^{-n}(1+n)^{1+n}}} | Sum[n=0 to ∞] {(e^n)/n!} |
A073226 | [15;6,2,13,1,3,6,2,1,1,5,1,1,1,9,4,1,1,1,6,7,...] | 15.1542622414792641897604302726299119 | ||
| 36,46215 96072 07911 77099 | Pi elevado a pi | π π {displaystyle pi ^{pi }} | π π {displaystyle pi ^{pi }} | pi^pi | A073233 | [36;2,6,9,2,1,2,5,1,1,6,2,1,291,1,38,50,1,2,...] | 36.4621596072079117709908260226921236 | |||
| 0,53964 54911 90413 18711 | Constante de Ioachimescu | 2 + ζ ( 1 2 ) {displaystyle 2+zeta ({tfrac {1}{2}})} | 2 − ( 1 + 2 ) ∑ n = 1 ∞ ( − 1 ) n + 1 n = γ + ∑ n = 1 ∞ ( − 1 ) 2 n γ n 2 n n ! {displaystyle {2{-}(1{+}{sqrt {2}})sum _{n=1}^{infty }{frac {(-1)^{n+1}}{sqrt {n}}}}=gamma +sum _{n=1}^{infty }{frac {(-1)^{2n};gamma _{n}}{2^{n}n!}}} | γ +N [sum[n=1 to ∞] {((-1)^(2n) gamma_n) /(2^n n!)}] |
2- A059750 |
[0;1,1,5,1,4,6,1,1,2,6,1,1,2,1,1,1,37,3,2,1,...] | 0.53964549119041318711050084748470198 | |||
| 2,58498 17595 79253 21706 | Constante de Sierpiński | 
|
K {displaystyle {K}} |
π
(
2
γ
+
ln
4
π
3
Γ
(
1
4
)
4
)
=
π
(
2
γ
+
4
ln
Γ
(
3
4
)
−
ln
π
)
{displaystyle pi left(2gamma +ln {frac {4pi ^{3}}{Gamma ({tfrac {1}{4}})^{4}}}right)=pi (2gamma +4ln Gamma ({tfrac {3}{4}})-ln pi)}
= π ( 2 ln 2 + 3 ln π + 2 γ − 4 ln Γ ( 1 4 ) ) {displaystyle =pi left(2ln 2+3ln pi +2gamma -4ln Gamma ({tfrac {1}{4}})right)} |
-Pi Log[Pi]+2 Pi EulerGamma +4 Pi Log [Gamma[3/4]] |
A062089 | [2;1,1,2,2,3,1,3,1,9,2,8,4,1,13,3,1,15,18,1,...] | 1907 | 2.58498175957925321706589358738317116 | |
| 1,83928 67552 14161 13255 | Constante Tribonacci | 
|
ϕ 3 {displaystyle {phi _{}}_{3}} | 1 + 19 + 3 33 3 + 19 − 3 33 3 3 = 1 + ( 1 2 + 1 2 + 1 2 + . . . 3 3 3 ) − 1 {displaystyle textstyle {frac {1+{sqrt[{3}]{19+3{sqrt {33}}}}+{sqrt[{3}]{19-3{sqrt {33}}}}}{3}}=scriptstyle ,1+left({sqrt[{3}]{{tfrac {1}{2}}+{sqrt[{3}]{{tfrac {1}{2}}+{sqrt[{3}]{{tfrac {1}{2}}+...}}}}}}right)^{-1}} | (1/3)*(1+(19+3 *sqrt(33))^(1/3) +(19-3 *sqrt(33))^(1/3)) |
A | A058265 | [1;1,5,4,2,305,1,8,2,1,4,6,14,3,1,13,5,1,7,...] | 1.83928675521416113255185256465328660 | |
| 0,69220 06275 55346 35386 | Valor mínimo de la función ƒ(x) = xx |
( 1 e ) 1 e {displaystyle {left({frac {1}{e}}right)}^{frac {1}{e}}} | e − 1 e {displaystyle {e}^{-{frac {1}{e}}}} = Inverso de: Número de Steiner | e^(-1/e) | A072364 | [0;1,2,4,55,27,1,1,16,9,3,2,8,3,2,1,1,4,1,9,...] | 0.69220062755534635386542199718278976 | |||
| 0,70710 67811 86547 52440 +0,70710 67811 86547 52440 i |
Raíz cuadrada de i | 
|
i {displaystyle {sqrt {i}}} | − 1 4 = 1 + i 2 = e i π 4 = cos ( π 4 ) + i sin ( π 4 ) {displaystyle {sqrt[{4}]{-1}}={frac {1+i}{sqrt {2}}}=e^{frac {ipi }{4}}=cos left({frac {pi }{4}}right)+isin left({frac {pi }{4}}right)} | (1+i)/(sqrt 2) | C A | A010503 A010503 |
[0;1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,..] = [0;1,2,...] [0;1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,..] i = [0;1,2,...] i |
0.70710678118654752440084436210484903 + 0.70710678118654752440084436210484 i | |
| 1,15636 26843 32269 71685 | Constante de recurrencia cúbica | σ 3 {displaystyle {sigma _{3}}} | ∏ n = 1 ∞ n 3 − n = 1 2 3 ⋯ 3 3 3 = 1 1 / 3 2 1 / 9 3 1 / 27 ⋯ {displaystyle prod _{n=1}^{infty }n^{{3}^{-n}}={sqrt[{3}]{1{sqrt[{3}]{2{sqrt[{3}]{3cdots }}}}}}=1^{1/3};2^{1/9};3^{1/27}cdots } | prod[n=1 to ∞] {n ^(1/3)^n} |
A123852 | [1;6,2,1,1,8,13,1,3,2,2,6,2,1,2,1,1,1,10,33,...] | 1.15636268433226971685337032288736935 | |||
| 1,66168 79496 33594 12129 | Recurrencia cuadrática de Somos | σ {displaystyle {sigma }} | ∏ n = 1 ∞ n 1 / 2 n = 1 2 3 4 ⋯ = 1 1 / 2 2 1 / 4 3 1 / 8 ⋯ {displaystyle prod _{n=1}^{infty }n^{{1/2}^{n}}={sqrt {1{sqrt {2{sqrt {3{sqrt {4cdots }}}}}}}}=1^{1/2};2^{1/4};3^{1/8}cdots } | prod[n=1 to ∞] {n ^(1/2)^n} |
T ? | A065481 | [1;1,1,1,21,1,1,1,6,4,2,1,1,2,1,3,1,13,13,...] | 1.66168794963359412129581892274995074 | ||
| 0,95531 66181 24509 27816 | Ángulo mágico | 
|
θ m {displaystyle {theta _{m}}} | arctan ( 2 ) = arccos ( 1 3 ) ≈ 54 , 7356 ∘ {displaystyle arctan left({sqrt {2}}right)=arccos left({sqrt {tfrac {1}{3}}}right)approx textstyle {54,7356}^{circ }} | arctan(sqrt(2)) | T | A195696 | [0;1,21,2,1,1,1,2,1,2,2,4,1,2,9,1,2,1,1,1,3,...] | 0.95531661812450927816385710251575775 | |
| 0,59634 73623 23194 07434 | Constante de Euler-Gompertz | G {displaystyle {G}} | − e E i ( − 1 ) = ∫ 0 ∞ e − n 1 + n d n = 1 1 + 1 1 + 1 1 + 2 1 + 2 1 + 3 1 + 3 1 + 4 / . . . {displaystyle -emathrm {Ei} (-1)=int limits _{0}^{infty }{frac {e^{-n}}{1{+}n}},dn=textstyle {frac {1}{1+{frac {1}{1+{frac {1}{1+{frac {2}{1+{frac {2}{1+{frac {3}{1+{frac {3}{1+4{/...}}}}}}}}}}}}}}}} | N[int[0 to ∞] {(e^-n)/(1+n)}] |
I | A073003 | [0;1,1,2,10,1,1,4,2,2,13,2,4,1,32,4,8,1,1,1,...] | 0.59634736232319407434107849936927937 | ||
| 0,69777 46579 64007 98200 | Constante de fracción continua, función de Bessel | C C F {displaystyle {C}_{CF}} | I 1 ( 2 ) I 0 ( 2 ) = ∑ n = 0 ∞ n n ! n ! ∑ n = 0 ∞ 1 n ! n ! = 1 1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + 1 / . . . {displaystyle {frac {I_{1}(2)}{I_{0}(2)}}={frac {sum limits _{n=0}^{infty }{frac {n}{n!n!}}}{sum limits _{n=0}^{infty }{frac {1}{n!n!}}}}=textstyle {frac {1}{1+{frac {1}{2+{frac {1}{3+{frac {1}{4+{frac {1}{5+{frac {1}{6+1{/...}}}}}}}}}}}}}} | (Sum {n=0 to ∞} n/(n!n!)) / (Sum {n=0 to ∞} 1/(n!n!)) |
I | A052119 | [0;1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,...] = [0;p+1], p∈ℕ |
0.69777465796400798200679059255175260 | ||
| 0,36651 29205 81664 32701 | Mediana distribución de Gumbel | 
|
l l 2 {displaystyle {ll_{2}}} | − ln ( ln ( 2 ) ) {displaystyle -ln(ln(2))} | -ln(ln(2)) | A074785 | [0;2,1,2,1,2,6,1,6,6,2,2,2,1,12,1,8,1,1,3,1,...] | 0.36816512920566432701243915823266947 | ||
| 0,64624 54398 94813 30426 | Constante de Masser-Gramain | C {displaystyle {C}} | γ β ( 1 ) + β ′ ( 1 ) = π ( − ln Γ ( 1 4 ) + 3 4 π + 1 2 ln 2 + 1 2 γ ) {displaystyle gamma {beta }(1){+}{beta }'(1)=pi !left(-!ln Gamma ({tfrac {1}{4}})+{tfrac {3}{4}}pi +{tfrac {1}{2}}ln 2+{tfrac {1}{2}}gamma right)} = π ( − ln ( 1 4 ! ) + 3 4 ln π − 3 2 ln 2 + 1 2 γ ) {displaystyle =pi !left(-!ln({tfrac {1}{4}}!)+{tfrac {3}{4}}ln pi -{tfrac {3}{2}}ln 2+{tfrac {1}{2}},gamma right)} γ = Constante de Euler–Mascheroni = 0,5772156649... {displaystyle scriptstyle gamma ,{text{= Constante de Euler–Mascheroni = 0,5772156649...}}} β() = Función beta, Γ() = Función Gamma | Pi/4*(2*Gamma + 2*Log[2] + 3*Log[Pi] - 4 Log[Gamma[1/4]]) |
A086057 | [0;1,1,1,4,1,3,2,3,9,1,33,1,4,3,3,5,3,1,3,4,...] | 0.64624543989481330426647339684579279 | |||
| 0.69034 71261 14964 31946 | Límite superior exponencial iterado | 
|
H 2 n + 1 {displaystyle {H}_{2n+1}} | lim n → ∞ H 2 n + 1 = ( 1 2 ) ( 1 3 ) ( 1 4 ) ⋅ ⋅ ( 1 2 n + 1 ) = 2 − 3 − 4 ⋅ ⋅ − 2 n − 1 {displaystyle lim _{nto infty }{H}_{2n+1}=textstyle left({frac {1}{2}}right)^{left({frac {1}{3}}right)^{left({frac {1}{4}}right)^{cdot ^{cdot ^{left({frac {1}{2n+1}}right)}}}}}={2}^{-3^{-4^{cdot ^{cdot ^{-2n-1}}}}}} | 2^-3^-4^-5^-6^ -7^-8^-9^-10^ -11^-12^-13 … |
A242760 | [0;1,2,4,2,1,3,1,2,2,1,4,1,2,4,3,1,1,10,1,3,2,...] | 0.69034712611496431946732843846418942 | ||
| 0,65836 55992 | Límite inferior exponencial iterado | H 2 n {displaystyle {H}_{2n}} | lim n → ∞ H 2 n = ( 1 2 ) ( 1 3 ) ( 1 4 ) ⋅ ⋅ ( 1 2 n ) = 2 − 3 − 4 ⋅ ⋅ − 2 n {displaystyle lim _{nto infty }{H}_{2n}=textstyle left({frac {1}{2}}right)^{left({frac {1}{3}}right)^{left({frac {1}{4}}right)^{cdot ^{cdot ^{left({frac {1}{2n}}right)}}}}}={2}^{-3^{-4^{cdot ^{cdot ^{-2n}}}}}} | 2^-3^-4^-5^-6^ -7^-8^-9^-10^ -11^-12 … |
[0;1,1,1,12,1,2,1,1,4,3,1,1,2,1,2,1,51,2,2,1,...] | 0.6583655992... | ||||
| 2,71828 18284 59045 23536 | Número e, constante de Euler | 
|
e {displaystyle {e}} | ∑ n = 0 ∞ 1 n ! = 1 0 ! + 1 1 + 1 2 ! + 1 3 ! + 1 4 ! + 1 5 ! + ⋯ {displaystyle sum _{n=0}^{infty }{frac {1}{n!}}={frac {1}{0!}}+{frac {1}{1}}+{frac {1}{2!}}+{frac {1}{3!}}+{frac {1}{4!}}+{frac {1}{5!}}+cdots } 2 ∏ n = 1 ∞ ∏ i = 1 2 n − 1 ( 2 n + 2 i ) ∏ i = 1 2 n − 1 ( 2 n + 2 i − 1 ) 2 n = 2 4 3 6 ⋅ 8 5 ⋅ 7 4 10 ⋅ 12 ⋅ 14 ⋅ 16 9 ⋅ 11 ⋅ 13 ⋅ 15 8 ⋯ {displaystyle 2!prod _{n=1}^{infty }!!textstyle {sqrt[{2^{n}}]{frac {prod _{i=1}^{2^{n-1}}(2^{n}+2i)}{prod _{i=1}^{2^{n-1}}!(2^{n}+2i-1)}}}=2{sqrt {frac {4}{3}}}{sqrt[{4}]{frac {6cdot 8}{5cdot 7}}}{sqrt[{8}]{frac {10cdot 12cdot 14cdot 16}{9cdot 11cdot 13cdot 15}}}cdots } | Sum[n=0 to ∞] {1/n!} |
T | A001113 | [2;1,2,1,1,4,1,1,6,1,1,8,1,1,10,1,1,12,1,...] = [2;1,2p,1], p∈ℕ |
1618 | 2.71828182845904523536028747135266250 |
| 2,74723 82749 32304 33305 | Raíces anidadas de Ramanujan R5 | R 5 {displaystyle R_{5}} | 5 + 5 + 5 − 5 + 5 + 5 + 5 − ⋯ = 2 + 5 + 15 − 6 5 2 {displaystyle scriptstyle {sqrt {5+{sqrt {5+{sqrt {5-{sqrt {5+{sqrt {5+{sqrt {5+{sqrt {5-cdots }}}}}}}}}}}}}};=textstyle {frac {2+{sqrt {5}}+{sqrt {15-6{sqrt {5}}}}}{2}}} | (2+sqrt(5) +sqrt(15 -6 sqrt(5)))/2 |
A | [2;1,2,1,21,1,7,2,1,1,2,1,2,1,17,4,4,1,1,4,2,...] | 2.74723827493230433305746518613420282 | |||
| 2,23606 79774 99789 69640 | Raíz cuadrada de cinco Suma de Gauss |
|
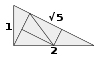
5 {displaystyle {sqrt {5}}} | ( n = 5 ) ∑ k = 0 n − 1 e 2 k 2 π i n = 1 + e 2 π i 5 + e 8 π i 5 + e 18 π i 5 + e 32 π i 5 {displaystyle scriptstyle (n=5)displaystyle sum _{k=0}^{n-1}e^{frac {2k^{2}pi i}{n}}=1+e^{frac {2pi i}{5}}+e^{frac {8pi i}{5}}+e^{frac {18pi i}{5}}+e^{frac {32pi i}{5}}} | Sum[k=0 to 4] {e^(2k^2 pi i/5)} |
A | A002163 | [2;4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,...] = [2;4,...] |
2.23606797749978969640917366873127624 | |
| 1,09864 19643 94156 48573 | Constante París | C P a {displaystyle C_{Pa}} | ∏ n = 2 ∞ 2 φ φ + φ n , φ = F i {displaystyle prod _{n=2}^{infty }{frac {2varphi }{varphi +varphi _{n}}};,;varphi {=}{Fi}} con φ n = 1 + φ n − 1 {displaystyle varphi _{n}{=}{sqrt {1{+}varphi _{n{-}1}}}} y φ 1 = 1 {displaystyle varphi _{1}{=}1} | A105415 | [1;10,7,3,1,3,1,5,1,4,2,7,1,2,3,22,1,2,5,2,1,...] | 1.09864196439415648573466891734359621 | ||||
| 0,11494 20448 53296 20070 | Constante de Kepler–Bouwkamp | 
|
ρ {displaystyle {rho }} | ∏ n = 3 ∞ cos ( π n ) = cos ( π 3 ) cos ( π 4 ) cos ( π 5 ) . . . {displaystyle prod _{n=3}^{infty }cos left({frac {pi }{n}}right)=cos left({frac {pi }{3}}right)cos left({frac {pi }{4}}right)cos left({frac {pi }{5}}right)...} | prod[n=3 to ∞] {cos(pi/n)} |
A085365 | [0;8,1,2,2,1,272,2,1,41,6,1,3,1,1,26,4,1,1,...] | 0.11494204485329620070104015746959874 | ||
| 1,28242 71291 00622 63687 | Constante de Glaisher–Kinkelin | A {displaystyle {A}} | e 1 12 − ζ ′ ( − 1 ) = e 1 8 − 1 2 ∑ n = 0 ∞ 1 n + 1 ∑ k = 0 n ( − 1 ) k ( n k ) ( k + 1 ) 2 ln ( k + 1 ) {displaystyle e^{{frac {1}{12}}-zeta ^{prime }(-1)}=e^{{frac {1}{8}}-{frac {1}{2}}sum limits _{n=0}^{infty }{frac {1}{n+1}}sum limits _{k=0}^{n}left(-1right)^{k}{binom {n}{k}}left(k+1right)^{2}ln(k+1)}} | e^(1/2-zeta´{-1}) | T ? | A074962 | [1;3,1,1,5,1,1,1,3,12,4,1,271,1,1,2,7,1,35,...] | 1878 | 1.28242712910062263687534256886979172 | |
| 3,62560 99082 21908 31193 | Gamma(1/4) | 
|
Γ ( 1 4 ) {displaystyle Gamma ({tfrac {1}{4}})} | 4 ( 1 4 ) ! = ( 2 π ) 3 4 ∏ k = 1 ∞ tanh ( π k 2 ) {displaystyle 4left({frac {1}{4}}right)!=(2pi)^{frac {3}{4}}prod _{k=1}^{infty }tanh left({frac {pi k}{2}}right)} | 4(1/4)! | T | A068466 | [3;1,1,1,2,25,4,9,1,1,8,4,1,6,1,1,19,1,1,4,1,...] | 1729 | 3.62560990822190831193068515586767200 |
| 1,78107 24179 90197 98523 | Exp.gamma por función G-Barnes | e γ {displaystyle e^{gamma }} |
∏
n
=
1
∞
e
1
n
1
+
1
n
=
∏
n
=
0
∞
(
∏
k
=
0
n
(
k
+
1
)
(
−
1
)
k
+
1
(
n
k
)
)
1
n
+
1
=
{displaystyle prod _{n=1}^{infty }{frac {e^{frac {1}{n}}}{1+{tfrac {1}{n}}}}=prod _{n=0}^{infty }left(prod _{k=0}^{n}(k+1)^{(-1)^{k+1}{n choose k}}right)^{frac {1}{n+1}}=}
( 2 1 ) 1 / 2 ( 2 2 1 ⋅ 3 ) 1 / 3 ( 2 3 ⋅ 4 1 ⋅ 3 3 ) 1 / 4 ( 2 4 ⋅ 4 4 1 ⋅ 3 6 ⋅ 5 ) 1 / 5 . . . {displaystyle textstyle left({frac {2}{1}}right)^{1/2}left({frac {2^{2}}{1cdot 3}}right)^{1/3}left({frac {2^{3}cdot 4}{1cdot 3^{3}}}right)^{1/4}left({frac {2^{4}cdot 4^{4}}{1cdot 3^{6}cdot 5}}right)^{1/5}...} |
Prod[n=1 to ∞] {e^(1/n)}/{1 + 1/n} |
A073004 | [1;1,3,1,1,3,5,4,1,1,2,2,1,7,9,1,16,1,1,1,2,...] | 1900 | 1.78107241799019798523650410310717954 | ||
| 0,18785 96424 62067 12024 | MRB Constant, Marvin Ray Burns | 
|
C M R B {displaystyle C_{{}_{MRB}}} | ∑ n = 1 ∞ ( − 1 ) n ( n 1 / n − 1 ) = − 1 1 + 2 2 − 3 3 + 4 4 . . . {displaystyle sum _{n=1}^{infty }({-}1)^{n}(n^{1/n}{-}1)=-{sqrt[{1}]{1}}+{sqrt[{2}]{2}}-{sqrt[{3}]{3}}+{sqrt[{4}]{4}},...} | Sum[n=1 to ∞] {(-1)^n (n^(1/n)-1)} |
A037077 | [0;5,3,10,1,1,4,1,1,1,1,9,1,1,12,2,17,2,2,1,...] | 1999 | 0.18785964246206712024851793405427323 | |
| 1,01494 16064 09653 62502 | Constante de Gieseking | π ln β {displaystyle {pi ln beta }} |
3
3
4
(
1
−
∑
n
=
0
∞
1
(
3
n
+
2
)
2
+
∑
n
=
1
∞
1
(
3
n
+
1
)
2
)
=
{displaystyle {frac {3{sqrt {3}}}{4}}left(1-sum _{n=0}^{infty }{frac {1}{(3n+2)^{2}}}+sum _{n=1}^{infty }{frac {1}{(3n+1)^{2}}}right)=}
3 3 4 ( 1 − 1 2 2 + 1 4 2 − 1 5 2 + 1 7 2 ± . . . ) = ∫ 0 2 π 3 ln ( 2 cos t 2 ) d t {displaystyle textstyle {frac {3{sqrt {3}}}{4}}left(1{-}{frac {1}{2^{2}}}{+}{frac {1}{4^{2}}}{-}{frac {1}{5^{2}}}{+}{frac {1}{7^{2}}}{pm }...right)=displaystyle !int _{0}^{frac {2pi }{3}}!ln !left(2cos {tfrac {t}{2}}right){mathrm {d} }t} |
sqrt(3)*3/4 *(1 -Sum[n=0 to ∞] {1/((3n+2)^2)} +Sum[n=1 to ∞] {1/((3n+1)^2)}) |
A143298 | [1;66,1,12,1,2,1,4,2,1,3,3,1,4,1,56,2,2,11,...] | 1912 | 1.01494160640965362502120255427452028 | ||
| 2,62205 75542 92119 81046 | Constante Lemniscata | 
|
ϖ {displaystyle {varpi }} | π G = 4 2 π Γ ( 5 4 ) 2 = 1 4 2 π Γ ( 1 4 ) 2 = 4 2 π ( 1 4 ! ) 2 {displaystyle pi ,{G}=4{sqrt {tfrac {2}{pi }}},Gamma {left({tfrac {5}{4}}right)^{2}}={tfrac {1}{4}}{sqrt {tfrac {2}{pi }}},Gamma {left({tfrac {1}{4}}right)^{2}}=4{sqrt {tfrac {2}{pi }}}left({tfrac {1}{4}}!right)^{2}} | 4 sqrt(2/pi) ((1/4)!)^2 |
T | A062539 | [2;1,1,1,1,1,4,1,2,5,1,1,1,14,9,2,6,2,9,4,1,...] | 1798 | 2.62205755429211981046483958989111941 |
| 0,83462 68416 74073 18628 | Constante de Gauss | G {displaystyle {G}} | 1 a g m ( 1 , 2 ) = 4 2 ( 1 4 ! ) 2 π 3 / 2 a g m : M e d i a a r i t m e ´ t i c a − g e o m e ´ t r i c a {displaystyle {underset {agm:;Media;aritm{acute {e}}tica-geom{acute {e}}trica}{{frac {1}{mathrm {agm} (1,{sqrt {2}})}}={frac {4{sqrt {2}},({tfrac {1}{4}}!)^{2}}{pi ^{3/2}}}}}} | (4 sqrt(2) ((1/4)!)^2) /pi^(3/2) |
T | A014549 | [0;1,5,21,3,4,14,1,1,1,1,1,3,1,15,1,3,7,1,...] | 1799 | 0.83462684167407318628142973279904680 | |
| 0,00787 49969 97812 3844 | Constante de Chaitin | 
|
Ω {displaystyle {Omega }} |
∑
p
∈
P
2
−
|
p
|
|
p
|
:
T
a
m
a
n
~
o
d
e
l
p
r
o
g
r
a
m
a
P
:
C
o
n
j
u
n
t
o
d
e
t
o
d
o
s
l
o
s
p
r
o
g
r
a
m
a
s
q
u
e
s
e
p
a
r
a
n
.
p
:
P
r
o
g
r
a
m
a
q
u
e
s
e
p
a
r
a
{displaystyle sum _{pin P}2^{-|p|}{overset {p:;{Programa;que;se;para}}{underset {P:;Conjunto;de;todos;los;programas;que;se;paran.}{scriptstyle {|p|}:;Tama{tilde {n}}o;del;programa}}}}
Ver también: Problema de la parada |
T | A100264 | [0; 126, 1, 62, 5, 5, 3, 3, 21, 1, 4, 1] | 1975 | 0.0078749969978123844 | |
| 2,80777 02420 28519 36522 | Constante Fransén–Robinson | F {displaystyle {F}} | ∫ 0 ∞ 1 Γ ( x ) d x . = e + ∫ 0 ∞ e − x π 2 + ln 2 x d x {displaystyle int _{0}^{infty }{frac {1}{Gamma (x)}},dx.=e+int _{0}^{infty }{frac {e^{-x}}{pi ^{2}+ln ^{2}x}},dx} | N[int[0 to ∞] {1/Gamma(x)}] |
A058655 | [2;1,4,4,1,18,5,1,3,4,1,5,3,6,1,1,1,5,1,1,1...] | 1978 | 2.80777024202851936522150118655777293 | ||
| 1,01734 30619 84449 13971 | Zeta(6) | 
|
ζ ( 6 ) {displaystyle zeta (6)} |
π
6
945
=
∏
n
=
1
∞
1
1
−
p
n
−
6
p
n
:
p
r
i
m
o
=
1
1
−
2
−
6
⋅
1
1
−
3
−
6
⋅
1
1
−
5
−
6
.
.
.
{displaystyle {frac {pi ^{6}}{945}}=prod _{n=1}^{infty }{underset {p_{n}:,{primo}}{frac {1}{{1-p_{n}}^{-6}}}}={frac {1}{1{-}2^{-6}}}{cdot }{frac {1}{1{-}3^{-6}}}{cdot }{frac {1}{1{-}5^{-6}}}...}
= ∑ n = 1 ∞ 1 n 6 = 1 1 6 + 1 2 6 + 1 3 6 + 1 4 6 + 1 5 6 + . . . {displaystyle textstyle =sum _{n=1}^{infty }{frac {1}{n^{6}}}={frac {1}{1^{6}}}+{frac {1}{2^{6}}}+{frac {1}{3^{6}}}+{frac {1}{4^{6}}}+{frac {1}{5^{6}}}+...} |
Prod[n=1 to ∞] {1/(1 -prime(n)^-6)} |
T | A013664 | [1;57,1,1,1,15,1,6,3,61,1,5,3,1,6,1,3,3,6,1,...] | 1.01734306198444913971451792979092052 | |
| 1,64872 12707 00128 14684 | Raíz cuadrada del número e | e {displaystyle {sqrt {e}}} | ∑ n = 0 ∞ 1 2 n n ! = ∑ n = 0 ∞ 1 ( 2 n ) ! ! = 1 1 + 1 2 + 1 8 + 1 48 + ⋯ {displaystyle sum _{n=0}^{infty }{frac {1}{2^{n}n!}}=sum _{n=0}^{infty }{frac {1}{(2n)!!}}={frac {1}{1}}+{frac {1}{2}}+{frac {1}{8}}+{frac {1}{48}}+cdots } | sum[n=0 to ∞] {1/(2^n n!)} |
T | A019774 | [1;1,1,1,5,1,1,9,1,1,13,1,1,17,1,1,21,1,1,...] = [1;1,1,1,4p+1], p∈ℕ |
1.64872127070012814684865078781416357 | ||
| i... | Número imaginario | 
|
i {displaystyle {i}} | − 1 = ln ( − 1 ) π e i π = − 1 {displaystyle {sqrt {-1}}={frac {ln(-1)}{pi }}qquad qquad mathrm {e} ^{i,pi }=-1} | sqrt(-1) | CI | 1501 à 1576 |
i | ||
| 4,81047 73809 65351 65547 | Constante de John | γ {displaystyle gamma } | i i = i − i = i 1 i = ( i i ) − 1 = e π 2 {displaystyle {sqrt[{i}]{i}}=i^{-i}=i^{frac {1}{i}}=(i^{i})^{-1}=e^{frac {pi }{2}}} | e^(π/2) | T | A042972 | [4;1,4,3,1,1,1,1,1,1,1,1,7,1,20,1,3,6,10,3,...] | 4.81047738096535165547303566670383313 | ||
| 0.49801 56681 18356 04271 0.15494 98283 01810 68512 i |
Factorial de i | i ! {displaystyle {i},!} | Γ ( 1 + i ) = i Γ ( i ) = ∫ 0 ∞ t i e t d t {displaystyle Gamma (1+i)=i,Gamma (i)=int limits _{0}^{infty }{frac {t^{i}}{e^{t}}}mathrm {d} t} | Gamma(1+i) | C | A212877 A212878 |
[0;6,2,4,1,8,1,46,2,2,3,5,1,10,7,5,1,7,2,...] - [0;2,125,2,18,1,2,1,1,19,1,1,1,2,3,34,...] i |
0.49801566811835604271369111746219809 - 0.15494982830181068512495513048388 i | ||
| 0,43828 29367 27032 11162 0,36059 24718 71385 485 i |
Tetración infinita de i | ∞ i {displaystyle {}^{infty }{i}} | lim n → ∞ n i = lim n → ∞ i i ⋅ ⋅ i ⏟ n {displaystyle lim _{nto infty }{}^{n}i=lim _{nto infty }underbrace {i^{i^{cdot ^{cdot ^{i}}}}} _{n}} | i^i^i^... | C | A077589 A077590 |
[0;2,3,1,1,4,2,2,1,10,2,1,3,1,8,2,1,2,1,...] + [0;2,1,3,2,2,3,1,5,5,1,2,1,10,10,6,1,1...] i |
0.43828293672703211162697516355126482 + 0.36059247187138548595294052690600 i | ||
| 0,56755 51633 06957 82538 | Módulo de la Tetración infinita de i |
| ∞ i | {displaystyle |{}^{infty }{i}|} | lim n → ∞ | n i | = | lim n → ∞ i i ⋅ ⋅ i ⏟ n | {displaystyle lim _{nto infty }left|{}^{n}iright|=left|lim _{nto infty }underbrace {i^{i^{cdot ^{cdot ^{i}}}}} _{n}right|} | Mod(i^i^i^...) | A212479 | [0;1,1,3,4,1,58,12,1,51,1,4,12,1,1,2,2,3,...] | 0.56755516330695782538461314419245334 | |||
| 0,26149 72128 47642 78375 | Constante de Meissel-Mertens | 
|
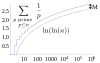
M {displaystyle {M}} | lim n → ∞ ( ∑ p ≤ n 1 p − ln ( ln ( n ) ) ) = γ + ∑ p ( ln ( 1 − 1 p ) + 1 p ) γ : Constante de Euler , p : primo {displaystyle lim _{nrightarrow infty }!!left(sum _{pleq n}{frac {1}{p}}!-ln(ln(n))!right)!!={underset {!!!!gamma:,{text{Constante de Euler}},,,p:,{text{primo}}}{!gamma !+!!sum _{p}!left(!ln !left(!1!-!{frac {1}{p}}!right)!!+!{frac {1}{p}}!right)}}} | gamma+ Sum[n=1 to ∞] {ln(1-1/prime(n)) +1/prime(n)} |
A077761 | [0;3,1,4,1,2,5,2,1,1,1,1,13,4,2,4,2,1,33,296,...] | 1866 y 1873 |
0.26149721284764278375542683860869585 | |
| 1,92878 00... | Constante de Wright | ω {displaystyle {omega }} | ⌊ 2 2 2 ⋅ ⋅ 2 ω ⌋ {displaystyle leftlfloor 2^{2^{2^{cdot ^{cdot ^{2^{omega }}}}}}rightrfloor } = primos: {displaystyle quad } ⌊ 2 ω ⌋ {displaystyle leftlfloor 2^{omega }rightrfloor } =3, ⌊ 2 2 ω ⌋ {displaystyle leftlfloor 2^{2^{omega }}rightrfloor } =13, ⌊ 2 2 2 ω ⌋ {displaystyle leftlfloor 2^{2^{2^{omega }}}rightrfloor } =16381, … {displaystyle dots } | A086238 | [1; 1, 13, 24, 2, 1, 1, 3, 1, 1, 3] | 1.9287800.. | ||||
| 0,37395 58136 19202 28805 | Constante de Artin | C A r t i n {displaystyle {C}_{Artin}} | ∏ n = 1 ∞ ( 1 − 1 p n ( p n − 1 ) ) p n = primos {displaystyle prod _{n=1}^{infty }left(1-{frac {1}{p_{n}(p_{n}-1)}}right)quad p_{n}scriptstyle {text{ = primos}}} | Prod[n=1 to ∞] {1-1/(prime(n) (prime(n)-1))} |
A005596 | [0;2,1,2,14,1,1,2,3,5,1,3,1,5,1,1,2,3,5,46,...] | 1999 | 0.37395581361920228805472805434641641 | ||
| 4,66920 16091 02990 67185 | Constante δ de Feigenbaum δ | 
|
δ {displaystyle {delta }} |
lim
n
→
∞
x
n
+
1
−
x
n
x
n
+
2
−
x
n
+
1
x
∈
(
3
,
8284
;
3
,
8495
)
{displaystyle lim _{nto infty }{frac {x_{n+1}-x_{n}}{x_{n+2}-x_{n+1}}}qquad scriptstyle xin (3,8284;,3,8495)}
x n + 1 = a x n ( 1 − x n ) o x n + 1 = a sin ( x n ) {displaystyle scriptstyle x_{n+1}=,ax_{n}(1-x_{n})quad {o}quad x_{n+1}=,asin(x_{n})} |
A006890 | [4;1,2,43,2,163,2,3,1,1,2,5,1,2,3,80,2,5,...] | 1975 | 4.66920160910299067185320382046620161 | ||
| 2,50290 78750 95892 82228 | Constante α de Feigenbaum | 
|
α {displaystyle alpha } | lim n → ∞ d n d n + 1 {displaystyle lim _{nto infty }{frac {d_{n}}{d_{n+1}}}} | A006891 | [2;1,1,85,2,8,1,10,16,3,8,9,2,1,40,1,2,3,...] | 1979 | 2.50290787509589282228390287321821578 | ||
| 5,97798 68121 78349 12266 | Constante hexagonal Madelung 2 | H 2 ( 2 ) {displaystyle {H}_{2}(2)} | π ln ( 3 ) 3 {displaystyle pi ln(3){sqrt {3}}} | Pi Log[3]Sqrt[3] | A086055 | [5;1,44,2,2,1,15,1,1,12,1,65,11,1,3,1,1,...] | 5.97798681217834912266905331933922774 | |||
| 0,96894 61462 59369 38048 | Constante Beta(3) | β ( 3 ) {displaystyle {beta }(3)} | π 3 32 = ∑ n = 1 ∞ − 1 n + 1 ( − 1 + 2 n ) 3 = 1 1 3 − 1 3 3 + 1 5 3 − 1 7 3 + . . . {displaystyle {frac {pi ^{3}}{32}}=sum _{n=1}^{infty }{frac {-1^{n+1}}{(-1+2n)^{3}}}={frac {1}{1^{3}}}{-}{frac {1}{3^{3}}}{+}{frac {1}{5^{3}}}{-}{frac {1}{7^{3}}}{+}...} | Sum[n=1 to ∞] {(-1)^(n+1) /(-1+2n)^3} |
T | A153071 | [0;1,31,4,1,18,21,1,1,2,1,2,1,3,6,3,28,1,...] | 0.96894614625936938048363484584691860 | ||
| 1,90216 05831 04 | Constante de Brun 2 = Σ inverso primos gemelos |
|
B 2 {displaystyle {B}_{,2}} | ∑ ( 1 p + 1 p + 2 ) p , p + 2 : p r i m o s = ( 1 3 + 1 5 ) + ( 1 5 + 1 7 ) + ( 1 11 + 1 13 ) + . . . {displaystyle textstyle {underset {p,,p+2:,{primos}}{sum ({frac {1}{p}}+{frac {1}{p+2}})}}=({frac {1}{3}}{+}{frac {1}{5}})+({tfrac {1}{5}}{+}{tfrac {1}{7}})+({tfrac {1}{11}}{+}{tfrac {1}{13}})+...} | N[prod[n=2 to 0,870∞] [1-1/(prime(n) -1)^2]] |
A065421 | [1; 1, 9, 4, 1, 1, 8, 3, 4, 4, 2, 2] | 1919 | 1.902160583104 | |
| 0,87058 83799 75 | Constante de Brun 4 = Σ inverso primos gemelos |
B 4 {displaystyle {B}_{,4}} | ( 1 5 + 1 7 + 1 11 + 1 13 ) p , p + 2 , p + 6 , p + 8 : p r i m o s + ( 1 11 + 1 13 + 1 17 + 1 19 ) + … {displaystyle {underset {p,,p+2,,p+6,,p+8:,{primos}}{left({tfrac {1}{5}}+{tfrac {1}{7}}+{tfrac {1}{11}}+{tfrac {1}{13}}right)}}+left({tfrac {1}{11}}+{tfrac {1}{13}}+{tfrac {1}{17}}+{tfrac {1}{19}}right)+dots } | A213007 | [0; 1, 6, 1, 2, 1, 2, 956, 3, 1, 1] | 1919 | 0.87058837997 | |||
| 22,45915 77183 61045 47342 | pi^e | π e {displaystyle pi ^{e}} | π e {displaystyle pi ^{e}} | pi^e | A059850 | [22;2,5,1,1,1,1,1,3,2,1,1,3,9,15,25,1,1,5,...] | 22.4591577183610454734271522045437350 | |||
| 3,14159 26535 89793 23846 | Número π, constante de Arquímedes · | 
|
π {displaystyle {pi }} | lim n → ∞ 2 n 2 − 2 + 2 + ... + 2 ⏟ n {displaystyle lim _{nto infty },2^{n}underbrace {sqrt {2-{sqrt {2+{sqrt {2+{text{...}}+{sqrt {2}}}}}}}} _{n}} | Sum[n=0 to ∞] {(-1)^n 4/(2n+1)} |
T | A000796 | [3;7,15,1,292,1,1,1,2,1,3,1,14,2,1,1,2,2,2,...] | -250 ~ | 3.14159265358979323846264338327950288 |
| 0,28878 80950 86602 42127 | Flajolet and Richmond | Q {displaystyle {Q}} | ∏ n = 1 ∞ ( 1 − 1 2 n ) = ( 1 − 1 2 1 ) ( 1 − 1 2 2 ) ( 1 − 1 2 3 ) . . . {displaystyle prod _{n=1}^{infty }left(1-{frac {1}{2^{n}}}right)=left(1{-}{frac {1}{2^{1}}}right)left(1{-}{frac {1}{2^{2}}}right)left(1{-}{frac {1}{2^{3}}}right)...} | prod[n=1 to ∞] {1-1/2^n} |
A048651 | [0;3,2,6,4,1,2,1,9,2,1,2,3,2,3,5,1,2,1,1,6,1,...] | 1992 | 0.28878809508660242127889972192923078 | ||
| 0,06598 80358 45312 53707 | Límite inferior de Tetración | 
|
e − e {displaystyle {e}^{-e}} | ( 1 e ) e {displaystyle left({frac {1}{e}}right)^{e}} | 1/(e^e) | A073230 | [0;15,6,2,13,1,3,6,2,1,1,5,1,1,1,9,4,1,1,1,...] | 0.06598803584531253707679018759684642 | ||
| 0,31830 98861 83790 67153 | Inverso de Pi, Ramanujan | 1 π {displaystyle {frac {1}{pi }}} | 2 2 9801 ∑ n = 0 ∞ ( 4 n ) ! ( 1103 + 26390 n ) ( n ! ) 4 396 4 n {displaystyle {frac {2{sqrt {2}}}{9801}}sum _{n=0}^{infty }{frac {(4n)!,(1103+26390;n)}{(n!)^{4},396^{4n}}}} | 2 sqrt(2)/9801 *Sum[n=0 to ∞] {((4n)!/n!^4)*(1103+ 26390n)/396^(4n)} |
T | A049541 | [0;3,7,15,292,1,1,1,2,1,3,1,14,2,1,1,2,2,2,...] | 0.31830988618379067153776752674502872 | ||
| 0,63661 97723 67581 34307
|
Constante de Buffon |  Aguja interseca línea
|
2 π {displaystyle {frac {2}{pi }}} |
2
2
⋅
2
+
2
2
⋅
2
+
2
+
2
2
⋯
{displaystyle {frac {sqrt {2}}{2}}cdot {frac {sqrt {2+{sqrt {2}}}}{2}}cdot {frac {sqrt {2+{sqrt {2+{sqrt {2}}}}}}{2}}cdots }
Producto de François Viète |
2/Pi | T | A060294 | [0;1,1,1,3,31,1,145,1,4,2,8,1,6,1,2,3,1,4,...] | 1540 a 1603 |
0.63661977236758134307553505349005745 |
| 0,47494 93799 87920 65033 | Constante de Weierstrass | σ ( 1 2 ) {displaystyle sigma ({tfrac {1}{2}})} | e π 8 π 4 ∗ 2 3 / 4 ( 1 4 ! ) 2 {displaystyle {frac {e^{frac {pi }{8}}{sqrt {pi }}}{4*2^{3/4}{({frac {1}{4}}!)^{2}}}}} | (E^(Pi/8) Sqrt[Pi]) /(4 2^(3/4) (1/4)!^2) |
A094692 | [0;2,9,2,11,1,6,1,4,6,3,19,9,217,1,2,4,8,6...] | 1872 ? | 0.47494937998792065033250463632798297 | ||
| 0,57721 56649 01532 86060 | Constante de Euler-Mascheroni | 
|
γ {displaystyle {gamma }} | ∑ n = 1 ∞ ∑ k = 0 ∞ ( − 1 ) k 2 n + k = ∑ n = 1 ∞ 1 n − ln ( n ) = ∫ 0 1 − ln ( ln 1 x ) d x {displaystyle sum _{n=1}^{infty }sum _{k=0}^{infty }{frac {(-1)^{k}}{2^{n}+k}}!=!sum _{n=1}^{infty }{frac {1}{n}}-ln(n)!=!!int _{0}^{1}!!-ln(ln {frac {1}{x}}),dx} | sum[n=1 to ∞] |sum[k=0 to ∞] {((-1)^k)/(2^n+k)} |
A001620 | [0;1,1,2,1,2,1,4,3,13,5,1,1,8,1,2,4,1,1,40,1,...] | 1735 | 0.57721566490153286060651209008240243 | |
| 1,70521 11401 05367 76428 | Constante de Niven | C {displaystyle {C}} | 1 + ∑ n = 2 ∞ ( 1 − 1 ζ ( n ) ) {displaystyle 1+sum _{n=2}^{infty }left(1-{frac {1}{zeta (n)}}right)} | 1+ Sum[n=2 to ∞] {1-(1/Zeta(n))} |
A033150 | [1;1,2,2,1,1,4,1,1,3,4,4,8,4,1,1,2,1,1,11,1,...] | 1969 | 1.70521114010536776428855145343450816 | ||
| 0,60459 97880 78072 61686 | Relación entre el área de un triángulo equilátero y su círculo inscrito. | 
|
π 3 3 {displaystyle {frac {pi }{3{sqrt {3}}}}} | ∑ n = 1 ∞ 1 n ( 2 n n ) = 1 − 1 2 + 1 4 − 1 5 + 1 7 − 1 8 + ⋯ {displaystyle sum _{n=1}^{infty }{frac {1}{n{2n choose n}}}=1-{frac {1}{2}}+{frac {1}{4}}-{frac {1}{5}}+{frac {1}{7}}-{frac {1}{8}}+cdots } Serie de Dirichlet | Sum[1/(n Binomial[2 n, n]) , {n, 1, ∞}] |
T | A073010 | [0;1,1,1,1,8,10,2,2,3,3,1,9,2,5,4,1,27,27,6,6,...] | 0.60459978807807261686469275254738524 | |
| 3,24697 96037 17467 06105 | Constante Silver de Tutte–Beraha | ς {displaystyle varsigma } | 2 + 2 cos 2 π 7 = 2 + 2 + 7 + 7 7 + 7 7 + ⋯ 3 3 3 1 + 7 + 7 7 + 7 7 + ⋯ 3 3 3 {displaystyle 2+2cos {frac {2pi }{7}}=textstyle 2+{frac {2+{sqrt[{3}]{7+7{sqrt[{3}]{7+7{sqrt[{3}]{,7+cdots }}}}}}}{1+{sqrt[{3}]{7+7{sqrt[{3}]{7+7{sqrt[{3}]{,7+cdots }}}}}}}}} | 2+2 cos(2Pi/7) | A | A116425 | [3;4,20,2,3,1,6,10,5,2,2,1,2,2,1,18,1,1,3,2,...] | 3.24697960371746706105000976800847962 | ||
| 0,69314 71805 59945 30941 | Logaritmo natural de 2 | 
|
L n ( 2 ) {displaystyle Ln(2)} | ∑ n = 1 ∞ 1 n 2 n = ∑ n = 1 ∞ ( − 1 ) n + 1 n = 1 1 − 1 2 + 1 3 − 1 4 + ⋯ {displaystyle sum _{n=1}^{infty }{frac {1}{n2^{n}}}=sum _{n=1}^{infty }{frac {({-}1)^{n+1}}{n}}={frac {1}{1}}-{frac {1}{2}}+{frac {1}{3}}-{frac {1}{4}}+{cdots }} | Sum[n=1 to ∞] {(-1)^(n+1)/n} |
T | A002162 | [0;1,2,3,1,6,3,1,1,2,1,1,1,1,3,10,1,1,1,2,1,1,...] | 1550 a 1617 |
0.69314718055994530941723212145817657 |
| 0,66016 18158 46869 57392 | Constante de los primos gemelos | C 2 {displaystyle {C}_{2}} | ∏ p = 3 ∞ p ( p − 2 ) ( p − 1 ) 2 {displaystyle prod _{p=3}^{infty }{frac {p(p-2)}{(p-1)^{2}}}} | prod[p=3 to ∞] {p(p-2)/(p-1)^2 |
A005597 | [0;1,1,1,16,2,2,2,2,1,18,2,2,11,1,1,2,4,1,...] | 1922 | 0.66016181584686957392781211001455577 | ||
| 0,66274 34193 49181 58097 | Constante límite de Laplace | 
|
λ {displaystyle {lambda }} | x e x 2 + 1 x 2 + 1 + 1 = 1 {displaystyle {frac {x;e^{sqrt {x^{2}+1}}}{{sqrt {x^{2}+1}}+1}}=1} | (x e^sqrt(x^2+1)) /(sqrt(x^2+1)+1) = 1 |
A033259 | [0;1,1,1,27,1,1,1,8,2,154,2,4,1,5,1,1,2,1601,...] | 1782 ~ | 0.66274341934918158097474209710925290 | |
| 0,28016 94990 23869 13303 | Constante de Bernstein | β {displaystyle {beta }} | 1 2 π {displaystyle {frac {1}{2{sqrt {pi }}}}} | 1/(2 sqrt(pi)) | T | A073001 | [0;3,1,1,3,9,6,3,1,3,14,34,2,1,1,60,2,2,1,1,...] | 1913 | 0.28016949902386913303643649123067200 | |
| 0,78343 05107 12134 40705 | Sophomore's Dream 1 Johann Bernoulli |
|
I 1 {displaystyle {I}_{1}} | ∫ 0 1 x − x d x = ∑ n = 1 ∞ ( − 1 ) n + 1 n n = 1 1 1 − 1 2 2 + 1 3 3 − ⋯ {displaystyle int _{0}^{1}!x^{-x},dx=sum _{n=1}^{infty }{frac {(-1)^{n+1}}{n^{n}}}={frac {1}{1^{1}}}-{frac {1}{2^{2}}}+{frac {1}{3^{3}}}-{cdots }} | Sum[n=1 to ∞] {-(-1)^n /n^n} |
A083648 | [0;1,3,1,1,1,1,1,1,2,4,7,2,1,2,1,1,1,2,1,14,...] | 1697 | 0.78343051071213440705926438652697546 | |
| 1,29128 59970 62663 54040 | Sophomore's Dream 2 Johann Bernoulli | 
|
I 2 {displaystyle {I}_{2}} | ∫ 0 1 1 x x d x = ∑ n = 1 ∞ 1 n n = 1 1 1 + 1 2 2 + 1 3 3 + 1 4 4 + ⋯ {displaystyle int _{0}^{1}!{frac {1}{x^{x}}},dx=sum _{n=1}^{infty }{frac {1}{n^{n}}}={frac {1}{1^{1}}}+{frac {1}{2^{2}}}+{frac {1}{3^{3}}}+{frac {1}{4^{4}}}+cdots } | Sum[n=1 to ∞] {1/(n^n)} |
A073009 | [1;3,2,3,4,3,1,2,1,1,6,7,2,5,3,1,2,1,8,1,2,4,...] | 1697 | 1.29128599706266354040728259059560054 | |
| 0,82246 70334 24113 21823 | Constante Nielsen-Ramanujan | ζ ( 2 ) 2 {displaystyle {frac {{zeta }(2)}{2}}} | π 2 12 = ∑ n = 1 ∞ ( − 1 ) n + 1 n 2 = 1 1 2 − 1 2 2 + 1 3 2 − 1 4 2 + 1 5 2 − . . . {displaystyle {frac {pi ^{2}}{12}}=sum _{n=1}^{infty }{frac {(-1)^{n+1}}{n^{2}}}={frac {1}{1^{2}}}{-}{frac {1}{2^{2}}}{+}{frac {1}{3^{2}}}{-}{frac {1}{4^{2}}}{+}{frac {1}{5^{2}}}{-}...} | Sum[n=1 to ∞] {((-1)^(n+1))/n^2} |
T | A072691 | [0;1,4,1,1,1,2,1,1,1,1,3,2,2,4,1,1,1,1,1,1,4...] | 1909 | 0.82246703342411321823620758332301259 | |
| 0,78539 81633 97448 30961 | Beta(1) | 
|
β ( 1 ) {displaystyle {beta }(1)} | π 4 = ∑ n = 0 ∞ ( − 1 ) n 2 n + 1 = 1 1 − 1 3 + 1 5 − 1 7 + 1 9 − ⋯ {displaystyle {frac {pi }{4}}=sum _{n=0}^{infty }{frac {(-1)^{n}}{2n+1}}={frac {1}{1}}-{frac {1}{3}}+{frac {1}{5}}-{frac {1}{7}}+{frac {1}{9}}-cdots } | Sum[n=0 to ∞] {(-1)^n/(2n+1)} |
T | A003881 | [0; 1,3,1,1,1,15,2,72,1,9,1,17,1,2,1,5,...] | 1805 a 1859 |
0.78539816339744830961566084581987572 |
| 0,91596 55941 77219 01505 | Constante de Catalan | C {displaystyle {C}} | ∫ 0 1 ∫ 0 1 1 1 + x 2 y 2 d x d y = ∑ n = 0 ∞ ( − 1 ) n ( 2 n + 1 ) 2 = 1 1 2 − 1 3 2 + ⋯ {displaystyle int _{0}^{1}!!int _{0}^{1}!!{frac {1}{1{+}x^{2}y^{2}}},dx,dy=!sum _{n=0}^{infty }!{frac {(-1)^{n}}{(2n{+}1)^{2}}}!=!{frac {1}{1^{2}}}{-}{frac {1}{3^{2}}}{+}{cdots }} | Sum[n=0 to ∞] {(-1)^n/(2n+1)^2} |
T ? | A006752 | [0;1,10,1,8,1,88,4,1,1,7,22,1,2,3,26,1,11,...] | 1864 | 0.91596559417721901505460351493238411 | |
| 1,05946 30943 59295 26456 | Intervalo entre semitonos de la escala musical | 
|
2 12 {displaystyle {sqrt[{12}]{2}}} |
440
H
z
.
2
1
12
2
2
12
2
3
12
2
4
12
2
5
12
2
6
12
2
7
12
2
8
12
2
9
12
2
10
12
2
11
12
2
{displaystyle scriptstyle 440,Hz.textstyle 2^{frac {1}{12}},2^{frac {2}{12}},2^{frac {3}{12}},2^{frac {4}{12}},2^{frac {5}{12}},2^{frac {6}{12}},2^{frac {7}{12}},2^{frac {8}{12}},2^{frac {9}{12}},2^{frac {10}{12}},2^{frac {11}{12}},2}
. . . D o 1 D o # R e R e # M i F a F a # S o l S o l # L a L a # S i D o 2 {displaystyle scriptstyle {color {white}...color {black}Do_{1};;Do#;,Re;,Re#;,Mi;;Fa;;Fa#;Sol;,Sol#,La;;La#;;Si;,Do_{2}}} . . . . C 1 C # D D # E F F # G G # A A # B C 2 {displaystyle scriptstyle {color {white}....color {black}C_{1};;;;C#;;;,D;;;D#;;,E;;;;,F;;;,F#;;;G;;;;G#;;;A;;;,A#;;;,B;;;C_{2}}} |
2^(1/12) | A | A010774 | [1;16,1,4,2,7,1,1,2,2,7,4,1,2,1,60,1,3,1,2,...] | 1.05946309435929526456182529494634170 | |
| 1,13198 82487 943 | Constante de Viswanath | C V i {displaystyle {C}_{Vi}} | lim n → ∞ | a n | 1 n {displaystyle lim _{nto infty }|a_{n}|^{frac {1}{n}}} donde an = Sucesión de Fibonacci | lim_(n->∞) |a_n|^(1/n) |
T ? | A078416 | [1;7,1,1,2,1,3,2,1,2,1,8,1,5,1,1,1,9,1,...] | 1997 | 1.1319882487943... | |
| 1,20205 69031 59594 28539 | Constante de Apéry | 
|
ζ ( 3 ) {displaystyle zeta (3)} |
∑
n
=
1
∞
1
n
3
=
1
1
3
+
1
2
3
+
1
3
3
+
1
4
3
+
1
5
3
+
⋯
=
{displaystyle sum _{n=1}^{infty }{frac {1}{n^{3}}}={frac {1}{1^{3}}}+{frac {1}{2^{3}}}+{frac {1}{3^{3}}}+{frac {1}{4^{3}}}+{frac {1}{5^{3}}}+cdots =}
1 2 ∑ n = 1 ∞ H n n 2 = 1 2 ∑ i = 1 ∞ ∑ j = 1 ∞ 1 i j ( i + j ) = ∫ 0 1 ∫ 0 1 ∫ 0 1 d x d y d z 1 − x y z {displaystyle {frac {1}{2}}sum _{n=1}^{infty }{frac {H_{n}}{n^{2}}}={frac {1}{2}}sum _{i=1}^{infty }sum _{j=1}^{infty }{frac {1}{ij(i{+}j)}}=!!int limits _{0}^{1}!!int limits _{0}^{1}!!int limits _{0}^{1}{frac {mathrm {d} xmathrm {d} ymathrm {d} z}{1-xyz}}} |
Sum[n=1 to ∞] {1/n^3} |
I | A010774 | [1;4,1,18,1,1,1,4,1,9,9,2,1,1,1,2,7,1,1,7,11,...] | 1979 | 1.20205690315959428539973816151144999 |
| 1,22541 67024 65177 64512 | Gamma(3/4) | Γ ( 3 4 ) {displaystyle Gamma ({tfrac {3}{4}})} | ( − 1 + 3 4 ) ! = ( − 1 4 ) ! {displaystyle left(-1+{frac {3}{4}}right)!=left(-{frac {1}{4}}right)!} | (-1+3/4)! | A068465 | [1;4,2,3,2,2,1,1,1,2,1,4,7,1,171,3,2,3,1,1,8,...] | 1.22541670246517764512909830336289053 | |||
| 1,25992 10498 94873 16476 | Raíz cúbica de dos, constante Delian | 
|
2 3 {displaystyle {sqrt[{3}]{2}}} | 2 3 {displaystyle {sqrt[{3}]{2}}} | 2^(1/3) | A | A002580 | [1;3,1,5,1,1,4,1,1,8,1,14,1,10,2,1,4,12,2,3,...] | 1.25992104989487316476721060727822835 | |
| 9,86960 44010 89358 61883 | Pi al Cuadrado | π 2 {displaystyle {pi }^{2}} | 6 ζ ( 2 ) = 6 ∑ n = 1 ∞ 1 n 2 = 6 1 2 + 6 2 2 + 6 3 2 + 6 4 2 + ⋯ {displaystyle 6zeta (2)=6sum _{n=1}^{infty }{frac {1}{n^{2}}}={frac {6}{1^{2}}}+{frac {6}{2^{2}}}+{frac {6}{3^{2}}}+{frac {6}{4^{2}}}+cdots } | 6 Sum[n=1 to ∞] {1/n^2} |
T | A002388 | [9;1,6,1,2,47,1,8,1,1,2,2,1,1,8,3,1,10,5,...] | 9.86960440108935861883449099987615114 | ||
| 1,41421 35623 73095 04880 | Raíz cuadrada de 2, constante de Pitágoras | 
|
2 {displaystyle {sqrt {2}}} | ∏ n = 1 ∞ 1 + ( − 1 ) n + 1 2 n − 1 = ( 1 + 1 1 ) ( 1 − 1 3 ) ( 1 + 1 5 ) ⋯ {displaystyle prod _{n=1}^{infty }1+{frac {(-1)^{n+1}}{2n-1}}=left(1{+}{frac {1}{1}}right)left(1{-}{frac {1}{3}}right)left(1{+}{frac {1}{5}}right)cdots } | prod[n=1 to ∞] {1+(-1)^(n+1) /(2n-1)} |
A | A002193 | [1;2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,...] = [1;2...] |
< -800 | 1.41421356237309504880168872420969808 |
| 262 53741 26407 68743 99999 99999 99250 073 |
Constante de Hermite-Ramanujan | R {displaystyle {R}} | e π 163 {displaystyle e^{pi {sqrt {163}}}} | e^(π sqrt(163)) | T | A060295 | [262537412640768743;1,1333462407511,1,8,1,1,5,...] | 1859 | 262537412640768743.999999999999250073 | |
| 0,76159 41559 55764 88811 | Tangente hiperbólica de 1 | 
|
t h 1 {displaystyle {th},1} | − i tan ( i ) = e − 1 e e + 1 e = e 2 − 1 e 2 + 1 {displaystyle -itan(i)={frac {e-{frac {1}{e}}}{e+{frac {1}{e}}}}={frac {e^{2}-1}{e^{2}+1}}} | (e-1/e)/(e+1/e) | T | A073744 | [0;1,3,5,7,9,11,13,15,17,19,21,23,25,27,...] = [0;2p+1], p∈ℕ |
0.76159415595576488811945828260479359 | |
| 0,36787 94411 71442 32159 | Inverso del Número e | 1 e {displaystyle {frac {1}{e}}} | ∑ n = 0 ∞ ( − 1 ) n n ! = 1 0 ! − 1 1 ! + 1 2 ! − 1 3 ! + 1 4 ! − 1 5 ! + ⋯ {displaystyle sum _{n=0}^{infty }{frac {(-1)^{n}}{n!}}={frac {1}{0!}}-{frac {1}{1!}}+{frac {1}{2!}}-{frac {1}{3!}}+{frac {1}{4!}}-{frac {1}{5!}}+cdots } | sum[n=2 to ∞] {(-1)^n/n!} |
T | A068985 | [0;2,1,1,2,1,1,4,1,1,6,1,1,8,1,1,10,1,1,12,...] = [0;2,1,1,2p,1], p∈ℕ |
1618 | 0.36787944117144232159552377016146086 | |
| 1,53960 07178 39002 03869 | Constante Square Ice de Lieb | 
|
W 2 D {displaystyle {W}_{2D}} | lim n → ∞ ( f ( n ) ) n − 2 = ( 4 3 ) 3 2 = 8 3 9 {displaystyle lim _{nto infty }(f(n))^{n^{-2}}=left({frac {4}{3}}right)^{frac {3}{2}}={frac {8{sqrt {3}}}{9}}} | (4/3)^(3/2) | A | A118273 | [1;1,1,5,1,4,2,1,6,1,6,1,2,4,1,5,1,1,2,...] | 1967 | 1.53960071783900203869106341467188655 |
| 1,23370 05501 36169 82735 | Constante de Favard | 3 4 ζ ( 2 ) {displaystyle {tfrac {3}{4}}zeta (2)} | π 2 8 = ∑ n = 0 ∞ 1 ( 2 n − 1 ) 2 = 1 1 2 + 1 3 2 + 1 5 2 + 1 7 2 + ⋯ {displaystyle {frac {pi ^{2}}{8}}=sum _{n=0}^{infty }{frac {1}{(2n-1)^{2}}}={frac {1}{1^{2}}}+{frac {1}{3^{2}}}+{frac {1}{5^{2}}}+{frac {1}{7^{2}}}+cdots } | sum[n=1 to ∞] {1/((2n-1)^2)} |
T | A111003 | [1;4,3,1,1,2,2,5,1,1,1,1,2,1,2,1,10,4,3,1,1,...] | 1902 a 1965 |
1.23370055013616982735431137498451889 | |
| 7,38905 60989 30650 22723 | Constante cónica de Schwarzschild | 
|
e 2 {displaystyle e^{2}} | ∑ n = 0 ∞ 2 n n ! = 1 + 2 + 2 2 2 ! + 2 3 3 ! + 2 4 4 ! + 2 5 5 ! + . . . {displaystyle sum _{n=0}^{infty }{frac {2^{n}}{n!}}=1+2+{frac {2^{2}}{2!}}+{frac {2^{3}}{3!}}+{frac {2^{4}}{4!}}+{frac {2^{5}}{5!}}+...} | Sum[n=0 to ∞] {2^n/n!} |
T | A072334 | [7;2,1,1,3,18,5,1,1,6,30,8,1,1,9,42,11,1,...] = [7,2,1,1,n,4*n+6,n+2], n = 3, 6, 9, etc. |
7.38905609893065022723042746057500781 | |
| 0,20787 95763 50761 90854 | i^i | i i {displaystyle {i}^{i}} | e − π 2 {displaystyle e^{frac {-pi }{2}}} | e^(-pi/2) | T | A049006 | [0;4,1,4,3,1,1,1,1,1,1,1,1,7,1,20,1,3,6,10,...] | 1746 | 0.20787957635076190854695561983497877 | |
| 1,44466 78610 09766 13365 | Número de Steiner |
|
e e {displaystyle {sqrt[{e}]{e}}} | e 1 / e {displaystyle e^{1/e}} Límite superior de Tetración | e^(1/e) | A073229 | [1;2,4,55,27,1,1,16,9,3,2,8,3,2,1,1,4,1,9,...] | 1796 a 1863 |
1.44466786100976613365833910859643022 | |
| 4,53236 01418 27193 80962 | Constante de van der Pauw | α {displaystyle {alpha }} | π l n ( 2 ) = ∑ n = 0 ∞ 4 ( − 1 ) n 2 n + 1 ∑ n = 1 ∞ ( − 1 ) n + 1 n = 4 1 − 4 3 + 4 5 − 4 7 + 4 9 − . . . 1 1 − 1 2 + 1 3 − 1 4 + 1 5 − . . . {displaystyle {frac {pi }{ln(2)}}={frac {sum _{n=0}^{infty }{frac {4(-1)^{n}}{2n+1}}}{sum _{n=1}^{infty }{frac {(-1)^{n+1}}{n}}}}={frac {{frac {4}{1}}{-}{frac {4}{3}}{+}{frac {4}{5}}{-}{frac {4}{7}}{+}{frac {4}{9}}-...}{{frac {1}{1}}{-}{frac {1}{2}}{+}{frac {1}{3}}{-}{frac {1}{4}}{+}{frac {1}{5}}-...}}} | π/ln(2) | A163973 | [4;1,1,7,4,2,3,3,1,4,1,1,4,7,2,3,3,12,2,1,...] | 4.53236014182719380962768294571666681 | |||
| 1,57079 63267 94896 61923 | Constante de Favard K1 Producto de Wallis |
|
π 2 {displaystyle {frac {pi }{2}}} | ∏ n = 1 ∞ ( 4 n 2 4 n 2 − 1 ) = 2 1 ⋅ 2 3 ⋅ 4 3 ⋅ 4 5 ⋅ 6 5 ⋅ 6 7 ⋅ 8 7 ⋅ 8 9 ⋯ {displaystyle prod _{n=1}^{infty }left({frac {4n^{2}}{4n^{2}-1}}right)={frac {2}{1}}cdot {frac {2}{3}}cdot {frac {4}{3}}cdot {frac {4}{5}}cdot {frac {6}{5}}cdot {frac {6}{7}}cdot {frac {8}{7}}cdot {frac {8}{9}}cdots } | Prod[n=1 to ∞] {(4n^2)/(4n^2-1)} |
A019669 | [1;1,1,3,31,1,145,1,4,2,8,1,6,1,2,3,1,4,1,5,1...] | 1655 | 1.57079632679489661923132169163975144 | |
| 3,27582 29187 21811 15978 | Constante de Khinchin-Lévy · | γ {displaystyle gamma } | e π 2 / ( 12 ln 2 ) {displaystyle e^{pi ^{2}/(12ln 2)}} | e^(pi^2/(12 ln(2)) | A086702 | [3;3,1,1,1,2,29,1,130,1,12,3,8,2,4,1,3,55,...] | 1936 | 3.27582291872181115978768188245384386 | ||
| 1,61803 39887 49894 84820 | Fi, Número áureo · | 
|
φ {displaystyle {varphi }} | 1 + 5 2 = 1 + 1 + 1 + 1 + ⋯ {displaystyle {frac {1+{sqrt {5}}}{2}}={sqrt {1+{sqrt {1+{sqrt {1+{sqrt {1+cdots }}}}}}}}} | (1+5^(1/2))/2 | A | A001622 | [0;1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,...] = [0;1,...] |
-300 ~ | 1.61803398874989484820458683436563811 |
| 1,64493 40668 48226 43647 | Función Zeta (2) de Riemann | ζ ( 2 ) {displaystyle {zeta }(,2)} | π 2 6 = ∑ n = 1 ∞ 1 n 2 = 1 1 2 + 1 2 2 + 1 3 2 + 1 4 2 + ⋯ {displaystyle {frac {pi ^{2}}{6}}=sum _{n=1}^{infty }{frac {1}{n^{2}}}={frac {1}{1^{2}}}+{frac {1}{2^{2}}}+{frac {1}{3^{2}}}+{frac {1}{4^{2}}}+cdots } | Sum[n=1 to ∞] {1/n^2} |
T | A013661 | [1;1,1,1,4,2,4,7,1,4,2,3,4,10 1,2,1,1,1,15,...] | 1826 a 1866 |
1.64493406684822643647241516664602519 | |
| 1,73205 08075 68877 29352 | Constante de Theodorus | 
|
3 {displaystyle {sqrt {3}}} | 3 3 3 3 3 ⋯ 3 3 3 3 3 {displaystyle {sqrt[{3}]{3,{sqrt[{3}]{3,{sqrt[{3}]{3,{sqrt[{3}]{3,{sqrt[{3}]{3,cdots }}}}}}}}}}} | (3(3(3(3(3(3(3) ^1/3)^1/3)^1/3) ^1/3)^1/3)^1/3) ^1/3... |
A | A002194 | [1;1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,...] = [1;1,2,...] |
-465 a -398 |
1.73205080756887729352744634150587237 |
| 1,75793 27566 18004 53270 | Número de Kasner | R {displaystyle {R}} | 1 + 2 + 3 + 4 + ⋯ {displaystyle {sqrt {1+{sqrt {2+{sqrt {3+{sqrt {4+cdots }}}}}}}}} | A072449 | [1;1,3,7,1,1,1,2,3,1,4,1,1,2,1,2,20,1,2,2,...] | 1878 a 1955 |
1.75793275661800453270881963821813852 | |||
| 2,29558 71493 92638 07403 | Constante universal parabólica | 
|
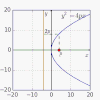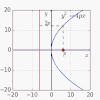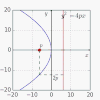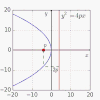
P 2 {displaystyle {P}_{,2}} | ln ( 1 + 2 ) + 2 = arcsinh ( 1 ) + 2 {displaystyle ln(1+{sqrt {2}})+{sqrt {2}};=;operatorname {arcsinh} (1)+{sqrt {2}}} | ln(1+sqrt 2)+sqrt 2 | T | A103710 | [2;3,2,1,1,1,1,3,3,1,1,4,2,3,2,7,1,6,1,8,7,2,1,...] | 2.29558714939263807403429804918949038 | |
| 3,30277 56377 31994 64655 | Número de bronce | σ R r {displaystyle {sigma }_{,Rr}} | 3 + 13 2 = 1 + 3 + 3 + 3 + 3 + ⋯ {displaystyle {frac {3+{sqrt {13}}}{2}}=1+{sqrt {3+{sqrt {3+{sqrt {3+{sqrt {3+cdots }}}}}}}}} | (3+sqrt 13)/2 | A | A098316 | [3;3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,...] = [3;3,...] |
3.30277563773199464655961063373524797 | ||
| 2,37313 82208 31250 90564 | Constante de Lévy 2 | 2 l n γ {displaystyle 2,ln,gamma } | π 2 6 l n ( 2 ) {displaystyle {frac {pi ^{2}}{6ln(2)}}} | Pi^(2)/(6*ln(2)) | T | A174606 | [2;2,1,2,8,57,9,32,1,1,2,1,2,1,2,1,2,1,3,2,...] | 1936 | 2.37313822083125090564344595189447424 | |
| 2,50662 82746 31000 50241 | Raíz cuadrada de 2 pi | 
|
2 π {displaystyle {sqrt {2pi }}} | 2 π = lim n → ∞ n ! e n n n n . . . . {displaystyle {sqrt {2pi }}=lim _{nto infty }{frac {n!;e^{n}}{n^{n}{sqrt {n}}}}{color {white}....color {black}}} Fórmula de Stirling | sqrt (2*pi) | T | A019727 | [2;1,1,37,4,1,1,1,1,9,1,1,2,8,6,1,2,2,1,3,...] | 1692 a 1770 |
2.50662827463100050241576528481104525 |
| 2,66514 41426 90225 18865 | Constante de Gelfond-Schneider | G G S {displaystyle G_{,GS}} | 2 2 {displaystyle 2^{sqrt {2}}} | 2^sqrt{2} | T | A007507 | [2;1,1,1,72,3,4,1,3,2,1,1,1,14,1,2,1,1,3,1,...] | 1934 | 2.66514414269022518865029724987313985 | |
| 2,68545 20010 65306 44530 | Constante de Khinchin | 
|
K 0 {displaystyle K_{,0}} |
∏
n
=
1
∞
[
1
+
1
n
(
n
+
2
)
]
ln
n
ln
2
=
lim
n
→
∞
(
∏
k
=
1
n
a
k
)
1
n
{displaystyle prod _{n=1}^{infty }left[{1{+}{1 over n(n{+}2)}}right]^{frac {ln n}{ln 2}}=lim _{nto infty }left(prod _{k=1}^{n}a_{k}right)^{frac {1}{n}}}
... donde ak son elementos de la fracción continua [a0; a1, a2, a3,...] |
prod[n=1 to ∞] {(1+1/(n(n+2))) ^((ln(n)/ln(2))} |
T | A002210 | [2;1,2,5,1,1,2,1,1,3,10,2,1,3,2,24,1,3,2,...] | 1934 | 2.68545200106530644530971483548179569 |
| 3,35988 56662 43177 55317 | Constante de Prévost, sum. inversos de Fibonacci | Ψ {displaystyle Psi } | ∑ n = 1 ∞ 1 F n = 1 1 + 1 1 + 1 2 + 1 3 + 1 5 + 1 8 + 1 13 + ⋯ {displaystyle sum _{n=1}^{infty }{frac {1}{F_{n}}}={frac {1}{1}}+{frac {1}{1}}+{frac {1}{2}}+{frac {1}{3}}+{frac {1}{5}}+{frac {1}{8}}+{frac {1}{13}}+cdots } | I | A079586 | [3;2,1,3,1,1,13,2,3,3,2,1,1,6,3,2,4,362,...] | 1977 | 3.35988566624317755317201130291892717 | ||
| 1,32471 79572 44746 02596 | Número plástico | 
|
ρ {displaystyle {rho }} | 1 + 1 + 1 + ⋯ 3 3 3 = 1 2 + 1 6 23 3 3 + 1 2 − 1 6 23 3 3 {displaystyle textstyle {sqrt[{3}]{1{+}{sqrt[{3}]{1{+}{sqrt[{3}]{1{+}cdots }}}}}}={sqrt[{3}]{{frac {1}{2}}+{frac {1}{6}}{sqrt {frac {23}{3}}}}}+{sqrt[{3}]{{frac {1}{2}}-{frac {1}{6}}{sqrt {frac {23}{3}}}}}} | A | A060006 | [1;3,12,1,1,3,2,3,2,4,2,141,80,2,5,1,2,8,...] | 1929 | 1.32471795724474602596090885447809734 | |
| 4,13273 13541 22492 93846 | Raíz de 2 e pi | 2 e π {displaystyle {sqrt {2epi }}} | 2 e π {displaystyle {sqrt {2epi }}} | sqrt(2e pi) | A019633 | [4;7,1,1,6,1,5,1,1,1,8,3,1,2,2,15,2,1,1,2,4,...] | 4.13273135412249293846939188429985264 | |||
| 2,66514 41426 90225 18865 | Constante de Gelfond | e π {displaystyle {e}^{pi }} | ( − 1 ) − i = i − 2 i = ∑ n = 0 ∞ π n n ! = π 1 1 + π 2 2 ! + π 3 3 ! + ⋯ {displaystyle (-1)^{-i}=i^{-2i}=sum _{n=0}^{infty }{frac {pi ^{n}}{n!}}={frac {pi ^{1}}{1}}+{frac {pi ^{2}}{2!}}+{frac {pi ^{3}}{3!}}+cdots } | Sum[n=0 to ∞] {(pi^n)/n!} |
T | A039661 | [23;7,9,3,1,1,591,2,9,1,2,34,1,16,1,30,1,...] | 1906 a 1968 |
23.1406926327792690057290863679485474 |
![{displaystyle lim _{nrightarrow infty }int _{1}^{2n}(-1)^{x}~{sqrt[{x}]{x}}~dx=int _{1}^{2n}e^{ipi x}~x^{1/x}~dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8a5f7620cf389898c275ed984f8688bbdf200b1)
![{displaystyle sum _{n=0}^{infty }{frac {1}{n!!}}={sqrt {e}}left[{frac {1}{sqrt {2}}}+gamma ({tfrac {1}{2}},{tfrac {1}{2}})right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e51ab5b1eae938ed34d7dd811be48e359de7b97)
![{displaystyle {frac {[Gamma ({tfrac {1}{4}})]^{2}}{sqrt {2pi }}}=4int _{0}^{1}{frac {dx}{sqrt {(1-x^{2})(2-x^{2})}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/838230a1a8781844335c2977f729a38f594a7da6)
![{displaystyle {sqrt[{4}]{5}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ca317d0c75e7b6f908151e893d8a05f990ee060)
![{displaystyle {sqrt[{5}]{5,{sqrt[{5}]{5,{sqrt[{5}]{5,{sqrt[{5}]{5,{sqrt[{5}]{5,cdots }}}}}}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3127d3db98c6e81870992019a1d56264a39f7a90)
![{displaystyle prod _{n=1}^{infty }{frac {n!}{{sqrt {2pi n}}left({frac {n}{e}}right)^{n}{sqrt[{12}]{1+{tfrac {1}{n}}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81ce7cd71c37a3c97c3b4244332953b626c26900)
![{displaystyle {sqrt[{3}]{1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/911022b24127c88770950e9ebfe48fbd12d3fddf)
![{displaystyle {frac {log left({frac {1+{sqrt[{3}]{73-6{sqrt {87}}}}+{sqrt[{3}]{73+6{sqrt {87}}}}}{3}}right)}{log(2)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a4162d90ad47ab451e6a198868b1d38f9a4f305)
![{displaystyle textstyle [1,0,8,4,1,0,1,5,1,2,2,3,1,1,1,3,6,...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b68851379d89009d2aa551f5f625d15a16c033f)
![{displaystyle {sqrt[{3}]{frac {45-{sqrt {1929}}}{18}}}+{sqrt[{3}]{frac {45+{sqrt {1929}}}{18}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4a477d1c213e6e2b9bad2f5190a12810278e06a)
![{displaystyle prod _{k=1}^{infty }left{1-left[1-prod _{j=1}^{n}(1-p_{k}^{-j})right]^{2}right}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c604e073b81c602f0926f2a05bc337eea83dcfc)
![{displaystyle textstyle {frac {1+{sqrt[{3}]{19+3{sqrt {33}}}}+{sqrt[{3}]{19-3{sqrt {33}}}}}{3}}=scriptstyle ,1+left({sqrt[{3}]{{tfrac {1}{2}}+{sqrt[{3}]{{tfrac {1}{2}}+{sqrt[{3}]{{tfrac {1}{2}}+...}}}}}}right)^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dae9951b8fe98213be5c592eca8d81e10dcbc441)
![{displaystyle {sqrt[{4}]{-1}}={frac {1+i}{sqrt {2}}}=e^{frac {ipi }{4}}=cos left({frac {pi }{4}}right)+isin left({frac {pi }{4}}right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37c0f3410cad402cfea4cf785416d99e3b2f417d)
![{displaystyle prod _{n=1}^{infty }n^{{3}^{-n}}={sqrt[{3}]{1{sqrt[{3}]{2{sqrt[{3}]{3cdots }}}}}}=1^{1/3};2^{1/9};3^{1/27}cdots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9e06c4b0df773f89d608077c7e00b4356a59994)
![{displaystyle 2!prod _{n=1}^{infty }!!textstyle {sqrt[{2^{n}}]{frac {prod _{i=1}^{2^{n-1}}(2^{n}+2i)}{prod _{i=1}^{2^{n-1}}!(2^{n}+2i-1)}}}=2{sqrt {frac {4}{3}}}{sqrt[{4}]{frac {6cdot 8}{5cdot 7}}}{sqrt[{8}]{frac {10cdot 12cdot 14cdot 16}{9cdot 11cdot 13cdot 15}}}cdots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6c0c981eac3e5b5b1d2f133e2e05b631a7d6d92)
![{displaystyle sum _{n=1}^{infty }({-}1)^{n}(n^{1/n}{-}1)=-{sqrt[{1}]{1}}+{sqrt[{2}]{2}}-{sqrt[{3}]{3}}+{sqrt[{4}]{4}},...}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d24fe745eaaccd7b633f9fbe8f9f447729e1f17d)
![{displaystyle {sqrt[{i}]{i}}=i^{-i}=i^{frac {1}{i}}=(i^{i})^{-1}=e^{frac {pi }{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/904fff5ea95018fde18c45c94097a379edad291e)
![{displaystyle 2+2cos {frac {2pi }{7}}=textstyle 2+{frac {2+{sqrt[{3}]{7+7{sqrt[{3}]{7+7{sqrt[{3}]{,7+cdots }}}}}}}{1+{sqrt[{3}]{7+7{sqrt[{3}]{7+7{sqrt[{3}]{,7+cdots }}}}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df4b6dfb762686eef1476628b27712ce19606c54)
![{displaystyle {sqrt[{12}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc835f27425fb3140e1f75a5faa35b1e8b9efc35)
![{displaystyle {sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710)
![{displaystyle {sqrt[{e}]{e}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96733766fde42bf61b329fba3cc27c54f46b21e5)
![{displaystyle {sqrt[{3}]{3,{sqrt[{3}]{3,{sqrt[{3}]{3,{sqrt[{3}]{3,{sqrt[{3}]{3,cdots }}}}}}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6a7a7a3adada2776b2b2ade49205f1f22eafca1)
![{displaystyle prod _{n=1}^{infty }left[{1{+}{1 over n(n{+}2)}}right]^{frac {ln n}{ln 2}}=lim _{nto infty }left(prod _{k=1}^{n}a_{k}right)^{frac {1}{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/527566b0fceb254898a4ff152297b8e0c5921ae6)
![{displaystyle textstyle {sqrt[{3}]{1{+}{sqrt[{3}]{1{+}{sqrt[{3}]{1{+}cdots }}}}}}={sqrt[{3}]{{frac {1}{2}}+{frac {1}{6}}{sqrt {frac {23}{3}}}}}+{sqrt[{3}]{{frac {1}{2}}-{frac {1}{6}}{sqrt {frac {23}{3}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/971c5e9de7ce0ab9336ef8da0dd6591aede8f98d)
Table of mathematical constants
Abbreviations used:
- R - Rational number
- I - Algebraic irrational number
- T - transcendental irrational number
- - Unknown
| 0 | 0 | zero | R | - | - |
| 1 | 1 | One | R | - | - |
| 2 | 2 | Two. | R | - | - |
| π π {displaystyle pi ,} | 3,14159 26535 89793 23846 26433 83279 50288 41971 | Pi, constant of Archimedes or number of Ludolph | T | 10.000.000.050 | 22/10/2011 |
| e=limn→ → ∞ ∞ (1+1n)n{displaystyle e=lim _{nto infty }left(1+{frac {1}{n}{n}right)^{n}}} | 2,71828 18284 59045 23536 02874 71352 66249 77572 | Constant of Napier, natural logarithm base | T | 1,000,000.000. | 2010 |
| 2{displaystyle {sqrt {2}}} | 1,41421 35623 73095 04880 16887 24209 69807 85696 | Square root of twoPythagoras constant. | I | 1,000,000.000. | 2010 |
| 3{displaystyle {sqrt {3}}} | 1,73205 08075 68877 29352 74463 41505 87236 69428 | Square three | I | 10,000.000 | |
| 5{displaystyle {sqrt {5}}} | 2,23606 79774 99789 69640 91736 68731 27623 54406 | Square root of five | I | 10,000.000 | 20/12/1999 |
| φ φ ,Δ Δ =1+52{displaystyle phitau ={frac {1+{sqrt {5}}}{2}}}}} | 1.61803 39887 49894 84820 45868 34365 63811 77203 | Authentic number, symbolized both φ and τ. | I | 1,000,000.000. | 2010 |
| γ γ =limn→ → ∞ ∞ [chuckles]␡ ␡ k=1n1k− − ln (n)]{displaystyle gamma =lim _{nrightarrow infty }left[sum _{k=1^{n}{frac {1}{k}}}-ln(right)}}}}}}} | 0.557721 56649 01532 86060 65120 90082 40243 10421 | Constant of Euler-Mascheroni | ? | 29.844.489.545 | 2009 |
| α α {displaystyle alpha ,} | -2,50290 78750 95892 82228 39028 73218 21578 63812 | Constant α de Feigenbaum | 1018 | 1999 | |
| δ δ {displaystyle delta ,} | 4,66920 16091 02990 67185 32038 20466 20161 72581 | Constant δ de Feigenbaum | 1018 | 1999 | |
| Cartin= pprimor(1− − 1p(p− − 1)){displaystyle C_{artin}=prod _{p,primo}left(1-{frac {1}{p(p-1)}}right)} | 0.3395 58136 19202 28805 47280 54346 41641 51116 | Constant of Artin | 1000 | 1999 | |
| C2= p≥ ≥ 3p(p− − 2)(p− − 1)2{displaystyle C_{2}=prod _{pgeq 3}{frac {p(p-2)}{(p-1)^{2}}}}}} | 0.66016 18158 46869 57392 78121 10014 55577 84326 | Constant twin cousins | 5.020 | 2001 | |
| B2{displaystyle B_{2},} | 1,90216 0582 | Constant of Brun for twin cousins | 9 | 1999 / 2002 |
![{displaystyle gamma =lim _{nrightarrow infty }left[sum _{k=1}^{n}{frac {1}{k}}-ln(n)right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8569bc7e2125dd8b06ab300011c683a0d82147e)
Books
- Finch, Steven (2003). Mathematical constants. Cambridge University Press. ISBN 978-0-521-81805-6.
- Daniel Zwillinger (2012). Standard Mathematical Tables and Formulae. Imperial College Press. ISBN 978-1-4398-3548-7.
- Eric W. Weisstein (2003). CRC Concise Encyclopedia of Mathematics. Chapman & Hall/CRC. ISBN 1-58488-347-2.
- Lloyd Kilford (2008). Modular Forms, a Classical and Computational Introduction. Imperial College Press. ISBN 978-1-84816-213-6.