Angular moment

The angular momentum or kinetic momentum is a physical quantity, rotational equivalent of linear momentum and represents the amount of rotational movement of an object. It is a vector quantity that characterizes the inertial properties of a body, which rotates in relation to a certain point. It is found in all three mechanics (classical, quantum and relativistic mechanics). In the International System of Units, the angular momentum is measured in kg·m²/s. With respect to rotations, this magnitude plays a role analogous to linear momentum in translations.

The traditional name in Spanish is momento kinético; "angular momentum" is in common use due to the influence of the English angular momentum.

Under certain conditions of rotational symmetry of systems, it is a physical magnitude that remains constant over time as the system changes, which gives rise to the so-called law of conservation of kinetic momentum. The kinetic moment for a rigid body that rotates about an axis is the resistance that said body offers to the variation of the angular velocity. However, that does not imply that it is an exclusive magnitude of the rotations; for example, the angular momentum of a particle moving freely with constant velocity (in magnitude and direction) is also conserved.

Kinetic moment in classical mechanics

Kinetic momentum of a point mass

The kinetic moment of a particle regarding the point O{displaystyle scriptstyle {O}} is the vector product of its linear moment mv{displaystyle scriptstyle {mmathbf {v}}}} by the vector r{displaystyle scriptstyle {mathbf {r}}}}.

In Newtonian mechanics, the kinetic moment of a particle or punctual mass regarding a point O of space is defined as the moment of its amount of movement p{displaystyle mathbf {p} } on that point. Normally designated by symbol L{displaystyle mathbf {L} }. Being r{displaystyle mathbf {r} } the vector that unites point O with the position of the punctual mass (also known as the radius of the trajectory), will be:

L=r× × p=r× × mv{displaystyle mathbf {L} =mathbf {r} times mathbf {p} =mathbf {r} times mmathbf {v} }

The vector L{displaystyle mathbf {L} ,} is perpendicular to the plane it contains r{displaystyle mathbf {r} ,} and v{displaystyle mathbf {v} ,}, in the direction indicated by the rule of the vector product or right hand rule and its module or intensity is:

L =mrvwithout θ θ =prwithout θ θ =pbp{displaystyle lVert mathbf {L} rVert =mrvsin theta =p,rsin theta =p,b_{p}}}}

this is, the product of the module of the linear moment for its arm (bp{displaystyle b_{p},} in drawing), defined this as the distance of the point from which the moment is taken to the straight that contains the velocity of the particle.

Kinetic moment and dynamic moment

Let's derive the angular momentum with respect to time:

dLdt=ddt(r× × p)=(drdt× × p)+(r× × dpdt){displaystyle {dmathbf {L} over dt}={dover dt}(mathbf {r} times mathbf {p})=left({dmathbf {r} over dt}}times mathbf {p} right)+left(bf {rth} times

The first of the parenthesis is zero as the derivative r{displaystyle mathbf {r} ,} about time is nothing but speed v{displaystyle mathbf {v} ,} and, as the vector speed is parallel to the vector number of movement p{displaystyle mathbf {p},}, the vector product is zero. As for the second parenthesis, we have:

dLdt=r× × dpdt=r× × ddt(mv)=r× × (ma){displaystyle {dmathbf {L} over dt}=mathbf {r} times {dmathbf {p} over dt}=mathbf {r} times {d over dt}left(mmathbf {v} right)=mathbf {r} times {mmathbb

where a{displaystyle scriptstyle {mathbf {a}}}} is the acceleration of the particle, so ma=F{displaystyle mmathbf {a} =mathbf {F} ,}It's the force that acts on it. Since the vector product r{displaystyle mathbf {r} ,} by force is the dynamic moment or moment applied to the mass, we have:

dLdt=r× × F=M{displaystyle {dmathbf {L} over dt}=mathbf {r} times mathbf {F} =mathbf {M} }

Thus, the temporary derivative of the kinetic moment is equal to the dynamic moment that acts on the particle. It should be noted that in this expression both moments, L{displaystyle mathbf {L} ,} and M{displaystyle mathbf {M} ,} they must be referred to the same point O.

As an example, the fact that the variation of the angular velocity depends on the moment of force is what allows a wrench to tighten or loosen a nut much more than simply turning it by hand. Because the wrench and the nut are a rigid system, they must all turn at the same time. As the spanner is much longer than the radius of the nut, applying a little force to the spanner forces the nut to exert a much greater force in order to slow down its advance, which implies that larger spanners allow nuts to be tightened at higher pressures.

Kinetic momentum of a set of point particles

The kinetic momentum of a set of particles is the sum of the angular momenta of each one:

L=␡ ␡ kr→ → k× × p→ → k=␡ ␡ Li{displaystyle mathbf {L} =sum _{k}{vec {r}}_{k}times {vec {p}}_{k}=sum mathbf {L} _{i},}

The temporal variation is:

dLdt=␡ ␡ dLidt=␡ ␡ Mi{displaystyle {dmathbf {L} over dt}=sum {dmathbf {L} _{i} over dt}=sum mathbf {M} _{i},}

The term on the right is the sum of all the moments produced by all the forces acting on the particles. A part of these forces can be of external origin to the set of particles. Another part may be forces between particles. But each force between particles has its reaction that is equal but of opposite direction and collinear. This means that the moments produced by each of the forces of an action-reaction pair are equal and of opposite sign and that their sum is null. That is, the sum of all moments of internal origin is zero and cannot change the value of the angular momentum of the assembly. Only the external moments remain:

dLdt=␡ ␡ dLidt=Mext.{displaystyle {dmathbf {L} over dt}=sum {dmathbf {L} _{i} over dt}=mathbf {M} _{ext.},}

The angular momentum of a system of particles is conserved in the absence of external momentum. This statement is valid for any set of particles: from atomic nuclei to groups of galaxies.

Kinetic moment of a rigid body

We have that in an inertial system the equation of movement is:

dLdt=ddt[chuckles]I(t)ω ω (t)]{displaystyle {frac {dmathbf {L} }{dt}}}={frac {d}{dt}}}left[mathbf {I} (t)mathbf {omega } (t)right]}

Where:

• ω ω {displaystyle scriptstyle {mathbf {omega } }}} is the angular speed of the solid.
• I{displaystyle scriptstyle {mathbf {I} }} It's the body's inertia tensor.

Now, normally for a rigid solid the inertia tensor I{displaystyle mathbf {I} }, it depends on time and therefore in the inertial system there is usually no analogue to Newton's second law, and unless the body turns around one of the main axes of inertia it happens that:

dLdtI was. I was. Idω ω dt=Iα α {displaystyle {dmathbf {L} over dt}neq mathbf {I} {dmathbf {omega } over dt}=mathbf {I} mathbf {alpha } } }

Where α α {displaystyle scriptstyle {mathbf {alpha } }}} is the angular acceleration of the body. That is why it is more useful to raise the equations of movement in a non-inertial system formed by the main axes of solid inertia, so it is achieved that I=cte.{displaystyle mathbf {I} ={mbox{cte}}}}, although then it is necessary to have the forces of inertia:

dLdt=Idω ω dt+ω ω × × (Iω ω ){displaystyle {dmathbf {L} over dt}=mathbf {I} {dmathbf {omega } over dt}+mathbf {omega } times (mathbf {I} mathbf {omega }}}}}}}

Which turns out to be a nonlinear equation in angular velocity.

Conservation of classical angular momentum

When the sum of external moments is zero M=0{displaystyle scriptstyle {mathbf {M} =0}}We've seen that:

dLdt=0{displaystyle {dmathbf {L} over dt}=0,}

That means that L=cornstante{displaystyle scriptstyle {mathbf {L} =mathrm {constant} }}}}. And like L{displaystyle scriptstyle {mathbf {L} }} is a vector, it is constant both in module and in direction.

Consider an object that can change shape. In one of those ways, your Inertia Moment is I1{displaystyle scriptstyle {I_{1}}}} and its angular speed ω ω 1{displaystyle scriptstyle {mathbf {omega } _{1}}}}. If the object changes shape (without intervention of an external moment) and that the new mass distribution makes its new Moment of inertia I2{displaystyle scriptstyle {I_{2}}}}, its angular speed will change in such a way that:

I1ω ω 1=I2ω ω 2{displaystyle mathbf {I} _{1}mathbf {omega } _{1}=mathbf {I} _{2}mathbf {omega } _{2},}

In some cases the moment of inertia can be considered a scalar. So the direction of the angular velocity vector will not change. Only the speed of rotation will change.

There are many phenomena in which the conservation of angular momentum is very important. For example:

• In all the arts and sports in which they turn, pirouettes, etc. For example, to make a pirouette, a dancer or a skater take momentum with the arms and an extended leg to increase their inertia moments around the vertical. Then, closing the arms and the leg, diminishing their moments of inertia, which increases the speed of rotation. To finish the pirueta, the extension of the arms and a leg, it allows to decrease the speed of rotation. The same happens with the platform jump or the trampoline. It is also important in cycling and motorcycling, since the conservation of the kinetic moment is responsible for the simplicity with which it is possible to maintain balance.
• To control the angular orientation of a satellite or space probe. As external moments may be considered to be zero, the kinetic moment and then the satellite orientation does not change. To change this orientation, an electric motor spins an inertia steering wheel. To preserve the kinetic moment, the satellite is turning in the opposite direction. Once in good orientation, just stop the inertia steering wheel, which for the satellite. The inertia flyer is also used to stop the small rotations caused by the small inevitable moments, such as the one produced by the solar wind.
• Some stars are contracted becoming a pulp (neutron star). Its diameter decreases up to a few kilometers, its inertia time decreases and its rotation speed increases enormously. Pressures have been detected with rotation periods of just a milliseconds.
• Because of the tides, the Moon exercises a moment on Earth. This decreases the kinetic moment of the Earth and, due to the preservation of the kinetic moment, that of the Moon increases. Consequently, the Moon increases its energy by moving away from Earth and decreasing its rotation rate (but increasing its kinetic moment). The Moon moves away and the lunar days and months elongate.

Example

In the drawing on the right we have a rotating mass, held by a thread of negligible mass that passes through a thin tube. We assume the set without friction and we do not take gravity into account.

The force that the thread exerts on the mass is radial and cannot exert a moment on the mass. If we pull the thread, the radius of gyration will decrease. Since, in the absence of external moments, angular momentum is conserved, the rate of rotation of the mass must increase.

A pull on the thread communicates a radial velocity Δ Δ V{displaystyle scriptstyle {Delta V}} to the mass. The new speed is the vector sum of the previous speed and Δ Δ V{displaystyle scriptstyle {Delta V}}

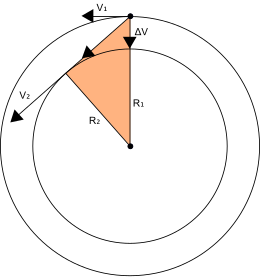
In the following drawing appears the mass that rotates with a radio R1{displaystyle scriptstyle {R_{1}}}} at the time when a yarn is given. The correct term of the physical "trum" is an impulse, that is to say a force applied for an instant of time. That impulse communicates radial speed Δ Δ V{displaystyle scriptstyle {Delta V}} to the mass. The new speed will be the vector sum of the previous speed V{displaystyle scriptstyle {V}} with Δ Δ V{displaystyle scriptstyle {Delta V}}. The direction of that new speed is not tangential, but incoming. When the dough passes through the nearest point in the center, at a distance R2{displaystyle scriptstyle {R_{2}}}}, we charge the loose thread and the dough will continue to spin with the new radio R2{displaystyle scriptstyle {R_{2}}}}. In drawing, the yellow triangle and the pink triangle are similar. Which allows us to write:

V2V1=R1R2{displaystyle {V_{2} over V_{1}}={R_{1} over R_{2}},}

that is:

V1R1=V2R2{displaystyle V_{1}R_{1}=V_{2}R_{2},}

And if we multiply by the mass m{displaystyle scriptstyle {m}}We get the kinetic moment preserved, as we expected:

mV1R1=mV2R2{displaystyle mV_{1}R_{1}=mV_{2}R_{2},}

We see how the kinetic momentum has been conserved: To reduce the radius of gyration, a radial velocity must be communicated, which increases the total velocity of the mass.

You can also do the experiment in the other direction. If the string is released, the mass follows the tangent of the trajectory and its angular momentum does not change. At a certain moment we brake the thread so that the radius is constant again. The fact of braking the wire, communicates a radial velocity (towards the center) to the mass. This time this radial speed decreases the total speed and only the component of the tangential speed to the wire remains in the position in which it was braked.

It is not necessary to do the experience by pulling. It can be done continuously, since the force that is made by recovering and releasing the thread can be broken down into a succession of small impulses.

Kinetic moment in relativistic mechanics

In Newtonian mechanics the angular momentum is a pseudovector or axial vector, so in relativistic mechanics it must be treated as the Hodge dual of the spatial components of an antisymmetric tensor. A representation of the angular momentum in the special theory of relativity is therefore as an antisymmetric quadritensor:

L=(0ctpx− − Ex/cctpand− − Eand/cctpz− − Ez/cEx/c− − ctpx0xpand− − andpxxpz− − zpxEand/c− − ctpandandpx− − xpand0andpz− − andpzEz/c− − ctpzzpx− − xpzzpand− − andpz0)=(0rxrandrz− − rx0Lz− − Land− − rand− − Lz0Lx− − rzLand− − Lx0)### ##########################################################################################################################################

It can be seen that the 3 space components form the kinetic moment of Newtonian mechanics L=(Lx,Land,Lz){displaystyle mathbf {L} =(L_{x},L_{y},L_{z}}}}}} and other components (rx,rand,rz){displaystyle (r_{x},r_{y},r_{z}),} describe the movement of the relativist mass center.

Kinetic momentum in quantum mechanics

In quantum mechanics the kinetic moment is a set of three operators for which there is a set of linearly independent states 日本語α α ,β β {displaystyle Δalphabeta rangle } which satisfies:

A^ ^ 2日本語α α ,β β = 2α α (α α +1)日本語α α ,β β ;A^ ^ 3日本語α α ,β β = β β 日本語α α ,β β {displaystyle {hat {mathbf {A}}}{alphabeta rangle ={hbar }^{2}alpha (alpha +1)

And that also satisfy the following canonical commutation relations:

[chuckles]A^ ^ i,A^ ^ j]=i ε ε ijkA^ ^ k,[chuckles]A^ ^ i,A^ ^ 2]=0{displaystyle [{hat {A}}_{i},{hat {A}}_{j}]=ihbar epsilon _{ijk}{hat {A}_{k},qquad left[{hat {A}}}_{i},{hat {mathbf {A} }{2}{2}{right}=0}

where

ε ε ijk{displaystyle epsilon} is the symbol of Levi-Civita and

A^ ^ 2:=A^ ^ x2+A^ ^ and2+A^ ^ z2{displaystyle {hat {mathbf {a}}}}{{2}:={hat {a}}_{x}{2}+{hat {a}_{y}}{2}}{hat {a}}}_{z^}{2}}

These commutation relations guarantee that these operators constitute a Lie algebra representation su(2) (which is related, to the universal covering group of the three-dimensional group of rotations).

For example the orbital kinetic moment L{displaystyle mathbf {L} }the thorn S{displaystyle mathbf {S} } (or intrinsic kinetic moment), isospin I{displaystyle mathbf {I} }the total kinetic moment J{displaystyle mathbf {J} }etc.

Orbital angular momentum

The orbital kinetic moment, such as the one with a two-particle system that rotates around the other, can be transformed to an operator L^ ^ {displaystyle {hat {L}}} through its classic expression:

L^ ^ =− − i (r× × ► ► ){displaystyle mathbf {hat {L}} =-ihbar left(mathbf {r} times {boldsymbol {blah}}}right)}}

being r{displaystyle mathbf {r} } the distance that separates them.

Using Cartesian coordinates the three components of the kinetic moment are expressed in the usual Hilbert space for wave functions, L2(R3){displaystyle L^{2}(mathbb {R} ^{3}}}like:

L^ ^ x=− − i (and▪ ▪ ▪ ▪ z− − z▪ ▪ ▪ ▪ and)L^ ^ and=− − i (z▪ ▪ ▪ ▪ x− − x▪ ▪ ▪ ▪ z)L^ ^ z=− − i (x▪ ▪ ▪ ▪ and− − and▪ ▪ ▪ ▪ x){cHFFFFFF}{cHFFFFFF}{cHFFFFFF}{cHFFFFFF00} {cHFFFFFFFF}{cHFFFFFFFFFF00}{cHFFFFFFFF00}{cHFFFFFFFFFF}{cHFFFFFFFF}{cHFFFFFFFFFFFF}{cHFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF}{c}{c}{cH00}{cHFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00}{}{cHFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF}{cH00}{} {c}{c} {cH00} {cHFFFFFFFFFFFFFFFFFFFFFF

On the other hand, in spherical angular coordinates, the square of the kinetic moment and the Z component are expressed as:

L^ ^ 2=− − 2[chuckles]1without θ θ ▪ ▪ ▪ ▪ θ θ (without θ θ ▪ ▪ ▪ ▪ θ θ )+1without2 θ θ ▪ ▪ 2▪ ▪ φ φ 2]L^ ^ z=− − i (▪ ▪ ▪ ▪ φ φ ){cHFFFFFF}{cHFFFFFF}{cHFFFFFFFF}{cHFFFFFF}{cHFFFFFF}{cHFFFFFFFF}{cHFFFFFFFFFFFF}{cHFFFFFFFFFF}{cHFFFFFFFF}{cHFFFFFFFF}{cHFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF}{c}{c}{cH00}{c}{cHFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF}{c}{c}{cHFFFFFFFFFFFFFFFFFFFFFFFF00}{c}{cH00}{cHFFFFFFFFFFFFFFFFFFFFFFFFFF}{c}{cHFFFFFFFFFFFFFFFFFFFFFFFFFFFF00}{c}{cH00}{c}{

The vectors themselves or states of the orbital kinetic moment depend on two whole quantum numbers l{displaystyle l} and m{displaystyle m}, are designated as 日本語l,m {displaystyle Δl,mrangle } and satisfy relationships:

L^ ^ 2日本語l,m = 2l(l+1)日本語l,m L^ ^ z日本語l,m = m日本語l,m {displaystyle {hat {L}}{2}{2}{2}{2}{rangle ={hbar }{2}{2}l(l+1)ёl,mrangle qquad {hat {L}}}_{z}

These eigenvectors expressed in terms of the spherical angular coordinates are the so-called spherical harmonics Y_{l, m}(θ,φ), which are built from the Legendre polynomials:

θ θ ,φ φ 日本語l,m =Andl,m(θ θ ,φ φ )Andl,m(θ θ ,φ φ )=Neimφ φ Plm(# θ θ ){displaystyle langle thetaphi Δl,mrangle =Y_{l,m}(thetavarphi)qquad Y_{l,m}(thetavarphi)=N,e^{imvarphi },P_{l}^{m}(cos {theta }}}}}}

They are especially important because they are the angular component of atomic orbitals.

Conservation of quantum angular momentum

It is important to note that if the Hamiltonian does not depend on the angular variables, as happens for example in problems with potential spherical symmetry then all the components of the angular momentum commute with the Hamiltonian:

[chuckles]L^ ^ i,H]=0{displaystyle left[{hat {L}}_{i},Hright]=0}

and, as a consequence, the square of the angular momentum also commutes with the Hamiltonian:

[chuckles]L^ ^ 2,H]=0{displaystyle left[{hat {L}}^{2},Hright]=0}.

And we have the kinetic moment preserved, that means that throughout the evolution in the time of the quantum system the probability distribution of the values of the kinetic moment will not vary. Note, however, that since the components of the kinetic moment do not switch to one another, they cannot be defined simultaneously. However, the square of the kinetic moment and one of its components can be defined simultaneously (the Z component is usually chosen). In particular if we have well-defined quantum states of time these will remain well-defined quantum states with the same quantum numbers values l{displaystyle l} and m{displaystyle m}.