Alternating current

Figure 1: Synusoidal form.

It is called alternating current (CA or AC, for its acronym in English of Alternating current) to the electric current in which the magnitude and direction vary cyclically.

The most commonly used form of alternating current oscillation is sinusoidal oscillationwith which a more efficient transmission of energy is achieved, to such an extent that when speaking of alternating current it is understood that it refers to the sinusoidal alternating current.

However, in certain applications other forms of periodic oscillation are used, such as triangular or rectangular.

Used generically, alternating current refers to the way in which electricity reaches homes and industries. However, audio and radio signals transmitted by electrical wires are also examples of alternating current. In these uses, the most important purpose is usually the transmission and recovery of the encoded (or modulated) information on the alternating current signal.

History

The first alternator to produce alternating current was a dynamoelectric generator based on Michael Faraday's principles, built by the French instrument maker Hippolyte Pixii in 1832. Pixii later added a commutator to his device to produce direct current (most used). The earliest recorded practical application of alternating current is by Guillaume Duchenne, inventor and developer of electrotherapy. In 1855, he announced that AC was superior to direct current for the electrotherapeutic activation of muscle contractions. Alternating current technology had first been developed in Europe due to the work of Guillaume Duchenne (1850s), the company Hungarian Ganz Works (1870s) and in the 1880s by William Stanley, Sebastian Ziani de Ferranti, Lucien Gaulard and Galileo Ferraris.

In 1876, Russian engineer Pavel Yablochkov invented a lighting system where sets of induction coils were installed along a high-voltage AC line. Instead of changing the voltage, the primary windings transferred power to the secondary windings which were connected to one or more 'electric candles'. (arc lamps) of his own design, used to prevent the failure of one lamp from disabling the entire circuit. In 1878, the Ganz Works company in Budapest, Hungary, began manufacturing equipment for electric lighting, and by 1883, it had installed more than fifty systems in Austria-Hungary. Their AC systems used incandescent arc lamps, generators, and other equipment.

Transformers

Alternating current systems can use transformers to switch current from low to high voltage and vice versa, allowing generation and transmission over long distances at high voltage, saving on conductor costs and energy losses, and consumption in low voltage.

An open core bipolar power transformer developed by Lucien Gaulard and John Dixon Gibbs was demonstrated in London in 1881, attracting the interest of Westinghouse. They also exhibited the invention in Turin in 1884. However, these early induction coils with open magnetic circuits are inefficient in transferring power to loads. Until about 1880, the paradigm for transmitting AC from a high-voltage source to a low-voltage load was a series circuit.

Open-core transformers with a ratio close to 1:1 were connected with their primaries in series to allow high voltage to be used for transmission and to present low voltage to lamps.

The inherent flaw in this method was that turning off a single lamp (or other electrical device) affected the voltage supplied to all others on the same circuit. Many adjustable transformer designs were introduced to compensate for this problematic characteristic of the series circuit, including those that employ methods to adjust the core or prevent magnetic flux around a coil. Direct current systems did not have these drawbacks, allowing gives significant advantages over early AC systems.

Nikola Tesla

In 1888, the Serbian inventor and engineer Nikola Tesla designed and built the first alternating current induction motor, a device capable of converting a certain form of energy into rotational mechanical energy, which allows powering a motor with alternating current, before transforming into direct current.

In the distribution of alternating current, Tesla notes that this energy travels in gaps at the peaks of the Sinusoids, so he creates a second signal out of sync with the first to fill those gaps, allowing amplification of the AC, without the need to build a new power plant as the direct current warranted.

However, the biggest fear of using AC was the danger that such a lot of energy represented in homes. To solve the problem, Tesla investigates a device developed by the European engineers called a transformer, with this component you can increase the voltage for transmission and then decrease it for the end user. With the improvements in the transformer, the invention of the electric motor, the power to amplify/decrease the AC voltage, among others, Nikola Tesla wins the war of currents competing with Thomas Edison who favored direct current.

Later, the physicist William Stanley reused, in 1885, the principle of induction to transfer alternating current between two electrically isolated circuits. The central idea was to wind a pair of coils on a common iron base, called an induction coil.

The system used today was fundamentally devised by Nikola Tesla; alternating current distribution was commercialized by George Westinghouse. Alternating current overcame the limitations that appeared when using direct current (DC), which is an inefficient system for large-scale power distribution due to problems in power transmission, marketed in its day with great aggressiveness by Thomas Alva Edison.

All the patents referring to this current were assigned by Nikola Tesla to the Westinghouse Electric company to raise capital and be able to continue the projects with alternating current.

The first long-distance transmission of alternating current occurred in 1891 near Telluride, Colorado, followed a few months later by another from Lauffen to Frankfurt in Germany. Despite the notorious advantages of alternating current over direct current, Thomas Edison continued to advocate strongly for the use of direct current, which cost him his position at the company he founded, Edison Electric, changing its name to the current General Electric.

Alternating Current vs. Direct Current

The reason for the wide use of alternating current is determined by its ease of transformation, a quality that direct current lacks. In the case of direct current, the increase in voltage is achieved by connecting dynamos in series, which is not very practical; on the contrary, in alternating current there is a device, the transformer, which allows the voltage to be raised efficiently.

Electrical energy is given by the product of voltage, current and time. Since the section of the conductors of the electric power lines depends on the intensity, by means of a transformer the voltage can be raised to high values (high voltage), decreasing the current intensity in equal proportion. With this, the same energy can be distributed over long distances with low current intensity and, therefore, with low losses due to the Joule effect and other effects associated with the passage of current, such as hysteresis or Eddy currents. Once at the point of consumption or in its vicinity, the voltage can again be reduced for industrial, domestic or commercial use in a comfortable and safe way.

Mathematics and sinusoidal alternating current

Some types of periodic oscillations have the drawback of not having their mathematical expression defined, so they cannot be operated analytically. By contrast, sinusoidal oscillation does not have this mathematical indeterminacy and has the following advantages:

• The sinus function is perfectly defined by its analytical and graphic expression. Through the theory of complex numbers the alternating circuits are analyzed with great ease.
• Non-sinusoryal periodic oscillations can be broken down in addition to a series of sinusory oscillations of different frequencies that receive the name of harmonics. This is a direct application of the Fourier series.
• They can be generated easily and in quantities of high values to facilitate the transport of electrical energy.
• Its transformation into other oscillations of different magnitude is easily achieved through the use of transformers.

Sinusoidal oscillation

Figure 2: Parameters characteristic of a sinusoidal oscillation.

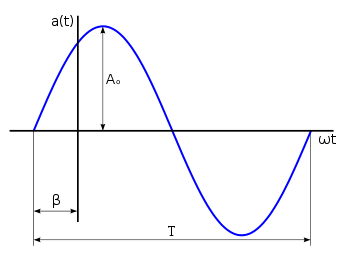
A senoidal or sinusoidal signal, a(t){displaystyle a(t)}, tension, v(t){displaystyle v(t)}Or ordinary, i(t){displaystyle i(t)}, you can express mathematically according to its characteristic parameters (Figure 2), as a function of time through the following equation:

a(t)=A0⋅ ⋅ without (ω ω t+β β ){displaystyle a(t)=A_{0}cdot sin(omega t+beta)}

where

A0{displaystyle A_{0}} It's the amplitude in volts or ampers (also called maximum or peak value),

ω ω {displaystyle omega } pulse in radian/second,

t{displaystyle t} time in seconds, and

β β {displaystyle beta } the initial phase angle in radians.

Since angular velocity is more interesting for mathematicians than for engineers, the above formula is often expressed as:

a(t)=A0⋅ ⋅ without (2π π ft+β β ){displaystyle a(t)=A_{0}cdot sin(2pi ft+beta)}

where f is the frequency in hertz (Hz) and equals the reverse of the period f=1T{displaystyle f={frac {1}{T}}}}. The most used values in the distribution are 50 Hz and 60 Hz.

Meaningful values

The following are other significant values of a sinusoidal signal:

• Instant value (a(t)): it is the one who takes the order in an instant, t, determined.

• Scope value (A)_pp): difference between its peak or maximum positive and its negative peak. Since the maximum value of sen(x) is +1 and the minimum value is -1, a sinusoidal signal that oscillates between +A₀ and...A₀. The peak value, written as A_P-P, it is therefore (+A₀)-(-A₀= 2×A₀.

• Average value (A)_med): value of the area that forms with the axis of abscises left for its period. The average value can be interpreted as the continuous component of the sinusoidal oscillation. The area is considered positive if it is above the axis of abscises and negative if it is below. As in a sinusoidal signal the positive semicycle is identical to the negative, its average value is zero. That is why the average value of a sinusoidal oscillation refers to a semi-cycle. By comprehensive calculation you can prove that your expression is the following;

Amed=2A0π π {displaystyle A_{med}={2A_{0} over {pi }}}}

• Pico or crest: maximum value, of positive sign (+), which takes the sinusoidal oscillation of the electromagnetic spectrum, each medium cycle, from the point “0”. This value increases or decreases as the "A" range of the oscillation itself grows or decreases positively above the "0" value.

• Effective value (A): the effective value is defined as the value of a continuous current (or voltage) that produces the same caloric effects as its alternating equivalent. That is to say that for a certain alternating current, its effective value (Ief) will be the continuous current that produces the same power dissipation (P) in a resistance (R). Mathematically, the effective value of a variable magnitude over time, is defined as the square root of the mean of the squares of the instant values reached during a period:

A=1T∫ ∫ 0Ta2(t)dt{displaystyle A={sqrt {{1 over {T}}{int _{0}{T}a^{2}(t)dt}}}}}}}

In English literature this value is known as the root mean square value of a function. In the industrial field, the effective value is of great importance, since almost all operations with energy magnitudes are made with said value. Hence, for speed and clarity it is represented with the capital letter of the magnitude in question (I, V, P, etc.). Mathematically, it is shown that for a sinusoidal alternating current the effective value is given by the expression:

A=A02{displaystyle A={A_{0} over {sqrt {2}}}}}}

The A value, voltage or current, is useful for calculating the power consumed by a load. Thus, if an alternating voltage develops a certain power P in a given resistive load, a direct voltage of V_rms will develop the same power P in the same load, therefore V _rms x I = V_AC x I (see Power in alternating current).

Phasor representation

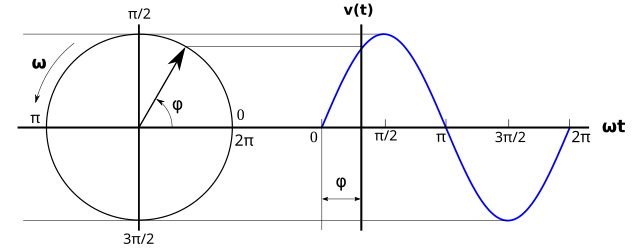
A sinusoidal function can be represented by a complex number whose argument grows linearly with time (figure 3), which is called a phasor or Fresnel representation, which will have the following characteristics:

• It will rotate with a ω angular speed.
• Your module will be the maximum or effective value, as appropriate.

Figure 3: Fasorial representation of a sinusoidal oscillation.

The reason for using the phasor representation lies in the simplification that it entails. Mathematically, a phasor can be easily defined by a complex number, so the calculation theory of these numbers can be used for the analysis of alternating current systems.

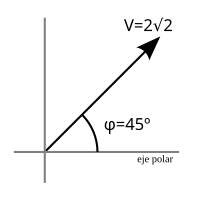
Let us consider, as an example, an alternating current voltage whose instantaneous value is the following:

Figure 4: Example of tension fasor.

v(t)=4without (1000t+π π 4){displaystyle v(t)=4sin left(1000t+{pi over {4}right)}

Taking its effective value as the module of the phasor, the graphical representation of the previous voltage will be the one that can be seen in figure 4, and it will be noted:

V→ → =22ejπ π 4=22 45 {displaystyle {vec {V}}=2{sqrt {2}}{mathrm {e} ^{mathrm {j} {frac {pi }{4}}}}}}}{2{sqrt {2} angle 45^{circ}}}}}

called polar forms, or:

V→ → =2+2j{displaystyle {vec {V}}=2+2mathrm {j} }

called a binomial, binomial, or rectangular form.

Three-phase current

Three-phase generation of electrical energy is the most common form and the one that provides the most efficient use of conductors. The use of electricity in triphasic form is common mostly for use in industries where many of the machines work with motors for this voltage.

Figure 5: Voltage of the phases of a three phase system. Between each of the phases there is a 120o dephase.

The triphasic current is formed by a set of three forms of oscillation, out of phase with respect to each other by 120º, according to the diagram shown in figure 5.

Three-phase currents are generated by alternators equipped with three coils or groups of coils, wound on three systems of equidistant pole pieces. The return of each of these circuits or phases is coupled at a point, called neutral, where the sum of the three currents, if the system is balanced, is zero, with which the transport can be carried out using only three cables.

This arrangement would be the so-called star connection, and there is also a triangle or delta connection in which the coils are coupled according to this geometric figure and the line threads start from the vertices.

There are therefore four possible interconnections between generator and load:

1. Star - Star
2. Star - Delta
3. Delta - Star
4. Delta - Delta

In the type circuits star, phase currents and line currents are equal and, when the system is balanced, line tensions are equal 3{displaystyle {sqrt {3}}} times higher than phase tensions and are advanced 30° to these:

Vlinea=[chuckles]3Vfase](φ φ +30){displaystyle V_{linea}=left[{sqrt {3}}V_{fase}right]_{left(phi +30right)}}}}

In the type circuits triangle or delta, the opposite happens, the phase and line tensions are equal and, when the system is balanced, the phase current is 3{displaystyle {sqrt {3}}} times smaller than the line current and is advanced 30° to this:

Ifase=[chuckles]Ilinea3](φ φ +30){displaystyle I_{fase}=left[{frac {I_{linea}{sqrt {3}}}{right]_{left(phi +30right)}}}}}}}

The three-phase system is a particular type within the polyphase power generation systems, although it is by far the most widely used.