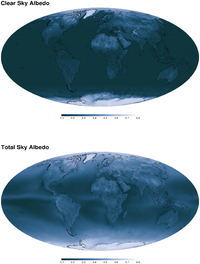
Albedo
The albedo is the percentage of radiation that any surface reflects with respect to the radiation that falls on it. Light surfaces have higher albedo values than dark ones, and shiny surfaces more than matte ones. The mean albedo of the Earth is approximately 0.3. This value is dimensionless and is measured on a scale from zero (corresponding to a black body absorbing all incident radiation) to one (corresponding to a white body reflecting all incident radiation).).
It is a measure of the tendency of a surface to reflect incident radiation.
A high albedo cools the planet, because the light (radiation) absorbed and used to heat it is minimal. Conversely, a low albedo warms the planet, because most of the light is absorbed by the planet.
The presence of water on Earth creates an interesting positive feedback for albedo, as low temperatures increase the amount of ice on its surface, making the planet whiter and increasing its albedo, which in turn cools the planet further, creating new amounts of ice; in this way, theoretically at least, the point could be reached where the entire Earth would snowball.
In astronomy, it offers an indirect means of ascertaining the nature of a star by comparing its albedo with that of known matter. The highest recorded so far in the solar system corresponds to that of Saturn's satellite Enceladus, and the lowest, to that of some carbonaceous asteroids, as well as the Martian satellites Phobos and Deimos.
Earth's albedo
| Surface | Albedo typical |
| Overland | |
| Fresh asphalt Expended asphalt | 0.04 0.12 |
| Open ocean | 0.06 (0.05 to 0.10) |
| Ceniza volcanic | 0.07 |
| Coniferous forest (summer) | 0.08 0.09 to 0.15 |
| Deciduous trees | 0.15 - 0.18 |
| Naked floor | 0.17 |
| Land deserts | 0.21 |
| Green herb | 0.25 |
| Desert sand | 0.40 |
| Clouds (average) Bright clouds | 0.50 0.78 |
| Ocean ice | 0.5-0.7 |
| New concrete | 0.55 |
| Fresh snow | 0.80-0.90 |
| Planets of the solar system | |
| Mercury | 0.06 |
| Moon | 0.07 |
| Mars | 0.15 |
| Earth (from space) | 0.3 |
| Jupiter | 0.41 |
| Saturn | 0.42 |
| Uranus | 0.45 |
| Neptune | 0.55 |
| Venus (atmosphere) | 0.70 |
| Other bodies of the solar system | |
| Cometa Halley | 0.04 |
| We | 0.06 |
| Fobos | 0.06 |
| Meteoroid | 0.07 |
| Ice cream. | 0.99 (later registered) |
| Extraordinary | |
| TrES-2b | 0.0004 (recorded amount) |
Any albedo in visible light falls within a range of about 0.9 for fresh snow to about 0.04 for charcoal, one of the darkest substances. Deeply shadowed cavities can achieve an effective albedo approaching zero for a black body. When viewed from a distance, the ocean surface has a low albedo, as do most forests, while desert areas have some of the highest albedos among landforms. Most land areas are in the albedo range of 0.1 to 0.4. The Earth's average albedo is approximately 0.3. This is much higher than for the ocean mainly due to the contribution of clouds.
The albedo of the Earth's surface is regularly estimated using Earth-observing satellite sensors such as NASA's MODIS instruments aboard the Terra and Aqua satellites. Since the total amount of reflected radiation cannot be directly measured by satellite, a mathematical model is used to translate a sample set of satellite reflectance measurements into estimates of directional hemispherical reflectance and bi-hemispherical reflectance. These calculations are based on the bi-directional reflectance distribution function (BRDF), which describes how the reflectance of a given surface depends on the observer's viewing angle and the solar angle. Therefore, the BRDF allows to translate reflectance observations into albedo. The average temperature of the Earth's surface due to its albedo and the greenhouse effect is currently about 15 °C. If the Earth were frozen solid (and therefore more reflective), the planet's average temperature would drop below -40°C. If only the continental landmasses were covered by glaciers, the planet's average temperature would drop to around 0°C. Conversely, if the entire Earth were covered by water - a so-called aquaplanet - the average temperature of the planet would rise to almost 27 °C.
Albedo of white sky and black sky
For terrestrial surfaces, it has been shown that the albedo at a solar cenital angle determined θi can be approximated by the proportional sum of two terms: the directional-hemispheric reflectance at that solar cenital angle, α α ! ! (θ θ i){displaystyle {{bar {alpha }}(theta _{i}}}}}}and bi-hemispheric reflectance, α α ! ! ! ! {displaystyle {bar {alpha }}}}, being D− − 1{displaystyle {D-1} the direct radiation ratio of a given solar angle, and D{displaystyle {D} the proportion of diffuse lighting. Therefore, the actual albedo α α {displaystyle {alpha }} (also called blue sky albedo) can be given as:
- α α =(1− − D)α α ! ! (θ θ i)+Dα α ! ! ! ! .{displaystyle {alpha }=(1-D){bar {alpha }}(theta _{i})+D{bar {alpha }}}}}}}. !
Hemispherical-directional reflectance is sometimes referred to as the black-sky albedo and bi-hemispherical reflectance as the white-sky albedo. These terms are important because they allow the albedo to be calculated for any given lighting condition from knowledge of the intrinsic properties of the surface.
Albedo variation
Global albedo variations are a natural fact that has continuously occurred throughout geological history, due to variations of exogenous and endogenous origin (continental drift and changes in the distribution of seas and continents).
These variations are superimposed by the intense environmental changes promoted by human activity (use of fossil fuels for vehicular traffic, industrial activity and domestic use).
These activities cause a dangerous increase in greenhouse gases, consequently a decrease in albedo and global warming.
A drop of as little as 0.01 in the earth's albedo would have a greater influence on climate than the effect of doubling the amount of carbon dioxide in the atmosphere.
Nuclear Physics
In nuclear physics, the albedo is the ability of a substance to reflect neutrons. It is measured by the ratio between the number of reflected neutrons and the total number of incident neutrons.
Contenido relacionado
Greece
The orchards
Electronvolt