Acid dissociation constant
An acid dissociation constant, Ka, (also known as the acidity constant, or acid ionization constant) is a quantitative measure of the strength of an acid in solution. It is the equilibrium constant for a reaction known as dissociation in the context of acid-base reactions. The equilibrium can be written symbolically as:
- Ha.
 A- + H+
A- + H+
where HA is a generic acid that dissociates by splitting into A-, known as the conjugate base of the acid, and the hydrogen ion or proton, H+, which, in the case of aqueous solutions, exists as a solvated hydronium ion. In the example shown in the figure, HA represents acetic acid, and A- the acetate ion. The chemical species HA, A-, and H+ are said to be in equilibrium when their concentrations do not change with time. The dissociation constant is usually written as a quotient of the equilibrium concentrations (in mol/L), represented by [HA], [A-], and [H+]:
- Ka=[chuckles]A− − ][chuckles]H+][chuckles]HA]{displaystyle K_{mathrm {a} }=mathrm {frac {[A^{-}][H^{+}}{[HA]}}}}}}
Due to the many orders of magnitude that the values of K a can span, in practice The acidity constant is often expressed by a logarithmic measure of the acidity constant, pKa, which is equal to -log10, and which is also often called the acid dissociation constant:
- pKa=− − log10 Ka{displaystyle mathrm {p} K_{mathrm {a} }=-log _{10}K_{mathrm {a} }}}
The higher the value of pKa, the less the extent of dissociation. A weak acid has a pKa value in the approximate range of 2 to 12 in water. Acids with pKa values less than about 2 are said to be strong acids; a strong acid is almost completely dissociated in aqueous solution, to the extent that the concentration of the undissociated acid is undetectable. Values of pKa for strong acids can be estimated by theoretical means or by extrapolation from measurements in non-aqueous media, in which the dissociation constant is lower, such as acetonitrile and dimethylsulfoxide.
Introduction
The acid dissociation constant is a direct consequence of the thermodynamics underlying the dissociation reaction, the pKa value being directly proportional to the standard Gibbs free energy change for the reaction. The value of pKa changes with temperature and can be understood qualitatively based on Le Châtelier's principle: when the reaction is endothermic, the value of pKa decreases with increasing temperature, the opposite is true for exothermic reactions. The underlying structural factors that influence the magnitude of the acid dissociation constant include Pauling's rules for acidity constants, inductive effects, mesomeric effects, and hydrogen bonding.
The quantitative behavior of acids and bases in solution can only be understood if the pKa values are known. In particular, the pH of a solution can be predicted when the analytical concentration and pKa values of all acids and bases are known; Conversely, it is also possible to calculate the equilibrium concentrations of acids and their bases in solution when the pH is known. These calculations have applications in different areas of chemistry, biology, medicine and geology. For example, many of the compounds used for medication are weak acids or bases, and knowledge of the pKa values, along with the octanol- water, can be used to estimate the extent to which the compound enters the bloodstream.
Acid dissociation constants are also essential in aqueous solution chemistry and chemical oceanography, where the acidity of water plays a key role. In living organisms, acid-base hemostasis and enzyme kinetics are dependent on the pKa values of many of the acids and bases present in the cell and in the body.
In chemistry, knowledge of pKa values is necessary for the preparation of buffer solutions, and is also a prerequisite for a quantitative understanding of the interaction between acids or bases and metal ions to form complexes. Experimentally, pKa values can be determined by potentiometric (pH) titration, but for pKa less than about 2 or about greater than 11, NMR or spectrophotometric measurements may be required due to practical difficulties with pH measurements.
Definitions
According to Arrhenius's original definition, an acid is a substance that dissociates in aqueous solution, releasing the hydrogen ion H+ (a proton):
- Ha.
 A- + H+
A- + H+
The equilibrium constant for this dissociation reaction is known as the dissociation constant. The released proton combines with a water molecule to give a (hydronium or oxonium ion) H3O+, and so on later Arrhenius proposed that the dissociation should be written as an acid-base reaction:
- HA + H2O
 A- + H3O+
A- + H3O+
The Brønsted–Lowry Theory generalizes this further by considering it as a proton exchange reaction:
- acid + base
 conjugated base + conjugated acid
conjugated base + conjugated acid
The acid loses a proton, giving the conjugate base, the proton is transferred to the base, giving the conjugate acid. For aqueous solutions of an HA acid, the base is water, the conjugate base of the acid is A-, and the conjugate acid of the base is hydronium ion. The Brønsted-Lowry definition applies to other solvents, such as dimethyl sulfoxide: solvent S acts as a base, accepting a proton and forming the conjugate acid SH+.
In solution chemistry it is common to use H+ as an abbreviation for the solvated hydrogen ion, regardless of the solvent. In aqueous solution, H+ denotes a solvated hydronium ion instead of a proton.
The designation of an acid or base as a "conjugate" depends on the context. The conjugate acid BH+ of a base B dissociates according to the equation:
- BH+ + OH-
 B + H2O
B + H2O
which is the inverse of equilibrium:
- H2O (acid) + B (base)
 OH− (base conjugada) + BH+ (conjugated acid)
OH− (base conjugada) + BH+ (conjugated acid)
The hydroxide ion OH−, a well-known base, acts here as the conjugate base of the acid water. Acids and bases are thus considered simply as proton donors or proton acceptors, respectively.
Water is amphiprotic: it can react as either an acid or a base. Another example of an amphiprotic molecule is the bicarbonate ion HCO3- which is the conjugate base of carbonic acid H2CO3 in balance:
- H2CO3 + H2O
 HCO3- + H3O+
HCO3- + H3O+
but also the conjugate acid of the carbonate ion CO32- in the reverse equilibrium reaction:
- HCO3- + OH-
 CO32- + H2O
CO32- + H2O
The balance of carbonic acid is important for acid-base homeostasis in the human body.
A broader definition of acid dissociation includes hydrolysis, in which protons are produced by the splitting of water molecules. For example, boric acid (B(OH)3) acts as a weak acid, although it is not a proton donor, due to hydrolysis:
- B(OH)3 + 2 H2O
 B(OH)4- + H3O+
B(OH)4- + H3O+
Similarly, the hydrolysis of metal ions produces ions such as [Al(H2O)6]3+ which behave as weak acids:
- [Al(H)2O)6]3+ + H2O
 [Al(H)2O)5(OH)]2+ + H3O+
[Al(H)2O)5(OH)]2+ + H3O+
Equilibrium constant
An acid dissociation constant is a particular example of an equilibrium constant. For the specific equilibrium between a monoprotic acid, HA, and its conjugate base A- in water:
- HA + H2O
 A- + H3O+
A- + H3O+
the constant thermodynamic balance, K![]() can be defined by:
can be defined by:
- K ={A− − !{H3O+!{HA!{H2O!{displaystyle K^{ominus }=mathrm {frac {{A^{{A^{}}{H_{3}O^{+}{}{{HA}{H_{2}O}}}}}}}{{{{{}{{{{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}
where {A} is the activity of the chemical species A, etc. K![]() is dimensional since the activity has no dimensions. The activities of dissociation products are placed in the numerator, the activities of the reagents are placed in the denominator. See activity coefficient for a deduction of this expression.
is dimensional since the activity has no dimensions. The activities of dissociation products are placed in the numerator, the activities of the reagents are placed in the denominator. See activity coefficient for a deduction of this expression.
Since the activity is the product of the concentration and the activity coefficient (γ) the definition could also be written as:
- K =[chuckles]A− − ][chuckles]H3O+][chuckles]HA][chuckles]H2O]× × γ γ A− − γ γ H3O+γ γ HAγ γ H2O=[chuckles]A− − ][chuckles]H3O+][chuckles]HA][chuckles]H2O]× × Interpreter Interpreter {displaystyle K^{ominus }{mathrm {{frac} {[A^{-}{3}O^{+}}{[HA][H_{2}{2}}}{frac}{frac} {gamma _{A^{-}}{H_{H_{3}{m}{
where [HA] represents the concentration of HA and Γ is a ratio of activity coefficients.
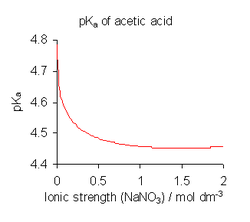
To avoid the complications involved in the use of activities, the dissociation constants are determined, when possible, in a medium of high ionic force, i.e., under conditions in which ↓ can be assumed to be always constant. for example, the medium can be a solution of 0.1 M of sodium nitrate or 3 M of potassium perchlorate (1 M = 1 mol·dm−3, a molar concentration unit). In addition, in all, except in the most concentrated solutions, water concentration may be assumed, [H2O], it's constant, approximately 55 mol·dm−3. Splitting K![]() by constant terms and writing [H+] for the concentration of hydronium, the expression is obtained:
by constant terms and writing [H+] for the concentration of hydronium, the expression is obtained:
- Ka=[chuckles]A− − ][chuckles]H+][chuckles]HA]{displaystyle K_{mathrm {a} }=mathrm {frac {[A^{-}][H^{+}}{[HA]}}}}}}
This is the commonly used definition. pKa is defined as -log10K a. Note, however, that all published dissociation constant values refer to the specific ionic medium used in their determination and that different values are obtained under different conditions, as shown for acetic acid in the illustration above. When published constants refer to an ionic strength other than that required for a particular application, it can be adjusted using Specific Ion Theory (SIT) and other theories.
Although Ka appears to have the dimension of concentration, in fact, it must be dimensionless or it would not be possible to obtain its logarithm. The illusion is the result of omitting the constant term [H_2O] from the definition of the expression. However, it is not unusual, especially in texts dealing with biochemical equilibria, to see a value quoted with a dimension such as "Ka = 300 M".
Monoprotic acids
After modifying the expression that defines Ka taking logarithms and putting pH =-log 10 [H+] we get:
- pH=pKa+log [chuckles]A− − ][chuckles]HA]{displaystyle mathrm {pH} =mathrm {p} K_{mathrm {a} }+log mathrm {frac {[A^{-}}}{[HA]}}}}} }
This is a form of the Henderson-Hasselbalch equation, from which the following conclusions can be drawn:
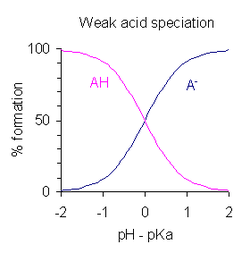
- Half of neutralization [AH]/[A-] = 1; since log (1) = 0, pH in the middle of neutralization is numerically equal to pKa. Conversely, when pH = pKaAH concentration is equal to AH concentration-.
- The tamponada region extends over the approximate interval pKa ± 2, although tamponing is weak outside the p rangeKa ±1. WhenKa ± 1, then [AH]/[A-] = 10 or 1/10.
- If pH is known, you can calculate the relationship [AH]/[A-]. This relationship is independent of the analytical concentration of acid.
In water, measurable values of pKa vary over a range from about -2 for a strong acid to about 12 for a strong acid. very weak (or strong base). All acids with a pKa value less than -2 are more than 99% dissociated at pH 0 (1 M acid). This is known as the leveling effect of the solvent since all acids appear to be at the same level of strong acids, regardless of their pKa. Likewise, all bases with a pKa value greater than the upper limit are more than 99% deprotonated for all possible pH values and are classified as strong bases.
An example of a strong acid is hydrochloric acid, HCl which has a pKa value, estimated from thermodynamic measurements of -9.3 in water. The concentration of undissociated acid in a 1 mol dm−3 solution would be less than 0.01% of the concentrations of the dissociation products. Hydrochloric acid is said to be completely dissociated in aqueous solution because the amount of undissociated acid is negligible. When the pKa and the analytical concentration of the acid are known, the extent of dissociation and the pH of a solution of a monoprotic acid can be easily calculated using a table ICE (initial concentrations, change and equilibrium concentrations).
A buffer of a desired pH can be prepared as a mixture of a weak acid and its conjugate base. In practice, the mixture can be created by dissolving the acid in water, and adding the necessary amount of strong acid or base. The pKa of the acid must be less than two units from the target pH.
Polyprotic acids
Polyprotic acids are acids that can lose more than one proton. The dissociation constant for the first proton can be written as Ka1 and the dissociation constants for successive protons as Ka2 etc Phosphoric acid, H3PO4, is an example of a polyprotide acid that can lose three protons.
balance P valueKa H3PO4  H2PO4− + H+
H2PO4− + H+pKa1 = 2.15 H2PO4−  HPO42− + H+
HPO42− + H+pKa2 = 7.20 HPO42−  PO43− + H+
PO43− + H+pKa3 = 12.37
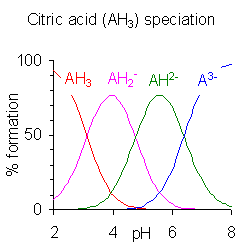
When the difference between successive values of pK is around four units or more, as in this example, each species can be considered an acid in its own right. In fact, salts of H2PO4− can be crystallized from solution by adjusting the pH around 5.5 and the salts of HPO4 >2− can crystallize from solution by adjusting the pH to around 10. The species distribution diagram shows that the concentrations of the two ions are highest at pH 5.5 and 10.
When the difference between successive values of pK is less than approximately four, there is an overlap between the pH range of existence of the species in equilibrium. The smaller the difference, the greater the overlap. The citric acid case is shown on the right; citric acid solutions are buffered over the full pH range of 2.5 to 7.5.
In general, it is true that successive values of pK increase (Pauling's First Rule). for example, for a diprotic acid, H2A, the two equilibria are:
- H2A
 Ha.− + H+
Ha.− + H+ - Ha.−
 A2− + H+
A2− + H+
it can be seen that the second proton is removed from a negatively charged species. Since the proton has a positive charge, extra work is needed to kick it off; this is the cause of the trend noted above. The (above) values for phosphoric acid illustrate this rule, as do the values for vanadic acid, H3VO4. When an exception to the rule is found, it indicates that a major change in the structure is occurring. In the case of VO2+ (aq), vanadium has an octahedral molecular geometry, (coordination number 6), while vanadic acid has a tetrahedral molecular geometry, (coordination number 4). This is the explanation why pKa1 > pKa2 for vanadium(V) oxoacids.
balance P valueKa [VOVING]2(H2O)4]+  H3VOO4 + H+ + 2H2O
H3VOO4 + H+ + 2H2O
pKa1 = 4.2 H3VOO4  H2VOO4− + H+
H2VOO4− + H+pKa2 = 2.60 H2VOO4−  HVO42− + H+
HVO42− + H+pKa3 = 7.92 HVO42−  VOO43− + H+
VOO43− + H+pKa4 = 13.27
Autoionization of DPPE&DVPE water
Water has both acidic and basic properties. The equilibrium constant for equilibrium:
- 2 H2O
 OH− + H3O+
OH− + H3O+
is given by:
- Ka=[chuckles]H3O+][chuckles]OH− − ][chuckles]H2O]2{displaystyle K_{mathrm {a} }=mathrm {frac {[H_{3}O^{+}][OH^{-}]}{[H_{2}O]{2}{2}}}}}} }
When, as usual, the concentration of water can be considered constant, this expression can be replaced by:
- Kw=[chuckles]H3O+][chuckles]OH− − ]{displaystyle K_{mathrm {w} }=[mathrm {H_{3}O} ^{+}[mathrm {OH} ^{-}],}
The value of Kw under standard conditions is 1.0×10−14. The autoionization constant of water, Kw, is therefore a special case of the acid dissociation constant.
Fundamentals
Historically, the equilibrium constant Kb for a base has been defined as the association constant for the protonation of the base, B, to the conjugated acid form, HB+. It is usually obtained from the value of Ka.
- B + H2O
 HB+ + OH−
HB+ + OH−
Using similar reasoning to the one used above:
- Kb=[chuckles]HB+][chuckles]OH− − ][chuckles]B]{displaystyle K_{mathrm {b} }=mathrm {frac {[HB^{+}][OH^{-}}{[B]}}}} }
In water, the concentration of the hydroxide ion, [OH−], is related to the concentration of the hydrogen ion by Kw = [H+] [OH−], therefore:
- [chuckles]OH− − ]=Kw[chuckles]H+]{displaystyle mathrm {[OH^{-}}}} ={frac {K_{mathrm {w}}{mathrm {[H^{+}}}}}}}}}}}}}}}}{mathrm {[m {[H^{m}}}}}}}}}}}}}}
Substitution of the expression of [OH−] into the expression of Kb gives:
- Kb=[chuckles]HB+]Kw[chuckles]B][chuckles]H+]=KwKa{displaystyle K_{mathrm {b} } }={mathrm {HB^{+} ]K_{mathrm {w}}{mathrm {[B][H^{+}}}}}}}{mathrm {w}}}{K_{mathrm {w}}}{K_{mathrm {a}}}}
When Ka, Kb and Kw are determined under the same conditions of temperature and ionic strength, it follows, taking logarithms, that pKb = pKw -pKa. In aqueous solution at 25 °C, pKw is 13.9965, thus pKb ~ 14 - pKa. Indeed, there is no need to define pKb separately from pKa, but it is done here because the values of pKb can be found in the old literature.
Temperature dependence
All equilibrium constants vary with temperature according to the van't Hoff equation
- d ln Kd T=Δ Δ H RT2{displaystyle {frac {operatorname {d} ln K}{operatorname {d}}}{frac {{delta H}^{ominus }}{RT^{2}}}}}}}}{{{{{{{displaystyle}}}}}}}{{{{{{displaystyle {exoperatorname {f} {f} {f}}{f}{f}}}{f}{f}}{f}}{f}{f}}}}}{f}{f}{f}}{f}}{f}}{f}{f}}{f}}}}}{f}{f}}}}{f}}}}{f}{f}{f}}{f}}}{f}}}}}{f}{f}}}{f}{f}}{f
R is the Universal Constant of ideal gases and T It's the absolute temperature. Thus, for exothermal reactions, (the change of standard detail, ΔH![]() , it's negative) K decreases with temperature, but for endothermal reactions (Δ)H
, it's negative) K decreases with temperature, but for endothermal reactions (Δ)H![]() is positive) K increases with temperature.
is positive) K increases with temperature.
Acidity in non-aqueous solutions
Classification of solvents
A solvent is a substance that allows the dispersion of another within it. Solvents can be classified according to their polarity as:
1. polar. They are substances in whose molecules the distribution of the electronic cloud is asymmetric; therefore, the molecule has a positive and a negative pole separated by a certain distance, so there is a permanent dipole. Water is the classic example of a polar solvent. Polar solvents can be subdivided into:
- Forecasts. They contain an O-H or N-H link. Examples: Water (H-O-H), ethanol (CH)3-CH2-OH) and acetic acid (CH)3-COOH) are prothetic polar solvents.
- Prosthetic. This type of solvent does not give or accept protons. The acetone (CH)3-CO-CH3), acetonytrile, dimethylformmide or THF (Tetrahydrofuran) are polar solvents
2. Apolar solvents. In general they are organic type substances, in whose molecules the distribution of the electronic cloud is symmetrical; so they lack permanent dipoles. Depending on the geometry of its molecules, if the individual dipole moments of its bonds are balanced, the molecule will be, as a whole, nonpolar. Some solvents of this type are: ethyl ether, benzene, toluene, xylene, ketones, hexane, cyclohexane and carbon tetrachloride.
Solvent system
The definition of a solvent system applies to any solvent that can dissociate into an anion and a cation (self-dissociation), where the resulting cation is the acid and the anion is the base. In water, autoionization corresponds to the transfer of a proton from one solvent molecule to another, being an example of amphoteric behavior.
2 H2O ▪ H3O++ -OH
Where the cation H3O+ is the acid and the anion -OH is the base.
Whereas in liquid NH3, proton transfer leads to the formation of [NH4]+, so in a solution of liquid ammonia, an acid can be described as a substance that produces [NH4]+ ions, while a base produces [NH2 ions sub>]-
2 NH3 ↔ [NH4]++ [NH2]-
In general in a self-dissociated solvent:
- An acid is a substance that increases the concentration of the protein characteristic of the solvent
- A base is a substance that increases the concentration of the characteristic anion of the solvent.
The size of the pH scale is conditioned by the index of the autoprotolysis constant (pKs), which is a measure of the solvent to generate in-situm the acidic particle (cation) and the basic particle (anion) of the solvent.
Properties of some protic solvents
| Disolvente | Acid (cation) | Base (anion) | pKs | Evaporation point (°C) |
|---|---|---|---|---|
| H2Or water | H3O+ | -OH | 14 | 100 |
| CH3OH Methanel | CH3OH2+ | CH3O- | 19.52 | 64.7 |
| NH3 Amonia | NH4+ | NH2- | 27.7 | -33.4 |
| CH3COOH Acetic acid | CH3COOH2+ | CH3COO- | 10 | 118.2 |
| CH3CN Acetonitrilo | CH3CNH+ | CH3CN- | 28.6 | 81 |
Relative strength of acids and bases
The relative strength of acids and bases is measured by how much they react with the solvent in which they are found. In aqueous solution the strength of an acid, HA, depends on the relative proton donating capacity of HA and of H3O+.
- HA + H2O ▪ H3O+ + A-
In an analogous way, the strength of a base B, in aqueous solution depends on the relative ability to accept protons from B and -OH
- B + H2O ▪ BH+ + -OH
The values of Ka (or Kb) generally refer to the ionization of acids in aqueous solutions and, when saying that “HCl is a strong acid”, it is understood that it is in aqueous media. However, if HCl is dissolved in acetic acid (a more acidic solvent than water), its ionization is much less than in water and so HCl behaves like a weak acid in this solvent.
Calculation of pH in solution in solvents analogous to H2O
| Type of substance | Equation |
|---|---|
| Strong acid | pH=− − log c0{displaystyle mathrm {pH} =-log c_{0}}} |
| weak acid | pH=12(pKa− − log c0){displaystyle mathrm {pH} ={tfrac {1}{2}}}(mathrm {p} K_{rm {a}}-log c_{0})}} |
| Par conjugado | pH=pKa+log (ca/cb){displaystyle mathrm {pH} =mathrm {p} K_{rm {a}}+log(c_{rm {a}}}/c_{rm {b}}}})} |
| Strong base | pH=14+log c0{displaystyle mathrm {pH} =14+log c_{0}} |
| weak base | pH=7+12(pKa+log c0){displaystyle mathrm {pH} =7+{tfrac {1}{2}(mathrm {p} K_{rm {a}}}+log c_{0})}} |
In the above equations, c0 is the formal or analytical concentration, ca the concentration of acid and cb the base concentration.
Non-aqueous solvents that are good proton acceptors (solvents more basic than water, for example, NH3), favor acids to ionize in them; so that in a basic solvent, all acids are strong; Therefore, it is said that the solvent has a leveling effect on the acid, since the strength of the dissolved acid cannot exceed that of the protonated solvent. For example, in aqueous solution, there can be no acid species that is a stronger acid than [H3O]+. In acidic solvents, such as CH3CO2H, H2SO4), the ionization of the bases; and therefore most acids are relatively weak under these conditions and some even ionize like bases.
A solvent is more likely to promote ionization of a dissolved acid molecule under the following circumstances.
- If it is a neurotic solvent, able to form hydrogen links.
- If you have a high donor number, so it's a strong Lewis base.
- If you have a high dielectric constant (relative permitivity), so it is a good solvent of ionic species.
pKa values of organic compounds are often obtained using aprotic solvents dimethyl sulfoxide (DMSO) and acetonitrile (ACN).
| Disolvente | Donor number | Dielectric constant |
|---|---|---|
| Acetonitrilo | 14 | 37 |
| dimethylsulfoxide | 30 | 47 |
| Water | 18 | 78 |
DMSO is widely used as an alternative to water because it has a lower dielectric constant than water, and is less polar, thereby more easily dissolving nonpolar hydrophobic substances. It has a measurable pKa range between 1 and 30. Acetonitrile is less basic than DMSO, and therefore acids are generally weaker and more the strongest bases in this solvent. Some pKa values at 25 o C for acetonitrile (ACN) and dimethyl sulfoxide (DMSO) are shown in the following tables. The values for water are included for comparison purposes.
| Ha. | ACN | DMSO | water |
|---|---|---|---|
| P-Toluenosulfonic acid | 8.5 | 0.9 | strong |
| 2,4-Dinitrophenol | 16.66 | 5.1 | 3.9 |
| Benzoic acid | 21.51 | 11.1 | 4.2 |
| Acetic acid | 23.51 | 12.6 | 4.756 |
| Fenol | 29.14 | 18.0 | 9.99 |
| BH+ | |||
| Pirrolidina | 19.56 | 10.8 | 11.4 |
| Trietilamina | 18.82 | 9.0 | 10.72 |
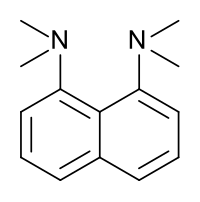
| 1.8-Bis(dimethylamine)naftaleno{{{ cult11}}}} | 18.62 | 7.5 | 12.1 |
| Piridina | 12.53 | 3.4 | 5.2 |
| Anilina | 10.62 | 3.6 | 9.4 |
The ionization of acids is less in an acidic solvent than in water. For example, hydrogen chloride is a weak acid when dissolved in acetic acid. This is because acetic acid is a much weaker base than water.
- HCl + CH3CO2H
 Cl− + CH3C(OH)2+
Cl− + CH3C(OH)2+
- acid + base
 conjugated base + conjugated acid
conjugated base + conjugated acid
Compare this reaction to what happens when acetic acid is dissolved in the more acidic solvent pure sulfuric acid
- H2SO4 + CH3CO2H
 HSO4− + CH3C(OH)2+
HSO4− + CH3C(OH)2+
The unlikely species diol geminal diol CH3C(OH)2+ is stable in these environments. For aqueous solutions the most suitable acidity function is the pH scale. Other acidity functions have been proposed for non-aqueous media, most notably the Hammett acidity function, H 0, for superacid media and its modified version H− for superbasic media.
In aprotic solvents, oligomers can be formed by hydrogen bonding, such as the well-known dimer of acetic acid. An acid can also form hydrogen bonds with its conjugate base. This process, known as homoconjugation, has the effect of increasing the acidity of acids, reducing their effective pKa values, by stabilizing the conjugate base. Homoconjugation increases the proton-donating power of toluenesulfonic acid in acetonitrile solution by a factor of nearly 800. In aqueous solutions, homoconjugation does not occur, because water forms stronger hydrogen bonds to the conjugate base than to the acid.
Mixture of solvents
When a compound has limited solubility in water it is common practice (in the pharmaceutical industry, for example) to determine the pKa values in a mixture of solvents such as water/dioxane or water/methanol, in which the compound is more soluble. In the example shown to the right, the value of pKa increases sharply with increasing percentage of dioxane as the dielectric constant of the mixture decreases.
A pKa value obtained in a mixed solvent cannot be used directly for aqueous solutions. The reason for this is that when the solvent is in its standard state its activity is "defined" as unity. For example, the standard state of water:dioxane 9:1 is just the mixed solvent, with no added solutes. To obtain the value of pKa for use in aqueous solutions they have to be extrapolated to a cosolvent concentration of zero from values obtained from various cosolvent mixtures.
These facts are obscured by the omission of the solvent in the expression that is normally used to define pKa but the values of pKa obtained in a certain given solvent mixture can be compared with any other, giving the relative acid strengths. The same is true for pKa values obtained in a particular non-aqueous solvent such as DMSO.
Until now, a universal and solvent-independent scale of dissociation constants has not been developed, since it is not known how to compare the standard states of two different solvents.
Factors Affecting pKa Values
Pauling's second rule states that pKa,1 for acids of formula Xm O(OH)n is approximately independent of n and X, such that pK<raises, 1(m = 0) ≈ 8; pKa,1(m = 1) ≈ 2; pKa,1(m = 2) ≈ -3; pKa,1(m = 3) < -10. This is related to the oxidation state of the central atom X: the higher the oxidation state, the stronger the strength of the oxoacid. For example, pKa(HClO) = 7.2; pKa(HClO2) = 2.0; pKa(HClO3) = -1 and HClO4 is a strong acid.
With organic acids the inductive effects and the mesomeric effects affect the pKa values. A simple example is provided by the effect of replacing the hydrogen atoms in acetic acid by the more electronegative chlorine atom. The effect of attraction of the electrons of the substituents makes the ionization easier, so that the successive values of pKa decrease in the series 4,7, 2, 8, 1.3, and 0.7, when 0, 1, 2, or 3 chlorine atoms are present. Hammett's equation provides a general expression for the effect of substituents.
log Ka=log K0+ρ ρ σ σ {displaystyle log K_{rm {a}}=log K_{0}+rho sigma }
Ka is the dissociation constant of a substituted compound, K0 is the dissociation constant when the substituent is hydrogen, ρ is a property of the unsubstituted compound and σ has a certain value for each substituent. A plot of log Ka against σ is a straight line, with intercept log K0 and slope ρ. This is an example of a linear Gibbs energy relationship where the log Ka is proportional to the standard Gibbs energy change. Originally Hammett formulated the relationship with the data for benzoic acid with different substituents in ortho- and para- positions: some numerical values are in Hammett's equation. This and other studies make it possible to order substituents according to their electron-withdrawing or electron-repelling power, and to distinguish between inductive and mesomeric effects.
Alcohols do not normally behave as acids in water, but the presence of a double bond adjacent to the OH group can considerably lower the pKa by the mechanism of keto-enol tautomerism. Ascorbic acid is an example of this effect. Diketone 2,4-pentanedione (acetylacetone) is also a weak acid because of the keto-enol equilibrium. In aromatic compounds, such as phenol, that have an OH substituent, conjugation to the aromatic ring as a whole greatly increases the stability of the deprotonated form.
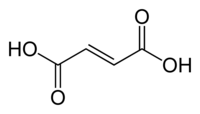
Structural effects can also be important. The difference between fumaric acid and maleic acid is a classic example. Fumaric acid is (E)-1,4-but-2-enedioic acid, a trans isomer, while maleic acid is the corresponding cis isomer, it is that is, (Z)-1,4-but-2-enedioic acid (see cis-trans isomerism). Fumaric acid has pKa values of approximately 3.5 and 4.5. In contrast, maleic acid has pKa values of approximately 1.5 and 6.5. The reason for this large difference is that when an electron is removed from the cis- (maleic acid) isomer, a strong intramolecular hydrogen bond is formed with the nearby remaining carboxyl group. This favors the formation of the maleate-H+, and opposes the removal of the second proton from that species. In the trans isomer, the two carboxyl groups are always far apart, so hydrogen bonding is not observed.
1,8-bis(dimethylamino)naphthalene has a pKa value of 12.1. This is one of the strongest amine bases known. The high basicity is attributed to stress relief on protonation and strong internal hydrogen bonding.
Also worth mentioning in this section are the effects of solvent and solvation. As it turns out, these influences are more subtle than those of a dielectric medium like the one mentioned above. For example, the order of basicity expected for methylamines in the gas phase (by the electronic effects of the methyl substituents) and observed:
Me3N > Me2NH > MeNH2 > NH3
is modified by water to:
Me2NH > MeNH2 > Me3N > NH3
Neutral methylamine molecules are hydrogen bonded to water molecules mainly by interaction through an acceptor, N-HOH, and only occasionally with more than one donor bond, NH-OH 2. Therefore, methylamines are stabilized to almost the same extent by hydration, regardless of the number of methyl groups. In stark contrast, the corresponding methylammonium cations always use 'all' of the protons available for the NH-OH 2-bond donors. The relative stabilization of the methylammonium ions therefore decreases with the number of methyl groups, explaining the order of basicity in water of the methylamines.
Thermodynamics
An equilibrium constant is related to the change in the standard Gibbs energy of the reaction ΔrG°, thus for an acid dissociation constant:
Δ Δ rG =− − RTln Ka{displaystyle Delta _{rm {r}}G^{circ}=-RTln K_{rm {a}}}}
R is the gas constant and T is the absolute temperature. Experimentally it can be considered that ΔrG°(25 °C) ≈ 5.708 pKa (in kJ mol−1). The Gibbs energy is made up of an enthalpy term and an entropy term.
G=H− − TS{displaystyle G=H-TS}
Considering that the reaction takes place under isothermal conditions, the standard Gibbs energy variation will be expressed such that
Δ Δ G =Δ Δ H − − TΔ Δ S {displaystyle Delta G^{circ }=Delta H^{circ }-TDelta S^{circ }}}
The standard enthalpy change can be determined either by calorimetry or by using the Van't Hoff equation, although the calorimetric method is preferable. When the standard enthalpy change and the acid dissociation constant are measured, the standard entropy change is easily calculated from the above equation. In the table below, the entropy terms have been calculated from the experimental values of pKa and ΔH°. The data was carefully selected and referred to 25 °C and null ionic strength, in water.
| Compound | Balance | pKa | ΔH° /kJ·mol−1 | −TΔS° /kJ·mol−1 |
|---|---|---|---|---|
| HA = acetic acid | Ha. | 4.756 | −0.41 | 27.56 |
| H2A+ = GlicinaH+ | H2A+ | 2.351 | 4.00 | 9.419 |
| Ha. | 9.78 | 44.20 | 11.6 | |
| H2A = Male acid | H2A | 1.92 | 1.10 | 9.85 |
| Ha.− | 6.27 | −3.60 | 39.4 | |
| H3A = Citric acid | H3A | 3.128 | 4.07 | 13.78 |
| H2A− | 4.76 | 2.23 | 24.9 | |
| Ha.2− | 6.40 | −3.38 | 39.9 | |
| HA = Boric acid | Ha. | 9.237 | 13.80 | 38.92 |
| H3A = Phosphoric acid | H3A | 2.148 | −8.00 | 20.26 |
| H2A− | 7.20 | 3.60 | 37.5 | |
| Ha.2− | 12.35 | 4 p.m. | 54.49 | |
| Ha.− = sulfate hydrogen | Ha.− | 1.99 | −22.40 | 33.74 |
| H2A = Oxalic acid | H2A | 1.27 | −3.90 | 11.15 |
| Ha.− | 4.266 | 7.00 | 31.35 |
| Compound | Balance | pKa | ΔH° /kJ·mol−1 | −TΔS° /kJ·mol−1 |
|---|---|---|---|---|
| B = Ammonium | HB+ | 9.245 | 51.95 | 0.8205 |
| B = methylamine | HB+ | 10.645 | 55.34 | 5.422 |
| B = Trietilamina | HB+ | 10.72 | 43.13 | 18.06 |
The first point to note is that when pKa > 0, the standard Gibbs energy change for the dissociation reaction is also positive; that is, the dissociation of a weak acid is not a spontaneous process. Second, some reactions are exothermic and others are endothermic, but when ΔH° < 0, the term −TΔS° is the dominant factor, which determines that ΔG° > 0. Finally, the entropy contribution is always unfavorable in these reactions.
Note that the standard energy change of the reaction is for the changes from the reactants in their standard states to the products in their standard states. The Gibbs energy change at equilibrium is zero, since the chemical potentials of reactants and products are equal at equilibrium.
Experimental determination
Experimental determination of pKa values is normally performed by means of titrations (or titrations) in a medium of high ionic strength and at constant temperature. A typical procedure might be as follows. A solution of the compound in the medium is acidified with a strong acid to the point that the compound is fully protonated. The solution is then titrated with a strong base until all the protons have been removed. At each titration point, the pH is measured using a glass electrode and a pH-meter. Equilibrium constants are found by fitting calculated pH values to observed values, using the method of least squares.
The total volume of strong base added should be small compared to the initial volume of solution to be titrated, in order to keep the ionic strength approximately constant. This will ensure that pKa remains unchanged during the titration.
A calculated titration curve for oxalic acid is shown on the right. Oxalic acid has pKa values of 1.27 and 4.27. Therefore, the buffering regions will be centered around pH 1.3 and pH 4.3. The buffer regions carry the necessary information to obtain the pKa values as well as the variation of the concentrations of the acid and its conjugate base in a buffer region.
Between the two buffer regions there is an end point of the titration or equivalence point, where the pH changes by around two units. This end point is unclear and is typical of a diprotic acid whose buffer zones overlap somewhat: pKa2 - pKa1 is roughly three units in this example. (If the difference in pK values were around two or less, the end point might not be detectable.) The second end point starts near pH 6.3 and is sharp. This indicates that all the protons have been removed. When this occurs, the solution is not buffered and the pH rises abruptly with the addition of a small amount of strong base. However, the pH will not continue to rise indefinitely. A new buffering region begins around pH 11 (pKw - 3), which is where autoionization of water becomes important.
It is very difficult to measure pH values less than two in aqueous solution with a glass electrode, because the Nernst equation stops working at such low pH values. To determine pK values of less than about 2 or more than about 11, or values of less than about 2 or more than about 11, spectrophotometric or NMR measurements can be used instead of, or combined with, pH measurements.
When the glass electrode cannot be used, such as in non-aqueous solutions, spectrophotometric methods are often used. This may include absorbance or fluorescence measurements. In both cases it is assumed that the amount measured is proportional to the sum of the contributions of each photoactive species; with absorbance measurements the Beer-Lambert law is assumed to apply.
Aqueous solutions with normal water cannot be used for 1H NMR measurements but heavy water, D2, must be used instead Or. 13C NMR data, however, can be used with normal water and 1H NMR spectra can be used with non-aqueous media. Quantities measured with NMR are the average duration of chemical shifts, as proton exchange is rapid on the NMR time scale, other chemical shifts, such as those of 31P, can be measured.
Microconstants
A base like spermine has a few different sites where protonation can occur. In this example, the first proton can go to the terminal -NH2 group, or to any of the internal -NH- groups. The pKa values for dissociation of protonated spermine at one or the other of the sites are examples of microconstants. They cannot be directly determined by pH, absorbance, fluorescence, or NMR measurements. However, the protonation site is very important for biological functions, so mathematical methods have been developed for the determination of microconstants.
Applications and importance
Knowledge of pKa values is important for the quantitative treatment of systems involving acid-base equilibria in solution. There are many applications in biochemistry; for example, the pKa values of protein side chains and amino acids are of great importance for enzyme activity and protein stability. Protein pKa values cannot always be measured directly, but can be calculated using theoretical methods. Buffer solutions are widely used to provide solutions at or near physiological pH for the study of biochemical reactions; the design of these solutions depends on a knowledge of pKa values. of its components. Important buffer solutions include MOPS, which provides a pH 7.2 solution, and tricine, which is used in gel electrophoresis. Buffering is an essential part of acid-base physiology including acid-base hemostasis, and is key to understanding disorders such as acid-base imbalance. The isoelectric point of a given molecule is a function of its pK values, thus different molecules have different isoelectric points. This enables a technique called isoelectric focusing, which is used for the separation of proteins by two-dimensional gel electrophoresis.
Buffer solutions also play a key role in analytical chemistry. They are used when there is a need to fix the pH of a solution to a certain value. Compared to an aqueous solution, the pH of a buffer solution is relatively insensitive to the addition of a small amount of strong acid or strong base. The buffering capacity of a single buffer solution is greatest when pH = pKa. In acid-base extraction, the efficiency of extraction of a compound into an organic phase, such as an ether, can be optimized by adjusting the pH of the aqueous phase using a suitable buffer. At the optimum pH, the concentration of electrically neutral species is maximized, such a species being more soluble in organic solvents that have a lower dielectric constant than it is in water. This technique is used for the purification of weak acids and bases.
A pH indicator is a weak acid or base that changes color in the pH transition range, which is approximately pKa ± 1. The design of a universal indicator requires a mixture of indicators whose pKa values differ by about two units such that their pH transition ranges exactly overlap.
In pharmacology, the ionization of a compound alters its physical behavior and its macroscopic properties, such as solubility and lipophilicity (log p). For example, ionization of a compound will increase solubility in water, but decrease lipophilicity. This is exploited in drug development to increase the concentration of a compound in the blood by adjusting the pKa of an ionizable group.
Knowledge of the values of pKa is important for understanding coordination complexes, which are formed by the interaction of a metal ion, M+, acting as a Lewis acid, with a ligand, L, acting as a Lewis base. However, the ligand can also undergo protonation reactions, so the formation of a complex in aqueous solution could be represented symbolically by the reaction:
- [M(H)2O)n]m+ +LH
 [M(H)2O)n−1L](m−1)+ + H3O/sup mentioned in Pine et al.+
[M(H)2O)n−1L](m−1)+ + H3O/sup mentioned in Pine et al.+
- [M(H)2O)n]m+ +LH
To determine the equilibrium constant for this reaction, in which the ligand loses a proton, the pKa of the protonated ligands must be known. In practice, the ligand can be polyprotic, for example EDTA4- can accept four protons; in which case, all values of pKa must be known. In addition, the metal ion is subject to hydrolysis, that is, it behaves like a weak acid, so the pK values for the hydrolysis reactions must also be known. The risks associated with an acid or a base require a knowledge of the pKa values. For example, hydrogen cyanide is a highly toxic gas, because the ion Cyanide inhibits the iron-containing enzyme cytochrome c oxidase. Hydrogen cyanide is a weak acid in aqueous solution, with a pKa of about 9. In strongly alkaline solutions, around pH 11, it follows that hydrogen cyanide sodium cyanide is "totally dissociated" so the risk due to hydrogen cyanide gas is very low. In acid solution, on the other hand, it is very dangerous because all the cyanide is in the acid form. Oral ingestion of cyanide is potentially fatal, independent of pH, due to reaction with cytochrome c oxidase.
In environmental sciences, acid–base balances are important for lakes and rivers; for example, humic acids are important components of natural waters. Another example occurs in chemical oceanography: In order to quantify the solubility of Fe(III) in seawater at various salinities, the pKa values for the formation of the hydrolysis products of Fe(III) were determined. Fe(III), Fe(OH)2+, Fe(OH)2+ and Fe(OH)3, together with the solubility product of iron hydroxides.
Values for common substances
There are multiple techniques to determine the pK, one of a chemical substance, giving rise to some discrepancies between different sources. Thus the measured values typically vary by 0.1 units from one to the other. The data presented here refer to 25 °C, in water. More values can be found in thermodynamics, above.
| Name of chemical compound | Balance | pKa |
|---|---|---|
| B = Adenine | BH22+ | 4.17 |
| BH+ | 9.65 | |
| H3A = arsenic acid | H3A | 2.22 |
| H2A− | 6.98 | |
| Ha.2− | 11.53 | |
| HA = benzoic acid | Ha. | 4.204 |
| HA = Butanoic acid | Ha. | 4.82 |
| H2A = Crymal acid | H2A | 0.98 |
| Ha.− | 6.5 | |
| B = codeine | BH+ | 8.17 |
| HA = Cresol | Ha. | 10.29 |
| HA = Formic acid | Ha. | 3.751 |
| HA = fluoride acid | Ha. | 3.17 |
| HA = Cyanide acid | Ha. | 9.21 |
| HA = Hydrogen Seleniide | Ha. | 3.89 |
| HA = Hydrogen peroxide (90 %) | Ha. | 11.7 |
| HA = dairy acid | Ha. | 3.86 |
| HA = Propanoic acid | Ha. | 4.87 |
| HA = Fenol | Ha. | 9.99 |
| H2A = L-(+)-ascorbic acid | H2A | 4.17 |
| Ha.− | 11.57 |
Further reading
- Albert, A.; Serjeant, E.P. (1971). The Determination of Ionization Constants: A Laboratory Manual. Chapman & Hall. ISBN 0412103001. The reference uses the obsolete parameter
|coautores=(help) (Previous edition published as Ionization constants of acids and bases. London (UK): Methuen. 1962.) - Atkins, P.W.; Jones, L. (2008). Chemical Principles: The Quest for Insight (4th edition). W.H. Freeman. ISBN 1-4292-0965-8. The reference uses the obsolete parameter
|coautores=(help) - Housecroft, C.E.; Sharpe, A.G. (2008). Inorganic chemistry (3rd edition). Prentice Hall. ISBN 0131755536. The reference uses the obsolete parameter
|coautores=(help) (non-aqueous solvents) - Hulanicki, A. (1987). Reactions of Acids and Bases in Analytical Chemistry. Horwood. ISBN 0853123306. (Translation Editor: Mary R. Masson)
- Perrin, D.D.; Dempsey, B.; Serjeant, E.P. (1981). pKa Prediction for Organic Acids and Bases. Chapman & Hall. ISBN 041222190X.
- Reichardt, C. (2003). Solvents and Solvent Effects in Organic Chemistry (3rd edition). Wiley-VCH. ISBN 3-527-30618-8. Chapter 4: Solvent Effects on the Position of Homogeneous Chemical Equilibria.
- Skoog, D.A.; West, D.M.; Holler, J.F.; Crouch, S.R. (2004). Fundamentals of Analytical Chemistry (8th edition). Thomson Brooks/Cole. ISBN 0-035523-0.
Contenido relacionado
Livermorio
Heterocyclic compound
Radical (chemistry)

![{displaystyle K_{mathrm {a} }=mathrm {frac {[A^{-}][H^{+}]}{[HA]}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/4df1424aa532585fc7ad6dd660a596705ee31a2b)


![{displaystyle K^{ominus }=mathrm {{frac {[A^{-}][H_{3}O^{+}]}{[HA][H_{2}O]}}times {frac {gamma _{A^{-}}gamma _{H_{3}O^{+}}}{gamma _{HA}gamma _{H_{2}O}}}=mathrm {frac {[A^{-}][H_{3}O^{+}]}{[HA][H_{2}O]}} times Gamma } }](https://wikimedia.org/api/rest_v1/media/math/render/svg/98e5acdd208e3a6eda8213278e88c22d19e4c509)
![{displaystyle mathrm {pH} =mathrm {p} K_{mathrm {a} }+log mathrm {frac {[A^{-}]}{[HA]}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e741bfd0c07772fa2abd205e79cd865a398268e)

![{displaystyle K_{mathrm {a} }=mathrm {frac {[H_{3}O^{+}][OH^{-}]}{[H_{2}O]^{2}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0fd2af6a4e208433b23af32cd7afa504c549f0e)
![{displaystyle K_{mathrm {w} }=[mathrm {H_{3}O} ^{+}][mathrm {OH} ^{-}],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b28e22a7001351bdc196d0c1d2e7ea94f3b2842f)
![{displaystyle K_{mathrm {b} }=mathrm {frac {[HB^{+}][OH^{-}]}{[B]}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e8602a5fa0751164332991a802fe0f0a9226ba2)
![{displaystyle mathrm {[OH^{-}]} ={frac {K_{mathrm {w} }}{mathrm {[H^{+}]} }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab7f583da9f8b50145990ffa4342919930edfa16)
![{displaystyle K_{mathrm {b} }={frac {[mathrm {HB^{+}} ]K_{mathrm {w} }}{mathrm {[B][H^{+}]} }}={frac {K_{mathrm {w} }}{K_{mathrm {a} }}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55e99b9289faff1c69f7cc5b289e461e363515a5)