Accuracy and Precision
In a set of measurements, accuracy is how close the measurements are to a specific value, while precision is how close the measurements are to each other.
Precision has two definitions:
- Most commonly, it is a description of systematic errors, a measure of statistical bias; low precision causes a difference between a result and a 'true' value. ISO calls this truthfulness.
- Alternatively, ISO defines precision as describing a combination of the above two types of observation error (random and systematic), so high precision requires both high precision and high trueness.
Precision is a description of random errors, a measure of statistical variability.
In simpler terms, given a set of data points of repeated measurements of the same quantity, the set can be said to be accurate if their average is close to the true value of the quantity being measured, whereas the set can be said to be accurate. set is accurate if the values are close to each other. In the first, most common definition of "accuracy" above, the two concepts are independent of each other, so a particular set of data can be said to be accurate, precise, both, or neither.
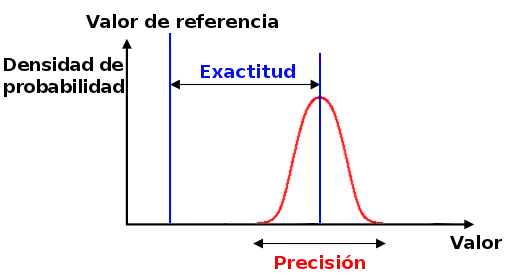
Common Technical Definition
In the fields of science and engineering, the precision of a measurement system is the degree to which the measurements of a quantity closely approximate the actual value of that quantity. The precision of a measurement system, related to reproducibility and repeatability, is the degree to which repeated measurements under unchanged conditions show the same results. Although the two words precision and accuracy may be synonymous in colloquial usage, they are deliberately contrasted in the context of the scientific method.
The field of statistics, where the interpretation of measurements plays a central role, prefers to use the terms bias and variability rather than accuracy and precision: bias is the amount of inaccuracy and variability is the amount of imprecision.
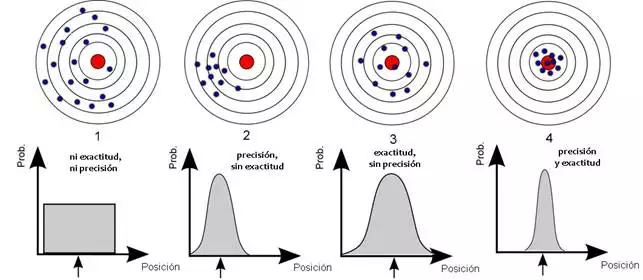
A measurement system can be exact but not exact, precise but not exact, neither, or both. For example, if an experiment contains a systematic error, then increasing the sample size generally increases precision but does not improve accuracy. The result would be a series of consistent but inaccurate results from the flawed experiment. Removing the systematic error improves the precision but does not change the precision.
A measurement system is considered valid if it is accurate and precise . Related terms include bias (nonrandom or driven effects caused by a factor or factors unrelated to the independent variable) and error (random variability).
The terminology is also applied to indirect measurements, that is, values obtained by a computational procedure from observed data.
In addition to accuracy and precision, measurements can also have a measurement resolution, which is the smallest change in the underlying physical quantity that produces a measurement response.
In numerical analysis, precision is also the closeness of a calculation to the true value; while precision is the resolution of the representation, typically defined by the number of decimal or binary digits.
In military terms, accuracy primarily refers to the accuracy of fire ( justesse de tir ), the precision of fire expressed by the closeness of a grouping of shots to and around the center of the target.
Quantification
In industrial instrumentation, precision is the measurement tolerance, or transmission, of the instrument and defines the limits of errors made when the instrument is used under normal operating conditions.
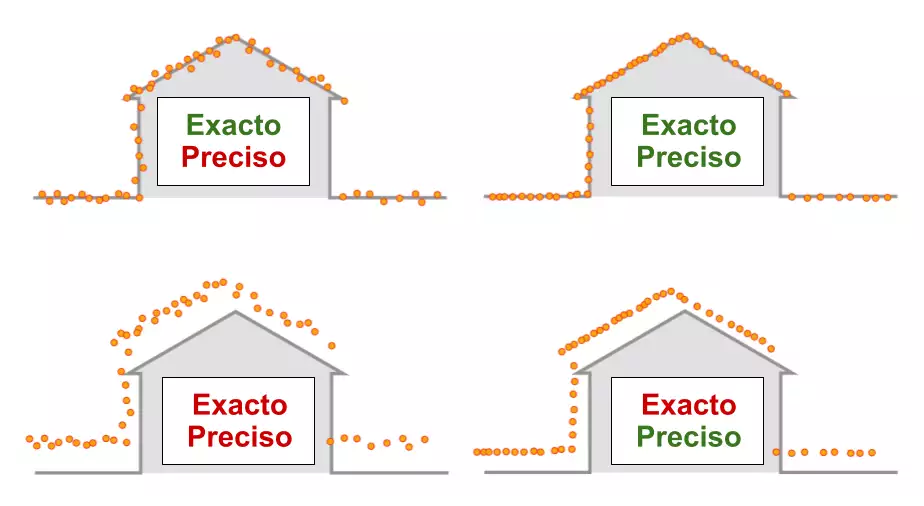
Ideally, a measurement device is accurate and precise, with measurements all close and tightly packed around the true value. The accuracy and precision of a measurement process is usually established by repeatedly measuring some traceable reference standard. Such standards are defined in the International System of Units (abbreviated SI from French: Système international d'unités ) and maintained by national standards organizations such as the National Institute of Standards and Technology in the United States.
This also applies when measurements are repeated and averaged. In that case, the term standard error is correctly applied: the precision of the average is equal to the known standard deviation of the process divided by the square root of the number of measurements averaged. Also, the central limit theorem shows that the probability distribution of the averaged measurements will be closer to a normal distribution than that of the individual measurements.
With regard to precision we can distinguish:
- the difference between the mean of the measurements and the reference value, the bias. It is necessary to set and correct the bias for calibration.
- the combined effect of that and accuracy.
A common convention in science and engineering is to express accuracy and/or precision implicitly by means of significant figures. When not expressly indicated, it is understood that the margin of error is half the value of the last significant place. For example, a record of 843.6 m, or 843.0 m, or 800.0 m would imply a margin of 0.05 m (last significant place is the tenths place), while a record of 843 m would imply a margin of error of 0.5 m (the last significant digits are the units).
A reading of 8000m, with trailing zeros and no decimal point, is ambiguous; trailing zeros may or may not be considered significant figures. To avoid this ambiguity, the number could be represented in scientific notation: 8.0 × 10 m indicates that the first zero is significant (thus a margin of 50 m) while 8,000 × 10 m indicates that all three zeros are significant , giving a margin of 0.5 meters Similarly, a multiple of the basic unit of measurement can be used: 8.0 km equals 8.0 × 10 meter. Indicates a margin of 0.05 km (50 m). However, relying on this convention can lead to false precision errors when accepting data from sources that do not obey it. For example, a source that reports a number like 153,753 with a precision of +/- 5,000 appears to have a precision of +/- 0.5. According to convention,
Alternatively, in a scientific context, if you want to indicate the margin of error more precisely, you can use a notation such as 7.54398(23) × 10 m, which means a range between 7.54375 and 7.54421 × 10m
Accuracy includes:
- repeatability — the variation that arises when every effort is made to keep conditions constant using the same instrument and operator, and repeating over a short period of time; and
- reproducibility — the variation that arises using the same measurement process between different instruments and operators, and over longer periods of time.
In engineering, precision is often taken as three times the standard deviation of the measurements taken, which represents the range in which 99.73% of the measurements can occur. For example, an ergonomist measuring the human body can be confident that 99.73% of his extracted measurements are within ± 0.7 cm, using the GRYPHON processing system, or ± 13 cm, using GRYPHON data. without processing.
ISO definition (ISO 5725)
A change in the meaning of these terms appeared with the publication of the ISO 5725 series of standards in 1994, which is also reflected in the 2008 edition of the "BIPM International Vocabulary of Metrology" (VIM), articles 2.13 and 2.14.
According to ISO 5725-1, the general term "accuracy" is used to describe how close a measurement is to the true value. When the term is applied to sets of measurements of the same measurand, it implies a random error component and a systematic error component. In this case, trueness is the closeness of the mean of a set of measurement results to the actual (true) value, and precision is the closeness of agreement between a set of results.
ISO 5725-1 and VIM also avoid the use of the term "bias", previously specified in BS 5497-1, because it has different connotations outside the fields of science and engineering, such as medicine and law. Precision of a target grouping according to BIPM and ISO 5725.
In binary classification
Precision is also used as a statistical measure of how well a binary classification test correctly identifies or excludes a condition. That is, precision is the proportion of correct predictions (both true positives and true negatives) among the total number of cases examined. As such, it compares probability estimates before and after the test. To clarify the context for semantics, it is often referred to as "Rand precision" or "Rand index". It is a test parameter. The formula for quantifying binary precision is:

Please note that in this context the concepts of trueness and precision defined in ISO 5725-1 are not applicable. One of the reasons is that there is not a single “true value” of a quantity, but two possible true values for each case, while precision is an average of all cases and therefore takes both values into account. However, the term accuracy is used in this context to refer to a different metric originating from the field of information retrieval (see below).
In psychometry and psychophysics
In psychometrics and psychophysics, the term precision is used interchangeably with constant validity and error . Precision is synonymous with reliability and variable error . The validity of a measurement instrument or psychological test is established through experimentation or correlation with behavior. Reliability is established with a variety of statistical techniques, classically through an internal consistency test such as Cronbach's alpha to ensure that sets of related questions have related answers, and then comparison of those related questions among the reference population. and the target population.
In logic simulation
In logic simulation, a common mistake in evaluating accurate models is to compare a logic simulation model with a transistor circuit simulation model. This is a comparison of differences in precision, not accuracy. Precision is measured with respect to detail and accuracy is measured with respect to reality.
In information systems
Information retrieval systems, such as databases and web search engines, are evaluated using many different metrics, some of which are derived from the confusion matrix, which divides results into true positives (correctly retrieved documents). , true negatives (documents not correctly retrieved), false positives (documents incorrectly retrieved), and false negatives (documents not incorrectly retrieved). Commonly used metrics include the notions of accuracy and recall. In this context, accuracy is defined as the fraction of retrieved documents that are relevant to the query (true positives divided by true+false positives), using a human-selected set of relevant results. Retrieval is defined as the fraction of relevant documents retrieved compared to the total number of relevant documents (true positives divided by true positives + false negatives). Less commonly, the precision metric is used, which is defined as the total number of correct classifications (true positives plus true negatives) divided by the total number of documents.
None of these metrics take into account the ranking of results. Ranking is very important to web search engines because readers rarely get past the first page of results, and there are too many documents on the web to manually rank as to whether they should be included or excluded from a given search. Adding a limit on a particular number of results takes ranking into account to some extent. The precision of the measure in k, for example, is a measure of precision that looks at only the top ten (k=10) search results. More sophisticated metrics, such as discounted cumulative profit, take into account each individual rating and are more commonly used where this matters.
Contenido relacionado
Dragon curve
Decimal separator
Incenter

