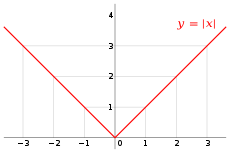
Absolute value

In mathematics, the absolute value or moduleof a real number x{displaystyle x}, denoted by 日本語x日本語{displaystyle 日本語x, is the value of x{displaystyle x} without considering the sign, be it positive or negative. For example, the absolute value of 3{displaystyle 3} That's it. 3{displaystyle 3} and the absolute value of − − 3{displaystyle} That's it. 3{displaystyle 3}. Some authors extend the notion of absolute value to complex numbers, where the absolute value coincides with the module.

Absolute value is linked to the notions of magnitude, distance and norm in different mathematical and physical contexts. The concept of absolute value of a real number can be generalized to many other mathematical objects, such as quaternions, ordered rings, fields, or vector spaces.

Function Graphic absolute value.

Definition

Real numbers

For any real number x{displaystyle x}, the absolute value or module of x{displaystyle x} denotes by 日本語x日本語{displaystyle 日本語x and is defined as:

<math alttext="{displaystyle |x|=left{{begin{array}{rcl}x,&{mbox{si}}&xgeq 0\-x,&{mbox{si}}&x日本語x日本語={x,Yeah.x≥ ≥ 0− − x,Yeah.x.0{displaystyle Șx:}{left{begin{array}{rcl}x, fake{mbox{si}}}}{x agesgeq 0-x, stranger{mbox{si}}{others}{end{array}}}right. !<img alt="{displaystyle |x|=left{{begin{array}{rcl}x,&{mbox{si}}&xgeq 0\-x,&{mbox{si}}&x

The absolute value of x{displaystyle x} is always a positive number or zero but never negative: when x{displaystyle x} It's a negative number. <math alttext="{displaystyle (x(x.0){displaystyle (x.<img alt="{displaystyle (x then its absolute value is necessarily positive 0)}" xmlns="http://www.w3.org/1998/Math/MathML">(日本語x日本語=− − x▪0){displaystyle (VAS =-x)}0)}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/c1814db01308b1fe3992c15abb9f3f1c95c8dddd" style="vertical-align: -0.838ex; width:14.93ex; height:2.843ex;"/>.

From a geometric point of view, the absolute value of a real number can be seen as the distance between that number and zero. In general, the absolute value of the difference between two numbers is the distance between them.

Properties

Absolute value has the following four fundamental properties, consider a,b한 한 R{displaystyle a,bin mathbb {R} } then.

日本語a日本語≥ ≥ 0No-negative日本語a日本語=0 a=0Positive definition日本語ab日本語=日本語a日本語日本語b日本語Multiplicity property日本語a+b日本語≤ ≤ 日本語a日本語+日本語b日本語Triangular inequality{displaystyle {begin{aligned}{aligned}{aligned}{geq 0 fake{text{No-negativity}}}}}}{iff a=0}{{text{Definition positive}}}}{posstimabficient}{experienced}{text{Property multiplied}{positive}{positive}{experiodus}{exa+bsexperiodexperindibsexperindibsexperindileq}{experindibsexperimentally triangular}{experindibsexperimentally unsexperimentality}{exority}{exority}{lection}{experimentally hypothesexperimentally unsexperimentally unsexperiedsexority}{exority}{exority}{experiedsexperimentally hypothesexperimentally hypothesexperiment}{experimentally

Other useful properties are as follows

日本語日本語a日本語日本語=日本語a日本語日本語− − a日本語=日本語a日本語日本語a− − b日本語=0 a=b日本語a− − b日本語≤ ≤ 日本語a− − c日本語+日本語c− − b日本語日本語ab日本語=日本語a日本語日本語b日本語Yeah.bI was. I was. 0日本語a− − b日本語≥ ≥ 日本語日本語a日本語− − 日本語b日本語日本語{displaystyle {begin{aligned}

these are a consequence of the definition or the first four properties.

Two other properties that use inequalities are

日本語a日本語≤ ≤ b − − b≤ ≤ a≤ ≤ b日本語a日本語≥ ≥ b a≤ ≤ − − bora≥ ≥ b{displaystyle {begin{aligned}{aligned}{leq biff -bleq aleq aleq b idol}{geq biff aleq -bquad {mbox{o}}}}quad ageq bend{aligned}}}}}}}

These relations can be used to solve inequalities involving absolute value, for example:

日本語x− − 3日本語≤ ≤ 9 − − 9≤ ≤ x− − 3≤ ≤ 9 − − 6≤ ≤ x≤ ≤ 12{displaystyle {begin{aligned}Provx-3associatedleq 9 strangeriff -9leq x-3leq 9leq `6leq xleq 12end{aligned}}}}}}

Equivalent definition

Yeah. x{displaystyle x} is a real number, its absolute value is a real non-negative number defined in the following two ways:

1. 日本語x日本語=x2{displaystyle Șx: {sqrt {x^{2}}}}}}
2. 日本語x日本語{displaystyle 日本語x equals the maximum {− − x,x!{displaystyle {-x,x}.

Absolute value function

The real absolute value function is defined on the set of all real numbers by assigning to each real number its respective absolute value.

Formally, the absolute value of all real numbers x{displaystyle x,} is defined by:

日本語日本語:R→ → R+ {0!x 日本語x日本語{displaystyle {begin{aligned}{quad Δ:mathbb {R} &to mathbb {R} ^{+}cup {0}x imaginarmapsto Șx{aligned}}}}}}}

which is usually expressed as:

<math alttext="{displaystyle {text{abs}}(x)=|x|=left{{begin{array}{rcl}x,&{mbox{si}}&xgeq 0\-x,&{mbox{si}}&xabs(x)=日本語x日本語={x,Yeah.x≥ ≥ 0− − x,Yeah.x.0{displaystyle {text{abs}{cHFFFFFF}}(x)= infox1left{{begin{array}{rcl}x, fake{mbox{si}}}}}{geq 0-x, fake{mbox{si}}}{end{array}}right. !<img alt="{displaystyle {text{abs}}(x)=|x|=left{{begin{array}{rcl}x,&{mbox{si}}&xgeq 0\-x,&{mbox{si}}&x

By definition, the absolute value of x{displaystyle x,} will always be greater or equal than zero and never negative.

This function is continuous in all the real straight and is differential in R{displaystyle mathbb {R} } less x=0{displaystyle x=0}.

Relation to the sign function

The real absolute value function of a real number returns its value regardless of sign while the sign function returns the sign of a number regardless of its value. The following equations show the relationship between these two functions:

日本語x日本語=xsgn (x)(x)}

or

日本語x日本語sgn (x)=x{displaystyle Șx1operatorname {sgn} (x)=x}

and stop xI was. I was. 0{displaystyle xneq 0}

sgn (x)=日本語x日本語x=x日本語x日本語{displaystyle operatorname {sgn} (x)={frac {intx1}{x1}}}{frac {x}{intx1}}}}}{displaystyle operatorname {sgn}

Derivative

The actual function absolute value is derived for each xI was. I was. 0{displaystyle xneq 0} But it's not differential x=0{displaystyle x=0}. Your derivative, stop xI was. I was. 0{displaystyle xneq 0}, is given by the following function

<math alttext="{displaystyle {frac {d}{dx}}|x|={frac {x}{|x|}}={begin{cases}-1&x0end{cases}}}" xmlns="http://www.w3.org/1998/Math/MathML">ddx日本語x日本語=x日本語x日本語={− − 1x.01x▪0{displaystyle {frac {d}{dx}{dx}{frac {x{x}{x}{x}{s}}}}={begin{cases}––––1 fakex}{1}{1st}}}}}}<img alt="{displaystyle {frac {d}{dx}}|x|={frac {x}{|x|}}={begin{cases}-1&x0end{cases}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/543b9978aeec9e3924cf2552243df554c2f9c364" style="vertical-align: -2.671ex; width:29.04ex; height:6.343ex;"/>

Stop. xI was. I was. 0{displaystyle xneq 0} the derivative of the function absolute value is the function sign

ddx日本語x日本語=sgn x{displaystyle {frac {d}{dx}{dx}})

Antiderivative

The antiderivative (indefinite integral) of the real absolute value function is

∫ ∫ 日本語x日本語dx=x日本語x日本語2+C{displaystyle int Δx1⁄4x1⁄2}{frac {x1}{2}{2}}+C}

where C{displaystyle C} is a constant of arbitrary integration.

Distance

In general, the absolute value of the difference of two real numbers is used to find the distance between them. In fact, the concept of a distance or metric function in mathematics can be seen as a generalization of the absolute value that expresses the distance along the real number line.

• La function absolute value is a continuous function in all its domain, with its derivative function essential discontinue in (0;0), with two branches of constant values.
• The function and = xDoxSD, using absolute value, is a growing and continuous function, its graph is obtained from the parable graph and=x², reflecting the left branch over the Ox axis.

The set of reals with the norm defined by absolute value (R,日本語⋅ ⋅ 日本語){displaystyle (mathbb {R} ultimate knowledge}} It's a Banach space.

Absolute value of a complex number

The absolute value of a complex number z{displaystyle z,} It's distance. r{displaystyle r,} from z{displaystyle z,} to the origin. Here we see that z{displaystyle z,} and its conjugate z! ! {displaystyle {bar {z},} They have the same absolute value.

Generalization is possible. because in R and C they are going to express the notion of distance.

Since complex numbers do not form an ordered set in the sense of real numbers, the generalization of the concept is not direct, but requires the following identity, which provides an alternative and equivalent definition for absolute value:

日本語z日本語=zz↓ ↓ {displaystyle 日本語={sqrt {zz^{}}}}}} where z^♪ is the conjugate of the complex number z.

In this way, given any complex number of the form

z=x+iand{displaystyle z=x+iy,}

with x and y real numbers, the absolute value or module of z is formally defined by:

日本語z日本語=x2+and2{displaystyle 日本語={sqrt {x^{2}+y^{2}}}}}}

Since complex numbers are a generalization of real numbers, it is logical that we can represent the latter in this way as well:

日本語x+i0日本語=x2+02=x2=日本語x日本語{displaystyle Δx+i0ё={sqrt {x^{2}+0^{2}}}}}={sqrt {x^{2}}}}

Similar to the geometric interpretation of absolute value for real numbers, it follows from the Pythagorean Theorem that the absolute value of a complex number corresponds to the distance in the complex plane of that number from the origin, and more so in In general, that the absolute value of the difference of two complex numbers is equal to the distance between them.

Properties

The absolute value of complexes shares all the properties seen above for real numbers. Furthermore, if

z=x+iand=r(# φ φ +iwithout φ φ ),z! ! =x− − iand{displaystyle z=x+iy=r(cos phi +isin phi),qquad {bar {z}=x-iy}

is the conjugate of z, then it is verified that:

日本語z日本語=r{displaystyle 日本語=r,}

日本語z日本語=日本語z! ! 日本語{displaystyle 日本語 繁體字 Français Español}

日本語z日本語=zz! ! {displaystyle 日本語={sqrt {z{bar {z}}}}}}

This last formula is the complex version of the first identity in reals that we mentioned in this section.

Since the positive real numbers form a subgroup of the complex numbers under the multiplication operator, we can think of absolute value as an endomorphism of the multiplicative group of complex numbers.

Generalizations

Hypercomplex numbers

In addition to complex numbers, the absolute value function can be extended to hypercomplex numbers such as quaternions or octonions. In these algebras about the real numbers the absolute value of a number h is defined as:

日本語h日本語=hh! ! {displaystyle Δh1⁄1⁄2⁄4⁄2⁄4⁄4}}}}}{displaystyle

Where h! ! {displaystyle {bar {h}}} represents the hyperset h.

Vector Spaces

In vector spaces that are not algebras over real numbers, the concepts of modulus, norm, and seminorm generalize the notion of absolute value of real numbers.

P-adic numbers

Ostrowski's theorem shows that on the body of rational numbers Q{displaystyle mathbb {Q} } only a certain number of non-trivial rules can be defined with the properties of absolute value. In addition to the ordinary absolute value, the p-addic standards can be defined 日本語⋅ ⋅ 日本語p{displaystyle 日本語_{p}}, which are non-acquimedean and which have essentially the same defining properties of the ordinary absolute value, but it gives rise to a totally different topological structure.

Absolute value programming

In programming, the commonly used mathematical function to compute absolute value is abs(). This is used in the programming languages Fortran, Matlab and GNU Octave (which support it for integers, reals and complex numbers), and also in the C Language, where the labs() , llabs(), fabs(), fabsf(), and fabsl().

Coding the absolute value function for integer values is simple:

int abs (int i){ if (i . 0) return -i; else return i;!

However, when dealing with floating point the encoding becomes more complicated, since it must deal with infinity and NaN values.^{[citation needed]}

With assembly language it is possible to calculate the absolute value of a number using only three instructions. For example, for a 32-bit register on x86 architecture, using the Intel syntax:

cdq
xor eax, edx
sub eax, edx

cdq extends the sign bit of eax into edx. If eax is non-negative, then edx becomes zero, and the last two instructions have no effect, leaving eax unchanged. If eax is negative, then edx becomes 0xFFFFFFFF, or -1. The next two instructions are converted to a two's complement inversion, leaving the absolute value of the negative value in eax.

References and notes