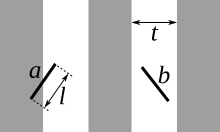Π number
The number π (pi) is the ratio between the length of a circle and its diameter in Euclidean geometry. It is an irrational number and one of the constants most important math. It is often used in mathematics, physics and engineering. The numerical value of π, truncated to its first digits, is the following:
- π π =3.141592653589793238462...... {displaystyle pi =3.141;592;653;589;793;238;462dots ,}(A000796 succession in OEIS)
The value of π has been obtained with various approaches throughout history, being one of the mathematical constants that appears the most in physics equations, along with the number e. It should be noted that the ratio between the length of any circle and its diameter is not constant in non-Euclidean geometries.
The name π
The notation with the Greek letter π comes from the initial of the words of Greek origin περιφέρεια «periphery» and περίμετρον «perimeter» of a circle, a notation that was first used by William Oughtred (1574-1660) and whose use it was proposed by the Welsh mathematician William Jones (1675-1749); although it was the mathematician Leonhard Euler, with his work Introduction to infinitesimal calculus , from 1748, who popularized it. It was formerly known as Ludolph's constant (after the mathematician Ludolph van Ceulen) or as Archimedes' constant (not to be confused with Archimedean number). Jones raises the name and symbol of this number in 1706 and Euler begins to spread it in 1736.
Archimedes calculated it with the approximation of <math alttext="{displaystyle 3+{frac {10}{71}}<pi 3+1071.π π .3+17{displaystyle 3+{frac {10}{71}}}{pi σ3+{frac {1}{7}}{7}}}}<img alt="{displaystyle 3+{frac {10}{71}}<pi as he assigned in his work Circle measurementcertainly with another notation.
History of the calculation of the value π
The search for the largest number of decimals π π {displaystyle pi } has made a constant effort by many scientists throughout history. Some historical approximations of π π {displaystyle pi } are the following.
Ancient Rome
Early Roman mathematicians discovered a relationship between the foot length of the circumference and the number 3.14.
Mesopotamia
Towards 1900-1600 a. C., some mesopotamian mathematicians used, in the calculation of segments, values of π π {displaystyle pi } equal to 3, reaching in some cases more approximate values, such as:
- π π ≈ ≈ 3+17=3.142857{displaystyle pi approx 3+{frac {1}{7}}}=3.142857}
Ancient Egypt
The approximate value of π π {displaystyle pi } in ancient cultures dates back to the time of the Egyptian scribe Ahmes in the year 1800 B.C., described in the papiro Rhind, where an approximate value of π π {displaystyle pi } asserting that the area of a circle is similar to that of a square whose side is equal to the diameter of the circle decreased in 1/9; that is, equal to 8/9 of the diameter. In modern notation:
- S=π π r2 (89⋅ ⋅ d)2=6481d2=6481(4r2){displaystyle S=pi r^{2}simeq left({frac {8{9}}}}}}cdot dright)^{2}={frac {64}{81}}}d^{2}{frac {64}{81}}{left(4r^{2}right}}
- π π 25681=3.16049...... {displaystyle pi simeq {frac {256}{81}}}=3{}16049ldots }
Among the eight mathematical documents found in the ancient Egyptian culture, two speak of circles. One is Daddy Rhind and the other is the papyrus of Moscow. Only in the first one speaks of the approximate value of the number π π {displaystyle pi }. Researcher Otto Neugebauer, in an annex to his book The Exact Sciences in Antiquity, describes a method inspired by the problems of the Ahmes papyrus to find out the value of π, through the approximation of the area of a square side 8, to that of a circle of diameter 9.
In the Bible
One of the oldest indirect references to the approximate value of π can be found in a verse from the Bible:
He made the Sea of molten metal that had ten cubits of edge to edge; it was entirely round, and five cubits high; a cord of thirty cubits measured its outline. Under the edge were pumpkins all around; they turned the Sea along thirty cubits; there were two rows of pumpkins cast into one piece.I Kings (Bible of Jerusalem)
A similar quote can be found in the Second Book of Chronicles. It appears in a list of requirements for the construction of the Great Temple of Solomon, built around 950 BC. c.:
He made the Sea of molten metal, ten cubits from edge to edge. It was entirely round and five cubits high. A cord of thirty cubits measured his outline.II Chronicles (Bible of Jerusalem)
Both citations give 3 as the value of π, which represents a notable loss of precision with respect to previous Egyptian and Mesopotamian estimates. In this regard, Christian apologetics point out that the lack of precision can be attributed to the rounding of the dimensions reported by the text.
Classical Antiquity
The Greek mathematician Archimedes (3rd century BC) was able to determine the value of π between the interval between 3 10/71, as the minimum value, and 3 1/7, as the maximum value. With this Archimedean approximation, a value is obtained with an error that oscillates between 0.024% and 0.040% of the real value. The method used by Archimedes was very simple and consisted of circumscribing and inscribing regular polygons with n-sides in circles and calculating the perimeter of said polygons. Archimedes started with circumscribed and inscribed hexagons, and doubled the number of sides until he reached polygons with 96 sides.
Around 20 AD. C., the Roman architect and engineer Vitruvius calculates π as the fractional value 25/8 by measuring the distance traveled in one revolution by a wheel of known diameter.
In the 2nd century, Claudius Ptolemy provided a fractional value by approximation:
- π π ≈ ≈ 377120=3.1416...... {displaystyle pi approx {frac {377}{120}}}}=3{}1416ldots }
The number π (“pi”) in the vigesimal system
The number π is a coefficient that multiplied by the diameter indicates the length of the circumference. That is, three times the diameter is close to the length of the circumference, but falls short. Actually, you have to multiply the diameter by 3.14159... We are expressing it as three units and a proper quotient of the decimal system.
Decimal system:
- π = 3.14159...
Vigesimal system:
- π = 03.02.16.08.18.04...
Explanation of its obtaining:
STEP 1.
Decimal quotient Multiplier Patient 20simal 0.1 (decimation) × 2 00.02. 0.01 (thousand) × 4 00.00 04 (tetracentesimas) 0.001 (thousand) × 8 00.00 00 08 (ochomilésimas) 0.0001 (diezmilésima) × 16 00.00 00 0.00001 (scientific) × 32 00.00 00 01 02 ... ... ...
STEP 2.
We have to take into account the carried ones.
3. 1 4 1 5 9 ... 03. 02 16 08 04 04 ... 14 ... 03. 02 16 08 18 04 ...
Chinese Mathematics
The calculation of pi was an attraction for expert mathematicians of all cultures. Around 120, the Chinese astronomer Zhang Heng (78-139) was one of the first to use the approximation √10, which he deduced from the ratio between the volume of a cube and the respective inscribed sphere. A century later, the astronomer Wang Fang estimated it to be 142/45 (3.155555), although the method used is unknown. A few years later, around 263, the mathematician Liu Hui was the first to suggest that 3.14 was a good approximation, using a 96 or 192 sided polygon. He subsequently estimated π as 3.14159 using a 3072-sided polygon.
At the end of the 5th century, Chinese mathematician and astronomer Zu Chongzhi calculated the value of π π {displaystyle pi } in 3.1415926, which he called “default value”, and 3.1415927, “overvalue value”, and gave two rational approximations of π π {displaystyle pi }, 22/7 and 355/113, well known both, being the last approach so good and accurate that it was not equaled up to more than nine centuries later, in the fifteenth century.
Indian Mathematics
Using a regular polygon registered from 384 sides, at the end of the centuryV the Indian mathematician Aryabhata estimated the value in 3.1416. In the middle of the seventh century, estimating incorrect the approach of Aryabhata, Brahmagupta calculates π π {displaystyle pi } Like √10calculates much less accurate than his predecessor. Around 1400 Madhava gets an exact approximation up to 11 digits (3.14159265359), being the first to use series to perform the estimate.
Islamic Mathematics
In the 9th century Al-Jwarizmi, Algebra (Hisab al yabr ua al muqabala), notes that the practical man uses 22/7 as value of π π {displaystyle pi }The geómetra uses 3, and astronomer 3.1416. In the 15th century, Persian mathematician Ghiyath al-Kashi was able to calculate the approximate value of π π {displaystyle pi } with nine digits, using a sexagesimal numerical base, which is equivalent to an approximation of 16 digits decimals: 2π π {displaystyle pi } = 6.2831853071795865_
European Renaissance
From the 12th century, with the use of Arabic numerals in calculations, the possibility of obtaining better calculations for π was greatly facilitated. The mathematician Fibonacci (1170-1250), in his Practica Geometriae, amplifies Archimedes' method, providing a narrower interval. Some 17th-century mathematicians, such as Viète, used polygons with up to 393,216 sides to approximate 3.141592653 with good precision. In 1593 the Flemish Adriaan van Roomen (Adrianus Romanus) obtained a precision of 16 decimal digits using the Archimedean method.
Modern Times (Precomputational)
In 1610 the mathematician Ludolph van Ceulen calculated the first 35 decimal places of π. It is said that he was so proud of this feat that he had it engraved on his tombstone. German mathematics textbooks for many years called π the Ludolfian number. In 1665 Isaac Newton developed the series
- arcsin x=x+12⋅ ⋅ x33+1⋅ ⋅ 32⋅ ⋅ 4⋅ ⋅ x55+1⋅ ⋅ 3⋅ ⋅ 52⋅ ⋅ 4⋅ ⋅ 6⋅ ⋅ x77+...... {displaystyle arcsin {x}=x+{frac {1}{2}}}{x^{3}}{3}}} +{frac {1cdot}{1}{2cdot}{cdot}}{cdot}{cdot}{x1}{x2}{xdot}{c}{c}{cdot}{c}}}{c}{cd}{c#
With x=12{displaystyle x={frac {1}{2}}}} got a series for:
- arcsin (12)=π π 6{displaystyle arcsin left({frac {1}{2}}}{right)={frac {pi }{6}}}}}
The English mathematician John Wallis developed in 1655 the well-known series Wallis Product:
- 21⋅ ⋅ 23⋅ ⋅ 43⋅ ⋅ 45⋅ ⋅ 65⋅ ⋅ 67⋅ ⋅ 87⋅ ⋅ 89⋅ ⋅ =π π 2{displaystyle {frac {2}{1}{1}cdot {frac}{2}{3}}}{4}{3}{3}{cdot {frac}{4}{5}}{cdot {c}{6}}{6}{6}{7frac}{7}}{cdot} {
In 1699, at the suggestion of Edmond Halley, the English mathematician Abraham Sharp (1651-1742) calculated pi to a precision of 71 decimal digits using the Gregory series:
- arctan (x)=x− − x33+x55− − ...... {displaystyle arctan(x)=x-{frac {x^{3}}{3}+}{frac {x^{5}}{5}}}-ldots }
With x=13{displaystyle x={frac {1}{sqrt {3}}}}}} a series is obtained for:
- arctan (13)=π π 6{displaystyle arctan left({frac {1}{sqrt {3}}right)={frac {pi }{6}}}}}
To achieve the precision obtained, he had to use about three hundred terms in the series. In 1720 the Frenchman Thomas de Lagny used the same method to obtain an approximation of 127 digits (only the first 112 were correct).
Leibniz calculated in a more complicated way in 1682 the following mathematical series that bears his name:
- ␡ ␡ n=0∞ ∞ (− − 1)n2n+1=1− − 13+15− − =π π 4{displaystyle sum _{n=0}^{infty }{frac {(-1)^{n}}}{2n+1}}}}=1-{frac {1}{3}}}}{frac {1}{5}}-dots ={frac {{pi }{4}}}}}}}}}}}}.
The Englishman William Oughtred was the first to use the Greek letter π as a symbol for the ratio between the lengths of a circle and its diameter. It was in the year 1706 when the Welshman William Jones stated: «3.14159 andc. = π» and proposed to always use the symbol π, and it was Leonhard Euler who, by adopting it in 1737, made it the usual notation used to this day.
The Japanese mathematician Takebe began to calculate the number π in the year 1722, with the same method exposed by Archimedes, and he was expanding the number of sides for circumscribed and inscribed polygons until he reached 1024 sides. This enormous work managed to determine π with 41 decimal places.
In 1789, the Slovenian mathematician Jurij Vega, using John Machin's formula, discovered in 1706, was the first to find out the first 140 decimal places of π, of which 126 were correct; this record stood for 52 years, until in 1841 William Rutherford calculated 208 decimal places, of which 152 were correct.
The English-born amateur mathematician William Shanks worked for 20 years to find the decimal digits of π, having obtained 707 decimal places in 1873. In 1944, D. F. Ferguson found an error in the fifty-twenty-eighth decimal digit (528th) of the Shanks series, after which all subsequent digits were wrong. In 1948, Ferguson recalculated π to 808 decimal places with the aid of an electronic calculator.
Some historical approximations of values of π, prior to the computational age, are shown in the following table:
| Year | Mathematics or document | Culture | Approximately | Error (in parts per million) |
| ~1900 a. C. | Ahmes sigh | Egyptian | 28/34 ~ 3.1605 | 6016 ppm |
| ~1600 a. C. | Susa tablet | Babylonian | 25/8 = 3.125 | 5282 ppm |
| ~600 a. C. | The Bible (Kings I, 7:23) | Jewish | 3 | 45 070 ppm |
| ~500 a. C. | Bandhayana | India | 3.09 | 16 422 ppm |
| ~250 a. C. | Syracuse Archimedes | Greek | between 3 10/71 and 3 1/7 employed 211875/67441 ~ 3.14163 | ≥402 ppm 13.45 ppm |
| ~150 | Claudio Ptolomeo | Grecoegipcia | 377/120 = 3.141666... | 23.56 ppm |
| 263 | Liu Hui | China | 3.14159 | 0.84 ppm |
| 263 | Wang Fan | China | 157/50 = 3.14 | 507 ppm |
| ~300 | Chang Hong | China | 101/2 ~ 3.1623 | 6584 ppm |
| ~ 500 | Zu Chongzhi | China | between 3.1415926 and 3.1415929 employed 355/113 ~ 3.1415929 | ≤0.078 ppm 0.085 ppm |
| ~ 500 | Aryabhata | India | 3.1416 | 2.34 ppm |
| ~600 | Brahmagupta | India | 101/2 ~ 3.1623 | 6584 ppm |
| ~ 800 | Al-Juarismi | Persian | 3.1416 | 2.34 ppm |
| 1220 | Fibonacci | Italiana | 3.141818 | 72.73 ppm |
| 1400 | Madhava | India | 3.14159265359 | 0.085 ppm |
| 1424 | Al-Kashi | Persian | 2π = 6.2831853071795865 | 0.1 ppm |
Modern Age (Computational)
Since the design of the first computer began to develop programs for the calculation of the π number with as many figures possible. Thus, in 1949 an ENIAC was able to break the record, obtaining 2037 decimal figures in 70 hours. Little by little computers were emerging that beat records and, in this way, a few years later (1954) a NORAC reached 3092 figures. For almost the whole decade of the 1960s IBMs were beating records, until an IBM 7030 could reach 250 000 decimal figures in 1966 (in 8 h and 23 min). During this time new computers were tested with algorithms for the generation of numbers from π π {displaystyle pi }.
In the 2000s, computers are capable of deriving numbers that have a huge number of decimal places. In 2009, more than two and a half trillion decimal places of pi were found using a T2K Tsukuba System supercomputer, made up of 640 high-performance computers, which together achieve processing speeds of 95 teraflops. They got it in 73 hours and 36 minutes.
| Year | Discovery | Computer used | Number of decimal figures |
| 1949 | G.W. Reitwiesner and others | ENIAC | 2037 |
| 1954 | NORAC | 3092 | |
| 1959 | Guilloud | IBM 704 | 16 |
| 1967 | CDC 6600 | 500 000 | |
| 1973 | Guillord and Bouyer | CDC 7600 | 1 001 250 |
| 1981 | Miyoshi and Kanada | FACOM M-200 | 2 000 036 |
| 1982 | Guilloud | 2 000 050 | |
| 1986 | Bailey | CRAY-2 | 29 360 111 |
| 1986 | Kanada and Tamura | HITAC S-810/20 | 67 108 839 |
| 1987 | Kanada, Tamura, Kobo and others | NEC SX-2 | 134 217 700 |
| 1988 | Kanada and Tamura | Hitachi S-820 | 201 326 000 |
| 1989 | Brothers Chudnovsky | CRAY-2 and IBM-3090/VF | 480 000 |
| 1989 | Brothers Chudnovsky | IBM 3090 | 1 011 196 691 |
| 1991 | Brothers Chudnovsky | 260 000 | |
| 1994 | Brothers Chudnovsky | 4 044 000 | |
| 1995 | Kanada and Takahashi | HITAC S-3800/480 | 6 442 450 000 |
| 1997 | Kanada and Takahashi | Hitachi SR2201 | 51 539 600 000 |
| 1999 | Kanada and Takahashi | Hitachi SR8000 | 68 719 470 000 |
| 1999 | Kanada and Takahashi | Hitachi SR8000 | 206 158 430 000 |
| 2002 | Kanada and others | Hitachi SR8000/MP | 1 241 100 000 |
| 2004 | Hitachi | 1 351 100 000 | |
| 2009 | Daisuke Takahashi | T2K Tsukuba System | 2 576 980 370 000 |
| 2009 | Fabrice Bellard | Core i7 CPU, 2.93 GHz; RAM: 6GiB | 2 699 999 990 000 |
| 2010 | Shigeru Kondo | 2 x Intel Xeon X5680, 3.33 GHz | 5 000 000 000 000 |
| 2011 | Shigeru Kondo | 10 000 000 000 000 | |
| 2019 | Emma Haruka Iwao | Google Cloud cruncher | 31 000 000 000 |
| 2020 | Timothy Mullican | 50 000 000 000 | |
| 2021 | Team DAViS of the University of Applied Sciences of the Grisons | 62 831 853 071 796 |
In the computational age of calculating π the figures have skyrocketed, not only due to the computing power that these machines are capable of generating, but also because of the prestige that this entails for the builder of the machine when its brand appears on the list of records, and for the ability to use advanced computing to chain millions of machines if desired and thus increase the computing power, which in the above cases only comes from a single machine, the last example being the use of a combination of processing power and the use of calculation programs and/or assisted machine entanglement.
Mathematical features
Definitions and characterizations
Euclides was the first to show that the relationship between a circumference and its diameter is a constant amount. However, there are various definitions of the number π π {displaystyle pi }But the most common is:
- π π {displaystyle pi } is the reason between the length of any circumference and that of its diameter.
Plus π π {displaystyle pi } is:
- The area of a unitary circle (radio that has length 1, in the usual geometric plane or euclid plane).
- The lowest real number x{displaystyle x} positive without (x)=0{displaystyle sin(x)=0}.
It is also possible to define analytically π π {displaystyle pi }; two definitions are possible:
- The equation on complex numbers eix+1=0{displaystyle e^{ix}+1=0} supports an infinity of positive real solutions, the smallest of which is precisely π π {displaystyle pi } (see identity of Euler).
- The differential equation S♫(x)+S(x)=0{displaystyle S'(x)+S(x)=0} with the conditions of contour S(0)=0,S♫(0)=1{displaystyle S(0)=0,S'(0)=1} for which there is a unique solution, guaranteed by the Picard-Lindelöf theorem, is an analytical function (the trigonometric function without (x){displaystyle sin(x)}) whose smallest positive root is precisely π π {displaystyle pi }.
- Through a defined integral you get the value of π π {displaystyle pi }/4. The function f(x) = 1/ (1 + x20 to 1.
- All statistical tests on the succession of decimal decimal depi digits have corroborated their random character. There is no order or regularity, there are several series of 7777 and the shock 9999, there are appearances that confuse or please the intuiistas.
Irrational and transcendental number
It is an irrational number, which means that it cannot be expressed as a fraction of two whole numbers, as Johann Heinrich Lambert proved in 1761 (or 1767). It is also a transcendental number, that is, it is not the root of any polynomial with integer coefficients. In the 19th century, the German mathematician Ferdinand Lindemann demonstrated this fact, thereby definitively closing the permanent and arduous investigation into the problem of squaring the circle, indicating that it has no solution.
It is also known that π is not a Liouville number either (Mahler, 1953), that is, it is not only transcendental but cannot be approximated by a “rapidly converging” sequence of rationals (Stoneham 1970[ citation required]).
First fifty decimal places
Despite being an irrational number, the maximum possible number of decimals continues to be found. The first fifty are:
- π π ≈ ≈ 3.14159265358979323846264338327950288419716939937510{displaystyle pi approx 3.1415926535;8979323846;2643383279;5028841971;6939937510}
To see sequences greater than this number, consult the references (5·1012 decimal places), as well as The first ten thousand decimal places A00796 and OEIS.
In science and engineering, this constant can be used, most of the time, with a precision of only a dozen decimal places. Forty decimal places could accurately describe the curvature of the Milky Way with an error smaller than the size of a proton.
Formulas containing the number π
In geometry
- Radio circumference length r: C = 2 π r
Areas of conic sections:
- Radio circle area r: A = π r2
- Interior area of the ellipse with semies a and b: A = π ab
Areas of bodies of revolution:
- Cylinder area: 2 π r (r+h)
- Cone area: π r2 + π r g
- Area of the sphere: 4 π r2
Volumes of bodies of revolution:
- Volume of the radio sphere r: V = (4/3) π r3
- Volume of a straight radio cylinder r and height hV = π r2 h
- Volume of a straight radio cone r and height hV = π r2 h / 3
Equations expressed in radians:
- Angles: 180 degrees are equivalent to π radian.
- The volume of the bull carries π to the square
In calculus
- Area limited by astroid: (3/8) π a2
- Area of the region covered by the axis X and a cycloid bow: 3 π a2
- Area enclosed by cardioid: (3/2) π a2
- Area of the region between the polar axis and the first two rounds of the spiral of Archimedes r = aα is 8π3 a2
- Area between the curve of Agnesi and the asymptote is S = πa2.
- Cisoide
- Strophoid
- Pascal's snail. The area using this curve and any of the above carries in the formula the pi value
In probability
- The probability of two randomly chosen positive integers to be cousins is: 6/π2
- If two positive numbers are chosen at random less than 1, the probability that together with the number 1 can be the sides of an obtussive triangle is: (π-2)/4
- The average number of ways to write a positive integer as a sum of two perfect squares is π/4 (the order is relevant).
- Buffon Needle: If we randomly throw a L-length needle on a surface where parallel lines are drawn separate a D distance, the probability that the needle cut to a line is: 2L/Dπ
In mathematical analysis
- Leibniz Formula:
- ␡ ␡ n=0∞ ∞ (− − 1)n2n+1=11− − 13+15− − 17+19− − =π π 4{displaystyle sum _{n=0}^{infty }{{{left(-1right)^{n} over {2,n+1}}{frac {1}{1}{1}{1}{frac}{1}{1}{1}{1}{frac}{1}{1}{1}{1}{1}{frac}}{1}{1}}}{1}{1}{1st}}}{1st}}{1st}}}{1st}{1st}}}}}{1st}}}{1st}{f}}{f}}}}}}}{1st}{1st}{f}}}}}}}}{f}}}}{f}}{1st}}{1st}{f}{f}{f}}}{f}}{f}{f}}}}}}{f}}}}}}{
- Wallis product:
- n=1∞ ∞ (2n2n− − 1⋅ ⋅ 2n2n+1)=21⋅ ⋅ 23⋅ ⋅ 43⋅ ⋅ 45⋅ ⋅ 65⋅ ⋅ 67⋅ ⋅ 87⋅ ⋅ 89 =π π 2{cHFFFFFF}{cH00FF} {cHFFFFFF}{cHFFFFFF}{cHFFFF} {cHFFFFFF}{cHFFFF} {cHFFFFFF}{cHFFFF}{cH}{cHFFFF} {cHFFFF}{cH}{cHFFFFFF}{cHFFFFFFFFFF}{cH}{cH}{cH}{cHFFFFFFFFFFFFFFFF}{cH}{cH}{cH}{cH}{cH}{cHFFFFFFFF}{cHFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF}{cH}{cHFFFFFF}{cH}{cH}{cH}{cHFFFFFFFFFF}{cH}{cH}{cHFFFFFF}{cH}{c
- Euler:
- ␡ ␡ n=0∞ ∞ 2nn!2(2n+1)!=1+13+1⋅ ⋅ 23⋅ ⋅ 5+1⋅ ⋅ 2⋅ ⋅ 33⋅ ⋅ 5⋅ ⋅ 7+ =π π 2{displaystyle sum _{n=0}^{infty }{cfrac {2^{n}n}{2}{(2n+1)}}{1+{frac}{1}{3}{1}{1}{1⁄cdot 2}{3cdot 5}+}{frac {1cdot 2cdot}{c}{1}{c}{1}{1}{1}{1}{1}{1}{1}{1}{1}{1}{1}{1}{1}{1}{1}{1⁄2}{1}{1}{1⁄2}{cd}{cd}{cd}{cd}{cd}{cd}{cd}{cd}{cd}{cd}{cd}}}}{cd}}}{cd}}{cd}{cd}}}{c
- Identity of Euler
- eπ π i+1=0{displaystyle e^{pi i}+1=0;}
- Area under the bell of Gauss:
- ∫ ∫ − − ∞ ∞ ∞ ∞ e− − x2dx=π π {displaystyle int _{-infty }^{infty }e^{-x^{2}dx={sqrt {pi }}}}
- Stirling Formula:
- n!≈ ≈ 2π π n(ne)n{displaystyle n!approx {sqrt {2pi n}}{left({frac {n}{n}{e}{right}{n}}}{n}}}}
- Formula resulting from the limit when k tends to infinite the function of Riemann for 2k:
- 2π π =limk→ → ∞ ∞ (2(2k)!B(2k))12k{displaystyle 2pi =lim _{kto infty }left({frac {2(2k)}{B(2k)}}}{right)^{frac {1}{2k}}}}}}
Where B(2k) is the 2k-th Bernoulli number.
- Basel problem, solved by Euler in 1735:
- γ γ (2)=112+122+132+142+ =π π 26{displaystyle zeta (2)={frac {1}{1^{2}}}}}+{frac {1}{2}{2}}}}}{2}}{1}{3^{2}}}}}{1}{4^{2}}}}}{cdots ={frac {pi ^{2}{6}}}}}}{1}}}}}{1}}}}{3}}{1⁄2}}}}}}}}}{4^
- Euler:
- γ γ (4)=114+124+134+144+ =π π 490{displaystyle zeta (4)={frac {1}{1^{4}}}}} +{frac {1}{2^{4}}}}}}{frac {1}{3^{4}}}}}{1}{4^{4}}}}}}}{cdots ={frac {pi ^{4}{4}{frac}{4}}}{4}}{4}}{4}}}}}{4}{4}}}{4}}}}}}}{1{4}}}}}}{4}}}}{1⁄4}}}}}}}}}{
- Nilakantha Formula:
- π π =3+4␡ ␡ n=1∞ ∞ (− − 1)n+1(2n)(2n+1)(2n+2){displaystyle pi =3+4sum _{n=1}^{infty }{(-1)^{n+1} over (2n)(2n+1)(2n+2)}}}}
- Ramanujan Formula:
- 1π π =229801␡ ␡ n=0∞ ∞ (4n)!(26390n+1103)(n!)4(396)4n{displaystyle {frac {1}{pi }}}={frac {2{sqrt {2}}}}{9801}}}{n=0}{infty }{(4n)}!(26390n+1103) over (n!)^{4}(396)^{4n}}}}}
- Chudnovsky Formula: (14 decimals are obtained with each iteration)
- 1π π =12␡ ␡ n=0∞ ∞ (− − 1)n(6n)!(545140134n+13591409)(n!)3(3n)!(640320)3n+3/2{displaystyle {frac {1}{pi }}}=12sum _{n=0}^{infty }{(1)^{n}(6n)!(545140134n+13591409) over (n!)^{3n!(640320)^{3n+3/2}}}}}
- In addition, π has several representations as continuous fractions:
- π π 4=11+13+45+97+169+2511+3613+49 {displaystyle {frac {pi }{4}}{cfrac {1}{1}{1+{cfrac {1}{3+{cfrac {4}{5+{cfrac {9}{7}{7+{cfrac} {16}{9+{cfrac {25}{11+{cfrac {36}{3}{cfr}}}}}{1}}{1}}}}{1}}{1}{1}}{1}{1⁄4}}{1}}}}{1}{1}{1}{1}{1}}{1⁄4}}{1}}}}{1}{1}}{cfr}}}}{1}}}}}}}{1}}}}}{1}{1}{1}{1}{1}{1}{1}{1}{1}}{1}{cfr}{1}}}}}}{1}}}{1}}}}}{
- 4π π =1+122+322+522+ =1+1323+3525+5727+ {cHFFFF}{cHFFFF}{cHFFFF}{cHFFFF}{cHFFFF}{cHFFFF}{cHFFFF}{cH00} {cHFFFF}{cHFF}{cHFF}{cHFF}{cHFF}{cHFF}{cH00}{cH00}{cHFF}{cHFF}{cH00}{cH00}{cH00}{cH00}{cH00}{cHFF}{cH00}{cH00}{cHFF}{cH00}{cH00}{cH00}{cH00}{cH00}{cHFF}{cHFF}{cFFF}{cH00}{cH00}{cHFF}{cH00}{cH00}{cH00}{
- Also as development in series:
- π π =␡ ␡ k=0∞ ∞ 2(− − 1)k312− − k2k+1{displaystyle pi =sum _{k=0}^{infty }{frac {2(-1)^{k;3^{{frac {1}{2}}}-k}}}{2k+1}}}}}}}}
- Forms of representation approximate to π π {displaystyle pi }
- 355113≈ ≈ 3.141592...{displaystyle {frac {355}{113}}}approx 3.141592}
- 26142451328446129≈ ≈ π π {displaystyle {sqrt[{29}]{261424513284461}}}approx pi }
- Monte Carlo Method
- In a circle of radio r inscribed in a square side 2r (2 times the radius), the circle area is πr2 and the square (2r)2. From this it follows that the relation of area between the square and the circle of π/4.
- Srinivāsa Rāmānujan Formula demonstrated in 1985 by Jonathan and Peter Borwein, discovered in 1910. It is very effective because it brings 8 decimals to each iteration:
- 1π π =229801␡ ␡ k=0∞ ∞ (4k)!(1103+26390k)(k!)43964k{displaystyle {frac {1}{pi }}}={frac {2{sqrt {2}}}}}{9801}}}{k=0}{infty }{frac {(4k)}{(1103+26390k)}{(k!)^{4}396^{4k}}}}}}}}}}}
Computations of π
Π and prime numbers
Using the inverse of the Euler product for the Riemann zeta function and for the value of the argument equal to 2, we obtain:
- 1γ γ (2)=limn→ → ∞ ∞ pn한 한 P(1− − 122)(1− − 132)(1− − 152)(1− − 172)(1− − 1112)...(1− − 1pn2)=6π π 2{cHFFFFFF}{cHFFFFFF}{cHFFFFFF}{cHFFFFFF}{cHFFFFFF}{cHFFFFFF00}{1}{cHFFFFFFFF00}{1}{cHFFFFFFFFFF}{1}{cHFFFFFFFFFFFFFF}{1}{1}{cHFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00}{1}{c}{1}{cHFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00}{c}{c}{c}{c}{1}{cHFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00}{c}{c}{c}{cHFFFFFFFFFFFFFFFF00}{c}{
where pn is the nth prime number. Euler was the first to find this value of the zeta function (using the summation expression) and thus solving the famous Basel Problem.
Machin's Formula
An exact way to calculate π in terms of inverse tangents of unit fractions is Machin's formula, discovered in 1706:
- π π 4=4arctan 15− − arctan 1239{displaystyle {frac {pi }{4}}=4arctan {frac {1}{5}{5}-arctan {frac {1}{239}}}}}}}}}
Many mathematicians used this formula to find digits above 100 (for example, the aforementioned Shanks, who with this formula calculated 707 decimal places of π).
Efficient methods
The first million digits of π and 1/π can be found at Project Gutenberg (see external links). One of the most recent records was set in December 2002 by Yasumasa Kanada of the University of Tokyo, setting the number pi to 1,241,100,000,000 digits; It took about 602 hours with a 64-node Hitachi SR8000 supercomputer with a terabyte memory capable of performing two trillion operations per second, more than six times the previous record (206 billion digits). For this, the following modified Machin formulas were used:
- K. Takano (1982).
- π π 4=12arctan 149+32arctan 157− − 5arctan 1239+12arctan 1110443{displaystyle {frac {pi }{4}}}=12arctan {frac {1}{49}{49}{arctan {frac {1}{57}}}}}{frac {1}{1}{1}{1}{frac}{1}{110443}}}}
- F. C. W. Störmer (1986).
- π π 4=44arctan 157+7arctan 1239− − 12arctan 1682+24arctan 112943{displaystyle {frac {pi }{4}}}=44arctan {frac {1}{57}{57}}{+7arctan {frac {1}{239}}}}{frac {1}{682}}}} +24arctan {frac {1}{12943}}}}}{1}{1}}{1}}
These approximations provided such a huge number of digits that it can be said that it is no longer useful except to check the operation of supercomputers. The limitation is not in the computation but in the memory needed to store a string with such a large amount of numbers.
Geometric approximations to π
It is possible to obtain an approximation to the value of π geometrically. In fact, the Greeks already tried unsuccessfully to obtain an exact solution to the problem of the value of π by using a ruler and compass. The Greek problem known as squaring the circle or, what is the same, obtaining a square with an area equal to the area of any circle, implies the calculation of the exact value of π.
Once it was shown that it was impossible to obtain π by using a ruler and compass, several approximate methods were developed. Two of the most elegant approximate solutions are those due to Kochanski (using straightedge and compass) and Mascheroni's (using only a compass).
Kochanski's method
Draw a circle of radius R. Inscribe the equilateral triangle OEG. Draw a straight line parallel to the segment EG that passes through A, extending it until it intersects the segment OE, obtaining D. From point D and on that segment, transport 3 times the radius of the circumference and obtain point C. The segment BC is about half the length of the circumference.
- Demonstration (assuming R = 1)
BC2=AB2+(3− − DA)2{displaystyle BC^{2}=AB^{2}+(3-DA)^{2},!}
OF=32{displaystyle OF={frac {sqrt {3}}{2}}}}
DAEF=OAOF→ → DA1/2=13/2→ → DA=33{displaystyle {frac {DA}{EF}}}={frac {OA}{OF}rightarrow {frac {frac}{1/2}}}={frac {1}{{{sqrt {3}}}}{rightarrow DA={frac {sqrt {3}}}{3}}}}}{3}}}}}}}}}}{
Substituting in the first formula:
BC2=22+(3− − 33)2→ → BC=40− − 633=3.141533...{displaystyle BC^{2}=2^{2}+left(3-{frac {sqrt {3}{3}}{3}}}{2}rightarrow BC={sqrt {40-6{sqrt {3}}} over 3}}=3.141533... !
Mascheroni's method
Method developed by Lorenzo Mascheroni: a circle of radius R is drawn and a regular hexagon is inscribed. Point D is the intersection of two circumference arcs: BD with center in A', and CD with center in A. We obtain point E as the intersection of arc DE, with center in B, and the circumference. The segment AE is a quarter of the length of the circle, approximately.
- Demonstration (assuming R = 1)
AD=AC=3{displaystyle AD=AC={sqrt {3}}} OD=3− − 1=2{displaystyle OD={sqrt {3-1}}={sqrt {2}
BE=BD=(OD− − MB)2+MO2{displaystyle BE=BD={sqrt {(OD-MB)^{2}+MO^{2}}}}}}}BE=BD=(2− − 32)2+14=3− − 6{displaystyle BE=BD={sqrt {left({sqrt {2}-{frac {sqrt {3}{2}}{2}}}{2}+{frac {1}{4}}}}}}}{{{sqrt {3-{sqrt {6}}}}}}}}}}}}}}
By Ptolemy's theorem, in the quadrilateral ABEB'
BB♫⋅ ⋅ AE=AB⋅ ⋅ EB♫+BE⋅ ⋅ AB♫{displaystyle BB'cdot AE=ABcdot EB'+BEcdot AB'}
2⋅ ⋅ AE=1+6+9− − 3⋅ ⋅ 6=3.142399...{displaystyle 2cdot AE={sqrt {1+{sqrt {6}}}}}}+{sqrt {9-3cdot {sqrt {6}}}}}}}}=3.142399... !
Use in math and science
π is ubiquitous in mathematics; it appears even in places that lack a direct connection to the circles of Euclidean geometry.
Geometry and trigonometry
For any circle of radius r and diameter d = 2r, the length of the circle is πd and the area of the circle is πr2. In addition, π appears in formulas for areas and volumes of many other geometric figures related to circles, such as ellipses, spheres, cones, and toroids. π appears in definite integrals that describe the circumference, area, or volume of figures generated by circles and circles. In the basic case, half the area of a unit circle is:
- ∫ ∫ − − 111− − x2dx=π π 2{displaystyle int _{-1}{1}{sqrt {1-x^{2}},dx={frac {pi }{2}}}}{2}}}}}
and half the length of the unit circle is:
- ∫ ∫ − − 1111− − x2dx=π π {displaystyle int _{-1}{1}{frac {1}{sqrt {1-x^{2}}}}{,dx=pi }
You can integrate more complex shapes like solids of revolution.
From the definition of the trigonometric functions from the unit circle, it is concluded that the sine and cosine have period 2π. Which means, for all x and integers n, sin(x) = sin(x + 2πn) and cos(x) = cos(x + 2πn). Because sin(0) = 0, sin(2πn) = 0 for all integers n. Also, the angle 180° is equal to π radians. In other words 1° = (π/180) radians.
In modern mathematics, π is often defined using trigonometric functions, for example as the smallest positive integer x for which sinx= 0, to avoid unnecessary dependencies on the niceties of Euclidean geometry and integration. Equivalently, π can be defined using inverse trigonometric functions, for example as π = 2 arccos(0) or π = 4 arctan(1). Expanding inverse trigonometric functions as power series is the easiest way to obtain infinite series for π.
Complex variable
The frequent appearance of π in complex analysis can be related to the behavior of the exponential function of a complex variable, described by Euler's formula
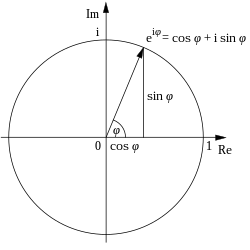
- eiφ φ =# φ φ +iwithout φ φ {displaystyle e^{ivarphi }=cos varphi +isin varphi !}
where i is the imaginary unity that satisfies the equation i2=− − 1{displaystyle i^{2}=1} and e ≈ 2.71828 is the number of Euler. This formula implies that the imaginary powers of e describe rotations a unitary circle in the complex plane; these rotations have a period of 360o = 2π. In particular, the rotation of 180o φ = π results in the remarkable identity of Euler
- eiπ π +1=0.{displaystyle e^{ipi }+1=0. !
There are n different nth roots of unity
- e2π π ik/n(k=0,1,2,...... ,n− − 1).{displaystyle e^{2pi ik/n}qquad (k=0,1,2,dotsn-1). !
Superior Calculus
The Gaussian integral
- ∫ ∫ − − ∞ ∞ ∞ ∞ e− − x2dx=π π .{displaystyle int _{-infty }^{infty }e^{-x^{2}dx={sqrt {pi }}}. !
A consequence is that the result of the division between the gamma function of a semi-integer (half of an odd number) and √π is a rational number.
Physics
Although not a physical constant, π appears routinely in equations describing the fundamental principles of the Universe, not necessarily related to the geometric characteristics of the circle, but used, for example, to describe periodic phenomena Like waves and cycles. Due in large part to its relationship with the nature of the circle and, correspondingly, with the spherical coordinate system (a system widely used in physics for its radial symmetry properties). Using units such as Planck units can sometimes eliminate π from formulas.
- The cosmological constant:
- .... =8π π G3c2ρ ρ {displaystyle lambda ={{8pi G} over {3c^{2}}{rho }
- Heisenberg's uncertainty principle:
- Δ Δ xΔ Δ p≥ ≥ h4π π {displaystyle Delta x,Delta pgeq {frac {h}{4pi }}}}
The use of pi in this fundamental relationship of quantum mechanics is related to the periodicity of the wave function, describing a minimum value in which you can correctly locate a wave function simultaneously in coordinate space (x{displaystyle x}) and in frequency space (p{displaystyle p}), interconnected by Fourier's transformation. The frequency is directly related to the time of the wave function. For example: for the photon p= ω ω {displaystyle p=hbar omega }Where ω ω =2π π f{displaystyle omega =2pi f}and f{displaystyle f}It is its frequency).
- Equation of Einstein's field of general relativity:
- Rik− − gikR2+.... gik=8π π Gc4Tik{displaystyle R_{ik}-{g_{ik}R over 2}+Lambda g_{ik}={8pi G over c^{4}}T_{ik}}}}
- Coulomb Law for Electric Power:
- F=日本語q1q2日本語4π π ε ε 0r2{displaystyle F={frac {left entailq_{1}q_{2}{2}{4pi varepsilon _{0}r^{2}}}}}}}}}}}}}
- Magnetic Permeability of Vacuum:
- μ μ 0=4π π ⋅ ⋅ 10− − 7N/A2{displaystyle mu _{0}=4pi cdot 10^{-7},mathrm {N/A^{2}} ,}
- Kepler's Third Law:
- P2a3=(2π π )2G(M+m){displaystyle {frac {P^{2}}{a^{3}}}}={(2pi)^{2over G(M+m)}}}}
Probability and Statistics
In probability and statistics, there are many distributions whose formulas contain π, including:
- the probability density function for normal distribution with mean μ and standard σ deviation, which depends on the Gaussian integral:
- f(x)=1σ σ 2π π e− − (x− − μ μ )2/2σ σ 2{displaystyle f(x)={1 over sigma {sqrt {2pi }}}}{,e^{-(x-mu)^{2}/2sigma ^{2}}}}}}
- the probability density function for the distribution of Cauchy (standard):
- f(x)=1π π (1+x2).{displaystyle f(x)={frac {1}{pi (1+x^{2})}}}}. !
Note that for all probability density functions it is fulfilled that∫ ∫ − − ∞ ∞ ∞ ∞ f(x)dx=1{displaystyle int _{-infty }^{infty }f(x),dx=1}, then the previous formulas can be used to produce other integral formulas for π.
The Buffon needle problem is sometimes called an empirical approximation of π. It involves throwing a needle of length l repeatedly over a surface on which parallel straight lines have been drawn, spaced apart, in t units, uniformly (with t > l so that the needle cannot touch two lines). If the needle is thrown n times and x of those times it lands across a line, then π can be approximated using the Monte Carlo Method, throwing it a long way. number of times:
- π π ≈ ≈ 2nlxt.{displaystyle pi approx {frac {2nl}{xt}}}}. !
Although this result is mathematically flawless, it cannot be used more than to determine a few digits of π experimentally. Getting just three correct digits (including the leading "3") requires millions of tosses, and the number of tosses grows exponentially with the number of digits desired. Furthermore, any error in the measurement of the lengths l and t is transferred directly as an error in the approximation of π. For example, a difference of a single atom on a 10-centimeter needle could lead to errors in the ninth digit of the result. In practice, uncertainties in determining whether the needle actually crosses a line that appears to be just touching it pushes the limit of achievable precision to much less than 9 digits.
Mnemonic Rules
It is very common to use poems as a mnemonic rule to remember the first digits of the number pi.
- One way to memorize the first 20 digits is with this poem, you just have to count the letters of each word:
I'm and I'll be all defined.
My name I have to give
always immeasurable diametrical quotient
I'm from the round rings.
- Another version, which allows to list the first 27 digits, is the following:
«What? And how does π gather infinity of figures? There must be repeated periods! I also don't understand that in an unknowing amount something like this is affirmed, so daring!" Note that for the second 1 (3.14159...) is used the Greek letter π.
- A third poem:
I'll love alone, depressed
They will never know what I dream of finding you,
hard perimeter, hidden
that in my neurons beats...
I find the way to see
the secrets you hide
Can I find them?
- Another rule, which allows us to remember the first 32 figures:
"I am π, motto and ingenious reason of a wise man, which precious series valued, he spoke magistral. By his singular law, well measured the great orb finally reduced was to the usual ordinary system." (from the author Rafael Nieto Paris) Here is also used the Greek π letter for the first 1.
- Another way to remember the first 14 figures:
"How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics!"
There are long stories that are capable of making you memorize a large number of digits, such is the one entitled «Cadaeic Cadenza», written in 1996 by the mathematician Michael Keith and which offers the possibility of memorizing the first 3834 digits. Thus, taking "A" as 1, "B" as 2, "C" as 3, etc., the name of the story takes the digits out of π, as "Cadaeic" is the first 7-digit word of π:
C to d a
3.1 4 1 5 9 3
It is noteworthy that in each language there are different mnemonic rules (it is advisable to visit each Wikipedia to discover the art used in each language).
Pop Culture
Media appearance
- In 1998, a film by director Darren Aronofsky appeared Pi about a mathematician who believes the world is represented by numbers.
- Alfred Hitchcock in his film Curtain torn makes the symbol π appear as an organization of espionage.
- In the movie The Net, appears at the bottom right of a page of concerts and music, of a program called The Mozart Ghost. Apparently it is only an ornament, but when CRTL+ALT+Clic is pressed in π, you access the data interface of the Guardian of the Gate, a program of pretorians that requested a user and a password.
- In the cartoon series The Simpsons, in the episode "Bye Bye Nerdie", Professor Frink shouts, with a voice in the neck, that "π is exactly three!" to draw the attention of an auditorium composed of scientists. When everyone turns around to look at him, he apologizes for being forced into such a sacrilege.
- In the series Futurama There are different references to π, such as "oil π in 1", and "buy in πkea".
- The novel Contact by Carl Sagan—on which the film was then filmed—takes π (although not on decimal basis) as a number that hides the very essence of the universe.
Oddities
- The method of Archimedes was not overcome in almost two thousand years despite the great progress made in its numerical evaluation.
- The value of Pi used by Posidonio (135-51 BC) must have been correct in several decimal figures. The value he obtained for the circumference of the earth was adopted three centuries later by the Alexandrian astronomer Claudio Ptolomeo and much later by Christopher Columbus, among many others.
- On March 14 (3/14 in United States date format) it is also marked as the pi day on which fans of this number celebrate it with different actions. Curiously it's Albert Einstein's birthday and the anniversary of Stephen Hawking's passing.
- 355/113 (~3.1415929) is sometimes mentioned as a four-perfect simulation!
- The Nobel Prize in Literature Wisława Szymborska wrote a poem entitled "The Pi Number" (Liczba Pi) in which he uses, in his order, the first 25 digits of π.
- John Squire (from the band The Stone Roses) mentions π in a song written for his second band The Seahorses called "Something Tells Me". The song ends with a letter like: "What's the secret of life? It's 3.14159265, yeah yeah!!"
- The first million figures of π and its reverse 1/π can be consulted in the Gutenberg Project or in this link.
- The numbering of the versions of Donald Knuth's TeX text treatment program is performed according to π digits. The 2002 version was labeled with 3.141592.
- This number is used in the series of signals sent by the earth in order to be identified by an alien intelligent civilization.
- The probability that two randomly chosen positive integers are cousins to each other is 6/π π 2{displaystyle 6/pi ^{2}.
- There are internet programs that look for your phone number in the 50 000 first figures of π.
- In some programming languages you can find as many digits as you want with simply using expressions like: RealDigits[ N[ Pi, 105]] in "Mathematica".
- In the year 2002 the Japanese Akira Haraguchi broke the world record reciting for 13 hours 83 431 digits of the unstop pi number, bending the previous record in possession of the also Japanese Hiroyuki Goto. On 4 October 2006, at 1:30 in the morning, and after 16 and a half hours, Haraguchi broke his own record again, reciting 100,000 digits of the number pi, making a stop every two hours of 10 minutes to take air.
- The maximum number of π digits needed to search for any day-month-year sequence with four digits in the decimal expansion of pi is 60.872.
- There is a song by Kate Bush called "Pi" in which more than twenty digits of the number are recited.
- In Argentina, the mobile phone number for emergencies in train and underground stations is ▼1416.
- The main value of the expression ii{displaystyle i^{i} is a real number and is given by: ii=(eiπ π /2)i=ei2π π /2=e− − π π /2=0.207879...{displaystyle i^{i}=left(e^{ipi /2}right)^{i}=e^{i^{2}pi /2}=e^{-pi /2}=0.207879... !
- Srinivasa Ramanujan published an approximate solution, with rule and compass, at the square of the circle in 1913 in which he obtained a segment approximately equal to rπ π {displaystyle r{sqrt {pi }}}:
- The Hebrews consider the number pi as "the number of God." In the movie Pi: Faith in the Caos Torah students consider the first 216 (6x6x6) decimals as a representation of the true name of God. In the Bible (Jewish and Christian) the name of God appears in chapter 3 and verse 14 of the Book of Exodus (Exodus 3:14).
Days of Approach to π
According to certain numerical coincidences, the Days of Approach to Pi are:
- 14 March (3/14 in English date format).
- April 26th.
- 22 July (22/7 is a pi approach).
- 10 November (it is the 314th day of the Gregorian calendar).
- 21 December (it is 355 day, in reference to approx. 355/113).
Open questions about π
- Each of the decimal digits 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9, has an infinite appearance in the decimals of π?
- The so-called Brouwer question: In the decimal expansion of π, is there any position where there is a succession of thousand consecutive zeros?
- Is π simply normal in base 10? I mean, does each of the ten digits of the decimal system have the same probability of appearance in a decimal expansion?
- It is not known whether π+e, π/e, ln(π) are irrational. It is known that they are not roots of polynomials of grade less than nine and with integer coefficients of order 109.
Contenido relacionado
Algebraic number
ANNEX: 1 E4 S
Quadrilateral















































![{sqrt[ {29}]{261424513284461}}approx pi](https://wikimedia.org/api/rest_v1/media/math/render/svg/33610db86799eed45ddd30541627f4d960c4cdd3)