Teoria dos Números

ImprimirCitar

Matemática de propriedades de inteiro

A distribuição de números primos é um ponto central de estudo na teoria dos números. Esta espiral de Ulam serve para ilustrar, sugerindo, em particular, a independência condicional entre ser primo e ser um valor de certos polinômios quadráticos.

Teoria dos números (ou aritmética ou aritmética superior no uso mais antigo) é um ramo da matemática pura dedicado principalmente ao estudo dos números inteiros e funções aritméticas. O matemático alemão Carl Friedrich Gauss (1777-1855) disse: "A matemática é a rainha das ciências - e a teoria dos números é a rainha da matemática". Os teóricos dos números estudam os números primos, bem como as propriedades de objetos matemáticos construídos a partir de inteiros (por exemplo, números racionais) ou definidos como generalizações dos inteiros (por exemplo, inteiros algébricos).

Os inteiros podem ser considerados em si mesmos ou como soluções de equações (geometria diofantina). Questões na teoria dos números geralmente são melhor compreendidas através do estudo de objetos analíticos (por exemplo, a função zeta de Riemann) que codificam propriedades dos números inteiros, primos ou outros objetos da teoria dos números de alguma forma (teoria analítica dos números). Pode-se também estudar os números reais em relação aos números racionais, por exemplo, como aproximados por estes últimos (aproximação diofantina).

O termo mais antigo para a teoria dos números é aritmética. No início do século XX, ela foi substituída pela "teoria dos números". (A palavra "aritmética" é usada pelo público em geral para significar "cálculos elementares"; ela também adquiriu outros significados na lógica matemática, como na aritmética de Peano, e ciência da computação, como em aritmética de ponto flutuante.) O uso do termo aritmética para teoria dos números recuperou algum terreno no segundo semestre do século 20, sem dúvida em parte devido à influência francesa. Em particular, aritmético é comumente preferido como um adjetivo para número-teórico.

História

Origens

Alvorecer da aritmética

O tablet Plimpton 322

O mais antigo achado histórico de uma natureza aritmética é um fragmento de uma tabela: o comprimido de argila quebrado Plimpton 322 (Larsa, Mesopotâmia, ca. 1800 BC) contém uma lista de "Trigêmeos pitagóricos", ou seja, inteiros $(a,b,c)$ tal que $a^{2}+b^{2}=c^{2}$ . Os triplos são muitos e muito grandes para ter sido obtido pela força bruta. O cabeçalho sobre a primeira coluna lê: "O Não. da diagonal que foi subtraída tal que a largura..."

O layout da mesa sugere que ela foi construída por meio do que equivale, em linguagem moderna, à identidade

{displaystyle left({frac {1}{2}}left(x-{frac {1}{x}}right)right)^{2}+1=left({frac {1}{2}}left(x+{frac {1}{x}}right)right)^{2},}

que é implícito na rotina exercícios babilônicos antigos. Se algum outro método foi usado, os triplos foram construídos pela primeira vez e depois reordenados por $c/a$ , presumivelmente para uso real como uma "tabela", por exemplo, com vista a aplicações.

Não se sabe quais podem ter sido esses aplicativos, ou se poderia ter havido algum; A astronomia babilônica, por exemplo, só se destacou mais tarde. Em vez disso, foi sugerido que a tabela era uma fonte de exemplos numéricos para problemas escolares.

Enquanto a teoria dos números babilônicos - ou o que sobrevive da matemática babilônica que pode ser chamada assim - consiste neste fragmento único e notável, a álgebra babilônica (no sentido de "álgebra" do ensino médio) foi excepcionalmente bem desenvolvido. Fontes neoplatônicas tardias afirmam que Pitágoras aprendeu matemática com os babilônios. Fontes muito anteriores afirmam que Tales e Pitágoras viajaram e estudaram no Egito.

Euclid IX 21–34 é muito provavelmente Pythagorean; é material muito simples ("o tempo até é mesmo", "se um número ímpar mede [= divide] um número par, então também mede [= divide] metade dele"), mas é tudo o que é necessário para provar que ${sqrt {2}}$ é irracional. Os místicos pitagóricos deram grande importância ao ímpar e ao uniforme. A descoberta de que ${sqrt {2}}$ é irracional é creditado aos primeiros Pitágoreanos (pré-Teodoro). Ao revelar (em termos modernos) que os números poderiam ser irracionais, esta descoberta parece ter provocado a primeira crise fundamental na história matemática; sua prova ou sua divulgação são, por vezes, creditadas a Hippaso, que foi expulso ou dividido da seita pitágoriana. Isso forçou uma distinção entre números (intérpretes e racionais - os sujeitos da aritmética), por um lado, e comprimentos e proporções (que nos identificamos com números reais, sejam racionais ou não), por outro lado.

A tradição pitagórica também falava dos chamados números poligonais ou figurados. Embora os números quadrados, números cúbicos, etc.).

Não conhecemos nenhum material claramente aritmético nas fontes egípcias ou védicas antigas, embora haja alguma álgebra em cada uma. O teorema chinês do resto aparece como um exercício em Sunzi Suanjing (3º, 4º ou 5º século EC). (Há um passo importante encoberto na solução de Sunzi: é o problema que mais tarde foi resolvido por Kuṭṭaka de Āryabhaṭa - veja abaixo.)

Há também algum misticismo numérico na matemática chinesa, mas, ao contrário dos pitagóricos, parece não ter levado a lugar nenhum. Como os pitagóricos'; números perfeitos, os quadrados mágicos passaram da superstição para a recreação.

Grécia clássica e início do período helenístico

Além de alguns fragmentos, a matemática da Grécia Clássica é conhecida por nós através de relatos de não-matemáticos contemporâneos ou através de trabalhos matemáticos do início do período helenístico. No caso da teoria dos números, isso significa, em geral, Platão e Euclides, respectivamente.

Embora a matemática asiática tenha influenciado o aprendizado grego e helenístico, parece que a matemática grega também é uma tradição indígena.

Eusébio, PE X, capítulo 4 menciona Pitágoras:

"Na verdade, os ditos Pitágoras, enquanto estudavam a sabedoria de cada nação, visitaram a Babilônia, e o Egito, e toda a Pérsia, sendo instruído pelos Magos e pelos sacerdotes; e além disso, ele está relacionado a ter estudado sob os brâmanes (estes são filósofos indianos); e de alguns ele reuniu astrologia, de outros geometria, e aritmética e música de outros, e coisas diferentes de nações sábias, e somente os homens

Aristóteles afirmou que a filosofia de Platão seguia de perto os ensinamentos dos pitagóricos, e Cícero repete esta afirmação: Platonem ferunt didicisse Pythagorea omnia ("Dizem que Platão aprendeu todas as coisas pitagóricas").

Platão teve um grande interesse em matemática, e distinguiu-se claramente entre aritmética e cálculo. (By) Aritmética ele quis dizer, em parte, teorizar em número, em vez de o que Aritmética ou teoria do número ter chegado a significar.) É através de um dos diálogos de Platão, ou seja, Theaetetus, que sabemos que Teodoro tinha provado que ${sqrt {3}},{sqrt {5}},dots{sqrt {17}}$ são irracionais. Theaetetus era, como Platão, um discípulo de Teodoro; ele trabalhou em distinguir diferentes tipos de incommensuráveis, e foi, portanto, indiscutivelmente um pioneiro no estudo de sistemas de números. (O livro X dos Elementos de Euclides é descrito por Pappus como sendo em grande parte baseado no trabalho de Theaetetus.)

Euclides dedicou parte de seus Elementos aos números primos e à divisibilidade, tópicos que pertencem inequivocamente à teoria dos números e são básicos para ela (Livros VII a IX dos Elementos de Euclides). Em particular, ele deu um algoritmo para calcular o máximo divisor comum de dois números (o algoritmo euclidiano; Elementos, Prop. VII.2) e a primeira prova conhecida da infinitude dos primos ( Elementos, Prop. IX.20).

Em 1773, Lessing publicou um epigrama que havia encontrado em um manuscrito durante seu trabalho como bibliotecário; afirmava ser uma carta enviada por Arquimedes a Eratóstenes. O epigrama propunha o que ficou conhecido como o problema do gado de Arquimedes; sua solução (ausente do manuscrito) requer a resolução de uma equação quadrática indeterminada (que se reduz ao que mais tarde seria erroneamente chamada de equação de Pell). Tanto quanto sabemos, tais equações foram primeiro tratadas com sucesso pela escola indiana. Não se sabe se o próprio Arquimedes tinha um método de solução.

Diofanto

Título da edição de 1621 de Diófanto de Alexandria Aritmética, traduzido em latim por Claude Gaspard Bachet de Méziriac

Muito pouco se sabe sobre Diófanto de Alexandria; ele provavelmente viveu no século III d.C., ou seja, cerca de quinhentos anos após Euclides. Seis dos treze livros de Diófanto Aritmética sobreviver no grego original e mais quatro sobreviver em uma tradução árabe. O Aritmética é uma coleção de problemas trabalhados onde a tarefa é invariavelmente encontrar soluções racionais para um sistema de equações polinomiais, geralmente da forma $f(x,y)=z^{2}$ ou $f(x,y,z)=w^{2}$ . Assim, hoje em dia, falamos de Equações de diofantina quando falamos de equações polinomiais a que soluções racionais ou inteiros devem ser encontradas.

Pode-se dizer que Diófanto estava estudando pontos racionais, ou seja, pontos cujas coordenadas são racionais - em curvas e variedades algébricas; no entanto, ao contrário dos gregos do período clássico, que fizeram o que agora chamaríamos álgebra básica em termos geométricos, Diófanto fez o que agora chamaríamos geometria algébrica básica em termos puramente algébricos. Em linguagem moderna, o que Diófanto fez foi encontrar parametrizações racionais de variedades; isto é, dada uma equação da forma (diz) $f(x_{1},x_{2},x_{3})=0$ , seu objetivo era encontrar (em essência) três funções racionais $g_{1},g_{2},g_{3}$ tal que, para todos os valores de $r$ e $s$ , definição $x_{i}=g_{i}(r,s)$ para $i=1,2,3$ dá uma solução para $f(x_{1},x_{2},x_{3})=0.$

Diophantus também estudou as equações de algumas curvas não racionais, para as quais nenhuma parametrização racional é possível. Ele conseguiu encontrar alguns pontos racionais nessas curvas (curvas elípticas, aliás, no que parece ser sua primeira ocorrência conhecida) por meio do que equivale a uma construção tangente: traduzida em geometria coordenada (que não existia na época de Diofanto), seu método seria visualizado como desenhar uma tangente a uma curva em um ponto racional conhecido e, em seguida, encontrar o outro ponto de interseção da tangente com a curva; esse outro ponto é um novo ponto racional. (Diofanto também recorreu ao que poderia ser chamado de caso especial de uma construção secante.)

Enquanto Diofanto estava preocupado principalmente com soluções racionais, ele assumiu alguns resultados em números inteiros, em particular que todo inteiro é a soma de quatro quadrados (embora ele nunca tenha afirmado isso explicitamente).

Āryabhaṭa, Brahmagupta, Bhāskara

Embora a astronomia grega provavelmente tenha influenciado o aprendizado indiano, a ponto de introduzir a trigonometria, parece ser o caso que a matemática indiana é, de outra forma, uma tradição indígena; em particular, não há evidências de que os Elementos de Euclides tenham chegado à Índia antes do século XVIII.

Āryabhaṭa (476-550 AD) mostrou que pares de congruências simultâneas ${displaystyle nequiv a_{1}{bmod {m}}_{1}}$ , ${displaystyle nequiv a_{2}{bmod {m}}_{2}}$ poderia ser resolvido por um método chamado O que é isso?ou Máquina de perfuração; este é um procedimento próximo (uma generalização) do algoritmo euclidiano, que foi provavelmente descoberto independentemente na Índia. Āryabhaṭa parece ter tido em mente aplicações para cálculos astronômicos.

Brahmagupta (628 dC) iniciou o estudo sistemático de equações quadráticas indefinidas - em particular, a mal chamada equação de Pell, na qual Arquimedes pode ter se interessado pela primeira vez, e que não começou a ser resolvida no Ocidente até a época de Fermat e Euler. Autores sânscritos posteriores seguiriam, usando a terminologia técnica de Brahmagupta. Um procedimento geral (o chakravala, ou "método cíclico") para resolver a equação de Pell foi finalmente encontrado por Jayadeva (citado no século XI; seu trabalho está perdido); a exposição sobrevivente mais antiga aparece em Bhāskara II's Bīja-gaṇita (século XII).

A matemática indiana permaneceu amplamente desconhecida na Europa até o final do século XVIII; A obra de Brahmagupta e Bhāskara foi traduzida para o inglês em 1817 por Henry Colebrooke.

A aritmética na era de ouro islâmica

Al-Haytham como visto pelo Ocidente: no frontispiece de Selenographia Alhasen [Sic] representa o conhecimento através da razão e do conhecimento de Galileu através dos sentidos.

No início do século IX, o califa Al-Ma'mun ordenou traduções de muitas obras matemáticas gregas e pelo menos uma obra sânscrita (o Sindhind, que pode ou não ser Brahmagupta&# 39;s Brāhmasphuṭasiddhānta). A principal obra de Diofanto, a Arithmetica, foi traduzida para o árabe por Qusta ibn Luqa (820–912). Parte do tratado al-Fakhri (por al-Karajī, 953 – ca. 1029) se baseia nisso até certo ponto. De acordo com Rashed Roshdi, o contemporâneo de Al-Karajī, Ibn al-Haytham, sabia o que mais tarde seria chamado de teorema de Wilson.

Europa Ocidental na Idade Média

Além de um tratado sobre quadrados em progressão aritmética por Fibonacci - que viajou e estudou no norte da África e em Constantinopla - nenhuma teoria dos números foi feita na Europa Ocidental durante a Idade Média. As coisas começaram a mudar na Europa no final do Renascimento, graças a um estudo renovado das obras da antiguidade grega. Um catalisador foi a emenda textual e a tradução para o latim da obra de Diofanto. Aritmética.

Primeira teoria moderna dos números

Fermat

Pierre de Fermat

Pierre de Fermat (1607–1665) nunca publicou seus escritos; em particular, seu trabalho sobre teoria dos números está contido quase inteiramente em cartas a matemáticos e em notas marginais privadas. Em suas notas e cartas, ele quase não escreveu nenhuma prova - não tinha modelos na área.

Ao longo de sua vida, Fermat fez as seguintes contribuições para o campo:

Um dos primeiros interesses de Fermat foi números perfeitos (que aparecem em Euclid, Elementos IX) e números amicable; estes tópicos levaram-no a trabalhar em divisors inteiros, que foram desde o início entre os assuntos da correspondência (1636 em diante) que o colocaram em contato com a comunidade matemática do dia.
Em 1638, Fermat afirmou, sem prova, que todos os números podem ser expressos como a soma de quatro quadrados ou menos.
pequeno teorema de Fermat (1640): se um não é divisível por um primo p, então ${displaystyle a^{p-1}equiv 1{bmod {p}}.}$
Se um e b) são coprime, então $a^2 + b^2$ não é divisível por qualquer congruente principal a −1 modulo 4; e cada congruente primo a 1 modulo 4 pode ser escrito na forma $a^2 + b^2$ . Estas duas declarações também datam de 1640; em 1659, Fermat afirmou a Huígenos que ele tinha provado a última declaração pelo método de descendência infinita.
Em 1657, Fermat colocou o problema da resolução $x^{2}-Ny^{2}=1$ como um desafio para os matemáticos ingleses. O problema foi resolvido em poucos meses por Wallis e Brouncker. Fermat considerou sua solução válida, mas apontou que tinha fornecido um algoritmo sem uma prova (como tinha Jayadeva e Bhaskara, embora Fermat não estivesse ciente disso). Ele afirmou que uma prova poderia ser encontrada por descendência infinita.
Fermat declarou e provou (por descida infinita) no apêndice Observações sobre Diófanto (Obs. XLV) que $x^{{4}}+y^{{4}}=z^{{4}}$ não tem soluções não triviais nos inteiros. Fermat também mencionou aos seus correspondentes que $x^{3}+y^{3}=z^{3}$ não tem soluções não triviais, e que isso também poderia ser provado por descida infinita. A primeira prova conhecida é devido a Euler (1753; de fato por descida infinita).
Fermat reivindicado (Fermat's Last Theorem) para ter mostrado que não há soluções para $x^{n}+y^{n}=z^{n}$ para todos $ngeq 3$ ; esta afirmação aparece em suas anotações nas margens de sua cópia de Diófanto.

Euler

Leonhard Euler

O interesse de Leonhard Euler (1707–1783) pela teoria dos números foi estimulado pela primeira vez em 1729, quando um amigo seu, o amador Goldbach, indicou-lhe alguns dos trabalhos de Fermat sobre o assunto. Isso tem sido chamado de "renascimento" da moderna teoria dos números, após a relativa falta de sucesso de Fermat em conseguir que seus contemporâneos atenção para o assunto. O trabalho de Euler na teoria dos números inclui o seguinte:

Provas para declarações de Fermat. Isso inclui o teorema pequeno de Fermat (geralizado por Euler para moduli não primário); o fato de que $p=x^{2}+y^{2}$ se e somente se ${displaystyle pequiv 1{bmod {4}}}$ ; trabalho inicial em direção a uma prova de que cada inteiro é a soma de quatro quadrados (a primeira prova completa é de Joseph-Louis Lagrange (1770), logo melhorada pelo próprio Euler); a falta de soluções inteiros não-zero para $x^{4}+y^{4}=z^{2}$ (implicando o caso Não. do último teorema de Fermat, o caso Não. de que Euler também provou por um método relacionado).
Equação de Pell, primeiro mal-nomeado por Euler. Escreveu na ligação entre frações continuadas e a equação de Pell.
Primeiros passos para a teoria dos números analíticos. Em seu trabalho de somas de quatro quadrados, partições, números pentagonais e a distribuição de números primos, Euler foi pioneiro no uso do que pode ser visto como análise (em particular, série infinita) na teoria dos números. Desde que viveu antes do desenvolvimento da análise complexa, a maioria de seu trabalho é restrita à manipulação formal da série de poder. Ele fez, no entanto, fazer algum trabalho inicial muito notável (embora não totalmente rigoroso) sobre o que mais tarde seria chamado de função zeta Riemann.
Formas quadradas. Seguindo a liderança de Fermat, Euler fez mais pesquisas sobre a questão de quais primos podem ser expressos na forma $x^{2}+Ny^{2}$ , alguns deles prefigurando a reciprocidade quadrática.
Equações de diofantina. Euler trabalhou em algumas equações diofantinas do gênero 0 e 1. Em particular, estudou o trabalho de Diófanto; tentou sistemá-lo, mas o tempo ainda não estava maduro para tal esforço - a geometria algébrica ainda estava em sua infância. Ele notou que havia uma conexão entre problemas diofantinos e integrais elípticas, cujo estudo ele mesmo tinha iniciado.

"Aqui estava um problema, que eu, uma criança de dez anos, poderia entender, e eu sabia a partir daquele momento que eu nunca deixaria ir. Eu tive que resolvê-lo." — Sir Andrew Wiles sobre a sua prova do último teorema de Fermat.

Lagrange, Legendre e Gauss

Carl Friedrich Gauss Disquisitiones Arithmeticae, primeira edição

Joseph-Louis Lagrange (1736-1813) foi o primeiro a dar provas completas de alguns dos trabalhos e observações de Fermat e Euler - por exemplo, o teorema de quatro quadras e a teoria básica da equação de "Pell" (para a qual uma solução algorítmica foi encontrada por Fermat e seus contemporâneos, e também por Jayadeva e Bhaskara II antes deles). Ele também estudou formas quadráticas em total generalidade (ao contrário de $mX^{2}+nY^{2}$ ) — definir a sua relação de equivalência, mostrando como colocá-los em forma reduzida, etc.

Adrien-Marie Legendre (1752-1833) foi o primeiro a declarar a lei da reciprocidade quadrática. Ele também conjecturou o que equivale ao teorema do número primo e teorema de Dirichlet sobre progressões aritméticas. Ele deu um tratamento completo da equação $ax^{2}+by^{2}+cz^{2}=0$ e trabalhou em formas quadráticas ao longo das linhas mais tarde desenvolvidas totalmente por Gauss. Em sua velhice, ele foi o primeiro a provar o último teorema de Fermat para $n=5$ (completando trabalho de Peter Gustav Lejeune Dirichlet, e creditando tanto ele quanto Sophie Germain).

Carl Friedrich Gauss

Em suas Disquisitiones Arithmeticae (1798), Carl Friedrich Gauss (1777–1855) provou a lei da reciprocidade quadrática e desenvolveu a teoria das formas quadráticas (em particular, definindo sua composição). Ele também introduziu algumas notações básicas (congruências) e dedicou uma seção a questões computacionais, incluindo testes de primalidade. A última seção das Disquisitiones estabeleceu uma ligação entre as raízes da unidade e a teoria dos números:

A teoria da divisão do círculo... que é tratada no sec. 7 não pertence por si só à aritmética, mas seus princípios só podem ser extraídos da aritmética mais elevada.

Dessa forma, Gauss provavelmente fez uma primeira incursão no trabalho de Évariste Galois e na teoria algébrica dos números.

Maturidade e divisão em subcampos

Ernst Kummer

Peter Gustav Lejeune Dirichlet

A partir do início do século XIX, os seguintes desenvolvimentos ocorreram gradualmente:

A ascensão à autoconsciência da teoria dos números (ou aritmética superior) como um campo de estudo.
O desenvolvimento de grande parte da matemática moderna necessária para a teoria básica dos números modernos: análise complexa, teoria do grupo, teoria de Galois, acompanhada por maior rigor na análise e abstração na álgebra.
A subdivisão áspera da teoria dos números em seus subcampos modernos — em particular, a teoria dos números analíticos e algébricas.

Pode-se dizer que a teoria algébrica dos números começou com o estudo da reciprocidade e da ciclotomia, mas realmente se destacou com o desenvolvimento da álgebra abstrata e das primeiras teorias de ideal e avaliação; Veja abaixo. Um ponto de partida convencional para a teoria analítica dos números é o teorema de Dirichlet sobre progressões aritméticas (1837), cuja prova introduziu funções L e envolveu alguma análise assintótica e um processo de limitação em uma variável real. O primeiro uso de ideias analíticas na teoria dos números remonta a Euler (1730), que usou séries de potências formais e argumentos limitantes não rigorosos (ou implícitos). O uso da análise complexa na teoria dos números vem depois: o trabalho de Bernhard Riemann (1859) sobre a função zeta é o ponto de partida canônico; O teorema dos quatro quadrados de Jacobi (1839), que o antecede, pertence a uma vertente inicialmente diferente que agora assumiu um papel de liderança na teoria analítica dos números (formas modulares).

A história de cada subcampo é brevemente abordada em sua própria seção abaixo; veja o artigo principal de cada subcampo para tratamentos mais completos. Muitas das questões mais interessantes em cada área permanecem em aberto e estão sendo ativamente trabalhadas.

Principais subdivisões

Teoria elementar dos números

O termo elementar geralmente denota um método que não usa análise complexa. Por exemplo, o teorema dos números primos foi provado pela primeira vez usando análise complexa em 1896, mas uma prova elementar foi encontrada apenas em 1949 por Erdős e Selberg. O termo é um tanto ambíguo: por exemplo, provas baseadas em teoremas tauberianos complexos (por exemplo, Wiener-Ikehara) são frequentemente vistas como bastante esclarecedoras, mas não elementares, apesar de usar a análise de Fourier, em vez da análise complexa como tal. Aqui como em qualquer outro lugar, uma prova elementar pode ser mais longa e mais difícil para a maioria dos leitores do que uma não elementar.

Teoria dos números Paul Erdős e Terence Tao em 1985, quando Erdős era 72 e Tao era 10

A teoria dos números tem a reputação de ser um campo cujos resultados podem ser declarados ao leigo. Ao mesmo tempo, as provas desses resultados não são particularmente acessíveis, em parte porque a variedade de ferramentas que eles usam é, no mínimo, incomumente ampla na matemática.

Teoria analítica dos números

Riemann função zeta ((S) no plano complexo. A cor de um ponto S dá o valor de of(S): cores escuras denota valores perto de zero e tons dá o argumento do valor.

A ação do grupo modular no meio plano superior. A região em cinza é o domínio fundamental padrão.

teoria analítica dos números pode ser definida

em termos de suas ferramentas, como o estudo dos inteiros por meio de ferramentas de análise real e complexa; ou
em termos de suas preocupações, como o estudo dentro da teoria dos números de estimativas sobre tamanho e densidade, em oposição às identidades.

Alguns assuntos geralmente considerados como parte da teoria analítica dos números, por exemplo, a teoria da peneira, são melhor cobertos pela segunda definição do que pela primeira: alguns da teoria da peneira, por exemplo, usam pouca análise, mas pertencem a teoria analítica dos números.

Os seguintes são exemplos de problemas na teoria analítica dos números: o teorema dos números primos, a conjectura de Goldbach (ou a conjectura dos primos gêmeos, ou as conjecturas de Hardy-Littlewood), o problema de Waring e a hipótese de Riemann. Algumas das ferramentas mais importantes da teoria analítica dos números são o método do círculo, métodos da peneira e funções L (ou melhor, o estudo de suas propriedades). A teoria das formas modulares (e, de forma mais geral, das formas automórficas) também ocupa um lugar cada vez mais central na caixa de ferramentas da teoria analítica dos números.

Pode-se fazer perguntas analíticas sobre números algébricos e usar meios analíticos para responder a essas perguntas; é assim que a teoria algébrica e analítica dos números se cruzam. Por exemplo, pode-se definir ideais primos (generalizações de números primos no campo dos números algébricos) e perguntar quantos ideais primos existem até certo tamanho. Esta questão pode ser respondida por meio de um exame das funções zeta de Dedekind, que são generalizações da função zeta de Riemann, um objeto analítico chave nas raízes do assunto. Este é um exemplo de um procedimento geral na teoria analítica dos números: obter informações sobre a distribuição de uma sequência (aqui, ideais primos ou números primos) do comportamento analítico de uma função de valor complexo adequadamente construída.

Teoria dos números algébricos

Um número álgebra é qualquer número complexo que é uma solução para alguma equação polinomial $f(x)=0$ com coeficientes racionais; por exemplo, cada solução $x$ de $x^{5}+(11/2)x^{3}-7x^{2}+9=0$ É um número algébrica. Campos de números algébricas também são chamados campos de número algébricaou em breve campos de número. A teoria dos números algébrica estuda campos de número algébrica. Assim, a teoria analítica e algébrica de números pode e se sobrepõe: o primeiro é definido por seus métodos, o último por seus objetos de estudo.

Pode-se argumentar que o tipo mais simples de campos de número (viz., campos quadráticos) já foram estudados por Gauss, como a discussão de formas quadráticas em Disquisições aritméticae pode ser descansado em termos de ideais e normas em campos quadráticos. (A) campo quadrático consiste em todos números da forma $a+b{sqrt {d}}$ , onde $a$ e $b$ são números racionais e $d$ é um número racional fixo cuja raiz quadrada não é racional.) Para esse assunto, o método chakravala do século XI equivale - em termos modernos - a um algoritmo para encontrar as unidades de um campo de número quadrático real. No entanto, nem Bhāskara nem Gauss sabiam de campos de número como tal.

Os motivos do assunto como sabemos foram estabelecidos no final do século XIX, quando números ideais, o teoria dos ideais e Teoria da avaliação foram desenvolvidos; estas são três formas complementares de lidar com a falta de fatoração única em campos de número algébrica. (Por exemplo, no campo gerado pelas racionais e ${sqrt {-5}}$ , o número $6$ pode ser fatorada tanto como $6=2cdot 3$ e $6=(1+{sqrt {-5}})(1-{sqrt {-5}})$ ; todos $2$ , $3$ , $1+{sqrt {-5}}$ e $1-{sqrt {-5}}$ são irredutíveis, e assim, em sentido ingênuo, análogos a primos entre os inteiros.) O impulso inicial para o desenvolvimento de números ideais (por Kummer) parece ter vindo do estudo de leis de reciprocidade mais altas, ou seja, generalizações da reciprocidade quadrática.

Os campos numéricos são frequentemente estudados como extensões de campos numéricos menores: um campo L é considerado uma extensão de um campo K se L contém K. (Por exemplo, os números complexos C são uma extensão dos reais R, e os reais R são uma extensão dos racionais Q.) Classificar as possíveis extensões de um dado campo numérico é um problema difícil e parcialmente em aberto. Extensões abelianas—isto é, extensões L de K de modo que o grupo de Galois Gal(L/K) de L sobre K é um grupo abeliano—são relativamente bem compreendidos. Sua classificação foi o objeto do programa da teoria de campo de classe, que foi iniciado no final do século 19 (em parte por Kronecker e Eisenstein) e realizado em grande parte em 1900-1950.

Um exemplo de uma área ativa de pesquisa na teoria algébrica dos números é a teoria de Iwasawa. O programa de Langlands, um dos principais planos atuais de pesquisa em larga escala em matemática, às vezes é descrito como uma tentativa de generalizar a teoria de campos de classe para extensões não abelianas de campos numéricos.

Geometria diofantina

O problema central da geometria diofantina é determinar quando uma equação diofantina tem soluções e, se tiver, quantas. A abordagem adotada é pensar nas soluções de uma equação como um objeto geométrico.

Por exemplo, uma equação em duas variáveis define uma curva no plano. Mais geralmente, uma equação, ou sistema de equações, em duas ou mais variáveis define uma curva, uma superfície ou algum outro objeto no espaço ndimensional. Na geometria diofantina, pergunta-se se existem quaisquer pontos racionais (pontos cujas coordenadas são racionais) ou pontos integrais (pontos cujas coordenadas são inteiras) na curva ou superfície. Se houver tais pontos, o próximo passo é perguntar quantos são e como estão distribuídos. Uma questão básica nesse sentido é se existem finitamente ou infinitos pontos racionais em uma dada curva (ou superfície).

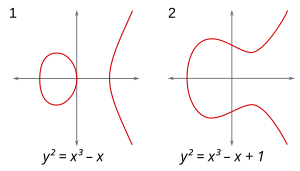
Na equação de Pythagorean ${displaystyle x^{2}+y^{2}=1,}$ nós gostaríamos de estudar suas soluções racionais, ou seja, suas soluções $(x,y)$ tal que x e Sim. são ambos racionais. Isso é o mesmo que pedir todas as soluções de inteiros para $a^{2}+b^{2}=c^{2}$ ; qualquer solução para a última equação nos dá uma solução $x = a/c$ , $y = b/c$ ao primeiro. É também o o mesmo que pedir por todos os pontos com coordenadas racionais na curva descrita por $x^2 + y^2 = 1$ . (Esta curva é um círculo de raio 1 em torno da origem.)

Dois exemplos de uma curva elíptica, ou seja, uma curva do gênero 1 com pelo menos um ponto racional. (Outro grafo pode ser visto como uma fatia de um toro no espaço de quatro dimensões.)

A reformulação de perguntas sobre equações em termos de pontos em curvas resulta em felicitous. A finitude ou não do número de pontos racionais ou inteiros em uma curva algébrica — isto é, soluções racionais ou integer para uma equação $f(x,y)=0$ , onde $f$ é um polinômio em duas variáveis - volta a depender crucialmente do género da curva. O género pode ser definido como segue: permitir as variáveis em $f(x,y)=0$ para ser números complexos; então $f(x,y)=0$ define uma superfície 2-dimensional em espaço 4-dimensional (uma vez que duas variáveis complexas podem ser decompostas em quatro variáveis reais, ou seja, quatro dimensões). Se contarmos o número de (doughnut) buracos na superfície; chamamos este número o género de $f(x,y)=0$ . Outras noções geométricas são tão cruciais.

Há também a área estreitamente ligada de aproximações de Diofantina: dado um número $x$ , então encontrar quão bem pode ser aproximado por racionais. (Estamos procurando aproximações que são boas em relação à quantidade de espaço que é preciso para escrever o racional: chamar $a/q$ (com $gcd(a,q)=1$ ) uma boa aproximação à $x$ se $<math alttext="{displaystyle |x-a/q||x- Sim. - Sim. um/q|<1qcNão. |x-a/q|<{frac {1}{q^{c}}<img alt="|x-a/q|$ , onde $c$ é grande.) Esta questão é de especial interesse se $x$ é um número algébrica. Se $x$ não pode ser bem aproximado, então algumas equações não têm soluções inteiras ou racionais. Além disso, vários conceitos (especialmente o de altura) resultam críticos tanto na geometria Diofantina quanto no estudo das aproximações Diofantinas. Esta questão também é de interesse especial na teoria transcendental dos números: se um número pode ser melhor aproximado do que qualquer número algébrica, então é um número transcendental. É por esse argumento que π e e foram mostrados para ser transcendental.

A geometria diofantina não deve ser confundida com a geometria dos números, que é uma coleção de métodos gráficos para responder a certas questões na teoria algébrica dos números. Geometria aritmética, no entanto, é um termo contemporâneo para praticamente o mesmo domínio coberto pelo termo Geometria diofantina. O termo geometria aritmética é indiscutivelmente usado com mais frequência quando se deseja enfatizar as conexões com a geometria algébrica moderna (como, por exemplo, o teorema de Faltings) em vez de técnicas de aproximações diofantinas.

Outros subcampos

As áreas abaixo datam não antes de meados do século XX, mesmo que sejam baseadas em material mais antigo. Por exemplo, conforme explicado abaixo, a questão dos algoritmos na teoria dos números é muito antiga, em certo sentido mais antiga que o conceito de prova; ao mesmo tempo, o estudo moderno da computabilidade data apenas das décadas de 1930 e 1940, e a teoria da complexidade computacional da década de 1970.

Teoria probabilística dos números

Grande parte da teoria probabilística dos números pode ser vista como um caso especial importante do estudo de variáveis que são quase, mas não totalmente, mutuamente independentes. Por exemplo, o evento de um inteiro aleatório entre um e um milhão ser divisível por dois e o evento de ser divisível por três são quase independentes, mas não totalmente.

É às vezes dito que a combinatória probabilística usa o fato de que o que acontece com probabilidade maior do que ${displaystyle 0}$ deve acontecer às vezes; pode-se dizer com justiça igual que muitas aplicações da teoria do número probabilístico dependem do fato de que o que é incomum deve ser raro. Se certos objetos algébricos (soluções de ensaio, racional ou inteiro a certas equações) podem ser mostrados na cauda de certas distribuições sensivelmente definidas, segue-se que deve haver poucos deles; esta é uma declaração não-probabilística muito concreta que segue de um probabilista.

Às vezes, uma abordagem probabilística não rigorosa leva a uma série de algoritmos heurísticos e problemas em aberto, principalmente a conjectura de Cramér.

Combinatória aritmética

Se começarmos de um conjunto infinito bastante "coisa" $A$ , ele contém muitos elementos na progressão aritmética: $a$ , ${displaystyle a+b,a+2b,a+3b,ldotsa+10b}$ Diz? Deve ser possível escrever grandes inteiros como somas de elementos de $A$ ?

Estas questões são características combinatória aritmética. Este é um campo de carvão atualmente; ele subsumes teoria dos números aditivos (que se preocupa com determinados conjuntos muito específicos) $A$ de significado aritmético, como os primos ou os quadrados) e, indiscutivelmente, alguns dos geometria de números, juntamente com algum material novo em rápido desenvolvimento. Seu foco em questões de crescimento e distribuição contas em parte por seus links em desenvolvimento com a teoria ergódica, teoria do grupo finito, teoria do modelo e outros campos. O termo combinatória aditiva é também usado; no entanto, os conjuntos $A$ ser estudado não precisa ser conjuntos de inteiros, mas sim subconjuntos de grupos não-comutativos, para os quais o símbolo de multiplicação, não o símbolo de adição, é tradicionalmente usado; eles também podem ser subconjuntos de anéis, nesse caso o crescimento de $A+A$ e $A$ · $A$ pode ser comparado.

Teoria computacional dos números

Um sieve Lehmer, um computador digital primitivo usado para encontrar primos e resolver equações diofantinas simples

Embora a palavra algoritmo remonte apenas a alguns leitores de al-Khwārizmī, descrições cuidadosas de métodos de solução são mais antigas que provas: tais métodos (ou seja, algoritmos) são tão antigos quanto qualquer outro reconhecível matemática — egípcio antigo, babilônico, védico, chinês — enquanto as provas apareceram apenas com os gregos do período clássico.

Um caso inicial é o que agora chamamos de algoritmo euclidiano. Em sua forma básica (nomeadamente, como um algoritmo para computar o maior divisor comum) aparece como Proposição 2 do Livro VII em Elementos, juntamente com uma prova de correção. No entanto, na forma que é frequentemente usada na teoria dos números (nomeadamente, como um algoritmo para encontrar soluções inteiras para uma equação $ax+by=c$ , ou, o que é o mesmo, para encontrar as quantidades cuja existência é assegurada pelo teorema restante chinês) ele aparece pela primeira vez nas obras de Āryabhaṭa (5o século VI CE) como um algoritmo chamado O que é isso? ("pulverizador"), sem prova de correção.

Existem duas questões principais: "Podemos calcular isso?" e "Podemos calculá-lo rapidamente?" Qualquer um pode testar se um número é primo ou, se não for, dividi-lo em fatores primos; fazê-lo rapidamente é outra questão. Agora conhecemos algoritmos rápidos para testar a primalidade, mas, apesar de muito trabalho (tanto teórico quanto prático), nenhum algoritmo verdadeiramente rápido para fatoração.

A dificuldade de um cálculo pode ser útil: protocolos modernos para criptografar mensagens (por exemplo, RSA) dependem de funções conhecidas por todos, mas cujos inversos são conhecidos apenas por alguns poucos escolhidos e levariam muito tempo tempo para descobrir por conta própria. Por exemplo, essas funções podem ser tais que seus inversos podem ser calculados apenas se certos inteiros grandes forem fatorados. Embora muitos problemas computacionais difíceis fora da teoria dos números sejam conhecidos, a maioria dos protocolos de criptografia de trabalho hoje em dia são baseados na dificuldade de alguns problemas teóricos dos números.

Algumas coisas podem não ser computáveis; na verdade, isso pode ser comprovado em alguns casos. Por exemplo, em 1970, provou-se, como solução para o décimo problema de Hilbert, que não existe máquina de Turing que resolva todas as equações diofantinas. Em particular, isso significa que, dado um conjunto de axiomas computavelmente enumerável, existem equações diofantinas para as quais não há prova, a partir dos axiomas, se o conjunto de equações tem ou não soluções inteiras. (Estaríamos necessariamente falando de equações diofantinas para as quais não há soluções inteiras, pois, dada uma equação diofantina com pelo menos uma solução, a própria solução fornece uma prova de que existe uma solução. Não podemos provar que um diofantino particular equação é desse tipo, pois isso implicaria que ela não tem soluções.)

Aplicativos

O teórico dos números Leonard Dickson (1874–1954) disse "Graças a Deus que a teoria dos números é imaculada por qualquer aplicação". Tal visão não é mais aplicável à teoria dos números. Em 1974, Donald Knuth disse "...praticamente todos os teoremas da teoria elementar dos números surgem de maneira natural e motivada em conexão com o problema de fazer os computadores fazerem cálculos numéricos de alta velocidade". A teoria elementar dos números é ensinada em cursos de matemática discreta para cientistas da computação; por outro lado, a teoria dos números também tem aplicações para o contínuo na análise numérica.

A teoria dos números tem agora várias aplicações modernas que abrangem diversas áreas, tais como:

Criptografia: esquemas de criptografia de chave pública como RSA são baseados na dificuldade de fatorar grandes números compostos em seus principais fatores.
Ciência da computação: O algoritmo de transformação rápida de Fourier (FFT), que é usado para calcular eficientemente a transformada de Fourier discreta, tem aplicações importantes no processamento de sinais e análise de dados.
Física: A hipótese de Riemann tem conexões com a distribuição de números primos e foi estudada para suas implicações potenciais na física.
Códigos de correção de erro: A teoria dos campos finitos e da geometria algébrica foram usados para construir códigos eficientes de correção de erros.
Comunicações: O design das redes telefônicas celulares requer conhecimento da teoria das formas modulares, que faz parte da teoria analítica dos números.
Estudo de escalas musicais: o conceito de "equal temperament", que é a base para a maioria da música ocidental moderna, envolve dividir a oitava em 12 partes iguais. Isso foi estudado usando teoria dos números e, em particular, as propriedades da 12a raiz de 2.

Prêmios

A American Mathematical Society concede o Prêmio Cole em Teoria dos Números. Além disso, a teoria dos números é uma das três subdisciplinas matemáticas premiadas pelo Prêmio Fermat.

Contenido relacionado

Más resultados...