Teoria do jogo
Teoria dos jogos é o estudo de modelos matemáticos de interações estratégicas entre agentes racionais. Tem aplicações em todos os campos das ciências sociais, bem como em lógica, ciência de sistemas e ciência da computação. Originalmente, abordava jogos de soma zero para duas pessoas, nos quais os ganhos ou perdas de cada participante são exatamente equilibrados pelos dos outros participantes. No século 21, a teoria dos jogos se aplica a uma ampla gama de relações comportamentais; agora é um termo genérico para a ciência da tomada de decisão lógica em humanos, animais e computadores.
A teoria moderna dos jogos começou com a ideia de equilíbrio de estratégia mista em um jogo de soma zero para duas pessoas e sua prova por John von Neumann. A prova original de Von Neumann usou o teorema do ponto fixo de Brouwer em mapeamentos contínuos em conjuntos convexos compactos, que se tornou um método padrão na teoria dos jogos e na economia matemática. Seu trabalho foi seguido pelo livro de 1944 Teoria dos Jogos e Comportamento Econômico, co-escrito com Oskar Morgenstern, que considerava jogos cooperativos de vários jogadores. A segunda edição deste livro forneceu uma teoria axiomática da utilidade esperada, que permitiu que estatísticos matemáticos e economistas tratassem a tomada de decisões sob incerteza.
A teoria dos jogos foi amplamente desenvolvida na década de 1950 por muitos estudiosos. Foi explicitamente aplicado à evolução na década de 1970, embora desenvolvimentos semelhantes remontem pelo menos até a década de 1930. A teoria dos jogos tem sido amplamente reconhecida como uma ferramenta importante em muitos campos. Em 2020, com o Prêmio Nobel de Ciências Econômicas indo para os teóricos dos jogos Paul Milgrom e Robert B. Wilson, quinze teóricos dos jogos ganharam o Prêmio Nobel de economia. John Maynard Smith recebeu o Prêmio Crafoord por sua aplicação da teoria evolutiva dos jogos.
História
Precursores
As discussões sobre a matemática dos jogos começaram muito antes do surgimento da moderna teoria matemática dos jogos. O trabalho de Cardano sobre jogos de azar em Liber de ludo aleae (Livro sobre jogos de azar), escrito por volta de 1564, mas publicado postumamente em 1663, formulou algumas das ideias básicas do campo. Na década de 1650, Pascal e Huygens desenvolveram o conceito de expectativa no raciocínio sobre a estrutura dos jogos de azar, e Huygens publicou seu cálculo de jogo em De ratiociniis in ludo aleæ (Sobre o raciocínio em jogos de Chance) em 1657.
Em 1713, uma carta atribuída a Charles Waldegrave analisava um jogo chamado "le Her". Ele era um jacobita ativo e tio de James Waldegrave, um diplomata britânico. Nesta carta, Waldegrave forneceu uma solução de estratégia mista minimax para uma versão para duas pessoas do jogo de cartas le Her, e o problema agora é conhecido como problema de Waldegrave. Em seu 1838 Recherches sur les principes mathématiques de la théorie des richesses (Pesquisas sobre os princípios matemáticos da the Theory of Wealth), Antoine Augustin Cournot considerou um duopólio e apresentou uma solução que é o equilíbrio de Nash do jogo.
Em 1913, Ernst Zermelo publicou Über eine Anwendung der Mengenlehre auf die Theorie des Schachspiels ( On an Application of Set Theory to the Theory of the Game of Chess), que provou que a estratégia ótima de xadrez é estritamente determinada. Isso abriu caminho para teoremas mais gerais.
Em 1938, o economista matemático dinamarquês Frederik Zeuthen provou que o modelo matemático tinha uma estratégia vencedora usando o teorema do ponto fixo de Brouwer. Em seu livro de 1938 Applications aux Jeux de Hasard e notas anteriores, Émile Borel provou um teorema minimax para duas pessoas jogos de matriz de soma zero apenas quando a matriz de pay-off é simétrica e fornece uma solução para um jogo infinito não trivial (conhecido em inglês como Blotto game). Borel conjecturou a inexistência de equilíbrios de estratégia mista em jogos finitos de soma zero de duas pessoas, uma conjectura que foi provada falsa por von Neumann.
Nascimento e primeiros desenvolvimentos
A teoria dos jogos não existia como um campo único até que John von Neumann publicou o artigo On the Theory of Games of Strategy em 1928. A prova original de Von Neumann usou a de Brouwer teorema do ponto fixo em mapeamentos contínuos em conjuntos convexos compactos, que se tornou um método padrão na teoria dos jogos e economia matemática. Seu artigo foi seguido por seu livro de 1944 Teoria dos Jogos e Comportamento Econômico em co-autoria com Oskar Morgenstern. A segunda edição deste livro forneceu uma teoria axiomática da utilidade, que reencarnou a antiga teoria da utilidade (do dinheiro) de Daniel Bernoulli como uma disciplina independente. O trabalho de Von Neumann na teoria dos jogos culminou neste livro de 1944. Este trabalho fundamental contém o método para encontrar soluções mutuamente consistentes para jogos de soma zero para duas pessoas. O trabalho subsequente focou principalmente na teoria dos jogos cooperativos, que analisa estratégias ótimas para grupos de indivíduos, presumindo que eles podem impor acordos entre eles sobre estratégias adequadas.
Em 1950, surgiu a primeira discussão matemática sobre o dilema do prisioneiro, e um experimento foi realizado pelos notáveis matemáticos Merrill M. Flood e Melvin Dresher, como parte das investigações da RAND Corporation sobre a teoria dos jogos. A RAND prosseguiu os estudos por causa de possíveis aplicações para a estratégia nuclear global. Mais ou menos na mesma época, John Nash desenvolveu um critério para a consistência mútua dos jogadores. estratégias conhecidas como equilíbrio de Nash, aplicáveis a uma variedade maior de jogos do que o critério proposto por von Neumann e Morgenstern. Nash provou que todo jogo não cooperativo finito de n jogadores e soma não zero (não apenas dois jogadores e soma zero) tem o que hoje é conhecido como equilíbrio de Nash em estratégias mistas.
A teoria dos jogos experimentou uma enxurrada de atividades na década de 1950, durante a qual foram desenvolvidos os conceitos de núcleo, jogo de forma extensiva, jogo fictício, jogos repetidos e o valor de Shapley. A década de 1950 também viu as primeiras aplicações da teoria dos jogos à filosofia e à ciência política.
Conquistas premiadas
Em 1965, Reinhard Selten introduziu seu conceito de solução de equilíbrios perfeitos de subjogos, que refinou ainda mais o equilíbrio de Nash. Mais tarde, ele também introduziria a perfeição das mãos trêmulas. Em 1994, Nash, Selten e Harsanyi se tornaram Prêmios Nobel de Economia por suas contribuições à teoria dos jogos econômicos.
Na década de 1970, a teoria dos jogos foi amplamente aplicada na biologia, em grande parte como resultado do trabalho de John Maynard Smith e sua estratégia evolutivamente estável. Além disso, os conceitos de equilíbrio correlacionado, perfeição da mão trêmula e conhecimento comum foram introduzidos e analisados.
Em 2005, os teóricos do jogo Thomas Schelling e Robert Aumann seguiram Nash, Selten e Harsanyi como ganhadores do Prêmio Nobel. Schelling trabalhou em modelos dinâmicos, primeiros exemplos da teoria evolutiva dos jogos. Aumann contribuiu mais para a escola do equilíbrio, introduzindo o enriquecimento do equilíbrio e os equilíbrios correlacionados e desenvolvendo uma extensa análise formal da suposição do conhecimento comum e de suas consequências.
Em 2007, Leonid Hurwicz, Eric Maskin e Roger Myerson receberam o Prêmio Nobel de Economia "por terem lançado as bases da teoria do projeto de mecanismos". As contribuições de Myerson incluem a noção de equilíbrio adequado e um importante texto de pós-graduação: Teoria dos Jogos, Análise de Conflito. Hurwicz introduziu e formalizou o conceito de compatibilidade de incentivos.
Em 2012, Alvin E. Roth e Lloyd S. Shapley receberam o Prêmio Nobel de Economia "pela teoria das alocações estáveis e pela prática do design de mercado". Em 2014, o Nobel foi para o teórico dos jogos Jean Tirole.
Tipos de jogo
Cooperativo / não cooperativo
Um jogo é cooperativo se os jogadores são capazes de assumir compromissos obrigatórios aplicados externamente (por exemplo, por meio de leis contratuais). Um jogo é não cooperativo se os jogadores não puderem formar alianças ou se todos os acordos precisarem ser autoaplicados (por exemplo, por meio de ameaças confiáveis).
Jogos cooperativos são frequentemente analisados por meio da estrutura da teoria dos jogos cooperativos, que se concentra em prever quais coalizões serão formadas, as ações conjuntas que os grupos realizam e os resultados coletivos resultantes. Ele se opõe à tradicional teoria dos jogos não cooperativos, que se concentra em prever o desempenho individual dos jogadores. ações e payoffs e analisando os equilíbrios de Nash. O foco no retorno individual pode resultar em um fenômeno conhecido como Tragedy of the Commons, onde os recursos são usados em um nível coletivamente ineficiente. A falta de negociação formal leva à deterioração dos bens públicos pelo uso excessivo e pela falta de provisão decorrente de incentivos privados.
A teoria dos jogos cooperativos fornece uma abordagem de alto nível, pois descreve apenas a estrutura, estratégias e recompensas das coalizões, enquanto a teoria dos jogos não cooperativos também analisa como os procedimentos de barganha afetarão a distribuição de recompensas dentro de cada coalizão. Como a teoria dos jogos não cooperativos é mais geral, os jogos cooperativos podem ser analisados através da abordagem da teoria dos jogos não cooperativos (o inverso não é válido), desde que sejam feitas suposições suficientes para abranger todas as estratégias possíveis disponíveis para os jogadores devido à possibilidade de imposição externa da cooperação. Embora o uso de uma única teoria possa ser desejável, em muitos casos, informações insuficientes estão disponíveis para modelar com precisão os procedimentos formais disponíveis durante o processo de negociação estratégica, ou o modelo resultante seria muito complexo para oferecer uma ferramenta prática no mundo real. Nesses casos, a teoria dos jogos cooperativos fornece uma abordagem simplificada que permite a análise do jogo como um todo sem ter que fazer qualquer suposição sobre os poderes de barganha.
Simétrico / assimétrico
| E | F | |
| E | 1, 2 | 0, 0 |
| F | 0, 0 | 1, 2 |
| Um jogo assimétrico | ||
Um jogo simétrico é um jogo em que os ganhos para jogar uma determinada estratégia dependem apenas das outras estratégias empregadas, não de quem as está jogando. Ou seja, se as identidades dos jogadores puderem ser alteradas sem alterar o resultado das estratégias, então um jogo é simétrico. Muitos dos jogos 2×2 comumente estudados são simétricos. As representações padrão de galinha, o dilema do prisioneiro e a caça ao veado são todos jogos simétricos. Alguns estudiosos considerariam certos jogos assimétricos como exemplos desses jogos também. No entanto, os pagamentos mais comuns para cada um desses jogos são simétricos.
Os jogos assimétricos mais comumente estudados são jogos em que não há conjuntos de estratégias idênticos para ambos os jogadores. Por exemplo, o jogo do ultimato e da mesma forma o jogo do ditador têm estratégias diferentes para cada jogador. É possível, no entanto, que um jogo tenha estratégias idênticas para ambos os jogadores, mas seja assimétrico. Por exemplo, o jogo retratado no gráfico desta seção é assimétrico, apesar de ter conjuntos de estratégias idênticos para ambos os jogadores.
Soma zero / soma diferente de zero
| A | B | |
| A | -1, 1 | 3, 3 |
| B | 0, 0 | -2, 2 |
| Um jogo de zero-sum | ||
Jogos de soma zero (mais geralmente, jogos de soma constante) são jogos em que as escolhas dos jogadores não podem aumentar nem diminuir os recursos disponíveis. Em jogos de soma zero, o benefício total vai para todos os jogadores em um jogo, para cada combinação de estratégias, sempre soma zero (mais informalmente, um jogador se beneficia apenas às custas iguais dos outros). O pôquer exemplifica um jogo de soma zero (ignorando a possibilidade do corte da casa), porque ganha-se exatamente o valor que os oponentes perdem. Outros jogos de soma zero incluem moedas de um centavo e a maioria dos jogos de tabuleiro clássicos, incluindo Go e xadrez.
Muitos jogos estudados por teóricos de jogos (incluindo o famoso dilema do prisioneiro) são jogos de soma diferente de zero, porque o resultado tem resultados líquidos maiores ou menores que zero. Informalmente, em jogos de soma diferente de zero, o ganho de um jogador não corresponde necessariamente à perda de outro.
Jogos de soma constante correspondem a atividades como roubo e jogos de azar, mas não à situação econômica fundamental em que há ganhos potenciais do comércio. É possível transformar qualquer jogo de soma constante em um jogo de soma zero (possivelmente assimétrico) adicionando um jogador fictício (muitas vezes chamado de "o tabuleiro") cujas perdas compensam as perdas dos jogadores; ganhos líquidos.
Simultâneo / sequencial
Jogos simultâneos são jogos em que ambos os jogadores se movem simultaneamente ou, em vez disso, os jogadores posteriores não têm conhecimento da posição dos jogadores anteriores. ações (tornando-as efetivamente simultâneas). Jogos sequenciais (ou jogos dinâmicos) são jogos em que os jogadores não tomam decisões simultaneamente e as ações anteriores do jogador afetam o resultado e as decisões de outros jogadores. Isso não precisa ser uma informação perfeita sobre todas as ações dos jogadores anteriores; pode ser muito pouco conhecimento. Por exemplo, um jogador pode saber que um jogador anterior não executou uma ação específica, embora não saiba qual das outras ações disponíveis o primeiro jogador realmente executou.
A diferença entre jogos simultâneos e sequenciais é capturada nas diferentes representações discutidas acima. Freqüentemente, a forma normal é usada para representar jogos simultâneos, enquanto a forma extensiva é usada para representar jogos sequenciais. A transformação da forma extensiva para normal é uma forma, o que significa que vários jogos de forma extensiva correspondem à mesma forma normal. Consequentemente, as noções de equilíbrio para jogos simultâneos são insuficientes para raciocinar sobre jogos sequenciais; veja a perfeição do subjogo.
Em resumo, as diferenças entre jogos sequenciais e simultâneos são as seguintes:
| Sequencial | Simultaneamente | |
|---|---|---|
| Normalmente denotado por | Árvores de decisão | Matrizes de pagamento |
Conhecimento prévio de movimento do adversário? | Sim. | Não. |
| Eixo do tempo? | Sim. | Não. |
| Também conhecido como | Jogo de forma extensiva Jogo extenso | Jogo de estratégia Jogo estratégico |
Competição do tribunal
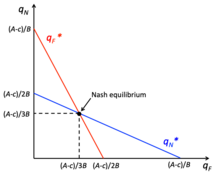
O modelo de competição de Cournot envolve jogadores que escolhem a quantidade de um produto homogêneo para produzir de forma independente e simultânea, onde o custo marginal pode ser diferente para cada empresa e o retorno da empresa é o lucro. Os custos de produção são informações públicas e a empresa visa encontrar a quantidade que maximiza o lucro com base no que acredita que a outra empresa produzirá e se comportará como monopólios. Nesse jogo, as firmas querem produzir na quantidade de monopólio, mas há um alto incentivo para se desviar e produzir mais, o que diminui o preço de equilíbrio do mercado. Por exemplo, as firmas podem ser tentadas a se desviar da quantidade de monopólio se houver uma quantidade de monopólio baixa e preço alto, com o objetivo de aumentar a produção para maximizar o lucro. No entanto, esta opção não oferece o maior retorno, pois a capacidade da empresa de maximizar os lucros depende de sua participação no mercado e da elasticidade da demanda do mercado. O equilíbrio de Cournot é alcançado quando cada empresa opera em sua função de reação sem nenhum incentivo para se desviar, pois tem a melhor resposta com base na produção das outras empresas. Dentro do jogo, as empresas atingem o equilíbrio de Nash quando o equilíbrio de Cournot é alcançado.
Concurso Bertrand
A competição de Bertrand assume produtos homogêneos e um custo marginal constante e os jogadores escolhem os preços. O equilíbrio de preços competitivos é onde o preço é igual aos custos marginais, assumindo informações completas sobre os concorrentes. custos. Portanto, as empresas têm um incentivo para se desviar do equilíbrio porque um produto homogêneo com preço mais baixo ganhará toda a participação de mercado, conhecida como vantagem de custo.
Informação perfeita e informação imperfeita
Um importante subconjunto de jogos sequenciais consiste em jogos de informação perfeita. Um jogo com informação perfeita significa que todos os jogadores, a cada jogada no jogo, conhecem a história anterior do jogo e as jogadas feitas anteriormente por todos os outros jogadores. Na realidade, isso pode ser aplicado a empresas e consumidores que possuem informações sobre preço e qualidade de todos os bens disponíveis em um mercado. Um jogo de informação imperfeita é jogado quando os jogadores não conhecem todos os movimentos já feitos pelo oponente, como um jogo de movimento simultâneo. A maioria dos jogos estudados na teoria dos jogos são jogos de informação imperfeita. Exemplos de jogos de informação perfeita incluem jogo da velha, damas, xadrez e Go.
Muitos jogos de cartas são jogos de informação imperfeita, como pôquer e bridge. A informação perfeita é muitas vezes confundida com a informação completa, que é um conceito semelhante pertencente ao conhecimento comum da sequência, estratégias e recompensas de cada jogador ao longo do jogo. A informação completa requer que cada jogador conheça as estratégias e recompensas disponíveis para os outros jogadores, mas não necessariamente as ações tomadas, enquanto a informação perfeita é o conhecimento de todos os aspectos do jogo e dos jogadores. Jogos de informação incompleta podem ser reduzidos, no entanto, a jogos de informação imperfeita, introduzindo "movimentos por natureza".
Jogo bayesiano
Uma das suposições do equilíbrio de Nash é que cada jogador tem crenças corretas sobre as ações dos outros jogadores. No entanto, existem muitas situações na teoria dos jogos em que os participantes não compreendem totalmente as características de seus oponentes. Os negociadores podem não estar cientes da avaliação de seus oponentes sobre o objeto da negociação, as empresas podem não estar cientes das funções de custo de seus oponentes, os combatentes podem não estar cientes dos pontos fortes de seus oponentes e os jurados podem não estar cientes da interpretação de seu colega das evidências no julgamento. Em alguns casos, os participantes podem conhecer bem o caráter de seu oponente, mas podem não saber o quão bem seu oponente conhece seu próprio caráter.
Jogo Bayesiano significa um jogo estratégico com informações incompletas. Para um jogo estratégico, os tomadores de decisão são os jogadores, e cada jogador tem um grupo de ações. Uma parte central da especificação de informação imperfeita é o conjunto de estados. Cada estado descreve completamente uma coleção de características relevantes para o jogador, como suas preferências e detalhes sobre eles. Deve haver um estado para cada conjunto de recursos que algum jogador acredita que possa existir.
Por exemplo, onde o Jogador 1 não tem certeza se o Jogador 2 prefere sair com ela ou se afastar dela, enquanto o Jogador 2 entende as preferências do Jogador 1 como antes. Para ser específico, supondo que o Jogador 1 acredite que o Jogador 2 quer sair com ela com uma probabilidade de 1/2 e fugir dela com uma probabilidade de 1/2 (esta avaliação vem da experiência do Jogador 1 provavelmente: ela enfrenta jogadores que querem sair com ela metade do tempo em tal caso e jogadores que querem evitá-la metade do tempo). Pela probabilidade envolvida, a análise dessa situação requer entender a preferência do jogador pelo empate, ainda que as pessoas estejam interessadas apenas no puro equilíbrio estratégico.
Jogos combinatórios
Os jogos em que a dificuldade de encontrar uma estratégia ótima decorre da multiplicidade de movimentos possíveis são chamados de jogos combinatórios. Exemplos incluem xadrez e Go. Os jogos que envolvem informação imperfeita também podem ter um forte caráter combinatório, como por exemplo o gamão. Não há uma teoria unificada abordando elementos combinatórios em jogos. Existem, no entanto, ferramentas matemáticas que podem resolver alguns problemas particulares e responder a algumas questões gerais.
Jogos de informação perfeita foram estudados na teoria combinatória dos jogos, que desenvolveu novas representações, por ex. números surreais, bem como métodos de prova combinatórios e algébricos (e às vezes não construtivos) para resolver jogos de certos tipos, incluindo jogos "loopy" jogos que podem resultar em sequências de movimentos infinitamente longas. Esses métodos abordam jogos com maior complexidade combinatória do que aqueles normalmente considerados na teoria dos jogos tradicional (ou "econômica"). Um jogo típico que foi resolvido dessa maneira é o Hex. Um campo de estudo relacionado, baseado na teoria da complexidade computacional, é a complexidade do jogo, que se preocupa em estimar a dificuldade computacional de encontrar estratégias ótimas.
A pesquisa em inteligência artificial abordou jogos de informação perfeitos e imperfeitos que possuem estruturas combinatórias muito complexas (como xadrez, go ou gamão) para os quais não foram encontradas estratégias ótimas comprováveis. As soluções práticas envolvem heurísticas computacionais, como poda alfa-beta ou uso de redes neurais artificiais treinadas por aprendizado por reforço, que tornam os jogos mais tratáveis na prática computacional.
Jogos infinitamente longos
Os jogos, conforme estudados por economistas e jogadores do mundo real, geralmente são finalizados em um número finito de movimentos. Matemáticos puros não são tão constrangidos, e teóricos de conjuntos em particular estudam jogos que duram infinitas jogadas, com o vencedor (ou outro pagamento) não conhecido até depois de todas essas jogadas serem concluídas.
O foco da atenção geralmente não está tanto na melhor maneira de jogar tal jogo, mas se um jogador tem uma estratégia vencedora. (Pode-se provar, usando o axioma da escolha, que existem jogos – mesmo com informações perfeitas e onde os únicos resultados são "ganhar" ou "perder" – para os quais nenhum dos jogadores tem uma estratégia vencedora.) A existência de tais estratégias, para jogos habilmente projetados, tem consequências importantes na teoria descritiva dos conjuntos.
Jogos discretos e contínuos
Grande parte da teoria dos jogos está preocupada com jogos finitos e discretos que têm um número finito de jogadores, movimentos, eventos, resultados, etc. Muitos conceitos podem ser estendidos, no entanto. Os jogos contínuos permitem que os jogadores escolham uma estratégia de um conjunto de estratégias contínuas. Por exemplo, a competição de Cournot é tipicamente modelada com o desempenho dos jogadores. estratégias sendo quaisquer quantidades não negativas, incluindo quantidades fracionárias.
Jogos diferenciais
Jogos diferenciados como o jogo de perseguição e evasão contínuas são jogos contínuos onde a evolução dos jogadores' variáveis de estado é governado por equações diferenciais. O problema de encontrar uma estratégia ótima em um jogo diferencial está intimamente relacionado com a teoria de controle ótimo. Em particular, existem dois tipos de estratégias: as estratégias de malha aberta são encontradas usando o princípio do máximo de Pontryagin, enquanto as estratégias de malha fechada são encontradas usando o método de Programação Dinâmica de Bellman.
Um caso particular de jogos diferenciais são os jogos com horizonte de tempo aleatório. Nesses jogos, o tempo terminal é uma variável aleatória com uma dada função de distribuição de probabilidade. Portanto, os jogadores maximizam a expectativa matemática da função de custo. Foi mostrado que o problema de otimização modificado pode ser reformulado como um jogo diferencial descontado em um intervalo de tempo infinito.
Teoria dos jogos evolutivos
A teoria evolutiva dos jogos estuda jogadores que ajustam suas estratégias ao longo do tempo de acordo com regras que não são necessariamente racionais ou perspicazes. Em geral, a evolução das estratégias ao longo do tempo de acordo com tais regras é modelada como uma cadeia de Markov com uma variável de estado, como o perfil da estratégia atual ou como o jogo foi jogado no passado recente. Tais regras podem apresentar imitação, otimização ou sobrevivência do mais apto.
Em biologia, tais modelos podem representar a evolução, em que os descendentes adotam o comportamento dos pais. estratégias e pais que jogam estratégias mais bem-sucedidas (ou seja, correspondendo a recompensas mais altas) têm um número maior de descendentes. Nas ciências sociais, tais modelos normalmente representam ajustes estratégicos por jogadores que jogam um jogo muitas vezes durante sua vida e, consciente ou inconscientemente, ocasionalmente ajustam suas estratégias.
Resultados estocásticos (e relação com outros campos)
Problemas de decisão individual com resultados estocásticos às vezes são considerados "jogos de um jogador". Eles podem ser modelados usando ferramentas semelhantes nas disciplinas relacionadas de teoria da decisão, pesquisa operacional e áreas de inteligência artificial, particularmente planejamento de IA (com incerteza) e sistema multiagente. Embora esses campos possam ter motivadores diferentes, a matemática envolvida é substancialmente a mesma, por exemplo, usando processos de decisão de Markov (MDP).
Os resultados estocásticos também podem ser modelados em termos de teoria dos jogos, adicionando um jogador de ação aleatória que faz "movimentos aleatórios" ("move-se por natureza"). Este jogador não é normalmente considerado um terceiro jogador no que de outra forma é um jogo para dois jogadores, mas serve apenas para fornecer uma jogada de dados quando exigido pelo jogo.
Para alguns problemas, abordagens diferentes para modelar resultados estocásticos podem levar a soluções diferentes. Por exemplo, a diferença de abordagem entre os MDPs e a solução minimax é que a última considera o pior caso sobre um conjunto de movimentos adversários, em vez de raciocinar na expectativa sobre esses movimentos, dada uma distribuição de probabilidade fixa. A abordagem minimax pode ser vantajosa onde modelos estocásticos de incerteza não estão disponíveis, mas também pode superestimar eventos extremamente improváveis (mas caros), influenciando drasticamente a estratégia em tais cenários se for assumido que um adversário pode forçar tal evento a acontecer. (Consulte a teoria do cisne negro para mais discussões sobre esse tipo de problema de modelagem, particularmente no que se refere à previsão e limitação de perdas em bancos de investimento.)
Modelos gerais que incluem todos os elementos de resultados estocásticos, adversários e observabilidade parcial ou ruidosa (de movimentos de outros jogadores) também foram estudados. O "padrão ouro" é considerado um jogo estocástico parcialmente observável (POSG), mas poucos problemas realistas são computacionalmente viáveis na representação POSG.
Metajogos
São jogos cujo jogo é o desenvolvimento das regras para outro jogo, o jogo alvo ou sujeito. Os metajogos buscam maximizar o valor de utilidade do conjunto de regras desenvolvido. A teoria dos metajogos está relacionada à teoria do design de mecanismos.
O termo análise de metajogo também é usado para se referir a uma abordagem prática desenvolvida por Nigel Howard, em que uma situação é enquadrada como um jogo estratégico no qual os participantes tentam realizar seus objetivos por meio das opções disponíveis. Desenvolvimentos subseqüentes levaram à formulação da análise de confrontação.
Jogos de sinuca
São jogos que prevalecem sobre todas as formas de sociedade. Os jogos de pool são jogadas repetidas com mudança na tabela de pagamento em geral ao longo de um caminho experiente, e suas estratégias de equilíbrio geralmente assumem uma forma de convenção social evolucionária e convenção econômica. A teoria dos jogos de pool surge para reconhecer formalmente a interação entre a escolha ideal em uma jogada e o surgimento do próximo caminho de atualização da tabela de pagamento, identificar a existência e a robustez da invariância e prever a variância ao longo do tempo. A teoria é baseada na classificação de transformação topológica da atualização da tabela de pagamento ao longo do tempo para prever variância e invariância, e também está dentro da jurisdição da lei computacional de otimalidade alcançável para sistema ordenado.
Teoria do jogo de campo médio
A teoria dos jogos de campo médio é o estudo da tomada de decisão estratégica em populações muito grandes de pequenos agentes em interação. Essa classe de problemas foi considerada na literatura econômica por Boyan Jovanovic e Robert W. Rosenthal, na literatura de engenharia por Peter E. Caines e pelos matemáticos Pierre-Louis Lions e Jean-Michel Lasry.
Representação de jogos
Os jogos estudados na teoria dos jogos são objetos matemáticos bem definidos. Para ser totalmente definido, um jogo deve especificar os seguintes elementos: os jogadores do jogo, as informações e as ações disponíveis para cada jogador em cada ponto de decisão e os retornos para cada resultado. (Eric Rasmusen refere-se a esses quatro "elementos essenciais" pelo acrônimo "PAPI".) Um teórico de jogos normalmente usa esses elementos, junto com um conceito de solução de sua escolha, para deduzir um conjunto de estratégias de equilíbrio para cada jogador, de modo que, quando essas estratégias são empregadas, nenhum jogador pode lucrar desviando-se unilateralmente de sua estratégia. Essas estratégias de equilíbrio determinam um equilíbrio para o jogo - um estado estável no qual ocorre um resultado ou um conjunto de resultados com probabilidade conhecida.
A maioria dos jogos cooperativos é apresentada na forma de função característica, enquanto as formas extensiva e normal são usadas para definir jogos não cooperativos.
Formulário extenso
O formulário extenso pode ser usado para formalizar jogos com uma sequência temporal de jogadas. Jogos de forma extensa podem ser visualizados usando árvores de jogo (como ilustrado aqui). Aqui cada vértice (ou nó) representa um ponto de escolha para um jogador. O jogador é especificado por um número listado pelo vértice. As linhas fora do vértice representam uma ação possível para aquele jogador. Os pagamentos são especificados na parte inferior da árvore. A forma extensa pode ser vista como uma generalização multijogador de uma árvore de decisão. Para resolver qualquer jogo de forma extensa, a indução reversa deve ser usada. Envolve trabalhar para trás na árvore do jogo para determinar o que um jogador racional faria no último vértice da árvore, o que o jogador com o movimento anterior faria dado que o jogador com o último movimento é racional, e assim por diante até o primeiro vértice da árvore é atingido.
O jogo ilustrado consiste em dois jogadores. A maneira como este jogo em particular é estruturado (ou seja, com tomada de decisão sequencial e informações perfeitas), Jogador 1 "move" primeiro escolhendo F ou U (justo ou injusto). O próximo na sequência, Jogador 2, que agora observou o Jogador 1's move, pode escolher jogar A ou R. Assim que o Jogador 2 fizer sua escolha, o jogo é considerado encerrado e cada jogador recebe seu respectivo pagamento, representado na imagem por dois números, onde o primeiro número representa o pagamento do Jogador 1 e o segundo número representa o pagamento do Jogador 2. Suponha que o Jogador 1 escolha U e então o Jogador 2 escolha A: Jogador 1 então recebe um pagamento de "oito" (que em termos do mundo real pode ser interpretado de várias maneiras, a mais simples das quais é em termos de dinheiro, mas pode significar coisas como oito dias de férias ou oito países conquistados ou ainda mais oito oportunidades de jogar o mesmo jogo contra outros jogadores) e o Jogador 2 recebe um pagamento de "dois".
O formulário extenso também pode capturar jogos com movimentos simultâneos e jogos com informações imperfeitas. Para representá-lo, uma linha pontilhada conecta diferentes vértices para representá-los como parte do mesmo conjunto de informações (ou seja, os jogadores não sabem em que ponto estão) ou uma linha fechada é desenhada em torno deles. (Veja o exemplo na seção de informações imperfeitas.)
Forma normal
| Jogador 2 escolhe Esquerda | Jogador 2 escolhe Certo. | |
| Jogador 1 escolhe Para cima | 4, 3 | -1, -1 |
| Jogador 1 escolhePara baixo. | 0, 0 | 3, 4 |
| Forma normal ou matriz de pagamento de um jogo de 2 jogadores, 2-estratégia | ||
O jogo normal (ou de forma estratégica) é geralmente representado por uma matriz que mostra os jogadores, estratégias e recompensas (veja o exemplo à direita). De maneira mais geral, pode ser representado por qualquer função que associe um pagamento para cada jogador a todas as combinações possíveis de ações. No exemplo a seguir, há dois jogadores; um escolhe a linha e o outro escolhe a coluna. Cada jogador tem duas estratégias, que são especificadas pelo número de linhas e pelo número de colunas. Os pagamentos são fornecidos no interior. O primeiro número é o pagamento recebido pelo jogador da linha (Jogador 1 em nosso exemplo); o segundo é o pagamento para o jogador da coluna (Jogador 2 em nosso exemplo). Suponha que o Jogador 1 jogue Cima e que o Jogador 2 jogue Esquerda. Então o jogador 1 recebe um pagamento de 4 e o jogador 2 recebe 3.
Quando um jogo é apresentado na forma normal, presume-se que cada jogador aja simultaneamente ou, pelo menos, sem conhecer as ações do outro. Se os jogadores tiverem alguma informação sobre as escolhas de outros jogadores, o jogo geralmente é apresentado de forma extensa.
Todo jogo de forma extensiva tem um jogo de forma normal equivalente, entretanto, a transformação para a forma normal pode resultar em uma explosão exponencial no tamanho da representação, tornando-a impraticável computacionalmente.
Formulário de função característica
Em jogos que possuem utilidade removível, recompensas separadas não são dadas; em vez disso, a função característica decide o pagamento de cada unidade. A ideia é que a unidade que está 'vazia', por assim dizer, não recebe recompensa alguma.
A origem desta forma deve ser encontrada no livro de John von Neumann e Oskar Morgenstern; ao olhar para estas instâncias, eles adivinharam que quando um sindicato C- Sim. aparece, funciona contra a fração (NC){displaystyle left({frac {mathbf] (N} }{mathbf {C} }}right)}como se dois indivíduos estivessem jogando um jogo normal. O pagamento equilibrado de C é uma função básica. Embora existam exemplos diferentes que ajudam a determinar quantidades coligacionais de jogos normais, nem todos parecem que em sua forma de função pode ser derivado de tal.
Formalmente, uma função característica é vista como: (N,v), onde N representa o grupo de pessoas e v:2N→ → R{displaystyle v:2^{N}to mathbf Não. é um utilitário normal.
Tais funções características foram expandidas para descrever jogos onde não há utilitário removível.
Representações alternativas do jogo
Formas alternativas de representação de jogos são utilizadas para algumas subclasses de jogos ou ajustadas às necessidades de pesquisas interdisciplinares. Além das representações clássicas do jogo, algumas das representações alternativas também codificam aspectos relacionados ao tempo.
| Nome | Ano | Meios | Tipo de jogos | Tempo |
|---|---|---|---|---|
| Jogo de Congestão | 1973 | funções | subconjunto de jogos n-person, movimentos simultâneos | Não. |
| Forma sequencial | 1994 | matrizes | Jogos de 2 pessoas de informações imperfeitas | Não. |
| Jogos em tempo real | 1994 | funções | Jogos de 2 pessoas | Sim. |
| Gala | 1997 | lógica | n-person jogos de informação imperfeita | Não. |
| Jogos gráficos | 2001 | gráficos, funções | n-person games, movimentos simultâneos | Não. |
| Jogos de efeito local | 2003 | funções | subconjunto de jogos n-person, movimentos simultâneos | Não. |
| GDL | 2005 | lógica | deterministic n-person games, movimentos simultâneos | Não. |
| Jogo Petri-nets | 2006 | Rede de Petri | deterministic n-person games, movimentos simultâneos | Não. |
| Jogos contínuos | 2007 | funções | subconjunto de jogos de 2 pessoas de informações imperfeitas | Sim. |
| PNSI | 2008 | Rede de Petri | n-person jogos de informação imperfeita | Sim. |
| Jogos de gráfico de ação | 2012 | gráficos, funções | n-person games, movimentos simultâneos | Não. |
Usos gerais e aplicados
Como método de matemática aplicada, a teoria dos jogos tem sido usada para estudar uma ampla variedade de comportamentos humanos e animais. Foi inicialmente desenvolvido em economia para entender uma grande coleção de comportamentos econômicos, incluindo comportamentos de empresas, mercados e consumidores. O primeiro uso da análise da teoria dos jogos foi por Antoine Augustin Cournot em 1838 com sua solução do duopólio de Cournot. O uso da teoria dos jogos nas ciências sociais se expandiu, e a teoria dos jogos também foi aplicada a comportamentos políticos, sociológicos e psicológicos.
Embora naturalistas anteriores ao século XX, como Charles Darwin, fizessem declarações do tipo teoria dos jogos, o uso da análise da teoria dos jogos na biologia começou com os estudos de comportamento animal de Ronald Fisher durante a década de 1930. Este trabalho é anterior ao nome "teoria dos jogos", mas compartilha muitas características importantes com este campo. Os desenvolvimentos na economia foram posteriormente aplicados à biologia em grande parte por John Maynard Smith em seu livro de 1982 Evolução e a Teoria dos Jogos.
Além de ser usada para descrever, prever e explicar o comportamento, a teoria dos jogos também foi usada para desenvolver teorias de comportamento ético ou normativo e para prescrever tal comportamento. Em economia e filosofia, os estudiosos aplicaram a teoria dos jogos para ajudar na compreensão do comportamento bom ou adequado. Argumentos da teoria dos jogos desse tipo podem ser encontrados desde Platão. Uma versão alternativa da teoria dos jogos, chamada de teoria química dos jogos, representa as escolhas do jogador como moléculas reagentes químicas metafóricas chamadas de "knowlecules". A teoria dos jogos químicos então calcula os resultados como soluções de equilíbrio para um sistema de reações químicas.
Descrição e modelagem
O principal uso da teoria dos jogos é descrever e modelar como as populações humanas se comportam. Alguns estudiosos acreditam que, ao encontrar o equilíbrio dos jogos, eles podem prever como as populações humanas reais se comportarão quando confrontadas com situações análogas ao jogo que está sendo estudado. Esta visão particular da teoria dos jogos tem sido criticada. Argumenta-se que as suposições feitas pelos teóricos dos jogos são frequentemente violadas quando aplicadas a situações do mundo real. Os teóricos dos jogos geralmente assumem que os jogadores agem racionalmente, mas, na prática, a racionalidade e/ou o comportamento humano muitas vezes se desviam do modelo de racionalidade usado na teoria dos jogos. Os teóricos dos jogos respondem comparando suas suposições com as usadas na física. Assim, embora suas suposições nem sempre sejam válidas, eles podem tratar a teoria dos jogos como um ideal científico razoável semelhante aos modelos usados pelos físicos. No entanto, o trabalho empírico mostrou que em alguns jogos clássicos, como o jogo da centopéia, adivinhar 2/3 do jogo médio e o jogo do ditador, as pessoas regularmente não jogam o equilíbrio de Nash. Há um debate em andamento sobre a importância desses experimentos e se a análise dos experimentos captura totalmente todos os aspectos da situação relevante.
Alguns teóricos dos jogos, seguindo o trabalho de John Maynard Smith e George R. Price, voltaram-se para a teoria evolutiva dos jogos para resolver esses problemas. Esses modelos presumem nenhuma racionalidade ou racionalidade limitada por parte dos jogadores. Apesar do nome, a teoria dos jogos evolutivos não pressupõe necessariamente a seleção natural no sentido biológico. A teoria evolutiva dos jogos inclui tanto a evolução biológica quanto a cultural e também modelos de aprendizagem individual (por exemplo, dinâmicas de jogos fictícios).
Análise prescritiva ou normativa
| Cooperar | Defeito | |
| Cooperar | -1,1 | -10, 0 |
| Defeito | 0, -10 | -5,5 |
| O dilema do prisioneiro | ||
Alguns estudiosos veem a teoria dos jogos não como uma ferramenta preditiva para o comportamento dos seres humanos, mas como uma sugestão de como as pessoas devem se comportar. Uma vez que uma estratégia, correspondente a um equilíbrio de Nash de um jogo, constitui a melhor resposta de alguém às ações dos outros jogadores – desde que estejam no (mesmo) equilíbrio de Nash – jogar uma estratégia que faz parte de um equilíbrio de Nash parece apropriado. Esse uso normativo da teoria dos jogos também foi criticado.
Economia e negócios
A teoria dos jogos é um método importante usado em economia matemática e negócios para modelar comportamentos competitivos de agentes que interagem. As aplicações incluem uma ampla gama de fenômenos e abordagens econômicas, como leilões, barganhas, preços de fusões e aquisições, divisão justa, duopólios, oligopólios, formação de redes sociais, economia computacional baseada em agentes, equilíbrio geral, design de mecanismos e sistemas de votação; e em áreas amplas como economia experimental, economia comportamental, economia da informação, organização industrial e economia política.
Essa pesquisa geralmente se concentra em conjuntos específicos de estratégias conhecidas como "conceitos de solução" ou "equilíbrio". Uma suposição comum é que os jogadores agem racionalmente. Em jogos não cooperativos, o mais famoso deles é o equilíbrio de Nash. Um conjunto de estratégias é um equilíbrio de Nash se cada uma representa a melhor resposta às outras estratégias. Se todos os jogadores estiverem jogando as estratégias em um equilíbrio de Nash, eles não terão nenhum incentivo unilateral para se desviar, pois sua estratégia é a melhor que podem fazer considerando o que os outros estão fazendo.
Os payoffs do jogo são geralmente usados para representar a utilidade de jogadores individuais.
Um artigo prototípico sobre teoria dos jogos em economia começa apresentando um jogo que é uma abstração de uma situação econômica particular. Um ou mais conceitos de solução são escolhidos e o autor demonstra quais conjuntos de estratégias no jogo apresentado são equilíbrios do tipo apropriado. Economistas e professores de administração sugerem dois usos principais (observados acima): descritivo e prescritivo.
O Chartered Institute of Procurement & Supply (CIPS) promove o conhecimento e o uso da teoria dos jogos no contexto da aquisição de negócios. A CIPS e a TWS Partners conduziram uma série de pesquisas destinadas a explorar a compreensão, conscientização e aplicação da teoria dos jogos entre os profissionais de compras. Algumas das principais descobertas em sua terceira pesquisa anual (2019) incluem:
- aplicação da teoria do jogo para a atividade de aquisição aumentou – no momento em que foi em 19% em todos os entrevistados de pesquisa
- 65% dos participantes prevêem que o uso de aplicações de teoria do jogo crescerá
- 70% dos entrevistados dizem que eles têm "apenas uma compreensão básica ou abaixo" da teoria do jogo
- 20% dos participantes realizaram treinamento no trabalho na teoria do jogo
- 50% dos entrevistados disseram que novas soluções de software foram desejáveis
- 90% dos entrevistados disseram que não têm o software que precisam para seu trabalho.
Gerenciamento de projetos
A tomada de decisão sensata é fundamental para o sucesso dos projetos. No gerenciamento de projetos, a teoria dos jogos é usada para modelar o processo de tomada de decisão dos atores, como investidores, gerentes de projetos, contratados, subcontratados, governos e clientes. Muitas vezes, esses jogadores têm interesses conflitantes e, às vezes, seus interesses são diretamente prejudiciais para outros jogadores, tornando os cenários de gerenciamento de projetos adequados para serem modelados pela teoria dos jogos.
Piraveenan (2019) em sua revisão fornece vários exemplos em que a teoria dos jogos é usada para modelar cenários de gerenciamento de projetos. Por exemplo, um investidor normalmente tem várias opções de investimento e cada opção provavelmente resultará em um projeto diferente e, portanto, uma das opções de investimento deve ser escolhida antes que o termo de abertura possa ser produzido. Da mesma forma, qualquer grande projeto envolvendo subcontratados, por exemplo, um projeto de construção, tem uma interação complexa entre o contratante principal (o gerente do projeto) e os subcontratados, ou entre os próprios subcontratados, que normalmente tem vários pontos de decisão. Por exemplo, se houver uma ambigüidade no contrato entre o empreiteiro e o subempreiteiro, cada um deve decidir até que ponto deve insistir em seu caso sem comprometer todo o projeto e, portanto, sua própria participação nele. Da mesma forma, quando projetos de organizações concorrentes são lançados, o pessoal de marketing deve decidir qual é o melhor momento e estratégia para comercializar o projeto, ou seu produto ou serviço resultante, para que possa ganhar força máxima diante da concorrência. Em cada um desses cenários, as decisões necessárias dependem das decisões de outros jogadores que, de alguma forma, têm interesses concorrentes aos interesses do tomador de decisão e, portanto, podem ser idealmente modelados usando a teoria dos jogos.
Piraveenan resume que os jogos de dois jogadores são predominantemente usados para modelar cenários de gerenciamento de projetos e, com base na identidade desses jogadores, cinco tipos distintos de jogos são usados no gerenciamento de projetos.
- Jogos do setor público-privado (jogos que modelam parcerias público-privadas)
- Jogos de contraste
- Jogos de contraste
- Subcontratado - jogos de subcontratação
- Jogos envolvendo outros jogadores
Em termos de tipos de jogos, tanto cooperativos quanto não cooperativos, de forma normal e extensiva e de soma zero e soma diferente de zero são usados para modelar vários cenários de gerenciamento de projetos.
Ciência política
A aplicação da teoria dos jogos à ciência política é focada nas áreas sobrepostas de divisão justa, economia política, escolha pública, barganha de guerra, teoria política positiva e teoria da escolha social. Em cada uma dessas áreas, os pesquisadores desenvolveram modelos de teoria dos jogos nos quais os jogadores são frequentemente eleitores, estados, grupos de interesses especiais e políticos.
Os primeiros exemplos de teoria dos jogos aplicados à ciência política são fornecidos por Anthony Downs. Em seu livro de 1957 An Economic Theory of Democracy, ele aplica o modelo de localização da empresa Hotelling ao processo político. No modelo downsiano, os candidatos políticos se comprometem com ideologias em um espaço político unidimensional. Downs primeiro mostra como os candidatos políticos irão convergir para a ideologia preferida pelo eleitor mediano se os eleitores forem totalmente informados, mas depois argumenta que os eleitores optam por permanecer racionalmente ignorantes, o que permite a divergência de candidatos. A teoria dos jogos foi aplicada em 1962 à Crise dos Mísseis de Cuba durante a presidência de John F. Kennedy.
Também foi proposto que a teoria dos jogos explica a estabilidade de qualquer forma de governo político. Tomando o caso mais simples de uma monarquia, por exemplo, o rei, sendo apenas uma pessoa, não mantém e não pode manter sua autoridade exercendo pessoalmente controle físico sobre todos ou mesmo sobre um número significativo de seus súditos. Em vez disso, o controle soberano é explicado pelo reconhecimento de cada cidadão de que todos os outros cidadãos esperam que os outros vejam o rei (ou outro governo estabelecido) como a pessoa cujas ordens serão seguidas. A comunicação coordenada entre os cidadãos para substituir o soberano é efetivamente proibida, uma vez que a conspiração para substituir o soberano é geralmente punível como crime. Assim, em um processo que pode ser modelado por variantes do dilema do prisioneiro, durante períodos de estabilidade nenhum cidadão achará racional mover-se para substituir o soberano, mesmo que todos os cidadãos saibam que estariam melhor se eles todos deveriam agir coletivamente.
Uma explicação da teoria dos jogos para a paz democrática é que o debate público e aberto nas democracias envia informações claras e confiáveis sobre suas intenções para outros estados. Em contraste, é difícil saber as intenções dos líderes não democráticos, que efeito terão as concessões e se as promessas serão cumpridas. Assim, haverá desconfiança e falta de vontade de fazer concessões se pelo menos uma das partes em disputa for uma não-democracia.
No entanto, a teoria dos jogos prevê que dois países ainda podem entrar em guerra, mesmo que seus líderes estejam cientes dos custos da luta. A guerra pode resultar de informação assimétrica; dois países podem ter incentivos para representar erroneamente a quantidade de recursos militares que têm em mãos, tornando-os incapazes de resolver disputas agradavelmente sem recorrer à luta. Além disso, a guerra pode surgir devido a problemas de compromisso: se dois países desejam resolver uma disputa por meios pacíficos, mas cada um deseja voltar atrás nos termos desse acordo, eles podem não ter escolha a não ser recorrer à guerra. Finalmente, a guerra pode resultar de indivisibilidades de questões.
A teoria dos jogos também pode ajudar a prever as respostas de uma nação quando há uma nova regra ou lei a ser aplicada a essa nação. Um exemplo é a pesquisa de Peter John Wood (2013) que analisa o que as nações podem fazer para ajudar a reduzir as mudanças climáticas. Wood pensou que isso poderia ser feito por meio de tratados com outras nações para reduzir as emissões de gases de efeito estufa. No entanto, ele concluiu que essa ideia não poderia funcionar porque criaria um dilema do prisioneiro para as nações.
Biologia
| Falcão | Dove | |
| Falcão | 20, 20 | 80, 40 |
| Dove | 40, 80 | 60, 60 |
| O jogo de pomba do falcão | ||
Ao contrário daqueles em economia, os resultados dos jogos em biologia são frequentemente interpretados como correspondentes ao condicionamento físico. Além disso, o foco tem sido menos nos equilíbrios que correspondem a uma noção de racionalidade e mais naqueles que seriam mantidos por forças evolutivas. O equilíbrio mais conhecido na biologia é conhecido como a estratégia evolutivamente estável (ESS), introduzido pela primeira vez em (Maynard Smith & Price 1973). Embora sua motivação inicial não envolva nenhum dos requisitos mentais do equilíbrio de Nash, toda EEE é um equilíbrio de Nash.
Na biologia, a teoria dos jogos tem sido usada como modelo para entender muitos fenômenos diferentes. Foi usado pela primeira vez para explicar a evolução (e estabilidade) das proporções aproximadas de 1:1 entre os sexos. (Fisher 1930) sugeriram que as proporções sexuais de 1:1 são resultado de forças evolucionárias agindo sobre indivíduos que poderiam ser vistos como tentando maximizar seu número de netos.
Além disso, os biólogos usaram a teoria evolutiva dos jogos e a ESS para explicar o surgimento da comunicação animal. A análise dos jogos de sinalização e outros jogos de comunicação forneceu informações sobre a evolução da comunicação entre os animais. Por exemplo, o comportamento de mobbing de muitas espécies, no qual um grande número de presas ataca um predador maior, parece ser um exemplo de organização emergente espontânea. As formigas também demonstraram exibir um comportamento de avanço semelhante à moda (consulte Economia da borboleta de Paul Ormerod).
Os biólogos usaram o jogo da galinha para analisar o comportamento de luta e a territorialidade.
De acordo com Maynard Smith, no prefácio de Evolution and the Theory of Games, "paradoxalmente, descobriu-se que a teoria dos jogos é mais facilmente aplicada à biologia do que ao campo da comportamento econômico para o qual foi originalmente projetado". A teoria dos jogos evolutivos tem sido usada para explicar muitos fenômenos aparentemente incongruentes na natureza.
Um desses fenômenos é conhecido como altruísmo biológico. Esta é uma situação em que um organismo parece agir de uma forma que beneficia outros organismos e é prejudicial a si mesmo. Isso é diferente das noções tradicionais de altruísmo porque tais ações não são conscientes, mas parecem ser adaptações evolutivas para aumentar a aptidão geral. Exemplos podem ser encontrados em espécies que vão desde morcegos vampiros que regurgitam o sangue que obtiveram em uma caçada noturna e o dão a membros do grupo que falharam em se alimentar, até abelhas operárias que cuidam da abelha rainha por toda a vida e nunca acasalar, para vervet macacos que alertam os membros do grupo sobre a aproximação de um predador, mesmo quando isso põe em risco a chance de sobrevivência desse indivíduo. Todas essas ações aumentam a aptidão geral de um grupo, mas ocorrem com um custo para o indivíduo.
A teoria evolutiva dos jogos explica esse altruísmo com a ideia de seleção de parentesco. Os altruístas discriminam entre os indivíduos que ajudam e favorecem os parentes. A regra de Hamilton explica a lógica evolutiva por trás dessa seleção com a equação c < b × r, onde o custo c para o altruísta deve ser menor que o benefício b para o destinatário multiplicado pelo coeficiente de parentesco r. Os dois organismos mais intimamente relacionados fazem com que as incidências de altruísmo aumentem porque eles compartilham muitos dos mesmos alelos. Isso significa que o indivíduo altruísta, ao garantir que os alelos de seu parente próximo sejam transmitidos por meio da sobrevivência de seus descendentes, pode renunciar à opção de ter filhos porque o mesmo número de alelos é transmitido. Por exemplo, ajudar um irmão (em animais diplóides) tem um coeficiente de 1⁄ 2, porque (em média) um indivíduo compartilha metade dos alelos na prole de seu irmão. Garantir que um número suficiente de descendentes de um irmão sobreviva até a idade adulta exclui a necessidade de o indivíduo altruísta produzir descendentes. Os valores dos coeficientes dependem fortemente do escopo do campo de jogo; por exemplo, se a escolha de quem favorecer inclui todos os seres vivos genéticos, não apenas todos os parentes, assumimos que a discrepância entre todos os humanos representa apenas aproximadamente 1% da diversidade no campo de jogo, um coeficiente que foi 1⁄2 no campo menor torna-se 0,995. Da mesma forma, se for considerado que a informação que não seja de natureza genética (por exemplo, epigenética, religião, ciência, etc.) persistiu ao longo do tempo, o campo de jogo torna-se ainda maior e as discrepâncias menores.
Ciência da computação e lógica
A teoria dos jogos passou a desempenhar um papel cada vez mais importante na lógica e na ciência da computação. Várias teorias lógicas têm base na semântica do jogo. Além disso, os cientistas da computação usaram jogos para modelar computações interativas. Além disso, a teoria dos jogos fornece uma base teórica para o campo de sistemas multiagentes.
Separadamente, a teoria dos jogos desempenhou um papel nos algoritmos online; em particular, o problema do k-server, que no passado foi referido como jogos com custos de movimentação e jogos de solicitação-resposta. O princípio de Yao é uma técnica de teoria dos jogos para provar limites inferiores na complexidade computacional de algoritmos aleatórios, especialmente algoritmos online.
O surgimento da Internet motivou o desenvolvimento de algoritmos para encontrar equilíbrios em jogos, mercados, leilões computacionais, sistemas peer-to-peer e mercados de segurança e informação. A teoria dos jogos algorítmicos e, dentro dela, o design de mecanismos algorítmicos combinam o design de algoritmos computacionais e a análise de sistemas complexos com a teoria econômica.
Filosofia
| Stag | Hare | |
| Stag | 3, 3 | 0, 2 |
| Hare | 2, 0 | 2, 2 |
| Caça de escada | ||
A teoria dos jogos tem vários usos na filosofia. Respondendo a dois artigos de W.V.O. Quine (1960, 1967), Lewis (1969) usaram a teoria dos jogos para desenvolver uma explicação filosófica da convenção. Ao fazer isso, ele forneceu a primeira análise do conhecimento comum e o empregou na análise do jogo em jogos de coordenação. Além disso, ele primeiro sugeriu que se pode entender o significado em termos de jogos de sinalização. Esta sugestão posterior foi seguida por vários filósofos desde Lewis. Seguindo a explicação das convenções da teoria dos jogos de Lewis (1969), Edna Ullmann-Margalit (1977) e Bicchieri (2006) desenvolveram teorias de normas sociais que as definem como equilíbrios de Nash que resultam da transformação de um jogo de motivos mistos em um jogo de coordenação.
A teoria dos jogos também desafiou os filósofos a pensar em termos de epistemologia interativa: o que significa para um coletivo ter crenças ou conhecimentos comuns e quais são as consequências desse conhecimento para os resultados sociais resultantes das interações dos agentes. Os filósofos que trabalharam nesta área incluem Bicchieri (1989, 1993), Skyrms (1990) e Stalnaker (1999).
Na ética, alguns autores (principalmente David Gauthier, Gregory Kavka e Jean Hampton) tentaram perseguir a filosofia de Thomas Hobbes. projeto de derivar a moralidade do interesse próprio. Uma vez que jogos como o dilema do prisioneiro apresentam um aparente conflito entre moralidade e interesse próprio, explicar por que a cooperação é exigida pelo interesse próprio é um componente importante deste projeto. Essa estratégia geral é um componente da visão geral do contrato social na filosofia política (para exemplos, ver Gauthier (1986) e Kavka (1986)).
Outros autores tentaram usar a teoria evolutiva dos jogos para explicar o surgimento de atitudes humanas sobre moralidade e comportamentos animais correspondentes. Esses autores analisam vários jogos, incluindo o dilema do prisioneiro, a caça ao veado e o jogo de barganha de Nash, fornecendo uma explicação para o surgimento de atitudes sobre moralidade (ver, por exemplo, Skyrms (1996, 2004) e Sober e Wilson (1998)).
Preços de produtos de varejo e de consumo
As aplicações da teoria dos jogos são freqüentemente usadas nas estratégias de precificação dos mercados de varejo e de consumo, particularmente para a venda de bens inelásticos. Com os varejistas competindo constantemente uns contra os outros pela participação no mercado consumidor, tornou-se uma prática bastante comum para os varejistas descontar certos produtos, de forma intermitente, na esperança de aumentar o tráfego de pedestres em locais físicos (visitas a sites para varejistas de comércio eletrônico) ou aumentar as vendas de produtos auxiliares ou complementares.
A Black Friday, um popular feriado de compras nos EUA, é quando muitos varejistas se concentram em estratégias de preços ideais para capturar o mercado de compras de fim de ano. No cenário da Black Friday, os varejistas que usam aplicações da teoria dos jogos normalmente perguntam "qual é a reação do concorrente dominante a mim?" Nesse cenário, o jogo tem dois jogadores: o varejista e o consumidor. O varejista está focado em uma estratégia de preço ideal, enquanto o consumidor está focado no melhor negócio. Nesse sistema fechado, muitas vezes não há estratégia dominante, pois ambos os jogadores têm opções alternativas. Ou seja, os varejistas podem encontrar um cliente diferente e os consumidores podem comprar em um varejista diferente. Dada a concorrência de mercado naquele dia, no entanto, a estratégia dominante para os varejistas consiste em superar os concorrentes. O sistema aberto assume vários varejistas vendendo produtos similares e um número finito de consumidores que demandam os produtos a um preço ótimo. Um blog de um professor da Cornell University forneceu um exemplo de tal estratégia, quando a Amazon precificou uma TV Samsung $ 100 abaixo do valor de varejo, efetivamente prejudicando os concorrentes. A Amazon compensou parte da diferença ao aumentar o preço dos cabos HDMI, pois constatou que os consumidores discriminam menos os preços na venda de itens secundários.
Os mercados de varejo continuam a desenvolver estratégias e aplicações da teoria dos jogos quando se trata de precificar bens de consumo. Os principais insights encontrados entre simulações em um ambiente controlado e experiências de varejo do mundo real mostram que as aplicações de tais estratégias são mais complexas, pois cada varejista precisa encontrar um equilíbrio ideal entre preços, relações com fornecedores, imagem de marca e o potencial de canibalizar a venda de itens mais lucrativos.
Epidemiologia
Uma vez que a decisão de tomar uma vacina para uma determinada doença é muitas vezes tomada por indivíduos, que podem considerar uma série de fatores e parâmetros ao tomar essa decisão (como a incidência e prevalência da doença, riscos percebidos e reais associados a contrair a doença, taxa de mortalidade, riscos percebidos e reais associados à vacinação e custo financeiro da vacinação), a teoria dos jogos tem sido usada para modelar e prever a adesão à vacinação em uma sociedade.
Na cultura popular
- Baseado no livro de 1998 de Sylvia Nasar, a história de vida do teórico do jogo e do matemático John Nash foi transformada em biopic Uma mente bonita, estrelando Russell Crowe como Nash.
- O romance de ficção científica militar de 1959 Troopers de Starship por Robert A. Heinlein mencionou "teoria dos jogos" e "teoria dos jogos". No filme de 1997 do mesmo nome, o personagem Carl Jenkins referiu-se à sua missão de inteligência militar como sendo atribuído a "jogos e teoria".
- O filme de 1964 Dr. Strangelove satiriza ideias teóricas do jogo sobre teoria da dissuasão. Por exemplo, a dissuasão nuclear depende da ameaça de retaliação catastrófica se um ataque nuclear for detectado. Um teórico do jogo pode argumentar que tais ameaças podem deixar de ser credível, no sentido de que eles podem levar ao subjogo equilibria imperfeita. O filme leva essa ideia um passo mais adiante, com a União Soviética comprometendo-se irrevogavelmente a uma resposta nuclear catastrófica sem tornar a ameaça pública.
- A banda de power pop da década de 1980 Game Theory foi fundada pelo cantor e compositor Scott Miller, que descreveu o nome da banda como aludindo ao "estudo de calcular a ação mais apropriada dada um adversário... dar-se a quantidade mínima de falha".
- Jogo de Liar, um mangá japonês de 2005 e série de televisão de 2007, apresenta os personagens principais em cada episódio com um jogo ou problema que é tipicamente extraído da teoria do jogo, como demonstrado pelas estratégias aplicadas pelos personagens.
- O romance de 1974 História do Spy por Len Deighton explora elementos da teoria do jogo em relação aos exercícios do exército de guerra fria.
- O romance de 2008 A Floresta Negra por Liu Cixin explora a relação entre vida extraterrestre, humanidade e teoria dos jogos.
- O antagonista principal Joker no filme O Cavaleiro das Trevas apresenta conceitos de teoria do jogo - notavelmente o dilema do prisioneiro em uma cena onde ele pede aos passageiros em dois ferries diferentes para bombardear o outro para salvar seus próprios.
- No filme de 2018 Asiáticos ricos loucos, a liderança feminina Rachel Chu é professora de economia e teoria dos jogos na Universidade de Nova York. No início do filme, ela é vista em sua sala de aula NYU jogando um jogo de poker com seu assistente de ensino e ganha o jogo por bluff; então no clímax do filme, ela joga um jogo de mahjong com a mãe desaprovante de seu amigo menino Eleanor, perdendo o jogo para Eleanor de propósito, mas ganhando sua aprovação como resultado.
- No filme de 2017 Molly's Game, Brad que é inexperiente jogador de poker, toma uma decisão de apostas irracionais sem perceber e faz com que seu oponente Harlan se desviar de sua estratégia Nash Equilibrium, resultando em uma perda significativa quando Harlan perde a mão.
Contenido relacionado
Pacto Kellogg-Briand
Giuseppe Peano
KRL (linguagem de programação)