Síntese aditiva

Exemplo de síntese aditiva

Um som semelhante ao sino gerado pela síntese aditiva de 21 parciais inharmônicos

---

Problemas com o arquivo? Veja ajuda na mídia.

Síntese aditiva é uma técnica de síntese de som que cria timbre adicionando ondas senoidais juntas.

O timbre dos instrumentos musicais pode ser considerado à luz da teoria de Fourier como consistindo de múltiplos harmônicos ou inarmônicos parciais ou harmônicos. Cada parcial é uma onda senoidal de frequência e amplitude diferentes que aumenta e diminui com o tempo devido à modulação de um envelope ADSR ou oscilador de baixa frequência.

A síntese aditiva gera som mais diretamente adicionando a saída de vários geradores de onda senoidal. Implementações alternativas podem usar tabelas de onda pré-computadas ou a transformada de Fourier rápida inversa.

Explicação

Os sons que se ouvem no dia-a-dia não são caracterizados por uma única frequência. Em vez disso, eles consistem em uma soma de frequências senoidais puras, cada uma em uma amplitude diferente. Quando os humanos ouvem essas frequências simultaneamente, podemos reconhecer o som. Isso é verdade tanto para "não-musicais" sons (por exemplo, salpicos de água, farfalhar de folhas, etc.) e para "sons musicais" (por exemplo, uma nota de piano, o canto de um pássaro, etc.). Este conjunto de parâmetros (frequências, suas amplitudes relativas e como as amplitudes relativas mudam ao longo do tempo) são encapsulados pelo timbre do som. A análise de Fourier é a técnica usada para determinar esses parâmetros de timbre exatos de um sinal sonoro geral; inversamente, o conjunto resultante de frequências e amplitudes é chamado de série de Fourier do sinal de som original.

No caso de uma nota musical, a frequência mais baixa de seu timbre é designada como frequência fundamental do som. Para simplificar, costumamos dizer que a nota está tocando nessa frequência fundamental (por exemplo, "middle C é 261,6 Hz"), mesmo que o som dessa nota consista em muitas outras frequências também. O conjunto das frequências restantes é chamado de harmônicos (ou harmônicos, se suas frequências forem múltiplos inteiros da frequência fundamental) do som. Em outras palavras, apenas a frequência fundamental é responsável pelo tom da nota, enquanto os harmônicos definem o timbre do som. Os harmônicos de um piano tocando o dó central serão bem diferentes dos harmônicos de um violino tocando a mesma nota; é isso que nos permite diferenciar os sons dos dois instrumentos. Existem até diferenças sutis de timbre entre diferentes versões do mesmo instrumento (por exemplo, um piano vertical versus um piano de cauda).

A síntese aditiva visa explorar essa propriedade do som para construir o timbre a partir do zero. Somando frequências puras (ondas senoidais) de frequências e amplitudes variadas, podemos definir com precisão o timbre do som que queremos criar.

Definições

Diagrama esquemático da síntese aditiva. As entradas para os osciladores são frequências fk{displaystyle f_{k}} e amplitudes RkNão. r_{k}}.

A síntese aditiva harmônica está intimamente relacionada ao conceito de série de Fourier, que é uma forma de expressar uma função periódica como a soma de funções senoidais com frequências iguais a múltiplos inteiros de uma frequência fundamental comum. Esses sinusóides são chamados de harmônicos, harmônicos ou, em geral, parciais. Em geral, uma série de Fourier contém um número infinito de componentes senoidais, sem limite superior para a frequência das funções senoidais e inclui um componente DC (um com frequência de 0 Hz). Frequências fora da faixa audível humana podem ser omitidas na síntese aditiva. Como resultado, apenas um número finito de termos senoidais com frequências dentro da faixa audível é modelado na síntese aditiva.

Uma forma de onda ou função é considerada periódica se

Sim.())= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Sim.()+P)(t)=y(t+P)}

para todos )Não. e por algum período PNão. P..

A série de Fourier de uma função periódica é expressa matematicamente como:

Sim.())= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =um02+Gerenciamento Gerenciamento k= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1∞ ∞ Não.umke⁡ ⁡ (2D D kf0))- Sim. - Sim. b)kpecado⁡ ⁡ (2D D kf0))]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =um02+Gerenciamento Gerenciamento k= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1∞ ∞ Rke⁡ ⁡ (2D D kf0)+φ φ k){displaystyle {begin{aligned}y(t)&={frac {a_{0}}{2}}+sum _{k=1}^{infty }left[a_{k}cos(2pi kf_{0}t)-b_{k}sin(2pi kf_{0}t)right]&={frac {a_{0}}{2}}+sum _{k=1}^{infty }r_{k}cos left(2pi kf_{0}t+phi _{k}right)\end{aligned}}}

onde

• f0= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1/PNão. f_{0}=1/P} é a frequência fundamental da forma de onda e é igual ao recíproco do período,
• umk= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Rke⁡ ⁡ (φ φ k)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2f0∫ ∫ 0PSim.())e⁡ ⁡ (2D D kf0))D),k≥ ≥ 0Não. a_{k}=r_{k}cos(phi _{k})=2f_{0}int _{0}^{P}y(t)cos(2pi kf_{0}t),dt,quad kgeq 0
• b)k= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Rkpecado⁡ ⁡ (φ φ k)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. 2f0∫ ∫ 0PSim.())pecado⁡ ⁡ (2D D kf0))D),k≥ ≥ 1Não. b_{k}=r_{k}sin(phi _{k})=-2f_{0}int _{0}^{P}y(t)sin(2pi kf_{0}t),dt,quad kgeq 1
• Rk= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =umk2+b)k2Não. ? {a_{k}^{2}+b_{k}^{2}}}} é a amplitude da kNão.a harmónica,
• φ φ k= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Atan2⁡ ⁡ (b)k,umk){displaystyle phi _{k}=operatorname {atan2} (b_{k},a_{k})} é o deslocamento de fase do kNão.A harmónica. o atan2 é a função arctangent de quatro quadrantes,

Sendo inaudível, o componente DC, um0/2Não. a_{0}/2}, e todos os componentes com frequências superiores a algum limite finito, KKf0{displaystyle Kf_{0}}, são omitidos nas seguintes expressões de síntese aditiva.

Forma harmônica

A síntese aditiva harmônica mais simples pode ser expressa matematicamente como:

Sim.())= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento k= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1KKRke⁡ ⁡ (2D D kf0)+φ φ k),{displaystyle y(t)=sum _{k=1}^{K}r_{k}cos left(2pi kf_{0}t+phi _{k}right),}

(1)

Onde? Sim.())(T)} é a saída de síntese, RkNão. r_{k}}, kf0{displaystyle kf_{0}}e φ φ k{displaystyle phi _{k}} são a amplitude, frequência e o deslocamento de fase, respectivamente, kNão.parciais de um total de KKNão. parciais harmônicos, e f0{displaystyle f_{0}} é a frequência fundamental da forma de onda e a frequência da nota musical.

Amplitudes dependentes do tempo

Exemplo de síntese aditiva harmônica em que cada harmônico tem uma amplitude dependente do tempo. A frequência fundamental é 440 Hz. Problemas ao ouvir este arquivo? Ver Ajuda na mídia

Mais geralmente, a amplitude de cada harmônico pode ser prescrita como uma função do tempo, Rk())(t)}, em que caso a saída de síntese é

Sim.())= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento k= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1KKRk())e⁡ ⁡ (2D D kf0)+φ φ k){displaystyle y(t)=sum _{k=1}^{K}r_{k}(t)cos left(2pi kf_{0}t+phi _{k}right)}.

(2)

Cada envelope Rk()){displaystyle r_{k}(t),} deve variar lentamente em relação ao espaçamento de frequência entre seios adjacentes. A largura de banda Rk())(t)} deve ser significativamente menor do que f0{displaystyle f_{0}}.

Forma inarmônica

A síntese aditiva também pode produzir sons inarmônicos (que são formas de onda aperiódicas) nos quais os harmônicos individuais não precisam ter frequências que sejam múltiplos inteiros de alguma frequência fundamental comum. Enquanto muitos instrumentos musicais convencionais têm parciais harmônicas (por exemplo, um oboé), alguns têm parciais inarmônicas (por exemplo, sinos). A síntese aditiva inarmônica pode ser descrita como

Sim.())= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento k= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1KKRk())e⁡ ⁡ (2D D fk)+φ φ k),{displaystyle y(t)=sum _{k=1}^{K}r_{k}(t)cos left(2pi f_{k}t+phi _{k}right),}

Onde? fk{displaystyle f_{k}} é a frequência constante de kNão.parcial.

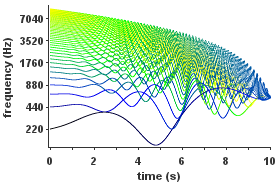Exemplo de síntese aditiva inharmônica em que tanto a amplitude e a frequência de cada parcial são dependentes do tempo. Problemas ao ouvir este arquivo? Ver Ajuda na mídia

Frequências dependentes do tempo

No caso geral, a frequência instantânea de um sinusóide é o derivado (com relação ao tempo) do argumento da função sine ou cosina. Se esta frequência é representada em hertz, em vez de em forma de frequência angular, então este derivado é dividido por 2D D - Sim.. Este é o caso se o parcial é harmônico ou inharmônico e se sua frequência é constante ou de tempo-varying.

Na forma mais geral, a frequência de cada parcial não-harmônico é uma função não negativa do tempo, fk())(t)}, cedendo

Sim.())= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento k= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1KKRk())e⁡ ⁡ (2D D ∫ ∫ 0)fk(u)Du+φ φ k).{displaystyle y(t)=sum _{k=1}^{K}r_{k}(t)cos left(2pi int _{0}^{t}f_{k}(u) du+phi _{k}right).}

(3)

Definições mais amplas

Síntese aditiva de forma mais ampla pode significar técnicas de síntese de som que somam elementos simples para criar timbres mais complexos, mesmo quando os elementos não são ondas senoidais. Por exemplo, F. Richard Moore listou a síntese aditiva como uma das "quatro categorias básicas" de síntese de som ao lado de síntese subtrativa, síntese não linear e modelagem física. Nesse sentido amplo, os órgãos de tubos, que também possuem tubos que produzem formas de onda não senoidais, podem ser considerados como uma forma variante de sintetizadores aditivos. A soma dos componentes principais e as funções de Walsh também foram classificadas como síntese aditiva.

Métodos de implementação

As implementações modernas de síntese aditiva são principalmente digitais. (Consulte a seção Equações de tempo discreto para a teoria de tempo discreto subjacente)

Síntese do banco oscilador

A síntese aditiva pode ser implementada usando um banco de osciladores senoidais, um para cada parcial.

Síntese ondulatória

No caso de tons musicais harmônicos e quase periódicos, a síntese wavetable pode ser tão geral quanto a síntese aditiva variável no tempo, mas requer menos computação durante a síntese. Como resultado, uma implementação eficiente da síntese aditiva variável no tempo de tons harmônicos pode ser realizada pelo uso da síntese de tabela de ondas.

Síntese de aditivo de grupo

A síntese aditiva de grupo é um método para agrupar parciais em grupos harmônicos (com diferentes frequências fundamentais) e sintetizar cada grupo separadamente com síntese de tabela de ondas antes de misturar os resultados.

Síntese FFT inversa

Uma transformada de Fourier rápida inversa pode ser usada para sintetizar com eficiência frequências que dividem uniformemente o período de transformação ou "quadro". Pela consideração cuidadosa da representação DFT no domínio da frequência, também é possível sintetizar eficientemente senoides de frequências arbitrárias usando uma série de quadros sobrepostos e a transformada rápida inversa de Fourier.

Análise aditiva/ressíntese

Sistema de análise/síntese Sinusoidal para Modelagem Sinusoidal (baseado em McAulay & Quatieri 1988, p. 161)

É possível analisar os componentes de frequência de um som gravado dando uma "soma de sinusóides" representação. Esta representação pode ser ressintetizada usando síntese aditiva. Um método de decompor um som em parciais sinusoidais variáveis no tempo é a Análise McAulay-Quatieri baseada na transformada de Fourier de curto prazo (STFT).

Ao modificar a representação da soma das sinusóides, alterações timbrais podem ser feitas antes da ressíntese. Por exemplo, um som harmônico pode ser reestruturado para soar inarmônico e vice-versa. Hibridação sonora ou "morfismo" foi implementada por ressíntese aditiva.

Análise/ressíntese aditiva tem sido empregada em várias técnicas, incluindo Modelagem Sinusoidal, Síntese de Modelagem Espectral (SMS) e Modelo de Som Aditivo Aprimorado de Largura de Banda Reatribuída. O software que implementa análise/ressíntese aditiva inclui: SPEAR, LEMUR, LORIS, SMSTools, ARSS.

Produtos

Re-síntese aditiva usando concatenação de timbre-quadro:

Concatenação com crossfades (em Synclavier)

Concatenação com interpolação de envelope espectral (no Vocaloid)

O New England Digital Synclavier tinha um recurso de ressíntese em que as amostras podiam ser analisadas e convertidas em "quadros de timbre" que faziam parte de seu mecanismo de síntese aditiva. A Technos acxel, lançada em 1987, utilizava o modelo de análise/resíntese aditiva, em uma implementação FFT.

Também um sintetizador vocal, o Vocaloid foi implementado com base na análise/ressíntese aditiva: seu modelo de voz espectral chamado Excitation plus Resonances (EpR) é estendido com base no Spectral Modeling Synthesis (SMS), e sua síntese concatenativa difona é processada usando Técnica de processamento de pico espectral (SPP) semelhante ao vocoder de bloqueio de fase modificado (um vocoder de fase aprimorado para processamento de formantes). Usando essas técnicas, os componentes espectrais (formantes) que consistem em parciais puramente harmônicos podem ser adequadamente transformados na forma desejada para modelagem de som e sequência de amostras curtas (difones ou fonemas) que constituem a frase desejada, podem ser conectados suavemente interpolando parciais correspondentes e picos de formantes, respectivamente, na região de transição inserida entre amostras diferentes. (Veja também timbres dinâmicos)

Aplicativos

Instrumentos musicais

A síntese aditiva é usada em instrumentos musicais eletrônicos. É a principal técnica de geração de som utilizada pelos órgãos Eminentes.

Síntese de fala

Na pesquisa linguística, a síntese aditiva harmônica foi usada na década de 1950 para reproduzir espectrogramas de fala modificados e sintéticos.

Mais tarde, no início da década de 1980, foram realizados testes de audição em fala sintética despojada de pistas acústicas para avaliar sua significância. Frequências e amplitudes de formantes variantes no tempo derivadas por codificação preditiva linear foram sintetizadas aditivamente como assobios de tom puro. Este método é chamado de síntese de onda senoidal. Além disso, a modelagem senoidal composta (CSM) usada em um recurso de síntese de fala cantada no Yamaha CX5M (1984) é conhecida por usar uma abordagem semelhante que foi desenvolvida independentemente durante 1966–1979. Esses métodos caracterizam-se pela extração e recomposição de um conjunto de picos espectrais significativos correspondentes aos diversos modos de ressonância ocorridos na cavidade oral e na cavidade nasal, do ponto de vista acústico. Este princípio também foi utilizado em um método de síntese de modelagem física, chamado de síntese modal.

História

Lord Kelvin's Tide-predicting máquina

Sintetizador harmônico

Analisador harmônico

A análise harmônica foi descoberta por Joseph Fourier, que publicou um extenso tratado de sua pesquisa no contexto da transferência de calor em 1822. A teoria encontrou uma aplicação inicial na previsão de marés. Por volta de 1876, William Thomson (mais tarde enobrecido como Lord Kelvin) construiu um previsor mecânico de marés. Consistia em um analisador de harmônicos e um sintetizador de harmônicos, como eram chamados já no século XIX. A análise das medições de maré foi feita usando a máquina integradora de James Thomson. Os coeficientes de Fourier resultantes foram inseridos no sintetizador, que então usou um sistema de cordas e polias para gerar e somar parciais senoidais harmônicos para prever as marés futuras. Em 1910, uma máquina semelhante foi construída para a análise das formas de onda periódicas do som. O sintetizador desenhou um gráfico da forma de onda de combinação, que foi usado principalmente para validação visual da análise.

Revisão de Helmholtz

Tom-generator utilizando-o

Georg Ohm aplicou a teoria de Fourier ao som em 1843. A linha de trabalho foi muito avançada por Hermann von Helmholtz, que publicou seus oito anos de pesquisa em 1863. Helmholtz acreditava que a percepção psicológica da cor do tom é sujeito à aprendizagem, enquanto a audição no sentido sensorial é puramente fisiológica. Ele apoiou a ideia de que a percepção do som deriva de sinais das células nervosas da membrana basilar e que os apêndices elásticos dessas células são vibrados simpaticamente por tons sinusoidais puros de frequências apropriadas. Helmholtz concordou com a descoberta de Ernst Chladni de 1787 de que certas fontes sonoras têm modos de vibração inarmônicos.

Analisador de som e sintetizador de Rudolph Koenig

sintetizador de som

analisador de som

Na época de Helmholtz, a amplificação eletrônica não estava disponível. Para a síntese de tons com parciais harmônicos, Helmholtz construiu uma matriz eletricamente excitada de diapasões e câmaras de ressonância acústica que permitiam o ajuste das amplitudes dos parciais. Construídos pelo menos já em 1862, eles foram por sua vez refinados por Rudolph Koenig, que demonstrou sua própria configuração em 1872. Para a síntese harmônica, Koenig também construiu um grande aparelho baseado em sua sirene de ondas. Era pneumático e utilizava tonewheels recortados, e foi criticado pela baixa pureza de seus tons parciais. Também os tubos de tíbia de órgãos de tubo têm formas de onda quase sinusoidais e podem ser combinados na forma de síntese aditiva.

Em 1938, com novas e significativas evidências de apoio, foi relatado nas páginas do Popular Science Monthly que as cordas vocais humanas funcionam como uma sirene de incêndio para produzir um tom rico em harmônicos, que é então filtrado pelo trato vocal para produzir diferentes tons de vogais. Na época, o órgão Hammond aditivo já estava no mercado. A maioria dos primeiros fabricantes de órgãos eletrônicos achava muito caro fabricar a pluralidade de osciladores exigidos pelos órgãos aditivos e, em vez disso, começaram a construir os subtrativos. Em uma reunião do Institute of Radio Engineers em 1940, o engenheiro-chefe de campo da Hammond elaborou o novo Novachord da empresa como tendo um "sistema subtrativo" em contraste com o órgão Hammond original em que "os tons finais foram construídos pela combinação de ondas sonoras". Alan Douglas usou os qualificadores aditivo e subtrativo para descrever diferentes tipos de órgãos eletrônicos em um artigo de 1948 apresentado à Royal Musical Association. As palavras contemporâneas síntese aditiva e síntese subtrativa podem ser encontradas em seu livro de 1957 A produção elétrica da música, no qual ele lista categoricamente três métodos de formação de tonalidades musicais, nas seções intituladas Síntese aditiva, Síntese subtrativa e Outras formas de combinações.

Um típico sintetizador aditivo moderno produz sua saída como um sinal elétrico, analógico ou como áudio digital, como no caso dos sintetizadores de software, que se tornaram populares por volta do ano 2000.

Cronograma

O seguinte é uma linha do tempo de sintetizadores e dispositivos analógicos e digitais notáveis histórica e tecnologicamente que implementam a síntese aditiva.

Implementação ou publicação de pesquisa	Disponível comercialmente	Empresa ou instituição	Dispositivo de sintetizador ou de síntese	Descrição	Amostras de áudio
1900	1906	New England Electric Music Company	Telhado	O primeiro sintetizador de música polifônico e sensível ao toque. Implementado síntese aditiva sinuosoidal usando rodas de tom e alternadores. Inventado por Thaddeus Cahill.	sem gravações conhecidas
1933	1935	Hammond Organ Company	Órgão Hammond	Um sintetizador aditivo eletrônico que foi comercialmente mais bem sucedido do que Telharmonium. Implementado síntese aditiva sinusoidal usando rodas de tom e captadores magnéticos. Inventado por Laurens Hammond.	Modelo A(help·info)
1950 ou mais cedo		Laboratórios de Haskins	Reprodução padrão	Um sistema de síntese de fala que controlava amplitudes de parciais harmônicas por um espectrograma que foi desenhado à mão ou um resultado de análise. As parciais foram geradas por uma multi-faixa de tom óptico.	amostras
1958			ANS	Um sintetizador aditivo que jogou microtonal espectrograma-como escores usando múltiplas multi-faixas ópticas Tomwheels. Inventado por Evgeny Murzin. Um instrumento semelhante que utilizou osciladores eletrônicos, o Banco de oscilação, e seu dispositivo de entrada Espectrograma foram realizados por Hugh Le Caine em 1959.	1964 modelo(help·info)
1963		MIT		Um sistema off-line para análise espectral digital e resíntese do ataque e porções de estado estável de timbres de instrumento musical por David Luce.
1964		Universidade de Illinois	Gerador de Tom harmônico	Um sistema eletrônico de síntese aditiva harmônica inventado por James Beauchamp.	amostras (info)
1974 ou anterior	1974	RMI	Sintetizador harmônico	O primeiro produto sintetizador que implementou a síntese aditiva usando osciladores digitais. O sintetizador também tinha um filtro analógico de tempo-varying. A RMI foi uma subsidiária da Allen Organ Company, que havia lançado o primeiro órgão comercial da igreja digital, o Órgão de computador Allen, em 1971, usando tecnologia digital desenvolvida pela North American Rockwell.	1 2 3 4 1 2 3 2 3 3 4 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 1 2 1 2 1 2 1 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3
1974		EMS (Londres)	Oscilador Digital Banco	Um banco de osciladores digitais com formas de onda arbitrárias, controles de frequência e amplitude individuais, destinados a uso em análise-resíntese com o digital Analisando o Banco de Filtro (AFB) também construído no EMS. Também conhecido como: DOB.	no novo som da música
1976	1976	Farol	Qasar M8	Um sintetizador tudo-digital que usou a transformação rápida de Fourier para criar amostras de envelopes de amplitude interativamente desenhados de harmônicos.	amostras
1977		Laboratório de Bell	Sintetizador Digital	Um sintetizador aditivo digital em tempo real que foi chamado o primeiro sintetizador digital verdadeiro. Também conhecido como: Linha de produção, Alice..	amostra (info)
1979	1979	Nova Inglaterra Digital	Sincronização II	Um sintetizador digital comercial que permitiu o desenvolvimento de timbre ao longo do tempo através de suaves cross-fades entre formas de onda geradas pela síntese aditiva.	Jon Appleton - Sashasonjon(help·info)

Equações de tempo discreto

Em implementações digitais de síntese aditiva, equações de tempo discreto são usadas no lugar das equações de síntese de tempo contínuo. Uma convenção nominal para sinais de tempo discreto usa colchetes ou seja. Sim.Não.n]- Sim. e o argumento n- Sim. só pode ser valores inteiros. Se a saída de síntese de tempo contínuo Sim.()){displaystyle y(t),} espera-se que seja suficientemente limitado; abaixo da metade da taxa de amostragem ou fS/2- Sim., basta amostrar diretamente a expressão contínua para obter a equação de síntese discreta. A saída de síntese contínua pode ser posteriormente reconstruída a partir das amostras usando um conversor digital para analógico. O período de amostragem é T= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1/fSNão. T=1/f_{mathrm {s} },}.

Começando com (3),

Sim.())= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento k= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1KKRk())e⁡ ⁡ (2D D ∫ ∫ 0)fk(u)Du+φ φ k){displaystyle y(t)=sum _{k=1}^{K}r_{k}(t)cos left(2pi int _{0}^{t}f_{k}(u) du+phi _{k}right)}

e amostragem em tempos discretos )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =nT= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =n/fSNão. t=nT=n/f_{mathrm {s} },} Resultados

Sim.Não.n]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Sim.(nT)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento k= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1KKRk(nT)e⁡ ⁡ (2D D ∫ ∫ 0nTfk(u)Du+φ φ k)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento k= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1KKRk(nT)e⁡ ⁡ (2D D Gerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1n∫ ∫ (Eu...- Sim. - Sim. 1)TEu...Tfk(u)Du+φ φ k)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento k= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1KKRk(nT)e⁡ ⁡ (2D D Gerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1n(TfkNão.Eu...])+φ φ k)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento k= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1KKRkNão.n]e⁡ ⁡ (2D D fSGerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1nfkNão.Eu...]+φ φ k){displaystyle {begin{aligned}y[n]&=y(nT)=sum _{k=1}^{K}r_{k}(nT)cos left(2pi int _{0}^{nT}f_{k}(u) Mais informações _{k}right)&=sum _{k=1}^{K}r_{k}(nT)cos left(2pi sum _{i=1}^{n}int _{(i-1)T}^{iT}f_{k}(u) Mais informações _{k}right)&=sum _{k=1}^{K}r_{k}(nT)cos left(2pi sum _{i=1}^{n}(Tf_{k}[i])+phi _{k}right)&=sum _{k=1}^{K}r_{k}[n]cos left({frac {2pi }{f_{mathrm {s} }}}sum _{i=1}^{n}f_{k}[i]+phi _{k}right)\end{aligned}}}

onde

RkNão.n]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Rk(nT)Não. r_{k}[n]=r_{k}(nT),} é o envelope de amplitude variável em tempo discreto

fkNão.n]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1T∫ ∫ (n- Sim. - Sim. 1)TnTfk())D){displaystyle f_{k}[n]={frac {1}{T}}int _{(n-1)T}^{nT}f_{k}(t) dt,} é a diferença de tempo discreto para trás frequência instantânea.

Isto é equivalente a

Sim.Não.n]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento k= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1KKRkNão.n]e⁡ ⁡ (θ θ kNão.n])- Sim. _{k=1}^{K}r_{k}[n]cos left(theta _{k}[n]right)}

onde

θ θ kNão.n]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2D D fSGerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1nfkNão.Eu...]+φ φ k= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =θ θ kNão.n- Sim. - Sim. 1]+2D D fSfkNão.n]{displaystyle {begin{aligned}theta _{k}[n]&={frac {2pi }{f_{mathrm {s} }}}sum _{i=1}^{n}f_{k}[i]+phi _{k}\&=theta _{k}[n-1]+{frac {2pi }{f_{mathrm {s} }}}f_{k}[n]\end{aligned}}} para todos 0,}" xmlns="http://www.w3.org/1998/Math/MathML">n>0- Sim.0," aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/947e5ee625b999ff1849997c89a25281e60d2240" style="vertical-align: -0.338ex; width:6.043ex; height:2.176ex;"/>

e

θ θ kNão.0]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ k.{displaystyle theta _{k}[0]=phi _{k}.,}