Seção transversal (física)

AjustarCompartirImprimirCitar

Probabilidade de um determinado processo ocorrendo em uma colisão de partículas

Na física, a seção transversal é uma medida da probabilidade de que um processo específico ocorrerá quando algum tipo de excitação radiante (por exemplo, um feixe de partículas, onda sonora, luz ou um X- raio) intercepta um fenômeno localizado (por exemplo, uma partícula ou flutuação de densidade). Por exemplo, a seção transversal de Rutherford é uma medida de probabilidade de que uma partícula alfa será desviada por um determinado ângulo durante uma interação com um núcleo atômico. A seção transversal é normalmente denotada $σ$ (sigma) e é expressa em unidades de área, mais especificamente em celeiros. De certa forma, pode ser pensado como o tamanho do objeto que a excitação deve atingir para que o processo ocorra, mas mais exatamente, é um parâmetro de um processo estocástico.

Na física clássica, essa probabilidade geralmente converge para uma proporção determinística da energia de excitação envolvida no processo, de modo que, por exemplo, com espalhamento de luz de uma partícula, a seção transversal especifica a quantidade de potência óptica espalhada pela luz de uma determinada irradiância (potência por área). É importante notar que, embora a seção transversal tenha as mesmas unidades de área, a seção transversal pode não corresponder necessariamente ao tamanho físico real do alvo dado por outras formas de medição. Não é incomum que a área real da seção transversal de um objeto de dispersão seja muito maior ou menor que a seção transversal relativa a algum processo físico. Por exemplo, as nanopartículas plasmônicas podem ter seções transversais de dispersão de luz para frequências específicas que são muito maiores do que suas áreas reais de seção transversal.

Quando duas partículas discretas interagem na física clássica, sua seção transversal mútua é a área transversal ao seu movimento relativo dentro da qual elas devem se encontrar para se espalharem uma da outra. Se as partículas são esferas inelásticas duras que interagem apenas no contato, sua seção transversal de dispersão está relacionada ao seu tamanho geométrico. Se as partículas interagirem por meio de alguma força de ação à distância, como eletromagnetismo ou gravidade, sua seção transversal de dispersão é geralmente maior que seu tamanho geométrico.

Quando uma seção transversal é especificada como o limite diferencial de uma função de alguma variável de estado final, como ângulo de partícula ou energia, ela é chamada de seção transversal diferencial (consulte a discussão detalhada abaixo). Quando uma seção transversal é integrada em todos os ângulos de dispersão (e possivelmente outras variáveis), ela é chamada de seção transversal total ou seção transversal total integrada. Por exemplo, na dispersão de Rayleigh, a intensidade espalhada nos ângulos para frente e para trás é maior que a intensidade espalhada lateralmente, de modo que a seção transversal de dispersão diferencial frontal é maior que a seção transversal diferencial perpendicular e adicionando todas as seções transversais infinitesimais sobre toda a gama de ângulos com cálculo integral, podemos encontrar a seção transversal total.

Seções transversais de dispersão podem ser definidas em física nuclear, atômica e de partículas para colisões de feixes acelerados de um tipo de partícula com alvos (estacionários ou móveis) de um segundo tipo de partícula. A probabilidade de qualquer reação ocorrer é proporcional à sua seção transversal. Assim, especificar a seção de choque para uma dada reação é um proxy para afirmar a probabilidade de que um determinado processo de espalhamento ocorrerá.

A taxa de reação medida de um determinado processo depende fortemente de variáveis experimentais, como a densidade do material alvo, a intensidade do feixe, a eficiência de detecção do aparelho ou o ajuste do ângulo do aparelho de detecção. No entanto, essas quantidades podem ser fatoradas, permitindo a medição da seção transversal colisional subjacente de duas partículas.

As seções de choque de espalhamento diferencial e total estão entre as quantidades mensuráveis mais importantes em física nuclear, atômica e de partículas.

Colisão entre partículas de gás

Figura 1. Em um gás de partículas de diâmetro individual

2 R

, a seção transversal

σ

, para colisões está relacionado com a densidade do número de partículas

n

, e significa caminho livre entre colisões

λ

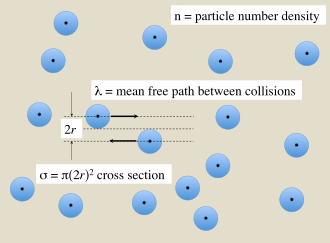
Em um gás de partículas de tamanho finito, há colisões entre partículas que dependem do tamanho de sua seção transversal. A distância média que uma partícula percorre entre as colisões depende da densidade das partículas de gás. Essas grandezas estão relacionadas por

{displaystyle sigma ={frac {1}{nlambda }},}

onde

σ

é a seção transversal de uma colisão de duas partículas (unidades SI: m²),

λ

é o caminho livre médio entre colisões (unidades SI: m),

n

é a densidade de número das partículas alvo (unidades SI: m^-3).

Se as partículas no gás puderem ser tratadas como esferas duras de raio $r$ que interagem por contato direto, conforme ilustrado na Figura 1, então a seção transversal efetiva para a colisão de um par é

{displaystyle sigma =pi left(2rright)^{2}}

Se as partículas no gás interagem por uma força com um alcance maior do que seu tamanho físico, então a seção transversal é uma área efetiva maior que pode depender de uma variedade de variáveis, como a energia das partículas.

As seções transversais podem ser calculadas para colisões atômicas, mas também são usadas no reino subatômico. Por exemplo, na física nuclear, um "gás" de nêutrons de baixa energia colide com núcleos em um reator ou outro dispositivo nuclear, com uma seção transversal dependente de energia e, portanto, também com caminho livre médio bem definido entre as colisões.

Atenuação de um feixe de partículas

Se um feixe de partículas entra em uma fina camada de material de espessura $d z$ , o fluxo $Φ$ do feixe diminuirá em $d Φ$ de acordo com

{displaystyle {frac {mathrm {d} Phi }{mathrm {d} z}}=-nsigma Phi}

onde $σ$ é a seção transversal total de todos os eventos, incluindo dispersão, absorção ou transformação em outra espécie. A densidade numérica volumétrica dos centros de dispersão é designada por $n$ . Resolver esta equação exibe a atenuação exponencial da intensidade do feixe:

{displaystyle Phi =Phi _{0}e^{-nsigma z},}

onde $Φ 0$ é o fluxo inicial e $z$ é a espessura total do material. Para a luz, isso é chamado de lei de Beer-Lambert.

Seção transversal diferencial

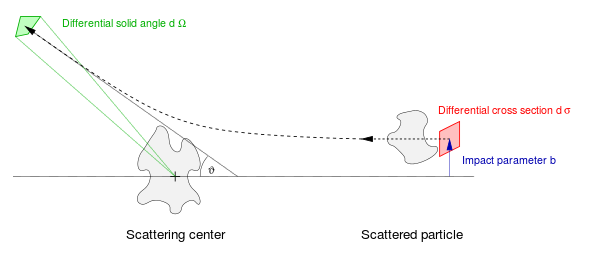
Considere uma medição clássica em que uma única partícula é espalhada por uma única partícula alvo estacionária. Convencionalmente, é utilizado um sistema de coordenadas esféricas, com o alvo colocado na origem e o eixo $z$ desse sistema de coordenadas alinhado com o feixe incidente. O ângulo $θ$ é o ângulo de dispersão, medido entre o feixe incidente e o feixe espalhado, e o $φ$ é o ângulo azimutal.

O parâmetro de impacto $b$ é o deslocamento perpendicular da trajetória da partícula que chega, e a partícula que sai emerge em um ângulo $θ$ . Para uma determinada interação (Coulômbica, magnética, gravitacional, contato, etc.), o parâmetro de impacto e o ângulo de dispersão têm uma dependência funcional um-para-um definida um do outro. Geralmente, o parâmetro de impacto não pode ser controlado nem medido de evento para evento e assume-se que assume todos os valores possíveis ao calcular a média de muitos eventos de dispersão. O tamanho diferencial da seção transversal é o elemento de área no plano do parâmetro de impacto, ou seja, $d σ = b d φ d b$ . A faixa angular diferencial da partícula espalhada no ângulo $θ$ é o elemento de ângulo sólido $d Ω = sin θ d θ d φ$ . A seção de choque diferencial é o quociente dessas quantidades, $d σ / d Ω$ .

É uma função do ângulo de dispersão (e, portanto, também do parâmetro de impacto), além de outros observáveis, como o momento da partícula que chega. A seção transversal diferencial é sempre considerada positiva, embora parâmetros de impacto maiores geralmente produzam menos deflexão. Em situações cilindricamente simétricas (em torno do eixo do feixe), o ângulo azimutal $φ$ não é alterado pelo processo de espalhamento, e a seção transversal diferencial pode ser escrita como

{displaystyle {frac {mathrm {d} sigma }{mathrm {d} (cos theta)}}=int _{0}^{2pi }{frac {mathrm {d} sigma }{mathrm {d} Omega }},mathrm {d} varphi }

Em situações em que o processo de espalhamento não é azimutalmente simétrico, como quando o feixe ou as partículas alvo possuem momentos magnéticos orientados perpendicularmente ao eixo do feixe, a seção de choque diferencial também deve ser expressa em função do ângulo azimutal.

Para dispersão de partículas de fluxo incidente $F inc$ de um alvo estacionário que consiste em muitas partículas, o cruzamento diferencial seção $d σ / d Ω$ em um ângulo $(θ, φ)$ está relacionado ao fluxo de detecção de partículas espalhadas $F out (θ, φ)$ em partículas por unidade de tempo por

{displaystyle {frac {mathrm {d} sigma }{mathrm {d} Omega }}(thetavarphi)={frac {1}{ntDelta Omega }}{frac {F_{text{out}}(thetavarphi)}{F_{text{inc}}}}.}

Aqui $Δ Ω$ é o tamanho angular finito do detector (unidade SI: sr), $n$ é a densidade numérica das partículas alvo (unidades SI: m⁻³) e $t$ é a espessura do alvo estacionário (unidades SI: m). Esta fórmula assume que o alvo é fino o suficiente para que cada partícula do feixe interaja com no máximo uma partícula alvo.

A seção transversal total $σ$ pode ser recuperada integrando a seção transversal diferencial $d σ / d Ω$ sobre o ângulo sólido completo ( $4π$ esterradianos):

{displaystyle sigma =oint _{4pi }{frac {mathrm {d} sigma }{mathrm {d} Omega }},mathrm {d} Omega =int _{0}^{2pi }int _{0}^{pi }{frac {mathrm {d} sigma }{mathrm {d} Omega }}sin theta ,mathrm {d} theta ,mathrm {d} varphi.}

É comum omitir o qualificador “diferencial” quando o tipo de seção transversal pode ser inferido a partir do contexto. Nesse caso, $σ$ pode ser chamado de seção transversal integral ou seção transversal total. O último termo pode ser confuso em contextos onde vários eventos estão envolvidos, já que “total” também pode se referir à soma das seções transversais de todos os eventos.

A seção de choque diferencial é uma quantidade extremamente útil em muitos campos da física, pois sua medição pode revelar uma grande quantidade de informações sobre a estrutura interna das partículas-alvo. Por exemplo, a seção de choque diferencial da dispersão de Rutherford forneceu fortes evidências para a existência do núcleo atômico.

Em vez do ângulo sólido, a transferência de momento pode ser usada como a variável independente das seções transversais diferenciais.

As seções de choque diferenciais no espalhamento inelástico contêm picos de ressonância que indicam a criação de estados metaestáveis e contêm informações sobre sua energia e tempo de vida.

Dispersão quântica

No formalismo independente do tempo do espalhamento quântico, a função de onda inicial (antes do espalhamento) é considerada uma onda plana com momento definido $k$ :

{displaystyle phi _{-}(mathbf {r});{stackrel {rto infty }{longrightarrow }};e^{ikz},}

onde $z$ e $r$ são os coordenadas relativas entre o projétil e o alvo. A seta indica que isso descreve apenas o comportamento assintótico da função de onda quando o projétil e o alvo estão muito distantes para que a interação tenha algum efeito.

Após o espalhamento, espera-se que a função de onda assuma a seguinte forma assintótica:

{displaystyle phi _{+}(mathbf {r});{stackrel {rto infty }{longrightarrow }};f(thetaphi){frac {e^{ikr}}{r}},}

onde $f$ é alguma função das coordenadas angulares conhecida como amplitude de dispersão. Esta forma geral é válida para qualquer interação de curto alcance e conservação de energia. Não é verdade para interações de longo alcance, então há complicações adicionais ao lidar com interações eletromagnéticas.

A função de onda completa do sistema se comporta assintoticamente como a soma

{displaystyle phi (mathbf {r});{stackrel {rto infty }{longrightarrow }};phi _{-}(mathbf {r})+phi _{+}(mathbf {r}).}

A seção transversal diferencial está relacionada à amplitude de dispersão:

{displaystyle {frac {mathrm {d} sigma }{mathrm {d} Omega }}(thetaphi)={bigl |}f(thetaphi){bigr |}^{2}.}

Isso tem uma interpretação simples como a densidade de probabilidade para encontrar o projétil espalhado em um determinado ângulo.

Uma seção transversal é, portanto, uma medida da área de superfície efetiva vista pelas partículas incidentes e, como tal, é expressa em unidades de área. A seção transversal de duas partículas (ou seja, observada quando as duas partículas estão colidindo uma com a outra) é uma medida do evento de interação entre as duas partículas. A seção transversal é proporcional à probabilidade de ocorrência de uma interação; por exemplo, em um experimento simples de espalhamento, o número de partículas espalhadas por unidade de tempo (corrente de partículas espalhadas $I r$ ) depende apenas do número de partículas incidentes por unidade de tempo (corrente de partículas incidentes $I i$ ), as características de alvo (por exemplo, o número de partículas por unidade de superfície $N$ ) e o tipo de interação. Para $Nσ ≪ 1$ temos

{displaystyle {begin{aligned}I_{text{r}}&=I_{text{i}}Nsigma\sigma &={frac {I_{text{r}}}{I_{text{i}}}}{frac {1}{N}}\&={text{probability of interaction}}times {frac {1}{N}}.end{aligned}}}

Relação com a matriz S

Se as massas reduzidas e os momentos do sistema em colisão forem $m i$ , $p i$ e $m f$ , $p f$ antes e depois da colisão, respectivamente, a seção transversal diferencial é dada por

{displaystyle {frac {mathrm {d} sigma }{mathrm {d} Omega }}=left(2pi right)^{4}m_{i}m_{f}{frac {p_{f}}{p_{i}}}{bigl |}T_{fi}{bigr |}^{2},}

onde a matriz $T$ on-shell é definida por

{displaystyle S_{fi}=delta _{fi}-2pi idelta left(E_{f}-E_{i}right)delta left(mathbf {p} _{i}-mathbf {p} _{f}right)T_{fi}}

em termos da matriz S. Aqui $δ$ é a função delta de Dirac. O cálculo da matriz S é o principal objetivo da teoria do espalhamento.

Unidades

Embora a unidade SI de seções transversais totais seja m2, unidades menores geralmente são usadas na prática.

Na física nuclear e de partículas, a unidade convencional é o celeiro b, onde 1 b = 10⁻²⁸ m² = 100 fm². Unidades prefixadas menores, como mb e μb, também são amplamente utilizadas. Correspondentemente, a seção transversal diferencial pode ser medida em unidades como mb/sr.

Quando a radiação espalhada é luz visível, é convencional medir o comprimento do caminho em centímetros. Para evitar a necessidade de fatores de conversão, a seção transversal de dispersão é expressa em cm² e a concentração numérica em cm⁻³. A medição da dispersão da luz visível é conhecida como nefelometria e é eficaz para partículas de 2 a 50 µm de diâmetro: como tal, é amplamente utilizada em meteorologia e na medição da poluição atmosférica.

A dispersão de raios-X também pode ser descrita em termos de seções transversais de dispersão, caso em que o quadrado ångström é uma unidade conveniente: 1 Å² = 10⁻²⁰ m² = 10000 pm² = 10⁸ b. A soma das seções transversais de espalhamento, fotoelétrico e produção de pares (em celeiros) é representada como o "coeficiente de atenuação atômica" (feixe estreito), em celeiros.

Dispersão de luz

Para a luz, como em outras configurações, a seção transversal de dispersão para partículas geralmente é diferente da seção transversal geométrica da partícula e depende do comprimento de onda da luz e da permissividade, forma e tamanho da partícula. A quantidade total de espalhamento em um meio esparso é proporcional ao produto da seção transversal de espalhamento e o número de partículas presentes.

Na interação da luz com as partículas, muitos processos ocorrem, cada um com suas próprias seções de choque, incluindo absorção, espalhamento e fotoluminescência. A soma das seções de choque de absorção e espalhamento às vezes é chamada de seção de choque de atenuação ou extinção.

{displaystyle sigma =sigma _{text{a}}+sigma _{text{s}}+sigma _{text{l}}.}

A seção de choque da extinção total está relacionada à atenuação da intensidade da luz por meio da lei de Beer-Lambert, que diz que a atenuação é proporcional à concentração de partículas:

{displaystyle A_{lambda }=Clsigma}

onde $A λ$ é a atenuação em um determinado comprimento de onda $λ$ , $C$ é a concentração de partículas como uma densidade numérica e $l$ é o comprimento do caminho. A absorbância da radiação é o logaritmo (decádico ou, mais comumente, natural) do recíproco da transmitância T:

A_{lambda }=-log {mathcal {T}}.

Combinar as seções transversais de espalhamento e absorção dessa maneira é muitas vezes necessário pela incapacidade de distingui-los experimentalmente, e muito esforço de pesquisa foi feito para desenvolver modelos que permitam distingui-los, sendo a teoria de Kubelka-Munk uma das mais importante nesta área.

Seção transversal e teoria de Mie

Seções cruzadas comumente calculadas usando A teoria de Mie inclui coeficientes de eficiência para extinção ${textstyle Q_{text{ext}}}$ , dispersão ${textstyle Q_{text{sc}}}$ e absorção ${textstyle Q_{text{abs}}}$ seções cruzadas. Esses são normalizados pelas seções geométricas da partícula ${textstyle sigma _{text{geom}}=pi a^{2}}$ como

{displaystyle Q_{alpha }={frac {sigma _{alpha }}{sigma _{text{geom}}}},qquad alpha ={text{ext}},{text{sc}},{text{abs}}.}

{displaystyle sigma _{alpha }={frac {W_{alpha }}{I_{text{inc}}}}}

Onde? ${displaystyle left[W_{alpha }right]=left[{text{W}}right]}$ é o fluxo de energia através da superfície circundante, e ${displaystyle left[I_{text{inc}}right]=left[{frac {text{W}}{{text{m}}^{2}}}right]}$ é a intensidade da onda incidente. Para uma onda de avião a intensidade vai ser ${displaystyle I_{text{inc}}=|mathbf {E} |^{2}/(2eta)}$ , onde ${displaystyle eta ={sqrt {mu mu _{0}/(varepsilon varepsilon _{0})}}}$ é a impedância do meio hospedeiro.

A abordagem principal é baseada no seguinte. Em primeiro lugar, construímos uma esfera imaginária de raio $r$ (superfície) $A$ ) em torno da partícula (o espalhador). A taxa líquida de energia eletromagnética cruza a superfície $A$ o

{displaystyle W_{a}=-oint _{A}mathbf {Pi } cdot {hat {mathbf {r} }}dA}

Onde? ${displaystyle mathbf {Pi } ={frac {1}{2}}operatorname {Re} left[mathbf {E} ^{*}times mathbf {H} right]}$ é a média de tempo Poynting vector. Se $0}" xmlns="http://www.w3.org/1998/Math/MathML">Wum>0- Sim. 0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e461554c7838486700a30e3a73f867ac350e882b" style="vertical-align: -0.671ex; width:7.556ex; height:2.509ex;"/>$ a energia é absorvida dentro da esfera, caso contrário a energia está sendo criada dentro da esfera. Excluímos da consideração posterior. Uma vez que o meio hospedeiro é não absorvente, a energia é absorvida pela partícula. Descompomos o campo total em partes incidentes e dispersas ${displaystyle mathbf {E} =mathbf {E} _{i}+mathbf {E} _{s}}$ , e o mesmo para o campo magnético $mathbf{H}$ . Assim, podemos decompor $W_a$ nos três termos ${displaystyle W_{a}=W_{i}-W_{s}+W_{text{ext}}}$ , onde

{displaystyle W_{i}=-oint _{A}mathbf {Pi } _{i}cdot {hat {mathbf {r} }}dAequiv 0,qquad W_{s}=oint _{A}mathbf {Pi } _{s}cdot {hat {mathbf {r} }}dA,qquad W_{text{ext}}=oint _{A}mathbf {Pi } _{text{ext}}cdot {hat {mathbf {r} }}dA.}

Onde? ${displaystyle mathbf {Pi } _{i}={frac {1}{2}}operatorname {Re} left[mathbf {E} _{i}^{*}times mathbf {H} _{i}right]}$ , ${displaystyle mathbf {Pi } _{s}={frac {1}{2}}operatorname {Re} left[mathbf {E} _{s}^{*}times mathbf {H} _{s}right]}$ e ${displaystyle mathbf {Pi } _{text{ext}}={frac {1}{2}}operatorname {Re} left[mathbf {E} _{s}^{*}times mathbf {H} _{i}+mathbf {E} _{i}^{*}times mathbf {H} _{s}right]}$ .

Todo o campo pode ser decomposto na série de harmônicos esféricos vetoriais (VSH). Depois disso, todas as integrais podem ser tomadas. No caso de um esfera uniforme de raio $a$ , permite $varepsilon$ , e permeabilidade $mu$ o problema tem uma solução precisa. Os coeficientes de dispersão e extinção são

{displaystyle Q_{text{sc}}={frac {2}{k^{2}a^{2}}}sum _{n=1}^{infty }(2n+1)(|a_{n}|^{2}+|b_{n}|^{2})}

{displaystyle Q_{text{ext}}={frac {2}{k^{2}a^{2}}}sum _{n=1}^{infty }(2n+1)Re (a_{n}+b_{n})}

{textstyle k=n_{text{host}}k_{0}}

{displaystyle sigma _{text{ext}}=sigma _{text{sc}}+sigma _{text{abs}}qquad {text{or}}qquad Q_{text{ext}}=Q_{text{sc}}+Q_{text{abs}}}

Aproximação de dipolo para a seção transversal de espalhamento

Vamos supor que as partículas suportam apenas os modos de dipolo elétrico e magnético com polarizabilidades ${textstyle mathbf {p} =alpha ^{e}mathbf {E} }$ e ${textstyle mathbf {m} =(mu mu _{0})^{-1}alpha ^{m}mathbf {H} }$ (aqui usamos a notação da polarização magnética da maneira de Bekshaev et al. ao invés da notação de Nieto-Vesperians et al.) expressa através dos coeficientes Mie como

{displaystyle alpha ^{e}=4pi varepsilon _{0}cdot i{frac {3varepsilon }{2k^{3}}}a_{1},qquad alpha ^{m}=4pi mu _{0}cdot i{frac {3mu }{2k^{3}}}b_{1}.}

{displaystyle sigma _{text{ext}}=sigma _{text{ext}}^{text{(e)}}+sigma _{text{ext}}^{text{(m)}}={frac {1}{4pi varepsilon varepsilon _{0}}}cdot 4pi kIm (alpha ^{e})+{frac {1}{4pi mu mu _{0}}}cdot 4pi kIm (alpha ^{m})}

{displaystyle sigma _{text{sc}}=sigma _{text{sc}}^{text{(e)}}+sigma _{text{sc}}^{text{(m)}}={frac {1}{(4pi varepsilon varepsilon _{0})^{2}}}cdot {frac {8pi }{3}}k^{4}|alpha ^{e}|^{2}+{frac {1}{(4pi mu mu _{0})^{2}}}cdot {frac {8pi }{3}}k^{4}|alpha ^{m}|^{2}}

{textstyle sigma _{text{abs}}=sigma _{text{abs}}^{text{(e)}}+sigma _{text{abs}}^{text{(m)}}}

{displaystyle sigma _{text{abs}}^{text{(e)}}={frac {1}{4pi varepsilon varepsilon _{0}}}cdot 4pi kleft[Im (alpha ^{e})-{frac {k^{3}}{6pi varepsilon varepsilon _{0}}}|alpha ^{e}|^{2}right]}

{displaystyle sigma _{text{abs}}^{text{(m)}}={frac {1}{4pi mu mu _{0}}}cdot 4pi kleft[Im (alpha ^{m})-{frac {k^{3}}{6pi mu mu _{0}}}|alpha ^{m}|^{2}right]}

Para o caso de partícula não-inside-gain, ou seja, não há energia emitida pela partícula internamente ( $0}" xmlns="http://www.w3.org/1998/Math/MathML">σ σ abs>0[textstyle sigma _{text{abs}}>0}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/d1c30c5d78a0b07062cebec71f8ce322c2bf4f1f" style="vertical-align: -0.671ex; width:8.204ex; height:2.509ex;"/>$ ), temos um caso particular do teorema Óptico

{displaystyle {frac {1}{4pi varepsilon varepsilon _{0}}}Im (alpha ^{e})+{frac {1}{4pi mu mu _{0}}}Im (alpha ^{m})geq {frac {2k^{3}}{3}}left[{frac {|alpha ^{e}|^{2}}{(4pi varepsilon varepsilon _{0})^{2}}}+{frac {|alpha ^{m}|^{2}}{(4pi mu mu _{0})^{2}}}right]}

{textstyle geq to =}

{textstyle Im (varepsilon)=Im (mu)=0}

Dispersão de luz em corpos estendidos

No contexto de dispersão de luz em corpos estendidos, a seção transversal de dispersão, $σ scat$ , descreve a probabilidade de luz sendo espalhada por uma partícula macroscópica. Em geral, a seção transversal de espalhamento é diferente da seção transversal geométrica de uma partícula, pois depende do comprimento de onda da luz e da permissividade, além da forma e tamanho da partícula. A quantidade total de espalhamento em um meio esparso é determinada pelo produto da seção transversal de espalhamento e o número de partículas presentes. Em termos de área, a seção transversal total ( $σ$ ) é a soma das seções transversais devido à absorção, espalhamento, e luminescência:

{displaystyle sigma =sigma _{text{a}}+sigma _{text{s}}+sigma _{text{l}}.}

A seção de choque total está relacionada à absorção da intensidade da luz por meio da lei de Beer–Lambert, que diz que a absorção é proporcional à concentração: $A λ = Clσ$ , onde $A λ$ é a absorbância em um determinado comprimento de onda $λ$ , $C$ é a concentração como uma densidade numérica e $l$ é o comprimento do caminho. A extinção ou absorbância da radiação é o logaritmo (decádico ou, mais comumente, natural) do recíproco da transmitância T:

{displaystyle A_{lambda }=-log {mathcal {T}}.}

Relação com o tamanho físico

Não existe uma relação simples entre a seção de choque de espalhamento e o tamanho físico das partículas, pois a seção de choque de espalhamento depende do comprimento de onda da radiação usada. Isso pode ser visto quando se olha para um halo ao redor da lua em uma noite de nevoeiro decente: os fótons de luz vermelha experimentam uma área de seção transversal maior de gotículas de água do que os fótons de energia mais alta. O halo ao redor da lua, portanto, tem um perímetro de luz vermelha devido aos fótons de energia mais baixa serem espalhados mais longe do centro da lua. Os fótons do restante do espectro visível são deixados no centro do halo e percebidos como luz branca.

Intervalo meteorológico

A seção transversal de espalhamento está relacionada ao alcance meteorológico $L V$ :

{displaystyle L_{text{V}}={frac {3.9}{Csigma _{text{scat}}}}.}

A quantidade $Cσ scat$ às vezes é denotada $b scat$ , o coeficiente de dispersão por unidade de comprimento.

Exemplos

Colisão elástica de duas esferas duras

As seguintes equações se aplicam a duas esferas duras que sofrem uma colisão perfeitamente elástica. Seja $R$ e $r$ denotam os raios do centro de dispersão e esfera espalhada, respectivamente. A seção transversal diferencial é

{displaystyle {frac {dsigma }{dOmega }}={frac {R^{2}}{4}},}

e a seção transversal total é

{displaystyle sigma _{text{tot}}=pi left(r+Rright)^{2}.}

Em outras palavras, a seção transversal de dispersão total é igual à área do círculo (com raio $r + R$ ) dentro do qual o centro de massa da esfera de entrada tem que chegar para que seja desviado.

Dispersão de Rutherford

No espalhamento de Rutherford, uma partícula incidente com carga $q$ e energia $E$ espalha uma partícula fixa com carga $Q$ . A seção transversal diferencial é

{displaystyle {frac {dsigma }{dOmega }}=left({frac {k_{text{e}}q,Q}{4Esin ^{2}(theta /2)}}right)^{2}}

onde $k e$ é a constante de Coulomb. A seção transversal total é infinita.

Dispersão de um espelho circular 2D

O exemplo a seguir trata de um feixe de luz se espalhando em um círculo com raio $r$ e um limite de reflexão perfeita. O feixe consiste em uma densidade uniforme de raios paralelos, e a interação feixe-círculo é modelada dentro da estrutura da óptica geométrica. Como o problema é genuinamente bidimensional, a seção transversal tem unidades de comprimento (por exemplo, metros). Seja $α$ o ângulo entre o raio de luz e o raio que une o ponto de reflexão do raio com o ponto central do espelho. Então o aumento do elemento de comprimento perpendicular à viga é

{displaystyle mathrm {d} x=rcos alpha ,mathrm {d} alpha.}

O ângulo de reflexão deste raio em relação ao raio incidente é $2 α$ , e o ângulo de dispersão é

{displaystyle theta =pi -2alpha.}

A relação diferencial entre intensidade incidente e refletida $I$ é

{displaystyle I,mathrm {d} sigma =I,mathrm {d} x(x)=Ircos alpha ,mathrm {d} alpha =I{frac {r}{2}}sin left({frac {theta }{2}}right),mathrm {d} theta =I{frac {mathrm {d} sigma }{mathrm {d} theta }},mathrm {d} theta.}

A seção transversal diferencial é, portanto, ( $d Ω = d θ$ )

{displaystyle {frac {mathrm {d} sigma }{mathrm {d} theta }}={frac {r}{2}}sin left({frac {theta }{2}}right).}

Seu máximo em $θ = π$ corresponde à dispersão reversa e seu mínimo em $θ = 0$ corresponde à dispersão da borda do círculo diretamente para frente. Essa expressão confirma as expectativas intuitivas de que o círculo do espelho age como uma lente divergente. A seção transversal total é igual ao diâmetro do círculo:

{displaystyle sigma =int _{0}^{2pi }{frac {mathrm {d} sigma }{mathrm {d} theta }},mathrm {d} theta =int _{0}^{2pi }{frac {r}{2}}sin left({frac {theta }{2}}right),mathrm {d} theta =2r.}

Dispersão de um espelho esférico 3D

O resultado do exemplo anterior pode ser usado para resolver o problema análogo em três dimensões, ou seja, espalhamento de uma esfera perfeitamente refletora de raio $a$ .

O plano perpendicular ao feixe de luz incidente pode ser parametrizado por coordenadas cilíndricas $r$ e $φ$ . Em qualquer plano do raio incidente e do raio refletido podemos escrever (do exemplo anterior):