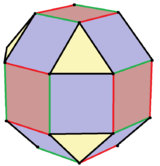
Rombicuboctaedro

Anúncio grátis para sua empresa
(Clique aqui para girar modelo)
Tipo	Solidariedade arqueológica Poliéster uniforme
Elementos	F - 26, E = 48, V = 24 (χ = 2)
Faces por lados	(6+12)}
Notação de saída	eC ou aaC AUXÍLIA
Símbolos de Schläfli	rr{4,3} ou R(43?{displaystyle r{begin{Bmatrix}43end{Bmatrix}}}
	)0,2{4,3}
Símbolo de Wythoff	3 4 | 2
Diagrama de Coxeador
Grupo de simetria	Oh, B3[4,3], (*432), ordem 48
Grupo de rotação	[4,3]+, (432), ordem 24
Ângulo dihedral	3-4: 144°44′08′′ (144.74°) 4-4: 135°
Referências	U10.C22,13
Propriedades	Convexo semi-regular
Rostos coloridos	3.4.4.4 (Vertex figure)
Linhas de produção (poliédron dual)	Rede

Em geometria, o rombicuboctaedro, ou pequeno rombicuboctaedro, é um poliedro com oito faces triangulares, seis quadradas e doze retangulares. Existem 24 vértices idênticos, com um triângulo, um quadrado e dois retângulos encontrando-se em cada um. Se todos os retângulos forem quadrados (equivalentemente, todas as arestas têm o mesmo comprimento, garantindo que os triângulos sejam equiláteros), é um sólido de Arquimedes. O poliedro tem simetria octaédrica, como o cubo e o octaedro. Seu dual é chamado de icositetraedro deltoidal ou icositetraedro trapezoidal, embora suas faces não sejam trapézios realmente verdadeiros.

Nomes

Johannes Kepler em Harmonices Mundi (1618) chamou este poliedro de rhombicuboctaedro, sendo a abreviação de losango cuboctaédrico truncado, com losango cuboctaédrico sendo seu nome para um dodecaedro rômbico. Existem diferentes truncamentos de um dodecaedro rômbico em um rombicuboctaedro topológico: proeminentemente sua retificação (esquerda), aquela que cria o sólido uniforme (centro), e a retificação do cuboctaedro dual (direita), que é o núcleo do composto dual.

Ele também pode ser chamado de cubo ou octaedro expandido ou cantelado, a partir de operações de truncamento em qualquer poliedro uniforme.

Did you mean:

Since its inclusion in Wings 3D as an n#34;octotoad n#34; this unofficial moniker is spreading.

Relações geométricas

Existem distorções do rombicuboctaedro que, embora algumas das faces não sejam polígonos regulares, ainda são vértice-uniformes. Alguns deles podem ser feitos pegando um cubo ou octaedro e cortando as bordas e depois aparando os cantos, de modo que o poliedro resultante tenha seis faces quadradas e doze retangulares. Estes têm simetria octaédrica e formam uma série contínua entre o cubo e o octaedro, análoga às distorções do rombicosidodecaedro ou às distorções tetraédricas do cuboctaedro. No entanto, o rombicuboctaedro também possui um segundo conjunto de distorções com seis faces retangulares e dezesseis trapezoidais, que não possuem simetria octaédrica, mas sim simetria T, portanto são invariantes sob as mesmas rotações do tetraedro, mas reflexões diferentes.

As linhas ao longo das quais um cubo de Rubik pode ser girado são projetadas em uma esfera, semelhante, topologicamente idêntica, às bordas de um rombicuboctaedro. Na verdade, foram produzidas variantes usando o mecanismo do Cubo de Rubik que se assemelham muito ao rombicuboctaedro.

O rombicuboctaedro é usado em três tesselações uniformes que preenchem o espaço: o favo de mel cúbico cantelado, o favo de mel cúbico runcitruncado e o favo de mel cúbico alternado runcinado.

Dissecção

O rombicuboctaedro pode ser dissecado em duas cúpulas quadradas e um prisma octogonal central. Uma rotação de 45 graus de uma cúpula cria o pseudo-hombicuboctaedro. Ambos os poliedros têm a mesma figura de vértice: 3.4.4.4.

Existem três pares de planos paralelos e cada um deles intercepta o rombicuboctaedro em um octógono regular. O rombicuboctaedro pode ser dividido ao longo de qualquer um deles para obter um prisma octogonal com faces regulares e dois poliedros adicionais chamados cúpulas quadradas, que contam entre os sólidos de Johnson; é, portanto, uma ortobicúpula quadrada alongada. Essas peças podem ser remontadas para dar um novo sólido chamado girobicúpula quadrada alongada ou pseudo-hombicuboctaedro, com a simetria de um antiprisma quadrado. Neste, os vértices são todos localmente iguais aos de um rombicuboctaedro, com um triângulo e três quadrados encontrando-se em cada um, mas não são todos idênticos em relação a todo o poliedro, uma vez que alguns estão mais próximos do eixo de simetria do que outros.

	Anúncio grátis para sua empresa
	Pseudorhombicuboctahedron

Projeções ortogonais

O rombicuboctaedro possui seis projeções ortogonais especiais, centradas em um vértice, em dois tipos de arestas e três tipos de faces: triângulos e dois quadrados. Os dois últimos correspondem aos planos B₂ e A₂ Coxeter.

Projeções ortogonais

Centro por	Verbos	Borda 3-4	Borda 4-4	Cara Quadrado 1	Cara Quadrado-2	Cara Triângulo
Sólido
Estrutura de fio
Projeto simetria	[2]	[2]	[2]	[2]	[4]	[6]
Dual

Ladrilhos esféricos

O rombicuboctaedro também pode ser representado como um ladrilho esférico e projetado no plano por meio de uma projeção estereográfica. Esta projeção é conforme, preservando ângulos, mas não áreas ou comprimentos. As linhas retas na esfera são projetadas como arcos circulares no plano.

	(6) quadrado centralizado	(6) quadrado centralizado	(8) triângulo centrado
Projeção ortogonal	Projeções estereográficas

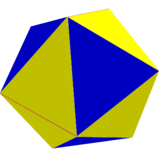
Simetria piritoédrica

Uma forma de meio simetria do rhombicuboctahedron, , existe com simetria pyritohedral, [4,3⁺], (3*2) como diagrama de Coxeter , símbolo de Schläfli₂{3,4}, e pode ser chamado de cantic snub octahedron. Esta forma pode ser visualizada colorindo alternadamente as bordas dos 6 quadrados. Estes quadrados podem então ser distorcidos em retângulos, enquanto os 8 triângulos permanecem equiláteros. As 12 faces quadradas diagonais se tornarão isosceles trapezoids. No limite, os retângulos podem ser reduzidos a bordas, e os trapezóides se tornam triângulos, e um icosaedro é formado, por um O que é isso? construção, , s{3,4}. (O composto de dois icosahedra é construído a partir de ambas as posições alternadas.)

Variações de simetria piritoedral
Geometria uniforme	Geometria não uniforme	Geometria não uniforme	No limite, um icosahedron Snub octahedron, , de uma das duas posições.	Composto por dois icosahedra de ambas as posições alternadas.

Propriedades algébricas

Coordenadas cartesianas

As coordenadas cartesianas para os vértices de um rombicuboctaedro centrado na origem, com comprimento de aresta 2 unidades, são todas as permutações pares de

(±1, ±1, ± 1, ± 1, + √2)).

Se o rombicuboctaedro original tem comprimento de aresta unitário, seu icositetraedro estrombico duplo tem comprimento de aresta

2710.- Sim. - Sim. 2e4- Sim. - Sim. 22.{displaystyle {frac {2}{7}}{sqrt {10-{sqrt {2}}}}quad {text{and}}quad {sqrt {4-2{sqrt {2}}}}}}}

Área e volume

A área A e o volume V do rombicuboctaedro de comprimento de aresta a são:

A= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(18.+23)um2? ? 21.4641016um2V= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =12+10.23um3? ? 8.71404521um3.{displaystyle {begin{aligned}A&=left(18+2{sqrt {3}}right)a^{2}&approx 21.464,1016a^{2}\V&={frac {12+10{sqrt {2}}}{3}}a^{3}&&approx 8.714,045,21a^{3}.end{aligned}}}

Densidade de empacotamento próximo

Did you mean:

The optimal packing fraction of rhombicuboctahedron is given by

? ? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =43(42- Sim. - Sim. 5){displaystyle eta ={tfrac {4}{3}}left(4{sqrt {2}}-5right)}.

Percebeu-se que este valor ótimo é obtido em uma rede de Bravais por de Graaf (2011). Como o rombicuboctaedro está contido em um dodecaedro rômbico cuja esfera inscrita é idêntica à sua própria esfera inscrita, o valor da fração de empacotamento ideal é um corolário da conjectura de Kepler: pode ser alcançado colocando um rombicuboctaedro em cada célula do dodecaedro rômbico favo de mel, e não pode ser superado, pois caso contrário a densidade ótima de empacotamento de esferas poderia ser superada colocando uma esfera em cada rombicuboctaedro do empacotamento hipotético que o ultrapassa.

Nas artes

O Retrato de Luca Pacioli de 1495, tradicionalmente atribuído a Jacopo de' Barbari, inclui um rombicuboctaedro de vidro cheio até a metade com água, que pode ter sido pintado por Leonardo da Vinci. A primeira versão impressa do rombicuboctaedro foi de Leonardo e apareceu na Divina proporcionale de Pacioli (1509).

Um panorama esférico de 180° × 360° pode ser projetado em qualquer poliedro; mas o rombicuboctaedro fornece uma aproximação boa o suficiente de uma esfera, ao mesmo tempo que é fácil de construir. Este tipo de projeção, chamada Philosphere, é possível a partir de alguns softwares de montagem de panoramas. É composto por duas imagens que são impressas separadamente e cortadas com tesoura deixando algumas abas para montagem com cola.

Objetos

Os jogos Freescape Driller e Dark Side tinham um mapa de jogo na forma de um rombicuboctaedro.

Did you mean:

The "Hurry-Scurry Galaxy A#34; and "Sea Slide Galaxy A#34; in the videogame Super Mario Galaxy have planets in the similar shape of a rhombicuboctahedron.

Did you mean:

Sonic the Hedgehog 3 's Icecap Zone features pillars topped with rhombicuboctahedron.

Did you mean:

During the Rubik 's Cube craze of the 1980s, at least two twisty puzzles sold had the form of a rhombicuboctahedron (the mechanism was similar to that of a Rubik's 's Cube).

• 

  Sundial (1596)

• 

  Sundial

• 

  Lâmpada de rua em Mainz

• 

  Morrer com 18 rostos rotulados

• 

  O alvo de tiro da Cabela

• 

  Serpente de Rubik

• 

  Variação do cubo de Rubik

• 

  Cristal de Pyrite

Poliedros relacionados

O rombicuboctaedro faz parte de uma família de poliedros uniformes relacionados ao cubo e ao octaedro regular.

Poliedros octahedral uniforme
Simetria: [4,3], (*432)							[4,3]+ (432)	[2]+[3,3] (*332)		[3]+,4] (3*2)
{4,3}	Não.	R{4,3} RECURSOS1.1?	T3,4 )1.1?	{3,4} (1.1?	rr,3 S2{3,4}	Não.	Sr.	H{4,3} (3,3)	H2{4,3} T3,3	- Sim. )1.1?
		= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =	= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =	= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =				= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = ou	= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = ou	= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =
Duals para polihedra uniforme
V43	V3.82	V(3.4)2	V4.62	V34	V3.43	V4.6.8	V34.4	V3	V3.62	V35

Mutações de simetria

Este poliedro está topologicamente relacionado como parte de uma sequência de poliedros cantelados com figura de vértice (3.4.n.4), e continua como ladrilhos do plano hiperbólico. Essas figuras transitivas de vértice têm (*n32) simetria reflexiva.

*n32 mutação simetria de camadas expandidas: 3.4.n.4
Simetria *n32 [n,3]	Esférica				Euclid.	Hiperb compacto.		Paracomp.
	*232 [2,3]	*332 [3,3]	*432 [4,3]	* 532 [5,3]	*632 [6,3]	*732 [7,3]	* 832 [8,3]...	* ∞32 [∞,3]
Figura
Config.	3.4.2.4	3.4.3.4	3.4.4.4	3.4.5.4	3.4.6.4	3.4.7.	3.4.8.4	3.4.∞.4

*n42 mutação simetria de camadas expandidas: n.4.4.4 v ) e
Simetria [n,4],n42)	Esférica	Euclidiano	Hiperbólica compacta				Paracomp.
	*342 [3,4]	*442 [4]	* 542 [5]	* 642 [6]	*742 [7]	* 842 [8]	* ∞42 [∞,4]
Expansão números
Config.	3.4.4.4	4.4.4.4	5.4.4.4	6.4.4.4	7.4.4.4	8.4.4.4	∞.4.4.4
Rhombic números config.	V3.4.4.4	V4.4.4.4	V5.4.4.4	V6.4.4.4	V7.4.4.4	V8.4.4.4	V∞.4.4.4

Organização de vértices

Ele compartilha seu arranjo de vértices com três poliedros uniformes não convexos: o hexaedro truncado estrelado, o pequeno rombihexaedro (tendo as faces triangulares e seis faces quadradas em comum) e o cububoctaedro pequeno (tendo doze faces quadradas em comum).

Anúncio grátis para sua empresa

Pequeno cubicuboctahedron

Rhombihexahedron pequeno

Hexahedron truncado estelar

Showing translation for

Rhombicuboctahedron graph

Did you mean:

The rhombicuboctahedron graph is the graph of vertices and edges of the rhombicuboctahedron. It has 24 vertices and 48 edges, and is a quartic Archimedean graph.