A relação binária tal que se A está relacionada com B e é diferente dele, então B não está relacionado com A
| Relações binárias transitivas |
|---|
| Symmetric | Antisymmetric | Conectado | Bem fundada | Tem uniões | Tem encontros | Reflexão | Irreflexível | Assimétrico | | | | Total, Semiconnex | | | | | Anti-
reflexivo | | | Relação de equivalência |  Y Y | ✗ | ✗ | ✗ | ✗ | ✗ |  Y Y | ✗ | ✗ | | Pré-ordem (Quasiorder) | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |  Y Y | ✗ | ✗ | | Ordem parcial | ✗ |  Y Y | ✗ | ✗ | ✗ | ✗ |  Y Y | ✗ | ✗ | | Entidade total | ✗ | ✗ |  Y Y | ✗ | ✗ | ✗ |  Y Y | ✗ | ✗ | | Ordem total | ✗ |  Y Y |  Y Y | ✗ | ✗ | ✗ |  Y Y | ✗ | ✗ | | Pré-encomendamento | ✗ | ✗ |  Y Y |  Y Y | ✗ | ✗ |  Y Y | ✗ | ✗ | | Ordenamento bem-quasi | ✗ | ✗ | ✗ |  Y Y | ✗ | ✗ |  Y Y | ✗ | ✗ | | Bem-ordenado | ✗ |  Y Y |  Y Y |  Y Y | ✗ | ✗ |  Y Y | ✗ | ✗ | | Lattice | ✗ |  Y Y | ✗ | ✗ |  Y Y |  Y Y |  Y Y | ✗ | ✗ | | Selecção | ✗ |  Y Y | ✗ | ✗ |  Y Y | ✗ |  Y Y | ✗ | ✗ | | Meet-semilattice | ✗ |  Y Y | ✗ | ✗ | ✗ |  Y Y |  Y Y | ✗ | ✗ | | Ordem parcial rigorosa | ✗ |  Y Y | ✗ | ✗ | ✗ | ✗ | ✗ |  Y Y |  Y Y | | Ordem fraca rigorosa | ✗ |  Y Y | ✗ | ✗ | ✗ | ✗ | ✗ |  Y Y |  Y Y | | Ordem total rigorosa | ✗ |  Y Y |  Y Y | ✗ | ✗ | ✗ | ✗ |  Y Y |  Y Y | | Symmetric | Antisymmetric | Conectado | Bem fundada | Tem uniões | Tem encontros | Reflexão | Irreflexível | Assimétrico | Definições, para todos um,b)Não. e S≠ ≠ ∅ ∅ :Não. Sneq varnothing:} e S≠ ≠ ∅ ∅ :Não. Sneq varnothing:} | umRb)⇒ ⇒ b)Rum{displaystyle {begin{aligned}&aRb\\Rightarrow {}&bRaend{aligned}}} | umRb)eb)Rum⇒ ⇒ um= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =b){displaystyle {begin{aligned}aRb{text{ and }}&bRa\Rightarrow a={}&bend{aligned}}} | um≠ ≠ b)⇒ ⇒ umRb)oub)Rum{displaystyle {begin{aligned}aneq {}&bRightarrow \aRb{text{ or }}&bRaend{aligned}}}}} | minSexiste{displaystyle {begin{aligned}min} S\{text{exists}}end{aligned}}} | um∨ ∨ b)existe{displaystyle {begin{aligned}avee b\{text{exists}}end{aligned}}} | um∧ ∧ b)existe{displaystyle {begin{aligned}awedge b\{text{exists}}end{aligned}}} | umRum- Sim. | nãoumRum{displaystyle {text{not }}a Ra. | umRb)⇒ ⇒ nãob)Rum- Sim. Direita \{text{not }}b Raend{aligned}}} |
|
 Y indica que a propriedade da coluna é sempre verdadeira o termo da linha (à esquerda), enquanto ✗ indica que a propriedade não é garantida em geral (pode, ou não, segure). Por exemplo, que cada relação de equivalência é simétrica, mas não necessariamente antissimétrica, é indicada por Y indica que a propriedade da coluna é sempre verdadeira o termo da linha (à esquerda), enquanto ✗ indica que a propriedade não é garantida em geral (pode, ou não, segure). Por exemplo, que cada relação de equivalência é simétrica, mas não necessariamente antissimétrica, é indicada por  Y na coluna "Simétrica" e ✗ na coluna "Antisymmetric", respectivamente. Y na coluna "Simétrica" e ✗ na coluna "Antisymmetric", respectivamente.
Todas as definições requerem tacitamente a relação homogênea RNão. R. ser transitivo: para todos um,b),c,- Sim. ser transitivo: para todos um,b),c,- Sim. se umRb)Não. ARB se umRb)Não. ARB e b)Rc- Sim. e b)Rc- Sim. então umRc.Não. então umRc.Não.
A definição de um termo pode exigir propriedades adicionais que não estão listadas nesta tabela.
|
Em matemática, uma relação binária RNão. R. em um conjunto X- Sim.
em um conjunto X- Sim. o anti-simétrico se não houver par de distinta elementos de X- Sim.
o anti-simétrico se não houver par de distinta elementos de X- Sim. cada um dos quais está relacionado por RNão. R.
cada um dos quais está relacionado por RNão. R. para o outro. Mais formalmente, RNão. R.
para o outro. Mais formalmente, RNão. R. é antissimétrico precisamente se para todos um,b)∈ ∈ X,- Sim.
é antissimétrico precisamente se para todos um,b)∈ ∈ X,- Sim.
seumRb)comum≠ ≠ b)entãob)Rumnão deve segurar,{displaystyle {text{if }},aRb,{text{ with }},aneq b,{text{ then }},bRa,{text{ must not hold}},}

seumRb)eb)Rumentãoum= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =b).{displaystyle {text{if }},aRb,{text{ e }},bRa,{text{ então }},a=b.}

 umNão.
umNão. RNão. R.
RNão. R. X- Sim.
X- Sim. umRum- Sim.
umRum- Sim. um∈ ∈ X- Sim.
um∈ ∈ X- Sim. umRum- Sim.
umRum- Sim. um∈ ∈ X- Sim.
um∈ ∈ X- Sim.
Exemplos
A relação de divisibilidade sobre os números naturais é um exemplo importante de uma relação antissimétrica. Neste contexto, a antisimetria significa que a única maneira de cada um de dois números pode ser divisível pelo outro é se os dois são, de fato, o mesmo número; equivalente, se nNão. e mNão.
e mNão. são distintos e nNão.
são distintos e nNão. é um fator de m,- Sim.
é um fator de m,- Sim. então mNão.
então mNão. não pode ser um fator de n.Não.
não pode ser um fator de n.Não. Por exemplo, 12 é divisível por 4, mas 4 não é divisível por 12.
Por exemplo, 12 é divisível por 4, mas 4 não é divisível por 12.
A relação de ordem habitual ≤ ≤ {displaystyle ,leq ,} nos números reais é antissimétrico: se para dois números reais xNão.
nos números reais é antissimétrico: se para dois números reais xNão. e Sim.- Sim.
e Sim.- Sim. ambas as desigualdades x≤ ≤ Sim.- Sim.
ambas as desigualdades x≤ ≤ Sim.- Sim. e Sim.≤ ≤ x- Sim.
e Sim.≤ ≤ x- Sim. Espere, então xNão.
Espere, então xNão. e Sim.- Sim.
e Sim.- Sim. deve ser igual. Da mesma forma, a ordem de subconjunto ⊆ ⊆ {displaystyle ,subseteq ,}
deve ser igual. Da mesma forma, a ordem de subconjunto ⊆ ⊆ {displaystyle ,subseteq ,} nos subconjuntos de qualquer conjunto dado é antissimétrico: dado dois conjuntos ANão. A.
nos subconjuntos de qualquer conjunto dado é antissimétrico: dado dois conjuntos ANão. A. e B,Não. B,
e B,Não. B, se cada elemento dentro ANão. A.
se cada elemento dentro ANão. A. também está em BNão.
também está em BNão. e cada elemento em BNão.
e cada elemento em BNão. também A,Não. A,
também A,Não. A, então ANão. A.
então ANão. A. e BNão.
e BNão. deve conter todos os mesmos elementos e, portanto, ser igual:
deve conter todos os mesmos elementos e, portanto, ser igual:
A⊆ ⊆ BeB⊆ ⊆ AimplicaA= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =BNão. Asubseteq B{text{ e }}Bsubseteq A{text{ implica }}A=B}

Propriedades
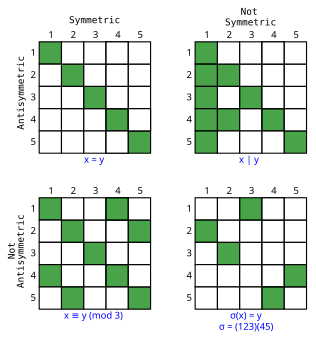
Relações simétricas e antisimétricas
Ordens parciais e totais são antissimétricas por definição. Uma relação pode ser simétrica e antisimétrica (neste caso, deve ser coreflexiva), e existem relações que não são nem simétricas nem antisimétricas (por exemplo, a relação "preda" sobre espécies biológicas).
A antisimetria é diferente da assimetria: uma relação é assimétrica se e somente se for antisimétrica e irreflexiva.
Más resultados...





































