Radiação eletromagnética

Uma onda eletromagnética linearmente polarizada que entra no eixo z, com E denotando o campo elétrico e o campo magnético perpendicular B que denota

Na física, radiação eletromagnética (EMR) consiste em ondas do campo eletromagnético (EM), que se propagam pelo espaço e carregam momento e energia radiante eletromagnética. Inclui ondas de rádio, microondas, infravermelho, luz (visível), ultravioleta, raios X e raios gama. Todas essas ondas fazem parte do espectro eletromagnético.

Classicamente, a radiação eletromagnética consiste em ondas eletromagnéticas, que são oscilações sincronizadas de campos elétricos e magnéticos. Dependendo da frequência de oscilação, diferentes comprimentos de onda do espectro eletromagnético são produzidos. No vácuo, as ondas eletromagnéticas viajam na velocidade da luz, comumente denotada como c. Em meios homogêneos e isotrópicos, as oscilações dos dois campos são perpendiculares entre si e perpendiculares à direção de propagação da energia e da onda, formando uma onda transversal. A posição de uma onda eletromagnética dentro do espectro eletromagnético pode ser caracterizada por sua frequência de oscilação ou seu comprimento de onda. Ondas eletromagnéticas de diferentes frequências são chamadas por nomes diferentes, pois têm diferentes fontes e efeitos na matéria. Em ordem crescente de frequência e decrescente de comprimento de onda são: ondas de rádio, microondas, radiação infravermelha, luz visível, radiação ultravioleta, raios X e raios gama.

As ondas eletromagnéticas são emitidas por partículas eletricamente carregadas em aceleração, e essas ondas podem posteriormente interagir com outras partículas carregadas, exercendo força sobre elas. As ondas EM transportam energia, momento e momento angular para longe de sua partícula de origem e podem transmitir essas quantidades à matéria com a qual interagem. A radiação eletromagnética está associada àquelas ondas EM que são livres para se propagar ("irradiar") sem a influência contínua das cargas em movimento que as produziram, porque alcançaram distância suficiente dessas cargas. Assim, o EMR às vezes é chamado de campo distante. Nesta linguagem, o campo próximo refere-se a campos EM próximos às cargas e correntes que os produziram diretamente, especificamente indução eletromagnética e fenômenos de indução eletrostática.

Na mecânica quântica, uma forma alternativa de ver o EMR é que ele consiste em fótons, partículas elementares não carregadas com massa de repouso zero que são os quanta do campo eletromagnético, responsáveis por todas as interações eletromagnéticas. A eletrodinâmica quântica é a teoria de como a EMR interage com a matéria em um nível atômico. Os efeitos quânticos fornecem fontes adicionais de EMR, como a transição de elétrons para níveis de energia mais baixos em um átomo e radiação de corpo negro. A energia de um fóton individual é quantizada e é maior para fótons de maior frequência. Essa relação é dada pela equação de Planck E = hf, onde E é a energia por fóton, f é a frequência do fóton e h é a constante de Planck. Um único fóton de raios gama, por exemplo, pode carregar cerca de 100.000 vezes a energia de um único fóton de luz visível.

Os efeitos da EMR sobre compostos químicos e organismos biológicos dependem tanto da potência da radiação quanto de sua frequência. EMR de frequências visíveis ou mais baixas (ou seja, luz visível, infravermelho, micro-ondas e ondas de rádio) é chamada de radiação não ionizante, porque seus fótons individualmente não têm energia suficiente para ionizar átomos ou moléculas, ou quebrar ligações químicas. Os efeitos dessas radiações em sistemas químicos e tecidos vivos são causados principalmente por efeitos de aquecimento da transferência combinada de energia de muitos fótons. Em contraste, ultravioleta de alta frequência, raios-X e raios gama são chamados de radiação ionizante, uma vez que fótons individuais de alta frequência têm energia suficiente para ionizar moléculas ou quebrar ligações químicas. Essas radiações têm a capacidade de causar reações químicas e danificar as células vivas além do que resulta do simples aquecimento e podem ser um perigo para a saúde.

Física

Teoria

Mostra os comprimentos de onda relativos das ondas eletromagnéticas de três cores diferentes de luz (azul, verde e vermelho) com uma escala de distância em micrômetros ao longo do eixo x.

Equações de Maxwell

James Clerk Maxwell derivou uma forma de onda das equações elétricas e magnéticas, revelando assim a natureza ondulatória dos campos elétrico e magnético e sua simetria. Como a velocidade das ondas EM previstas pela equação da onda coincidiu com a velocidade medida da luz, Maxwell concluiu que a própria luz é uma onda EM. As equações de Maxwell foram confirmadas por Heinrich Hertz através de experimentos com ondas de rádio.

Maxwell percebeu que, como grande parte da física é simétrica e matematicamente artística de certa forma, também deve haver uma simetria entre eletricidade e magnetismo. Ele percebeu que a luz é uma combinação de eletricidade e magnetismo e, portanto, os dois devem estar ligados. De acordo com as equações de Maxwell, um campo elétrico variando espacialmente está sempre associado a um campo magnético que muda com o tempo. Da mesma forma, um campo magnético variando espacialmente está associado a mudanças específicas ao longo do tempo no campo elétrico. Em uma onda eletromagnética, as mudanças no campo elétrico são sempre acompanhadas por uma onda no campo magnético em uma direção e vice-versa. Essa relação entre os dois ocorre sem que nenhum tipo de campo cause o outro; ao contrário, elas ocorrem juntas da mesma forma que as mudanças de tempo e espaço ocorrem juntas e estão interligadas na relatividade especial. Na verdade, os campos magnéticos podem ser vistos como campos elétricos em outro referencial, e os campos elétricos podem ser vistos como campos magnéticos em outro referencial, mas eles têm o mesmo significado, pois a física é a mesma em todos os referenciais. estreita relação entre as mudanças de espaço e tempo aqui é mais do que uma analogia. Juntos, esses campos formam uma onda eletromagnética em propagação, que se move para o espaço e nunca mais precisa interagir com a fonte. O distante campo EM formado desta forma pela aceleração de uma carga carrega consigo energia que "irradia" através do espaço, daí o termo.

Campos próximos e distantes

Na radiação eletromagnética (como micro-ondas de uma antena, mostrada aqui) o termo "radiação" aplica-se apenas às partes do campo eletromagnético que irradiam em espaço infinito e diminuem na intensidade por uma lei inversa-quadrado do poder, de modo que a energia total da radiação que atravessa uma superfície esférica imaginária é a mesma, não importa quão longe da antena a superfície esférica é desenhada. A radiação eletromagnética inclui assim a parte de campo distante do campo eletromagnético em torno de um transmissor. Uma parte do "near-field" perto do transmissor, faz parte do campo eletromagnético em mudança, mas não conta como radiação eletromagnética.

As equações de Maxwell estabeleceram que algumas cargas e correntes ("fontes") produzem um tipo de campo eletromagnético local perto delas que não tem o comportamento de EMR. As correntes produzem diretamente um campo magnético, mas é do tipo dipolo magnético que desaparece com a distância da corrente. De maneira semelhante, cargas em movimento afastadas em um condutor por um potencial elétrico variável (como em uma antena) produzem um campo elétrico do tipo dipolo elétrico, mas isso também diminui com a distância. Esses campos compõem o campo próximo próximo à fonte EMR. Nenhum desses comportamentos é responsável pela radiação EM. Em vez disso, eles causam um comportamento do campo eletromagnético que apenas transfere energia com eficiência para um receptor muito próximo à fonte, como a indução magnética dentro de um transformador ou o comportamento de feedback que ocorre próximo à bobina de um detector de metais. Normalmente, os campos próximos têm um efeito poderoso em suas próprias fontes, causando um aumento de "carga" (diminuição da reatância elétrica) na fonte ou transmissor, sempre que a energia é retirada do campo EM por um receptor. Caso contrário, esses campos não "se propagam" livremente no espaço, levando sua energia sem limite de distância, mas oscilando, devolvendo sua energia ao transmissor se não for recebida por um receptor.

Por outro lado, o campo distante EM é composto de radiação que está livre do transmissor no sentido de que (ao contrário do caso de um transformador elétrico) o transmissor requer a mesma potência para enviar esses alterações nos campos externos, quer o sinal seja captado imediatamente ou não. Esta parte distante do campo eletromagnético é "radiação eletromagnética" (também chamado de campo distante). Os campos distantes se propagam (irradiam) sem permitir que o transmissor os afete. Isso os torna independentes no sentido de que sua existência e sua energia, depois de deixarem o transmissor, são completamente independentes tanto do transmissor quanto do receptor. Devido à conservação de energia, a quantidade de energia que passa por qualquer superfície esférica desenhada em torno da fonte é a mesma. Como tal superfície tem uma área proporcional ao quadrado de sua distância da fonte, a densidade de potência da radiação EM sempre diminui com o inverso do quadrado da distância da fonte; isso é chamado de lei do inverso do quadrado. Isso contrasta com as partes do dipolo do campo EM próximas à fonte (o campo próximo), que variam em potência de acordo com uma lei de potência do cubo inverso e, portanto, não transportam uma quantidade conservada de energia em distâncias, mas em vez disso diminui com a distância, com sua energia (como observado) retornando rapidamente ao transmissor ou absorvida por um receptor próximo (como uma bobina secundária de transformador).

O campo distante (EMR) depende de um mecanismo diferente para sua produção do que o campo próximo e de termos diferentes nas equações de Maxwell. Considerando que a parte magnética do campo próximo é devido a correntes na fonte, o campo magnético em EMR é devido apenas à mudança local no campo elétrico. De maneira semelhante, enquanto o campo elétrico no campo próximo é devido diretamente às cargas e à separação de carga na fonte, o campo elétrico no EMR é devido a uma mudança no campo magnético local. Ambos os processos para produzir campos EMR elétricos e magnéticos têm uma dependência diferente da distância do que os campos elétricos e magnéticos de dipolo de campo próximo. É por isso que o tipo EMR de campo EM se torna dominante no poder "far" de fontes. O termo "longe das fontes" refere-se a quão longe da fonte (movendo-se à velocidade da luz) qualquer parte do campo EM em movimento externo está localizada, no momento em que as correntes da fonte são alteradas pela variação do potencial da fonte e, portanto, a fonte começou a gerar um campo EM movendo-se para fora de uma fase diferente.

Uma visão mais compacta do EMR é que o campo distante que compõe o EMR é geralmente aquela parte do campo EM que percorreu uma distância suficiente da fonte, que se tornou completamente desconectado de qualquer feedback para as cargas e correntes que foram originalmente responsáveis por isso. Agora, independente das cargas da fonte, o campo EM, à medida que se afasta, depende apenas das acelerações das cargas que o produziram. Não tem mais uma ligação forte com os campos diretos das cargas, nem com a velocidade das cargas (correntes).

Na formulação do potencial de Liénard-Wiechert dos campos elétrico e magnético devido ao movimento de uma única partícula (de acordo com as equações de Maxwell), os termos associados à aceleração da partícula são aqueles que são responsáveis pela parte do campo que é considerado como radiação eletromagnética. Por outro lado, o termo associado à mudança do campo elétrico estático da partícula e o termo magnético que resulta da velocidade uniforme da partícula, estão ambos associados ao campo próximo eletromagnético e não compreendem a radiação EM.

Propriedades

Ondas eletromagnéticas podem ser imaginadas como uma onda oscilante transversais autopropagadora de campos elétricos e magnéticos. Esta animação 3D mostra um plano de propagação linear de onda polarizada da esquerda para a direita. Os campos elétricos e magnéticos em tal onda são infase uns com os outros, alcançando minima e maxima juntos.

A eletrodinâmica é a física da radiação eletromagnética e o eletromagnetismo é o fenômeno físico associado à teoria da eletrodinâmica. Os campos elétrico e magnético obedecem às propriedades de superposição. Assim, um campo devido a qualquer partícula particular ou campo elétrico ou magnético variável no tempo contribui para os campos presentes no mesmo espaço devido a outras causas. Além disso, como são campos vetoriais, todos os vetores de campo magnético e elétrico se somam de acordo com a adição de vetores. Por exemplo, em óptica, duas ou mais ondas de luz coerentes podem interagir e, por interferência construtiva ou destrutiva, produzir uma irradiância resultante que se desvia da soma das irradiâncias componentes das ondas de luz individuais.

Os campos eletromagnéticos de luz não são afetados pela passagem através de campos elétricos ou magnéticos estáticos em um meio linear como o vácuo. No entanto, em meios não lineares, como alguns cristais, podem ocorrer interações entre a luz e os campos elétricos e magnéticos estáticos - essas interações incluem o efeito Faraday e o efeito Kerr.

Na refração, uma onda que passa de um meio para outro de densidade diferente altera sua velocidade e direção ao entrar no novo meio. A proporção dos índices de refração da mídia determina o grau de refração e é resumida pela lei de Snell. A luz de comprimentos de onda compostos (luz solar natural) se dispersa em um espectro visível passando por um prisma, devido ao índice de refração dependente do comprimento de onda do material do prisma (dispersão); isto é, cada onda componente dentro da luz composta é dobrada em um valor diferente.

A radiação EM exibe propriedades de onda e partículas ao mesmo tempo (ver dualidade onda-partícula). Ambas as características de onda e partícula foram confirmadas em muitos experimentos. As características das ondas são mais aparentes quando a radiação EM é medida em escalas de tempo relativamente grandes e em grandes distâncias, enquanto as características das partículas são mais evidentes ao medir pequenas escalas de tempo e distâncias. Por exemplo, quando a radiação eletromagnética é absorvida pela matéria, as propriedades de partículas serão mais óbvias quando o número médio de fótons no cubo do comprimento de onda relevante for muito menor que 1. Não é tão difícil observar experimentalmente a deposição não uniforme de energia quando a luz é absorvida, no entanto, isso por si só não é evidência de "partículas" comportamento. Em vez disso, reflete a natureza quântica da matéria. Demonstrar que a própria luz é quantizada, não apenas sua interação com a matéria, é uma questão mais sutil.

Alguns experimentos exibem as naturezas de onda e partícula de ondas eletromagnéticas, como a auto-interferência de um único fóton. Quando um único fóton é enviado por um interferômetro, ele passa por ambos os caminhos, interferindo consigo mesmo, como fazem as ondas, mas é detectado por um fotomultiplicador ou outro detector sensível apenas uma vez.

Uma teoria quântica da interação entre a radiação eletromagnética e a matéria, como os elétrons, é descrita pela teoria da eletrodinâmica quântica.

As ondas eletromagnéticas podem ser polarizadas, refletidas, refratadas, difratadas ou interferir umas nas outras.

Modelo de onda

Representação do vetor de campo elétrico de uma onda de radiação eletromagnética circularmente polarizada.

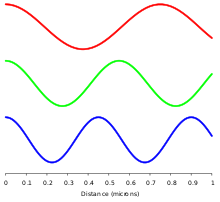
Em meios homogêneos e isotrópicos, a radiação eletromagnética é uma onda transversal, o que significa que suas oscilações são perpendiculares à direção da transferência e viagem de energia. Vem das seguintes equações:

? ? )) E= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0? ? )) B= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0{displaystyle {begin{aligned}nabla cdot mathbf] {E} &=0\\nabla cdot mathbf {B} &=0end{aligned}}}

As partes elétrica e magnética do campo em uma onda eletromagnética permanecem em uma proporção fixa de forças para satisfazer as duas equações de Maxwell que especificam como uma é produzida a partir da outra. Em meios sem dissipação (sem perdas), esses campos E e B também estão em fase, atingindo máximos e mínimos nos mesmos pontos no espaço (consulte as ilustrações). Um equívoco comum é que os campos E e B na radiação eletromagnética estão fora de fase porque uma mudança em um produz o outro, e isso produziria uma diferença de fase entre eles como funções senoidais (como de fato acontece na indução eletromagnética e no campo próximo próximo às antenas). No entanto, na radiação EM de campo distante, que é descrita pelas duas equações do operador rotacional de Maxwell sem fonte, uma descrição mais correta é que uma mudança de tempo em um tipo de campo é proporcional a uma mudança de espaço no outro. Essas derivadas exigem que os campos E e B no EMR estejam em fase (consulte a seção de matemática abaixo). Um aspecto importante da natureza da luz é sua frequência. A frequência de uma onda é a sua taxa de oscilação e é medida em hertz, a unidade SI de frequência, onde um hertz é igual a uma oscilação por segundo. A luz geralmente tem múltiplas frequências que se somam para formar a onda resultante. Diferentes frequências sofrem diferentes ângulos de refração, um fenômeno conhecido como dispersão.

Uma onda monocromática (uma onda de uma única frequência) consiste em depressões e cristas sucessivas, e a distância entre duas cristas ou depressões adjacentes é chamada de comprimento de onda. As ondas do espectro eletromagnético variam em tamanho, desde ondas de rádio muito longas, maiores que um continente, até raios gama muito curtos, menores que núcleos de átomos. A frequência é inversamente proporcional ao comprimento de onda, de acordo com a equação:

v= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =fλ λ {displaystyle displaystyle v=flambda ?

onde v é a velocidade da onda (c no vácuo ou menos em outro meio), f é a frequência e λ é o comprimento de onda. À medida que as ondas cruzam fronteiras entre diferentes meios, suas velocidades mudam, mas suas frequências permanecem constantes.

Ondas eletromagnéticas no espaço livre devem ser soluções da equação de onda eletromagnética de Maxwell. Duas classes principais de soluções são conhecidas, ou seja, ondas planas e ondas esféricas. As ondas planas podem ser vistas como o caso limite de ondas esféricas a uma distância muito grande (idealmente infinita) da fonte. Ambos os tipos de ondas podem ter uma forma de onda que é uma função de tempo arbitrária (desde que seja suficientemente diferenciável para estar em conformidade com a equação de onda). Como acontece com qualquer função de tempo, isso pode ser decomposto por meio da análise de Fourier em seu espectro de frequência ou componentes senoidais individuais, cada um dos quais contém uma única frequência, amplitude e fase. Tal onda componente é dita ser monocromática. Uma onda eletromagnética monocromática pode ser caracterizada por sua frequência ou comprimento de onda, sua amplitude de pico, sua fase em relação a alguma fase de referência, sua direção de propagação e sua polarização.

A interferência é a superposição de duas ou mais ondas resultando em um novo padrão de onda. Se os campos tiverem componentes na mesma direção, eles interferem construtivamente, enquanto direções opostas causam interferência destrutiva. Um exemplo de interferência causada por EMR é a interferência eletromagnética (EMI) ou, como é mais comumente conhecida como, interferência de radiofrequência (RFI). Além disso, vários sinais de polarização podem ser combinados (isto é, interferidos) para formar novos estados de polarização, o que é conhecido como geração de estado de polarização paralela.

A energia das ondas eletromagnéticas às vezes é chamada de energia radiante.

Modelo de partícula e teoria quântica

Uma anomalia surgiu no final do século 19 envolvendo uma contradição entre a teoria ondulatória da luz e as medições dos espectros eletromagnéticos que estavam sendo emitidos por radiadores térmicos conhecidos como corpos negros. Os físicos lutaram com esse problema sem sucesso por muitos anos. Mais tarde, ficou conhecido como a catástrofe ultravioleta. Em 1900, Max Planck desenvolveu uma nova teoria da radiação do corpo negro que explicava o espectro observado. A teoria de Planck foi baseada na ideia de que os corpos negros emitem luz (e outras radiações eletromagnéticas) apenas como feixes ou pacotes discretos de energia. Esses pacotes foram chamados de quanta. Em 1905, Albert Einstein propôs que os quanta de luz fossem considerados partículas reais. Mais tarde, a partícula de luz recebeu o nome de fóton, para corresponder a outras partículas descritas nessa época, como o elétron e o próton. Um fóton tem uma energia, E, proporcional à sua frequência, f, por

E= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =hf= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =hcλ λ Não. E depois? Não. }},!}

Onde? h é constante de Planck, λ λ - Sim. é o comprimento de onda e c é a velocidade da luz. Isso às vezes é conhecido como a equação Planck-Einstein. Na teoria quântica (ver primeira quantificação) a energia dos fótons é, portanto, diretamente proporcional à frequência da onda EMR.

Da mesma forma, o momento p de um fóton também é proporcional à sua frequência e inversamente proporcional ao seu comprimento de onda:

p= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Ec= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =hfc= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =hλ λ .{displaystyle p={E over c}={hf over c}={h over lambda }

A origem da proposta de Einstein de que a luz era composta de partículas (ou poderia agir como partículas em algumas circunstâncias) foi uma anomalia experimental não explicada pela teoria ondulatória: o efeito fotoelétrico, no qual a luz atinge uma superfície metálica ejetou elétrons da superfície, fazendo com que uma corrente elétrica fluísse através de uma voltagem aplicada. Medições experimentais demonstraram que a energia de elétrons ejetados individualmente era proporcional à frequência, em vez da intensidade, da luz. Além disso, abaixo de uma certa frequência mínima, que dependia do metal em particular, nenhuma corrente fluiria independentemente da intensidade. Essas observações pareciam contradizer a teoria das ondas e, durante anos, os físicos tentaram em vão encontrar uma explicação. Em 1905, Einstein explicou esse quebra-cabeça ressuscitando a teoria das partículas da luz para explicar o efeito observado. Devido à preponderância de evidências a favor da teoria ondulatória, no entanto, as ideias de Einstein foram recebidas inicialmente com grande ceticismo entre os físicos estabelecidos. Eventualmente, a explicação de Einstein foi aceita, pois foi observado um novo comportamento semelhante a partícula da luz, como o efeito Compton.

À medida que um fóton é absorvido por um átomo, ele excita o átomo, elevando um elétron a um nível de energia mais alto (um que está, em média, mais distante do núcleo). Quando um elétron em uma molécula ou átomo excitado desce para um nível de energia mais baixo, ele emite um fóton de luz em uma frequência correspondente à diferença de energia. Como os níveis de energia dos elétrons nos átomos são discretos, cada elemento e cada molécula emite e absorve suas próprias frequências características. A emissão imediata de fótons é chamada de fluorescência, um tipo de fotoluminescência. Um exemplo é a luz visível emitida por tintas fluorescentes, em resposta ao ultravioleta (luz negra). Muitas outras emissões fluorescentes são conhecidas em bandas espectrais além da luz visível. A emissão retardada é chamada de fosforescência.

Dualidade onda-partícula

A teoria moderna que explica a natureza da luz inclui a noção de dualidade onda-partícula. De forma mais geral, a teoria afirma que tudo tem tanto uma natureza de partícula quanto uma natureza de onda, e vários experimentos podem ser feitos para revelar uma ou outra. A natureza da partícula é mais facilmente discernida usando um objeto com uma grande massa. Uma proposição ousada de Louis de Broglie em 1924 levou a comunidade científica a perceber que a matéria (por exemplo, elétrons) também exibe dualidade onda-partícula.

Efeitos de onda e partícula da radiação eletromagnética

Juntos, os efeitos de onda e partícula explicam completamente os espectros de emissão e absorção da radiação EM. A composição da matéria do meio através do qual a luz viaja determina a natureza do espectro de absorção e emissão. Essas bandas correspondem aos níveis de energia permitidos nos átomos. As bandas escuras no espectro de absorção são devidas aos átomos em um meio intermediário entre a fonte e o observador. Os átomos absorvem certas frequências da luz entre o emissor e o detector/olho, e então as emitem em todas as direções. Uma faixa escura aparece para o detector, devido à radiação espalhada pelo feixe. Por exemplo, as bandas escuras na luz emitida por uma estrela distante são devidas aos átomos na atmosfera da estrela. Um fenômeno semelhante ocorre para a emissão, que é vista quando um gás emissor brilha devido à excitação dos átomos de qualquer mecanismo, incluindo o calor. À medida que os elétrons descem para níveis de energia mais baixos, é emitido um espectro que representa os saltos entre os níveis de energia dos elétrons, mas as linhas são vistas porque, novamente, a emissão ocorre apenas em energias específicas após a excitação. Um exemplo é o espectro de emissão de nebulosas. Elétrons que se movem rapidamente são mais rapidamente acelerados quando encontram uma região de força, então eles são responsáveis por produzir grande parte da radiação eletromagnética de frequência mais alta observada na natureza.

Esses fenômenos podem auxiliar várias determinações químicas para a composição de gases iluminados por trás (espectro de absorção) e para gases brilhantes (espectro de emissão). A espectroscopia (por exemplo) determina quais elementos químicos compõem uma estrela em particular. A espectroscopia também é usada na determinação da distância de uma estrela, usando o desvio para o vermelho.

Velocidade de propagação

Quando qualquer fio (ou outro objeto condutor, como uma antena) conduz corrente alternada, a radiação eletromagnética é propagada na mesma frequência que a corrente. Em muitas dessas situações é possível identificar um momento de dipolo elétrico que surge da separação de cargas devido ao potencial elétrico de excitação, e esse momento de dipolo oscila no tempo, conforme as cargas se movem para frente e para trás. Essa oscilação em uma determinada frequência dá origem a campos elétricos e magnéticos variáveis, que então colocam a radiação eletromagnética em movimento.

No nível quântico, a radiação eletromagnética é produzida quando o pacote de ondas de uma partícula carregada oscila ou acelera. Partículas carregadas em um estado estacionário não se movem, mas uma superposição de tais estados pode resultar em um estado de transição que possui um momento de dipolo elétrico que oscila no tempo. Este momento de dipolo oscilante é responsável pelo fenômeno de transição radiativa entre estados quânticos de uma partícula carregada. Tais estados ocorrem (por exemplo) em átomos quando os fótons são irradiados quando o átomo muda de um estado estacionário para outro.

Como uma onda, a luz é caracterizada por uma velocidade (a velocidade da luz), comprimento de onda e frequência. Como partículas, a luz é um fluxo de fótons. Cada um tem uma energia relacionada à frequência da onda dada pela relação de Planck E = hf, onde E é a energia do fóton, h é a constante de Planck, 6,626 × 10⁻³⁴ J·s, e f é a frequência da onda.

Uma regra é obedecida independentemente das circunstâncias: a radiação EM no vácuo viaja na velocidade da luz, em relação ao observador, independentemente da velocidade do observador. Em um meio (que não seja vácuo), o fator de velocidade ou o índice de refração são considerados, dependendo da frequência e da aplicação. Ambos são proporções da velocidade em um meio para a velocidade no vácuo.

Teoria especial da relatividade

No final do século XIX, várias anomalias experimentais não podiam ser explicadas pela teoria das ondas simples. Uma dessas anomalias envolveu uma controvérsia sobre a velocidade da luz. A velocidade da luz e outras EMR previstas pelas equações de Maxwell não apareceram a menos que as equações fossem modificadas de uma maneira sugerida pela primeira vez por FitzGerald e Lorentz (veja a história da relatividade especial), ou então essa velocidade dependeria da velocidade do observador em relação ao "meio" (chamado éter luminífero) que supostamente "carregava" a onda eletromagnética (de maneira análoga à maneira como o ar transporta as ondas sonoras). Os experimentos falharam em encontrar qualquer efeito do observador. Em 1905, Einstein propôs que o espaço e o tempo pareciam ser entidades com velocidade variável para a propagação da luz e todos os outros processos e leis. Essas mudanças foram responsáveis pela constância da velocidade da luz e de toda a radiação eletromagnética, do ponto de vista de todos os observadores – mesmo aqueles em movimento relativo.

História da descoberta

A radiação eletromagnética de comprimentos de onda diferentes dos da luz visível foi descoberta no início do século XIX. A descoberta da radiação infravermelha é atribuída ao astrônomo William Herschel, que publicou seus resultados em 1800 perante a Royal Society de Londres. Herschel usou um prisma de vidro para refratar a luz do Sol e detectou raios invisíveis que causavam aquecimento além da parte vermelha do espectro, por meio de um aumento na temperatura registrada com um termômetro. Esses "raios caloríficos" foram posteriormente denominados de infravermelho.

Em 1801, o físico alemão Johann Wilhelm Ritter descobriu o ultravioleta em um experimento semelhante ao de Herschel, usando a luz solar e um prisma de vidro. Ritter notou que os raios invisíveis perto da borda violeta de um espectro solar disperso por um prisma triangular escureciam as preparações de cloreto de prata mais rapidamente do que a luz violeta próxima. Os experimentos de Ritter foram um dos primeiros precursores do que se tornaria a fotografia. Ritter notou que os raios ultravioleta (que a princípio eram chamados de "raios químicos") eram capazes de causar reações químicas.

James Clerk Maxwell

Em 1862–64, James Clerk Maxwell desenvolveu equações para o campo eletromagnético que sugeriam que as ondas no campo viajariam com uma velocidade muito próxima da conhecida velocidade da luz. Maxwell, portanto, sugeriu que a luz visível (assim como os raios infravermelhos e ultravioleta invisíveis por inferência) consistia na propagação de perturbações (ou radiação) no campo eletromagnético. As ondas de rádio foram produzidas pela primeira vez deliberadamente por Heinrich Hertz em 1887, usando circuitos elétricos calculados para produzir oscilações em uma frequência muito menor que a da luz visível, seguindo receitas para produzir cargas e correntes oscilantes sugeridas pelas equações de Maxwell. Hertz também desenvolveu maneiras de detectar essas ondas e produziu e caracterizou o que mais tarde foi chamado de ondas de rádio e micro-ondas.

Wilhelm Röntgen descobriu e nomeou os raios-X. Depois de experimentar altas voltagens aplicadas a um tubo evacuado em 8 de novembro de 1895, ele notou uma fluorescência em uma placa próxima de vidro revestido. Em um mês, ele descobriu os raios-X'; propriedades principais.

A última porção do espectro EM a ser descoberta foi associada à radioatividade. Henri Becquerel descobriu que os sais de urânio causavam o embaçamento de uma placa fotográfica não exposta através de um papel de cobertura de maneira semelhante aos raios X, e Marie Curie descobriu que apenas certos elementos emitiam esses raios de energia, logo descobrindo a intensa radiação do rádio. A radiação da pechblenda foi diferenciada em raios alfa (partículas alfa) e raios beta (partículas beta) por Ernest Rutherford através de experimentos simples em 1899, mas estes provaram ser tipos de partículas carregadas de radiação. No entanto, em 1900, o cientista francês Paul Villard descobriu um terceiro tipo de radiação do rádio, com carga neutra e especialmente penetrante, e depois de descrevê-lo, Rutherford percebeu que deveria ser ainda um terceiro tipo de radiação, que em 1903 Rutherford denominou raios gama. Em 1910, o físico britânico William Henry Bragg demonstrou que os raios gama são radiação eletromagnética, não partículas, e em 1914 Rutherford e Edward Andrade mediram seus comprimentos de onda, descobrindo que eram semelhantes aos raios X, mas com comprimentos de onda mais curtos e frequência mais alta, embora um &# 39;cruzamento' entre raios X e gama torna possível ter raios X com uma energia maior (e, portanto, comprimento de onda mais curto) do que os raios gama e vice-versa. A origem do raio os diferencia, os raios gama tendem a ser fenômenos naturais originários do núcleo instável de um átomo e os raios X são gerados eletricamente (e, portanto, feitos pelo homem), a menos que sejam resultado da radiação X bremsstrahlung causada por a interação de partículas em movimento rápido (como partículas beta) colidindo com certos materiais, geralmente de números atômicos mais altos.

Espectro eletromagnético

Espectro eletromagnético com luz visível destacada

Legenda:
γ = raios gama

HX = Raios X duros
SX = X-Rays macios

EUV = Extreme-ultraviolet
NUV = Near-ultraviolet

Luz visível (bandas coloridas)

NIR = infravermelho próximo
MIR = Mid-infrared
FIR = infravermelho distante

EHF = Frequência extremamente alta (microondas)
SHF = Super-alta frequência (microondas)

UHF = Freqüência ultra-alta (ábio ondas)
VHF = Frequência muito alta (rádio)
HF = Alta frequência (rádio)
MF = Frequência média (rádio)
LF = Baixa frequência (rádio)
VLF = Frequência muito baixa (rádio)
VF = Frequência de voz
ULF = Frequência ultra-baixa (rádio)
SLF = Super-baixa frequência (rádio)
ELF = Frequência extremamente baixa (rádio)

A radiação EM (a designação 'radiação' exclui campos elétricos e magnéticos estáticos e próximos) é classificada por comprimento de onda em rádio, micro-ondas, infravermelho, visível, ultravioleta, raios-X e raios gama. Ondas eletromagnéticas arbitrárias podem ser expressas pela análise de Fourier em termos de ondas monocromáticas senoidais, que por sua vez podem ser classificadas nessas regiões do espectro EMR.

Para certas classes de ondas EM, a forma de onda é tratada de forma mais útil como aleatória e, em seguida, a análise espectral deve ser feita por técnicas matemáticas ligeiramente diferentes, apropriadas para processos aleatórios ou estocásticos. Nesses casos, os componentes de frequência individuais são representados em termos de seu conteúdo de potência e a informação de fase não é preservada. Tal representação é chamada de densidade espectral de potência do processo aleatório. A radiação eletromagnética aleatória que requer esse tipo de análise é, por exemplo, encontrada no interior das estrelas e em algumas outras formas de radiação de banda larga, como o campo de onda de ponto zero do vácuo eletromagnético.

O comportamento da radiação EM e sua interação com a matéria dependem de sua frequência e mudam qualitativamente conforme a frequência muda. As frequências mais baixas têm comprimentos de onda mais longos e as frequências mais altas têm comprimentos de onda mais curtos e estão associadas a fótons de energia mais alta. Não há limite fundamental conhecido para esses comprimentos de onda ou energias, em qualquer extremidade do espectro, embora os fótons com energias próximas à energia de Planck ou superiores a ela (altas demais para serem observadas) exigirão novas teorias físicas para serem descritas.

Rádio e micro-ondas

Quando as ondas de rádio incidem sobre um condutor, elas se acoplam ao condutor, viajam ao longo dele e induzem uma corrente elétrica na superfície do condutor movendo os elétrons do material condutor em feixes de carga correlacionados. Tais efeitos podem cobrir distâncias macroscópicas em condutores (como antenas de rádio), uma vez que o comprimento de onda das ondas de rádio é longo.

Fenômenos de radiação eletromagnética com comprimentos de onda que variam de um metro a um milímetro são chamados de micro-ondas; com frequências entre 300 MHz (0,3 GHz) e 300 GHz.

Nas frequências de rádio e micro-ondas, a EMR interage com a matéria em grande parte como uma coleção de cargas espalhadas por um grande número de átomos afetados. Em condutores elétricos, tal movimento induzido de cargas (correntes elétricas) resulta na absorção da EMR, ou então separações de cargas que causam a geração de uma nova EMR (reflexão efetiva da EMR). Um exemplo é a absorção ou emissão de ondas de rádio por antenas, ou absorção de micro-ondas por água ou outras moléculas com momento de dipolo elétrico, como por exemplo dentro de um forno de micro-ondas. Essas interações produzem correntes elétricas ou calor, ou ambos.

Infravermelho

Como o rádio e o micro-ondas, o infravermelho (IR) também é refletido pelos metais (e também pela maioria dos EMR, bem na faixa ultravioleta). No entanto, ao contrário da radiação de rádio e micro-ondas de baixa frequência, o EMR infravermelho geralmente interage com dipolos presentes em moléculas individuais, que mudam à medida que os átomos vibram nas extremidades de uma única ligação química. Conseqüentemente, é absorvido por uma ampla gama de substâncias, fazendo com que elas aumentem de temperatura à medida que as vibrações se dissipam na forma de calor. O mesmo processo, executado ao contrário, faz com que as substâncias a granel irradiem no infravermelho espontaneamente (consulte a seção de radiação térmica abaixo).

A radiação infravermelha é dividida em sub-regiões espectrais. Embora existam diferentes esquemas de subdivisão, o espectro é comumente dividido como infravermelho próximo (0,75–1,4 μm), infravermelho de comprimento de onda curto (1,4–3 μm), infravermelho de comprimento de onda médio (3–8 μm), infravermelho de comprimento de onda longo (8 –15 μm) e infravermelho distante (15–1000 μm).

Luz visível

Fontes naturais produzem radiação EM em todo o espectro. A radiação EM com um comprimento de onda entre aproximadamente 400 nm e 700 nm é detectada diretamente pelo olho humano e percebida como luz visível. Outros comprimentos de onda, especialmente infravermelho próximo (maior que 700 nm) e ultravioleta (menor que 400 nm) também são às vezes chamados de luz.

À medida que a frequência aumenta na faixa visível, os fótons têm energia suficiente para alterar a estrutura de ligação de algumas moléculas individuais. Não é por acaso que isso acontece na faixa do visível, pois o mecanismo da visão envolve a mudança na ligação de uma única molécula, o retinal, que absorve um único fóton. A mudança no retinal provoca uma mudança na forma da proteína rodopsina em que está contido, que inicia o processo bioquímico que faz com que a retina do olho humano sinta a luz.

A fotossíntese também se torna possível nesta faixa, pelo mesmo motivo. Uma única molécula de clorofila é excitada por um único fóton. Nos tecidos vegetais que conduzem a fotossíntese, os carotenóides agem para extinguir a clorofila excitada eletronicamente produzida pela luz visível em um processo chamado extinção não fotoquímica, para evitar reações que, de outra forma, interfeririam na fotossíntese em altos níveis de luz.

Os animais detetores de infravermelhos utilizam pequenos pacotes de água que mudam de temperatura, num processo essencialmente térmico que envolve muitos fotões.

Infravermelho, micro-ondas e ondas de rádio são conhecidos por danificar moléculas e tecidos biológicos apenas por aquecimento em massa, não por excitação de fótons individuais da radiação.

A luz visível é capaz de afetar apenas uma pequena porcentagem de todas as moléculas. Geralmente não de forma permanente ou prejudicial, mas o fóton excita um elétron que então emite outro fóton ao retornar à sua posição original. Esta é a fonte de cor produzida pela maioria dos corantes. A retina é uma exceção. Quando um fóton é absorvido, o retinal muda permanentemente a estrutura de cis para trans e requer uma proteína para convertê-lo de volta, ou seja, redefini-lo para poder funcionar como um detector de luz novamente.

Evidências limitadas indicam que algumas espécies reativas de oxigênio são criadas pela luz visível na pele e que podem ter algum papel no fotoenvelhecimento, da mesma forma que o ultravioleta A.

Ultravioleta

À medida que a frequência aumenta no ultravioleta, os fótons agora carregam energia suficiente (cerca de três elétron-volts ou mais) para excitar certas moléculas duplamente ligadas em um rearranjo químico permanente. No DNA, isso causa danos permanentes. O DNA também é indiretamente danificado por espécies reativas de oxigênio produzidas pelo ultravioleta A (UVA), que tem energia muito baixa para danificar o DNA diretamente. É por isso que o ultravioleta em todos os comprimentos de onda pode danificar o DNA e é capaz de causar câncer e (para UVB) queimaduras na pele (queimaduras solares) que são muito piores do que seriam produzidas por simples efeitos de aquecimento (aumento de temperatura). Esta propriedade de causar dano molecular desproporcional aos efeitos de aquecimento é característica de todos os EMR com frequências na faixa de luz visível e acima. Essas propriedades de EMR de alta frequência são devidas a efeitos quânticos que danificam permanentemente materiais e tecidos no nível molecular.

Na extremidade superior da faixa ultravioleta, a energia dos fótons torna-se grande o suficiente para transmitir energia suficiente aos elétrons para fazer com que sejam liberados do átomo, em um processo chamado fotoionização. A energia necessária para isso é sempre maior que cerca de 10 elétron-volt (eV) correspondendo a comprimentos de onda menores que 124 nm (algumas fontes sugerem um corte mais realista de 33 eV, que é a energia necessária para ionizar a água). Esta extremidade superior do espectro ultravioleta com energias na faixa aproximada de ionização, às vezes é chamada de "UV extremo." O UV ionizante é fortemente filtrado pela atmosfera da Terra.

Raios X e raios gama

A radiação eletromagnética composta por fótons que carregam energia de ionização mínima, ou mais, (que inclui todo o espectro com comprimentos de onda mais curtos), é, portanto, denominada radiação ionizante. (Muitos outros tipos de radiação ionizante são feitos de partículas não-EM). A radiação ionizante do tipo eletromagnético se estende do ultravioleta extremo a todas as frequências mais altas e comprimentos de onda mais curtos, o que significa que todos os raios X e raios gama se qualificam. Estes são capazes dos tipos mais graves de danos moleculares, que podem acontecer em biologia a qualquer tipo de biomolécula, incluindo mutação e câncer, e muitas vezes em grandes profundidades abaixo da pele, desde a extremidade superior do espectro de raios-X, e todos do espectro de raios gama, penetram na matéria.

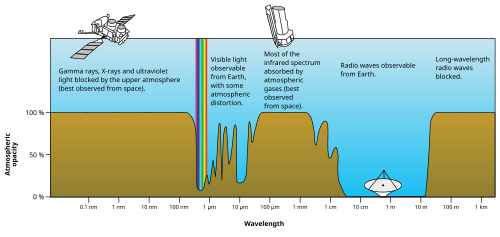
Atmosfera e magnetosfera

Terreno áspero de absorção e dispersão atmosférica da Terra (ou opacidade) de vários comprimentos de onda de radiação eletromagnética

A maioria dos raios UV e X são bloqueados pela absorção primeiro do nitrogênio molecular e depois (para comprimentos de onda no UV superior) da excitação eletrônica do dioxigênio e, finalmente, do ozônio na faixa intermediária do UV. Apenas 30% da luz ultravioleta do Sol atinge o solo e quase tudo isso é bem transmitido.

A luz visível é bem transmitida no ar, pois não é energética o suficiente para excitar nitrogênio, oxigênio ou ozônio, mas é muito energética para excitar frequências vibracionais moleculares de vapor d'água.

As bandas de absorção no infravermelho são devidas a modos de excitação vibracional no vapor d'água. No entanto, em energias muito baixas para excitar o vapor d'água, a atmosfera torna-se novamente transparente, permitindo a transmissão livre da maioria das ondas de rádio e microondas.

Finalmente, em comprimentos de onda de rádio maiores que 10 m ou mais (cerca de 30 MHz), o ar na baixa atmosfera permanece transparente ao rádio, mas o plasma em certas camadas da ionosfera começa a interagir com as ondas de rádio (consulte skywave). Essa propriedade permite que alguns comprimentos de onda mais longos (100 m ou 3 MHz) sejam refletidos e resultem em rádio de ondas curtas além da linha de visão. No entanto, certos efeitos ionosféricos começam a bloquear as ondas de rádio recebidas do espaço, quando sua frequência é inferior a cerca de 10 MHz (comprimento de onda superior a cerca de 30 m).

Radiação térmica e eletromagnética como forma de calor

A estrutura básica da matéria envolve partículas carregadas unidas. Quando a radiação eletromagnética incide sobre a matéria, ela faz com que as partículas carregadas oscilem e ganhem energia. O destino final dessa energia depende do contexto. Pode ser imediatamente irradiado novamente e aparecer como radiação espalhada, refletida ou transmitida. Ela pode se dissipar em outros movimentos microscópicos dentro da matéria, chegando ao equilíbrio térmico e se manifestando como energia térmica, ou mesmo energia cinética, no material. Com algumas exceções relacionadas a fótons de alta energia (como fluorescência, geração harmônica, reações fotoquímicas, efeito fotovoltaico para radiações ionizantes no ultravioleta distante, raios X e radiação gama), a radiação eletromagnética absorvida simplesmente deposita sua energia aquecendo o material. Isso acontece para infravermelho, microondas e radiação de ondas de rádio. Ondas de rádio intensas podem queimar termicamente tecidos vivos e cozinhar alimentos. Além dos lasers infravermelhos, lasers visíveis e ultravioleta suficientemente intensos podem facilmente incendiar o papel.

A radiação ionizante cria elétrons de alta velocidade em um material e quebra as ligações químicas, mas depois que esses elétrons colidem muitas vezes com outros átomos, a maior parte da energia se torna energia térmica em uma pequena fração de segundo. Este processo torna a radiação ionizante muito mais perigosa por unidade de energia do que a radiação não ionizante. Esta ressalva também se aplica ao UV, embora quase todo ele não seja ionizante, porque o UV pode danificar as moléculas devido à excitação eletrônica, que é muito maior por unidade de energia do que os efeitos do aquecimento.

A radiação infravermelha na distribuição espectral de um corpo negro é normalmente considerada uma forma de calor, uma vez que tem uma temperatura equivalente e está associada a uma variação de entropia por unidade de energia térmica. No entanto, "calor" é um termo técnico em física e termodinâmica e muitas vezes é confundido com energia térmica. Qualquer tipo de energia eletromagnética pode ser transformada em energia térmica em interação com a matéria. Assim, qualquer radiação eletromagnética pode "aquecer" (no sentido de aumentar a temperatura da energia térmica de) um material, quando ele é absorvido.

O processo de absorção inverso ou reverso no tempo é a radiação térmica. Grande parte da energia térmica na matéria consiste no movimento aleatório de partículas carregadas, e essa energia pode ser irradiada para longe da matéria. A radiação resultante pode posteriormente ser absorvida por outro pedaço de matéria, com a energia depositada aquecendo o material.

A radiação eletromagnética em uma cavidade opaca em equilíbrio térmico é efetivamente uma forma de energia térmica, tendo entropia de radiação máxima.

Efeitos biológicos

Bioeletromagnética é o estudo das interações e efeitos da radiação EM em organismos vivos. Os efeitos da radiação eletromagnética sobre as células vivas, incluindo as dos humanos, dependem da potência e frequência da radiação. Para radiação de baixa frequência (ondas de rádio à luz visível), os efeitos mais bem compreendidos são aqueles devidos apenas à potência da radiação, agindo por aquecimento quando a radiação é absorvida. Para esses efeitos térmicos, a frequência é importante, pois afeta a intensidade da radiação e a penetração no organismo (por exemplo, as micro-ondas penetram melhor que o infravermelho). É amplamente aceito que os campos de baixa frequência que são muito fracos para causar aquecimento significativo não podem ter nenhum efeito biológico.

Apesar dos resultados comumente aceitos, algumas pesquisas foram realizadas para mostrar que campos eletromagnéticos não térmicos mais fracos (incluindo campos magnéticos ELF fracos, embora o último não se qualifique estritamente como radiação EM) e modulados Os campos de RF e microondas têm efeitos biológicos. Os mecanismos fundamentais da interação entre material biológico e campos eletromagnéticos em níveis não térmicos não são totalmente compreendidos.

A Organização Mundial da Saúde classificou a radiação eletromagnética de radiofrequência como Grupo 2B – possivelmente cancerígena. Este grupo contém possíveis agentes cancerígenos, como chumbo, DDT e estireno. Por exemplo, estudos epidemiológicos que procuram uma relação entre o uso do telefone celular e o desenvolvimento de câncer no cérebro têm sido bastante inconclusivos, exceto para demonstrar que o efeito, se existir, não pode ser grande.

Em frequências mais altas (visíveis e além), os efeitos dos fótons individuais começam a se tornar importantes, pois agora eles têm energia suficiente individualmente para danificar direta ou indiretamente as moléculas biológicas. Todas as frequências UV foram classificadas como cancerígenas do Grupo 1 pela Organização Mundial de Saúde. A radiação ultravioleta da exposição ao sol é a principal causa de câncer de pele.

Assim, em frequências UV e superiores (e provavelmente um pouco também na faixa visível), a radiação eletromagnética causa mais danos aos sistemas biológicos do que o simples aquecimento prevê. Isso é mais óbvio no "distante" (ou "extremo") ultravioleta. UV, com raios X e radiação gama, são referidos como radiação ionizante devido à capacidade dos fótons dessa radiação de produzir íons e radicais livres em materiais (incluindo tecidos vivos). Como essa radiação pode danificar gravemente a vida em níveis de energia que produzem pouco aquecimento, ela é considerada muito mais perigosa (em termos de dano produzido por unidade de energia ou potência) do que o restante do espectro eletromagnético.

Usar como arma

O raio de calor é uma aplicação de EMR que faz uso de frequências de micro-ondas para criar um efeito de aquecimento desagradável na camada superior da pele. Uma arma de raios de calor conhecida publicamente chamada Active Denial System foi desenvolvida pelos militares dos EUA como uma arma experimental para impedir o acesso do inimigo a uma área. Um raio da morte é uma arma teórica que fornece raios de calor com base na energia eletromagnética em níveis capazes de ferir o tecido humano. Um inventor de um raio da morte, Harry Grindell Matthews, afirmou ter perdido a visão do olho esquerdo enquanto trabalhava em sua arma de raio da morte baseada em um magnetron de micro-ondas da década de 1920 (um forno de micro-ondas normal cria um efeito de cozimento prejudicial ao tecido dentro do forno em cerca de 2 kV/m).

Derivação da teoria eletromagnética

As ondas eletromagnéticas são previstas pelas leis clássicas da eletricidade e do magnetismo, conhecidas como equações de Maxwell. Existem soluções não triviais das equações homogêneas de Maxwell (sem cargas ou correntes), descrevendo ondas de campos elétricos e magnéticos variáveis. Começando com as equações de Maxwell no espaço livre:

? ? )) E= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0{displaystyle nabla cdot mathbf Não.

(1)

? ? × × E= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. ∂ ∂ B∂ ∂ ){displaystyle nabla times mathbf {E} =-{frac {partial mathbf (B) * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *

(2)

? ? )) B= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0{displaystyle nabla cdot mathbf Não.

(3)

? ? × × B= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =μ μ 0ε ε 0∂ ∂ E∂ ∂ ){displaystyle nabla times mathbf - Não. _{0}varepsilon _{0}{frac {displaystyle mathbf] Não, não.

(4)

onde

• E- Sim. e B- Sim. são o campo elétrico (medido em V/m ou N/C) e o campo magnético (medido em T ou Wb/m²), respectivamente;
• ? ? )) X{displaystyle nabla cdot mathbf Não. produz a divergência e ? ? × × X{displaystyle nabla times mathbf Não. o cacho de um campo vetorial X;{displaystyle mathbf {X};}
• ∂ ∂ B∂ ∂ ){displaystyle {displaystyle mathbf] (B) * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * e ∂ ∂ E∂ ∂ ){displaystyle {displaystyle mathbf] Não, não. são derivados parciais (taxa de mudança no tempo, com localização fixa) do campo magnético e elétrico;
• μ μ 0{displaystyle mu _{0}} é a permeabilidade de um vácuo (4D × 10^-7 (H/m) e ε ε 0{displaystyle varepsilon _{0}} é a permissão de um vácuo (8,85×10^-12. (F/m));

Além da solução trivial

E= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =B= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0,{displaystyle mathbf] {E} =mathbf {B} =mathbf {0}}

A(A)

? ? × × (? ? × × A)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =? ? (? ? )) A)- Sim. - Sim. ? ? 2A.{displaystyle nabla times left(nabla times mathbf {A} right)=nabla left(nabla cdot mathbf {A} right)-nabla ^{2}mathbf {A}.}

Tomando o rotacional da segunda equação de Maxwell (2) resulta:

? ? × × (? ? × × E)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =? ? × × (- Sim. - Sim. ∂ ∂ B∂ ∂ )){displaystyle nabla times left(nabla times mathbf {E} right)=nabla times left(-{frac {partial mathbf {B} }{partial t}}right)}

(5)

Avaliando o lado esquerdo de (5) com a identidade acima e simplificando usando (1), resulta:

? ? × × (? ? × × E)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =? ? (? ? )) E)- Sim. - Sim. ? ? 2E= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. ? ? 2E.{displaystyle nabla times left(nabla times mathbf {E} right)=nabla left(nabla cdot mathbf {E} right)-nabla ^{2}mathbf {E} =-nabla ^{2}mathbf Não.

(6)

Avaliando o lado direito de (5) trocando a sequência de derivações e inserindo a quarta equação de Maxwell (4), produz:

? ? × × (- Sim. - Sim. ∂ ∂ B∂ ∂ ))= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. ∂ ∂ ∂ ∂ )(? ? × × B)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. μ μ 0ε ε 0∂ ∂ 2E∂ ∂ )2{displaystyle nabla times left(-{frac {partial mathbf {B} }{partial t}}right)=-{frac {partial }{partial t}}left(nabla times mathbf {B} right)=-mu _{0}varepsilon _{0}{frac {partial ^{2}mathbf {E} }{partial t^{2}}}}}}

(7)

Combinar (6) e (7) novamente, fornece uma equação diferencial de valor vetorial para o campo elétrico, resolvendo as equações homogêneas de Maxwell:

Tomar o rotacional da quarta equação de Maxwell (4) resulta em uma equação diferencial semelhante para um campo magnético resolvendo as equações homogêneas de Maxwell:

Ambas as equações diferenciais têm a forma da equação de onda geral para as ondas que se propagam com velocidade c0,Não. Onde? fNão. é uma função de tempo e localização, que dá a amplitude da onda em algum momento em um determinado local:

? ? 2f= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1c02∂ ∂ 2f∂ ∂ )2{displaystyle nabla ^{2}f={frac {1}{c_{0}}^{2}}}{frac {partial ^{2}f}{partial t^{2}}}}}}

◻ ◻ f= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0{displaystyle Box f=0}

◻ ◻ - Sim.

◻ ◻ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =? ? 2- Sim. - Sim. 1c02∂ ∂ 2∂ ∂ )2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∂ ∂ 2∂ ∂ x2+∂ ∂ 2∂ ∂ Sim.2+∂ ∂ 2∂ ∂ zangão.2- Sim. - Sim. 1c02∂ ∂ 2∂ ∂ )2Não. Box =nabla ^{2}-{frac {1}{c_{0}}^{2}}}{frac {partial ^{2}}{partial t^{2}}}={frac {partial ^{2}}{partial x^{2}}}+{frac {partial ^{2}}{partial y^{2}}}+{frac {partial ^{2}}{partial z^{2}}}-{frac {1}{c_{0}}^{2}}}{frac {partial ^{2}}{partial t^{2}}} }

Comparando os termos para a velocidade de propagação, resulta no caso dos campos elétrico e magnético:

c0= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1μ μ 0ε ε 0.Não. ? - Não. _{0}varepsilon _{0}}}

Esta é a velocidade da luz no vácuo. Assim, as equações de Maxwell conectam a permissão de vácuo ε ε 0{displaystyle varepsilon _{0}}, a permeabilidade do vácuo μ μ 0{displaystyle mu _{0}}e a velocidade da luz, c₀, através da equação acima. Esta relação foi descoberta por Wilhelm Eduard Weber e Rudolf Kohlrausch antes do desenvolvimento da eletrodinâmica de Maxwell, no entanto Maxwell foi o primeiro a produzir uma teoria de campo consistente com ondas que viajam à velocidade da luz.

Estas são apenas duas equações versus as quatro originais, então mais informações pertencem a essas ondas escondidas nas equações de Maxwell. Uma onda vetorial genérica para o campo elétrico tem a forma

E= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =E0f(k^ ^ )) x- Sim. - Sim. c0)){displaystyle mathbf {E} =mathbf {E} _{0}f{left({hat {mathbf {k} }}cdot mathbf {x} -c_{0}tright)}}

Toma. E0{displaystyle mathbf {E} _{0}} é a amplitude constante, fNão. é qualquer segunda função diferencial, k^ ^ Não.) é um vetor unitário na direção da propagação, e x{displaystyle {mathbf {x} }} é um vetor de posição. f(k^ ^ )) x- Sim. - Sim. c0)){displaystyle f{left({hat {mathbf {k} }}cdot mathbf {x} -c_{0}tright)}} é uma solução genérica para a equação de onda. Em outras palavras,

? ? 2f(k^ ^ )) x- Sim. - Sim. c0))= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1c02∂ ∂ 2∂ ∂ )2f(k^ ^ )) x- Sim. - Sim. c0)),{displaystyle nabla ^{2}f{left({hat {mathbf {k} }}cdot mathbf {x} -c_{0}tright)}={frac {1}{c_{0}}^{2}}}{frac {partial ^{2}}{partial t^{2}}}f{left({hat {mathbf {k} }}cdot mathbf {x} -c_{0}tright)},}

k^ ^ Não.)

Da primeira das equações de Maxwell, obtemos

? ? )) E= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =k^ ^ )) E0f?(k^ ^ )) x- Sim. - Sim. c0))= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0{displaystyle nabla cdot mathbf {E} ={hat {mathbf {k} cdot mathbf {E} _{0}f'{left({hat {mathbf {k} }}cdot mathbf {x} -c_{0}tright)}=0}

Assim,

E)) k^ ^ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0{displaystyle mathbf {E} cdot {hat {mathbf {k}}} - Sim.

? ? × × E= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =k^ ^ × × E0f?(k^ ^ )) x- Sim. - Sim. c0))= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. ∂ ∂ B∂ ∂ ){displaystyle nabla times mathbf {E} ={hat {mathbf {k} }}times mathbf {E} _{0}f'{left({hat {mathbf {k} }}cdot mathbf {x} -c_{0}tright)}=-{frac {partial mathbf] (B) * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *

Assim,

B= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1c0k^ ^ × × E{displaystyle mathbf] Não. {1}{c_{0}}} }}times mathbf Não.

As equações restantes serão satisfeitas por esta escolha de E,B{displaystyle mathbf {E}mathbf} Não..

As ondas de campo elétricas e magnéticas no campo distante viajam à velocidade da luz. Eles têm uma orientação restrita especial e magnitudes proporcionais, E0= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =c0B0Não. E_{0}=c_{0}B_{0}}, que pode ser visto imediatamente do vetor Poynting. O campo elétrico, campo magnético e direção da propagação de ondas são todos ortogonais, e a onda se propaga na mesma direção que E× × B{displaystyle mathbf {E} times mathbf Não.. Também, E e B campos distantes no espaço livre, que como soluções de onda dependem principalmente dessas duas equações Maxwell, são infase uns com os outros. Isso é garantido, uma vez que a solução de onda genérica é a primeira ordem no espaço e no tempo, e o operador curl de um lado dessas equações resulta em derivados espaciais de primeira ordem da solução de onda, enquanto o tempo derivado do outro lado das equações, que dá o outro campo, é a primeira ordem no tempo, resultando na mesma fase de deslocamento para ambos os campos em cada operação matemática.

Do ponto de vista de uma onda eletromagnética se propagando, o campo elétrico pode estar oscilando para cima e para baixo, enquanto o campo magnético oscila para a direita e para a esquerda. Esta imagem pode ser girada com o campo elétrico oscilando para a direita e para a esquerda e o campo magnético oscilando para baixo e para cima. Esta é uma solução diferente que está viajando na mesma direção. Essa arbitrariedade na orientação em relação à direção de propagação é conhecida como polarização. Em um nível quântico, é descrito como polarização de fótons. A direção da polarização é definida como a direção do campo elétrico.

Formas mais gerais das equações de onda de segunda ordem dadas acima estão disponíveis, permitindo meios e fontes de propagação sem vácuo. Existem muitas derivações concorrentes, todas com níveis variados de aproximação e aplicações pretendidas. Um exemplo muito geral é uma forma da equação do campo elétrico, que foi fatorada em um par de equações de onda explicitamente direcionais e, então, eficientemente reduzida a uma única equação de onda unidirecional por meio de uma aproximação simples de evolução lenta.