Quadro de referência inercial

Na física clássica e na relatividade restrita, um referencial inercial (também chamado de referencial inercial, referencial inercial, referencial inercial espaço, ou referencial galileu) é um referencial que não sofre nenhuma aceleração. É um referencial no qual um objeto físico isolado – um objeto com força líquida nula atuando sobre ele – é percebido como movendo-se com uma velocidade constante (pode ser uma velocidade zero) ou, equivalentemente, é um referencial no qual Newton& #39;a primeira lei do movimento é válida. Todos os referenciais inerciais estão em um estado de movimento constante e retilíneo um em relação ao outro; em outras palavras, um acelerômetro se movendo com qualquer um deles detectaria aceleração zero.

Foi observado que objetos celestes que estão distantes de outros objetos e que estão em movimento uniforme em relação à radiação cósmica de fundo em micro-ondas mantêm esse movimento uniforme.

As medições em um referencial inercial podem ser convertidas em medições em outro por uma transformação simples, a transformação de Galileu na física newtoniana e a transformação de Lorentz na relatividade restrita.

Na mecânica analítica, um referencial inercial pode ser definido como um referencial que descreve o tempo e o espaço de maneira homogênea, isotropica e independente do tempo.

Na relatividade geral

• em qualquer região pequena o suficiente para a curvatura das forças espaciais e marés ser negligenciável, pode-se encontrar um conjunto de quadros inerciais que descrevem aproximadamente essa região.
• a física de um sistema pode ser descrita em termos de um quadro inercial sem causas externas ao respectivo sistema, com exceção de um efeito aparente devido às chamadas massas distantes.

Em um referencial não inercial, visto de uma perspectiva da física clássica e da relatividade especial, as interações entre os constituintes fundamentais do universo observável (a física de um sistema) variam dependendo da aceleração desse referencial em relação a um referencial inercial. Visto a partir desta perspectiva e devido ao fenômeno da inércia, o 'usual' as forças físicas entre dois corpos devem ser suplementadas por forças inerciais aparentemente sem fonte. Visto de uma perspectiva da teoria da relatividade geral, as forças inerciais aparentes (as causas externas suplementares) são atribuídas ao movimento geodésico no espaço-tempo.

Na física clássica, por exemplo, uma bola lançada em direção ao solo não se move exatamente para baixo porque a Terra está girando. Isso significa que o referencial de um observador na Terra não é inercial. Como consequência, a ciência da física tem que levar em conta o efeito de Coriolis – uma força aparente – para prever o respectivo pequeno movimento horizontal. Outro exemplo de uma força aparente que aparece em referenciais rotativos diz respeito ao efeito centrífugo, a força centrífuga.

Um conjunto de quadros onde as leis da física são simples

O movimento de um corpo só pode ser descrito em relação a outra coisa - outros corpos, observadores ou um conjunto de coordenadas do espaço-tempo. Estes são chamados de quadros de referência. Se as coordenadas forem mal escolhidas, as leis do movimento podem parecer mais complexas do que o necessário. Por exemplo, suponha que um corpo livre que não tem forças externas atuando sobre ele esteja em repouso em algum instante. Em muitos sistemas de coordenadas, ele começaria a se mover no instante seguinte, mesmo que não houvesse forças sobre ele. No entanto, sempre pode ser escolhido um referencial no qual ele permaneça estacionário. Da mesma forma, se o espaço não for descrito uniformemente ou o tempo independentemente, um sistema de coordenadas poderia descrever o simples voo de um corpo livre no espaço como um zigue-zague complicado em seu sistema de coordenadas. De fato, um resumo intuitivo dos referenciais inerciais pode ser dado: em um referencial inercial, as leis da mecânica assumem sua forma mais simples.

De acordo com o primeiro postulado da relatividade especial, todas as leis físicas assumem sua forma mais simples em um referencial inercial, e existem vários referenciais inerciais inter-relacionados por tradução uniforme:

Princípio especial da relatividade: Se um sistema de coordenadas K é escolhido para que, em relação a ele, as leis físicas se mantenham boas em sua forma mais simples, as mesmas leis têm bom em relação a qualquer outro sistema de coordenadas K' movendo-se em tradução uniforme relativamente a K.

—Albert Einstein: A fundação da teoria geral da relatividadeSecção A, §1

Essa simplicidade se manifesta no fato de que os referenciais inerciais têm física autocontida sem a necessidade de causas externas, enquanto a física em retratos não inerciais possui causas externas. O princípio da simplicidade pode ser usado na física newtoniana, bem como na relatividade restrita; veja Nagel e também Blagojević.

As leis da mecânica newtoniana nem sempre possuem em sua forma mais simples... Se, por exemplo, um observador é colocado em um disco girando em relação à terra, ele / ela vai sentir uma "força" empurrando-o para a periferia do disco, que não é causada por qualquer interação com outros corpos. Aqui, a aceleração não é a consequência da força habitual, mas da chamada força inercial. As leis de Newton possuem em sua forma mais simples apenas em uma família de quadros de referência, chamados quadros inerciais. Este fato representa a essência do princípio da relatividade da Galiléia:
As leis da mecânica têm a mesma forma em todos os quadros inerciais.

—Milutin Blagojević: Symmetries de gravidade e calibre, p. 4

Em termos práticos, a equivalência de referenciais inerciais significa que os cientistas dentro de uma caixa movendo-se uniformemente não podem determinar sua velocidade absoluta por nenhum experimento. Caso contrário, as diferenças estabeleceriam um quadro de referência padrão absoluto. De acordo com esta definição, complementada com a constância da velocidade da luz, os referenciais inerciais se transformam entre si segundo o grupo de transformações de simetria de Poincaré, do qual as transformações de Lorentz são um subgrupo. Na mecânica newtoniana, que pode ser vista como um caso limite da relatividade especial em que a velocidade da luz é infinita, os referenciais inerciais são relacionados pelo grupo galileano de simetrias.

Referencial inercial de Newton

Espaço absoluto

Newton postulou um espaço absoluto considerado bem aproximado por um referencial estacionário em relação às estrelas fixas. Um referencial inercial era então um em translação uniforme em relação ao espaço absoluto. No entanto, alguns cientistas (chamados de "relativistas" por Mach), ainda na época de Newton, achavam que o espaço absoluto era um defeito da formulação e deveria ser substituído.

De fato, a expressão referencial inercial (alemão: sistema inercial) foi cunhada por Ludwig Lange em 1885, para substituir a de Newton definições de "espaço e tempo absolutos" por uma definição mais operacional. Conforme traduzido por Iro, Lange propôs a seguinte definição:

Um quadro de referência em que um ponto de massa jogado do mesmo ponto em três direções diferentes (não co-planares) segue caminhos rectilineares cada vez que é jogado, é chamado de quadro inercial.

Uma discussão sobre a proposta de Lange pode ser encontrada em Mach.

A inadequação da noção de "espaço absoluto" na mecânica newtoniana é explicado por Blagojević:

• A existência de espaço absoluto contradiz a lógica interna da mecânica clássica, uma vez que, de acordo com o princípio da relatividade galileia, nenhum dos quadros inerciais pode ser destacado.
• O espaço absoluto não explica forças inerciais, uma vez que estão relacionadas à aceleração em relação a qualquer um dos quadros inerciais.
• O espaço absoluto atua em objetos físicos induzindo sua resistência à aceleração, mas não pode ser acionado.

—Milutin Blagojević: Symmetries de gravidade e calibre, p. 5

A utilidade das definições operacionais foi levada muito além na teoria especial da relatividade. Alguns antecedentes históricos, incluindo a definição de Lange, são fornecidos por DiSalle, que diz em resumo:

A pergunta original, "relativa a que quadro de referência fazem as leis do movimento prendem?" revela-se falsamente colocada. Para as leis do movimento determinam essencialmente uma classe de quadros de referência, e (em princípio) um procedimento para construí-los.

—Robert DiSalle Espaço e Hora: Quadros Inerciais

Mecânica newtoniana

Teorias clássicas que usam a transformação galileia postulam a equivalência de todos os quadros de referência inerciais. Algumas teorias podem até postular a existência de um quadro privilegiado que fornece espaço absoluto e tempo absoluto. A transformação da Galileia transforma coordenadas de um quadro de referência inercial, S- Sim., para outro, S? ? {displaystyle mathbf {s} ^{prime }}, por adição simples ou subtração de coordenadas:

R? ? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R- Sim. - Sim. R0- Sim. - Sim. v){displaystyle mathbf {r} ^{prime }=mathbf {r}} - Sim. _{0}-mathbf {v} t}

)? ? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =)- Sim. - Sim. )0{displaystyle t^{prime }=t-t_{0}}

onde r₀ e t₀ representam mudanças na origem do espaço e do tempo, e v é a velocidade relativa dos dois referenciais inerciais. Nas transformações galileanas, o tempo t₂ − t₁ entre dois eventos é o mesmo para todos os referenciais e a distância entre dois eventos simultâneos (ou, equivalentemente, o comprimento de qualquer objeto, |r₂ − r₁|) também é o mesmo.

Figura 1: Dois quadros de referência movendo-se com velocidade relativa v→ → (v}}{}}}. Quadro S ' tem uma rotação arbitrária, mas fixa em relação ao quadro S. Eles são ambos quadros inerciais desde que um corpo não sujeito a forças parece mover-se em uma linha reta. Se esse movimento for visto em um quadro, ele também aparecerá dessa maneira no outro.

Dentro do reino da mecânica newtoniana, um referencial inercial, ou referencial inercial, é aquele em que a primeira lei do movimento de Newton é válida. No entanto, o princípio da relatividade especial generaliza a noção de referencial inercial para incluir todas as leis físicas, não apenas a primeira lei de Newton.

Newton via a primeira lei como válida em qualquer referencial que esteja em movimento uniforme em relação às estrelas fixas; isto é, nem girando nem acelerando em relação às estrelas. Hoje, a noção de "espaço absoluto" é abandonado, e um referencial inercial no campo da mecânica clássica é definido como:

Um quadro inercial de referência é aquele em que o movimento de uma partícula não sujeita a forças está em linha reta a velocidade constante.

Portanto, com relação a um referencial inercial, um objeto ou corpo acelera apenas quando uma força física é aplicada e (seguindo a primeira lei do movimento de Newton), na ausência de uma força resultante, um corpo em resto permanecerá em repouso e um corpo em movimento continuará a se mover uniformemente - isto é, em linha reta e com velocidade constante. Os referenciais inerciais newtonianos se transformam entre si de acordo com o grupo galileano de simetrias.

Se esta regra for interpretada como dizendo que o movimento em linha reta é uma indicação de força resultante zero, a regra não identifica referenciais inerciais porque o movimento em linha reta pode ser observado em uma variedade de referenciais. Se a regra for interpretada como definindo um referencial inercial, então devemos ser capazes de determinar quando a força líquida zero é aplicada. O problema foi resumido por Einstein:

A fraqueza do princípio da inércia reside nisso, que envolve um argumento em um círculo: uma massa se move sem aceleração se está suficientemente longe de outros corpos; sabemos que está suficientemente longe de outros corpos apenas pelo fato de que se move sem aceleração.

—Albert Einstein: O Significado da Relatividade, p. 58

Existem várias abordagens para esse problema. Uma abordagem é argumentar que todas as forças reais diminuem com a distância de suas fontes de uma maneira conhecida, portanto, precisamos apenas ter certeza de que um corpo está longe o suficiente de todas as fontes para garantir que nenhuma força esteja presente. Um possível problema com essa abordagem é a visão historicamente duradoura de que o universo distante pode afetar as coisas (princípio de Mach). Outra abordagem é identificar todas as fontes reais de forças reais e responsabilizá-las. Um possível problema com essa abordagem é que podemos perder algo ou explicar inadequadamente sua influência, talvez, novamente, devido ao princípio de Mach e uma compreensão incompleta do universo. Uma terceira abordagem é observar a maneira como as forças se transformam quando mudamos os referenciais. Forças fictícias, aquelas que surgem devido à aceleração de um referencial, desaparecem em referenciais inerciais, e possuem complicadas regras de transformação em casos gerais. Com base na universalidade da lei física e na solicitação de referenciais onde as leis são expressas de maneira mais simples, os referenciais inerciais se distinguem pela ausência de tais forças fictícias.

O próprio Newton enunciou um princípio da relatividade em um de seus corolários às leis do movimento:

Os movimentos de corpos incluídos em um determinado espaço são os mesmos entre si, se esse espaço está em repouso ou se move uniformemente para a frente em uma linha reta.

—Isaac Newton: Principia, Corollary V, p. 88 na tradução Andrew Motte

Este princípio difere do princípio especial de duas maneiras: primeiro, é restrito à mecânica e, segundo, não faz menção à simplicidade. Compartilha com o princípio especial a invariância da forma da descrição entre referenciais que se traduzem mutuamente. O papel das forças fictícias na classificação dos referenciais é abordado mais adiante.

Comentários

É importante observar algumas suposições feitas acima sobre os vários referenciais inerciais. Newton, por exemplo, empregou o tempo universal, conforme explicado no exemplo a seguir. Suponha que você possua dois relógios, que funcionam exatamente na mesma velocidade. Você os sincroniza para que ambos sejam exibidos exatamente ao mesmo tempo. Os dois relógios agora estão separados e um relógio está em um trem em movimento rápido, viajando em velocidade constante em direção ao outro. De acordo com Newton, esses dois relógios ainda funcionarão no mesmo ritmo e mostrarão a mesma hora. Newton diz que a taxa de tempo medida em um referencial deve ser a mesma que a taxa de tempo em outro. Ou seja, existe um "universal" o tempo e todos os outros tempos em todos os outros quadros de referência serão executados na mesma taxa que este tempo universal, independentemente de sua posição e velocidade. Este conceito de tempo e simultaneidade foi posteriormente generalizado por Einstein em sua teoria especial da relatividade (1905), onde desenvolveu transformações entre sistemas de referência inerciais com base na natureza universal das leis físicas e sua economia de expressão (transformações de Lorentz).

Os quadros de referência são especialmente importantes na relatividade especial, porque quando um quadro de referência está se movendo a uma fração significativa da velocidade da luz, o fluxo de tempo nesse quadro não se aplica necessariamente a outro quadro. A velocidade da luz é considerada a única constante verdadeira entre os quadros de referência em movimento.

A definição de referencial inercial também pode ser estendida além do espaço euclidiano tridimensional. Newton assumiu um espaço euclidiano, mas a relatividade geral usa uma geometria mais geral. Como um exemplo de por que isso é importante, considere a geometria de um elipsóide. Nesta geometria, um "livre" partícula é definida como uma em repouso ou viajando a velocidade constante em um caminho geodésico. Duas partículas livres podem começar no mesmo ponto da superfície, viajando com a mesma velocidade constante em diferentes direções. Após um período de tempo, as duas partículas colidem no lado oposto do elipsóide. Ambos "grátis" as partículas viajaram com uma velocidade constante, satisfazendo a definição de que nenhuma força estava agindo. Nenhuma aceleração ocorreu e, portanto, a primeira lei de Newton se manteve verdadeira. Isso significa que as partículas estavam em referenciais inerciais. Como nenhuma força estava agindo, foi a geometria da situação que fez com que as duas partículas se encontrassem novamente. De maneira semelhante, agora é comum descrever que existimos em uma geometria quadridimensional conhecida como espaço-tempo. Nesta imagem, a curvatura deste espaço 4D é responsável pela maneira como dois corpos com massa são atraídos juntos, mesmo que nenhuma força esteja atuando. Essa curvatura do espaço-tempo substitui a força conhecida como gravidade na mecânica newtoniana e na relatividade especial.

Relatividade especial

A teoria da relatividade especial de Einstein, como a mecânica newtoniana, postula a equivalência de todos os referenciais inerciais. No entanto, como a relatividade especial postula que a velocidade da luz no espaço livre é invariante, a transformação entre referenciais inerciais é a transformação de Lorentz, não a transformação galileana que é usada na mecânica newtoniana. A invariância da velocidade da luz leva a fenômenos contra-intuitivos, como a dilatação do tempo e a contração do comprimento, e a relatividade da simultaneidade, que foram extensivamente verificados experimentalmente. A transformação de Lorentz se reduz à transformação de Galileu quando a velocidade da luz se aproxima do infinito ou quando a velocidade relativa entre os quadros se aproxima de zero.

Quadros não inerciais

Aqui é considerada a relação entre referenciais observacionais inerciais e não inerciais. A diferença básica entre esses pórticos é a necessidade em pórticos não inerciais de forças fictícias, conforme descrito a seguir.

Relatividade geral

A relatividade geral é baseada no princípio da equivalência:

Não há observadores de experimentos que possam realizar para distinguir se uma aceleração surge por causa de uma força gravitacional ou porque seu quadro de referência está acelerando.

—Douglas C. Giancoli, Física para cientistas e engenheiros com física modernaP. 155.

Essa ideia foi introduzida no artigo de Einstein de 1907, "Princípio da Relatividade e Gravitação" e posteriormente desenvolvido em 1911. O suporte para este princípio é encontrado no experimento de Eötvös, que determina se a proporção de massa inercial para massa gravitacional é a mesma para todos os corpos, independentemente de tamanho ou composição. Até o momento, nenhuma diferença foi encontrada em algumas partes em 10¹¹. Para alguma discussão sobre as sutilezas do experimento de Eötvös, como a distribuição de massa local ao redor do local experimental (incluindo uma piada sobre a massa do próprio Eötvös), veja Franklin.

A teoria geral de Einstein modifica a distinção entre valores nominalmente "inerciais" e "não inercial" substituindo os efeitos "planos" da relatividade especial; Espaço de Minkowski com uma métrica que produz curvatura diferente de zero. Na relatividade geral, o princípio da inércia é substituído pelo princípio do movimento geodésico, segundo o qual os objetos se movem de maneira ditada pela curvatura do espaço-tempo. Como consequência desta curvatura, não é um dado na relatividade geral que os objetos inerciais que se movem a uma taxa particular um em relação ao outro continuarão a fazê-lo. Esse fenômeno de desvio geodésico significa que os referenciais inerciais não existem globalmente como na mecânica newtoniana e na relatividade restrita.

No entanto, a teoria geral se reduz à teoria especial sobre regiões suficientemente pequenas do espaço-tempo, onde os efeitos da curvatura se tornam menos importantes e os argumentos anteriores do referencial inercial podem voltar ao jogo. Consequentemente, a relatividade especial moderna é agora descrita às vezes apenas como uma "teoria local". "Local" pode abranger, por exemplo, toda a Via Láctea: O astrônomo Karl Schwarzschild observou o movimento de pares de estrelas orbitando uma à outra. Ele descobriu que as duas órbitas das estrelas de tal sistema estão em um plano, e o periélio das órbitas das duas estrelas permanece apontando na mesma direção em relação ao sistema solar. Schwarzschild apontou que isso foi visto invariavelmente: a direção do momento angular de todos os sistemas estelares duplos observados permanece fixa em relação à direção do momento angular do Sistema Solar. Essas observações permitiram que ele concluísse que os referenciais inerciais dentro da galáxia não giram um em relação ao outro e que o espaço da Via Láctea é aproximadamente galileu ou minkowskiano.

Retratos inerciais e rotação

Em um referencial inercial, a primeira lei de Newton, a lei da inércia, é satisfeita: qualquer movimento livre tem magnitude e direção constantes. A segunda lei de Newton para uma partícula assume a forma:

F= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =mum,{displaystyle mathbf {F} =mmathbf {a} }}

com F a força resultante (um vetor), m a massa de uma partícula e a a aceleração da partícula (também um vetor) que seria medido por um observador em repouso no quadro. A força F é a soma vetorial de todas as forças "reais" forças na partícula, como forças de contato, forças eletromagnéticas, gravitacionais e nucleares.

Em contraste, a segunda lei de Newton em um referencial rotativo (um referencial não inercial), girando a uma taxa angular Ω em torno de um eixo, assume a forma:

F?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =mum,{displaystyle mathbf {F}=mmathbf {a} }}

que parece o mesmo que em um referencial inercial, mas agora a força F′ é resultante não apenas de F, mas também de termos adicionais (o parágrafo seguinte a este equação apresenta os pontos principais sem matemática detalhada):

F?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =F- Sim. - Sim. 2mΩ Ω × × vB- Sim. - Sim. mΩ Ω × × (Ω Ω × × xB)- Sim. - Sim. mDΩ Ω D)× × xB,{displaystyle mathbf {F}=mathbf {F} -2mmathbf - Sim. _{B}-mmathbf {Omega } times (mathbf {Omega } times mathbf {x} _{B})-m{frac {dmathbf {Omega } }{dt}}times mathbf {x} _{B}}

onde a rotação angular do quadro é expressa pelo vetor Ω apontando na direção do eixo de rotação, e com magnitude igual à taxa angular de rotação Ω, o símbolo × denota o produto vetorial vetorial, o vetor x_B localiza o corpo e o vetor v _B é a velocidade do corpo de acordo com um observador em rotação (diferente da velocidade vista pelo observador inercial).

Os termos extras na força F′ são os termos "fictícios" forças para este pórtico, cujas causas são externas ao sistema do pórtico. O primeiro termo extra é a força de Coriolis, o segundo a força centrífuga e o terceiro a força de Euler. Todos esses termos têm as seguintes propriedades: eles desaparecem quando Ω = 0; ou seja, são zero para um referencial inercial (que, claro, não gira); eles assumem uma magnitude e direção diferentes em cada referencial rotativo, dependendo de seu valor particular de Ω; eles são onipresentes no referencial rotativo (afetam todas as partículas, independentemente das circunstâncias); e eles não têm nenhuma fonte aparente em fontes físicas identificáveis, em particular, matéria. Além disso, as forças fictícias não diminuem com a distância (ao contrário, por exemplo, das forças nucleares ou elétricas). Por exemplo, a força centrífuga que parece emanar do eixo de rotação em uma estrutura rotativa aumenta com a distância do eixo.

Todos os observadores concordam com as forças reais, F; apenas observadores não inerciais precisam de forças fictícias. As leis da física no referencial inercial são mais simples porque forças desnecessárias não estão presentes.

Na época de Newton, as estrelas fixas eram invocadas como um referencial, supostamente em repouso em relação ao espaço absoluto. Em referenciais que estavam em repouso em relação às estrelas fixas ou em translação uniforme em relação a essas estrelas, supunha-se que as leis do movimento de Newton eram válidas. Em contraste, em referenciais acelerando em relação às estrelas fixas, um caso importante sendo os referenciais girando em relação às estrelas fixas, as leis do movimento não se sustentam em sua forma mais simples, mas devem ser suplementadas pela adição de forças fictícias, por exemplo exemplo, a força de Coriolis e a força centrífuga. Dois experimentos foram planejados por Newton para demonstrar como essas forças poderiam ser descobertas, revelando assim a um observador que elas não estavam em um referencial inercial: o exemplo da tensão na corda que liga duas esferas girando em torno de seu centro de gravidade e o exemplo da curvatura da superfície da água em um balde rotativo. Em ambos os casos, a aplicação da segunda lei de Newton não funcionaria para o observador em rotação sem invocar as forças centrífuga e de Coriolis para explicar suas observações (tensão no caso das esferas; superfície parabólica da água no caso do balde em rotação).

Como sabemos agora, as estrelas fixas não são fixas. Aqueles que residem na Via Láctea giram com a galáxia, exibindo movimentos próprios. Aqueles que estão fora de nossa galáxia (como as nebulosas que antes eram confundidas com estrelas) também participam de seu próprio movimento, em parte devido à expansão do universo e em parte devido a velocidades peculiares. Por exemplo, a Galáxia de Andrômeda está em rota de colisão com a Via Láctea a uma velocidade de 117 km/s. O conceito de referenciais inerciais não está mais vinculado nem às estrelas fixas nem ao espaço absoluto. Em vez disso, a identificação de um referencial inercial é baseada na simplicidade das leis da física no referencial. John Stachel escreveu: uma vez que desistimos da existência de um referencial privilegiado (o referencial do éter), não havia razão para pararmos na relatividade dos referenciais inerciais. A resposta convencional a tais dúvidas era que as leis da natureza tomavam uma forma mais simples nos referenciais inerciais porque nesses referenciais não era necessário introduzir forças inerciais ao escrever a lei de Newton de movimento.

Na prática, embora não seja um requisito, usar um referencial baseado nas estrelas fixas como se fosse um referencial inercial introduz muito pouca discrepância. Por exemplo, a aceleração centrífuga da Terra por causa de sua rotação em torno do Sol é cerca de trinta milhões de vezes maior que a do Sol em torno do centro galáctico.

Para ilustrar ainda mais, considere a questão: "Nosso Universo gira?" Para responder, podemos tentar explicar a forma da Via Láctea usando as leis da física, embora outras observações possam ser mais definitivas; ou seja, fornecem maiores discrepâncias ou menos incerteza de medição, como a anisotropia da radiação de fundo de micro-ondas ou a nucleossíntese do Big Bang. A planicidade da Via Láctea depende de sua taxa de rotação em um referencial inercial. Se atribuirmos sua aparente taxa de rotação inteiramente à rotação em um referencial inercial, uma "planicidade" é previsto do que se supusermos que parte dessa rotação realmente se deve à rotação do universo e não deveria ser incluída na rotação da própria galáxia. Com base nas leis da física, um modelo é configurado em que um parâmetro é a taxa de rotação do Universo. Se as leis da física concordam com mais precisão com as observações em um modelo com rotação do que sem ela, tendemos a selecionar o valor de melhor ajuste para rotação, sujeito a todas as outras observações experimentais pertinentes. Se nenhum valor do parâmetro de rotação for bem-sucedido e a teoria não estiver dentro do erro observacional, uma modificação da lei física é considerada, por exemplo, a matéria escura é invocada para explicar a curva de rotação galáctica. Até agora, as observações mostram que qualquer rotação do universo é muito lenta, não mais rápida do que uma vez a cada 6×10¹³ anos (10⁻¹³ rad/ano), e persiste o debate sobre se há qualquer rotação. No entanto, se a rotação fosse encontrada, a interpretação das observações em um referencial ligado ao universo teria que ser corrigida para as forças fictícias inerentes a tal rotação na física clássica e na relatividade especial, ou interpretada como a curvatura do espaço-tempo e o movimento da matéria ao longo a geodésica na relatividade geral.

Quando os efeitos quânticos são importantes, há complicações conceituais adicionais que surgem nos quadros de referência quânticos.

Quadros preparados

Um quadro de referência acelerado é muitas vezes delineado como sendo o "preparado" quadro e todas as variáveis que dependem desse quadro são notadas com primos, por exemplo x′, y′, a′.

O vetor da origem de um referencial inercial até a origem de um referencial acelerado é comumente notado como R. Dado um ponto de interesse que existe em ambos os referenciais, o vetor da origem inercial até o ponto é chamado r, e o vetor da origem acelerada até o ponto é chamado r′. Da geometria da situação, obtemos

R= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R+R?.{displaystyle mathbf {r}} =mathbf {R} +mathbf {r} '

Tomando a primeira e a segunda derivada disso em relação ao tempo, obtemos

v= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =V+v?,(v) =mathbf {V} +mathbf {v} ',}

um= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =A+um?.{displaystyle mathbf {a} =mathbf {A} +mathbf {a} '

onde V e A são a velocidade e a aceleração do sistema acelerado em relação ao sistema inercial e v e a são a velocidade e a aceleração do ponto de interesse em relação ao referencial inercial.

Estas equações permitem transformações entre os dois sistemas de coordenadas; por exemplo, agora podemos escrever a segunda lei de Newton como

F= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =mum= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =mA+mum?.{displaystyle mathbf {F} =mmathbf {a} =mmathbf {A} +mmathbf {a} '

Quando há movimento acelerado devido a uma força sendo exercida, há manifestação de inércia. Se um carro elétrico projetado para recarregar seu sistema de baterias ao desacelerar for colocado em frenagem, as baterias serão recarregadas, ilustrando a força física de manifestação da inércia. No entanto, a manifestação da inércia não impede a aceleração (ou desaceleração), pois a manifestação da inércia ocorre em resposta à mudança na velocidade devido a uma força. Visto da perspectiva de um quadro de referência rotativo, a manifestação da inércia parece exercer uma força (seja na direção centrífuga ou na direção ortogonal ao movimento de um objeto, o efeito Coriolis).

Um tipo comum de quadro de referência acelerado é um quadro que está girando e transladando (um exemplo é um quadro de referência anexado a um CD que está sendo reproduzido enquanto o reprodutor é transportado). Esse arranjo leva à equação (consulte Força fictícia para uma derivação):

um= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =um?+ω ω :: × × R?+2ω ω × × v?+ω ω × × (ω ω × × R?)+A0,{displaystyle mathbf {a} =mathbf {a} '+{dot {boldsymbol {omega }}}times mathbf {r}+2{boldsymbol {omega }}times mathbf {v} '+{boldsymbol {omega }}times ({boldsymbol {omega }}times mathb}

ou, para calcular a aceleração no quadro acelerado,

um?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =um- Sim. - Sim. ω ω :: × × R?- Sim. - Sim. 2ω ω × × v?- Sim. - Sim. ω ω × × (ω ω × × R?)- Sim. - Sim. A0.{displaystyle mathbf {a}=mathbf {a}} -{dot {boldsymbol {omega }}}times mathbf {r} '-2{boldsymbol {omega }}times mathbf {v} '-{boldsymbol {omega }}times ({boldsymbol {omega }}times mathbf {r} ')-mathbf}

Multiplicando pela massa m dá

F?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =FphSim.SEu...cumEu...+FEuEu...eR?+FCoREu...oEu...Eu...S?+Fcen)REu...pe)umEu...?- Sim. - Sim. mA0,{displaystyle mathbf {F}=mathbf {F} _{mathrm {physical} }+mathbf {F}_{mathrm {Euler}+mathbf {F}_{mathrm {Coriolis} }+mathbf {F}_{mathrm {centripetal} }-mmathbf {A} _{0},}

onde

FEuEu...eR?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. mω ω :: × × R?{displaystyle mathbf {F}_{mathrm {Euler} }=-m{dot {boldsymbol {omega }}}times mathbf {r} '} (Força Euler),

FCoREu...oEu...Eu...S?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. 2mω ω × × v?{displaystyle mathbf {F}_{mathrm {Coriolis} }=-2m{boldsymbol - Sim. (Coriolis force),

Fcen)REu...fugumEu...?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. mω ω × × (ω ω × × R?)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =m(ω ω 2R?- Sim. - Sim. (ω ω )) R?)ω ω ){displaystyle mathbf {F}_{mathrm {centrifugal} }=-m{boldsymbol {omega }}times ({boldsymbol {omega }}times mathbf {r} ')=m(omega ^{2}mathbf {r} '-({boldsymbol {omega }}cdot mathbf {r} '){boldsymbol (força centrífuga).

Separando referenciais não inerciais de inerciais

Teoria

Figura 2: Duas esferas amarradas com uma corda e girando a uma taxa angular ω. Por causa da rotação, a corda amarrando as esferas em conjunto está sob tensão.

Figura 3: Visão explosiva de esferas rotativas em um quadro inercial de referência mostrando as forças centrípetas nas esferas fornecidas pela tensão na cadeia.

Os referenciais inerciais e não inerciais podem ser distinguidos pela ausência ou presença de forças fictícias, conforme explicado brevemente.

O efeito deste ser no quadro não inercial é exigir que o observador introduza uma força fictícia em seus cálculos....

—Sidney Borowitz e Lawrence A Bornstein em Uma visão contemporânea da física elementar, p. 138

A presença de forças fictícias indica que as leis físicas não são as leis mais simples disponíveis, portanto, em termos do princípio da relatividade especial, um referencial onde forças fictícias estão presentes não é um referencial inercial:

As equações de movimento em um sistema não inercial diferem das equações em um sistema inercial por termos adicionais chamados de forças inerciais. Isso nos permite detectar experimentalmente a natureza não inercial de um sistema.

—V. I. Arnol'd: Métodos Matemáticos de Mecânica Clássica Segunda edição, p. 129

Corpos em referenciais não inerciais estão sujeitos às chamadas forças fictícias (pseudo-forças); ou seja, forças que resultam da aceleração do próprio referencial e não de qualquer força física agindo sobre o corpo. Exemplos de forças fictícias são a força centrífuga e a força de Coriolis em referenciais rotativos.

Como então, são "fictícios" forças a serem separadas do "real" forças? É difícil aplicar a definição newtoniana de referencial inercial sem essa separação. Por exemplo, considere um objeto estacionário em um referencial inercial. Estando em repouso, nenhuma força resultante é aplicada. Mas em um referencial girando em torno de um eixo fixo, o objeto parece se mover em um círculo e está sujeito à força centrípeta (que é composta pela força de Coriolis e pela força centrífuga). Como podemos decidir que o referencial rotativo é um referencial não inercial? Existem duas abordagens para esta resolução: uma abordagem é procurar a origem das forças fictícias (a força de Coriolis e a força centrífuga). Descobriremos que não há fontes para essas forças, nem portadores de força associados, nem corpos originários. Uma segunda abordagem é olhar para uma variedade de quadros de referência. Para qualquer referencial inercial, a força de Coriolis e a força centrífuga desaparecem, portanto, a aplicação do princípio da relatividade especial identificaria esses referenciais onde as forças desaparecem como compartilhando as mesmas e mais simples leis físicas e, portanto, determinaria que o referencial rotativo não é um referencial inercial. quadro inercial.

O próprio Newton examinou esse problema usando esferas em rotação, conforme mostrado na Figura 2 e na Figura 3. Ele apontou que, se as esferas não estiverem girando, a tensão no barbante é medida como zero em todos os referenciais. Se as esferas apenas parecem girar (ou seja, estamos observando esferas estacionárias de um referencial giratório), a tensão zero na corda é explicada observando que a força centrípeta é fornecida pela combinação das forças centrífuga e de Coriolis, de modo que não tensão é necessária. Se as esferas realmente estiverem girando, a tensão observada é exatamente a força centrípeta exigida pelo movimento circular. Assim, a medição da tensão no fio identifica o referencial inercial: é aquele em que a tensão no fio fornece exatamente a força centrípeta exigida pelo movimento conforme observado naquele referencial, e não um valor diferente. Ou seja, o referencial inercial é aquele onde as forças fictícias desaparecem.

Tanto para forças fictícias devido à rotação. No entanto, para aceleração linear, Newton expressou a ideia de indetectabilidade de acelerações em linha reta mantidas em comum:

Se os corpos, como se moviam entre si, forem instados na direção de linhas paralelas por forças acelerativas iguais, continuarão a se mover entre si, da mesma forma como se não tivessem sido instados por tais forças.

—Isaac Newton: Principia Corollary VI, p. 89, em Andrew Motte Tradução

Este princípio generaliza a noção de referencial inercial. Por exemplo, um observador confinado em um elevador em queda livre afirmará que ele próprio é um referencial inercial válido, mesmo que esteja acelerando sob a gravidade, desde que não tenha conhecimento de nada fora do elevador. Portanto, estritamente falando, referencial inercial é um conceito relativo. Com isso em mente, podemos definir referenciais inerciais coletivamente como um conjunto de referenciais estacionários ou em movimento com velocidade constante entre si, de modo que um único referencial inercial é definido como um elemento desse conjunto.

Para que essas ideias sejam aplicadas, tudo o que é observado no quadro deve estar sujeito a uma linha de base, uma aceleração comum compartilhada pelo próprio quadro. Essa situação se aplicaria, por exemplo, ao exemplo do elevador, onde todos os objetos estão sujeitos à mesma aceleração gravitacional e o próprio elevador acelera na mesma taxa.

Aplicativos

Os sistemas de navegação inercial usavam um conjunto de giroscópios e acelerômetros para determinar as acelerações relativas ao espaço inercial. Depois que um giroscópio é girado em uma orientação particular no espaço inercial, a lei de conservação do momento angular exige que ele mantenha essa orientação enquanto nenhuma força externa for aplicada a ele. Três giroscópios ortogonais estabelecem um referencial inercial e os aceleradores medem a aceleração relativa a esse referencial. As acelerações, junto com um relógio, podem então ser usadas para calcular a mudança na posição. Assim, a navegação inercial é uma forma de cálculo morto que não requer entrada externa e, portanto, não pode ser bloqueada por nenhuma fonte de sinal externa ou interna.

Um giroscópio, empregado para navegação de embarcações marítimas, encontra o norte geométrico. Ele faz isso, não detectando o campo magnético da Terra, mas usando o espaço inercial como referência. O invólucro externo do dispositivo giroscópio é mantido de tal forma que permanece alinhado com o fio de prumo local. Quando a roda do giroscópio dentro do dispositivo giroscópio é girada, a maneira como a roda do giroscópio é suspensa faz com que a roda do giroscópio alinhe gradualmente seu eixo giratório com o eixo da Terra. O alinhamento com o eixo da Terra é a única direção para a qual o eixo giratório do giroscópio pode ser estacionário em relação à Terra e não ser obrigado a mudar de direção em relação ao espaço inercial. Depois de ser girado, um giroscópio pode atingir a direção de alinhamento com o eixo da Terra em menos de um quarto de hora.

Exemplos

Exemplo simples

Figura 1: Dois carros movendo-se em velocidades diferentes, mas constantes observadas a partir do quadro inercial estacionário S anexado à estrada e movendo quadro inercial S. ligado ao primeiro carro.

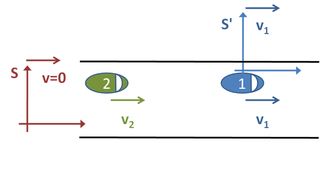
Considere uma situação comum na vida cotidiana. Dois carros viajam ao longo de uma estrada, ambos se movendo com velocidades constantes. Veja a Figura 1. Em algum momento particular, eles estão separados por 200 metros. O carro da frente está viajando a 22 metros por segundo e o carro de trás está viajando a 30 metros por segundo. Se quisermos descobrir quanto tempo o segundo carro levará para alcançar o primeiro, existem três "quadros de referência" que poderíamos escolher.

Primeiro, podíamos observar os dois carros do lado da estrada. Definimos o nosso "quadro de referência" S como segue. Ficamos no lado da estrada e começamos uma parada no momento exato que o segundo carro nos passa, o que acontece ser quando eles são uma distância D = 200 m separados. Como nenhum dos carros está acelerando, podemos determinar suas posições pelas seguintes fórmulas, onde x1())(t)} é a posição em metros de carro um após o tempo ) em segundos e x2())(t)} é a posição do carro dois após o tempo ).

x1())= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =D+v1)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =200+22),x2())= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =v2)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =30).(t)=d+v_{1}t=200+22t,quad x_{2}(t)=v_{2}t=30t.}

Observe que essas fórmulas prevêem em ) = 0 s o primeiro carro é 200 m abaixo da estrada e o segundo carro está ao nosso lado, como esperado. Queremos encontrar o momento em que x1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =x2Não. x_{1}=x_{2}}. Portanto, nós estabelecemos x1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =x2Não. x_{1}=x_{2}} e resolver para )Não.Isto é:

200+22)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =30),200+22t=30t,}

8)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =200,- Sim.

)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =25SeconDS.{displaystyle t=25 mathrm {seconds}.}

Alternativamente, poderíamos escolher um referencial S′ situado no primeiro vagão. Neste caso, o primeiro carro está parado e o segundo carro está se aproximando por trás com uma velocidade de v₂ − v ₁ = 8 m/s. Para alcançar o primeiro carro, levará um tempo de d /v₂ − v₁ = 200 /8 s, ou seja, 25 segundos, como antes. Observe como o problema se torna muito mais fácil ao escolher um referencial adequado. O terceiro quadro de referência possível seria anexado ao segundo carro. Esse exemplo lembra o caso que acabamos de discutir, exceto que o segundo carro está parado e o primeiro carro se move para trás em sua direção a 8 m/s.

Teria sido possível escolher um referencial em rotação e aceleração, movendo-se de maneira complicada, mas isso teria servido para complicar o problema desnecessariamente. Também é necessário observar que é possível converter medições feitas em um sistema de coordenadas para outro. Por exemplo, suponha que seu relógio esteja cinco minutos adiantado em comparação com o horário padrão local. Se você sabe que é esse o caso, quando alguém lhe pergunta que horas são, você pode deduzir cinco minutos da hora exibida em seu relógio para obter a hora correta. As medições que um observador faz sobre um sistema dependem, portanto, do referencial do observador (você pode dizer que o ônibus chegou às três e cinco, quando na verdade chegou às três).

Exemplo adicional

Figura 2: Exemplo de moldura de referência simples

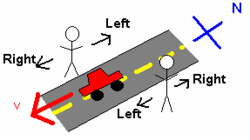
Para um exemplo simples envolvendo apenas a orientação de dois observadores, considere duas pessoas em pé, uma de frente para a outra, em ambos os lados de uma rua norte-sul. Veja a Figura 2. Um carro passa por eles em direção ao sul. Para a pessoa voltada para o leste, o carro estava se movendo para a direita. No entanto, para a pessoa voltada para o oeste, o carro estava se movendo para a esquerda. Essa discrepância ocorre porque as duas pessoas usaram dois quadros de referência diferentes para investigar esse sistema.

Para um exemplo mais complexo envolvendo observadores em movimento relativo, considere Alfred, que está parado na beira de uma estrada observando um carro passar por ele da esquerda para a direita. Em seu quadro de referência, Alfred define o local onde ele está como a origem, a estrada como o eixo x e a direção em frente ao ele como o eixo y positivo. Para ele, o carro se move ao longo do eixo x com alguma velocidade v na direção x positiva. O referencial de Alfred é considerado um referencial inercial porque ele não está acelerando (ignorando efeitos como a rotação e a gravidade da Terra).

Agora considere Betsy, a pessoa que dirige o carro. Betsy, ao escolher seu referencial, define sua localização como a origem, a direção à sua direita como o eixo x positivo e a direção na frente dela como o eixo y positivo. Nesse quadro de referência, é Betsy que está estacionária e o mundo ao seu redor que está se movendo – por exemplo, ao passar por Alfred, ela o observa se movendo com velocidade v na direção y negativa. Se ela estiver dirigindo para o norte, então o norte é a direção y positiva; se ela virar para o leste, o leste se torna a direção y positiva.

Finalmente, como exemplo de observadores não inerciais, suponha que Candace esteja acelerando seu carro. Quando ela passa por ele, Alfred mede sua aceleração e descobre que é a no negativo x -direção. Supondo que a aceleração de Candace seja constante, que aceleração Betsy mede? Se a velocidade de Betsy v for constante, ela está em um referencial inercial e descobrirá que a aceleração é a mesma que Alfred em seu quadro de referência, a no negativo y -direção. No entanto, se ela estiver acelerando a uma taxa A no negativo y-direção (em outras palavras, desacelerando), ela descobrirá que a aceleração de Candace é a′ = a − A na direção y negativa — um valor menor do que o medido por Alfred. Da mesma forma, se ela estiver acelerando na taxa A na direção y positiva (acelerando), ela observará Candace& #39;s aceleração como a′ = a + A no negativo y-direction—um valor maior que a medida de Alfred.