Relação entre duas quantidades cuja soma está na mesma proporção para a maior

Um retângulo dourado com lado longo
um e lado curto
b) (vermelho em forma, direito) e um quadrado com lados de comprimento
um (azul em forma, esquerda) combinar para formar um retângulo dourado semelhante com lado longo
a + b e lado curto
um. Isso ilustra a relação
um+b)um= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =umb))) φ φ .Não. - Não. (a) {b} - Não.
Em matemática, duas quantidades estão no rácio de ouro se a sua relação é a mesma que a relação de sua soma para maior das duas quantidades. Expressado algébrica, para quantidades umNão. e b)Não.
e b)Não. com b>0}" xmlns="http://www.w3.org/1998/Math/MathML">um>b)>0- Sim.
com b>0}" xmlns="http://www.w3.org/1998/Math/MathML">um>b)>0- Sim.![]() b > 0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/dc57e5721ebc7b851b968ea2545913848bf7a01e" style="vertical-align: -0.338ex; width:9.587ex; height:2.176ex;"/>,
b > 0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/dc57e5721ebc7b851b968ea2545913848bf7a01e" style="vertical-align: -0.338ex; width:9.587ex; height:2.176ex;"/>,
um+b)um= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =umb)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ Não. - Não. {a}{b}=varphi ?
onde a letra grega phi (φ φ - Sim. ou φ φ - Sim.
ou φ φ - Sim. ) denota a relação de ouro. A constante φ φ - Sim.
) denota a relação de ouro. A constante φ φ - Sim. satisfaz a equação quadrática φ φ 2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ +1{displaystyle varphi ^{2}=varphi +1
satisfaz a equação quadrática φ φ 2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ +1{displaystyle varphi ^{2}=varphi +1 e é um número irracional com um valor de
e é um número irracional com um valor de
φ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1+52= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = ={displaystyle varphi ={frac (em inglês) {5}}}{2}=} 1.618033988749...
1.618033988749... A proporção áurea foi chamada de proporção extrema e média por Euclides, e a proporção divina por Luca Pacioli, e também atende por vários outros nomes.
Os matemáticos estudaram as propriedades da relação dourada desde a antiguidade. É a proporção da diagonal de um pentágono regular ao seu lado e, portanto, aparece na construção do dodecaedro e icosaedro. Um retângulo dourado — isto é, um retângulo com uma relação de aspecto φ φ - Sim. — pode ser cortado em um quadrado e um retângulo menor com a mesma proporção. A proporção de ouro tem sido usada para analisar as proporções de objetos naturais e sistemas artificiais, como mercados financeiros, em alguns casos com base em dubious se encaixa aos dados. A proporção de ouro aparece em alguns padrões na natureza, incluindo o arranjo espiral de folhas e outras partes da vegetação.
— pode ser cortado em um quadrado e um retângulo menor com a mesma proporção. A proporção de ouro tem sido usada para analisar as proporções de objetos naturais e sistemas artificiais, como mercados financeiros, em alguns casos com base em dubious se encaixa aos dados. A proporção de ouro aparece em alguns padrões na natureza, incluindo o arranjo espiral de folhas e outras partes da vegetação.
Alguns artistas e arquitetos do século 20, incluindo Le Corbusier e Salvador Dalí, têm proporcionado suas obras para se aproximar da proporção áurea, acreditando ser esteticamente agradável. Esses usos geralmente aparecem na forma de um retângulo dourado.
Cálculo
Duas quantidades umNão. e b)Não.
e b)Não. estão no rácio de ouro φ φ - Sim.
estão no rácio de ouro φ φ - Sim. se
se
um+b)um= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =umb)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ .Não. - Não. {a}{b}}=varphi.}
Um método para encontrar φ φ - Sim. A forma fechada começa com a fração esquerda. Simplificando a fração e substituindo o recíproco b)/um= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1/φ φ Não. b/a=1/varphi }
A forma fechada começa com a fração esquerda. Simplificando a fração e substituindo o recíproco b)/um= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1/φ φ Não. b/a=1/varphi } ,
,
um+b)um= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =umum+b)um= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1+b)um= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1+1φ φ .Não. - Não. - Sim. Não. {b}{a}}=1+{frac {1}{varphi Sim.
Portanto,
1+1φ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ .{displaystyle 1+{frac {1}{varphi }}=varphi.}
Multiplicando-se φ φ - Sim. dá
dá
φ φ +1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ 2{displaystyle varphi +1=varphi ^{2}}
que pode ser reorganizado para
φ φ 2- Sim. - Sim. φ φ - Sim. - Sim. 1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0.{displaystyle {varphi }^{2}-varphi -1=0.
A fórmula quadrática produz duas soluções:
1+52= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1.618033...... (1+ {5}}}{2}}=1.618033dots }
e
1- Sim. - Sim. 52= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. 0,618033...... .Não. {5}}}{2}}=-0.618033dots.}
Porque... φ φ - Sim. é uma razão entre quantidades positivas, φ φ - Sim.
é uma razão entre quantidades positivas, φ φ - Sim. é necessariamente a raiz positiva. A raiz negativa é de fato o inverso negativo - Sim. - Sim. 1φ φ Não. - Sim.)
é necessariamente a raiz positiva. A raiz negativa é de fato o inverso negativo - Sim. - Sim. 1φ φ Não. - Sim.) , que compartilha muitas propriedades com a proporção de ouro.
, que compartilha muitas propriedades com a proporção de ouro.
História
Segundo Mário Livio,
Algumas das maiores mentes matemáticas de todas as idades, de Pitágoras e Euclides na Grécia antiga, através do matemático italiano medieval Leonardo de Pisa e do astrônomo renascentista Johannes Kepler, para figuras científicas atuais, como o físico de Oxford Roger Penrose, passaram horas infinitas sobre esta relação simples e suas propriedades.... Biólogos, artistas, músicos, historiadores, arquitetos, psicólogos e até mesmo místicos ponderaram e debateram a base de sua ubiquidade e apelo. Na verdade, provavelmente é justo dizer que o Golden Ratio inspirou pensadores de todas as disciplinas como nenhum outro número na história da matemática.
—The Golden Ratio: The Story of Phi, o maior número surpreendente do mundo
Os antigos matemáticos gregos estudaram pela primeira vez a proporção áurea por causa de sua frequente aparição na geometria; a divisão de uma linha em "razão extrema e média" (a seção áurea) é importante na geometria de pentagramas e pentágonos regulares. De acordo com uma história, o matemático Hippasus, do século V aC, descobriu que a proporção áurea não era nem um número inteiro nem uma fração (é irracional), surpreendendo os pitagóricos. Os Elementos de Euclides (c. 300 aC) fornecem várias proposições e suas provas empregando a proporção áurea e contém sua primeira definição conhecida que procede do seguinte modo:
Diz-se que uma linha reta foi cortada na relação extrema e média quando, como toda a linha é para o segmento maior, assim é o maior para o menor.

Michael Maestlin, o primeiro a escrever uma aproximação decimal da relação
A proporção áurea foi estudada perifericamente ao longo do próximo milênio. Abu Kamil (c. 850–930) o empregou em seus cálculos geométricos de pentágonos e decágonos; seus escritos influenciaram os de Fibonacci (Leonardo de Pisa) (c. 1170–1250), que usou a razão em problemas de geometria relacionados, mas não observou que ela estava conectada aos números de Fibonacci.
Luca Pacioli nomeou seu livro Divina proporcione (1509) após a proporção; o livro, em grande parte plagiado de Piero della Francesca, explorou suas propriedades, incluindo sua aparição em alguns dos sólidos platônicos. Leonardo da Vinci, que ilustrou o livro de Pacioli, chamou a razão de sectio aurea ('seção áurea'). Embora seja frequentemente dito que Pacioli defendeu a aplicação da proporção áurea para produzir proporções agradáveis e harmoniosas, Livio aponta que a interpretação foi atribuída a um erro em 1799 e que Pacioli realmente defendeu o sistema Vitruviano de proporções racionais. Pacioli também viu significado religioso católico na razão, o que levou ao título de sua obra. Matemáticos do século XVI, como Rafael Bombelli, resolveram problemas geométricos usando a razão.
O matemático alemão Simon Jacob (m. 1564) observou que os números de Fibonacci consecutivos convergem para a proporção de ouro; isso foi redescoberto por Johannes Kepler em 1608. A primeira aproximação decimal conhecida da relação de ouro (inverso) foi declarada como "sobre 0.6180340Não. " em 1597 por Michael Maestlin da Universidade de Tübingen em uma carta a Kepler, seu ex-aluno. No mesmo ano, Kepler escreveu a Maestlin do triângulo Kepler, que combina a relação dourada com o teorema de Pythagorean. Kepler disse sobre estes:
" em 1597 por Michael Maestlin da Universidade de Tübingen em uma carta a Kepler, seu ex-aluno. No mesmo ano, Kepler escreveu a Maestlin do triângulo Kepler, que combina a relação dourada com o teorema de Pythagorean. Kepler disse sobre estes:
Geometria tem dois grandes tesouros: um é o teorema de Pitágoras, o outro a divisão de uma linha em relação extrema e média. O primeiro que podemos comparar com uma massa de ouro, o segundo que podemos chamar uma jóia preciosa.
Os matemáticos do século XVIII Abraham de Moivre, Nicolaus I Bernoulli e Leonhard Euler usaram uma fórmula baseada na proporção áurea que encontra o valor de um número de Fibonacci com base em sua colocação na sequência; em 1843, isso foi redescoberto por Jacques Philippe Marie Binet, para quem foi chamado de "fórmula de Binet". Martin Ohm usou pela primeira vez o termo alemão goldener Schnitt ('seção áurea') para descrever a proporção em 1835. James Sully usou o termo inglês equivalente em 1875.
Em 1910, o inventor Mark Barr começou a usar a letra grega phi (φ φ - Sim. ) como um símbolo para a relação de ouro. Também foi representado por tau (? ? - Sim.
) como um símbolo para a relação de ouro. Também foi representado por tau (? ? - Sim. ), a primeira letra do grego antigo τομή ('cut' or 'section').
), a primeira letra do grego antigo τομή ('cut' or 'section').

Dan Shechtman demonstra quasicrystals no NIST em 1985 usando um modelo de Zometoy.
O sistema de construção zome, desenvolvido por Steve Baer no final dos anos 1960, é baseado no sistema de simetria do icosaedro/dodecaedro e usa a proporção áurea de forma onipresente. Entre 1973 e 1974, Roger Penrose desenvolveu o ladrilho Penrose, um padrão relacionado à proporção áurea tanto na proporção de áreas de seus dois ladrilhos rômbicos quanto em sua frequência relativa dentro do padrão. Isso ganhou interesse após a descoberta de quasicristais com simetria icosaédrica de Dan Shechtman, vencedor do Nobel de 1982, que logo depois foi explicado por meio de analogias com o ladrilho de Penrose.
Matemática
Irracionalidade
A proporção áurea é um número irracional. Abaixo estão duas pequenas provas de irracionalidade:
Contradição de uma expressão nos termos mais baixos

Se
φ eram racionais, então seria a proporção de lados de um retângulo com lados inteiros (o retângulo que compreende todo o diagrama). Mas também seria uma proporção de lados inteiros do retângulo menor (a parte mais direita do diagrama) obtida pela exclusão de um quadrado. A sequência de diminuição dos comprimentos laterais inteiros formados pela exclusão de quadrados não pode ser continuada indefinidamente porque os inteiros positivos têm um limite inferior, portanto
φ não pode ser racional.
Lembre-se que:
o todo é a parte mais longa mais a parte mais curta;
o todo é para a parte mais longa como a parte mais longa é para a parte mais curta.
Se ligarmos a todos nNão. e a parte mais longa m,- Sim.
e a parte mais longa m,- Sim. então a segunda declaração acima torna-se
então a segunda declaração acima torna-se
nNão.
a
mNão.
como
mNão.
a
n- Sim. - Sim. m.Não. Não.
Dizer que a relação de ouro φ φ - Sim. é racional significa que φ φ - Sim.
é racional significa que φ φ - Sim. é uma fração n/mNão. Não.
é uma fração n/mNão. Não. Onde? nNão.
Onde? nNão. e mNão.
e mNão. são inteiros. Podemos tomar n/mNão. Não.
são inteiros. Podemos tomar n/mNão. Não. ser em termos mais baixos e nNão.
ser em termos mais baixos e nNão. e mNão.
e mNão. para ser positivo. Mas se n/mNão. Não.
para ser positivo. Mas se n/mNão. Não. é em termos mais baixos, então o igualmente valorizado m/(n- Sim. - Sim. m)(n-m)}
é em termos mais baixos, então o igualmente valorizado m/(n- Sim. - Sim. m)(n-m)} é em termos ainda mais baixos. Essa é uma contradição que segue da suposição de que φ φ - Sim.
é em termos ainda mais baixos. Essa é uma contradição que segue da suposição de que φ φ - Sim. é racional.
é racional.
Por irracionalidade de √5
Outra prova curta – talvez mais comumente conhecida – da irracionalidade da relação dourada faz uso do fechamento de números racionais sob adição e multiplicação. Se φ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =12(1+5){displaystyle varphi ={tfrac {1}{2}}(1+{sqrt {5}}} é racional, então 2φ φ - Sim. - Sim. 1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =5{displaystyle 2varphi - Sim. (5)
é racional, então 2φ φ - Sim. - Sim. 1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =5{displaystyle 2varphi - Sim. (5) é também racional, que é uma contradição se já se sabe que a raiz quadrada de todos os números naturais não-quadrados são irracionais.
é também racional, que é uma contradição se já se sabe que a raiz quadrada de todos os números naturais não-quadrados são irracionais.
Polinômio mínimo
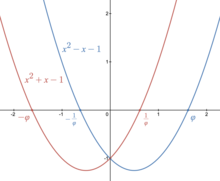
A relação de ouro
φ e seu reciprocal negativo
- Sim.φ- Sim. são as duas raízes do polinomial quadrático
x2 - Sim. x - 1. A relação de ouro é negativa
- Sim.φ e recíproco
φ- Sim. são as duas raízes do polinomial quadrático
x2 + x - 1.
A proporção áurea também é um número algébrico e até mesmo um inteiro algébrico. Tem polinômio mínimo
x2- Sim. - Sim. x- Sim. - Sim. 1.{displaystyle x^{2}-x-1.}
Este polinomial quadrático tem duas raízes, φ φ - Sim. e - Sim. - Sim. φ φ - Sim. - Sim. 1.Não. - varphi ^{-1}
e - Sim. - Sim. φ φ - Sim. - Sim. 1.Não. - varphi ^{-1}
A proporção áurea também está intimamente relacionada ao polinômio
x2+x- Sim. - Sim. 1,{displaystyle x^{2}+x-1,}
que tem raízes - Sim. - Sim. φ φ - Sim. e φ φ - Sim. - Sim. 1.{displaystyle varphi ^{-1}.}
e φ φ - Sim. - Sim. 1.{displaystyle varphi ^{-1}.} Como a raiz de um polinômio quadrático, a proporção de ouro é um número construível.
Como a raiz de um polinômio quadrático, a proporção de ouro é um número construível.
Proporção áurea conjugada e potências
A raiz conjugada para o polinomial mínimo x2- Sim. - Sim. x- Sim. - Sim. 1{displaystyle x^{2}-x-1} o
o
- Sim. - Sim. 1φ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1- Sim. - Sim. φ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1- Sim. - Sim. 52= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. 0,618033...... .- Sim. }}=1-varphi - Sim. Não. {5}}}{2}}=-0.618033dots.}
O valor absoluto desta quantidade (0.618...... } ) corresponde à relação de comprimento tomada em ordem reversa (pequeno comprimento do segmento ao longo do comprimento do segmento mais longo, b)/umNão.
) corresponde à relação de comprimento tomada em ordem reversa (pequeno comprimento do segmento ao longo do comprimento do segmento mais longo, b)/umNão. ).
).
Isto ilustra a propriedade única da proporção áurea entre números positivos, que
1φ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ - Sim. - Sim. 1,Não. }}=varphi -1,}
ou seu inverso:
11/φ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1φ φ +1.{displaystyle {frac {1}{1/varphi * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * - Sim.
O conjugado e a definição da relação polinomial quadrática levam a valores decimais que têm sua parte fracionada em comum com φ φ - Sim. :
:
φ φ 2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ +1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2.618033...... ,1φ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ - Sim. - Sim. 1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0,618033...... .{displaystyle {begin{aligned}varphi ^{2}&=varphi +1=2.618033dots\[5mu]{frac {1}{varphi }}&=varphi -1=0.618033dots.end{aligned}}}![{displaystyle {begin{aligned}varphi ^{2}&=varphi +1=2.618033dots\[5mu]{frac {1}{varphi }}&=varphi -1=0.618033dots.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff2e5225abf67548cf93c882add3a4b439c4aeb8)
A sequência de poderes de φ φ - Sim. contém estes valores 0,618033...... ,- Não.
contém estes valores 0,618033...... ,- Não. 1.0.,Não. 1.0.
1.0.,Não. 1.0. 1.618033...... ,- Sim.
1.618033...... ,- Sim. 2.618033...... ;{displaystyle 2.618033ldots;}
2.618033...... ;{displaystyle 2.618033ldots;} mais geralmente,
qualquer poder de φ φ - Sim.
mais geralmente,
qualquer poder de φ φ - Sim. é igual à soma dos dois poderes imediatamente anteriores:
é igual à soma dos dois poderes imediatamente anteriores:
φ φ n= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ n- Sim. - Sim. 1+φ φ n- Sim. - Sim. 2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ )) Fn+Fn- Sim. - Sim. 1.{displaystyle varphi ^{n}=varphi ^{n-1}+varphi ^{n-2}=varphi cdot operatorname {F} _{n}+operatorname _{n-1}
Como resultado, pode-se facilmente decompor qualquer poder de φ φ - Sim. em um múltiplo de φ φ - Sim.
em um múltiplo de φ φ - Sim. e uma constante. O múltiplo e a constante são sempre números Fibonacci adjacentes. Isso leva a outra propriedade dos poderes positivos de φ φ - Sim.
e uma constante. O múltiplo e a constante são sempre números Fibonacci adjacentes. Isso leva a outra propriedade dos poderes positivos de φ φ - Sim. :
:
Se ? ? n/2- Sim. - Sim. 1Gerenciamento de contas Gerenciamento de contas = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =m,{displaystyle lfloor n/2-1rfloor =m,} então:
então:
φ φ n= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ n- Sim. - Sim. 1+φ φ n- Sim. - Sim. 3+⋯ ⋯ +φ φ n- Sim. - Sim. 1- Sim. - Sim. 2m+φ φ n- Sim. - Sim. 2- Sim. - Sim. 2mφ φ n- Sim. - Sim. φ φ n- Sim. - Sim. 1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ n- Sim. - Sim. 2.{displaystyle {begin{aligned}varphi ^{n}&=varphi ^{n-1+varphi ^{n-3}+cdots +varphi ^{n-1-2m}+varphi ^{n-2m}\[5mu]varphi ^{n}-varphi ^{n-1}&=varphi ^{n-2}.end{aligned}}}![{displaystyle {begin{aligned}varphi ^{n}&=varphi ^{n-1}+varphi ^{n-3}+cdots +varphi ^{n-1-2m}+varphi ^{n-2-2m}\[5mu]varphi ^{n}-varphi ^{n-1}&=varphi ^{n-2}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/048f09b7012c7fbd3d9f32798de6dd5c01acabcd)
Fração contínua e raiz quadrada

Aproximações à relação de ouro recíproca por frações continuadas finitas ou razões de números de Fibonacci
A fórmula φ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1+1/φ φ {displaystyle varphi =1+1/varphi } pode ser expandido recursivamente para obter uma fração contínua para a relação de ouro:
pode ser expandido recursivamente para obter uma fração contínua para a relação de ouro:
φ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Não.1;1,1,1,...... ]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1+11+11+11+⋱ ⋱ {displaystyle varphi *[1;1,1dots ]=1+{cfrac Não. Não. {1}{1+ddots Sim.![varphi =[1;1,1,1,dots ]=1+{cfrac {1}{1+{cfrac {1}{1+{cfrac {1}{1+ddots }}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95682588ffee3530627c3a7b00ff08bbba6e97d4)
Na verdade, é a forma mais simples de uma fração contínua, ao lado de sua forma recíproca:
φ φ - Sim. - Sim. 1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Não.0;1,1,1,...... ]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0+11+11+11+⋱ ⋱ {displaystyle varphi ^{-1}=[0;1,1,dots ]=0+{cfrac Não. Não. {1}{1+ddots Sim.![varphi ^{-1}=[0;1,1,1,dots ]=0+{cfrac {1}{1+{cfrac {1}{1+{cfrac {1}{1+ddots }}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/165d255e32f4b9af1f9144f15302b147fc3fead2)
Os convergentes destas frações continuadas (1/1,1/1,} 2/1,- Sim.
2/1,- Sim. 2/1,- Sim.
2/1,- Sim. 3/2,3/2,}
3/2,3/2,} 5/3,- Sim.
5/3,- Sim. 8/5,8/5,}
8/5,8/5,} 13/8,Não. 13/8,
13/8,Não. 13/8, ... ou 1/1,1/1,}
... ou 1/1,1/1,} 1/2,- Sim.
1/2,- Sim. 2/3,- Sim.
2/3,- Sim. 3/5,3/5,}
3/5,3/5,} 5/8,{displaystyle 5/8,}
5/8,{displaystyle 5/8,} 8/13,{displaystyle 8/13,}
8/13,{displaystyle 8/13,} ... são razões de números Fibonacci sucessivos. Os termos consistentemente pequenos em sua fração contínua explicam por que os aproximantes convergem tão lentamente. Isso torna a proporção de ouro um caso extremo da desigualdade de Hurwitz para aproximações de Diofantina, que afirma que para cada irracional ? ? - Sim.
... são razões de números Fibonacci sucessivos. Os termos consistentemente pequenos em sua fração contínua explicam por que os aproximantes convergem tão lentamente. Isso torna a proporção de ouro um caso extremo da desigualdade de Hurwitz para aproximações de Diofantina, que afirma que para cada irracional ? ? - Sim. , há infinitamente muitas frações distintas p/q- Sim.
, há infinitamente muitas frações distintas p/q- Sim. tal que,
tal que,
<math alttext="{displaystyle left|xi -{frac {p}{q}}right||? ? - Sim. - Sim. pq|<15q2.{displaystyle left|xi - Sim. {p}{q}}right|<{frac Não. {5}}q^{2}}}.}<img alt="{displaystyle left|xi -{frac {p}{q}}right|
Isso significa que a constante 5(5}}} não pode ser melhorado sem excluir a relação de ouro. É, de fato, o menor número que deve ser excluído para gerar aproximações mais próximas de tais números Lagrange.
não pode ser melhorado sem excluir a relação de ouro. É, de fato, o menor número que deve ser excluído para gerar aproximações mais próximas de tais números Lagrange.
Uma forma de raiz quadrada contínua para φ φ - Sim. pode ser obtido a partir de φ φ 2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1+φ φ {displaystyle varphi ^{2}=1+varphi }
pode ser obtido a partir de φ φ 2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1+φ φ {displaystyle varphi ^{2}=1+varphi } , produzindo:
, produzindo:
φ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1+1+1+⋯ ⋯ .{displaystyle varphi ={sqrt (1+ {1+{sqrt {1+cdots - Sim.
Relação com os números de Fibonacci e Lucas
Uma espiral de Fibonacci (top) que aproxima a espiral dourada, usando tamanhos quadrados de sequência de Fibonacci até 21. Uma espiral dourada também é gerada (bottom) de quadrados de empilhamento cujos comprimentos de lados são números pertencentes à sequência de números Lucas, aqui até 76.
Os números de Fibonacci e Lucas têm uma relação intrincada com a relação de ouro. Na sequência de Fibonacci, cada número é igual à soma dos dois precedentes, começando com a sequência de base 0,1Não. :
:
0,Não. 1,- Sim.
1,- Sim. 1,- Sim.
1,- Sim. 2,- Sim.
2,- Sim. 3,- Sim.
3,- Sim. 5,Sim.
5,Sim. 8,Sim.
8,Sim. 13,Sim.
13,Sim. 21,Sim.
21,Sim. 34,Sim.
34,Sim. 55,- Sim.
55,- Sim. 89,Não.
89,Não. ...... }
...... }
(
OEIS: A000045).
A sequência de números de Lucas (não confundir com as sequências generalizadas de Lucas, das quais é parte) é como a sequência de Fibonacci, em que cada termo é a soma dos dois anteriores, no entanto, começa com 2,1Sim. :
:
2,- Sim. 1,- Sim.
1,- Sim. 3,- Sim.
3,- Sim. 4,- Sim.
4,- Sim. 7,Sim.
7,Sim. 11,Sim.
11,Sim. 18.,- Sim.
18.,- Sim. 29 de Março,- Sim.
29 de Março,- Sim. 47,- Sim.
47,- Sim. 76,Não.
76,Não. 123,Não.
123,Não. 199,- Sim.
199,- Sim. ...... }
...... }
(
OEIS: A000032).
Excepcionalmente, a proporção áurea é igual ao limite das razões de termos sucessivos na sequência de Fibonacci e na sequência dos números de Lucas:
Limpar.n→ → ∞ ∞ Fn+1Fn= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Limpar.n→ → ∞ ∞ Ln+1Ln= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ .{displaystyle lim _{nto infty }{frac {F_{n+1}}{F_{n}}}=lim _{nto infty }{frac {L_{n+1}}{L_{n}}}=varphi.}
Em outras palavras, se um número de Fibonacci e Lucas é dividido por seu antecessor imediato na sequência, o quociente aproxima φ φ - Sim. .
.
Por exemplo, F16.F15= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =987610= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1 de Janeiro de 1999...... ,{displaystyle {frac {F_{16}}{F_{15}}}={frac {987}{610}}=1.6180327ldots} e L16.L15= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =22071364= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1.6180351...... .Não. {L_{16}}{L_{15}}}={frac {2207}{1364}}=1.6180351ldots.}
e L16.L15= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =22071364= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1.6180351...... .Não. {L_{16}}{L_{15}}}={frac {2207}{1364}}=1.6180351ldots.}
Estas aproximações são alternadamente mais baixas e superiores do que φ φ ,- Sim. e convergir para φ φ - Sim.
e convergir para φ φ - Sim. como os números Fibonacci e Lucas aumentam.
como os números Fibonacci e Lucas aumentam.
As expressões de forma fechada para as sequências de Fibonacci e Lucas que envolvem a proporção áurea são:
F(n)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ n- Sim. - Sim. (1- Sim. - Sim. φ φ )n5= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ n- Sim. - Sim. (- Sim. - Sim. φ φ )- Sim. - Sim. n5,{displaystyle Fleft(nright)={{varphi ^{n}-(1-varphi)^{n}} - Sim. {5}}}={{varphi ^{n}-(-varphi)^{-n}} O que é isso?
L(n)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ n+(- Sim. - Sim. φ φ )- Sim. - Sim. n= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(1+52)n+(1- Sim. - Sim. 52)n.{displaystyle Lleft(nright)=varphi ^{n}+(-varphi)^{-n}=left({1+{sqrt {5}} over 2}right)^{n}+left({1-{sqrt {5}} over 2}right)^{n},}
Combinando ambas as fórmulas acima, obtém-se uma fórmula para φ φ n{displaystyle varphi ^{n}} que envolve números de Fibonacci e Lucas:
que envolve números de Fibonacci e Lucas:
φ φ n= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Ln+Fn52.{displaystyle varphi ^{n}={L_{n}+F_{n}{sqrt {5}}} over 2},.}
Entre Fibonacci e Lucas números um pode deduzir L2n= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =5Fn2+2(- Sim. - Sim. 1)n= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Ln2- Sim. - Sim. 2(- Sim. - Sim. 1)n,Não. L_{2n}=5F_{n}^{2}+2(-1)^{n}=L_{n}^{2}-2(-1)^{n}, ? que simplifica para expressar o limite do quociente dos números Lucas por números Fibonacci como igual à raiz quadrada de cinco:
que simplifica para expressar o limite do quociente dos números Lucas por números Fibonacci como igual à raiz quadrada de cinco:
Limpar.n→ → ∞ ∞ LnFn= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =5.{displaystyle lim _{nto infty }{frac {L_{n}}{F_{n}}}={sqrt {5}}.}
De fato, declarações muito mais fortes são verdadeiras:
- |Ln- Sim. - Sim. 5Fn|= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2φ φ n→ → 0{displaystyle vert L_{n}-{sqrt {5}}F_{n}vert ={frac {2}{varphi ^{n}}}to 0
 ,
, - (L3n/2)2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =5(F3n/2)2+(- Sim. - Sim. 1)nNão. (L_{3n}/2)^{2}=5(F_{3n}/2)^{2}+(-1)^{n}}
 .
.
Estes valores descrevem φ φ - Sim. como uma unidade fundamental do campo número algébrica Q(5){displaystyle mathbb {Q} ({sqrt {5}})}
como uma unidade fundamental do campo número algébrica Q(5){displaystyle mathbb {Q} ({sqrt {5}})} .
.
Os poderes bem sucedidos da relação dourada obedecem à recorrência de Fibonacci, ou seja. φ φ n+1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ n+φ φ n- Sim. - Sim. 1.{displaystyle varphi ^{n+1}=varphi ^{n}+varphi ^{n-1}.}
A redução para uma expressão linear pode ser realizada em uma etapa usando:
φ φ n= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Fnφ φ +Fn- Sim. - Sim. 1.{displaystyle varphi ^{n}=F_{n}varphi +F_{n-1}.}
Esta identidade permite qualquer polinomial φ φ - Sim. para ser reduzido a uma expressão linear, como em:
para ser reduzido a uma expressão linear, como em:
3φ φ 3- Sim. - Sim. 5φ φ 2+4= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =3(φ φ 2+φ φ )- Sim. - Sim. 5φ φ 2+4= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =3Não.(φ φ +1)+φ φ ]- Sim. - Sim. 5(φ φ +1)+4= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ +2? ? 3.618033.{displaystyle {begin{aligned}3varphi ^{3}-5varphi ^{2}+4&=3(varphi ^{2}+varphi)-5varphi ^{2}+4\[5mu]&=3[(varphi +1)+varphi ]-5(varphi) +1)+4\[5mu]&=varphi +2approx 3.618033.end{aligned}}}![{displaystyle {begin{aligned}3varphi ^{3}-5varphi ^{2}+4&=3(varphi ^{2}+varphi)-5varphi ^{2}+4\[5mu]&=3[(varphi +1)+varphi ]-5(varphi +1)+4\[5mu]&=varphi +2approx 3.618033.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60ff8508aa117064d60142d447fb0cb58a809848)
Os números consecutivos de Fibonacci também podem ser usados para obter uma fórmula semelhante para a proporção áurea, aqui por soma infinita:
Gerenciamento Gerenciamento n= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1∞ ∞ |Fnφ φ - Sim. - Sim. Fn+1|= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ .{displaystyle sum _{n=1}^{infty } |F_{n}varphi -F_{n+1}|=varphi.}
Em particular, os poderes de φ φ - Sim. em torno de Lucas números (em ordem, exceto para os dois primeiros poderes, φ φ 0{displaystyle varphi ^{0}}
em torno de Lucas números (em ordem, exceto para os dois primeiros poderes, φ φ 0{displaystyle varphi ^{0}} e φ φ - Sim.
e φ φ - Sim. , estão em ordem inversa):
, estão em ordem inversa):
φ φ 0= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1,φ φ 1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1.618033989...? ? 2,φ φ 2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2.618033989...? ? 3,φ φ 3= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =4.236067978...? ? 4,φ φ 4= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =6.854101967...? ? 7,{displaystyle {begin{aligned}varphi ^{0}&=1,\[5mu]varphi ^{1}&=1.618033989...approx 2,\[5mu]varphi ^{2}&=2.618033989...approx 3,\[5mu]varphi ^{3}&=4.236067978...approx 4,\[5mu]varphi ^{4}&=6.854101967...approx 7,end{aligned}}}![{displaystyle {begin{aligned}varphi ^{0}&=1,\[5mu]varphi ^{1}&=1.618033989...approx 2,\[5mu]varphi ^{2}&=2.618033989...approx 3,\[5mu]varphi ^{3}&=4.236067978...approx 4,\[5mu]varphi ^{4}&=6.854101967...approx 7,end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20c9bfd2f9bdc877282b290adc74c88f1dfa63c8)
e assim por diante. Os números Lucas também geram diretamente poderes da relação de ouro; para n≥ ≥ 2{displaystyle ngeq 2} :
:
φ φ n= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Ln- Sim. - Sim. (- Sim. - Sim. φ φ )- Sim. - Sim. n.{displaystyle varphi ^{n}=L_{n}-(-varphi)^{-n}.
Enraizada em sua relação de interconexão com a relação de ouro é a noção de que a soma de terceiro números Fibonacci consecutivos é igual a um número Lucas, ou seja, Ln= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Fn- Sim. - Sim. 1+Fn+1Não. L_{n}=F_{n-1}+F_{n+1}} ; e, importante, que Ln= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =F2nFnNão. {L_{n}}={frac {F_{2n}}{F_{n}}}}
; e, importante, que Ln= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =F2nFnNão. {L_{n}}={frac {F_{2n}}{F_{n}}}} .
.
Tanto a sequência de Fibonacci quanto a sequência dos números de Lucas podem ser usadas para gerar formas aproximadas da espiral áurea (que é uma forma especial de espiral logarítmica) usando quartos de círculo com raios dessas sequências, diferindo apenas ligeiramente da espiral logarítmica dourada verdadeira. Espiral de Fibonacci é geralmente o termo usado para espirais que se aproximam de espirais douradas usando quadrados e quartos de círculo sequenciados por números de Fibonacci.
Geometria
A proporção áurea aparece com destaque na geometria. Por exemplo, está intrinsecamente envolvido na simetria interna do pentágono, e se estende para formar parte das coordenadas dos vértices de um dodecaedro regular, bem como as de um 5-cell. Também aparece no triângulo de Kepler e nos ladrilhos de Penrose, bem como em vários outros politopos.
Construção
Dividindo um segmento de linha por divisão interior (top) e divisão exterior (bottom) de acordo com a relação de ouro.
Divisão por divisão interior
- Ter um segmento de linha AB,Não. AB,
 construir um perpendicular BCNão. AC.
construir um perpendicular BCNão. AC. ponto B,Não. B,
ponto B,Não. B, com BCNão. AC.
com BCNão. AC. metade do comprimento de AB.Não. AB.
metade do comprimento de AB.Não. AB. Desenhe a hipotenusa AC.Não. AC.
Desenhe a hipotenusa AC.Não. AC.
- Desenhe um arco com centro CNão. C.
 e raio BC.Não. BC.
e raio BC.Não. BC. Este arco cruza a hipotenusa ACNão. AC.
Este arco cruza a hipotenusa ACNão. AC. ponto D.Não. D.
ponto D.Não. D.
- Desenhe um arco com centro ANão. A.
 e raio AD.Não. AD.
e raio AD.Não. AD. Este arco cruza o segmento de linha original ABNão. AB
Este arco cruza o segmento de linha original ABNão. AB ponto S.Não. S.
ponto S.Não. S. Ponto SNão. S.
Ponto SNão. S. divide o segmento de linha original ABNão. AB
divide o segmento de linha original ABNão. AB em segmentos de linha ASNão. Como?
em segmentos de linha ASNão. Como? e SBNão. SB
e SBNão. SB com comprimentos na proporção de ouro.
com comprimentos na proporção de ouro.
Divisão por divisão externa
- Desenhe um segmento de linha ASNão. Como?
 e construir fora do ponto SNão. S.
e construir fora do ponto SNão. S. um segmento SCNão. SC
um segmento SCNão. SC perpendicular a ASNão. Como?
perpendicular a ASNão. Como? e com o mesmo comprimento que AS.Não. Como.
e com o mesmo comprimento que AS.Não. Como.
- Faça bisect o segmento de linha ASNão. Como?
 com M.Não. M.
com M.Não. M.
- Um arco circular ao redor MNão.
 com raio MCNão. MC
com raio MCNão. MC intersetos no ponto BNão.
intersetos no ponto BNão. a linha reta através de pontos ANão. A.
a linha reta através de pontos ANão. A. e SNão. S.
e SNão. S. (também conhecido como a extensão de ASNão. Como?
(também conhecido como a extensão de ASNão. Como? ). A relação de ASNão. Como?
). A relação de ASNão. Como? para o segmento construído SBNão. SB
para o segmento construído SBNão. SB é a proporção de ouro.
é a proporção de ouro.
Exemplos de aplicação que você pode ver nos artigos Pentágono com um determinado comprimento de lado, Decágono com determinado circuncírculo e Decágono com um determinado comprimento de lado.
Ambos os algoritmos diferentes exibidos acima produzem construções geométricas que determinam dois segmentos de linha alinhados, onde a proporção do mais longo para o mais curto é a proporção áurea.
Ângulo dourado
Quando dois ângulos que fazem um círculo completo têm medidas na proporção de ouro, o menor é chamado o ângulo de ouro, com medida g:: - Sim.
2D D - Sim. - Sim. gg= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2D D 2D D - Sim. - Sim. g= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ ,2D D - Sim. - Sim. g= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2D D φ φ ? ? 222.∘ ∘ ,g= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2D D φ φ 2? ? 137.∘ ∘ .{displaystyle {begin{aligned}{frac {2pi} -g}{g}}&={frac {2pi }{2pi -g}}=varphi\[8mu]2pi -g&={frac {2pi }{varphi }}approx 222.5^{circ },\[8mu]g&={frac {2pi }{varphi ^{2}}}approx 137.5^{circ }![{displaystyle {begin{aligned}{frac {2pi -g}{g}}&={frac {2pi }{2pi -g}}=varphi\[8mu]2pi -g&={frac {2pi }{varphi }}approx 222.5^{circ },\[8mu]g&={frac {2pi }{varphi ^{2}}}approx 137.5^{circ }.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd5f9122b38d09e0cd2992820f27b8587efd167a)
Esse ângulo ocorre nos padrões de crescimento da planta como o espaçamento ideal dos brotos das folhas ao redor dos caules das plantas, de modo que as folhas sucessivas não bloqueiem a luz solar das folhas abaixo delas.
Sistema de simetria pentagonal
Pentágono e pentagrama

Um pentagrama colorido para distinguir seus segmentos de linha de diferentes comprimentos. Os quatro comprimentos estão em proporção de ouro um ao outro.
Em um pentágono regular a relação de uma diagonal a um lado é a proporção de ouro, enquanto as diagonais se cruzam na proporção de ouro. As propriedades da razão de ouro de um pentágono regular podem ser confirmadas aplicando o teorema de Ptolemy ao quadrilateral formado pela remoção de um de seus vértices. Se a borda longa do quadrilateral e as diagonais são um,Não. e bordas curtas são b),Não.
e bordas curtas são b),Não. então o teorema de Ptolemy dá um2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =b)2+umb).{displaystyle a^{2}=b^{2}+ab.}
então o teorema de Ptolemy dá um2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =b)2+umb).{displaystyle a^{2}=b^{2}+ab.} Dividir ambos os lados por umb)Não.
Dividir ambos os lados por umb)Não. rendimentos (ver § Cálculo acima),
rendimentos (ver § Cálculo acima),
umb)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =um+b)um= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ .Não. Não. {a+b}{a}}=varphi.}
Os segmentos diagonais de um pentágono formam um pentagrama, ou poligono estrela de cinco pontos, cuja geometria é quintessentialmente descrita por φ φ - Sim. . Principalmente, cada interseção de bordas seções outras bordas na proporção de ouro. A relação do comprimento do segmento mais curto para o segmento limitado pelas duas bordas de interseção (isto é, um lado do pentágono invertido no centro do pentagrama) é φ φ ,- Sim.
. Principalmente, cada interseção de bordas seções outras bordas na proporção de ouro. A relação do comprimento do segmento mais curto para o segmento limitado pelas duas bordas de interseção (isto é, um lado do pentágono invertido no centro do pentagrama) é φ φ ,- Sim. como mostra a ilustração de quatro cores.
como mostra a ilustração de quatro cores.
A geometria pentagonal e pentagrammica nos permite calcular os seguintes valores para φ φ - Sim. :
:
φ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1+2pecado (D D /10.)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1+2pecado 18.∘ ∘ ,φ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =12CSC (D D /10.)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =12CSC 18.∘ ∘ ,φ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2e (D D /5)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2e 36∘ ∘ ,φ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2pecado (3D D /10.)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2pecado 54∘ ∘ .{displaystyle {begin{aligned}varphi &=1+2sin(pi /10)=1+2sin 18^{circ },\[5mu]varphi &={tfrac {1}{2}}csc(pi /10)={tfrac {1}{2}}csc 18^{circ },[5mu]varphi &=2cos(pi /5)=2cos 36^{circ },[5mu]varphi &=2sin(3pi /10)=2sin 54^{circ }.![{displaystyle {begin{aligned}varphi &=1+2sin(pi /10)=1+2sin 18^{circ },\[5mu]varphi &={tfrac {1}{2}}csc(pi /10)={tfrac {1}{2}}csc 18^{circ },\[5mu]varphi &=2cos(pi /5)=2cos 36^{circ },\[5mu]varphi &=2sin(3pi /10)=2sin 54^{circ }.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c42bbf25d6257a00fad895691aa2c5eb0c6f57a)
Triângulo dourado e gnômon dourado
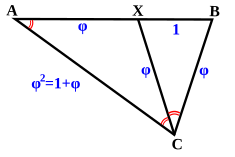
Um triângulo dourado
ABC pode ser subdividido por um bissetor de ângulo em um triângulo dourado menor
CXB e um gnomon dourado
XAC.
O triângulo formado por duas diagonais e um lado de um pentágono regular é chamado de triângulo dourado ou triângulo sublime. É um triângulo isósceles agudo com ângulo do vértice 36° e ângulos da base 72°. Seus dois lados iguais estão na proporção áurea de sua base. O triângulo formado por dois lados e uma diagonal de um pentágono regular é chamado de gnômon de ouro. É um triângulo isósceles obtuso com ângulo do vértice 108° e ângulo da base 36°. Sua base está na proporção áurea de seus dois lados iguais. O pentágono pode assim ser subdividido em dois gnômons dourados e um triângulo dourado central. Os cinco pontos de um pentagrama regular são triângulos de ouro, assim como os dez triângulos formados pela ligação dos vértices de um decágono regular ao seu ponto central.
A divisão de um dos ângulos da base do triângulo dourado o subdivide em um triângulo dourado menor e um gnômon dourado. Analogamente, qualquer triângulo isósceles agudo pode ser subdividido em um triângulo semelhante e um triângulo isósceles obtuso, mas o triângulo áureo é o único para o qual essa subdivisão é feita pela bissetriz do ângulo, pois é o único triângulo isósceles cujo ângulo da base é duas vezes seu ângulo de ápice. A bissetriz do triângulo áureo subdivide o lado que ela encontra na proporção áurea, e as áreas das duas partes subdivididas também estão na proporção áurea.
Se o ângulo do ápice do gnômon de ouro for trissecionado, o trissetor novamente o subdividirá em um gnômon de ouro menor e um triângulo de ouro. O trissector subdivide a base na proporção áurea, e as duas peças têm áreas na proporção áurea. Analogamente, qualquer triângulo obtuso pode ser subdividido em um triângulo semelhante e um triângulo isósceles agudo, mas o gnômon de ouro é o único para o qual essa subdivisão é feita pelo trissetor do ângulo, pois é o único triângulo isósceles cujo ângulo do ápice é três vezes seu ângulo de base.
Ladrilhos de Penrose

As telhas de papagaio e dardo do tiling de Penrose. Os arcos coloridos dividem cada borda na proporção de ouro; quando duas telhas compartilham uma borda, seus arcos devem combinar.
A proporção áurea aparece com destaque no ladrilho de Penrose, uma família de ladrilhos aperiódicos do plano desenvolvido por Roger Penrose, inspirado na observação de Johannes Kepler de que pentagramas, decágonos e outras formas poderia preencher lacunas que formas pentagonais sozinhas deixam quando lado a lado. Várias variações deste ladrilho foram estudadas, cujos protótipos exibem a proporção áurea:
- A versão original deste tiling de Penrose usou quatro formas: pentágonos regulares e pentagramas, figuras de "barco" com três pontos de um pentagrama, e "diamond" em forma de rhombi.
- O kite e dardo Penrose tiling usa kites com três ângulos interiores de 72° e um ângulo interior de 144°, e dardos, concave quadriláteros com dois ângulos interiores de 36°, um de 72°, e um ângulo não-convexo de 216°. Regras especiais de correspondência restringem como as telhas podem se encontrar em qualquer borda, resultando em sete combinações de telhas em qualquer vértice. Ambos os kites e dardos têm lados de dois comprimentos, na proporção de ouro um ao outro. As áreas destas duas formas de telha também estão na proporção de ouro um ao outro.
- O papagaio e o dardo podem ser cortados em seus eixos de simetria em um par de triângulos dourados e gnomons dourados, respectivamente. Com regras de correspondência adequadas, esses triângulos, chamados neste contexto Triângulos de Robinson, pode ser usado como os prototis para uma forma do tiling de Penrose.
- O tilingue penrose rhombic contém dois tipos de rhombus, um rhombus fino com ângulos de 36° e 144°, e um rhombus grosso com ângulos de 72° e 108°. Todos os comprimentos laterais são iguais, mas a proporção do comprimento dos lados para a diagonal curta no rhombus fino é igual 1:φ φ }
 , como faz a relação dos lados da diagonal longa do rhombus grosso. Tal como acontece com o gatinho e dardo, as áreas dos dois rhombi estão na proporção de ouro um ao outro. Novamente, esses rhombi podem ser decompostos em pares de triângulos Robinson.
, como faz a relação dos lados da diagonal longa do rhombus grosso. Tal como acontece com o gatinho e dardo, as áreas dos dois rhombi estão na proporção de ouro um ao outro. Novamente, esses rhombi podem ser decompostos em pares de triângulos Robinson.
Tintura de Penrose original de quatro partes
Toldos de pântano Rhombic
Em triângulos e quadriláteros
Construção de Odom
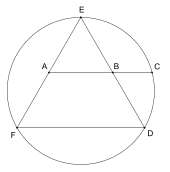
Construção de Odom:
AB: BC = AC: AB = φ: 1George Odom encontrou uma construção para φ φ - Sim. envolvendo um triângulo equilátero: se o segmento de linha que une os pontos médios de dois lados é estendido para intersetar o circuncírculo, então os dois pontos médios e o ponto de interseção com o círculo estão em proporção dourada.
envolvendo um triângulo equilátero: se o segmento de linha que une os pontos médios de dois lados é estendido para intersetar o circuncírculo, então os dois pontos médios e o ponto de interseção com o círculo estão em proporção dourada.
Triângulo de Kepler
Progressão geométrica de áreas de quadrados nos lados de um triângulo Kepler
Um triângulo isosceles formado a partir de dois triângulos Kepler maximiza a relação de seu inradius ao comprimento lateral
O triângulo de Kepler, em homenagem a Johannes Kepler, é o único triângulo retângulo com lados em progressão geométrica:
1:φ φ :φ φ {displaystyle 1mathbin {:} {sqrt {varphi }}mathbin {:}} - Sim.
.
Estes comprimentos laterais são os três meios pitagóricos dos dois números φ φ ± ± 1{displaystyle varphi pm 1 . Os três quadrados em seus lados têm áreas na progressão geométrica dourada 1:φ φ :φ φ 2{displaystyle 1mathbin {:} varphi mathbin {:} varphi ^{2}}
. Os três quadrados em seus lados têm áreas na progressão geométrica dourada 1:φ φ :φ φ 2{displaystyle 1mathbin {:} varphi mathbin {:} varphi ^{2}} .
.
Entre os triângulos isósceles, a razão entre o raio e o comprimento do lado é maximizada para o triângulo formado por duas cópias refletidas do triângulo de Kepler, compartilhando o maior de suas duas pernas. O mesmo triângulo isósceles maximiza a razão entre o raio de um semicírculo em sua base e seu perímetro.
Para um triângulo Kepler com menor comprimento lateral SNão. , a área e ângulos internos agudos são:
, a área e ângulos internos agudos são:
A= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =S22φ φ ,θ θ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =pecado- Sim. - Sim. 1 1φ φ ? ? 38.1727∘ ∘ ,θ θ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =e- Sim. - Sim. 1 1φ φ ? ? 51.8273∘ ∘ .A > {s^{2}}{2}}{sqrt {varphi }},[5mu]theta &=sin ^{-1}{frac {1}{varphi }}approx 38.1727^{circ },[5mu]theta &=cos ^{-1}{frac {1}{varphi }}approx 51.8273^{circ }.end{aligned}}}![{displaystyle {begin{aligned}A&={tfrac {s^{2}}{2}}{sqrt {varphi }},\[5mu]theta &=sin ^{-1}{frac {1}{varphi }}approx 38.1727^{circ },\[5mu]theta &=cos ^{-1}{frac {1}{varphi }}approx 51.8273^{circ }.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f96fa323a2e180a6198f05d33c13e1631854e840)
Retângulo dourado
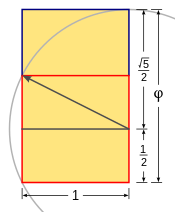
Para construir um retângulo dourado com apenas um straightedge e bússola em quatro etapas simples:
| Desenhe um quadrado. |
| Desenhe uma linha do ponto médio de um lado do quadrado a um canto oposto. |
| Use essa linha como o raio para desenhar um arco que define a altura do retângulo. |
| Complete o retângulo dourado. |
A proporção de ouro proporciona os comprimentos laterais adjacentes de um Retângulo dourado em 1:φ φ } ratio. Empilhar retângulos dourados produz retângulos dourados de novo, e remover ou adicionar quadrados de retângulos dourados folhas retângulos ainda proporcionados em φ φ - Sim.
ratio. Empilhar retângulos dourados produz retângulos dourados de novo, e remover ou adicionar quadrados de retângulos dourados folhas retângulos ainda proporcionados em φ φ - Sim. ratio. Eles podem ser gerados por espirais de ouro, através de sucessivas Fibonacci e Lucas quadrados de tamanho grande e círculos de quarto. Eles apresentam proeminentemente no icosahedron, bem como no dodecahedron (veja a seção abaixo para mais detalhes).
ratio. Eles podem ser gerados por espirais de ouro, através de sucessivas Fibonacci e Lucas quadrados de tamanho grande e círculos de quarto. Eles apresentam proeminentemente no icosahedron, bem como no dodecahedron (veja a seção abaixo para mais detalhes).
Rombo dourado
A rhombus de ouro é um rhombus cujas diagonais estão em proporção à proporção de ouro, mais comumente 1:φ φ } . Para um rhombus de tais proporções, seu ângulo agudo e ângulos obtusos são:
. Para um rhombus de tais proporções, seu ângulo agudo e ângulos obtusos são:
α α = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2arctan 1φ φ ? ? 63.43495∘ ∘ ,β β = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2arctan φ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =D D - Sim. - Sim. arctan 2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =arctan 1+arctan 3? ? 11,5 milhões de euros∘ ∘ .{displaystyle {begin{aligned}alpha &=2arctan {1 over varphi }approx 63.43495^{circ },[5mu]beta &=2arctan varphi =pi -arctan 2=arctan 1+arctan 3approx 116.56505^{circ }ed}![{displaystyle {begin{aligned}alpha &=2arctan {1 over varphi }approx 63.43495^{circ },\[5mu]beta &=2arctan varphi =pi -arctan 2=arctan 1+arctan 3approx 116.56505^{circ }.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c5a4321454f4ca1b41b0dbd8f2c6c4afd48467e)
Os comprimentos de suas diagonals curtas e longas DNão. e DNão.
e DNão. , em termos de comprimento lateral umNão.
, em termos de comprimento lateral umNão. são:
são:
D= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2um2+φ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =23- Sim. - Sim. φ φ 5um? ? 1.05146um,D= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =22+φ φ 5um? ? 1.70130um.{displaystyle {begin{aligned}d&={2a over {sqrt {2+varphi - Sim. {{3-varphi } over 5}}aapprox 1.05146a,[5mu]D&=2{sqrt {{2+varphi } over 5}}aapprox 1.70130a.end{aligned}}}![{displaystyle {begin{aligned}d&={2a over {sqrt {2+varphi }}}=2{sqrt {{3-varphi } over 5}}aapprox 1.05146a,\[5mu]D&=2{sqrt {{2+varphi } over 5}}aapprox 1.70130a.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d00bbc42679ab9e34fdf849ac68de75180cc92c7)
Sua área, em termos de umNão. e DNão.
e DNão. :
:
A= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(pecado (arctan 2))um2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =25um2? ? 0,9443um2,A= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ 2D2? ? 0,0902D2.{displaystyle {begin{aligned}A&=(sin(arctan 2))~a^{2}={2 over {sqrt {5}}}~a^{2}approx 0.89443a^{2},[5mu]A&={{varphi } over 2}d^{2}approx 0.80902d^{2}.end{aligned}}}![{displaystyle {begin{aligned}A&=(sin(arctan 2))~a^{2}={2 over {sqrt {5}}}~a^{2}approx 0.89443a^{2},\[5mu]A&={{varphi } over 2}d^{2}approx 0.80902d^{2}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7bed70dcf23f16f3f8241aeaf2b56f0897244ff3)
Seu inradius, em termos de lado umNão. :
:
R= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =um5.Não. - Sim.
Recurso de losango dourado no triacontaedro rômbico (veja a seção abaixo). Eles também são encontrados no romboedro de ouro, no dodecaedro de Bilinski e no hexecontaedro rômbico.
Espiral dourada

Uma espiral logarítmica dourada gira em torno de um triângulo dourado, tocando seus três vértices, movendo-se interiormente dentro de triângulos dourados fractais semelhantes.
Espirais logarítmicas são espirais auto-similar onde as distâncias cobertas por volta estão em progressão geométrica. Importante, os triângulos dourados isosceles podem ser envoltos por uma espiral logarítmica dourada, de modo que as voltas sucessivas de uma espiral geram novos triângulos dourados no interior. Este caso especial de espirais logarítmicas chama-se o espiral de ouro, e exibe crescimento contínuo na proporção de ouro. Isto é, para cada 90∘ ∘ {displaystyle 90^{circ }} turn, há um fator de crescimento de φ φ - Sim.
turn, há um fator de crescimento de φ φ - Sim. . Essas espirais podem ser aproximadas por quarto-círculos gerados a partir de Fibonacci e Lucas quadrados de tamanho grande que são azulejos juntos. Em sua forma exata, eles podem ser descritos pela equação polar com (R,θ θ )(r,theta)}
. Essas espirais podem ser aproximadas por quarto-círculos gerados a partir de Fibonacci e Lucas quadrados de tamanho grande que são azulejos juntos. Em sua forma exata, eles podem ser descritos pela equação polar com (R,θ θ )(r,theta)} :
:
R= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ 2θ θ /D D .Não. r=varphi ^{2theta /pi }.}
Como com qualquer espiral logarítmica, para R= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =umeb)θ θ {displaystyle r=ae^{btheta) com eb)θ θ REu...gh)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ {displaystyle e^{btheta _{mathrm {right} }}=varphi }
com eb)θ θ REu...gh)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ {displaystyle e^{btheta _{mathrm {right} }}=varphi } em ângulos retos:
em ângulos retos:
|b)|= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =I φ φ θ θ REu...gh)≐ ≐ 0.0053468∘ ∘ ≐ ≐ 0,063489Rad.{displaystyle |b|={ln {varphi } over theta _{mathrm {right} }}doteq 0.0053468^{circ }doteq 0.3063489{text{ rad}}}}}
Sua inclinação polar α α - Sim. pode ser calculado usando bronzeado α α = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =b){displaystyle tan alfa - O quê?
pode ser calculado usando bronzeado α α = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =b){displaystyle tan alfa - O quê? ao lado |b)||b|}
ao lado |b)||b|} de cima,
de cima,
α α = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =arctan (|b)|)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =arctan (I φ φ D D /2)≐ ≐ 17.03239113∘ ∘ ≐ ≐ 0,2972713047Rad.{displaystyle alpha =arctan(|b|)=arctan left({ln {varphi } over pi /2}right)doteq 17.03239113^{circ }doteq 0.2972713047{text{ rad.}}}
Tem um ângulo complementar, β β - Sim. :
:
β β = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =D D /2- Sim. - Sim. α α ≐ ≐ 72.96760887∘ ∘ ≐ ≐ 1 de Janeiro de 2002Rad.{displaystyle beta =pi /2-alpha doteq 72.96760887^{circ }doteq 1.273525022{text{ rad.}}}
As espirais douradas também podem ser colocadas simetricamente dentro de pentágonos e pentagramas, de modo que as cópias fractais da geometria subjacente sejam reproduzidas em todas as escalas.
No dodecaedro e icosaedro

| |
Coordenadas cartesianas do dodecaedro:
|
| (±1, ±1, ±1) |
| (0, ±φ, ±1/φ) |
| (1/φ, 0, ±φ) |
| (φ, ±1/φ, 0) |
| Um cubo aninhado dentro do dodecaedro é representado com pontilhada linhas. | |
O dodecaedro regular e seu poliedro duplo o icosahedron são sólidos platônicos cujas dimensões estão relacionadas com a relação de ouro. Um icosahedron é feito de 12Não. caras pentagonais regulares, enquanto o icosahedron é feito de 20.Não.
caras pentagonais regulares, enquanto o icosahedron é feito de 20.Não. triângulos equiláteros; ambos com 30Não.
triângulos equiláteros; ambos com 30Não. bordas.
bordas.
Para um dodecaedro do lado umNão. , o raio de uma esfera circunscrita e inscrita, e midradius são (Ru{displaystyle r_{u}}
, o raio de uma esfera circunscrita e inscrita, e midradius são (Ru{displaystyle r_{u}} , REu...Não. r_{i}}
, REu...Não. r_{i}} e RmNão. r_{m}}
e RmNão. r_{m}} , respectivamente):
, respectivamente):
Ru= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =um3φ φ 2{displaystyle r_{u}=a,{frac {{sqrt {3}}varphi ?
,
REu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =umφ φ 223- Sim. - Sim. φ φ Não. r_{i}=a,{frac {varphi ^{2}}{2{sqrt {3-varphi Sim.
e
Rm= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =umφ φ 22Não. r_{m}=a,{frac - Sim.
.
Enquanto para um icosahedron de lado umNão. , o raio de uma esfera circunscrita e inscrita, e midradius são:
, o raio de uma esfera circunscrita e inscrita, e midradius são:
Ru= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =umφ φ 52Não. r_{u=a{frac Não. Não. {5}}{2}}}
,
REu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =umφ φ 223Não. r_{i}=a{frac {varphi ^{2}}{2{sqrt {3}}}}}
e
Rm= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =umφ φ 2Não. r_{m}=a{frac {varphi }{2}}}
.
O volume e a superfície da dodecaedro podem ser expressos em termos de φ φ - Sim. :
:
AD= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =15φ φ 3- Sim. - Sim. φ φ Não. A_{d}={frac {15varphi }{sqrt {3-varphi Sim.
e
VD= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =5φ φ 36- Sim. - Sim. 2φ φ Não. V_{d}={frac {5varphi ^{3}}{6-2varphi }}}
.
Assim como para o icosaedro:
AEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =20.φ φ 22Não. A_{i}=20{frac {varphi ^{2}}{2}}}
e
VEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =56(1+φ φ ).Não. V_{i}={frac {5}{6}}(1+varphi).}
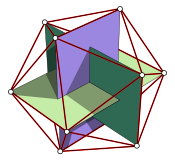
Três retângulos dourados tocam todos os
12 vértices de um icosahedron regular.
Esses valores geométricos podem ser calculados a partir de suas coordenadas cartesianas, que também podem ser dados usando fórmulas envolvendo φ φ - Sim. . As coordenadas do dodecaedro são exibidas na figura acima, enquanto as do icosaedro são as permutações cíclicas de:
. As coordenadas do dodecaedro são exibidas na figura acima, enquanto as do icosaedro são as permutações cíclicas de:
(0,± ± 1,± ± φ φ ){displaystyle (0,pm 1,pm varphi)}
,
(± ± 1,± ± φ φ ,0)(pm 1,pm varphi0)}
,
(± ± φ φ ,0,± ± 1).(pm varphi0,pm 1). ?
Conjuntos de três retângulos dourados se cruzam perpendicularmente dentro dodecahedra e icosahedra, formando anéis Borromean. Em dodecahedra, pares de vértices opostos em retângulos dourados encontram os centros de rostos pentagonais, e em icosahedra, encontram-se em seus vértices. No total, os três retângulos dourados contêm 12Não. vértices do icosahedron, ou equivalentemente, intersetem os centros de 12Não.
vértices do icosahedron, ou equivalentemente, intersetem os centros de 12Não. das caras do decaedro.
das caras do decaedro.
Um cubo pode ser inscrito em um dodecaedro regular, com algumas das diagonais das faces pentagonais do dodecaedro servindo como as bordas do cubo; portanto, os comprimentos da borda estão na proporção de ouro. O volume do cubo é 22+φ φ (2}{2+varphi) vezes o dodecaedro. De fato, os retângulos dourados dentro de um dodecaedro estão em proporções douradas a um cubo inscrito, tais que as bordas de um cubo e as bordas longas de um retângulo dourado estão em si mesmos φ φ :φ φ 2Não. varphi:varphi ^{2}}
vezes o dodecaedro. De fato, os retângulos dourados dentro de um dodecaedro estão em proporções douradas a um cubo inscrito, tais que as bordas de um cubo e as bordas longas de um retângulo dourado estão em si mesmos φ φ :φ φ 2Não. varphi:varphi ^{2}} ratio. Por outro lado, o octahedron, que é o poliedro duplo do cubo, pode inscrever um icosahedron, de tal forma que um icosahedron's 12Não.
ratio. Por outro lado, o octahedron, que é o poliedro duplo do cubo, pode inscrever um icosahedron, de tal forma que um icosahedron's 12Não. vértices tocar o 12Não.
vértices tocar o 12Não. bordas de um octahedron em pontos que dividem suas bordas em proporção de ouro.
bordas de um octahedron em pontos que dividem suas bordas em proporção de ouro.
Outros poliedros estão relacionados com o dodecaedro e o icosaedro ou suas simetrias e, portanto, têm relações correspondentes com a proporção áurea. Estes incluem o composto de cinco cubos, composto de cinco octaedros, composto de cinco tetraedros, o composto de dez tetraedros, triacontaedro rômbico, icosidodecaedro, icosaedro truncado, dodecaedro truncado e rombicosidodecaedro, eneacontaedro rômbico e poliedro Kepler-Poinsot e hexecontaedro rômbico. Em quatro dimensões, o dodecaedro e o icosaedro aparecem como faces das células 120 e 600, que novamente têm dimensões relacionadas à proporção áurea.
Outras propriedades
A relação de ouro expansão decimal pode ser calculado através de métodos de definição de raiz, como o método de Newton ou o método de Halley, na equação x2- Sim. - Sim. x- Sim. - Sim. 1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0{displaystyle x^{2}-x-1=0} ou em x2- Sim. - Sim. 5= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0Não. x^{2}-5=0}
ou em x2- Sim. - Sim. 5= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0Não. x^{2}-5=0} (para calcular 5(5}}}
(para calcular 5(5}}} primeiro). O tempo necessário para computar nNão.
primeiro). O tempo necessário para computar nNão. dígitos da relação de ouro usando o método de Newton é essencialmente O(M(n))(M(n)}
dígitos da relação de ouro usando o método de Newton é essencialmente O(M(n))(M(n)} , onde M(n)(n)}
, onde M(n)(n)} é a complexidade do tempo de multiplicar dois nNão.
é a complexidade do tempo de multiplicar dois nNão. - Números de dígitos. Isto é consideravelmente mais rápido do que algoritmos conhecidos para D D - Sim.
- Números de dígitos. Isto é consideravelmente mais rápido do que algoritmos conhecidos para D D - Sim. e eNão.
e eNão. . Uma alternativa facilmente programada usando apenas aritmética inteiro é calcular dois grandes números Fibonacci consecutivos e dividi-los. A proporção de números de Fibonacci F25000{displaystyle F_{25001}}
. Uma alternativa facilmente programada usando apenas aritmética inteiro é calcular dois grandes números Fibonacci consecutivos e dividi-los. A proporção de números de Fibonacci F25000{displaystyle F_{25001}} e F25000,- Sim.
e F25000,- Sim. cada um 5000.- Sim.
cada um 5000.- Sim. dígitos, rendimentos sobre 10.000- Sim.
dígitos, rendimentos sobre 10.000- Sim. dígitos significativos da relação de ouro. A expansão decimal da relação dourada φ φ - Sim.
dígitos significativos da relação de ouro. A expansão decimal da relação dourada φ φ - Sim. foi calculado para uma precisão de dez trilhões (1× × 10.13= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =10.000.10^{13}=10{,}000{,}000{,}000{,}000}
foi calculado para uma precisão de dez trilhões (1× × 10.13= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =10.000.10^{13}=10{,}000{,}000{,}000{,}000} ) dígitos.
) dígitos.
No plano complexo, as quintas raízes da unidade zangão.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =e2D D kEu.../5{displaystyle z=e^{2pi ki/5}} (para um inteiro k- Sim.
(para um inteiro k- Sim. ) satisfação zangão.5= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1- Sim.
) satisfação zangão.5= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1- Sim. são os vértices de um pentágono. Eles não formam um anel de inteiros quadráticos, contudo a soma de qualquer quinta raiz da unidade e sua conjugação complexa, zangão.+zangão.? ? ,{displaystyle z+{bar {z}},}
são os vértices de um pentágono. Eles não formam um anel de inteiros quadráticos, contudo a soma de qualquer quinta raiz da unidade e sua conjugação complexa, zangão.+zangão.? ? ,{displaystyle z+{bar {z}},} o um inteiro quadrático, um elemento de Z.Não.φ φ ].- Sim. Não.
o um inteiro quadrático, um elemento de Z.Não.φ φ ].- Sim. Não.![{textstyle mathbb {Z} [varphi ].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c19ab3d8278828be7f591bad1dc4482e4aaac6d) Especificamente,
Especificamente,
e0+e- Sim. - Sim. 0= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2,e2D D Eu.../5+e- Sim. - Sim. 2D D Eu.../5= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ - Sim. - Sim. 1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. 1+φ φ ,e4D D Eu.../5+e- Sim. - Sim. 4D D Eu.../5= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. φ φ .{displaystyle {begin{aligned}e^{0}+e^{-0}&=2,[5mu]e^{2pi i/5}+e^{-2pi i/5} > ^{-1}=-1+varphi[5mu]e^{4pi i/5}+e^{-4 i/5}&=-varphi.end{aligned}}}![{displaystyle {begin{aligned}e^{0}+e^{-0}&=2,\[5mu]e^{2pi i/5}+e^{-2pi i/5}&=varphi ^{-1}=-1+varphi\[5mu]e^{4pi i/5}+e^{-4pi i/5}&=-varphi.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bec7bcbd2e99aef0874eb163966c3e2dd9424b86)
Isto também é válido para as restantes dez raízes da unidade que satisfazem zangão.10.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1,{displaystyle z^{10}=1,}
eD D Eu...+e- Sim. - Sim. D D Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. 2,eD D Eu.../5+e- Sim. - Sim. D D Eu.../5= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ ,e3D D Eu.../5+e- Sim. - Sim. 3D D Eu.../5= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. φ φ - Sim. - Sim. 1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1- Sim. - Sim. φ φ .{displaystyle {begin{aligned}e^{pi i}+e^{-pi i}&=-2,[5mu]e^{pi i/5}+e^{-pi i/5}&=varphi[5mu]e^{3pi i/5}+e^{-3pi i/5}&=- ^{-1}=1-varphi.end{aligned}}}![{displaystyle {begin{aligned}e^{pi i}+e^{-pi i}&=-2,\[5mu]e^{pi i/5}+e^{-pi i/5}&=varphi\[5mu]e^{3pi i/5}+e^{-3pi i/5}&=-varphi ^{-1}=1-varphi.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9459634b32b6990a97eb560ce696a3bc2e722513)
Para a função gama )) Não. "Gamma" , as únicas soluções para a equação )) (zangão.- Sim. - Sim. 1)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =)) (zangão.+1){displaystyle Gamma (z-1)=Gamma (z+1)}
, as únicas soluções para a equação )) (zangão.- Sim. - Sim. 1)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =)) (zangão.+1){displaystyle Gamma (z-1)=Gamma (z+1)} são zangão.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ - Sim.
são zangão.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ - Sim. e zangão.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. φ φ - Sim. - Sim. 1{displaystyle z=-varphi ^{-1}}
e zangão.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. φ φ - Sim. - Sim. 1{displaystyle z=-varphi ^{-1}} .
.
Quando a proporção de ouro é usada como base de um sistema numeral (veja base de proporção de ouro, às vezes dublado phinary ou φ φ - Sim. - Nancy.), inteiros quadráticos no anel Z.Não.φ φ ]- Sim.
- Nancy.), inteiros quadráticos no anel Z.Não.φ φ ]- Sim.![{displaystyle mathbb {Z} [varphi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14f984c2710477c64fca0f16a71928134bdb8201) – isto é, números da forma um+b)φ φ - Sim.
– isto é, números da forma um+b)φ φ - Sim. para um,b)∈ ∈ Z.{displaystyle a,bin mathbb {Z} }
para um,b)∈ ∈ Z.{displaystyle a,bin mathbb {Z} } – têm representações terminantes, mas frações racionais têm representações não-terminantes.
– têm representações terminantes, mas frações racionais têm representações não-terminantes.
A proporção de ouro também aparece na geometria hiperbólica, como a distância máxima de um ponto em um lado de um triângulo ideal para o mais perto dos outros dois lados: esta distância, o comprimento lateral do triângulo equilátero formado pelos pontos de tangência de um círculo inscrito dentro do triângulo ideal, é 4log (φ φ ).{displaystyle 4log(varphi).}
A relação de ouro aparece também na teoria das funções modulares. Para <math alttext="{displaystyle left|qright||q|<1{displaystyle left|qright|<1}}<img alt="{displaystyle left|qright|, let
R(q)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =q1/51+q1+q21+q31+⋱ ⋱ .{displaystyle R(q)={cfrac {q^{1/5}}{1+{cfrac Não. {q^{2}}{1+{cfrac {q^{3}}{1+ddots }}}}}}.}
Então
R(e- Sim. - Sim. 2D D )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ 5- Sim. - Sim. φ φ ,R(- Sim. - Sim. e- Sim. - Sim. D D )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ - Sim. - Sim. 1- Sim. - Sim. 2- Sim. - Sim. φ φ - Sim. - Sim. 1{displaystyle R(e^{-2pi })={sqrt {5}}-varphiquad R(-e^{-pi })=varphi ^{-1}-{sqrt {2-varphi ^{-1}}}}}}
e
R(e- Sim. - Sim. 2D D Eu.../? ? )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1- Sim. - Sim. φ φ R(e2D D Eu...? ? )φ φ +R(e2D D Eu...? ? ){displaystyle R(e^{-2pi i/tau })={frac {1-varphi R(e^{2pi itau })}{varphi +R(e^{2pi itau })}}}
Onde? 0}" xmlns="http://www.w3.org/1998/Math/MathML">Eu... ? ? >0{displaystyle operatorname} Não.![]() 0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e3cbb8e8cc06392e462125f6bbe9c9cfe4906bae" style="vertical-align: -0.338ex; width:8.625ex; height:2.176ex;"/> e (ezangão.)1/5(e^{z})^{1/5}}
0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e3cbb8e8cc06392e462125f6bbe9c9cfe4906bae" style="vertical-align: -0.338ex; width:8.625ex; height:2.176ex;"/> e (ezangão.)1/5(e^{z})^{1/5}} na fração contínua deve ser avaliado como ezangão./5O que é isso?
na fração contínua deve ser avaliado como ezangão./5O que é isso? . A função ? ? ↦ ↦ R(e2D D Eu...? ? ){displaystyle tau mapsto R(e^{2pi itau })}
. A função ? ? ↦ ↦ R(e2D D Eu...? ? ){displaystyle tau mapsto R(e^{2pi itau })} é invariante sob )) (5){displaystyle Gamma (5)}
é invariante sob )) (5){displaystyle Gamma (5)} , um subgrupo de congruência do grupo modular. Também para números reais positivos um,b)∈ ∈ R+{displaystyle a,bin mathbb {R} ^{+}}
, um subgrupo de congruência do grupo modular. Também para números reais positivos um,b)∈ ∈ R+{displaystyle a,bin mathbb {R} ^{+}} e umb)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =D D 2,{displaystyle ab=pi ^{2},}
e umb)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =D D 2,{displaystyle ab=pi ^{2},} então
então
(φ φ +R(e- Sim. - Sim. 2um))(φ φ +R(e- Sim. - Sim. 2b)))= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ 5,(φ φ - Sim. - Sim. 1- Sim. - Sim. R(- Sim. - Sim. e- Sim. - Sim. um))(φ φ - Sim. - Sim. 1- Sim. - Sim. R(- Sim. - Sim. e- Sim. - Sim. b)))= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =φ φ - Sim. - Sim. 15.Não. Bigl (}varphi +R{{bigl (}e^{-2a}{bigr)}}{Bigr)}{Bigl (}varphi +R{{bigl (}e^{-2b}{bigr)}} Bigr)}&=varphi {sqrt {5}},[5mu]{Bigl (}varphi ^{-1}-R{{bigl (}{-e^{-a}}{bigr)}}{Bigr)} Bigl (}varphi ^{-1}-R{{bigl (}{-e^{-b}}{bigr)}} Bigr)}&=varphi ^{-1}{sqrt {5}}.end{aligned}}}![{displaystyle {begin{aligned}{Bigl (}varphi +R{{bigl (}e^{-2a}{bigr)}}{Bigr)}{Bigl (}varphi +R{{bigl (}e^{-2b}{bigr)}}{Bigr)}&=varphi {sqrt {5}},\[5mu]{Bigl (}varphi ^{-1}-R{{bigl (}{-e^{-a}}{bigr)}}{Bigr)}{Bigl (}varphi ^{-1}-R{{bigl (}{-e^{-b}}{bigr)}}{Bigr)}&=varphi ^{-1}{sqrt {5}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efa72855991c37845330a894d36b1d91647a265a)
φ φ - Sim. é um número Pisot-Vijayaraghavan.
é um número Pisot-Vijayaraghavan.
Aplicações e observações
Arquitetura
O arquiteto suíço Le Corbusier, famoso por suas contribuições ao estilo moderno internacional, centrou sua filosofia de design em sistemas de harmonia e proporção. A fé de Le Corbusier na ordem matemática do universo estava intimamente ligada à proporção áurea e à série de Fibonacci, que ele descreveu como "ritmos aparentes aos olhos e claros em suas relações uns com os outros". E esses ritmos estão na própria raiz das atividades humanas. Eles ressoam no homem por uma inevitabilidade orgânica, a mesma fina inevitabilidade que faz com que as crianças, os velhos, os selvagens e os eruditos desviem a Seção Áurea”.
Le Corbusier usou explicitamente a proporção áurea em seu sistema Modulor para a escala da proporção arquitetônica. Ele viu esse sistema como uma continuação da longa tradição de Vitruvius, o "Homem Vitruviano" de Leonardo da Vinci, o trabalho de Leon Battista Alberti e outros que usaram as proporções do corpo humano para melhorar a aparência e a função da arquitetura.
Além da proporção áurea, Le Corbusier baseou o sistema em medições humanas, números de Fibonacci e a unidade dupla. Ele levou a sugestão da proporção áurea em proporções humanas ao extremo: seccionou a altura de seu modelo de corpo humano no umbigo com as duas seções na proporção áurea, depois subdividiu essas seções na proporção áurea nos joelhos e na garganta; ele usou essas proporções áureas no sistema Modulor. A Villa Stein de 1927 de Le Corbusier em Garches exemplificou a aplicação do sistema Modulor. A planta retangular, a elevação e a estrutura interna da villa se aproximam dos retângulos dourados.
Outro arquiteto suíço, Mario Botta, baseia muitos de seus projetos em figuras geométricas. Várias casas particulares que ele projetou na Suíça são compostas de quadrados e círculos, cubos e cilindros. Em uma casa que projetou em Origlio, a proporção áurea é a proporção entre a seção central e as seções laterais da casa.
Arte
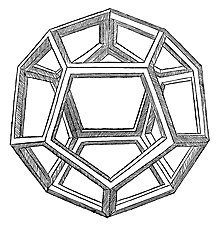
Ilustração de Da Vinci de um dodecaedro de Pacioli
Divina proporcional (1509)
As ilustrações de poliedros de Leonardo da Vinci em Divina ratio de Pacioli levaram alguns a especular que ele incorporou a proporção áurea em suas pinturas. Mas a sugestão de que sua Mona Lisa, por exemplo, emprega proporções áureas, não é apoiada pelos próprios escritos de Leonardo. Da mesma forma, embora o Homem Vitruviano de Leonardo seja frequentemente mostrado em conexão com a proporção áurea, as proporções da figura não correspondem a ela, e o texto apenas menciona proporções de números inteiros.
Salvador Dalí, influenciado pelas obras de Matila Ghyka, usou explicitamente a proporção áurea em sua obra-prima, O Sacramento da Última Ceia. As dimensões da tela são um retângulo dourado. Um enorme dodecaedro, em perspectiva de modo que as arestas apareçam em proporção áurea entre si, está suspenso acima e atrás de Jesus e domina a composição.
Um estudo estatístico sobre 565 obras de arte de diferentes grandes pintores, realizado em 1999, descobriu que esses artistas não tinham usado a proporção de ouro no tamanho de suas telas. O estudo concluiu que a relação média dos dois lados das pinturas estudadas é 1.3.,Não. com médias para artistas individuais que vão desde 1.04- Sim.
com médias para artistas individuais que vão desde 1.04- Sim. (Goya) para 1.4.46Não.
(Goya) para 1.4.46Não. (Bellini). Por outro lado, Pablo Tosto listou mais de 350 obras de artistas bem conhecidos, incluindo mais de 100 que têm telas com retângulo dourado e 5(5}}}
(Bellini). Por outro lado, Pablo Tosto listou mais de 350 obras de artistas bem conhecidos, incluindo mais de 100 que têm telas com retângulo dourado e 5(5}}} proporções, e outros com proporções como 2,{displaystyle {sqrt {2}},}
proporções, e outros com proporções como 2,{displaystyle {sqrt {2}},} 3,- Sim.
3,- Sim. 4,- Sim.
4,- Sim. e 6.Não. 6.
e 6.Não. 6.

Depicção das proporções em um manuscrito medieval. De acordo com Jan Tschichold: "Página proporção 2:3. Proporções de margem 1:1:2:3. Área de texto proporcionada na Seção de Ouro."
Livros e design
De acordo com Jan Tschichold,
Houve um tempo em que os desvios das proporções verdadeiramente belas da página 2:3,{displaystyle 2mathbin {:} 3,} 1:3,{displaystyle 1mathbin {:} {sqrt {3}},}
1:3,{displaystyle 1mathbin {:} {sqrt {3}},} e a Seção Dourada eram raras. Muitos livros produzidos entre 1550 e 1770 mostram essas proporções exatamente, para dentro de meio milímetro.
e a Seção Dourada eram raras. Muitos livros produzidos entre 1550 e 1770 mostram essas proporções exatamente, para dentro de meio milímetro.
De acordo com algumas fontes, a proporção áurea é usada no design cotidiano, por exemplo, nas proporções de cartas de baralho, cartões postais, pôsteres, placas de interruptores de luz e televisores widescreen.
Sinalizadores

A bandeira de Togo, cuja relação de aspecto usa a relação de ouro
A proporção (largura e altura) da bandeira do Togo foi planejada para ser a proporção áurea, de acordo com seu criador.
Música
Ernő Lendvai analisa as obras de Béla Bartók como sendo baseadas em dois sistemas opostos, o da proporção áurea e a escala acústica, embora outros estudiosos da música rejeitem essa análise. O compositor francês Erik Satie usou a proporção áurea em várias de suas peças, incluindo Sonneries de la Rose+Croix. A proporção áurea também é aparente na organização das seções na música de Reflets dans l'eau (Reflexões na Água) de Debussy, de Imagens (1ª série, 1905), em que "a sequência de teclas é marcada pelos intervalos 34, 21, 13 e 8, e o clímax principal fica na posição phi".
O musicólogo Roy Howat observou que os limites formais de La Mer de Debussy correspondem exatamente à seção áurea. Trezise considera a evidência intrínseca "notável", mas adverte que nenhuma evidência escrita ou relatada sugere que Debussy buscou conscientemente tais proporções.
Teóricos da música, incluindo Hans Zender e Heinz Bohlen, experimentaram a escala de 833 centavos, uma escala musical baseada no uso da proporção áurea como seu intervalo musical fundamental. Quando medida em centavos, uma escala logarítmica para intervalos musicais, a proporção áurea é de aproximadamente 833,09 centavos.
Natureza

Detalhe da planta do disco,
Aeonium tabuliforme, mostrando o arranjo espiral múltipla (parastichy)
Johannes Kepler escreveu que "a imagem do homem e da mulher decorre da proporção divina. Na minha opinião, a propagação de plantas e os atos progenitivos de animais estão na mesma proporção".
O psicólogo Adolf Zeising observou que a proporção áurea apareceu na filotaxia e argumentou a partir desses padrões na natureza que a proporção áurea era uma lei universal. Zeising escreveu em 1854 sobre uma lei ortogenética universal de "lutar pela beleza e completude nos reinos da natureza e da arte".
No entanto, alguns argumentaram que muitas manifestações aparentes da proporção áurea na natureza, especialmente no que diz respeito às dimensões dos animais, são fictícias.
Física
O ferromagneto Ising quase unidimensional CoNb2O6 (niobato de cobalto) tem 8 estados de excitação previstos (com simetria E8), que quando sondados com espalhamento de nêutrons, mostrou que seus dois menores estavam na proporção áurea. Especificamente, essas transições de fase quântica durante a excitação do spin, que ocorrem próximo à temperatura do zero absoluto, mostraram pares de kinks em sua fase ordenada para spin-flips em sua fase paramagnética; revelando, logo abaixo de seu campo crítico, uma dinâmica de spin com modos agudos em baixas energias aproximando-se da média áurea.
Otimização
Não há nenhum algoritmo geral conhecido para organizar um determinado número de nós uniformemente em uma esfera, para qualquer uma de várias definições de distribuição uniforme (veja, por exemplo, Problema de Thomson ou Problema de Tammes). No entanto, uma aproximação útil resulta de dividir a esfera em bandas paralelas de área de superfície igual e colocar um nó em cada banda em longitudes espaçadas por uma seção dourada do círculo, ou seja,. 360.∘ ∘ /φ φ ? ? 222.∘ ∘ .{displaystyle 360^{circ }/varphi approx 222.5^{circ }.} Este método foi usado para organizar os 1500 espelhos do satélite aluno-participatório Starshine-3.
Este método foi usado para organizar os 1500 espelhos do satélite aluno-participatório Starshine-3.
A proporção áurea também é um elemento crítico para a pesquisa da seção áurea.
Observações contestadas
Exemplos de observações contestadas da proporção áurea incluem o seguinte:

As conchas Nautilus são muitas vezes erroneamente reivindicadas como sendo de ouro proporcional.
- Proporções específicas nos corpos de vertebrados (incluindo humanos) são muitas vezes reivindicadas como sendo na proporção de ouro; por exemplo, a proporção de ossos falangeais e metacarpos sucessivos (ossos de dedos) foi dito para aproximar a proporção de ouro. Há uma grande variação nas medidas reais desses elementos em indivíduos específicos, no entanto, e a proporção em questão é muitas vezes significativamente diferente da proporção de ouro.
- As conchas de moluscos, como o nautilus, são muitas vezes alegadamente na proporção de ouro. O crescimento de conchas nautilus segue uma espiral logarítmica, e às vezes é erroneamente afirmado que qualquer espiral logarítmica está relacionada à relação de ouro, ou às vezes alegado que cada nova câmara é proporcional a ouro em relação à anterior. No entanto, as medidas de conchas nautilus não suportam esta reivindicação.
- Historiador John O homem afirma que as páginas e a área de texto da Bíblia de Gutenberg foram "baseadas na forma da seção dourada". No entanto, de acordo com suas próprias medidas, a proporção de altura para largura das páginas é 1.45.- Sim.

- Estudos por psicólogos, começando com Gustav Fechner c. 1876, foram concebidos para testar a ideia de que a proporção de ouro desempenha um papel na percepção humana da beleza. Enquanto Fechner encontrou uma preferência por rácios retângulos centrados na proporção de ouro, tentativas posteriores de testar cuidadosamente essa hipótese foram, na melhor das hipóteses, inconclusivas.
- No investimento, alguns praticantes de análise técnica usam a relação de ouro para indicar o suporte de um nível de preço, ou a resistência a aumentos de preços, de um estoque ou mercadoria; após mudanças significativas de preços para cima ou para baixo, novos níveis de apoio e resistência são supostamente encontrados a ou perto de preços relacionados com o preço inicial através da relação de ouro. O uso da relação de ouro no investimento também está relacionado a padrões mais complicados descritos pelos números de Fibonacci (por exemplo, princípio de onda Elliott e retracemento de Fibonacci). No entanto, outros analistas de mercado publicaram análises sugerindo que essas percentagens e padrões não são suportados pelos dados.
Pirâmides egípcias

A Grande Pirâmide de Giza
A Grande Pirâmide de Gizé (também conhecida como Pirâmide de Quéops ou Khufu) foi analisada por piramidologistas como tendo um triângulo duplo de Kepler como sua seção transversal. Se essa teoria fosse verdadeira, a proporção áurea descreveria a razão das distâncias do ponto médio de um dos lados da pirâmide ao seu ápice e do mesmo ponto médio ao centro da base da pirâmide. No entanto, a imprecisão na medição causada em parte pela remoção da superfície externa da pirâmide torna impossível distinguir esta teoria de outras teorias numéricas das proporções da pirâmide, baseadas em pi ou em proporções de números inteiros. O consenso dos estudiosos modernos é que as proporções dessa pirâmide não são baseadas na proporção áurea, porque tal base seria inconsistente tanto com o que se sabe sobre a matemática egípcia desde a época da construção da pirâmide quanto com as teorias egípcias. de arquitetura e proporção usados em suas outras obras.
O Partenon

Muitas das proporções do Parthenon são supostas para exibir a relação de ouro, mas isso foi amplamente desacreditado.
A fachada do Partenon (c. 432 aC), bem como os elementos de sua fachada e em outros lugares, são circunscritos por retângulos dourados. Outros estudiosos negam que os gregos tivessem qualquer associação estética com a proporção áurea. Por exemplo, Keith Devlin diz: "Certamente, a afirmação frequentemente repetida de que o Partenon em Atenas é baseado na proporção áurea não é suportada por medições reais. Na verdade, toda a história sobre os gregos e a proporção áurea parece não ter fundamento." Midhat J. Gazalé afirma que "Não foi até Euclides... que as propriedades matemáticas da proporção áurea foram estudadas."
A partir de medições de 15 templos, 18 túmulos monumentais, 8 sarcófagos e 58 estelas graves do século V aC ao século II dC, um pesquisador concluiu que a proporção áurea estava totalmente ausente da arquitetura grega do século V clássico aC, e quase ausente durante os seis séculos seguintes.
Fontes posteriores como Vitrúvio (primeiro século aC) discutem exclusivamente proporções que podem ser expressas em números inteiros, ou seja, proporcionais em oposição a proporções irracionais.
Arte moderna

Albert Gleizes,
Les Baigneuses (1912)
A Section d'Or ('Golden Section') era um coletivo de pintores, escultores, poetas e críticos associados ao cubismo e ao orfismo. Ativos de 1911 a cerca de 1914, eles adotaram o nome tanto para destacar que o cubismo representava a continuação de uma grande tradição, em vez de ser um movimento isolado, quanto em homenagem à harmonia matemática associada a Georges Seurat. (Vários autores afirmaram que Seurat empregou a proporção áurea em suas pinturas, mas os escritos e pinturas de Seurat sugerem que ele empregou proporções simples de números inteiros e qualquer aproximação da proporção áurea foi coincidência.) Os cubistas observaram em suas harmonias, estrutura geométrica de movimento e forma, "a primazia da ideia sobre a natureza", "uma absoluta clareza científica de concepção". No entanto, apesar desse interesse geral pela harmonia matemática, é mais difícil determinar se as pinturas apresentadas na célebre exposição Salon de la Section d'Or de 1912 usavam a proporção áurea em qualquer composição. Lívio, por exemplo, afirma que não, e Marcel Duchamp disse isso em uma entrevista. Por outro lado, uma análise sugere que Juan Gris utilizou a proporção áurea para compor obras que provavelmente, mas não definitivamente, seriam exibidas na exposição. O historiador de arte Daniel Robbins argumentou que, além de fazer referência ao termo matemático, o nome da exposição também se refere ao antigo grupo Bandeaux d'Or, com o qual Albert Gleizes e outros ex-membros da Abbaye de Créteil estava envolvido.
Diz-se que Piet Mondrian usou extensivamente a seção áurea em suas pinturas geométricas, embora outros especialistas (incluindo o crítico Yve-Alain Bois) tenham desacreditado essas afirmações.
Más resultados...

b > 0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/dc57e5721ebc7b851b968ea2545913848bf7a01e" style="vertical-align: -0.338ex; width:9.587ex; height:2.176ex;"/>,


0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e3cbb8e8cc06392e462125f6bbe9c9cfe4906bae" style="vertical-align: -0.338ex; width:8.625ex; height:2.176ex;"/> e (ezangão.)1/5(e^{z})^{1/5}} na fração contínua deve ser avaliado como ezangão./5O que é isso?. A função ? ? ↦ ↦ R(e2D D Eu...? ? ){displaystyle tau mapsto R(e^{2pi itau })} é invariante sob )) (5){displaystyle Gamma (5)}, um subgrupo de congruência do grupo modular. Também para números reais positivos um,b)∈ ∈ R+{displaystyle a,bin mathbb {R} ^{+}} e umb)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =D D 2,{displaystyle ab=pi ^{2},} então









































![{displaystyle {begin{aligned}varphi ^{2}&=varphi +1=2.618033dots\[5mu]{frac {1}{varphi }}&=varphi -1=0.618033dots.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff2e5225abf67548cf93c882add3a4b439c4aeb8)






![{displaystyle {begin{aligned}varphi ^{n}&=varphi ^{n-1}+varphi ^{n-3}+cdots +varphi ^{n-1-2m}+varphi ^{n-2-2m}\[5mu]varphi ^{n}-varphi ^{n-1}&=varphi ^{n-2}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/048f09b7012c7fbd3d9f32798de6dd5c01acabcd)


![varphi =[1;1,1,1,dots ]=1+{cfrac {1}{1+{cfrac {1}{1+{cfrac {1}{1+ddots }}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95682588ffee3530627c3a7b00ff08bbba6e97d4)
![varphi ^{-1}=[0;1,1,1,dots ]=0+{cfrac {1}{1+{cfrac {1}{1+{cfrac {1}{1+ddots }}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/165d255e32f4b9af1f9144f15302b147fc3fead2)
















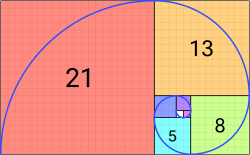
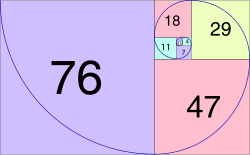






































![{displaystyle {begin{aligned}3varphi ^{3}-5varphi ^{2}+4&=3(varphi ^{2}+varphi)-5varphi ^{2}+4\[5mu]&=3[(varphi +1)+varphi ]-5(varphi +1)+4\[5mu]&=varphi +2approx 3.618033.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60ff8508aa117064d60142d447fb0cb58a809848)


![{displaystyle {begin{aligned}varphi ^{0}&=1,\[5mu]varphi ^{1}&=1.618033989...approx 2,\[5mu]varphi ^{2}&=2.618033989...approx 3,\[5mu]varphi ^{3}&=4.236067978...approx 4,\[5mu]varphi ^{4}&=6.854101967...approx 7,end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20c9bfd2f9bdc877282b290adc74c88f1dfa63c8)






























![{displaystyle {begin{aligned}{frac {2pi -g}{g}}&={frac {2pi }{2pi -g}}=varphi\[8mu]2pi -g&={frac {2pi }{varphi }}approx 222.5^{circ },\[8mu]g&={frac {2pi }{varphi ^{2}}}approx 137.5^{circ }.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd5f9122b38d09e0cd2992820f27b8587efd167a)






![{displaystyle {begin{aligned}varphi &=1+2sin(pi /10)=1+2sin 18^{circ },\[5mu]varphi &={tfrac {1}{2}}csc(pi /10)={tfrac {1}{2}}csc 18^{circ },\[5mu]varphi &=2cos(pi /5)=2cos 36^{circ },\[5mu]varphi &=2sin(3pi /10)=2sin 54^{circ }.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c42bbf25d6257a00fad895691aa2c5eb0c6f57a)



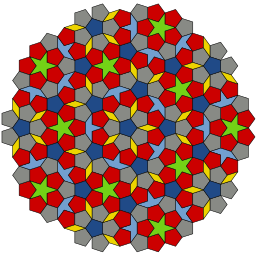


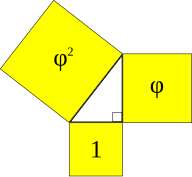




![{displaystyle {begin{aligned}A&={tfrac {s^{2}}{2}}{sqrt {varphi }},\[5mu]theta &=sin ^{-1}{frac {1}{varphi }}approx 38.1727^{circ },\[5mu]theta &=cos ^{-1}{frac {1}{varphi }}approx 51.8273^{circ }.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f96fa323a2e180a6198f05d33c13e1631854e840)
![{displaystyle {begin{aligned}alpha &=2arctan {1 over varphi }approx 63.43495^{circ },\[5mu]beta &=2arctan varphi =pi -arctan 2=arctan 1+arctan 3approx 116.56505^{circ }.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c5a4321454f4ca1b41b0dbd8f2c6c4afd48467e)


![{displaystyle {begin{aligned}d&={2a over {sqrt {2+varphi }}}=2{sqrt {{3-varphi } over 5}}aapprox 1.05146a,\[5mu]D&=2{sqrt {{2+varphi } over 5}}aapprox 1.70130a.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d00bbc42679ab9e34fdf849ac68de75180cc92c7)
![{displaystyle {begin{aligned}A&=(sin(arctan 2))~a^{2}={2 over {sqrt {5}}}~a^{2}approx 0.89443a^{2},\[5mu]A&={{varphi } over 2}d^{2}approx 0.80902d^{2}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7bed70dcf23f16f3f8241aeaf2b56f0897244ff3)




















































![{textstyle mathbb {Z} [varphi ].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c19ab3d8278828be7f591bad1dc4482e4aaac6d)
![{displaystyle {begin{aligned}e^{0}+e^{-0}&=2,\[5mu]e^{2pi i/5}+e^{-2pi i/5}&=varphi ^{-1}=-1+varphi\[5mu]e^{4pi i/5}+e^{-4pi i/5}&=-varphi.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bec7bcbd2e99aef0874eb163966c3e2dd9424b86)

![{displaystyle {begin{aligned}e^{pi i}+e^{-pi i}&=-2,\[5mu]e^{pi i/5}+e^{-pi i/5}&=varphi\[5mu]e^{3pi i/5}+e^{-3pi i/5}&=-varphi ^{-1}=1-varphi.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9459634b32b6990a97eb560ce696a3bc2e722513)




![{displaystyle mathbb {Z} [varphi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14f984c2710477c64fca0f16a71928134bdb8201)












![{displaystyle {begin{aligned}{Bigl (}varphi +R{{bigl (}e^{-2a}{bigr)}}{Bigr)}{Bigl (}varphi +R{{bigl (}e^{-2b}{bigr)}}{Bigr)}&=varphi {sqrt {5}},\[5mu]{Bigl (}varphi ^{-1}-R{{bigl (}{-e^{-a}}{bigr)}}{Bigr)}{Bigl (}varphi ^{-1}-R{{bigl (}{-e^{-b}}{bigr)}}{Bigr)}&=varphi ^{-1}{sqrt {5}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efa72855991c37845330a894d36b1d91647a265a)
















