Projeção de Mercator

Projeção de Mercator do mundo entre 85°S e 85°N. Note a comparação de tamanho da Groenlândia e África.

A projeção do Mercator com o indicador de deformação de Tissot.

Mercator 1569 mapa do mundo (Nova et Aucta Orbis Terrae Descriptio ad Usum Navigantium Emendar dados do Accommo) mostrando latitudes 66°S a 80°N.

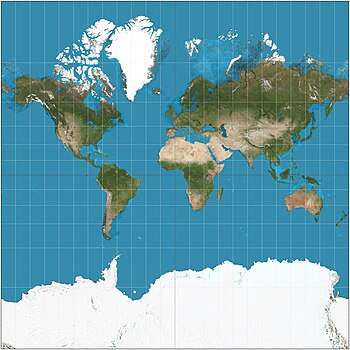
A projeção de Mercator () é uma projeção de mapa cilíndrica apresentada pelo geógrafo e cartógrafo flamengo Gerardus Mercator em 1569. Tornou-se a projeção de mapa padrão para navegação porque é única na representação do norte como para cima e para o sul como para baixo em todos os lugares, preservando as direções e formas locais. O mapa é assim conforme. Como efeito colateral, a projeção de Mercator aumenta o tamanho dos objetos longe do equador. Esta inflação é muito pequena perto do equador, mas acelera com o aumento da latitude para se tornar infinita nos pólos. Como resultado, as massas de terra como a Groenlândia, a Antártica, o Canadá e a Rússia parecem muito maiores do que realmente são em relação às massas de terra próximas ao equador, como a África Central.

História

Existe alguma controvérsia sobre as origens do Mercator. O polímata alemão Erhard Etzlaub gravou "mapas de bússola" em miniatura; (cerca de 10 × 8 cm) da Europa e partes da África que abrangem as latitudes de 0 ° a 67 ° para permitir o ajuste de seus relógios de sol portáteis de bolso. A projeção encontrada nesses mapas, datada de 1511, foi declarada por John Snyder em 1987 como sendo a mesma projeção de Mercator. No entanto, dada a geometria de um relógio de sol, esses mapas podem muito bem ter sido baseados na projeção cilíndrica central semelhante, um caso limite da projeção gnomônica, que é a base para um relógio de sol. Snyder alterou sua avaliação para "uma projeção semelhante" em 1993.

Joseph Needham, um historiador da China, escreveu que os chineses desenvolveram a projeção de Mercator centenas de anos antes de Mercator, usando-a em mapas estelares durante a Dinastia Song. No entanto, este foi um caso simples e comum de identificação incorreta. A projeção em uso foi a projeção equiretangular.

O matemático e cosmógrafo português Pedro Nunes foi o primeiro a descrever o princípio matemático do loxodromo e a sua utilização na navegação marítima. Em 1537, ele propôs a construção de um atlas náutico composto por várias folhas de grande escala na projeção cilíndrica equidistante como forma de minimizar a distorção das direções. Se essas folhas fossem colocadas na mesma escala e montadas, elas se aproximariam da projeção de Mercator.

Em 1569, Gerhard Kremer, conhecido por seu nome comercial Gerardus Mercator, anunciou uma nova projeção ao publicar um grande mapa planisférico medindo 202 por 124 cm (80 por 49 in) e impresso em dezoito folhas separadas. Mercator intitulou o mapa Nova et Aucta Orbis Terrae Descriptio ad Usum Navigantium Emendata: "Um novo e aumentado descrição da Terra corrigida para o uso dos marinheiros. Este título, juntamente com uma explicação elaborada para o uso da projeção que aparece como uma seção de texto no mapa, mostra que Mercator entendeu exatamente o que havia alcançado e que pretendia que a projeção ajudasse a navegação. Mercator nunca explicou o método de construção ou como chegou a ele. Várias hipóteses foram levantadas ao longo dos anos, mas, em qualquer caso, a amizade de Mercator com Pedro Nunes e seu acesso às tabelas loxodrômicas que Nunes criou provavelmente ajudaram seus esforços.

O matemático inglês Edward Wright publicou as primeiras tabelas precisas para a construção da projeção em 1599 e, com mais detalhes, em 1610, chamando seu tratado de "Certos erros na navegação". A primeira formulação matemática foi divulgada por volta de 1645 por um matemático chamado Henry Bond (c. 1600-1678). No entanto, a matemática envolvida foi desenvolvida, mas nunca publicada pelo matemático Thomas Harriot a partir de 1589.

O desenvolvimento da projeção de Mercator representou um grande avanço na cartografia náutica do século XVI. No entanto, estava muito à frente de seu tempo, pois as antigas técnicas de navegação e topografia não eram compatíveis com seu uso na navegação. Dois problemas principais impediam sua aplicação imediata: a impossibilidade de determinar a longitude no mar com precisão adequada e o fato de serem usadas direções magnéticas, em vez de direções geográficas, na navegação. Somente em meados do século 18, depois que o cronômetro marítimo foi inventado e a distribuição espacial da declinação magnética foi conhecida, a projeção de Mercator foi totalmente adotada pelos navegadores.

Apesar dessas limitações de localização, a projeção de Mercator pode ser encontrada em muitos mapas mundiais nos séculos seguintes à primeira publicação de Mercator. No entanto, não começou a dominar os mapas do mundo até o século 19, quando o problema da determinação da posição foi amplamente resolvido. Uma vez que o Mercator se tornou a projeção usual para mapas comerciais e educacionais, ele passou a sofrer críticas persistentes de cartógrafos por sua representação desequilibrada de massas de terra e sua incapacidade de mostrar as regiões polares de maneira útil.

As críticas levantadas contra o uso inapropriado da projeção de Mercator resultaram em uma enxurrada de novas invenções no final do século 19 e início do século 20, frequentemente apresentadas diretamente como alternativas ao Mercator. Devido a essas pressões, os editores reduziram gradualmente o uso da projeção ao longo do século XX. No entanto, o advento do mapeamento da Web deu à projeção um ressurgimento abrupto na forma da projeção da Web Mercator.

Hoje, o Mercator pode ser encontrado em cartas marítimas, mapas mundiais ocasionais e serviços de mapeamento da Web, mas os atlas comerciais o abandonaram em grande parte, e mapas murais do mundo podem ser encontrados em muitas projeções alternativas. O Google Maps, que dependia dele desde 2005, ainda o usa para mapas de áreas locais, mas abandonou a projeção de plataformas de desktop em 2017 para mapas com zoom reduzido de áreas locais. Muitos outros serviços de mapeamento online ainda usam exclusivamente o Web Mercator.

Propriedades

Comparação de formas tangentes e secantes de projeções normais, oblíquas e transversais do Mercator com paralelos padrão em vermelho

Como em todas as projeções cilíndricas, paralelos e meridianos no Mercator são retos e perpendiculares entre si. Ao conseguir isso, o inevitável alongamento leste-oeste do mapa, que aumenta à medida que a distância do equador aumenta, é acompanhado na projeção de Mercator por um correspondente alongamento norte-sul, de modo que em cada localização de ponto a escala leste-oeste é o mesmo que a escala norte-sul, tornando-se uma projeção de mapa conforme. As projeções conformes preservam os ângulos ao redor de todos os locais.

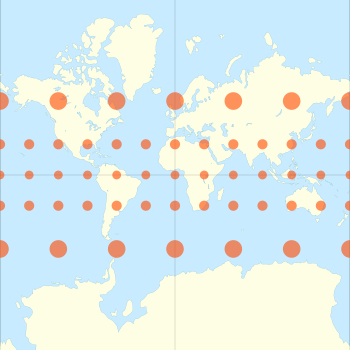
Como a escala linear de um mapa de Mercator aumenta com a latitude, ela distorce o tamanho dos objetos geográficos distantes do equador e transmite uma percepção distorcida da geometria geral do planeta. Em latitudes superiores a 70° norte ou sul, a projeção de Mercator é praticamente inutilizável, porque a escala linear torna-se infinitamente grande nos pólos. Um mapa de Mercator pode, portanto, nunca mostrar totalmente as áreas polares (desde que a projeção seja baseada em um cilindro centrado no eixo de rotação da Terra; veja a projeção transversal de Mercator para outra aplicação).

A projeção de Mercator mapeia trajetórias de orientação constante (chamadas linhas de loxodromia ou loxodromes) para linhas retas e, portanto, é adequada exclusivamente para a navegação marítima: cursos e orientações são medidos usando uma rosa dos ventos ou transferidor, e as direções correspondentes são facilmente transferidas de ponto a ponto, no mapa, por ex. com o auxílio de uma régua paralela.

A projeção de Mercator é frequentemente comparada e confundida com a projeção cilíndrica central, que é o resultado da projeção de pontos da esfera em um cilindro tangente ao longo de linhas radiais retas, como se fosse uma fonte de luz colocada na superfície da Terra. s centro. Ambos têm distorção extrema longe do equador e não podem mostrar os pólos. No entanto, são projeções diferentes e possuem propriedades diferentes.

Distorção de tamanhos

Proporções de tamanho aparente e tamanho real (animado)

Como em todas as projeções de mapas, formas ou tamanhos são distorções do verdadeiro layout da superfície da Terra.

A projeção de Mercator exagera áreas distantes do equador.

Exemplos de distorção de tamanho

• A Gronelândia aparece do mesmo tamanho que a África, quando na realidade a área da África é 14 vezes maior.
  • A área real da Gronelândia é comparável à única República Democrática do Congo.
  • A África parece ser aproximadamente o mesmo tamanho que a América do Sul, quando na realidade a África é mais de uma e meia vezes maior.

• Alasca parece ser o mesmo tamanho que a Austrália, embora a Austrália é na verdade 4,5 vezes maior.
  • O Alasca também ocupa tanto espaço no mapa como no Brasil, enquanto a área do Brasil é quase 5 vezes a do Alasca.

• Madagáscar e Grã-Bretanha olham sobre o mesmo tamanho, enquanto Madagascar é, na verdade, mais de duas vezes maior que a Grã-Bretanha.

Críticas

Devido às grandes distorções da área terrestre, críticos como George Kellaway e Irving Fisher consideram a projeção inadequada para mapas gerais do mundo. Por mostrar os países próximos ao Equador como muito pequenos quando comparados aos da Europa e da América do Norte, supostamente faz com que as pessoas considerem esses países como menos importantes. O próprio Mercator usou a projeção senoidal de área igual para mostrar as áreas relativas. No entanto, apesar de tais críticas, a projeção de Mercator foi, especialmente no final do século 19 e início do século 20, talvez a projeção mais comum usada em mapas do mundo.

Os atlas praticamente pararam de usar a projeção de Mercator para mapas do mundo ou para áreas distantes do equador na década de 1940, preferindo outras projeções cilíndricas ou formas de projeção de área igual. A projeção de Mercator, no entanto, ainda é comumente usada para áreas próximas ao equador onde a distorção é mínima. Também é freqüentemente encontrado em mapas de fusos horários. Por causa de seu uso comum, a projeção de Mercator supostamente influenciou a visão de mundo das pessoas.

Arno Peters gerou polêmica a partir de 1972, quando propôs o que agora é geralmente chamado de projeção de Gall-Peters para remediar os problemas do Mercator, alegando que era seu próprio trabalho original sem fazer referência a trabalhos anteriores de cartógrafos como Gall&#39 A obra de;s de 1855. A projeção que ele promoveu é uma parametrização específica da projeção cilíndrica de áreas iguais. Em resposta, uma resolução de 1989 de sete grupos geográficos norte-americanos desacreditou o uso de projeções cilíndricas para mapas mundiais de uso geral, que incluiriam tanto o Mercator quanto o Gall-Peters.

Usos

Praticamente todas as cartas náuticas impressas são baseadas na projeção de Mercator devido às suas propriedades exclusivamente favoráveis para a navegação. Também é comumente usado por serviços de mapa de ruas hospedados na Internet, devido às suas propriedades favoráveis exclusivas para mapas de área local calculados sob demanda. As projeções de Mercator também foram importantes no desenvolvimento matemático das placas tectônicas na década de 1960.

Navegação marítima

Uma linha de rhumb (azul) em comparação com um arco de grande círculo (vermelho) entre Lisboa, Portugal e Havana, Cuba. Top: projeção ortográfica. Parte de baixo: Projeção de Mercator.

A projeção de Mercator foi projetada para uso na navegação marítima por causa de sua propriedade única de representar qualquer curso de orientação constante como um segmento reto. Esse curso, conhecido como loxodromia (ou, matematicamente, loxodrômico) é preferido na navegação marítima porque os navios podem navegar em uma direção constante da bússola, reduzindo as correções de curso difíceis e propensas a erros que, de outra forma, seriam necessárias com frequência ao navegar em um rumo diferente. curso. Para distâncias pequenas em relação ao raio da Terra, a diferença entre a loxodromia e o curso tecnicamente mais curto, um grande segmento de círculo, é insignificante e, mesmo para distâncias maiores, a simplicidade do rumo constante o torna atraente. Conforme observado por Mercator, em tal curso, o navio não chegaria pelo caminho mais curto, mas com certeza chegará. Velejar um losango significava que tudo o que os marinheiros tinham que fazer era manter um curso constante, desde que soubessem onde estavam quando começaram, onde pretendiam estar quando terminassem e tivessem um mapa em projeção de Mercator que mostrasse corretamente esses dois coordenadas.

Web Mercator

Muitos dos principais serviços de mapeamento de ruas on-line (Bing Maps, Google Maps, Mapbox, MapQuest, OpenStreetMap, Yahoo! Maps e outros) usam uma variante da projeção de Mercator para suas imagens de mapa chamada Web Mercator ou Google Web Mercator. Apesar de sua óbvia variação de escala em pequenas escalas, a projeção é adequada como um mapa-múndi interativo que pode ser ampliado perfeitamente para mapas de grande escala (locais), onde há relativamente pouca distorção devido à proximidade da projeção variante. -conformidade.

Os principais serviços de mapeamento de ruas online' sistemas lado a lado exibem a maior parte do mundo no nível de zoom mais baixo como uma única imagem quadrada, excluindo as regiões polares por truncamento em latitudes de φ_max = ±85,05113°. (Veja abaixo.) Os valores de latitude fora desse intervalo são mapeados usando uma relação diferente que não diverge em φ = ±90°.

Matemática

Projeções cilíndricas

Embora a superfície da Terra seja melhor modelada por um elipsóide de revolução oblato, para mapas de pequena escala, o elipsóide é aproximado por uma esfera de raio a, onde a é aproximadamente 6.371 km. Esta aproximação esférica da Terra pode ser modelada por uma esfera menor de raio R, chamada de globo nesta seção. O globo determina a escala do mapa. As várias projeções cilíndricas especificam como o detalhe geográfico é transferido do globo para um cilindro tangente a ele no equador. O cilindro é então desenrolado para dar o mapa planar. A fração R/a é chamada de fração representativa (RF) ou escala principal da projeção. Por exemplo, um mapa de Mercator impresso em um livro pode ter uma largura equatorial de 13,4 cm correspondente a um raio de globo de 2,13 cm e um RF de aproximadamente 1/300M (M é usado como abreviação de 1.000.000 em escrevendo um RF), enquanto o mapa original de 1569 de Mercator tem uma largura de 198 cm correspondente a um raio de globo de 31,5 cm e um RF de cerca de 1/20M.

Uma projeção de mapa cilíndrica é especificada por fórmulas que ligam as coordenadas geográficas de latitude φ e longitude λ às coordenadas cartesianas no mapa com origem no equador e x-eixo ao longo do equador. Por construção, todos os pontos no mesmo meridiano estão no mesmo gerador do cilindro em um valor constante de x, mas a distância y ao longo o gerador (medido a partir do equador) é uma função arbitrária da latitude, y(φ). Em geral, esta função não descreve a projeção geométrica (como de raios de luz em uma tela) do centro do globo para o cilindro, que é apenas uma das inúmeras maneiras de projetar conceitualmente um mapa cilíndrico.

Como o cilindro é tangente ao globo no equador, o fator de escala entre o globo e o cilindro é a unidade no equador, mas em nenhum outro lugar. Em particular, como o raio de um paralelo, ou círculo de latitude, é R cos φ, o paralelo correspondente no mapa deve ter sido esticado por um fator de 1/cos φ = seg φ. Este fator de escala no paralelo é convencionalmente denotado por k e o fator de escala correspondente no meridiano é denotado por h.

Fator de escala

A projeção de Mercator é determinada pela exigência de que a projeção seja conforme. Uma implicação disso é a "isotropia dos fatores de escala", o que significa que o fator de escala do ponto é independente da direção, de modo que pequenas formas são preservadas pela projeção. Isso implica que o fator de escala vertical, h, é igual ao fator de escala horizontal, k. Já que k = seg φ, o mesmo deve acontecer com h.

O gráfico mostra a variação deste fator de escala com a latitude. Alguns valores numéricos estão listados abaixo.

na latitude 30° o fator de escala é k= seg 30° = 1.15,

a latitude 45° o fator de escala é k= seg 45° = 1.41,

na latitude 60° o fator de escala é k= sec 60° = 2,

na latitude 80° o fator de escala é k= sec 80° = 5.76,

a latitude 85° o fator de escala é k= seg 85° = 11.5

O fator de escala de área é o produto das escalas paralelas e meridianas hk = seg²φ . Para a Groenlândia, considerando 73° como latitude mediana, hk = 11,7. Para a Austrália, considerando 25° como latitude mediana, hk = 1,2. Para a Grã-Bretanha, tomando 55° como latitude mediana, hk = 3,04.

A variação com a latitude às vezes é indicada por várias escalas de barras, conforme mostrado abaixo.

Os indicadores de Tissot na projeção do Mercator

A forma clássica de mostrar a distorção inerente a uma projeção é usar a indicatriz de Tissot. Nicolas Tissot notou que os fatores de escala em um ponto em uma projeção de mapa, especificados pelos números h e k, definem uma elipse naquele ponto. Para projeções cilíndricas, os eixos da elipse são alinhados aos meridianos e paralelos. Para a projeção de Mercator, h = k, então as elipses degeneram em círculos com raio proporcional ao valor do fator de escala para aquela latitude. Esses círculos são renderizados no mapa projetado com extrema variação de tamanho, indicativo das variações de escala de Mercator.

Transformações de projeção de Mercator

Derivação

Conforme discutido acima, a condição de isotropia implica que h = k = sec φ. Considere um ponto no globo de raio R com longitude λ e latitude φ. Se φ é aumentado por uma quantidade infinitesimal, dφ, o ponto se move R dφ ao longo de um meridiano do globo do raio R, então a mudança correspondente em y, dy, deve ser hR dφ = R seg φ dφ. Portanto y′(φ) = R seg φ. Da mesma forma, aumentar λ em dλ move o ponto R cos φ dλ ao longo de um paralelo do globo, então dx = kR cos φ dλ = R dλ. Ou seja, x′(λ) = R. Integrando as equações

x?(λ λ )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R,Sim.?(φ φ )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R- Sim.⁡ ⁡ φ φ ,{displaystyle x'(lambda)=R,qquad y'(varphi)=Rsec varphi}

com x(λ₀) = 0 e y(0) = 0, dá x(λ) e y(φ). O valor λ₀ é a longitude de um meridiano central arbitrário que é geralmente, mas nem sempre, o de Greenwich (ou seja, zero). Os ângulos λ e φ são expressos em radianos. Pela integral da função secante,

x= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R(λ λ - Sim. - Sim. λ λ 0),Sim.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =RI⁡ ⁡ Não.bronzeado⁡ ⁡ (D D 4+φ φ 2)].{displaystyle x=R(lambda) -lambda _{0}),qquad y=Rln left[tan left({frac {pi }{4}}+{frac {varphi }{2}}right)right].}

A função y(φ) é plotada ao lado de φ para o caso R = 1: ela tende ao infinito nos pólos. Os valores lineares do eixo y geralmente não são mostrados em mapas impressos; em vez disso, alguns mapas mostram a escala não linear dos valores de latitude à direita. Na maioria das vezes, os mapas mostram apenas uma gratícula de meridianos e paralelos selecionados.

Transformações inversas

λ λ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =λ λ 0+xR,φ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2bronzeado- Sim. - Sim. 1⁡ ⁡ Não.exp⁡ ⁡ (Sim.R)]- Sim. - Sim. D D 2.{displaystyle lambda =lambda _{0}+{frac {x}{R}},qquad varphi =2tan ^{-1}left[exp left({frac {y}{R}}right)right]-{frac {pi }{2}},.}

A expressão à direita da segunda equação define a função Gudermanniana; ou seja, φ = gd(y/R): a equação direta pode, portanto, ser escrita como y = R·gd⁻¹(φ).

Expressões alternativas

Existem muitas expressões alternativas para y(φ), todas derivadas de manipulações elementares.

Sim.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R2I⁡ ⁡ Não.1+pecado⁡ ⁡ φ φ 1- Sim. - Sim. pecado⁡ ⁡ φ φ ]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =RI⁡ ⁡ Não.1+pecado⁡ ⁡ φ φ e⁡ ⁡ φ φ ]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =RI⁡ ⁡ (- Sim.⁡ ⁡ φ φ +bronzeado⁡ ⁡ φ φ )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =RTanh- Sim. - Sim. 1⁡ ⁡ (pecado⁡ ⁡ φ φ )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =RPecar!- Sim. - Sim. 1⁡ ⁡ (bronzeado⁡ ⁡ φ φ )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =RSgn⁡ ⁡ (φ φ )Cosh!- Sim. - Sim. 1⁡ ⁡ (- Sim.⁡ ⁡ φ φ )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =RGD- Sim. - Sim. 1⁡ ⁡ (φ φ ).{displaystyle {begin{aligned}y&=&{frac {R}{2}}ln left[{frac {1+sin varphi }{1-sin varphi }}right]&=&{R}ln left[{frac {1+sin varphi }{cos varphi }}right

Os inversos correspondentes são:

φ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =pecado- Sim. - Sim. 1⁡ ⁡ (Tanh⁡ ⁡ Sim.R)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =bronzeado- Sim. - Sim. 1⁡ ⁡ (Pecar!⁡ ⁡ Sim.R)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Sgn⁡ ⁡ (Sim.)- Sim.- Sim. - Sim. 1⁡ ⁡ (Cosh!⁡ ⁡ Sim.R)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =GD⁡ ⁡ Sim.R.{displaystyle varphi =sin ^{-1}left(tanh {frac {y}{R}}right)=tan ^{-1}left(sinh {frac {y}{R}}right)=operatorname {sgn} (y)sec ^{-1}left(cosh {frac {y}{R}}right)=operatorname {gd} {frac Não.

Para ângulos expressos em graus:

x= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =D D R(λ λ ∘ ∘ - Sim. - Sim. λ λ 0∘ ∘ )180,Sim.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =RI⁡ ⁡ Não.bronzeado⁡ ⁡ (45+φ φ ∘ ∘ 2)].Não. R(lambda) ? _{0}^{circ })}{180}},qquad quad y=Rln left[tan left(45+{frac {varphi ^{circ }}{2}}right].}

As fórmulas acima são escritas em termos do raio do globo R. Geralmente é conveniente trabalhar diretamente com a largura do mapa W = 2πR. Por exemplo, as equações básicas de transformação tornam-se

x= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =W2D D (λ λ - Sim. - Sim. λ λ 0),Sim.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =W2D D I⁡ ⁡ Não.bronzeado⁡ ⁡ (D D 4+φ φ 2)].{displaystyle x={frac {W}{2pi }}left(lambda) -lambda _{0}right),qquad quad y={frac {W}{2pi }}ln left[tan left({frac }{4}}+{frac {varphi }{2}}right)right].}

Truncação e proporção

A ordenada y da projeção de Mercator torna-se infinita nos pólos e o mapa deve ser truncado em alguma latitude menor que noventa graus. Isso não precisa ser feito simetricamente. O mapa original de Mercator é truncado em 80°N e 66°S com o resultado de que os países europeus foram movidos para o centro do mapa. A proporção do mapa dele é 198/120 = 1,65. Truncamentos ainda mais extremos foram usados: um atlas escolar finlandês foi truncado em aproximadamente 76°N e 56°S, uma proporção de 1,97.

Grande parte do mapeamento baseado na Web usa uma versão com zoom da projeção de Mercator com uma proporção de um. Nesse caso, a latitude máxima alcançada deve corresponder a y = ±W /2, ou equivalente y/R = π. Qualquer uma das fórmulas de transformação inversa pode ser usada para calcular as latitudes correspondentes:

φ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =bronzeado- Sim. - Sim. 1⁡ ⁡ Não.Pecar!⁡ ⁡ (Sim.R)]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =bronzeado- Sim. - Sim. 1⁡ ⁡ Não.Pecar!⁡ ⁡ D D ]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =bronzeado- Sim. - Sim. 1⁡ ⁡ Não.11.5487]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =85.05113∘ ∘ .{displaystyle varphi =tan ^{-1}left[sinh left({frac {y}{R}}right)right]=tan ^{-1}left[sinh pi right]=tan ^{-1}left[11.5487right]=85.05113^{circ }.}

Geometria de elementos pequenos

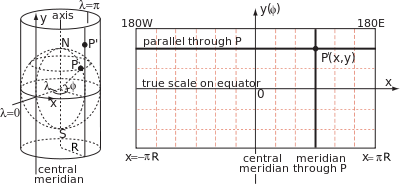
As relações entre y(φ) e as propriedades da projeção, como a transformação de ângulos e a variação de escala, decorrem da geometria do pequenos elementos no globo e no mapa. A figura abaixo mostra um ponto P na latitude φ e longitude λ no globo e um ponto próximo Q na latitude φ + δφ e longitude λ + δλ. As linhas verticais PK e MQ são arcos de meridianos de comprimento Rδφ. As linhas horizontais PM e KQ são arcos de paralelos de comprimento R(cos φ)δλ. Os pontos correspondentes na projeção definem um retângulo de largura δx e altura δy.

Para elementos pequenos, o ângulo PKQ é aproximadamente um ângulo reto e, portanto,

bronzeado⁡ ⁡ α α ? ? Re⁡ ⁡ φ φ δ δ λ λ Rδ δ φ φ ,bronzeado⁡ ⁡ β β = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =δ δ xδ δ Sim.,{displaystyle tan alpha approx {frac {Rcos varphi ,delta lambda }{R,delta varphi }},qquad qquad tan beta ={frac {delta x}{delta y}},}

Os fatores de escala mencionados anteriormente do globo para o cilindro são dados por

fator de escala paralela k(φ φ )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =P?M?PM= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =δ δ xRe⁡ ⁡ φ φ δ δ λ λ ,{displaystyle quad k(varphi);=;{frac {P'M'}{PM}};=;{frac x}{Rcos varphi ,delta lambda }},}

fator de escala de meridiano h(φ φ )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =P?KK?PKK= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =δ δ Sim.Rδ δ φ φ .{displaystyle quad h(varphi);=;{frac {P'K'}{PK}};=;{frac Sim. Rdelta varphi ,}}.}

Como os meridianos são mapeados para linhas de constante x, devemos ter x = R(λ − λ₀) e δx = Rδλ, (λ em radianos). Portanto, no limite de elementos infinitesimalmente pequenos

bronzeado⁡ ⁡ β β = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R- Sim.⁡ ⁡ φ φ Sim.?(φ φ )bronzeado⁡ ⁡ α α ,k= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim.⁡ ⁡ φ φ ,h= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Sim.?(φ φ )R.{displaystyle tan beta - Sim. {Rsec varphi }{y'(varphi)}}tan alpha ,qquad k=sec varphi ,qquad h={frac {y'(varphi)}{R}}.}

No caso da projeção de Mercator, y'(φ) = R seg φ, então isso nos dá h = k e α = β. O fato de que h = k é a isotropia dos fatores de escala discutidos acima. O fato de que α = β reflete outra implicação do mapeamento ser conforme, ou seja, o fato de que um curso de navegação de azimute constante no globo é mapeado na mesma grade constante rumo no mapa.

Fórmulas para distância

Converter a distância da régua no mapa de Mercator em distância real (grande círculo) na esfera é direto ao longo do equador, mas em nenhum outro lugar. Um problema é a variação da escala com a latitude, e outro é que as linhas retas no mapa (linhas de loxodromia), além dos meridianos ou do equador, não correspondem a grandes círculos.

A distinção entre distância de loxodromia (navegando) e distância de grande círculo (verdadeira) foi claramente compreendida por Mercator. (Veja a Legenda 12 no mapa de 1569.) Ele enfatizou que a distância da loxodromia é uma aproximação aceitável para a verdadeira distância do grande círculo para percursos de distância curta ou moderada, particularmente em latitudes mais baixas. Ele ainda quantifica sua afirmação: "Quando as grandes distâncias circulares que devem ser medidas nas proximidades do equador não excedem 20 graus de um grande círculo, ou 15 graus perto da Espanha e da França, ou 8 e até 10 graus nas partes do norte, é conveniente usar as distâncias da linha de loxodromia".

Para uma medida de régua de uma linha curta, com ponto médio na latitude φ, onde o fator de escala é k = seg φ = 1/cos φ:

Verdadeira distância = distância rhumb ≡ distância régua × cosφ / RF. (linhas curtas)

Com raio e circunferência do grande círculo iguais a 6.371 km e 40.030 km, respectivamente, um RF de 1/300M, para os quais R = 2,12 cm e W = 13,34 cm, implica que uma medida de régua de 3 mm. em qualquer direção a partir de um ponto no equador corresponde a aproximadamente 900 km. As distâncias correspondentes para as latitudes 20°, 40°, 60° e 80° são 846 km, 689 km, 450 km e 156 km, respectivamente.

As distâncias maiores requerem várias abordagens.

No equador

A escala é a unidade no equador (para uma projeção não secante). Portanto, interpretar as medidas da régua no equador é simples:

Distância verdadeira = distância de régua / RF (equator)

Para o modelo acima, com RF = 1/300M, 1 cm corresponde a 3.000 km.

Em outros paralelos

Em qualquer outro paralelo, o fator de escala é sec φ de modo que

Distância paralela = distância de régua × cosφ / RF (paralela).

Para o modelo acima, 1 cm corresponde a 1.500 km a uma latitude de 60°.

Esta não é a distância mais curta entre os pontos finais escolhidos no paralelo porque um paralelo não é um grande círculo. A diferença é pequena para distâncias curtas, mas aumenta à medida que λ, a separação longitudinal, aumenta. Para dois pontos, A e B, separados por 10° de longitude no paralelo a 60°, a distância ao longo do paralelo é aproximadamente 0,5 km maior que a distância do grande círculo. (A distância AB ao longo do paralelo é (a cos φ) λ. O comprimento da corda AB é 2(a cos φ) sin λ/2. Este acorde subtende um ângulo no centro igual a 2arcsin(cos φ sin λ/2) e a distância do grande círculo entre A e B é 2a arcsin(cos φ sin λ/ 2).) No caso extremo em que a separação longitudinal é de 180°, a distância ao longo do paralelo é metade da circunferência desse paralelo; ou seja, 10.007,5 km. Por outro lado, a geodésica entre esses pontos é um grande arco de círculo através do polo subtendendo um ângulo de 60° no centro: o comprimento desse arco é um sexto da circunferência do grande círculo, cerca de 6.672 km. A diferença é de 3.338 km, portanto, a distância da régua medida a partir do mapa é bastante enganosa, mesmo após a correção da variação de latitude do fator de escala.

Em um meridiano

Um meridiano do mapa é um grande círculo no globo, mas a variação contínua da escala significa que a medição da régua por si só não pode fornecer a verdadeira distância entre pontos distantes no meridiano. No entanto, se o mapa estiver marcado com uma escala de latitude precisa e espaçada com precisão, a partir da qual a latitude pode ser lida diretamente - como é o caso do mapa-múndi Mercator 1569 (folhas 3, 9, 15) e todas as cartas náuticas subsequentes - o meridiano distância entre duas latitudes φ₁ e φ₂ é simplesmente

m12= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =um|φ φ 1- Sim. - Sim. φ φ 2|.Não. m_{12}=a|varphi _{1}-varphi _{2}|.}

Se as latitudes dos pontos finais não puderem ser determinadas com confiança, elas poderão ser encontradas calculando a distância da régua. Chamando as distâncias da régua dos pontos finais no meridiano do mapa medidos a partir do equador y₁ e y₂, a verdadeira distância entre esses pontos na esfera é dada usando qualquer uma das fórmulas inversas de Mercator:

m12= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =um|bronzeado- Sim. - Sim. 1⁡ ⁡ Não.Pecar!⁡ ⁡ (Sim.1R)]- Sim. - Sim. bronzeado- Sim. - Sim. 1⁡ ⁡ Não.Pecar!⁡ ⁡ (Sim.2R)]|,Não. m_{12}=aleft|tan ^{-1}left[sinh left({frac {y_{1}}{R}}right]-tan ^{-1}left[sinh left({frac) {y_{2}}{R}}right)right]right|,}

onde R pode ser calculado a partir da largura W do mapa por R = W/2π. Por exemplo, em um mapa com R = 1, os valores de y = 0, 1, 2, 3 correspondem às latitudes de φ = 0 °, 50°, 75°, 84° e, portanto, os intervalos sucessivos de 1 cm no mapa correspondem a intervalos de latitude no globo de 50°, 25°, 9° e distâncias de 5.560 km, 2.780 km e 1.000 km em a Terra.

Em um rumo

Uma linha reta no mapa de Mercator no ângulo α dos meridianos é uma loxodromia. Quando α = π/2 ou 3π/2 a loxodromia corresponde a um dos paralelos; apenas um, o equador, é um grande círculo. Quando α = 0 ou π corresponde a um grande círculo meridiano (se continuado ao redor da Terra). Para todos os outros valores, é uma espiral de pólo a pólo no globo, interceptando todos os meridianos no mesmo ângulo e, portanto, não é um grande círculo. Esta seção discute apenas o último desses casos.

Se α não for 0 nem π então a figura acima dos elementos infinitesimais mostra que o comprimento de uma linha de rumo infinitesimal na esfera entre as latitudes φ; e φ + δφ é a sec α δφ. Uma vez que α é constante na loxodromia, esta expressão pode ser integrada para dar, para linhas de rumo finitas na Terra:

R12= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =um- Sim.⁡ ⁡ α α |φ φ 1- Sim. - Sim. φ φ 2|= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =um- Sim.⁡ ⁡ α α ? ? φ φ .Não. r_{12}=asec alpha ,|varphi _{1}-varphi _{2}|=a,sec alpha ;Delta varphi.}

Mais uma vez, se Δφ pode ser lido diretamente de uma escala de latitude precisa no mapa, então a distância de rumo entre os pontos do mapa com latitudes φ₁ e φ₂ são dados acima. Se não houver tal escala, a régua distancia entre os pontos finais e o equador, y₁ e y₂, dê o resultado por meio de uma fórmula inversa:

R12= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =um- Sim.⁡ ⁡ α α |bronzeado- Sim. - Sim. 1⁡ ⁡ Pecar!⁡ ⁡ (Sim.1R)- Sim. - Sim. bronzeado- Sim. - Sim. 1⁡ ⁡ Pecar!⁡ ⁡ (Sim.2R)|.Não. r_{12}=asec alpha left|tan ^{-1}sinh left({frac {y_{1}}{R}}right)-tan ^{-1}sinh left({frac {y_{2}}{R}}right)right|.}

Essas fórmulas fornecem distâncias loxodrômicas na esfera que podem diferir muito das distâncias verdadeiras cuja determinação requer cálculos mais sofisticados.

Generalização para o elipsóide

Quando a Terra é modelada por um esferóide (elipsóide de revolução), a projeção de Mercator deve ser modificada para permanecer conforme. As equações de transformação e fator de escala para a versão não secante são

x= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R(λ λ - Sim. - Sim. λ λ 0),Sim.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =RI⁡ ⁡ Não.bronzeado⁡ ⁡ (D D 4+φ φ 2)(1- Sim. - Sim. epecado⁡ ⁡ φ φ 1+epecado⁡ ⁡ φ φ )e2]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R(Pecar!- Sim. - Sim. 1⁡ ⁡ (bronzeado⁡ ⁡ φ φ )- Sim. - Sim. eTanh- Sim. - Sim. 1⁡ ⁡ (epecado⁡ ⁡ φ φ )),k= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim.⁡ ⁡ φ φ 1- Sim. - Sim. e2pecado2⁡ ⁡ φ φ .{displaystyle {begin{aligned}x&=Rleft(lambda) -lambda _{0}right),\y&=Rln left[tan left({frac {pi }{4}}+{frac {varphi }{2}}right)left({frac {1-esin varphi }{1+esin varphi }}right)^{frac {e}{2}}right]=Rleft(sinh ^{-1}left(tan varphi right)-etanh ^{-1}(esin varphi)right),k&=sec varphi {sqrt {1-e^{2}sin ^{2}varphi }}.end{aligned}}}

O fator de escala é a unidade no equador, pois deve ser uma vez que o cilindro é tangente ao elipsóide no equador. A correção elipsoidal do fator de escala aumenta com a latitude, mas nunca é maior que e², uma correção inferior a 1%. (O valor de e² é cerca de 0,006 para todos os elipsóides de referência.) Isso é muito menor do que a imprecisão da escala, exceto muito perto do equador. Somente projeções precisas de Mercator de regiões próximas ao equador necessitarão de correções elipsoidais.

O inverso é resolvido iterativamente, pois a latitude isométrica está envolvida.