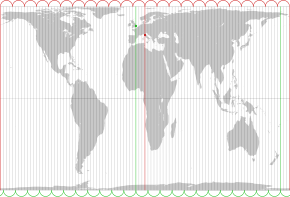
Projeção de Gall-Peters

A projeção Gall–Peters do mapa mundial

A projeção de Gall-Peters é uma projeção retangular de mapa de área igual. Como todas as projeções de área igual, ela distorce a maioria das formas. É uma projeção cilíndrica de área igual com latitudes 45° norte e sul como as regiões no mapa que não têm distorção.

A projeção recebeu o nome de James Gall e Arno Peters. Gall descreveu a projeção em 1855 em uma convenção científica e publicou um artigo sobre ela em 1885. Peters trouxe a projeção para um público mais amplo no início dos anos 1970 por meio de seu "Peters World Map". O nome "projeção de Gall-Peters" foi usado pela primeira vez por Arthur H. Robinson em um panfleto publicado pela American Cartographic Association em 1986.

Os mapas baseados na projeção são promovidos pela UNESCO e também são amplamente utilizados pelas escolas britânicas. O estado americano de Massachusetts e as escolas públicas de Boston começaram a incluir esses mapas em março de 2017, tornando-se o primeiro distrito escolar público e estado nos Estados Unidos a adotar os mapas Gall-Peters como padrão.

A projeção de Gall-Peters alcançou notoriedade no final do século 20 como peça central de uma controvérsia sobre as implicações políticas do design do mapa.

Descrição

A projeção da área igual cilíndrica Gall-Peters com os indicadores de deformação de Tissot

Fórmula

A projeção é convencionalmente definida como:

x= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =RD D λ λ e⁡ ⁡ 45∘ ∘ 180∘ ∘ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =RD D λ λ 180∘ ∘ 2Sim.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Rpecado⁡ ⁡ φ φ e⁡ ⁡ 45∘ ∘ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R2pecado⁡ ⁡ φ φ {displaystyle {begin{aligned}x&={frac {Rpi lambda cos 45^{circ rc{180^{circ Sim. (Rpi lambda }{180^{circ }{sqrt {2}}y&={frac {Rsin varphi }{cos 45^{circ }}}=R{sqrt {2}}sin varphi end{aligned}}}

onde λ é a longitude do meridiano central em graus, φ é a latitude e R é o raio do globo usado como o modelo da Terra para projeção. Para longitude dada em radianos, remova o π /180° fatores.

Fórmula simplificada

Retirando a conversão de unidades e escala uniforme, as fórmulas podem ser escritas:

x= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Rλ λ Sim.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2Rpecado⁡ ⁡ φ φ - Sim. Rlambda \y&=2Rsin varphi end{aligned}}}

Onde? λ λ - Sim. é a longitude do meridiano central (em radianos), φ φ - Sim. é a latitude, e R é o raio do globo usado como o modelo da terra para projeção. Daí a esfera é mapeada para o cilindro vertical, e o cilindro é esticado para dobrar seu comprimento. O fator estiramento, 2 neste caso, é o que distingue as variações da projeção cilíndrica da área igual.

Relação com projeções cilíndricas de área igual

As várias especializações da projeção cilíndrica de área igual diferem apenas na proporção do eixo vertical para o horizontal. Essa relação determina o paralelo padrão da projeção, que é o paralelo no qual não há distorção e ao longo do qual as distâncias correspondem à escala indicada. Os paralelos padrão do Gall-Peters são 45° N e 45° S. Várias outras especializações do cilíndrico de área igual foram descritas, promovidas ou nomeadas de outra forma.

Origens e nomenclatura

A projeção de Gall-Peters foi descrita pela primeira vez em 1855 pelo clérigo James Gall, que a apresentou junto com duas outras projeções na reunião de Glasgow da Associação Britânica para o Avanço da Ciência (BA). Ele deu o nome de "ortográfico" e publicou formalmente seu trabalho em 1885 na Scottish Geographical Magazine. A projeção é sugestiva da projeção ortográfica em que as distâncias entre os paralelos do Gall-Peters são um múltiplo constante das distâncias entre os paralelos do ortográfico. Essa constante é √2.

Em 1967, o cineasta alemão Arno Peters concebeu de forma independente uma projeção semelhante, que apresentou em 1973 como o "mapa do mundo de Peters". A descrição original de Peters de sua projeção continha um erro geométrico que, tomado literalmente, implica em paralelos padrão de 46°02′ N/S. No entanto, o texto que acompanha a descrição deixou claro que ele pretendia que os paralelos padrão fossem 45° N/S, tornando sua projeção idêntica à ortográfica de Gall. Em qualquer caso, a diferença é insignificante em um mapa-múndi.

O nome "projeção de Gall-Peters" parece ter sido usado pela primeira vez por Arthur H. Robinson em um panfleto publicado pela American Cartographic Association em 1986. Antes de 1973, era conhecido, quando referido, como o "Gall ortográfico" ou "Gall's ortográfico." A maioria dos apoiadores de Peters hoje se refere a isso apenas como a "projeção de Peters" Durante os anos de controvérsia, a literatura cartográfica tendeu a mencionar ambas as atribuições, optando por uma ou por outra para efeitos do artigo. Nos últimos anos, "Gall-Peters" parece dominar.

Controvérsia do mapa mundi de Peter

Mural em uma escola que retrata a projeção Gall-Peters, com continentes coloridos.

As bordas direita e esquerda do mapa de Peters estão no Estreito de Bering, então toda a Rússia é exibida no lado direito.

Greenwich grande círculo

Bering Strait grande círculo (traversing Florence in Italy, ver Florença meridiano)

A projeção de Gall-Peters inicialmente passou despercebida quando apresentada por Gall em 1855. Ela alcançou uma atenção mais ampla depois que Arno Peters a reintroduziu em 1973. Ele a promoveu como uma alternativa superior à projeção de Mercator comumente usada, com base em que a projeção A projeção de Mercator distorce muito os tamanhos relativos das regiões em um mapa. Em particular, ele criticou que a projeção de Mercator faz com que a Europa e a América do Norte ricas pareçam muito grandes em relação à África e à América do Sul mais pobres. Esses argumentos influenciaram muitos grupos socialmente preocupados a adotar a projeção de Gall-Peters, incluindo o Conselho Nacional de Igrejas e a revista New Internationalist.

Sua campanha foi reforçada pela afirmação imprecisa de que a projeção de Gall-Peters era a única "área correta" mapa. Na verdade, algumas das projeções mais antigas são de área igual (como a projeção senoidal) e centenas foram descritas. Ele também afirmou incorretamente que possuía "conformidade angular absoluta", não tinha "distorções extremas de forma" e era "totalmente factual à distância". Peters enquadrou suas críticas à projeção de Mercator com críticas à comunidade cartográfica mais ampla. Em particular, Peters escreveu em The New Cartography,

Pela autoridade de sua profissão [cartógrafos] impediu seu desenvolvimento. Desde que Mercator produziu seu mapa global há mais de quatrocentos anos para a idade da dominação mundial dos europeus, cartógrafos têm se agarrado a ele apesar de ter sido muito ultrapassado por eventos. Eles têm procurado torná-lo tópico por correções cosméticas.... A profissão cartográfica é, por sua retenção de preceitos antigos baseados no conceito global eurocêntrico, incapaz de desenvolver este mapa mundial igualitário que só pode demonstrar a paridade de todos os povos da terra.

À medida que as promoções de Peters ganhavam popularidade, a comunidade cartográfica reagia com hostilidade às suas críticas, bem como à imprecisão e falta de novidade de suas afirmações. Eles chamaram a atenção para a longa lista de cartógrafos que, ao longo do século anterior, expressaram formalmente sua frustração com as críticas dos editores. uso excessivo do Mercator e defendeu alternativas. Além disso, vários estudiosos criticaram as distorções particularmente grandes presentes na projeção de Gall-Peters e comentaram sobre a ironia de sua apresentação não distorcida das latitudes médias, incluindo a Alemanha natal de Peters, às custas das baixas latitudes, que acolher mais nações tecnologicamente subdesenvolvidas.

A crescente publicidade das reivindicações de Peter em 1986 motivou a American Cartographic Association (agora Cartography and Geographic Information Society) a produzir uma série de livretos (incluindo Which Map Is Best) projetados para educar o público sobre projeções de mapas e distorções em mapas. Em 1989 e 1990, após algum debate interno, sete organizações geográficas norte-americanas adotaram uma resolução rejeitando todos os mapas-múndi retangulares, uma categoria que inclui tanto as projeções de Mercator quanto as de Gall-Peters, embora a North American Cartographic Information Society tenha se recusado notavelmente a endossá-la..

Os dois campos nunca fizeram nenhuma tentativa real de reconciliação. O campo de Peters ignorou em grande parte os protestos dos cartógrafos e não reconheceu o trabalho anterior de Gall até que a controvérsia terminasse em grande parte, no final da vida de Peters. Embora ele provavelmente tenha planejado a projeção de forma independente, sua conduta não acadêmica e sua recusa em envolver a comunidade cartográfica sem dúvida contribuíram para a polarização e o impasse.

Nas décadas seguintes, J. Brian Harley atribuiu ao fenômeno Peters a demonstração das implicações sociais das projeções cartográficas, enquanto Jeremy Crampton considera todos os mapas políticos e vê a condenação da comunidade cartográfica como reacionária e talvez demonstrativa de imaturidade na profissão.