Problema de satisfatibilidade booleana
Na lógica e na ciência da computação, o problema de satisfatibilidade booleana (às vezes chamado de problema de satisfatibilidade proposicional e abreviado como SATISFIABILITY, SAT ou B-SAT) é o problema de determinar se existe uma interpretação que satisfaça uma determinada fórmula booleana. Em outras palavras, ele pergunta se as variáveis de uma determinada fórmula booleana podem ser consistentemente substituídas pelos valores TRUE ou FALSE de forma que a fórmula seja avaliada como TRUE. Se for esse o caso, a fórmula é chamada satisfatível. Por outro lado, se tal atribuição não existir, a função expressa pela fórmula é FALSE para todas as atribuições de variáveis possíveis e a fórmula é insatisfatível. Por exemplo, a fórmula "a AND NOT b" é satisfatível porque é possível encontrar os valores a = VERDADEIRO e b = FALSO, o que torna (a E NÃO b) = VERDADEIRO. Em contraste, "a E NÃO a" é insatisfatório.
SAT é o primeiro problema que provou ser NP-completo; veja o teorema de Cook–Levin. Isso significa que todos os problemas na classe de complexidade NP, que inclui uma ampla gama de problemas naturais de decisão e otimização, são no máximo tão difíceis de resolver quanto SAT. Não existe nenhum algoritmo conhecido que resolva eficientemente cada problema SAT, e geralmente acredita-se que tal algoritmo não exista; ainda esta crença não foi provada matematicamente, e resolver a questão de saber se SAT tem um algoritmo de tempo polinomial é equivalente ao problema P versus NP, que é um famoso problema em aberto na teoria da computação.
No entanto, a partir de 2007, os algoritmos SAT heurísticos são capazes de resolver instâncias de problemas envolvendo dezenas de milhares de variáveis e fórmulas que consistem em milhões de símbolos, o que é suficiente para muitos problemas SAT práticos de, por exemplo, inteligência artificial, design de circuito, e prova automática de teoremas.
Definições
Uma fórmula lógica proposicional, também chamada de expressão booleana, é construída a partir de variáveis, operadores AND (conjunção, também denotada por ∧), OR (disjunção, ∨), NOT (negação, ¬) e parênteses. Diz-se que uma fórmula é satisfatória se puder ser transformada em VERDADEIRO atribuindo valores lógicos apropriados (ou seja, VERDADEIRO, FALSO) às suas variáveis. O problema de satisfatibilidade booleana (SAT) é, dada uma fórmula, verificar se é satisfatível. Este problema de decisão é de importância central em muitas áreas da ciência da computação, incluindo ciência da computação teórica, teoria da complexidade, algoritmos, criptografia e inteligência artificial.
Forma normal conjuntiva
Um literal é uma variável (neste caso é chamado de literal positivo) ou a negação de uma variável (chamada de literal negativo). Uma cláusula é uma disjunção de literais (ou um único literal). Uma cláusula é chamada de Cláusula de Horn se contiver no máximo um literal positivo. Uma fórmula está na forma normal conjuntiva (CNF) se for uma conjunção de cláusulas (ou uma única cláusula). Por exemplo, x1 é um literal positivo, ¬x2 é um literal negativo, x1 ∨ ¬x2 é uma cláusula. A fórmula (x1 ∨ ¬x2) ∧ (¬x1 ∨ x2 ∨ x3) ∧ ¬x1 está na forma normal conjuntiva; sua primeira e terceira cláusulas são cláusulas de Horn, mas sua segunda cláusula não é. A fórmula pode ser satisfeita, escolhendo x1 = FALSE, x2 = FALSE e x 3 arbitrariamente, pois (FALSE ∨ ¬FALSE) ∧ (¬FALSE ∨ FALSE ∨ x3) ∧ ¬FALSE resulta em (FALSO ∨ VERDADEIRO) ∧ (VERDADEIRO ∨ FALSO ∨ x3) ∧ VERDADEIRO, e por sua vez para VERDADEIRO ∧ VERDADEIRO ∧ VERDADEIRO (ou seja, VERDADEIRO). Em contraste, a fórmula CNF a ∧ ¬a, que consiste em duas cláusulas de um literal, é insatisfatível, pois para a=TRUE ou a=FALSE ele avalia como TRUE ∧ ¬TRUE (ou seja, FALSE) ou FALSE ∧ ¬FALSE (ou seja, novamente FALSE), respectivamente.
Para algumas versões do problema SAT, é útil definir a noção de uma fórmula de forma normal conjuntiva generalizada, viz. como uma conjunção de muitas cláusulas generalizadas arbitrariamente, sendo a última da forma R(l 1,...,ln) para alguma função booleana R e literais (comuns) li. Diferentes conjuntos de funções booleanas permitidas levam a diferentes versões do problema. Por exemplo, R(¬x,a,b) é uma cláusula generalizada e R(¬x,a,b) ∧ R(b,y,c) ∧ R(c,d,¬ z) é uma forma normal conjuntiva generalizada. Esta fórmula é usada abaixo, com R sendo o operador ternário que é TRUE exatamente quando exatamente um de seus argumentos é.
Usando as leis da álgebra booleana, toda fórmula lógica proposicional pode ser transformada em uma forma normal conjuntiva equivalente, que pode, no entanto, ser exponencialmente mais longa. Por exemplo, transformando a fórmula (x1∧y1) ∨ (x2∧y2) ∨... ∨ (xn ∧yn) na forma normal conjuntiva produz
- (x1∨x2∨...xn)
- (Sim.1∨x2∨...xn)
- (x1∨Sim.2∨...xn)
- (Sim.1∨Sim.2∨...xn) ∧... ∧
- (x1∨x2∨...Sim.n)
- (Sim.1∨x2∨...Sim.n)
- (x1∨Sim.2∨...Sim.n)
- (Sim.1∨Sim.2∨...Sim.n);
enquanto o primeiro é uma disjunção de n conjunções de 2 variáveis, o último consiste em 2n cláusulas de n variáveis.
No entanto, com o uso da transformação de Tseytin, podemos encontrar uma fórmula de forma normal conjuntiva equisatisfatível com comprimento linear no tamanho da fórmula lógica proposicional original.
Complexidade
SAT foi o primeiro problema NP-completo conhecido, comprovado por Stephen Cook na Universidade de Toronto em 1971 e independentemente por Leonid Levin na Academia Russa de Ciências em 1973. Até então, o conceito de um NP-completo problema nem existia. A prova mostra como todo problema de decisão na classe de complexidade NP pode ser reduzido ao problema SAT para fórmulas CNF, às vezes chamado de CNFSAT. Uma propriedade útil da redução de Cook é que ela preserva o número de respostas aceitas. Por exemplo, decidir se um determinado grafo tem 3 cores é outro problema em NP; se um gráfico tiver 17 3 colorações válidas, a fórmula SAT produzida pela redução de Cook-Levin terá 17 atribuições satisfatórias.
A NP-completude refere-se apenas ao tempo de execução das instâncias do pior caso. Muitas das instâncias que ocorrem em aplicações práticas podem ser resolvidas muito mais rapidamente. Consulte Algoritmos para resolver o SAT abaixo.
3-satisfabilidade
Como o problema de satisfatibilidade para fórmulas arbitrárias, determinar a satisfatibilidade de uma fórmula na forma normal conjuntiva onde cada cláusula é limitada a no máximo três literais também é NP-completo; esse problema é chamado de 3-SAT, 3CNFSAT ou 3-satisfabilidade. Para reduzir o problema SAT irrestrito para 3-SAT, transforme cada cláusula l1 ∨ ⋯ ∨ ln para uma conjunção de cláusulas n - 2
- (Eu...1 ∨ Eu...2 ∨ x2)
- Não.x2 ∨ Eu...3 ∨ x3)
- Não.x3 ∨ Eu...4 ∨ x4) ∧ ≡ ∧
- Não.xn - 3 ∨ Eu...n - 2 ∨ xn - 2)
- Não.xn - 2 ∨ Eu...n - 1 ∨ Eu...n)
onde x2, ⋯ , xn − 2 são variáveis novas que não ocorrem em outro lugar. Embora as duas fórmulas não sejam logicamente equivalentes, elas são equisatisfatíveis. A fórmula resultante da transformação de todas as cláusulas é no máximo 3 vezes maior que a original, ou seja, o crescimento do comprimento é polinomial.
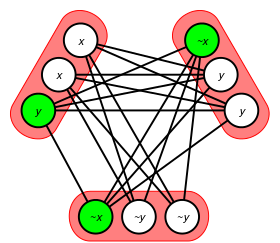
3-SAT é um dos 21 problemas NP-completos de Karp, e é usado como ponto de partida para provar que outros problemas também são NP-difíceis. Isso é feito pela redução de tempo polinomial de 3-SAT para o outro problema. Um exemplo de problema em que esse método foi usado é o problema do clique: dada uma fórmula CNF que consiste em cláusulas c, o grafo correspondente consiste em um vértice para cada literal e uma aresta entre cada dois não -contradizendo literais de diferentes cláusulas, cf. foto. O gráfico tem um clique c se e somente se a fórmula for satisfatível.
Existe um algoritmo aleatório simples devido a Schöning (1999) que é executado no tempo (4/3)n onde n é o número de variáveis na proposição 3-SAT, e consegue com alta probabilidade decidir corretamente 3-SAT.
A hipótese de tempo exponencial afirma que nenhum algoritmo pode resolver 3-SAT (ou de fato k-SAT para qualquer 2}" xmlns="http://www.w3.org/1998/Math/MathML">k>2Não.2}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/fa7a4bb0e17a911cb4b3f6c4e455be472a295299" style="vertical-align: -0.338ex; width:5.472ex; height:2.176ex;"/>) em exp(o)n) tempo (ou seja, fundamentalmente mais rápido do que exponencial em n).
Selman, Mitchell e Levesque (1996) fornecem dados empíricos sobre a dificuldade de fórmulas 3-SAT geradas aleatoriamente, dependendo de seus parâmetros de tamanho. A dificuldade é medida em número de chamadas recursivas feitas por um algoritmo DPLL. Eles identificaram uma região de transição de fase de fórmulas quase certamente satisfatórias para fórmulas quase certamente insatisfatórias na proporção de cláusulas para variáveis em cerca de 4,26.
3-satisfabilidade pode ser generalizada para k-satisfabilidade (k-SAT, também k-CNF-SAT), quando fórmulas em CNF são consideradas com cada cláusula contendo até k literais. No entanto, como para qualquer k ≥ 3, esse problema não pode ser nem mais fácil que 3-SAT nem mais difícil que SAT, e os dois últimos são NP-completos, então deve ser k-SAT.
Alguns autores restringem k-SAT a fórmulas CNF com exatamente k literais. Isso também não leva a uma classe de complexidade diferente, pois cada cláusula l1 ∨ ⋯ ∨ lj com j < Os literais k podem ser preenchidos com variáveis fictícias fixas para l1 ∨ ⋯ ∨ lj ∨ dj+1 ∨ ⋯ ∨ dk. Depois de preencher todas as cláusulas, 2k-1 cláusulas extras devem ser anexadas para garantir que apenas d1 = ⋯ = dk=FALSE pode levar a uma atribuição satisfatória. Como k não depende do comprimento da fórmula, as cláusulas extras levam a um aumento constante no comprimento. Pela mesma razão, não importa se literais duplicados são permitidos em cláusulas, como em ¬x ∨ ¬y ∨ ¬y.
Casos especiais de SAT
Forma normal conjuntiva
A forma normal conjuntiva (em particular com 3 literais por cláusula) é frequentemente considerada a representação canônica para fórmulas SAT. Como mostrado acima, o problema SAT geral se reduz a 3-SAT, o problema de determinar a satisfatibilidade para fórmulas nesta forma.
Forma normal disjuntiva
SAT é trivial se as fórmulas se restringem àquelas na forma normal disjuntiva, ou seja, são uma disjunção de conjunções de literais. Tal fórmula é de fato satisfatível se e somente se pelo menos uma de suas conjunções for satisfatível, e uma conjunção é satisfatível se e somente se ela não contiver x e NOT x para alguma variável x. Isso pode ser verificado em tempo linear. Além disso, se eles estiverem restritos a estar na forma normal disjuntiva completa, na qual cada variável aparece exatamente uma vez em cada conjunção, eles podem ser verificados em tempo constante (cada conjunção representa uma atribuição satisfatória). Mas pode levar tempo e espaço exponenciais para converter um problema SAT geral para a forma normal disjuntiva; para um exemplo de troca "∧" e "∨" no exemplo de explosão exponencial acima para formas normais conjuntivas.
Exatamente-1 3-satisfabilidade

Uma variante do problema de 3 satisfatibilidade é o um em três 3-SAT (também conhecido como 1-em-3-SAT e exatamente-1 3-SAT). Dada uma forma normal conjuntiva com três literais por cláusula, o problema é determinar se existe uma atribuição de verdade às variáveis de modo que cada cláusula tenha exatamente um literal VERDADEIRO (e, portanto, exatamente dois literais FALSO). Em contraste, o 3-SAT comum requer que cada cláusula tenha pelo menos um literal VERDADEIRO. Formalmente, um problema 3-SAT um em três é dado como uma forma normal conjuntiva generalizada com todas as cláusulas generalizadas usando um operador ternário R que é VERDADEIRO apenas se exatamente um de seus argumentos for. Quando todos os literais de uma fórmula 3-SAT um em três são positivos, o problema de satisfatibilidade é chamado de 3-SAT positivo um em três.
Um em três 3-SAT, junto com seu caso positivo, é listado como problema NP-completo "LO4" na referência padrão, Computers and Intractability: A Guide to the Theory of NP-Completeness por Michael R. Garey e David S. Johnson. Um em três 3-SAT provou ser NP-completo por Thomas Jerome Schaefer como um caso especial do teorema da dicotomia de Schaefer, que afirma que qualquer problema generalizando a satisfazibilidade booleana de uma certa maneira está na classe P ou é NP-completo.
Schaefer fornece uma construção que permite uma fácil redução de tempo polinomial de 3-SAT para um em três 3-SAT. Deixe "(x ou y ou z)" ser uma cláusula em uma fórmula 3CNF. Adicione seis novas variáveis booleanas a, b, c, d, e, e f, para ser usado para simular esta cláusula e nenhuma outra. Então a fórmula R(x,a,d) ∧ R(y,b,d) ∧ R(a,b,e) ∧ R(c,d,f) ∧ R(z,c,FALSE) é satisfazível por alguma configuração das novas variáveis se e somente se pelo menos um de x, y ou z é VERDADEIRO, veja a figura (à esquerda). Assim, qualquer instância 3-SAT com cláusulas m e variáveis n pode ser convertida em uma instância 3-SAT um em três equisatisfatível com 5m cláusulas e n+6m variáveis. Outra redução envolve apenas quatro novas variáveis e três cláusulas: R(¬x,a,b) ∧ R(b,y,c) ∧ R(c, d,¬z), veja a imagem (à direita).
3-satisfabilidade não igual para todos
Outra variante é o problema not-all-equal 3-satisfiability (também chamado de NAE3SAT). Dada uma forma normal conjuntiva com três literais por cláusula, o problema é determinar se existe uma atribuição às variáveis de modo que em nenhuma cláusula todos os três literais tenham o mesmo valor de verdade. Este problema também é NP-completo, mesmo que nenhum símbolo de negação seja admitido, pelo teorema da dicotomia de Schaefer.
SAT linear
Uma fórmula 3-SAT é Linear SAT (LSAT) se cada cláusula (vista como um conjunto de literais) intercepta no máximo uma outra cláusula e, além disso, se duas cláusulas se cruzam, elas têm exatamente um literal em comum. Uma fórmula LSAT pode ser representada como um conjunto de intervalos semi-fechados disjuntos em uma linha. Decidir se uma fórmula LSAT é satisfatível é NP-completo.
2-satisfabilidade
SAT é mais fácil se o número de literais em uma cláusula for limitado a no máximo 2, caso em que o problema é chamado de 2-SAT. Este problema pode ser resolvido em tempo polinomial, e de fato é completo para a classe de complexidade NL. Se adicionalmente todas as operações OR em literais forem alteradas para operações XOR, o resultado é chamado de exclusive-or 2-satisfiability, que é um problema completo para a classe de complexidade SL = L.
Satisfabilidade do chifre
O problema de decidir a satisfazibilidade de uma dada conjunção de cláusulas de Horn é chamado de Horn-satisfabilidade, ou HORN-SAT. Pode ser resolvido em tempo polinomial por uma única etapa do algoritmo de propagação da unidade, que produz o modelo mínimo único do conjunto de cláusulas de Horn (w.r.t. o conjunto de literais atribuídos a TRUE). A satisfatibilidade de chifre é P-completa. Pode ser visto como a versão de P do problema de satisfatibilidade booleana. Além disso, decidir a verdade das fórmulas de Horn quantificadas pode ser feito em tempo polinomial.
As cláusulas de Horn são interessantes porque são capazes de expressar a implicação de uma variável de um conjunto de outras variáveis. De fato, uma dessas cláusulas ¬x1 ∨... ∨ ¬xn ∨ y pode ser reescrito como x1 ∧... ∧ xn → y, ou seja, se x1,...,xn são todos TRUE, então y também precisa ser TRUE.
Uma generalização da classe das fórmulas de Horn é a das fórmulas renameable-Horn, que é o conjunto de fórmulas que podem ser colocadas na forma de Horn substituindo algumas variáveis por suas respectivas negações. Por exemplo, (x1 ∨ ¬x2) ∧ (¬x 1 ∨ x2 ∨ x3) ∧ ¬x1 não é uma fórmula de Horn, mas pode ser renomeada para fórmula de Horn (x1 ∨ ¬x2) ∧ (¬x1 ∨ x2 ∨ ¬y3) ∧ ¬x1 introduzindo y3 como negação de x3. Em contraste, nenhuma renomeação de (x1 ∨ ¬x2 ∨ ¬x3) ∧ (¬x1 ∨ x2 ∨ x3) ∧ ¬x1 leva a uma fórmula de Horn. A verificação da existência de tal substituição pode ser feita em tempo linear; portanto, a satisfazibilidade de tais fórmulas está em P, pois pode ser resolvida realizando primeiro essa substituição e, em seguida, verificando a satisfatibilidade da fórmula de Horn resultante.
Satisfabilidade de XOR
| Resolvendo um exemplo XOR-SAT por eliminação gaussiana | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Outro caso especial é a classe de problemas em que cada cláusula contém operadores XOR (isto é, ou exclusivo) em vez de OU (simples). Isso está em P, pois uma fórmula XOR-SAT também pode ser vista como um sistema de equações lineares mod 2 e pode ser resolvida em tempo cúbico por eliminação gaussiana; veja a caixa para um exemplo. Esta reformulação é baseada no parentesco entre álgebras booleanas e anéis booleanos, e no fato de que o módulo aritmético dois forma um corpo finito. Como a XOR b XOR c é avaliado como TRUE se e somente se exatamente 1 ou 3 membros de {a, b,c} são TRUE, cada solução do problema 1-em-3-SAT para uma dada fórmula CNF é também uma solução do problema XOR-3-SAT, e por sua vez cada solução de XOR-3-SAT é uma solução de 3-SAT, cf. foto. Como consequência, para cada fórmula CNF, é possível resolver o problema XOR-3-SAT definido pela fórmula e, com base no resultado, inferir que o problema 3-SAT é solucionável ou que o problema 1-em-3- O problema do SAT é insolúvel.
Desde que as classes de complexidade P e NP não sejam iguais, nem 2-, nem Horn-, nem XOR-satisfabilidade é NP-completo, ao contrário de SAT.
Teorema da dicotomia de Schaefer
As restrições acima (CNF, 2CNF, 3CNF, Horn, XOR-SAT) obrigam as fórmulas consideradas a serem conjunções de subfórmulas; cada restrição estabelece uma forma específica para todas as subfórmulas: por exemplo, apenas cláusulas binárias podem ser subfórmulas em 2CNF.
O teorema da dicotomia de Schaefer afirma que, para qualquer restrição a funções booleanas que podem ser usadas para formar essas subfórmulas, o problema de satisfatibilidade correspondente está em P ou NP-completo. A associação em P da satisfazibilidade das fórmulas 2CNF, Horn e XOR-SAT são casos especiais desse teorema.
A tabela a seguir resume algumas variantes comuns do SAT.
| Código | Nome | Restrições | Requisitos | Classe |
|---|---|---|---|---|
| 3SAT | 3-satisfação | Cada cláusula contém 3 literais. | Pelo menos um literal deve ser verdade. | NP-c |
| 2SAT | 2-satisfação | Cada cláusula contém 2 literais. | Pelo menos um literal deve ser verdade. | NL-C |
| 1-em-3-SAT | Exatamente-1 3-SAT | Cada cláusula contém 3 literais. | Exactamente um literal deve ser verdade. | NP-c |
| 1-em-3-SAT+ | Exatamente-1 Positivo 3-SAT | Cada cláusula contém 3 literais positivos. | Exactamente um literal deve ser verdade. | NP-c |
| NAE3SAT | Não tudo igual 3-satisfabilidade | Cada cláusula contém 3 literais. | Ou um ou dois literais devem ser verdadeiros. | NP-c |
| NAE3SAT+ | Not-all-equal positivo 3-SAT | Cada cláusula contém 3 literais positivos. | Ou um ou dois literais devem ser verdadeiros. | NP-c |
| PL-SAT | SAT de Planar | O grafo de incidência (grafo variável de coral) é planar. | Pelo menos um literal deve ser verdade. | NP-c |
| LSAT | SAT linear | Cada cláusula contém 3 litros, intersetos no máximo uma outra cláusula, e a interseção é exatamente um literal. | Pelo menos um literal deve ser verdade. | NP-c |
| HORN-SAT | Satisfação do chifre | Cláusulas de chifre (na maioria um literal positivo). | Pelo menos um literal deve ser verdade. | P-c |
| XOR-SAT | Satisfação Xor | Cada cláusula contém operações XOR em vez de OR. | O XOR de todos os literais deve ser verdadeiro. | P |
Extensões do SAT
Uma extensão que ganhou popularidade significativa desde 2003 são as teorias de módulo de satisfação (SMT) que podem enriquecer fórmulas CNF com restrições lineares, matrizes, restrições totalmente diferentes, não interpretadas funções, etc. Essas extensões normalmente permanecem NP-completas, mas agora estão disponíveis solucionadores muito eficientes que podem lidar com muitos desses tipos de restrições.
O problema de satisfatibilidade se torna mais difícil se ambos "para todos" (∀) e "existe" (∃) quantificadores são permitidos para vincular as variáveis booleanas. Um exemplo de tal expressão seria ∀x ∀y ∃z (x ∨ y ∨ z) ∧ (¬x ∨ ¬y ∨ ¬z); é válido, pois para todos os valores de x e y, um valor apropriado de z pode ser encontrado, viz. z=TRUE se x e y forem FALSE, e z=FALSE caso contrário. O próprio SAT (tacitamente) usa apenas quantificadores ∃. Se apenas ∀ quantificadores forem permitidos, o chamado problema de tautologia é obtido, que é co-NP-completo. Se ambos os quantificadores forem permitidos, o problema é chamado de problema de fórmula booleana quantificada (QBF), que pode ser mostrado como PSPACE-completo. Acredita-se amplamente que os problemas PSPACE-completos são estritamente mais difíceis do que qualquer problema em NP, embora isso ainda não tenha sido provado. Usando sistemas P altamente paralelos, problemas QBF-SAT podem ser resolvidos em tempo linear.
SAT comum pergunta se há pelo menos uma atribuição de variável que torna a fórmula verdadeira. Uma variedade de variantes lida com o número de tais atribuições:
- MAJ-SAT pergunta se a maioria de todas as tarefas fazem a fórmula TRUE. É conhecido por estar completo para PP, uma classe probabilística.
- #SAT #, o problema de contar quantas tarefas variáveis satisfazem uma fórmula, é um problema de contagem, não um problema de decisão, e é #P-completo.
- UNIQUES é o problema de determinar se uma fórmula tem exatamente uma atribuição. É completo para os EUA, a classe de complexidade descrevendo problemas solváveis por uma máquina de Turing tempo polinomial não determinística que aceita quando há exatamente um caminho de aceitação não-determinístico e rejeita o contrário.
- UNAMBIGUOUS-SAT é o nome dado ao problema de satisfação quando a entrada é restrita a fórmulas que têm no máximo uma atribuição satisfatória. O problema também é chamado EUAT. Um algoritmo de solução para UNAMBIGUOUS-SAT é permitido exibir qualquer comportamento, incluindo looping interminável, em uma fórmula com várias tarefas satisfatórias. Embora este problema pareça mais fácil, Valiant e Vazirani mostraram que se houver um algoritmo prático (isto é, polinomial-tempo randomizado) para resolvê-lo, então todos os problemas em NP podem ser resolvidos tão facilmente.
- Max., o problema máximo de satisfação, é uma generalização FNP do SAT. Ele pede o número máximo de cláusulas que podem ser satisfeitas por qualquer atribuição. Tem algoritmos de aproximação eficientes, mas é NP-hard para resolver exatamente. Pior ainda, é APX-completo, o que significa que não há esquema de aproximação de tempo polinomial (PTAS) para este problema a menos que P=NP.
- WMSAT é o problema de encontrar uma atribuição de peso mínimo que satisfaça uma fórmula booleana monotone (ou seja, uma fórmula sem qualquer negação). Pesos de variáveis proposicionais são dados na entrada do problema. O peso de uma atribuição é a soma de pesos de variáveis verdadeiras. Esse problema é NP-completo (veja Th. 1 de).
Outras generalizações incluem satisfatibilidade para lógica de primeira e segunda ordem, problemas de satisfação de restrição, programação inteira 0-1.
Encontrar uma tarefa satisfatória
Enquanto SAT é um problema de decisão, o problema de busca de encontrar uma atribuição satisfatória reduz-se a SAT. Ou seja, cada algoritmo que responde corretamente se uma instância de SAT é solucionável pode ser usado para encontrar uma atribuição satisfatória. Primeiro, a pergunta é feita sobre a fórmula dada Φ. Se a resposta for "não", a fórmula é insatisfatória. Caso contrário, a pergunta é feita na fórmula parcialmente instanciada Φ{x1=TRUE}, ou seja, Φ com a primeira variável x1 substituída por TRUE e simplificada de acordo. Se a resposta for "sim", então x1=TRUE, caso contrário x1 =FALSO. Os valores de outras variáveis podem ser encontrados subsequentemente da mesma maneira. No total, são necessárias n+1 execuções do algoritmo, onde n é o número de variáveis distintas em Φ.
Esta propriedade é usada em vários teoremas na teoria da complexidade:
- NP ⊆ P/poli ⇒ PH = Σ2 (teorema de karp–Lipton)
- NP ⊆ BPP ⇒ NP = RP
- P = NP ⇒ FP = FNP
Algoritmos para resolver SAT
Como o problema SAT é NP-completo, apenas algoritmos com complexidade exponencial de pior caso são conhecidos por ele. Apesar disso, algoritmos eficientes e escaláveis para SAT foram desenvolvidos durante os anos 2000 e contribuíram para avanços dramáticos em nossa capacidade de resolver automaticamente instâncias de problemas envolvendo dezenas de milhares de variáveis e milhões de restrições (ou seja, cláusulas). Exemplos de tais problemas em automação de projeto eletrônico (EDA) incluem verificação de equivalência formal, verificação de modelo, verificação formal de microprocessadores em pipeline, geração automática de padrões de teste, roteamento de FPGAs, problemas de planejamento e agendamento e assim por diante. Um mecanismo de resolução SAT também é considerado um componente essencial na caixa de ferramentas de automação de design eletrônico.
As principais técnicas usadas pelos solucionadores SAT modernos incluem o algoritmo Davis–Putnam–Logemann–Loveland (ou DPLL), aprendizado de cláusula orientado por conflito (CDCL) e algoritmos estocásticos de pesquisa local, como WalkSAT. Quase todos os solucionadores SAT incluem tempos limite, portanto, eles serão encerrados em um tempo razoável, mesmo que não consigam encontrar uma solução. Diferentes solucionadores SAT acharão diferentes instâncias fáceis ou difíceis, e alguns se destacam em provar insatisfabilidade e outros em encontrar soluções. Tentativas recentes foram feitas para aprender a satisfatibilidade de uma instância usando técnicas de aprendizado profundo.
Os solucionadores SAT são desenvolvidos e comparados em concursos de resolução SAT. Os solucionadores SAT modernos também estão tendo um impacto significativo nos campos de verificação de software, resolução de restrições em inteligência artificial e pesquisa operacional, entre outros.
Contenido relacionado
Erlang (linguagem de programação)
André S. Tanenbaum
APL (linguagem de programação)