Orbital molecular

Conjunto orbital molecular de acetileno completo (H-C≡C-H). A coluna esquerda mostra MO's que estão ocupados no estado do solo, com a menor energia orbital no topo. A linha branca e cinza visível em alguns MO's é o eixo molecular passando pelos núcleos. As funções de onda orbital são positivas nas regiões vermelhas e negativas no azul. A coluna direita mostra MO virtual que estão vazios no estado do solo, mas podem ser ocupados em estados excitados.

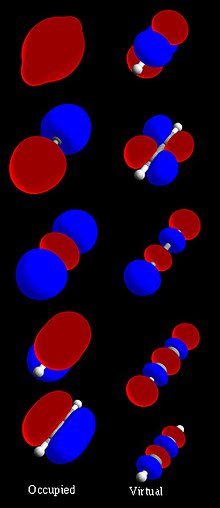
Em química, um orbital molecular () é uma função matemática que descreve a localização e o comportamento ondulatório de um elétron em uma molécula. Essa função pode ser usada para calcular propriedades químicas e físicas, como a probabilidade de encontrar um elétron em qualquer região específica. Os termos orbital atômico e orbital molecular foram introduzidos por Robert S. Mulliken em 1932 para significar funções de onda orbital de um elétron. Em um nível elementar, eles são usados para descrever a região do espaço em que uma função tem uma amplitude significativa.

Em um átomo isolado, os elétrons orbitais' a localização é determinada por funções chamadas orbitais atômicos. Quando vários átomos se combinam quimicamente em uma molécula, os elétrons' as localizações são determinadas pela molécula como um todo, de modo que os orbitais atômicos se combinam para formar orbitais moleculares. Os elétrons dos átomos constituintes ocupam os orbitais moleculares. Matematicamente, os orbitais moleculares são uma solução aproximada da equação de Schrödinger para os elétrons no campo dos núcleos atômicos da molécula. Eles geralmente são construídos combinando orbitais atômicos ou orbitais híbridos de cada átomo da molécula, ou outros orbitais moleculares de grupos de átomos. Eles podem ser calculados quantitativamente usando os métodos de Hartree-Fock ou de campo autoconsistente (SCF).

Os orbitais moleculares são de três tipos: orbitais ligantes que possuem uma energia menor que a energia dos orbitais atômicos que os formaram, e assim promovem as ligações químicas que mantêm a molécula unida; orbitais antiligantes que têm uma energia maior que a energia de seus orbitais atômicos constituintes, e assim se opõem à ligação da molécula, e orbitais não ligantes que têm a mesma energia que seus orbitais atômicos constituintes e, portanto, não têm efeito sobre a ligação da molécula.

Visão geral

Um orbital molecular (MO) pode ser usado para representar as regiões em uma molécula onde é provável que um elétron ocupando esse orbital seja encontrado. Orbitais moleculares são soluções aproximadas da equação de Schrödinger para os elétrons no campo elétrico dos núcleos atômicos da molécula. No entanto, calcular os orbitais diretamente a partir desta equação é um problema muito intratável. Em vez disso, eles são obtidos a partir da combinação de orbitais atômicos, que prevêem a localização de um elétron em um átomo. Um orbital molecular pode especificar a configuração eletrônica de uma molécula: a distribuição espacial e a energia de um (ou um par de) elétron(s). Mais comumente, um MO é representado como uma combinação linear de orbitais atômicos (o método LCAO-MO), especialmente em uso qualitativo ou muito aproximado. Eles são inestimáveis ao fornecer um modelo simples de ligação em moléculas, compreendido por meio da teoria do orbital molecular. A maioria dos métodos atuais em química computacional começa calculando os MOs do sistema. Um orbital molecular descreve o comportamento de um elétron no campo elétrico gerado pelos núcleos e alguma distribuição média dos outros elétrons. No caso de dois elétrons ocupando o mesmo orbital, o princípio de Pauli exige que eles tenham spins opostos. Necessariamente, isso é uma aproximação, e descrições altamente precisas da função de onda eletrônica molecular não possuem orbitais (consulte interação de configuração).

Os orbitais moleculares são, em geral, deslocalizados ao longo de toda a molécula. Além disso, se a molécula tiver elementos de simetria, seus orbitais moleculares não degenerados serão simétricos ou antissimétricos em relação a qualquer uma dessas simetrias. Em outras palavras, a aplicação de uma operação de simetria S (por exemplo, uma reflexão, rotação ou inversão) ao orbital molecular ψ resulta no orbital molecular inalterado ou na reversão de seu sinal matemático: Sψ = ±ψ. Em moléculas planares, por exemplo, os orbitais moleculares são simétricos (sigma) ou antissimétricos (pi) em relação à reflexão no plano molecular. Se moléculas com energias orbitais degeneradas também forem consideradas, uma afirmação mais geral de que os orbitais moleculares formam bases para as representações irredutíveis do grupo de simetria da molécula se mantém. As propriedades de simetria dos orbitais moleculares significam que a deslocalização é uma característica inerente da teoria dos orbitais moleculares e a torna fundamentalmente diferente (e complementar) da teoria das ligações de valência, na qual as ligações são vistas como pares de elétrons localizados, com permissão para ressonância para explicar a deslocalização.

Em contraste com esses orbitais moleculares canônicos adaptados à simetria, os orbitais moleculares localizados podem ser formados aplicando certas transformações matemáticas aos orbitais canônicos. A vantagem dessa abordagem é que os orbitais corresponderão mais de perto às "ligações" de uma molécula representada por uma estrutura de Lewis. Como desvantagem, os níveis de energia desses orbitais localizados não têm mais significado físico. (A discussão no restante deste artigo se concentrará em orbitais moleculares canônicos. Para mais discussões sobre orbitais moleculares localizados, consulte: orbital de ligação natural e sigma-pi e modelos de orbitais equivalentes.)

Formação de orbitais moleculares

Os orbitais moleculares surgem de interações permitidas entre orbitais atômicos, que são permitidas se as simetrias (determinadas pela teoria de grupos) dos orbitais atômicos forem compatíveis entre si. A eficiência das interações orbitais atômicas é determinada a partir da sobreposição (uma medida de quão bem dois orbitais interagem construtivamente um com o outro) entre dois orbitais atômicos, o que é significativo se os orbitais atômicos estiverem próximos em energia. Finalmente, o número de orbitais moleculares formados deve ser igual ao número de orbitais atômicos nos átomos que estão sendo combinados para formar a molécula.

Discussão qualitativa

Para uma discussão imprecisa, mas qualitativamente útil, da estrutura molecular, os orbitais moleculares podem ser obtidos a partir do método de "Combinação linear de orbitais atômicos de orbitais moleculares" ansatz. Aqui, os orbitais moleculares são expressos como combinações lineares de orbitais atômicos.

Combinações lineares de orbitais atômicos (LCAO)

Os orbitais moleculares foram introduzidos pela primeira vez por Friedrich Hund e Robert S. Mulliken em 1927 e 1928. A combinação linear de orbitais atômicos ou "LCAO" A aproximação para orbitais moleculares foi introduzida em 1929 por Sir John Lennard-Jones. Seu artigo inovador mostrou como derivar a estrutura eletrônica das moléculas de flúor e oxigênio a partir de princípios quânticos. Essa abordagem qualitativa da teoria do orbital molecular faz parte do início da química quântica moderna. Combinações lineares de orbitais atômicos (LCAO) podem ser usadas para estimar os orbitais moleculares que são formados após a ligação entre os átomos constituintes da molécula. Semelhante a um orbital atômico, uma equação de Schrödinger, que descreve o comportamento de um elétron, também pode ser construída para um orbital molecular. Combinações lineares de orbitais atômicos, ou as somas e diferenças das funções de onda atômicas, fornecem soluções aproximadas para as equações Hartree-Fock que correspondem à aproximação de partícula independente da equação molecular de Schrödinger. Para moléculas diatômicas simples, as funções de onda obtidas são representadas matematicamente pelas equações

Telecomunicações Telecomunicações = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =cum? ? um+cb)? ? b){displaystyle Psi =c_{a}psi _{a}+c_{b}psi _{b}}

Telecomunicações Telecomunicações ∗ ∗ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =cum? ? um- Sim. - Sim. cb)? ? b)Não. Psi ^{*}=c_{a}psi _{a}-c_{b}psi _{b}}

Onde? Telecomunicações Telecomunicações - Sim. e Telecomunicações Telecomunicações ∗ ∗ Não. Psi ^{*}} são as funções de onda molecular para a ligação e orbitais moleculares antiaderentes, respectivamente, ? ? um{displaystyle psi _{a}} e ? ? b){displaystyle psi _{b}} são as funções de onda atômica de átomos a e b, respectivamente, e cum{displaystyle c_{a}} e cb)Não. c_{b}} são coeficientes ajustáveis. Estes coeficientes podem ser positivos ou negativos, dependendo das energias e simetrias dos orbitais atômicos individuais. À medida que os dois átomos se aproximam, suas órbitas atômicas se sobrepõem para produzir áreas de alta densidade de elétrons, e, como consequência, orbitais moleculares são formados entre os dois átomos. Os átomos são mantidos juntos pela atração eletrostática entre os núcleos carregados positivamente e os elétrons carregados negativamente ocupando orbitais moleculares ligados.

MOs ligantes, antiligantes e não ligantes

Quando os orbitais atômicos interagem, o orbital molecular resultante pode ser de três tipos: ligante, antiligante ou não ligante.

Mos de ligação:

• As interações de ligação entre orbitais atômicos são interações construtivas (infase).
• Ligação MOs são menores em energia do que os orbitais atômicos que se combinam para produzi-los.

MOs antiligantes:

• As interações antiaderente entre orbitais atômicos são interações destrutivas (fora da fase), com um plano nodal onde a função de onda do orbital antiaderente é zero entre os dois átomos que interagem
• Antibonding MOs são mais elevados em energia do que os orbitais atômicos que combinam para produzi-los.

MOs não aderentes:

• Nonbonding MOs são o resultado de nenhuma interação entre orbitais atômicos por causa da falta de simetrias compatíveis.
• Nonbonding Os MOs terão a mesma energia que os orbitais atômicos de um dos átomos da molécula.

Rótulos Sigma e pi para MOs

O tipo de interação entre os orbitais atômicos pode ser ainda categorizado pelos rótulos de simetria orbital molecular σ (sigma), π (pi), δ (delta), φ (phi), γ (gama) etc. Letras gregas correspondentes aos orbitais atômicos s, p, d, f e g, respectivamente. O número de planos nodais contendo o eixo internuclear entre os átomos envolvidos é zero para σ MOs, um para π, dois para δ, três para φ e quatro para γ.

Σ simetria

Um MO com simetria σ resulta da interação de dois orbitais s atômicos ou dois orbitais p_z atômicos. Um MO terá simetria σ se o orbital for simétrico em relação ao eixo que une os dois centros nucleares, o eixo internuclear. Isso significa que a rotação do MO em torno do eixo internuclear não resulta em uma mudança de fase. Um orbital σ*, orbital antiligante sigma, também mantém a mesma fase quando girado em torno do eixo internuclear. O orbital σ* tem um plano nodal que está entre os núcleos e perpendicular ao eixo internuclear.

Π simetria

Um MO com simetria π resulta da interação de dois orbitais p_x atômicos ou orbitais p_y. Um MO terá simetria π se o orbital for assimétrico em relação à rotação em torno do eixo internuclear. Isso significa que a rotação do MO em torno do eixo internuclear resultará em uma mudança de fase. Existe um plano nodal contendo o eixo internuclear, se orbitais reais forem considerados.

Um orbital π*, orbital antiligante pi, também produzirá uma mudança de fase quando girado em torno do eixo internuclear. O orbital π* também possui um segundo plano nodal entre os núcleos.

Simetria Δ

Um MO com simetria δ resulta da interação de dois átomos d_xy ou d_x²-y² orbitais. Como esses orbitais moleculares envolvem orbitais atômicos d de baixa energia, eles são vistos em complexos de metais de transição. Um orbital ligante δ tem dois planos nodais contendo o eixo internuclear, e um orbital antiligante δ* também tem um terceiro plano nodal entre os núcleos.

Φ simetria

Orbitais atômicos alinhados de forma adequada sobrepõem-se à forma phi orbital molecular (uma ligação phi)

Químicos teóricos conjecturaram que ligações de ordem superior, como ligações phi correspondentes à sobreposição de f orbitais atômicos, são possíveis. Não há nenhum exemplo conhecido de uma molécula que supostamente contenha uma ligação phi.

Simetria gerada e não gerada

Para moléculas que possuem um centro de inversão (moléculas centrosimétricas), existem rótulos adicionais de simetria que podem ser aplicados aos orbitais moleculares. Moléculas centrosimétricas incluem:

• Diatômica Homonuclear, X₂
• Octaedral, EX₆
• Planar quadrado, EX₄.

Moléculas não centrossimétricas incluem:

• Diatômica heteronuclear, XY
• Tetraedral, EX₄.

Se a inversão através do centro de simetria em uma molécula resulta nas mesmas fases para o orbital molecular, então diz-se que o MO tem simetria gerade (g), da palavra alemã para par. Se a inversão através do centro de simetria em uma molécula resulta em uma mudança de fase para o orbital molecular, diz-se que o MO tem simetria ungerada (u), da palavra alemã para ímpar. Para um MO ligante com σ-simetria, o orbital é σ_g (s' + s'' é simétrico), enquanto um MO antiligante com σ-simetria o orbital é σ_u, porque a inversão de s' – s'' é antisimétrico. Para um MO de ligação com π-simetria, o orbital é π_u porque a inversão através do centro de simetria para produziria uma mudança de sinal (os dois orbitais atômicos p estão em fase um com o outro, mas os dois lóbulos têm sinais opostos), enquanto um MO antiligante com π-simetria é π_g porque a inversão através do centro de simetria para não produziria uma mudança de sinal (os dois orbitais p são antisimétricos por fase).

Diagramas MO

A abordagem qualitativa da análise MO usa um diagrama orbital molecular para visualizar as interações de ligação em uma molécula. Nesse tipo de diagrama, os orbitais moleculares são representados por linhas horizontais; quanto maior a linha, maior a energia do orbital, e os orbitais degenerados são colocados no mesmo nível com um espaço entre eles. Em seguida, os elétrons a serem colocados nos orbitais moleculares são encaixados um a um, tendo em mente o princípio de exclusão de Pauli e a regra de multiplicidade máxima de Hund (apenas 2 elétrons, com spins opostos, por orbital; coloque quantos elétrons desemparelhados em um nível de energia possível antes de começar a emparelhá-los). Para moléculas mais complicadas, a abordagem da mecânica ondulatória perde utilidade em uma compreensão qualitativa da ligação (embora ainda seja necessária para uma abordagem quantitativa). Algumas propriedades:

• Um conjunto de bases de orbitais inclui aqueles orbitais atômicos que estão disponíveis para interações orbitais moleculares, que podem ser ligação ou antibonding
• O número de orbitais moleculares é igual ao número de orbitais atômicos incluídos na expansão linear ou no conjunto de base
• Se a molécula tiver alguma simetria, os orbitais atômicos degenerados (com a mesma energia atômica) são agrupados em combinações lineares (chamadas de orbitais atômicos adaptados à simetria (SO)), que pertencem à representação do grupo de simetria, de modo que as funções de onda que descrevem o grupo são conhecidas como combinações lineares adaptadas à simetria (SALC).
• O número de orbitais moleculares pertencentes a uma representação de grupo é igual ao número de orbitais atômicos adaptados à simetria pertencentes a esta representação
• Dentro de uma representação particular, os orbitais atômicos adaptados à simetria misturam mais se seus níveis de energia atômica estão mais próximos.

O procedimento geral para a construção de um diagrama de orbitais moleculares para uma molécula razoavelmente simples pode ser resumido da seguinte forma:

1. Atribua um grupo pontual à molécula.

2. Procure as formas dos SALCs.

3. Organize os SALCs de cada fragmento molecular em ordem decrescente de energia, observando primeiro se eles se originam dos orbitais s, p ou d (e coloque-os na ordem s < p < d) e, em seguida, seu número de nós internucleares.

4. Combine SALCs do mesmo tipo de simetria dos dois fragmentos e, a partir de N SALCs, forme N orbitais moleculares.

5. Estime as energias relativas dos orbitais moleculares a partir de considerações de sobreposição e energias relativas dos orbitais pais e desenhe os níveis em um diagrama de nível de energia do orbital molecular (mostrando a origem dos orbitais).

6. Confirme, corrija e revise esta ordem qualitativa realizando um cálculo de orbital molecular usando software comercial.

Ligação em orbitais moleculares

Degenerescência orbital

Orbitais moleculares são considerados degenerados se tiverem a mesma energia. Por exemplo, nas moléculas diatômicas homonucleares dos dez primeiros elementos, os orbitais moleculares derivados dos orbitais atômicos p_x e p_y resultam em dois orbitais ligantes degenerados (de baixa energia) e dois orbitais antiligantes degenerados (de alta energia).

Ligações iônicas

Quando a diferença de energia entre os orbitais atômicos de dois átomos é muito grande, os orbitais de um átomo contribuem quase inteiramente para os orbitais ligantes, e os orbitais do outro átomo contribuem quase inteiramente para os orbitais antiligantes. Assim, a situação é efetivamente que um ou mais elétrons foram transferidos de um átomo para o outro. Isso é chamado de ligação (principalmente) iônica.

Ordem de títulos

A ordem de ligação, ou número de ligações, de uma molécula pode ser determinada pela combinação do número de elétrons em orbitais moleculares ligantes e antiligantes. Um par de elétrons em um orbital ligante cria uma ligação, enquanto um par de elétrons em um orbital antiligante nega uma ligação. Por exemplo, N₂, com oito elétrons em orbitais ligantes e dois elétrons em orbitais antiligantes, tem uma ordem de ligação de três, o que constitui uma ligação tripla.

A força da ligação é proporcional à ordem da ligação - uma quantidade maior de ligação produz uma ligação mais estável - e o comprimento da ligação é inversamente proporcional a ela - uma ligação mais forte é mais curta.

Existem raras exceções ao requisito da molécula ter uma ordem de ligação positiva. Embora Be₂ tenha uma ordem de ligação de 0 de acordo com a análise MO, há evidências experimentais de uma molécula Be₂ altamente instável com um comprimento de ligação de 245 pm e energia de ligação de 10 kJ/mol.

HOMO e LUMO

O orbital molecular ocupado mais alto e o orbital molecular desocupado mais baixo são frequentemente referidos como HOMO e LUMO, respectivamente. A diferença das energias do HOMO e LUMO é chamada de lacuna HOMO-LUMO. Essa noção costuma ser motivo de confusão na literatura e deve ser considerada com cautela. Seu valor geralmente está localizado entre o gap fundamental (diferença entre o potencial de ionização e a afinidade eletrônica) e o gap óptico. Além disso, o gap HOMO-LUMO pode estar relacionado a um gap de material a granel ou gap de transporte, que geralmente é muito menor que o gap fundamental.

Exemplos

Diatômica homonuclear

Os MOs diatômicos homonucleares contêm contribuições iguais de cada orbital atômico no conjunto de base. Isso é mostrado nos diagramas MO diatômicos homonucleares para H₂, He₂ e Li₂, todos contendo orbitais simétricos.

H2

Função de onda eletron para os 1s orbital de um átomo de hidrogênio solitário (esquerda e direita) e a ligação correspondente (bottom) e orbitais moleculares antibonding (top) dos H₂ molécula. A parte real da função de onda é a curva azul, e a parte imaginária é a curva vermelha. Os pontos vermelhos marcam os locais dos núcleos. A função de onda eletrônica oscila de acordo com a equação de onda Schrödinger, e orbitais são suas ondas permanentes. A frequência de onda permanente é proporcional à energia cinética da órbita. (Esta trama é uma fatia unidimensional através do sistema tridimensional.)

Como um exemplo simples de MO, considere os elétrons em uma molécula de hidrogênio, H₂ (veja o diagrama do orbital molecular), com os dois átomos marcados como H' e H". Os orbitais atômicos de menor energia, 1s' e 1s", não se transformam de acordo com as simetrias da molécula. No entanto, os seguintes orbitais atômicos adaptados à simetria fazem:

A combinação simétrica (chamada orbital ligante) tem energia mais baixa do que os orbitais básicos, e a combinação antissimétrica (chamada orbital antiligante) é mais alta. Como a molécula H₂ tem dois elétrons, ambos podem ir no orbital de ligação, tornando o sistema com menos energia (portanto, mais estável) do que dois átomos de hidrogênio livres. Isso é chamado de ligação covalente. A ordem de ligação é igual ao número de elétrons ligantes menos o número de elétrons antiligantes, dividido por 2. Neste exemplo, há 2 elétrons no orbital ligante e nenhum no orbital antiligante; a ordem de ligação é 1, e há uma ligação simples entre os dois átomos de hidrogênio.

He2

Por outro lado, considere a molécula hipotética de He₂ com os átomos marcados como He' e Ele'. Como com H₂, os orbitais atômicos de energia mais baixa são os 1s' e 1s", e não se transformam de acordo com as simetrias da molécula, enquanto os orbitais atômicos adaptados à simetria o fazem. A combinação simétrica — o orbital ligante — tem menor energia do que os orbitais de base, e a combinação antissimétrica — o orbital antiligante — é maior. Ao contrário de H₂, com dois elétrons de valência, He₂ tem quatro em seu estado fundamental neutro. Dois elétrons preenchem o orbital ligante de energia mais baixa, σ_g(1s), enquanto os dois restantes preenchem o orbital antiligante de energia mais alta, σ_u*(1s). Assim, a densidade eletrônica resultante ao redor da molécula não suporta a formação de uma ligação entre os dois átomos; sem uma ligação estável mantendo os átomos juntos, não se esperaria que a molécula existisse. Outra maneira de ver isso é que existem dois elétrons ligantes e dois elétrons antiligantes; portanto, a ordem da ligação é 0 e não existe nenhuma ligação (a molécula tem um estado ligado suportado pelo potencial de Van der Waals).

Li2

Dilithium Li₂ é formado a partir da sobreposição dos orbitais atômicos 1s e 2s (o conjunto de base) de dois átomos de Li. Cada átomo de Li contribui com três elétrons para interações de ligação, e os seis elétrons preenchem os três MOs de menor energia, σ_g(1s), σ_u*(1s) e σ_g(2s). Usando a equação para ordem de ligação, descobriu-se que o dilítio tem uma ordem de ligação de um, uma ligação simples.

Gases nobres

Considerando uma molécula hipotética de He₂, uma vez que o conjunto base de orbitais atômicos é o mesmo que no caso de H₂, descobrimos que tanto a ligação quanto orbitais antiligantes são preenchidos, então não há vantagem energética para o par. HeH teria uma ligeira vantagem energética, mas não tanto quanto H₂ + 2 He, então a molécula é muito instável e existe apenas brevemente antes de se decompor em hidrogênio e hélio. Em geral, descobrimos que átomos como o He, que possuem camadas de energia completas, raramente se ligam a outros átomos. Exceto pelos complexos de Van der Waals de vida curta, existem muito poucos compostos de gases nobres conhecidos.

Diatômicas heteronucleares

Enquanto os MOs para moléculas diatômicas homonucleares contêm contribuições iguais de cada orbital atômico em interação, os MOs para diatômicos heteronucleares contêm contribuições orbitais atômicas diferentes. As interações orbitais para produzir orbitais ligantes ou antiligantes em diatômicos heteronucleares ocorrem se houver sobreposição suficiente entre os orbitais atômicos conforme determinado por suas simetrias e similaridade nas energias orbitais.

AF

No fluoreto de hidrogênio, a sobreposição HF entre os orbitais H 1s e F 2s é permitida por simetria, mas a diferença de energia entre os dois orbitais atômicos os impede de interagir para criar um orbital molecular. A sobreposição entre os orbitais H 1s e F 2p_z também é permitida por simetria, e esses dois orbitais atômicos têm uma pequena separação de energia. Assim, eles interagem, levando à criação de MOs σ e σ* e uma molécula com ordem de ligação 1. Como HF é uma molécula não centrosimétrica, os rótulos de simetria g e u não se aplicam aos seus orbitais moleculares.

Abordagem quantitativa

Para obter valores quantitativos para os níveis de energia molecular, é preciso ter orbitais moleculares que sejam tais que a expansão da interação de configuração (CI) converja rapidamente para o limite CI completo. O método mais comum para obter tais funções é o método de Hartree-Fock, que expressa os orbitais moleculares como autofunções do operador de Fock. Geralmente se resolve esse problema expandindo os orbitais moleculares como combinações lineares de funções gaussianas centradas nos núcleos atômicos (ver combinação linear de orbitais atômicos e conjunto de base (química)). A equação para os coeficientes dessas combinações lineares é uma equação de autovalor generalizada conhecida como equações de Roothaan, que são de fato uma representação particular da equação de Hartree-Fock. Existem vários programas nos quais cálculos químicos quânticos de MOs podem ser realizados, incluindo o Spartan.

Contas simples geralmente sugerem que as energias orbitais moleculares experimentais podem ser obtidas pelos métodos de espectroscopia de fotoelétrons ultravioleta para orbitais de valência e espectroscopia de fotoelétrons de raios-X para orbitais centrais. Isso, no entanto, é incorreto, pois esses experimentos medem a energia de ionização, a diferença de energia entre a molécula e um dos íons resultante da remoção de um elétron. As energias de ionização estão ligadas aproximadamente às energias orbitais por Koopmans'. teorema. Embora a concordância entre esses dois valores possa ser próxima para algumas moléculas, pode ser muito ruim em outros casos.