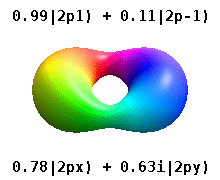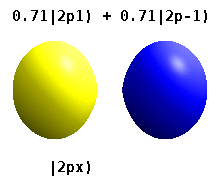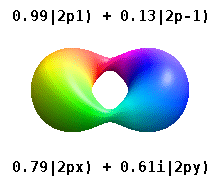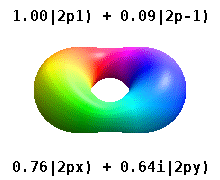Orbital atômico

Na teoria atômica e na mecânica quântica, um orbital atômico é uma função que descreve a localização e o comportamento ondulatório de um elétron em um átomo. Esta função pode ser usada para calcular a probabilidade de encontrar qualquer elétron de um átomo em qualquer região específica ao redor do núcleo do átomo. O termo orbital atômico também pode se referir à região física ou espaço onde o elétron pode estar presente, conforme previsto pela forma matemática particular do orbital.
Cada orbital em um átomo é caracterizado por um conjunto de valores dos três números quânticos n, Eu...e mEu..., que correspondem, respectivamente, à energia do elétron, ao impulso angular e a um componente angular do vetor momentum (número quântico magnético). Alternativa ao número quântico magnético, os orbitais são frequentemente rotulados pelos polinômios harmônicos associados (por exemplo, Xy!, x2 - Sim. Sim.2). Cada orbital pode ser ocupado por um máximo de dois elétrons, cada um com sua própria projeção de rotação mSNão. m_{s}}. Os nomes simples s orbital, P orbital, d orbitale f orbital referem-se a orbitais com momentum angular número quântico Eu... = 0, 1, 2, e 3 respectivamente. Estes nomes, juntamente com o valor den, são usados para descrever as configurações de elétrons de átomos. Eles são derivados da descrição pelos primeiros espectroscopistas de certas séries de linhas espectroscópicas de metal alcalino como afiada, principal, difusa e fundamental. Orbitals para Eu... > 3 continuar alfabeticamente (g, h, i, k,...), omitindo j porque algumas línguas não distinguem entre as letras "i" e "j".
Os orbitais atômicos são os blocos de construção básicos do modelo orbital atômico (ou nuvem de elétrons ou modelo de mecânica de onda), uma estrutura moderna para visualizar o comportamento submicroscópico dos elétrons na matéria. Neste modelo, a nuvem eletrônica de um átomo pode ser vista como sendo construída (em aproximação) em uma configuração eletrônica que é um produto de orbitais atômicos semelhantes ao hidrogênio mais simples. A periodicidade repetida de blocos de 2, 6, 10 e 14 elementos dentro das seções da tabela periódica surge naturalmente do número total de elétrons que ocupam um conjunto completo de s, p, d e f orbitais, respectivamente, embora para valores mais altos de número quântico n, particularmente quando o átomo carrega uma carga positiva, as energias de certos sub -shells tornam-se muito semelhantes e, portanto, a ordem em que dizem ser preenchidos por elétrons (por exemplo, Cr = [Ar]4s13d5 e Cr 2+ = [Ar]3d4) pode ser racionalizado apenas de forma um tanto arbitrária.
Propriedades do elétron
Com o desenvolvimento da mecânica quântica e descobertas experimentais (como a difração de elétrons em duas fendas), descobriu-se que os elétrons orbitando um núcleo não podiam ser totalmente descritos como partículas, mas precisavam ser explicados pela dualidade onda-partícula. Nesse sentido, os elétrons têm as seguintes propriedades:
Propriedades semelhantes a ondas:
- Os elétrons não orbitam um núcleo da maneira de um planeta orbitando o Sol, mas em vez disso existem como ondas permanentes. Assim, a menor energia possível que um elétron pode tomar é semelhante à frequência fundamental de uma onda em uma corda. Os estados de energia mais elevados são semelhantes às harmônicas dessa frequência fundamental.
- Os elétrons nunca estão em um único ponto, embora a probabilidade de interagir com o elétron em um único ponto possa ser encontrada a partir da função de onda do elétron. A carga do elétron funciona como se fosse manchada no espaço em uma distribuição contínua, proporcional em qualquer ponto à magnitude quadrada da função de onda do elétron.
Propriedades semelhantes a partículas:
- O número de elétrons orbitando um núcleo pode ser apenas um inteiro.
- Os electrões saltam entre orbitais como partículas. Por exemplo, se um fóton atinge os elétrons, apenas um elétron muda de estado como resultado.
- Os elétrons mantêm propriedades semelhantes a partículas, como: cada estado de onda tem a mesma carga elétrica que sua partícula de elétrons. Cada estado de onda tem um único spin discreto (pinar para cima ou girar para baixo) dependendo de sua superposição.
Assim, os elétrons não podem ser descritos simplesmente como partículas sólidas. Uma analogia pode ser a de uma "atmosfera" (o elétron), distribuído em torno de um planeta relativamente pequeno (o núcleo). Orbitais atômicos descrevem exatamente a forma dessa "atmosfera" somente quando um elétron está presente. Quando mais elétrons são adicionados, os elétrons adicionais tendem a preencher mais uniformemente um volume de espaço ao redor do núcleo, de modo que a coleção resultante ("nuvem de elétrons") tende para uma zona de probabilidade geralmente esférica que descreve o elétron" 39;s localização, por causa do princípio da incerteza.
Definição formal da mecânica quântica
Os orbitais atômicos podem ser definidos com mais precisão na linguagem formal da mecânica quântica. Eles são soluções aproximadas da equação de Schrödinger para os elétrons ligados ao átomo pelo campo elétrico do núcleo do átomo. Especificamente, na mecânica quântica, o estado de um átomo, isto é, um autoestado do hamiltoniano atômico, é aproximado por uma expansão (ver expansão de interação de configuração e conjunto de base) em combinações lineares de produtos anti-simétricos (determinantes de Slater) de um- funções eletrônicas. Os componentes espaciais dessas funções de um elétron são chamados de orbitais atômicos. (Quando se considera também seu componente de spin, fala-se de orbitais de spin atômico.) Um estado é, na verdade, uma função das coordenadas de todos os elétrons, de modo que seu movimento está correlacionado, mas isso geralmente é aproximado por este modelo de partículas independentes de produtos de funções de onda de um único elétron. (A força de dispersão de London, por exemplo, depende das correlações do movimento dos elétrons.)
Na física atômica, as linhas espectrais atômicas correspondem a transições (saltos quânticos) entre estados quânticos de um átomo. Esses estados são rotulados por um conjunto de números quânticos resumidos no termo símbolo e geralmente associados a configurações eletrônicas particulares, ou seja, por esquemas de ocupação de orbitais atômicos (por exemplo, 1s2 2s2 2p6 para o estado fundamental do símbolo do termo neon: 1S0).
Esta notação significa que os determinantes de Slater correspondentes têm um peso claramente maior na expansão da interação de configuração. O conceito de orbital atômico é, portanto, um conceito-chave para visualizar o processo de excitação associado a uma determinada transição. Por exemplo, pode-se dizer para uma dada transição que ela corresponde à excitação de um elétron de um orbital ocupado para um dado orbital desocupado. No entanto, deve-se ter em mente que os elétrons são férmions regidos pelo princípio de exclusão de Pauli e não podem ser distinguidos uns dos outros. Além disso, às vezes acontece que a expansão da interação de configuração converge muito lentamente e que não se pode falar sobre função de onda simples de um determinante. Este é o caso quando a correlação eletrônica é grande.
Fundamentalmente, um orbital atômico é uma função de onda de um elétron, embora muitos elétrons não estejam em átomos de um elétron e, portanto, a visão de um elétron é uma aproximação. Ao pensar em orbitais, muitas vezes recebemos uma visualização orbital fortemente influenciada pela aproximação Hartree-Fock, que é uma maneira de reduzir as complexidades da teoria orbital molecular.
Tipos de orbital
Os orbitais atômicos podem ser os "orbitais" que são soluções exatas para a equação de Schrödinger para um "átomo" (isto é, átomo com um elétron). Alternativamente, orbitais atômicos referem-se a funções que dependem das coordenadas de um elétron (isto é, orbitais), mas são usadas como pontos de partida para aproximar funções de onda que dependem das coordenadas simultâneas de todos os elétrons em um átomo ou molécula. Os sistemas de coordenadas escolhidos para orbitais são geralmente coordenadas esféricas (r, θ, φ) em átomos e (x, y, z) cartesiano em moléculas poliatômicas. A vantagem das coordenadas esféricas aqui é que uma função de onda orbital é um produto de três fatores, cada um dependente de uma única coordenada: ψ(r, θ, φ) = R(r) Θ(θ) Φ (φ). Os fatores angulares dos orbitais atômicos Θ(θ) Φ(φ) geram funções s, p, d, etc. como combinações reais de harmônicos esféricos Yℓm(θ, φ) (onde ℓ e m são números quânticos). Normalmente existem três formas matemáticas para as funções radiais R(r) que podem ser escolhidas como ponto de partida para o cálculo das propriedades de átomos e moléculas com muitos elétrons:
- O orbitais semelhantes a hidrogénio são derivados das soluções exatas da Equação de Schrödinger para um elétron e um núcleo, para um átomo de hidrogênio. A parte da função que depende da distância R do núcleo tem nós radiais e decai como e- Sim. - Sim. α α R{displaystyle e^{-alpha r}}.
- O orbital tipo Slater (STO) é uma forma sem nós radiais, mas decai do núcleo como faz um orbital semelhante a hidrogênio.
- A forma do tipo gaussiano orbital (Gaussianos) não tem nós radiais e decai como e- Sim. - Sim. α α R2{displaystyle e^{-alpha r^{2}}}.
Embora orbitais semelhantes ao hidrogênio ainda sejam usados como ferramentas pedagógicas, o advento dos computadores tornou os STOs preferíveis para átomos e moléculas diatômicas, uma vez que combinações de STOs podem substituir os nós em orbitais semelhantes ao hidrogênio. Gaussianas são tipicamente usadas em moléculas com três ou mais átomos. Embora não sejam tão precisos quanto os STOs, as combinações de muitos gaussianos podem atingir a precisão dos orbitais semelhantes ao hidrogênio.
História
O termo "orbital" foi cunhado por Robert Mulliken em 1932 como abreviação de função de onda orbital de um elétron. Niels Bohr explicou por volta de 1913 que os elétrons podem girar em torno de um núcleo compacto com momento angular definido. O modelo de Bohr foi uma melhoria nas explicações de 1911 de Ernest Rutherford, que do elétron se movendo em torno de um núcleo. O físico japonês Hantaro Nagaoka publicou uma hipótese baseada em órbita para o comportamento do elétron já em 1904. Cada uma dessas teorias foi construída sobre novas observações começando com uma compreensão simples e tornando-se mais correta e complexa. Explicando o comportamento dessas "órbitas" foi uma das forças motrizes por trás do desenvolvimento da mecânica quântica.
Primeiros modelos
Com a descoberta do elétron por J. J. Thomson em 1897, ficou claro que os átomos não eram os menores blocos de construção da natureza, mas sim partículas compostas. A estrutura recém-descoberta dentro dos átomos tentou muitos a imaginar como as partes constituintes do átomo podem interagir umas com as outras. Thomson teorizou que múltiplos elétrons giram em anéis parecidos com órbitas dentro de uma substância gelatinosa carregada positivamente, e entre a descoberta do elétron e 1909, esse "modelo de pudim de ameixa" foi a explicação mais amplamente aceita da estrutura atômica.
Pouco depois da descoberta de Thomson, Hantaro Nagaoka previu um modelo diferente para a estrutura eletrônica. Ao contrário do modelo do pudim de ameixa, a carga positiva no "Modelo Saturniano" estava concentrado em um núcleo central, puxando os elétrons para órbitas circulares que lembram os anéis de Saturno. Poucas pessoas notaram o trabalho de Nagaoka na época, e o próprio Nagaoka reconheceu um defeito fundamental na teoria mesmo em sua concepção, ou seja, que um objeto carregado clássico não pode sustentar o movimento orbital porque está acelerando e, portanto, perde energia devido à radiação eletromagnética. No entanto, o modelo saturnino revelou ter mais em comum com a teoria moderna do que qualquer um de seus contemporâneos.
Átomo de Bohr
Em 1909, Ernest Rutherford descobriu que a maior parte da massa atômica estava fortemente condensada em um núcleo, que também era carregado positivamente. Ficou claro a partir de sua análise em 1911 que o modelo do pudim de passas não poderia explicar a estrutura atômica. Em 1913, o aluno de pós-doutorado de Rutherford, Niels Bohr, propôs um novo modelo do átomo, em que os elétrons orbitavam o núcleo com períodos clássicos, mas podiam ter apenas valores discretos de momento angular, quantizados em unidades ħ. Essa restrição permitia automaticamente apenas certas energias de elétrons. O modelo de Bohr do átomo corrigiu o problema da perda de energia da radiação de um estado fundamental (declarando que não havia nenhum estado abaixo deste) e, mais importante, explicou a origem das linhas espectrais.
Após o uso de Bohr da explicação de Einstein sobre o efeito fotoelétrico para relacionar os níveis de energia nos átomos com o comprimento de onda da luz emitida, a conexão entre a estrutura dos elétrons nos átomos e os espectros de emissão e absorção de os átomos tornaram-se uma ferramenta cada vez mais útil na compreensão dos elétrons nos átomos. A característica mais proeminente dos espectros de emissão e absorção (conhecida experimentalmente desde meados do século XIX) era que esses espectros atômicos continham linhas discretas. A importância do modelo de Bohr era que ele relacionava as linhas nos espectros de emissão e absorção com as diferenças de energia entre as órbitas que os elétrons poderiam tomar em torno de um átomo. Isso, no entanto, não foi alcançado por Bohr dando aos elétrons algum tipo de propriedade ondulatória, uma vez que a ideia de que os elétrons poderiam se comportar como ondas de matéria não foi sugerida até onze anos depois. Ainda assim, o uso do modelo de Bohr de momentos angulares quantizados e, portanto, níveis de energia quantizados foi um passo significativo para a compreensão dos elétrons nos átomos, e também um passo significativo para o desenvolvimento da mecânica quântica ao sugerir que as restrições quantizadas devem explicar todos os níveis de energia descontínuos e espectros em átomos.
Com a sugestão de de Broglie da existência de ondas de matéria eletrônica em 1924, e por um curto período de tempo antes do tratamento completo da equação de Schrödinger de 1926 de átomos semelhantes ao hidrogênio, um elétron de Bohr "comprimento de onda" pode ser visto como uma função de seu momento; assim, um elétron em órbita de Bohr foi visto orbitando em um círculo em um múltiplo de seu meio comprimento de onda. O modelo de Bohr por um curto período de tempo pode ser visto como um modelo clássico com uma restrição adicional fornecida pelo 'comprimento de onda' argumento. No entanto, esse período foi imediatamente substituído pela mecânica de onda tridimensional completa de 1926. Em nossa compreensão atual da física, o modelo de Bohr é chamado de modelo semiclássico por causa de sua quantização do momento angular, não principalmente por causa de sua relação com comprimento de onda do elétron, que apareceu em retrospectiva doze anos depois que o modelo de Bohr foi proposto.
O modelo de Bohr foi capaz de explicar os espectros de emissão e absorção do hidrogênio. As energias dos elétrons nos estados n = 1, 2, 3 etc. no modelo de Bohr correspondem às da física atual. No entanto, isso não explica as semelhanças entre átomos diferentes, expressas pela tabela periódica, como o fato de o hélio (dois elétrons), o néon (10 elétrons) e o argônio (18 elétrons) apresentarem inércia química semelhante. A mecânica quântica moderna explica isso em termos de camadas e subcamadas de elétrons, cada uma podendo conter um número de elétrons determinado pelo princípio de exclusão de Pauli. Assim, o estado n = 1 pode conter um ou dois elétrons, enquanto o estado n = 2 pode conter até oito elétrons em subcamadas 2s e 2p. No hélio, todos os estados n = 1 estão totalmente ocupados; o mesmo vale para n = 1 e n = 2 em neon. No argônio, os subníveis 3s e 3p são igualmente ocupados por oito elétrons; a mecânica quântica também permite um subnível 3d, mas com energia mais alta que 3s e 3p no argônio (ao contrário da situação do hidrogênio) e permanece vazio.
Concepções modernas e conexões com o princípio da incerteza de Heisenberg
Imediatamente após Heisenberg descobrir seu princípio da incerteza, Bohr observou que a existência de qualquer tipo de pacote de ondas implica incerteza na frequência e no comprimento de onda da onda, uma vez que é necessário um espalhamento de frequências para criar o próprio pacote. Na mecânica quântica, onde todos os momentos das partículas estão associados a ondas, é a formação de tal pacote de ondas que localiza a onda e, portanto, a partícula no espaço. Nos estados em que uma partícula da mecânica quântica está ligada, ela deve ser localizada como um pacote de ondas, e a existência do pacote e seu tamanho mínimo implicam uma propagação e um valor mínimo no comprimento de onda da partícula e, portanto, também no momento e na energia. Na mecânica quântica, como uma partícula está localizada em uma região menor no espaço, o pacote de onda comprimido associado requer uma gama cada vez maior de momentos e, portanto, maior energia cinética. Assim, a energia de ligação para conter ou aprisionar uma partícula em uma região menor do espaço aumenta sem limites à medida que a região do espaço diminui. As partículas não podem ser restritas a um ponto geométrico no espaço, pois isso exigiria um momento infinito de partícula.
Em química, Schrödinger, Pauling, Mulliken e outros observaram que a consequência da relação de Heisenberg era que o elétron, como um pacote de ondas, não poderia ser considerado como tendo uma localização exata em seu orbital. Max Born sugeriu que a posição do elétron precisava ser descrita por uma distribuição de probabilidade relacionada com a localização do elétron em algum ponto da função de onda que descrevia seu pacote de onda associado. A nova mecânica quântica não forneceu resultados exatos, mas apenas as probabilidades de ocorrência de uma variedade de resultados possíveis. Heisenberg sustentou que o caminho de uma partícula em movimento não tem sentido se não pudermos observá-lo, como não podemos com os elétrons em um átomo.
Na imagem quântica de Heisenberg, Schrödinger e outros, o número do átomo de Bohr n para cada orbital tornou-se conhecido como uma n-esfera em um átomo tridimensional e foi retratado como a energia mais provável da nuvem de probabilidade do pacote de ondas do elétron que envolveu o átomo.
Nomes de orbitais
Notação orbital e subshells
Os orbitais receberam nomes, que geralmente são dados na forma:
- X)Sim.peNão. X,mathrm {type} }
onde X é o nível de energia correspondente ao número quântico principal n; tipo é uma letra minúscula que denota a forma ou subcamada do orbital, correspondendo ao número quântico do momento angular ℓ .
Por exemplo, o orbital 1s (pronunciado como os números e letras individuais: "'one' 'ess'") é o nível de energia mais baixo (n = 1) e tem um número quântico angular de ℓ = 0, denotado como s. Orbitais com ℓ = 1, 2 e 3 são denotados como p, d e f, respectivamente.
O conjunto de orbitais para um determinado n e ℓ é chamado de subshell, denotado
- X)Sim.peSim.Não. X,mathrm {type} ^{y} }.
O expoente y mostra o número de elétrons no subnível. Por exemplo, a notação 2p4 indica que o subnível 2p de um átomo contém 4 elétrons. Este subnível tem 3 orbitais, cada um com n = 2 e ℓ = 1.
Notação de raios X
Há também outro sistema menos comum ainda usado na ciência de raios-X, conhecido como notação de raios-X, que é uma continuação das notações usadas antes que a teoria orbital fosse bem compreendida. Nesse sistema, o número quântico principal recebe uma letra associada a ele. Para n = 1, 2, 3, 4, 5, ..., as letras associadas a esses números são K, L, M, N, O,... respectivamente.
Orbitais semelhantes ao hidrogênio
Os orbitais atômicos mais simples são aqueles calculados para sistemas com um único elétron, como o átomo de hidrogênio. Um átomo de qualquer outro elemento ionizado em um único elétron é muito semelhante ao hidrogênio, e os orbitais assumem a mesma forma. Na equação de Schrödinger para este sistema de uma partícula negativa e uma positiva, os orbitais atômicos são os autoestados do operador hamiltoniano para a energia. Eles podem ser obtidos analiticamente, o que significa que os orbitais resultantes são produtos de uma série polinomial e funções exponenciais e trigonométricas. (ver átomo de hidrogênio).
Para átomos com dois ou mais elétrons, as equações governantes podem ser resolvidas apenas com o uso de métodos de aproximação iterativa. Orbitais de átomos multieletrônicos são qualitativamente semelhantes aos do hidrogênio e, nos modelos mais simples, eles são considerados como tendo a mesma forma. Para análises mais rigorosas e precisas, aproximações numéricas devem ser usadas.
Um determinado orbital atômico (semelhante ao hidrogênio) é identificado por valores únicos de três números quânticos: n, ℓ e mℓ. As regras que restringem os valores dos números quânticos e suas energias (veja abaixo) explicam a configuração eletrônica dos átomos e a tabela periódica.
Os estados estacionários (estados quânticos) dos átomos semelhantes ao hidrogênio são seus orbitais atômicos. No entanto, em geral, o comportamento de um elétron não é totalmente descrito por um único orbital. Os estados de elétrons são melhor representados por "misturas" (combinações lineares) de múltiplos orbitais. Consulte Combinação linear de orbitais atômicos método de orbitais moleculares.
O número quântico n apareceu pela primeira vez no modelo de Bohr, onde determina o raio de cada órbita circular do elétron. Entretanto, na mecânica quântica moderna, n determina a distância média do elétron do núcleo; todos os elétrons com o mesmo valor de n estão na mesma distância média. Por esta razão, orbitais com o mesmo valor de n são considerados uma "casca". Orbitais com o mesmo valor de n e também o mesmo valor de ℓ estão ainda mais relacionados, e dizem que compreendem um "subshell".
Números quânticos
Devido à natureza da mecânica quântica dos elétrons ao redor de um núcleo, os orbitais atômicos podem ser definidos exclusivamente por um conjunto de números inteiros conhecidos como números quânticos. Esses números quânticos ocorrem apenas em certas combinações de valores, e sua interpretação física muda dependendo se versões reais ou complexas dos orbitais atômicos são empregadas.
Orbitais complexos
Na física, as descrições orbitais mais comuns são baseadas nas soluções para o átomo de hidrogênio, onde os orbitais são dados pelo produto entre uma função radial e um harmônico esférico puro. Os números quânticos, juntamente com as regras que regem seus possíveis valores, são os seguintes:
O número quântico principal n descreve a energia do elétron e é sempre um inteiro positivo. Na verdade, pode ser qualquer número inteiro positivo, mas, pelas razões discutidas abaixo, números grandes raramente são encontrados. Cada átomo tem, em geral, muitos orbitais associados a cada valor de n; esses orbitais juntos às vezes são chamados de invólucros de elétrons.
O número quântico azimutal Eu... descreve o momento angular orbital de cada elétron e é um inteiro não negativo. Dentro de uma concha onde n é algum inteiro n0, Eu... varia em todos os valores (inteiros) que satisfazem a relação 0≤ ≤ Eu... Eu... ≤ ≤ n0- Sim. - Sim. 1{displaystyle 0leq ell leq N_{0}-1. Por exemplo, o n = 1shell tem apenas orbitais com Eu... Eu... = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0- Sim., e n = 2shell tem apenas orbitais com Eu... Eu... = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0- Sim.e Eu... Eu... = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1{displaystyle ell =1}. O conjunto de orbitais associados com um valor particular deEu... às vezes são coletivamente chamados de Subshell.
O número quântico magnético, mEu... Eu... Não. M_{ell), descreve o momento magnético de um elétron em uma direção arbitrária, e também é sempre um inteiro. Dentro de um subshell onde Eu... Eu... - Sim. é algum inteiro Eu... Eu... 0{displaystyle ell _{0}}, mEu... Eu... Não. M_{ell) intervalos assim: - Sim. - Sim. Eu... Eu... 0≤ ≤ mEu... Eu... ≤ ≤ Eu... Eu... 0Não. -ell _{0}leq m_{ell }leq ell _{0}}.
Os resultados acima podem ser resumidos na tabela a seguir. Cada célula representa uma sub-marca, e lista os valores de mEu... Eu... Não. M_{ell) disponível nesse sub-shell. Células vazias representam subvenções que não existem.
| Eu... = 0 (s) | Eu... = 1 (p) | Eu... = 2 (d) | Eu... = 3 (f) | Eu... = 4 (g) | ... | |
|---|---|---|---|---|---|---|
| n = 1 | mEu... Eu... = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0Não. - Sim. | ... | ||||
| n = 2 | 0 | -1, 0, 1 | ... | |||
| n = 3 | 0 | -1, 0, 1 | -2, −1, 0, 1, 2 | ... | ||
| n = 4 | 0 | -1, 0, 1 | -2, −1, 0, 1, 2 | −3, −2, −1, 0, 1, 2, 3 | ... | |
| n = 5 | 0 | -1, 0, 1 | -2, −1, 0, 1, 2 | −3, −2, −1, 0, 1, 2, 3 | −4, −3, −2, −1, 0, 1, 2, 3, 4 | ... |
| ... | ... | ... | ... | ... | ... | ... |
Subchetes são geralmente identificados por seus nNão.- e Eu... Eu... - Sim.-valores. nNão. é representado pelo seu valor numérico, mas Eu... Eu... - Sim. é representado por uma carta como segue: 0 é representado por 's', 1 por 'p', 2 por 'd', 3 por 'f' e 4 por 'g'. Por exemplo, pode-se falar do subshell com n= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2Não. e Eu... Eu... = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0- Sim. como um "2s subshell".
Cada elétron também tem um número quântico de spin, s, que descreve o spin de cada elétron (spin up ou spin down). O número s pode ser +1 /2 ou −1/2.
O princípio de exclusão de Pauli afirma que dois elétrons em um átomo não podem ter os mesmos valores de todos os quatro números quânticos. Se houver dois elétrons em um orbital com valores dados para três números quânticos, (n, ℓ, m), esses dois elétrons devem diferir em seus rodar.
As convenções acima implicam um eixo preferencial (por exemplo, a direção z em coordenadas cartesianas) e também implicam uma direção preferencial ao longo desse eixo preferencial. Caso contrário, não faria sentido distinguir m = +1 de m = − 1. Como tal, o modelo é mais útil quando aplicado a sistemas físicos que compartilham essas simetrias. O experimento de Stern-Gerlach — em que um átomo é exposto a um campo magnético — fornece um desses exemplos.
Orbitais reais
Além dos complexos orbitais descritos acima, é comum, especialmente na literatura química, usar real orbitais atômicos. Estes orbitais reais surgem de combinações lineares simples de orbitais complexos. Usando a convenção de fase Condon-Shortley, orbitais reais estão relacionados a orbitais complexos da mesma forma que os harmônicos esféricos reais estão relacionados com harmônicos esféricos complexos. Deixando ? ? n,Eu... Eu... ,m{displaystyle psi _{n,ellm}} denote uma órbita complexa com números quânticos nNão., Eu...Não.e mNão., os orbitais reais ? ? n,Eu... Eu... ,mreal{displaystyle psi _{n,ellm}^{text{real}}} pode ser definido por
- <math alttext="{displaystyle psi _{n,ellm}^{text{real}}={begin{cases}{sqrt {2}}(-1)^{m}{text{Im}}left{psi _{n,ell|m|}right}&{text{ for }}m0end{cases}}={begin{cases}{frac {i}{sqrt {2}}}left(psi _{n,ell-|m|}-(-1)^{m}psi _{n,ell|m|}right)&{text{ for }}m0\end{cases}}}" xmlns="http://www.w3.org/1998/Math/MathML">? ? n,Eu... Eu... ,mreal= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(2(- Sim. - Sim. 1)mEu...(? ? n,Eu... Eu... ,|m|?param<0? ? n,Eu... Eu... ,|m|param= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =02(- Sim. - Sim. 1)mRepito(? ? n,Eu... Eu... ,|m|?param>0= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(Eu...2(? ? n,Eu... Eu... ,- Sim. - Sim. |m|- Sim. - Sim. (- Sim. - Sim. 1)m? ? n,Eu... Eu... ,|m|)param<0? ? n,Eu... Eu... ,|m|param= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =012(? ? n,Eu... Eu... ,- Sim. - Sim. |m|+(- Sim. - Sim. 1)m? ? n,Eu... Eu... ,|m|)param>0{displaystyle psi _{n,ellm}^{text{real}}={begin{cases}{sqrt {2}}(-1)^{m}{text{Im}}left{psi _{n,ell|m|}right}&{text{ for }}m0end{cases}}={begin{cases}{frac {i}{sqrt {2}}}left(psi _{n,ell-|m|}-(-1)^{m}psi _{n,ell|m|}right)&{sqrt {2}m<0\psi _{n,ell|m|m|}&{text{=0{frac {1}{sqrt {2}n}}<img alt="{displaystyle psi _{n,ellm}^{text{real}}={begin{cases}{sqrt {2}}(-1)^{m}{text{Im}}left{psi _{n,ell|m|}right}&{text{ for }}m0end{cases}}={begin{cases}{frac {i}{sqrt {2}}}left(psi _{n,ell-|m|}-(-1)^{m}psi _{n,ell|m|}right)&{text{ for }}m0\end{cases}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/7bf4dcadba666e2e8d5422a09290fda36ff2995a" style="vertical-align: -4.985ex; margin-bottom: -0.187ex; width:94.362ex; height:11.509ex;"/>
Se ? ? n,Eu... Eu... ,m(R,θ θ ,φ φ )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =RnEu...(R)YEu... Eu... m(θ θ ,φ φ ){displaystyle psi _{n,ellm}(r,thetaphi)=R_{nl}(r)Y_{ell }^{m}(thetaphi)}, com RnEu...(R)(r)} a parte radial da órbita, esta definição é equivalente a ? ? n,Eu... Eu... ,mreal(R,θ θ ,φ φ )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =RnEu...(R)YEu... Eu... m(θ θ ,φ φ ){displaystyle psi _{n,ellm}^{text{real}}(r,thetaphi)=R_{nl}(r) Y_{ell m}(thetaphi)} Onde? YEu... Eu... mNão. Sim. é a verdadeira harmônica esférica relacionada com a parte real ou imaginária do complexo harmônico esférico YEu... Eu... mNão. Y_{ell }^{m}}.
harmônicos esféricos reais são fisicamente relevantes quando um átomo é incorporado em um sólido cristalino, em que caso há múltiplos eixos de simetria preferidos, mas nenhuma direção preferida. Os orbitais atômicos reais também são mais freqüentemente encontrados em livros didáticos de química introdutória e mostrados em visualizações orbitais comuns. Em orbitais reais de hidrogênio, números quânticos nNão. e Eu... Eu... - Sim. têm a mesma interpretação e significado como suas contrapartes complexas, mas mNão. não é mais um bom número quântico (mas seu valor absoluto é).
Alguns orbitais reais recebem nomes específicos além do simples ? ? n,Eu... Eu... ,m{displaystyle psi _{n,ellm}} designação. Orbitais com número quântico Eu... Eu... - Sim. igual a 0,1,2,3,4,5,6...... Não. 0,1,2,3,4,5,6ldots } são chamados S,p,D,f,g,h,...... {displaystyle s,p,d,f,g,h,ldots } orbitais. Com este já pode atribuir nomes a orbitais complexos, como 2p± ± 1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =? ? 2,1,± ± 1{displaystyle 2p_{pm 1}=psi _{2,1,pm 1; o primeiro símbolo é o nNão. número quântico, o segundo número é o símbolo para esse particular Eu... Eu... - Sim. número quântico e o subscript é o mNão. Número quântico.
Como exemplo de como os nomes orbitais completos são gerados para orbitais reais, pode-se calcular ? ? n,1,± ± 1real{displaystyle psi _{n,1,pm 1}^{text{real}}}. Da mesa dos harmônicos esféricos, ? ? n,1,± ± 1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Rn,1Y1± ± 1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∓ ∓ Rn,13/8D D )) (x± ± Eu...Sim.)/R{displaystyle psi _{n,1,pm 1}=R_{n,1}Y_{1}^{pm 1}=mp R_{n,1}{sqrt {3/8pi }}cdot (xpm iy)/r} com R= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =x2+Sim.2+zangão.2- Sim. (x^{2}+y^{2}+z^{2}}}}. Então...
- ? ? n,1,+1real= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Rn,134D D )) xR? ? n,1,- Sim. - Sim. 1real= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Rn,134D D )) Sim.R{displaystyle {begin{aligned}psi} _{n,1,+1}^{text{real}}=&R_{n,1}{sqrt ? frac}cdot {x}{r}}\\psi _{n,1,-1}^{text{real}}=&R_{n,1}{sqrt ? frac}cdot {y}{r}}end{aligned}}}
Da mesma forma ? ? n,1,0= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Rn,13/4D D )) zangão./R{displaystyle psi _{n,1,0}=R_{n,1}{sqrt {3/4pi }}cdot z/r}. Como um exemplo mais complicado:
- ? ? n,3,+1real= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Rn,314212D D )) x)) (5zangão.2- Sim. - Sim. R2)R3{displaystyle psi _{n,3,+1}^{text{real}}=R_{n,3}{frac {1}{4}}{sqrt {frac {21}{2pi }}}cdot {frac {xcdot (5z^{2}-r^{2})}{r^{3}}}}}}
Em todos estes casos, geramos um rótulo cartesiano para o orbital examinando, e abreviando, o polinomial em xNão., Sim.- Sim.e zangão.Não. aparecendo no numerador. Nós ignoramos quaisquer termos no zangão.,R- Sim. polinomial exceto para o termo com o expoente mais alto em zangão.Não.. Em seguida, usamos o polinômio abreviado como um rótulo subscrito para o estado atômico, usando a mesma nomenclatura acima para indicar o nNão. e Eu... Eu... - Sim. Números quânticos.
- ? ? n,1,- Sim. - Sim. 1real= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =npSim.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...2(np- Sim. - Sim. 1+np+1)? ? n,1,0real= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =npzangão.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2p0? ? n,1,+1real= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =npx= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =12(np- Sim. - Sim. 1- Sim. - Sim. np+1)? ? n,3,+1real= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =nfxzangão.2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =12(nf- Sim. - Sim. 1- Sim. - Sim. nf+1){displaystyle {begin{aligned}psi} _{n,1,-1}^{text{real}}=&np_{y}={frac {i}{sqrt {2}}}left (np_{-1}+np_{+1}right)\psi _{n,1,0}^{text{real}}=&np_{z}=2p_{0}\psi _{n,1,+1}^{text{real}}=&np_{x}={frac {1}{sqrt {2}}}left(np_{-1}-np_{+1}right)\psi _{n,3,+1}^{text{real}}=&nf_{xz^{2}}={frac {1}{sqrt {2}}}left(nf_{-1}-nf_{+1}right)end{aligned}}}
A expressão acima de tudo usa a convenção de fase Condon–Shortley que é favorecida por físicos quânticos. Outras convenções para a fase dos harmônicos esféricos existe. Sob estas diferentes convenções os px{displaystyle p_{x}} e pSim.Não. p_{y}} orbitais podem aparecer, por exemplo, como a soma e a diferença de p+1Não. p_{+1}} e p- Sim. - Sim. 1Não. p_{-1}}, ao contrário do que é mostrado acima.
Abaixo está uma lista destes nomes polinomiais cartesianos para os orbitais atômicos. Note que não parece haver referência na literatura sobre como abreviar os longos polinômios harmônicos esféricos cartesianos para 3}" xmlns="http://www.w3.org/1998/Math/MathML">Eu... Eu... >3- Sim.3}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e91b5f299aefad76e097dcf7b13d5557d4fbcc2f" style="vertical-align: -0.338ex; width:5.231ex; height:2.176ex;"/> por isso não parece haver consenso sobre a nomeação de gNão. orbitais ou superiores de acordo com esta nomenclatura.
| m = -3 | m = −2 | m = −1 | m = 0 | m = + | m = + | m = +3 | |
|---|---|---|---|---|---|---|---|
| Eu... Eu... = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0- Sim. | SNão. | ||||||
| Eu... Eu... = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1{displaystyle ell =1} | pSim.Não. p_{y}} | pzangão.{displaystyle p_{z}} | px{displaystyle p_{x}} | ||||
| Eu... Eu... = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2- Sim. | DxSim.{displaystyle d_{xy}} | DSim.zangão.{displaystyle d_{yz}} | Dzangão.2{displaystyle d_{z^{2}}} | Dxzangão.{displaystyle d_{xz}} | Dx2- Sim. - Sim. Sim.2Não. d_{x^{2}-y^{2}}} | ||
| Eu... Eu... = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =3Não. | fSim.(3x2- Sim. - Sim. Sim.2){displaystyle f_{y(3x^{2}-y^{2})}} | fxSim.zangão.{displaystyle f_{xyz}} | fSim.zangão.2{displaystyle f_{yz^{2}}} | fzangão.3{displaystyle f_{z^{3}}} | fxzangão.2{displaystyle f_{xz^{2}}} | fzangão.(x2- Sim. - Sim. Sim.2)(x^{2}-y^{2})}} | fx(x2- Sim. - Sim. 3Sim.2)(x^{2}-3y^{2})}} |
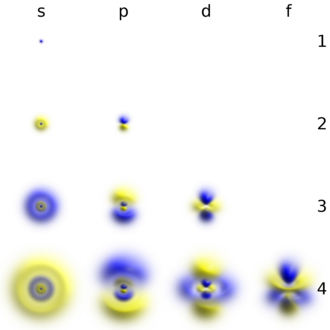
Formas de orbitais
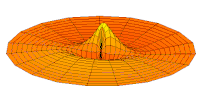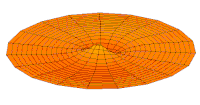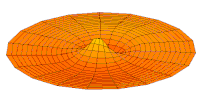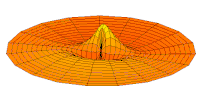
Imagens simples que mostram formas orbitais destinam-se a descrever as formas angulares de regiões no espaço onde os elétrons que ocupam o orbital provavelmente serão encontrados. Os diagramas não podem mostrar toda a região onde um elétron pode ser encontrado, pois de acordo com a mecânica quântica existe uma probabilidade diferente de zero de encontrar o elétron (quase) em qualquer lugar do espaço. Em vez disso, os diagramas são representações aproximadas de contornos ou superfícies de contorno onde a densidade de probabilidade | ψ(r, θ, φ) |2 tem um valor constante, escolhido de forma que existe uma certa probabilidade (por exemplo 90%) de encontrar o elétron dentro do contorno. Embora | ψ |2 como o quadrado de um valor absoluto é sempre não negativo, o sinal da função de onda ψ(r, θ, φ) é frequentemente indicado em cada sub-região da imagem orbital.
Às vezes, a função ψ é representada graficamente para mostrar suas fases, em vez de | ψ(r, θ, φ) |2 que mostra a densidade de probabilidade, mas não tem fase (que se perde ao tomar o valor absoluto, pois ψ(r, θ, φ) é um número complexo). |ψ(r, θ , φ)|2 grafos orbitais tendem a ter lóbulos menos esféricos e mais finos do que ψ(r, θ, φ) gráficos, mas têm o mesmo número de lóbulos nos mesmos lugares e, caso contrário, são reconhecível. Este artigo, para mostrar a fase da função de onda, mostra principalmente ψ(r, θ, φ) gráficos.
Os lóbulos podem ser vistos como padrões de interferência de ondas estacionárias entre as duas ondas viajantes ressonantes de anel em rotação contrária m e −m; a projeção do orbital no plano xy tem um comprimento de onda ressonante m ao redor da circunferência. Embora raramente mostradas, as soluções de ondas viajantes podem ser vistas como toros de bandas rotativas; as bandas representam informações de fase. Para cada m existem duas soluções de onda estacionária ⟨m⟩ + ⟨−m⟩ e ⟨m⟩ − ⟨−m⟩. Se m = 0, o orbital é vertical, as informações de rotação contrária são desconhecidas e o orbital é simétrico no eixo z. Se ℓ = 0 não há modos de rotação contrária. Existem apenas modos radiais e a forma é esfericamente simétrica. Para qualquer n, o menor ℓ é, mais nós radiais existem. Para qualquer ℓ, o menor n é, menos nós radiais existem (zero para qualquer n primeiro que tenha ℓ orbital). Falando vagamente, n é energia, ℓ é análogo à excentricidade e m é a orientação. No caso clássico, uma onda viajante ressonante de anel, por exemplo em uma linha de transmissão circular, a menos que seja ativamente forçada, decai espontaneamente em uma onda estacionária ressonante de anel porque as reflexões se acumulam ao longo do tempo mesmo na menor imperfeição ou descontinuidade.
Em geral, n determina o tamanho e a energia do orbital para um dado núcleo; conforme n aumenta, o tamanho do orbital aumenta. A carga nuclear mais alta Z de elementos mais pesados faz com que seus orbitais se contraiam em comparação com os mais leves, de modo que o tamanho do átomo permanece aproximadamente constante, mesmo quando o número de elétrons aumenta.
Também em termos gerais, ℓ determina a forma de um orbital e mℓ sua orientação. No entanto, como alguns orbitais são descritos por equações em números complexos, a forma às vezes depende de mℓ também. Juntos, todo o conjunto de orbitais para um dado ℓ e n preencher o espaço o mais simetricamente possível, embora com conjuntos cada vez mais complexos de lóbulos e nós.
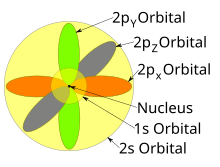
O único s-orbitals (Eu... Eu... = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0- Sim.) são moldados como esferas. Para n = 1 é aproximadamente uma bola sólida (densto no centro e desaparece para fora exponencialmente), mas para n ≥ 2, cada único s-orbital é feito de superfícies esfericamente simétricas que são conchas aninhadas (ou seja, a "estrutura de onda" é radial, seguindo um componente radial sinusoidal também). Veja a ilustração de uma seção transversal dessas conchas aninhadas, à direita. Os s-orbitais para todos n os números são os únicos orbitais com um anti-nodo (uma região de alta densidade de função de onda) no centro do núcleo. Todos os outros orbitais (p, d, f, etc.) têm impulso angular, e assim evitar o núcleo (tendo um nó de onda em o núcleo). Recentemente, houve um esforço para fotografar experimentalmente os orbitais 1s e 2p em um SrTiO3 cristal usando microscopia eletrônica de transmissão de varredura com espectroscopia de raios-x dispersiva de energia. Como a imagem foi realizada usando um feixe de elétrons, a interação coulmóbica do feixe-orbital que é frequentemente denominada como o efeito do parâmetro de impacto é incluído no resultado final (veja a figura à direita).
As formas dos orbitais p, d e f são descritas verbalmente aqui e mostradas graficamente na tabela de orbitais abaixo. Os três orbitais p para n = 2 têm a forma de dois elipsoides com um ponto de tangência no núcleo (a forma de dois lóbulos às vezes é referido como um "haltere"—há dois lóbulos apontando em direções opostas um do outro). Os três orbitais p em cada camada são orientados em ângulos retos entre si, conforme determinado por sua respectiva combinação linear de valores de m ℓ. O resultado geral é um lóbulo apontando ao longo de cada direção dos eixos primários.
Quatro dos cinco orbitais d para n = 3 parecem semelhantes, cada um com quatro lóbulos em forma de pêra, cada lóbulo tangente em ângulos retos a outros dois, e os centros de todos os quatro situados em um plano. Três desses planos são os planos xy, xz e yz - os lóbulos estão entre os pares de eixos primários - e o quarto tem o centro ao longo dos próprios eixos x e y. O quinto e último orbital d consiste em três regiões de alta densidade de probabilidade: um toro entre duas regiões em forma de pêra colocadas simetricamente em seu eixo z. O total geral de 18 lóbulos direcionais aponta em cada direção do eixo primário e entre cada par.
Existem sete orbitais f, cada um com formas mais complexas que as dos orbitais d.
Além disso, como é o caso dos orbitais s, orbitais p, d, f e g individuais com valores n maiores do que o valor mais baixo possível, exibem uma estrutura de nó radial adicional que é reminiscente de ondas harmônicas do mesmo tipo, em comparação com o modo mais baixo (ou fundamental) da onda. Assim como os orbitais s, esse fenômeno fornece os orbitais p, d, f e g no próximo valor mais alto possível de n (para exemplo, orbitais 3p vs. o 2p fundamental), um nó adicional em cada lóbulo. Valores ainda maiores de n aumentam ainda mais o número de nós radiais, para cada tipo de orbital.
As formas dos orbitais atômicos no átomo de um elétron estão relacionadas aos harmônicos esféricos tridimensionais. Essas formas não são únicas, e qualquer combinação linear é válida, como uma transformação para harmônicos cúbicos, na verdade é possível gerar conjuntos onde todos os d's tenham a mesma forma, assim como o px, py, e p z são da mesma forma.
Embora os orbitais individuais sejam frequentemente mostrados independentes uns dos outros, os orbitais coexistem em torno do núcleo ao mesmo tempo. Além disso, em 1927, Albrecht Unsöld provou que se alguém somar a densidade eletrônica de todos os orbitais de um determinado número quântico azimutal ℓ do mesmo shell n (por exemplo, todos os três orbitais 2p ou todos os cinco orbitais 3d) onde cada orbital é ocupado por um elétron ou cada é ocupado por um par de elétrons, então toda dependência angular desaparece; isto é, a densidade total resultante de todos os orbitais atômicos naquele subnível (aqueles com o mesmo ℓ) é esférica. Isso é conhecido como teorema de Unsöld.
Tabela de orbitais
Esta tabela mostra as funções de onda reais semelhantes ao hidrogênio para todos os orbitais atômicos até 7s e, portanto, cobre os orbitais ocupados no estado fundamental de todos os elementos da tabela periódica até o rádio e alguns além. "ψ" os gráficos são mostrados com fases de função de onda − e + mostradas em duas cores diferentes (arbitrariamente vermelho e azul). O orbital pz é igual ao orbital p0 orbital, mas o px e py são formados por combinações lineares de p+1 e p−1 orbitais (é por isso que eles estão listados sob m = ±1 rótulo). Além disso, p+1 e p-1 não são a mesma forma que o p0, pois são harmônicos esféricos puros.
* Nenhum elemento com elétrons 6f, 7d ou 7f foi descoberto ainda.
† Elementos com 7p elétrons foram descobertos, mas suas configurações eletrônicas são apenas previstas.
‡ Para os elementos cujo orbital ocupado mais alto é um orbital 6d, apenas algumas configurações eletrônicas foram confirmadas. (faltam ainda Ds, Rg e Cn).
Estes são os orbitais reais comumente usados em química. Só o m= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0Não. orbitais onde estão eigenstates do operador de momentum angular orbital, L^ ^ zangão.{displaystyle {hat {L}}_{z}}. As colunas com m= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =± ± 1,± ± 2,⋯ ⋯ {displaystyle m=pm 1,pm 2,cdots } são combinações de dois eigenstates. Veja a comparação na seguinte imagem:
Compreensão qualitativa das formas
As formas dos orbitais atômicos podem ser entendidas qualitativamente considerando o caso análogo de ondas estacionárias em um tambor circular. Para ver a analogia, o deslocamento vibracional médio de cada pedaço da membrana do tambor a partir do ponto de equilíbrio ao longo de muitos ciclos (uma medida da velocidade média da membrana do tambor e momento naquele ponto) deve ser considerado em relação à distância desse ponto do ponto centro da cabeça do tambor. Se esse deslocamento for considerado análogo à probabilidade de encontrar um elétron a uma determinada distância do núcleo, veremos que os vários modos do disco vibratório formam padrões que traçam as várias formas dos orbitais atômicos. A razão básica para esta correspondência reside no fato de que a distribuição de energia cinética e momento em uma onda de matéria é preditiva de onde a partícula associada com a onda estará. Ou seja, a probabilidade de encontrar um elétron em um determinado local também é uma função do momento médio do elétron naquele ponto, uma vez que o alto momento do elétron em uma determinada posição tende a "localizar" o elétron nessa posição, por meio das propriedades dos pacotes de ondas de elétrons (consulte o princípio da incerteza de Heisenberg para obter detalhes do mecanismo).
Essa relação significa que certas características-chave podem ser observadas em ambos os modos de membrana de tambor e orbitais atômicos. Por exemplo, em todos os modos análogos aos orbitais s (a linha superior na ilustração animada abaixo), pode-se ver que o centro da membrana do tambor vibra mais fortemente, correspondendo ao antinodo em todos os orbitais s em um átomo. Esse antinó significa que o elétron provavelmente está na posição física do núcleo (pelo qual ele passa direto sem se espalhar ou colidir com ele), uma vez que está se movendo (em média) mais rapidamente nesse ponto, dando-lhe impulso máximo.
Uma "órbita planetária" A imagem mais próxima do comportamento dos elétrons em orbitais s, todos sem momento angular, talvez seja a de uma órbita Kepleriana com a excentricidade orbital de 1, mas um eixo principal finito, não fisicamente possível (porque as partículas iriam colidir), mas pode ser imaginado como um limite de órbitas com eixos principais iguais, mas com excentricidade crescente.
Abaixo, vários modos de vibração da membrana do tambor e as respectivas funções de onda do átomo de hidrogênio são mostrados. Uma correspondência pode ser considerada onde as funções de onda de uma cabeça de tambor vibrante são para um sistema de duas coordenadas ψ(r, θ) e as funções de onda para uma esfera vibrante são três coordenadas ψ(r, θ, φ).
- modos de bateria tipo s e funções de onda
Função de onda de 1s orbital (parte real, 2D-corte, Rmumx= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2um0Não. r_{max}=2a_{0}})
Função de onda de 2s orbital (parte real, 2D-corte, Rmumx= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =10.um0Não. r_{max}=10a_{0}})
Função de onda de 3s orbital (parte real, 2D-corte, Rmumx= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =20.um0Não. r_{max}=20a_{0}})
Nenhum dos outros conjuntos de modos em uma membrana de tambor tem um antinó central, e em todos eles o centro do tambor não se move. Estes correspondem a um nó no núcleo para todos os orbitais não-s em um átomo. Todos esses orbitais têm algum momento angular e, no modelo planetário, correspondem a partículas em órbita com excentricidade menor que 1,0, de modo que não passam diretamente pelo centro do corpo primário, mas se afastam um pouco dele.
Além disso, os modos de bateria análogos aos modos p e d em um átomo mostram irregularidade espacial ao longo das diferentes direções radiais do centro do tambor, enquanto todos os modos análogos aos modos s são perfeitamente simétricos na direção radial. As propriedades de não simetria radial dos orbitais não-s são necessárias para localizar uma partícula com momento angular e natureza ondulatória em um orbital onde ela deve tender a ficar longe da força de atração central, pois qualquer partícula localizada no ponto de atração central não poderia ter nenhum momento angular. Para esses modos, as ondas na pele do tambor tendem a evitar o ponto central. Tais características novamente enfatizam que as formas dos orbitais atômicos são uma consequência direta da natureza ondulatória dos elétrons.
- modos de tambor tipo p e funções de onda
Função de onda de 2p orbital (parte real, 2D-corte, Rmumx= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =10.um0Não. r_{max}=10a_{0}})
Função de onda de 3p orbital (parte real, 2D-corte, Rmumx= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =20.um0Não. r_{max}=20a_{0}})
Função de onda de 4p orbital (parte real, 2D-corte, Rmumx= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =25um0Não. r_{max}=25a_{0}})
- modos de bateria do tipo d
Energia orbital
Em átomos com um elétron (um átomo semelhante a hidrogênio), a energia de um orbital (e, consequentemente, qualquer elétron na órbita) é determinada principalmente por nNão.. O n= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1Não. orbital tem a menor energia possível no átomo. Cada valor sucessivamente maior de nNão. tem uma energia maior, mas a diferença diminui como nNão. aumentos. Para alta nNão., a energia torna-se tão alta que o elétron pode facilmente escapar do átomo. Em átomos de elétron únicos, todos os níveis com diferentes Eu... Eu... - Sim. dentro de um dado nNão. são degenerados na aproximação de Schrödinger, e têm a mesma energia. Esta aproximação é quebrada ligeiramente na solução para a equação de Dirac (onde a energia depende de n e outro número quântico JJ), e pelo efeito do campo magnético do núcleo e efeitos eletrodinâmicos quânticos. Este último induz pequenas diferenças de energia de ligação especialmente para Selétrons que se aproximam do núcleo, uma vez que estes sentem uma carga nuclear muito ligeiramente diferente, mesmo em átomos de um elétron; veja a mudança do Cordeiro.
Em átomos com múltiplos elétrons, a energia de um elétron depende não apenas de sua órbita, mas também de suas interações com outros elétrons. Estas interações dependem do detalhe de sua distribuição de probabilidade espacial, e assim os níveis de energia dos orbitais dependem não só de nNão. mas também sobre Eu... Eu... - Sim.. Valores mais elevados de Eu... Eu... - Sim. estão associados a valores mais elevados de energia; por exemplo, o estado 2p é maior do que o estado 2s. Quando Eu... Eu... = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2- Sim., o aumento da energia da órbita torna-se tão grande quanto empurrar a energia de orbital acima da energia do s-orbital no próximo shell superior; quando Eu... Eu... = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =3Não. a energia é empurrada para o shell dois passos mais alto. O enchimento dos orbitais 3D não ocorre até que os 4s orbitais tenham sido preenchidos.
O aumento da energia para sub-venções de aumento do impulso angular em átomos maiores é devido a efeitos de interação elétron-eletrônica, e está especificamente relacionado com a capacidade de elétrons de impulso angular baixo para penetrar mais efetivamente em direção ao núcleo, onde eles estão sujeitos a menos rastreamento da carga de elétrons intervenientes. Assim, em átomos com maior número atômico, o Eu... Eu... - Sim. de elétrons torna-se cada vez mais um fator determinante em sua energia, e os principais números quânticos nNão. de elétrons torna-se cada vez menos importante em sua colocação de energia.
A sequência de energia das primeiras 35 sub-venções (por exemplo, 1s, 2p, 3d, etc.) é dada na tabela a seguir. Cada célula representa um subshell com nNão. e Eu... Eu... - Sim. dada por seus índices de linha e coluna, respectivamente. O número na célula é a posição do sub-shell na sequência. Para uma listagem linear das subvenções em termos de energias crescentes em átomos multieletrônicos, consulte a seção abaixo.
Eu... n | S | p | D | f | g | h |
|---|---|---|---|---|---|---|
| 1 | 1 | |||||
| 2 | 2 | 3 | ||||
| 3 | 4 | 5 | 7 | |||
| 4 | 6 | 8 | 10. | 13 | ||
| 5 | 9 | 11 | 14 | 17. | 21 | |
| 6 | 12 | 15 | 18. | 22 | 26 | 31 |
| 7 | 16. | 19 | 23 | 27 | 32 | 37 |
| 8 | 20. | 24. | 28 | 33 | 38 | 44 |
| 9 | 25 | 29 de Março | 34 | 39 | 45 | 51 |
| 10. | 30 | 35 | 40 | 46. | 52 | 59 |
Nota: células vazias indicam subníveis inexistentes, enquanto números em itálico indicam subníveis que poderiam (potencialmente) existir, mas que não possuem elétrons em nenhum elemento atualmente conhecido.
Colocação de elétrons e a tabela periódica

Várias regras governam a colocação de elétrons em orbitais (configuração eletrônica). A primeira determina que dois elétrons em um átomo não podem ter o mesmo conjunto de valores de números quânticos (este é o princípio de exclusão de Pauli). Esses números quânticos incluem os três que definem orbitais, bem como s, ou número quântico de spin. Assim, dois elétrons podem ocupar um único orbital, desde que tenham valores diferentes de s. No entanto, apenas dois elétrons, devido ao seu spin, podem ser associados a cada orbital.
Além disso, um elétron sempre tende a cair para o estado de energia mais baixo possível. É possível que ele ocupe qualquer orbital desde que não viole o princípio de exclusão de Pauli, mas se orbitais de menor energia estiverem disponíveis, essa condição é instável. O elétron eventualmente perderá energia (liberando um fóton) e cairá no orbital inferior. Assim, os elétrons preenchem os orbitais na ordem especificada pela sequência de energia dada acima.
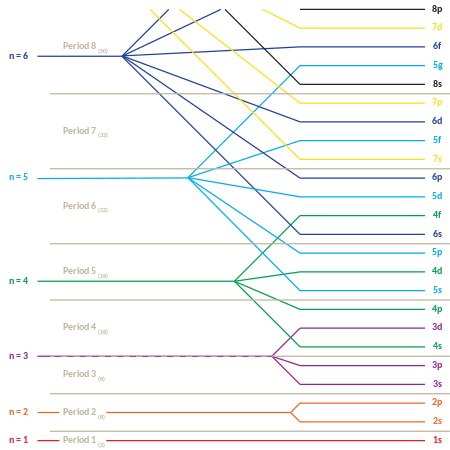
Este comportamento é responsável pela estrutura da tabela periódica. A tabela pode ser dividida em várias linhas (chamadas 'períodos'), numeradas começando com 1 no topo. Os elementos atualmente conhecidos ocupam sete períodos. Se um determinado período tem o número i, ele consiste em elementos cujos elétrons mais externos estão na camada i. Niels Bohr foi o primeiro a propor (1923) que a periodicidade nas propriedades dos elementos poderia ser explicada pelo preenchimento periódico dos níveis de energia dos elétrons, resultando na estrutura eletrônica do átomo.
A tabela periódica também pode ser dividida em vários 'blocos' retangulares numerados. Os elementos pertencentes a um determinado bloco têm esta característica comum: seus elétrons de maior energia pertencem todos ao mesmo ℓ-state (mas o n associado a esse ℓ-state depende do período). Por exemplo, as duas colunas mais à esquerda constituem o 's-block'. Os elétrons mais externos de Li e Be pertencem, respectivamente, ao subnível 2s e os de Na e Mg ao subnível 3s.
A seguir está a ordem de preenchimento do "subshell" orbitais, que também dá a ordem dos "blocos" na tabela periódica:
- 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, 7p
O "periódico" natureza do preenchimento dos orbitais, bem como a emergência dos s, p, d e f & #34;blocos", é mais óbvio se esta ordem de preenchimento for dada na forma de matriz, com números quânticos principais crescentes iniciando as novas linhas ("períodos") na matriz. Em seguida, cada subnível (composto pelos dois primeiros números quânticos) é repetido quantas vezes forem necessárias para cada par de elétrons que possa conter. O resultado é uma tabela periódica compactada, com cada entrada representando dois elementos sucessivos:
| 1 | |||||||||||||||
| 2 | 2 p | 2 p | 2 p | ||||||||||||
| 3 | 3p | 3p | 3p | ||||||||||||
| 4 | 3D | 3D | 3D | 3D | 3D | 4p | 4p | 4p | |||||||
| 5 | 4D | 4D | 4D | 4D | 4D | 5p | 5p | 5p | |||||||
| 6 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 5d | 5d | 5d | 5d | 5d | 6p | 6p | 6p |
| 7 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 6d | 6d | 6d | 6d | 6d | 7p | 7p | 7p |
Embora esta seja a ordem geral de preenchimento orbital de acordo com a regra de Madelung, há exceções, e as energias eletrônicas reais de cada elemento também dependem de detalhes adicionais dos átomos (consulte Configuração eletrônica § Átomos: princípio de Aufbau e Madelung regra).
O número de elétrons em um átomo eletricamente neutro aumenta com o número atômico. Os elétrons na camada mais externa, ou elétrons de valência, tendem a ser responsáveis pelo comportamento químico de um elemento. Elementos que contêm o mesmo número de elétrons de valência podem ser agrupados e exibir propriedades químicas semelhantes.
Efeitos relativísticos
Para elementos com alto número atômico Z, os efeitos da relatividade tornam-se mais pronunciados, especialmente para s elétrons, que movem-se em velocidades relativísticas à medida que penetram nos elétrons de blindagem próximos ao núcleo de átomos de Z. Este aumento relativístico no momento para elétrons de alta velocidade causa uma diminuição correspondente no comprimento de onda e contração dos orbitais 6s em relação aos orbitais 5d (em comparação com os elétrons s e d correspondentes em elementos mais leves na mesma coluna da tabela periódica); isso resulta em elétrons de valência 6s tornando-se mais baixos em energia.
Exemplos de resultados físicos significativos desse efeito incluem a temperatura de fusão reduzida do mercúrio (que resulta da indisponibilidade dos elétrons 6s para a ligação de metais) e a cor dourada do ouro e do césio.
No modelo Bohr, um n = 1elétron tem uma velocidade dada por v= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Z.α α c{displaystyle v=Zalpha C., onde Z. é o número atômico, α α - Sim. é a estrutura fina constante, e c é a velocidade da luz. Na mecânica quântica não-relativista, portanto, qualquer átomo com um número atômico maior que 137 exigiria que seus elétrons 1s viajassem mais rápido do que a velocidade da luz. Mesmo na equação de Dirac, que responde por efeitos relativísticos, a função de onda do elétron para átomos com 137}" xmlns="http://www.w3.org/1998/Math/MathML">Z.>137- Sim.137}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/c5e1614dcfe75f6096afe244e3d5ba573b2f462e" style="vertical-align: -0.338ex; width:8.266ex; height:2.176ex;"/> é oscilatório e unbounded. O significado do elemento 137, também conhecido como untriseptium, foi apontado pela primeira vez pelo físico Richard Feynman. Elemento 137 é às vezes informalmente chamado feynmanium (symbol Fy). No entanto, a aproximação de Feynman não consegue prever o valor crítico exato deZ. devido à natureza não-ponto-carga do núcleo e um raio orbital muito pequeno de elétrons internos, resultando em um potencial visto por elétrons internos que é efetivamente menos do que Z.. A crítica Z.valor, o que torna o átomo instável em relação à quebra de alto campo do vácuo e produção de pares de elétrons-positrons, não ocorre até Z. é cerca de 173. Estas condições não são vistas, exceto transientemente em colisões de núcleos muito pesados, como chumbo ou urânio em aceleradores, onde a produção de electrões-positron destes efeitos foi reivindicada a ser observada.
Não há nós em densidades orbitais relativísticas, embora componentes individuais da função de onda tenham nós.
Hibridação Pp (conjecturada)
No final do período 8 elementos, espera-se que exista um híbrido de 8p3/2 e 9p1/2, onde "3/2" e "1/2" referem-se ao número quântico do momento angular total. Este "pp" híbrido pode ser responsável pelo bloco p do período devido a propriedades semelhantes aos subníveis p em camadas de valência comuns. Os níveis de energia de 8p3/2 e 9p1/2 se aproximam devido aos efeitos relativísticos de rotação-órbita; o subnível 9s também deve participar, pois espera-se que esses elementos sejam análogos aos respectivos elementos 5p de índio a xenônio.
Transições entre orbitais
Os estados quânticos vinculados têm níveis de energia discretos. Quando aplicado a orbitais atômicos, isso significa que as diferenças de energia entre os estados também são discretas. Uma transição entre esses estados (ou seja, um elétron absorvendo ou emitindo um fóton) só pode acontecer se o fóton tiver uma energia correspondente à diferença de energia exata entre os referidos estados.
Considere dois estados do átomo de hidrogênio:
- Estado n = 1, Eu... = 0, mEu... = 0 e mS = +1/2
- Estado n = 2, Eu... = 0, mEu... = 0 e mS = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1/2
Pela teoria quântica, o estado 1 tem uma energia fixa de E1, e o estado 2 tem uma energia fixa de E2. Agora, o que aconteceria se um elétron no estado 1 passasse para o estado 2? Para isso acontecer, o elétron precisaria ganhar uma energia de exatamente E2 − E1. Se o elétron receber energia menor ou maior que esse valor, ele não poderá pular do estado 1 para o estado 2. Agora, suponha que irradiemos o átomo com um amplo espectro de luz. Fótons que atingem o átomo que tem uma energia de exatamente E2 − E1 será absorvido pelo elétron no estado 1, e esse elétron saltará para o estado 2. No entanto, os fótons com maior ou menor energia não podem ser absorvidos pelo elétron, porque o elétron pode saltar apenas para um dos orbitais, ele não pode pular para um estado entre orbitais. O resultado é que apenas os fótons de uma frequência específica serão absorvidos pelo átomo. Isso cria uma linha no espectro, conhecida como linha de absorção, que corresponde à diferença de energia entre os estados 1 e 2.
O modelo orbital atômico prevê assim espectros de linha, que são observados experimentalmente. Esta é uma das principais validações do modelo orbital atômico.
O modelo orbital atômico é, no entanto, uma aproximação da teoria quântica completa, que reconhece apenas muitos estados de elétrons. As previsões dos espectros de linha são qualitativamente úteis, mas não são quantitativamente precisas para átomos e íons que não contenham apenas um elétron.
Contenido relacionado
Ácido benzóico
Camada Kennelly-Heaviside
Boro