Número complexo

ImprimirCitar

Número com uma parte real e imaginária

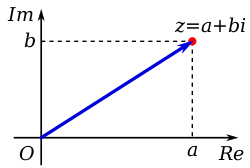
Um número complexo pode ser visualmente representado como um par de números

(um, b))

formando um vetor em um diagrama chamado um diagrama Argand, representando o plano complexo. Repito é o verdadeiro eixo, Eu... é o eixo imaginário, e

Eu...

é a "unidade imaginária", que satisfaz

Eu... 2 = -1

Em matemática, número complexo é um elemento de um sistema de números que estende os números reais com um elemento específico denotado $Eu...$ , chamado de unidade imaginária e satisfazendo a equação ${displaystyle i^{2}=-1}$ ; cada número complexo pode ser expresso na forma $a + bi$ , onde $um$ e $b)$ são números reais. Porque nenhum número real satisfaz a equação acima, $Eu...$ foi chamado de número imaginário de René Descartes. Para o número complexo $a+bi$ , $um$ é chamado de parte reale $b)$ é chamado de parte imaginária. O conjunto de números complexos é denotado por qualquer um dos símbolos $mathbb {C}$ ou $C$ . Apesar da nomenclatura histórica "imaginaria", números complexos são considerados nas ciências matemáticas como "real" como os números reais e são fundamentais em muitos aspectos da descrição científica do mundo natural.

Os números complexos permitem soluções para todas as equações polinomiais, mesmo aquelas que não têm soluções em números reais. Mais precisamente, o teorema fundamental da álgebra afirma que cada equação polinomial não constante com coeficientes reais ou complexos tem uma solução que é um número complexo. Por exemplo, a equação ${displaystyle (x+1)^{2}=-9}$ não tem nenhuma solução real, uma vez que o quadrado de um número real não pode ser negativo, mas tem as duas soluções complexas não reais ${displaystyle -1+3i}$ e ${displaystyle -1-3i}$ .

A adição, subtração e multiplicação de números complexos podem ser definidos naturalmente usando a regra ${displaystyle i^{2}=-1}$ combinada com as leis associativas, comutativas e distributivas. Cada número complexo nonzero tem um inverso multiplicativo. Isso torna os números complexos um campo que tem os números reais como um subcampo. Os números complexos também formam um espaço vetorial real da dimensão dois, com $(Eu... ?$ como uma base padrão.

Essa base padrão torna os números complexos um plano cartesiano, chamado de plano complexo. Isso permite uma interpretação geométrica dos números complexos e suas operações e, inversamente, expressar em termos de números complexos algumas propriedades e construções geométricas. Por exemplo, os números reais formam a reta real que se identifica com o eixo horizontal do plano complexo. Os números complexos de valor absoluto um formam o círculo unitário. A adição de um número complexo é uma translação no plano complexo, e a multiplicação por um número complexo é uma semelhança centrada na origem. A conjugação complexa é a simetria de reflexão em relação ao eixo real. O valor absoluto complexo é uma norma euclidiana.

Em resumo, os números complexos formam uma estrutura rica que é simultaneamente um corpo algebricamente fechado, uma álgebra comutativa sobre os reais e um espaço vetorial euclidiano de dimensão dois.

Definição

Uma ilustração do número complexo

zangão. = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = x + Olá.

no plano complexo. A parte real é

x

, e sua parte imaginária é

Sim.

Um número complexo é um número na forma $a + bi$ , onde $a$ e $b$ são números reais e $i$ é um indeterminado satisfatório $i 2 = -1. Por exemplo, 2 + 3 i é um número complexo.$

Desta forma, um número complexo é definido como um polinômio com coeficientes reais no único indeterminado $i$ , para o qual a relação $i 2 + 1 = 0$ é imposto. Com base nessa definição, os números complexos podem ser adicionados e multiplicados, usando a adição e a multiplicação para polinômios. A relação $i 2 + 1 = 0$ induz as igualdades $i 4 k = 1, i 4 k +1 = i, i 4 k +2 = -1,$ e $i 4 k +3 = - i,$ que vale para todos os inteiros $k$ ; estes permitem a redução de qualquer polinômio resultante da adição e multiplicação de números complexos a um polinômio linear em $i$ , novamente do forma $a + bi$ com coeficientes reais $a, b.$

O número real $a$ é chamado de parte real do número complexo $a + bi$ ; o número real $b$ é chamado de parte imaginária. Para enfatizar, a parte imaginária não inclui um fator $i$ ; ou seja, a parte imaginária é $b$ , não $bi$ .

Formalmente, os números complexos são definidos como o anel quociente do anel polinomial no indeterminado $i$ , pelo ideal gerado pelo polinômio $i 2 + 1$ (veja abaixo).

Notação

Um número real $a$ pode ser considerado um número complexo $a + 0 i$ , cuja parte imaginária é 0. Um número puramente imaginário $bi$ é um número complexo $0 + bi$ , cuja parte real é zero. Assim como os polinômios, é comum escrever $a$ para $a + 0 i$ e $bi$ para $0 + bi$ . Além disso, quando a parte imaginária é negativa, ou seja, $b = - |b| < 0$ , é comum escrever $a - |b|i$ ao invés de $a + (- |b|) i$ ; por exemplo, para $b = -4$ , $3 - 4 i$ pode ser escrito no lugar de $3 + (-4) i$ .

Como a multiplicação do indeterminado $i$ e um real é comutativa em polinômios com coeficientes reais, o polinômio $a + bi$ pode ser escrito como $a + ib .$ Isso geralmente é conveniente para partes imaginárias denotadas por expressões, por exemplo, quando $b$ é um radical.

A parte real de um número complexo $zangão.$ é denotado por $Re(zangão.)$ , ${displaystyle {mathcal {Re}}(z)}$ ou ${displaystyle {mathfrak {R}}(z)}$ ; a parte imaginária de um número complexo $zangão.$ é denotado por $Im. zangão.)$ , ${displaystyle {mathcal {Im}}(z)}$ ou ${displaystyle {mathfrak {I}}(z).}$ Por exemplo,

{displaystyle operatorname {Re} (2+3i)=2quad {text{ and }}quad operatorname {Im} (2+3i)=3~.}

O conjunto de todos os números complexos é denotado por $mathbb{C}$ (blackboard bold) ou $C$ (direitamente ousada).

Em algumas disciplinas, particularmente em eletromagnetismo e engenharia elétrica, $j$ é usado em vez de $i$ como $i$ é freqüentemente usado para representar a corrente elétrica. Nesses casos, os números complexos são escritos como $a + bj$ ou $a + jb$ .

Visualização

Um número complexo

zangão.

, como ponto (preto) e seu vetor de posição (azul)

Um número complexo $zangão.$ pode assim ser identificado com um par ordenado ${displaystyle (Re (z),Im (z))}$ de números reais, que por sua vez pode ser interpretado como coordenadas de um ponto em um espaço bidimensional. O espaço mais imediato é o plano euclidiano com coordenadas adequadas, que é então chamado plano complexo ou Diagrama de Argand, nomeado após Jean-Robert Argand. Outro espaço proeminente no qual as coordenadas podem ser projetadas é a superfície bidimensional de uma esfera, que é então chamada de esfera de Riemann.

Plano complexo cartesiano

A definição dos números complexos envolvendo dois valores reais arbitrários sugere imediatamente o uso de coordenadas cartesianas no plano complexo. O eixo horizontal (real) geralmente é usado para exibir a parte real, com valores crescentes à direita, e a parte imaginária marca o eixo vertical (imaginário), com valores crescentes valores para cima.

Um número cartografado pode ser visto como o ponto coordenado ou como um vetor de posição desde a origem até este ponto. Os valores de coordenadas de um número complexo $z$ podem, portanto, ser expressos em sua forma cartesiana, retangular ou forma algébrica.

Notavelmente, as operações de adição e multiplicação assumem um caráter geométrico muito natural, quando os números complexos são vistos como vetores de posição: a adição corresponde à adição de vetores, enquanto a multiplicação (veja abaixo) corresponde à multiplicação de suas magnitudes e à adição dos ângulos que eles fazer com o eixo real. Visto desta forma, a multiplicação de um número complexo por $i$ corresponde a girar o vetor de posição no sentido anti-horário em um quarto de volta (90°) sobre a origem — um fato que pode ser expresso algebricamente como

{displaystyle (a+bi),i=-b+ai.}

Plano complexo polar

Argumento

φ

e modulus

R

localizar um ponto no plano complexo.

Módulo e argumento

Uma opção alternativa para coordenadas no plano complexo é o sistema de coordenadas polares que usa a distância do ponto $z$ do origem ( $O$ ) e o ângulo subtendido entre o eixo real positivo e o segmento de reta estilo $Oz$ no sentido anti-horário. Isso leva à forma polar

{displaystyle z=re^{ivarphi }=r(cos varphi +isin varphi)}

de um número complexo, onde $R$ é o valor absoluto de $zangão.$ e $varphi$ é o argumento de $zangão.$ .

O valor absoluto (ou módulo ou magnitude) de um número complexo $z = x + yi$ é

{displaystyle r=|z|={sqrt {x^{2}+y^{2}}}.}

zangão.

Sim. = 0

R | x |

Por Pitágoras N#39; teorema, o valor absoluto de um número complexo é a distância até a origem do ponto que representa o número complexo no plano complexo.

O argumento de $z$ (em muitos aplicativos chamado de "fase& #34; $φ$ ) é o ângulo do raio $Oz$ com o eixo real positivo e é escrito como $arg z$ . Assim como o módulo, o argumento pode ser encontrado na forma retangular $x + yi$ —aplicando a tangente inversa ao quociente de partes imaginárias por reais. Ao usar uma identidade de meio ângulo, um único ramo do arctan é suficiente para cobrir o intervalo $(- π, π]$ da função $arg$ e evita uma análise caso a caso mais sutil

0,\pi &{text{if }}xφ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Arg⁡ ⁡ (x+Sim.Eu...)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(2arctan⁡ ⁡ (Sim.x2+Sim.2+x)seSim.≠ ≠ 0oux>0,D D sex<0eSim.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0,indefinidosex= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0eSim.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0.{displaystyle varphi =arg(x+yi)={begin{cases}2arctan left({dfrac Não. {x^{2}+y^{2}}}+x}}right)&{text{if }}yneq 0{text{ or }}x>0,\pi &{text{if }}x<0{text{ and }}y=0,{text{undefinida}}&{text{if }}x=0{text{ e }}y=0.end{cases}}}0,\pi &{text{if }}x

Normalmente, conforme informado acima, o valor principal no intervalo $(- π, π]$ é escolhido. Se o valor arg for negativo, valores no intervalo $(- π, π]$ ou $[0, 2 π)$ pode pode ser obtido adicionando $2 π$ . O valor de $φ$ é expresso em radianos neste artigo. Ele pode aumentar em qualquer múltiplo inteiro de $2 π$ e ainda fornecer o mesmo ângulo, visto como subtendido pelos raios do eixo real positivo e da origem até $z$ . Portanto, a função arg às vezes é considerada multivalorada. O ângulo polar para o número complexo 0 é indeterminado, mas a escolha arbitrária do ângulo polar 0 é comum.

O valor de $φ$ é igual ao resultado de atan2:

{displaystyle varphi =operatorname {atan2} left(operatorname {Im} (z),operatorname {Re} (z)right).}

Juntos, $r$ e $φ$ fornecem outra maneira de representar números complexos, a forma polar, pois a combinação de módulo e argumento especifica totalmente a posição de um ponto no plano. A recuperação das coordenadas retangulares originais da forma polar é feita pela fórmula chamada forma trigonométrica

{displaystyle z=r(cos varphi +isin varphi).}

Usando a fórmula de Euler, isso pode ser escrito como

{displaystyle z=re^{ivarphi }{text{ or }}z=rexp ivarphi.}

Usando a função $cis$ , isso às vezes é abreviado para

{displaystyle z=roperatorname {mathrm {cis} } varphi.}

Na notação de ângulo, frequentemente usado em eletrônica para representar um fasor com amplitude $r$ e fase $φ$ , é escrito como

{displaystyle z=rangle varphi.}

Gráficos complexos

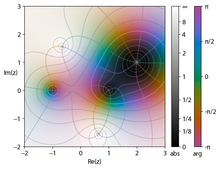
Um gráfico de roda colorida da expressão

(zangão. 2 - 1) zangão. - 2 - Eu...) 2 / zangão. 2 + 2 + 2 Eu...

Ao visualizar funções complexas, uma entrada e uma saída complexas são necessárias. Como cada número complexo é representado em duas dimensões, representar graficamente uma função complexa exigiria a percepção de um espaço quadridimensional, o que só é possível em projeções. Por causa disso, outras formas de visualizar funções complexas foram projetadas.

Na coloração de domínio as dimensões de saída são representadas pela cor e brilho, respectivamente. Cada ponto no plano complexo como domínio é ornado, tipicamente com cor da cor representando o argumento do número complexo, e brilho brilho brilho brilho brilho brilho representando a magnitude. Pontos escuros marcam moduli perto de zero, pontos mais brilhantes estão mais distantes da origem, a gradação pode ser descontínua, mas é assumida como monótona. As cores muitas vezes variam em passos de $D$ /3 para $0$ para $2 D$ de vermelho, amarelo, verde, ciano, azul, para magenta. Estes gráficos são chamados gráficos de roda de cor. Isso fornece uma maneira simples de visualizar as funções sem perder informações. A imagem mostra zeros para $\pm1, (2 + Eu...)$ e postes em ${displaystyle pm {sqrt {-2-2i}}.}$

História

A solução em radicais (sem funções trigonométricas) de uma equação cúbica geral, quando todas as suas três raízes são números reais, contém as raízes quadradas de números negativos, situação que não pode ser corrigida pela fatoração auxiliada pelo teste da raiz racional, se a cúbica for irredutível; este é o chamado casus irreducibilis ("caso irredutível"). Este enigma levou o matemático italiano Gerolamo Cardano a conceber números complexos por volta de 1545 em seu Ars Magna, embora sua compreensão fosse rudimentar; além disso, ele mais tarde descartou os números complexos como "sutis e inúteis". Cardano usou números imaginários, mas descreveu usá-los como “tortura mental”. Isso foi antes do uso do plano complexo gráfico. Cardano e outros matemáticos italianos, principalmente Scipione del Ferro, criaram nos anos 1500 um algoritmo para resolver equações cúbicas que geralmente tinham uma solução real e duas soluções contendo um número imaginário. Como ignoravam as respostas com os números imaginários, Cardano as considerava inúteis.

Trabalhar no problema de polinômios gerais acabou levando ao teorema fundamental da álgebra, que mostra que, com números complexos, existe uma solução para cada equação polinomial de grau um ou superior. Os números complexos formam, assim, um corpo algebricamente fechado, onde qualquer equação polinomial tem uma raiz.

Muitos matemáticos contribuíram para o desenvolvimento dos números complexos. As regras para adição, subtração, multiplicação e extração de raízes de números complexos foram desenvolvidas pelo matemático italiano Rafael Bombelli. Um formalismo mais abstrato para os números complexos foi desenvolvido pelo matemático irlandês William Rowan Hamilton, que estendeu essa abstração à teoria dos quaternions.

A primeira referência fugaz às raízes quadradas de números negativos pode talvez ser dito ocorrer no trabalho do herói matemático grego de Alexandria no século I dC, onde em seu Estereométrico ele considerou, aparentemente em erro, o volume de um frustum impossível de uma pirâmide para chegar ao termo $sqrt{81 - 144}$ em seus cálculos, que hoje simplificaria para ${displaystyle {sqrt {-63}}=3i{sqrt {7}}}$ . Quantidades negativas não foram concebidas em matemática helenística e Hero simplesmente substituiu-a por seu positivo ${displaystyle {sqrt {144-81}}=3{sqrt {7}}.}$

O ímpeto de estudar números complexos como um tópico em si surgiu pela primeira vez no século 16, quando soluções algébricas para as raízes de polinômios cúbicos e quárticos foram descobertas por matemáticos italianos (ver Niccolò Fontana Tartaglia, Gerolamo Cardano). Logo se percebeu (mas provou muito mais tarde) que essas fórmulas, mesmo que alguém estivesse interessado apenas em soluções reais, às vezes exigiam a manipulação de raízes quadradas de números negativos. Como exemplo, a fórmula de Tartaglia para uma equação cúbica da forma $x 3 = px + q$ fornece a solução para a equação $x 3 = x$ como

{displaystyle {tfrac {1}{sqrt {3}}}left(left({sqrt {-1}}right)^{1/3}+left({sqrt {-1}}right)^{-1/3}right).}

À primeira vista isto parece um disparate. No entanto, cálculos formais com números complexos mostram que a equação $zangão. 3 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = Eu...$ tem três soluções: ${displaystyle -i,{frac {{sqrt {3}}+i}{2}},{frac {-{sqrt {3}}+i}{2}}.}$ Substituir estes por sua vez ${displaystyle {sqrt {-1}}^{1/3}}$ na fórmula cúbica de Tartaglia e simplificando, um recebe 0, 1 e −1 como as soluções de $x 3 - Sim. x = 0$ . Naturalmente esta equação particular pode ser resolvida à vista, mas ilustra que quando as fórmulas gerais são usadas para resolver equações cúbicos com raízes reais, então, como os matemáticos posteriores mostraram rigorosamente, o uso de números complexos é inevitável. Rafael Bombelli foi o primeiro a abordar explicitamente essas soluções aparentemente paradoxais de equações cúbicas e desenvolveu as regras para a aritmética complexa tentando resolver essas questões.

O termo "imaginário" para essas quantidades foi cunhado por René Descartes em 1637, que se esforçou para enfatizar sua natureza irreal

... às vezes apenas imaginário, que é um pode imaginar como muitos como eu disse em cada equação, mas às vezes não há quantidade que corresponda ao que imaginamos.
Não.... quelquefois seulement imaginaires c'est-à-dire que l'on peut toujours en imaginer autant que j'ai dit en chaque équation, mais qu'il n'y a quelquefois aucune quantité qui corresponde à celle qu'on imagine.]

Uma outra fonte de confusão foi que a equação ${displaystyle {sqrt {-1}}^{2}={sqrt {-1}}{sqrt {-1}}=-1}$ parecia ser caprichosamente inconsistente com a identidade algébrica ${displaystyle {sqrt {a}}{sqrt {b}}={sqrt {ab}}}$ , que é válido para números reais não negativos $um$ e $b)$ , e que também foi usado em cálculos de números complexos com um de $um$ , $b)$ positivo e o outro negativo. O uso incorreto desta identidade (e a identidade relacionada ${textstyle {frac {1}{sqrt {a}}}={sqrt {frac {1}{a}}}}$ ) no caso em que ambos $um$ e $b)$ são negativas até mesmo serviled Leonhard Euler. Esta dificuldade eventualmente levou à convenção de usar o símbolo especial $Eu...$ no lugar de ${sqrt {-1}}$ para proteger contra este erro. Mesmo assim, Euler considerou natural introduzir os alunos a números complexos muito mais cedo do que nós hoje. Em seu livro de texto de álgebra elementar, Elementos de Algebra, ele introduz esses números quase de uma vez e, em seguida, usa-los de uma forma natural ao longo.

No século XVIII, os números complexos ganharam uso mais amplo, pois percebeu-se que a manipulação formal de expressões complexas poderia ser usada para simplificar cálculos envolvendo funções trigonométricas. Por exemplo, em 1730, Abraham de Moivre notou que as identidades relacionando funções trigonométricas de um múltiplo inteiro de um ângulo com potências de funções trigonométricas daquele ângulo poderiam ser reexpressas pela seguinte fórmula de Moivre:

{displaystyle (cos theta +isin theta)^{n}=cos ntheta +isin ntheta.}

Em 1748, Euler foi mais longe e obteve a fórmula de análise complexa de Euler:

{displaystyle cos theta +isin theta =e^{itheta }}

manipulando formalmente séries de potências complexas e observou que essa fórmula poderia ser usada para reduzir qualquer identidade trigonométrica a identidades exponenciais muito mais simples.

A ideia de um número complexo como um ponto no plano complexo (acima) foi descrita pela primeira vez pelo matemático dinamarquês-norueguês Caspar Wessel em 1799, embora tenha sido antecipada já em 1685 no de Wallis Um Tratado de Álgebra.

As memórias de Wessel apareceram no Proceedings of the Copenhagen Academy, mas passaram despercebidas. Em 1806, Jean-Robert Argand publicou independentemente um panfleto sobre números complexos e forneceu uma prova rigorosa do teorema fundamental da álgebra. Carl Friedrich Gauss havia publicado anteriormente uma prova essencialmente topológica do teorema em 1797, mas expressou suas dúvidas na época sobre "a verdadeira metafísica da raiz quadrada de -1". Somente em 1831 ele superou essas dúvidas e publicou seu tratado sobre números complexos como pontos no plano, estabelecendo amplamente a notação e a terminologia modernas:

Se um anteriormente contemplado este assunto de um ponto de vista falso e, portanto, encontrou uma escuridão misteriosa, isso é em grande parte atribuível à terminologia desajeitada. Tinha um não chamado +1, -1, ${sqrt {-1}}$ unidades positivas, negativas ou imaginárias (ou até mesmo impossíveis), mas em vez disso, digamos, unidades diretas, inversas ou laterais, então não poderia ter sido mal falar de tais trevas.

No início do século XIX, outros matemáticos descobriram de forma independente a representação geométrica dos números complexos: Buée, Mourey, Warren, Français e seu irmão, Bellavitis.

O matemático inglês G.H. Hardy observou que Gauss foi o primeiro matemático a usar números complexos de "uma maneira realmente confiável e científica". embora matemáticos como o norueguês Niels Henrik Abel e Carl Gustav Jacob Jacobi os estivessem usando rotineiramente antes de Gauss publicar seu tratado de 1831.

Augustin-Louis Cauchy e Bernhard Riemann juntos levaram as ideias fundamentais da análise complexa a um alto estado de conclusão, começando por volta de 1825 no caso de Cauchy.

Os termos comuns utilizados na teoria são principalmente devido aos fundadores. Argand chamado $e φ + Eu... pecado φ$ o fator de direçãoe ${displaystyle r={sqrt {a^{2}+b^{2}}}}$ o Modulus; Cauchy (1821) chamado $e φ + Eu... pecado φ$ o formulário reduzido (I'expression réduite) e, aparentemente, introduziu o termo argumento; Gauss usado $Eu...$ para ${sqrt {-1}}$ , introduziu o termo número complexo para $um + b)$ e chamado $um 2 + b) 2$ o normas. A expressão coeficiente de direção, frequentemente usado para $e φ + Eu... pecado φ$ , é devido a Hankel (1867), e valor absoluto, para modulus, é devido a Weierstrass.

Escritores clássicos posteriores sobre a teoria geral incluem Richard Dedekind, Otto Hölder, Felix Klein, Henri Poincaré, Hermann Schwarz, Karl Weierstrass e muitos outros. Trabalhos importantes (incluindo uma sistematização) em cálculo multivariado complexo foram iniciados no início do século XX. Resultados importantes foram alcançados por Wilhelm Wirtinger em 1927.

Relações e operações

Igualdade

Os números complexos têm uma definição de igualdade semelhante aos números reais; dois números complexos $a 1 + b 1 i$ e $a 2 + b 2 i$ são iguais se e somente se suas partes reais e imaginárias são iguais, isto é, se $a 1 = a 2$ e $b 1 = b 2$ . Números complexos diferentes de zero escritos na forma polar são iguais se e somente se tiverem a mesma magnitude e seus argumentos diferirem por um múltiplo inteiro de $2 π$ .

Pedido

Ao contrário dos números reais, não há ordenação natural dos números complexos. Em particular, não há ordenação linear nos números complexos que seja compatível com adição e multiplicação. Assim, os números complexos não têm a estrutura de um corpo ordenado. Uma explicação para isso é que toda soma não trivial de quadrados em um campo ordenado é diferente de zero e $i 2 + 1 2 = 0$ é uma soma não trivial de quadrados. Assim, os números complexos são naturalmente pensados como existindo em um plano bidimensional.

Conjugado

Representação geométrica

zangão.

e sua conjugação

zangão.

no plano complexo

O conjugado complexo do número complexo $z = x + yi$ é dado por $x - yi$ . É indicado por $z$ ou $z *$ . Essa operação unária em números complexos não pode ser expressa aplicando apenas suas operações básicas de adição, subtração, multiplicação e divisão.

Geometricamente, $z$ é o &# 34;reflexão" de $z$ sobre o eixo real. A conjugação duas vezes dá o número complexo original

{displaystyle {overline {overline {z}}}=z,}

o que torna esta operação uma involução. A reflexão deixa a parte real e a magnitude de $z$ inalteradas, ou seja

{displaystyle operatorname {Re} ({overline {z}})=operatorname {Re} (z)quad }

{displaystyle quad |{overline {z}}|=|z|.}

A parte imaginária e o argumento de um número complexo $z$ mudam de sinal na conjugação

{displaystyle operatorname {Im} ({overline {z}})=-operatorname {Im} (z)quad {text{ and }}quad operatorname {arg} {overline {z}}equiv -operatorname {arg} z{pmod {2pi }}.}

Para obter detalhes sobre argumento e magnitude, consulte a seção Forma polar.

O produto de um número complexo $z = x + yi$ e seu conjugado é conhecido como o quadrado absoluto. É sempre um número real não negativo e é igual ao quadrado da magnitude de cada um:

{displaystyle zcdot {overline {z}}=x^{2}+y^{2}=|z|^{2}=|{overline {z}}|^{2}.}

Esta propriedade pode ser usada para converter uma fração com um denominador complexo em uma fração equivalente com um denominador real, expandindo o numerador e o denominador da fração pelo conjugado do denominador dado. Às vezes, esse processo é chamado de "racionalização" do denominador (embora o denominador na expressão final possa ser um número real irracional), porque se assemelha ao método para remover raízes de expressões simples em um denominador.

As partes reais e imaginárias de um número complexo $z$ podem ser extraídas usando a conjugação:

{displaystyle operatorname {Re} (z)={dfrac {z+{overline {z}}}{2}},quad {text{ and }}quad operatorname {Im} (z)={dfrac {z-{overline {z}}}{2i}}.}

A conjugação distribui sobre as operações aritméticas complexas básicas:

{displaystyle {begin{aligned}{overline {zpm w}}&={overline {z}}pm {overline {w}},\{overline {zcdot w}}&={overline {z}}cdot {overline {w}},\{overline {z/w}}&={overline {z}}/{overline {w}}.end{aligned}}}

A conjugação também é empregada na geometria inversa, um ramo da geometria que estuda reflexões mais gerais do que aquelas sobre uma linha. Na análise de rede de circuitos elétricos, o conjugado complexo é usado para encontrar a impedância equivalente quando o teorema de transferência de potência máxima é procurado.

Adição e subtração

A adição de dois números complexos pode ser feita geometricamente através da construção de um paralelograma.

Dois números complexos ${displaystyle a=x+yi}$ e ${displaystyle b=u+vi}$ são mais facilmente adicionados adicionando separadamente suas partes reais e imaginárias. Isso é dizer:

{displaystyle a+b=(x+yi)+(u+vi)=(x+u)+(y+v)i.}

{displaystyle a-b=(x+yi)-(u+vi)=(x-u)+(y-v)i.}

Multiplicação de um número complexo ${displaystyle a=x+yi}$ e um número real $R$ pode ser feito de forma semelhante, multiplicando-se separadamente $R$ e as partes reais e imaginárias de $um$ :

{displaystyle ra=r(x+yi)=rx+ryi.}

-1

{displaystyle a-b=a+(-1),b.}

Usando a visualização de números complexos no plano complexo, a adição tem a seguinte interpretação geométrica: a soma de dois números complexos $a$ e $b$ , interpretado como pontos no plano complexo, é o ponto obtido construindo um paralelogramo a partir dos três vértices $O$ , e as pontas das setas rotuladas $a$ e $b$ (desde que não estejam em uma linha). Equivalentemente, chamando esses pontos de $A$ , $B$ , respectivamente e o quarto ponto do paralelogramo $X$ os triângulos $OAB$ e $XBA$ são congruentes.

Multiplicação e quadrado

As regras da propriedade distributiva, as propriedades comutativas (de adição e multiplicação) e a propriedade definidora $i 2 = - 1$ se aplica a números complexos. Segue que

{displaystyle (x+yi),(u+vi)=(xu-yv)+(xv+yu)i.}

Em particular,

{displaystyle (x+yi)^{2}=x^{2}-y^{2}+2xyi.}

Recíproco e divisão

Usando a conjugação, o recíproco de um número complexo diferente de zero $z = x + yi$ sempre pode ser dividido em

{displaystyle {frac {1}{z}}={frac {overline {z}}{z{overline {z}}}}={frac {overline {z}}{|z|^{2}}}={frac {overline {z}}{x^{2}+y^{2}}}={frac {x}{x^{2}+y^{2}}}-{frac {y}{x^{2}+y^{2}}}i,}

uma vez que diferente de zero implica que <é² + y² é maior que zero.

Isso pode ser usado para expressar uma divisão de um número complexo arbitrário $w = u + vi$ por um número complexo diferente de zero $z$ como

{displaystyle {frac {w}{z}}=wcdot {frac {1}{z}}=(u+vi)cdot left({frac {x}{x^{2}+y^{2}}}-{frac {y}{x^{2}+y^{2}}}iright)={frac {(ux+vy)+(vx-uy)i}{x^{2}+y^{2}}}.}

Multiplicação e divisão na forma polar

Multiplicação de $2 + Eu...$ (triângulo azul) e $3 + Eu...$ (triângulo vermelho). O triângulo vermelho é girado para combinar o vértice do azul (a adição de ambos os ângulos nos termos φ₁+φ₂ na equação) e esticado pelo comprimento da hipotenusa do triângulo azul (a multiplicação de ambos os raios, conforme o termo R₁R₂ na equação).

As fórmulas para multiplicação, divisão e exponenciação são mais simples na forma polar do que as fórmulas correspondentes em coordenadas cartesianas. Dados dois números complexos $z 1 = r 1 (cos φ 1 + i sin φ 1)$ e $z 2 = r 2 (cos φ 2 + i sin φ 2)$ , por causa das identidades trigonométricas

{displaystyle {begin{alignedat}{4}cos acos b&-sin asin b&{}={}&cos(a+b)\cos asin b&+sin acos b&{}={}&sin(a+b).end{alignedat}}}

podemos derivar

{displaystyle z_{1}z_{2}=r_{1}r_{2}(cos(varphi _{1}+varphi _{2})+isin(varphi _{1}+varphi _{2})).}

$Eu...$ $Eu... 2 = -1$ ${displaystyle (2+i)(3+i)=5+5i.}$ $5 + 5 Eu...$ $D /4$ ${displaystyle {frac {pi }{4}}=arctan left({frac {1}{2}}right)+arctan left({frac {1}{3}}right)}$
Da mesma forma, a divisão é dada por
${displaystyle {frac {z_{1}}{z_{2}}}={frac {r_{1}}{r_{2}}}left(cos(varphi _{1}-varphi _{2})+isin(varphi _{1}-varphi _{2})right).}$
Raiz quadrada
As raízes quadradas de $um + b)$ (com $b) \neq 0$ ) são $pm (gamma +delta i)$ , onde
${displaystyle gamma ={sqrt {frac {a+{sqrt {a^{2}+b^{2}}}}{2}}}}$
e
${displaystyle delta =(operatorname {sgn} b){sqrt {frac {-a+{sqrt {a^{2}+b^{2}}}}{2}}},}$
Onde? $Sgn$ é a função de sinalização. Isso pode ser visto por squaring $pm (gamma +delta i)$ para obter $um + b)$ . Aqui. ${sqrt {a^{2}+b^{2}}}$ é chamado de módulo de $um + b)$ , e o sinal de raiz quadrada indica a raiz quadrada com parte real não negativa, chamado o raiz quadrada principal; também ${displaystyle {sqrt {a^{2}+b^{2}}}={sqrt {z{overline {z}}}},}$ Onde? $zangão. = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = um + b)$ .
Função exponencial
A função exponencial ${displaystyle exp colon mathbb {C} to mathbb {C};zmapsto exp z}$ pode ser definido para cada número complexo $zangão.$ pela série de energia
${displaystyle exp z=sum _{n=0}^{infty }{frac {z^{n}}{n!}},}$
O valor em $1$ da função exponencial é o número de Euler
${displaystyle e=exp 1=sum _{n=0}^{infty }{frac {1}{n!}}approx 2.71828.}$ $zangão.$ ${displaystyle exp z=e^{z}.}$ $zangão.$ $e$ ${displaystyle e^{z}=exp z.}$
Equação funcional
A função exponencial satisfaz a equação funcional ${displaystyle e^{z+t}=e^{z}e^{t}.}$ Isso pode ser provado comparando a expansão da série de potência de ambos os membros ou aplicando a continuação analítica da restrição da equação a argumentos reais.
Fórmula de Euler
A fórmula de Euler afirma que, para qualquer número real $y$ ,
${displaystyle e^{iy}=cos y+isin y.}$
A equação funcional implica então que, se $x$ e $y$ são reais, tem-se
${displaystyle e^{x+iy}=e^{x}(cos y+isin y)=e^{x}cos y+ie^{x}sin y,}$
Logaritmo complexo
No caso real, o logaritmo natural pode ser definido como o inverso ${displaystyle ln colon mathbb {R} ^{+}to mathbb {R};xmapsto ln x}$ da função exponencial. Para estender isso ao domínio complexo, pode-se começar a partir da fórmula de Euler. Isso implica que, se um número complexo ${displaystyle zin mathbb {C} ^{times }}$ é escrito em forma polar
${displaystyle z=r(cos varphi +isin varphi)}$ ${displaystyle r,varphi in mathbb {R}}$ ${displaystyle ln z=ln r+ivarphi }$ ${displaystyle exp ln z=exp(ln r+ivarphi)=rexp ivarphi =r(cos varphi +isin varphi)=z.}$
No entanto, como o cosseno e o seno são funções periódicas, a adição de um múltiplo inteiro de $2 π$ a $φ$ não altera $z$ . Por exemplo, $e iπ = e 3 iπ = -1$ então ambos $iπ$ e $3 iπ$ são valores possíveis para o logaritmo natural de $-1$ .
Portanto, se o logaritmo complexo não for definido como uma função multivalorada
${displaystyle ln z=left{ln r+i(varphi +2pi k)mid kin mathbb {Z} right},}$ ${displaystyle ln colon ;mathbb {C} ^{times };to ;;;mathbb {R} ^{+}+;i,left(-pipi right].}$
Se ${displaystyle zin mathbb {C} setminus left(-mathbb {R} _{geq 0}right)}$ não é um número real não positivo (um número positivo ou não real), o valor principal resultante do logaritmo complexo é obtido com $- Sim. D < φ < D$ . É uma função analítica fora dos números reais negativos, mas não pode ser prolongada a uma função que é contínua em qualquer número real negativo ${displaystyle zin -mathbb {R} ^{+}}$ , onde o valor principal é $I zangão. = ln (-) zangão.) + IND$ .
Exponenciação
Se $x > 0$ é real e $z$ complexo, a exponenciação é definida como
${displaystyle x^{z}=e^{zln x},}$ $I$
Parece natural estender esta fórmula para valores complexos de $x$ , mas existem algumas dificuldades resultantes do fato de que o logaritmo complexo não é realmente uma função, mas uma função multivalorada.
Segue-se que se $z$ for como acima, e se $t$ é outro número complexo, então a exponenciação é a função multivalorada
${displaystyle z^{t}=left{e^{tln r},(cos(varphi t+2pi kt)+isin(varphi t+2pi kt))mid kin mathbb {Z} right}}$
Expoentes inteiros e fracionários

Representação geométrica das raízes 2 a 6 de um número complexo $zangão.$ , em forma polar $re Eu...$ Onde? $R | zangão. |$ e $φ = zangão.$ . Se $zangão.$ é real, $φ = 0$ ou $D$ . As raízes principais são mostradas em preto.
Se, na fórmula anterior, $t$ for um número inteiro, então o seno e o cosseno são independentes de $k$ . Assim, se o expoente $n$ for um número inteiro, então $z n$ está bem definido, e a fórmula de exponenciação é simplificada para a fórmula de de Moivre:
${displaystyle z^{n}=(r(cos varphi +isin varphi))^{n}=r^{n},(cos nvarphi +isin nvarphi).}$
As $n$ enésimas raízes de um número complexo $z$ são dados por
${displaystyle z^{1/n}={sqrt[{n}]{r}}left(cos left({frac {varphi +2kpi }{n}}right)+isin left({frac {varphi +2kpi }{n}}right)right)}$ $0 \leq k \leq n - 1$ ${displaystyle {sqrt[{n}]{r}}}$ $n$ $R$ $k$
Enquanto a $n$ ésima raiz de um número real positivo $r$ é escolhido para ser o número real positivo $c$ satisfatório $c n = r$ , não há uma maneira natural de distinguir um complexo particular $n$ ésima raiz de um número complexo. Portanto, a $n$ ésima raiz é uma função com valor n de $z$ . Isso implica que, ao contrário do caso dos números reais positivos, tem-se
${displaystyle (z^{n})^{1/n}neq z,}$ $n$
Propriedades
Estrutura de campo
O conjunto $mathbb{C}$ de números complexos é um campo. Resumidamente, isso significa que os seguintes fatos possuem: primeiro, qualquer dois números complexos podem ser adicionados e multiplicados para produzir outro número complexo. Segundo, para qualquer número complexo $zangão.$ , seu aditivo inverso $- zangão.$ é também um número complexo; e terceiro, cada número complexo nonzero tem um número complexo recíproco. Além disso, essas operações satisfazem uma série de leis, por exemplo, a lei da comutividade da adição e da multiplicação para qualquer dois números complexos $zangão. 1$ e $zangão. 2$ :
${displaystyle {begin{aligned}z_{1}+z_{2}&=z_{2}+z_{1},\z_{1}z_{2}&=z_{2}z_{1}.end{aligned}}}$
Ao contrário dos reais, $mathbb{C}$ não é um campo ordenado, ou seja, não é possível definir uma relação $zangão. 1 < zangão. 2$ que é compatível com a adição e multiplicação. Na verdade, em qualquer campo ordenado, o quadrado de qualquer elemento é necessariamente positivo, então $Eu... 2 = -1$ exclui a existência de um pedido ${displaystyle mathbb {C}.}$
Quando o campo subjacente para um tópico ou construção matemática é o campo de números complexos, o nome do tópico geralmente é modificado para refletir esse fato. Por exemplo: análise complexa, matriz complexa, polinômio complexo e álgebra de Lie complexa.
Soluções de equações polinomiais
Dados quaisquer números complexos (chamados coeficientes) $a 0, ..., a n$ , a equação
${displaystyle a_{n}z^{n}+dotsb +a_{1}z+a_{0}=0}$ zangão. $um 1, um n$ $mathbb{C}$ $mathbb {Q}$ $x 2 - 2$ $mathbb {R}$ $x 2 + um$ $um > 0$ $x$ $x$
Existem várias provas deste teorema, quer por métodos analíticos como o teorema de Liouville, quer topológicos como o número sinuoso, ou uma prova que combina a teoria de Galois e o facto de que qualquer polinómio real de ímpar grau tem pelo menos uma raiz real.
Por causa deste fato, teoremas que prendem para qualquer campo algébrica fechado aplicar a ${displaystyle mathbb {C}.}$ Por exemplo, qualquer matriz quadrada complexa não vazia tem pelo menos um (complexo) eigenvalue.
Caracterização algébrica
O campo $mathbb{C}$ tem as seguintes três propriedades:
Primeiro, tem característica 0. Isso significa que $1 + 1 + \equiv + 1 \neq 0$ para qualquer número de resumos (todos iguais).
Segundo, seu grau de transcendência sobre $mathbb {Q}$ , o campo principal de ${displaystyle mathbb {C}}$ é a cardinalidade do continuum.
Em terceiro lugar, é algébricamente fechado (veja acima).
Pode-se mostrar que qualquer campo com essas propriedades é isomorfo (como um campo) para ${displaystyle mathbb {C}.}$ Por exemplo, o fechamento algébrico do campo ${displaystyle mathbb {Q} _{p}}$ do número p-ádico também satisfaz essas três propriedades, de modo que estes dois campos são isomorfos (como campos, mas não como campos topológicos). Também, $mathbb{C}$ é isomorfo para o campo da série Puiseux complexa. No entanto, especificar um isomorfismo requer o axioma da escolha. Outra consequência desta caracterização algébrica é que $mathbb{C}$ contém muitos subcampos adequados que são isomórficos para $mathbb{C}$ .
Caracterização como um campo topológico
A caracterização anterior de $mathbb{C}$ descreve apenas os aspectos algébricas de ${displaystyle mathbb {C}.}$ Ou seja, as propriedades de proximidade e continuidade, que importam em áreas como análise e topologia, não são tratadas. A seguinte descrição: $mathbb{C}$ como um campo topológico (ou seja, um campo equipado com uma topologia, que permite a noção de convergência) leva em conta as propriedades topológicas. $mathbb{C}$ contém um subconjunto $P$ (nomeadamente o conjunto de números reais positivos) de elementos nonzero satisfazendo as seguintes três condições:
$P$ é fechado sob adição, multiplicação e tomando inversos.
Se $x$ e $Sim.$ são elementos distintos de $P$ , então ou $x - Sim. Sim.$ ou $Sim. - Sim. x$ em $P$ .
Se $S$ é qualquer subconjunto vazio de $P$ , então $S + P = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = x + P$ para alguns $x$ em ${displaystyle mathbb {C}.}$
Além disso, $mathbb{C}$ tem um automorfismo não trivial $x \mapsto x *$ (nomeadamente a conjugação complexa), tal que $x x x x x *$ em $P$ para qualquer nonzero $x$ em ${displaystyle mathbb {C}.}$
Qualquer campo $F$ com estas propriedades podem ser dotadas com uma topologia, tomando os conjuntos $B (x, p) = {Sim. | p - Sim. Sim. - Sim. x) Sim. - Sim. x)* \in P ?$ como base, onde $x$ escalas sobre o campo e $p$ escalas sobre $P$ . Com esta topologia $F$ é isomorfo como um topologia campo para ${displaystyle mathbb {C}.}$
Os únicos campos topológicos conectados localmente compactos são $mathbb {R}$ e ${displaystyle mathbb {C}.}$ Isso dá outra caracterização de $mathbb{C}$ como um campo topológico, desde $mathbb{C}$ pode ser distinguido $mathbb {R}$ porque os números complexos nonzero estão conectados, enquanto os números reais nonzero não são.
Construção formal
Construção como pares ordenados
William Rowan Hamilton introduziu a abordagem para definir o conjunto $mathbb{C}$ de números complexos como o conjunto $mathbb {R} ^{2}$ de pares ordenados $(um, b))$ de números reais, em que as seguintes regras para adição e multiplicação são impostas:
${displaystyle {begin{aligned}(a,b)+(c,d)&=(a+c,b+d)\(a,b)cdot (c,d)&=(ac-bd,bc+ad).end{aligned}}}$
É então apenas uma questão de notação para expressar $(a, b)$ como $a + bi$ .
Construção como um campo quociente
Embora esta construção de baixo nível descreva com precisão a estrutura dos números complexos, a seguinte definição equivalente revela a natureza algébrica de $mathbb{C}$ mais imediatamente. Esta caracterização depende da noção de campos e polinomiais. Um campo é um conjunto dotado de operações de adição, subtração, multiplicação e divisão que se comportam como é familiar de, por exemplo, números racionais. Por exemplo, a lei distributiva
${displaystyle (x+y)z=xz+yz}$ $x$ $Sim.$ $zangão.$ $mathbb {R}$ $p (X)$ ${displaystyle a_{n}X^{n}+dotsb +a_{1}X+a_{0},}$ $um 0, um n$ ${displaystyle mathbb {R} [X]}$
O conjunto de números complexos é definido como o anel quociente ${displaystyle mathbb {R} [X]/(X^{2}+1).}$ Este campo de extensão contém duas raízes quadradas de $- Sim.$ , nomeadamente (os cosets de) $X$ e $- Sim. X$ , respectivamente. (Os conjuntos de) $1$ e $X$ forma uma base de ${displaystyle mathbb {R} [X]/(X^{2}+1)}$ como um espaço vetorial real, o que significa que cada elemento do campo de extensão pode ser exclusivamente escrito como uma combinação linear nestes dois elementos. Equivalentemente, os elementos do campo de extensão podem ser escritos como pares ordenados $(um, b))$ de números reais. O anel quociente é um campo, porque $X 2 + 1$ é irredutível ${displaystyle mathbb {R}}$ assim o ideal que gera é maximal.
As fórmulas para adição e multiplicação no anel ${displaystyle mathbb {R} [X],}$ modulo a relação $X 2 = -1$ , correspondem às fórmulas para adição e multiplicação de números complexos definidos como pares ordenados. Então as duas definições do campo $mathbb{C}$ são isomorfos (como campos).
Aceitando isso $mathbb{C}$ é algébricamente fechado, uma vez que é uma extensão algébrica de $mathbb {R}$ nesta abordagem, $mathbb{C}$ é, portanto, o fechamento algébrico de ${displaystyle mathbb {R}.}$
Representação matricial de números complexos
Números complexos $a + bi$ também podem ser representados por $2 \times 2$ matrizes que têm a forma:
${displaystyle {begin{pmatrix}a&-b\b&;;aend{pmatrix}}}$ $um$ $b)$ $2 \times 2$
Um cálculo simples mostra que o mapa:
${displaystyle a+ibmapsto {begin{pmatrix}a&-b\b&;;aend{pmatrix}}}$
A descrição geométrica da multiplicação de números complexos também pode ser expressa em termos de matrizes de rotação usando esta correspondência entre números complexos e tais matrizes. A ação da matriz em um vetor $(x, y)$ corresponde à multiplicação de $x + iy$ por $a + ib$ . Em particular, se o determinante for $1$ , existe um número real $t$ tal que a matriz tem a forma:
${displaystyle {begin{pmatrix}cos t&-sin t\sin t&;;cos tend{pmatrix}}}$ ${displaystyle cos t+isin t}$ $)$
Análise complexa

Gráfico de roda de cor de $pecado (1 zangão.)$ . Partes brancas no interior referem-se a números com grandes valores absolutos.
O estudo das funções de uma variável complexa é conhecido como análise complexa e tem enorme uso prático na matemática aplicada, bem como em outros ramos da matemática. Freqüentemente, as provas mais naturais para declarações em análise real ou até mesmo em teoria dos números empregam técnicas de análise complexa (veja o teorema dos números primos para um exemplo). Ao contrário das funções reais, que são comumente representadas como gráficos bidimensionais, as funções complexas têm gráficos quadridimensionais e podem ser ilustradas de maneira útil codificando por cores um gráfico tridimensional para sugerir quatro dimensões ou animando os gráficos da função complexa. transformação dinâmica do plano complexo.
Funções exponenciais complexas e relacionadas
As noções de série convergente e funções contínuas na análise (real) têm análogos naturais em análise complexa. Uma seqüência de números complexos é dito para convergir se e somente se suas partes reais e imaginárias fazem. Isso é equivalente à definição de limites (ε, δ), onde o valor absoluto dos números reais é substituído por um dos números complexos. De um ponto de vista mais abstrato, $mathbb {C}$ , dotado da métrica
${displaystyle operatorname {d} (z_{1},z_{2})=|z_{1}-z_{2}|}$ ${displaystyle |z_{1}+z_{2}|leq |z_{1}|+|z_{2}|}$ $zangão. 1$ $zangão. 2$
Como na análise real, esta noção de convergência é usada para construir uma série de funções elementares: a função exponencial $exp z$ , também escrito $e z$ , é definido como a série infinita
${displaystyle exp z:=1+z+{frac {z^{2}}{2cdot 1}}+{frac {z^{3}}{3cdot 2cdot 1}}+cdots =sum _{n=0}^{infty }{frac {z^{n}}{n!}}.}$
A série que define as funções trigonométricas reais seno e cosseno, bem como as funções hiperbólicas sinh e cosh, também são transportadas para argumentos complexos sem alteração. Para as outras funções trigonométricas e hiperbólicas, como a tangente, as coisas são um pouco mais complicadas, pois as séries definidoras não convergem para todos os valores complexos. Portanto, deve-se defini-los em termos de seno, cosseno e exponencial, ou, de forma equivalente, usando o método de continuação analítica.
A fórmula de Euler afirma:
${displaystyle exp(ivarphi)=cos varphi +isin varphi }$ $φ$ ${displaystyle exp(ipi)=-1}$ $zangão.$ ${displaystyle exp z=w}$ $O quê? \neq 0$ $zangão.$ $O quê?$ ${displaystyle log w=ln |w|+iarg w,}$ $2 D$ $(D, D]$
Exponenciação complexa $z ω$ é definida como
${displaystyle z^{omega }=exp(omega ln z),}$ $ω$ $ω = 1 / n$ $n$ $n$
Os números complexos, ao contrário dos números reais, em geral não satisfazem as identidades de potência e logaritmo não modificadas, particularmente quando ingenuamente tratados como funções de valor único; ver falha de poder e identidades logarítmicas. Por exemplo, eles não satisfazem
${displaystyle a^{bc}=left(a^{b}right)^{c}.}$
Funções holomórficas
Uma função f: $mathbb {C}$ → $mathbb {C}$ é chamado holomórfico se satisfizer as equações de Cauchy-Riemann. Por exemplo, qualquer $mathbb {R}$ -linear mapa $mathbb {C}$ → $mathbb {C}$ pode ser escrito no formulário
${displaystyle f(z)=az+b{overline {z}}}$ $um$ $b)$ $b) = 0$ $b{overline {z}}$
A análise complexa mostra algumas características não aparentes na análise real. Por exemplo, quaisquer duas funções holomórficas $f$ e $g$ que concorda em um pequeno subconjunto aberto arbitrariamente de $mathbb {C}$ necessariamente concorda em todos os lugares. Funções meromórficas, funções que podem ser escritas localmente $f (zangão.) zangão. - Sim. zangão. 0) n$ com uma função holomorfo $f$ , ainda compartilhar algumas das características de funções holomórficas. Outras funções têm singularidades essenciais, tais como $pecado (1 zangão.)$ em $zangão. = 0$ .
Aplicativos
Os números complexos têm aplicações em muitas áreas científicas, incluindo processamento de sinais, teoria de controle, eletromagnetismo, dinâmica de fluidos, mecânica quântica, cartografia e análise de vibração. Algumas dessas aplicações são descritas a seguir.
Geometria
Formas
Três pontos não coloniais $u,v,w$ no plano determinar a forma do triângulo ${displaystyle {u,v,w}}$ . Localizando os pontos no plano complexo, esta forma de um triângulo pode ser expressa por aritmética complexa como
${displaystyle S(u,v,w)={frac {u-w}{u-v}}.}$ $S$ ${displaystyle {u,v,w}}$
Geometria fractal

O Mandelbrot estabeleceu-se com os eixos reais e imaginários rotulados.
O conjunto Mandelbrot é um exemplo popular de um fractal formado no plano complexo. É definido traçando cada local $c$ onde iterar a sequência ${displaystyle f_{c}(z)=z^{2}+c}$ não diverge quando iterado infinitamente. Da mesma forma, os conjuntos de Julia têm as mesmas regras, exceto onde $c$ permanece constante.
Triângulos
Cada triângulo tem um inellipse Steiner único – uma elipse dentro do triângulo e tangente aos midpoints dos três lados do triângulo. Os focos da inellipse de Steiner de um triângulo podem ser encontrados da seguinte forma, de acordo com o teorema de Marden: Denote os vértices do triângulo no plano complexo como $um = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = x A + Sim. A Eu...$ , $b) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = x B + Sim. B Eu...$ e $c = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = x C + Sim. C Eu...$ . Escreva a equação cúbico $(x-a)(x-b)(x-c)=0$ , tome seu derivado e equate o derivado (quadrático) a zero. O teorema de Marden diz que as soluções desta equação são os números complexos que denotam os locais dos dois focos da inellipse Steiner.
Teoria dos números algébricos

Construção de um pentágono regular usando straightedge e bússola.
Como mencionado acima, qualquer equação polinomial não constante (em coeficientes complexos) tem uma solução em $mathbb {C}$ . A fortiori, o mesmo é verdade se a equação tem coeficientes racionais. As raízes de tais equações são chamadas de números algébricas – eles são um objeto principal de estudo em teoria dos números algébrica. Comparado a ${overline {mathbb {Q} }}$ , o fechamento algébrica de $mathbb {Q}$ , que também contém todos os números algébricas, $mathbb {C}$ tem a vantagem de ser facilmente compreensível em termos geométricos. Desta forma, métodos algébricas podem ser usados para estudar questões geométricas e vice-versa. Com métodos algébricas, mais especificamente aplicando as máquinas da teoria do campo ao campo número contendo raízes da unidade, pode-se mostrar que não é possível construir um nonagon regular usando apenas bússola e borda reta – um problema puramente geométrico.
Outro exemplo são os inteiros Gaussianos; ou seja, números na forma $x + iy$ , onde $x$ e $y$ são inteiros, que podem ser usados para classificar somas de quadrados.
Teoria analítica dos números
A teoria analítica dos números estuda os números, geralmente inteiros ou racionais, aproveitando o fato de que eles podem ser considerados como números complexos, nos quais métodos analíticos podem ser usados. Isso é feito pela codificação de informações teóricas de números em funções de valor complexo. Por exemplo, a função zeta de Riemann $ζ(s)$ está relacionada à distribuição de números primos.
Integrais impróprias
Nos campos aplicados, os números complexos são frequentemente usados para calcular certas integrais impróprias de valor real, por meio de funções de valor complexo. Existem vários métodos para fazer isso; veja métodos de integração de contorno.
Equações dinâmicas
Em equações diferenciais, é comum encontrar primeiro todas as raízes complexas $r$ da equação característica de uma equação diferencial linear ou sistema de equações e, em seguida, tentar resolver o sistema em termos de funções básicas da forma $f (t) = e rt$ . Da mesma forma, em equações de diferenças, as raízes complexas $r$ da equação característica do sistema de equações de diferenças são usadas, para tentar resolver o sistema em termos de funções básicas da forma $f (t) = r t$ .
Álgebra linear
Eigendecomposition é uma ferramenta útil para calcular potências de matrizes e exponenciais de matrizes. No entanto, muitas vezes requer o uso de números complexos, mesmo que a matriz seja real (por exemplo, uma matriz de rotação).
Números complexos geralmente generalizam conceitos originalmente concebidos nos números reais. Por exemplo, a transposta conjugada generaliza a transposta, as matrizes hermitianas generalizam as matrizes simétricas e as matrizes unitárias generalizam as matrizes ortogonais.
Em matemática aplicada
Teoria de controle
Na teoria de controle, os sistemas são frequentemente transformados do domínio do tempo para o domínio da frequência complexa usando a transformada de Laplace. Os zeros e polos do sistema são então analisados no plano complexo. O lugar geométrico das raízes, o gráfico de Nyquist e as técnicas de gráfico de Nichols fazem uso do plano complexo.
No método do lugar das raízes, é importante saber se os zeros e pólos estão nos semiplanos esquerdo ou direito, ou seja, se têm parte real maior ou menor que zero. Se um sistema linear, invariante no tempo (LTI) tem pólos que são
no meio avião direito, será instável,
tudo no meio plano esquerdo, será estável,
no eixo imaginário, terá estabilidade marginal.
Se um sistema tem zeros no semiplano direito, é um sistema de fase não mínima.
Análise de sinal
Números complexos são usados na análise de sinal e outros campos para uma descrição conveniente para sinais que variam periodicamente. Para funções reais dadas que representam quantidades físicas reais, geralmente em termos de senos e cossenos, são consideradas funções complexas correspondentes cujas partes reais são as quantidades originais. Para uma onda senoidal de uma determinada frequência, o valor absoluto $| z |$ do correspondente $z$ é a amplitude e o argumento $arg z$ é a fase.
Se a análise de Fourier for empregada para escrever um dado sinal de valor real como uma soma de funções periódicas, essas funções periódicas são frequentemente escritas como funções de valor complexo da forma
${displaystyle x(t)=operatorname {Re} {X(t)}}$
e
${displaystyle X(t)=Ae^{iomega t}=ae^{iphi }e^{iomega t}=ae^{i(omega t+phi)}}$
onde ω representa a frequência angular e o número complexo A codifica a fase e a amplitude conforme explicado acima.
Esse uso também é estendido ao processamento de sinal digital e processamento de imagem digital, que usam versões digitais da análise de Fourier (e análise de wavelet) para transmitir, compactar, restaurar e processar sinais de áudio digital, imagens estáticas e sinais de vídeo.
Outro exemplo, relevante para as duas bandas laterais de modulação de amplitude do rádio AM, é:
${displaystyle {begin{aligned}cos((omega +alpha)t)+cos left((omega -alpha)tright)&=operatorname {Re} left(e^{i(omega +alpha)t}+e^{i(omega -alpha)t}right)\&=operatorname {Re} left(left(e^{ialpha t}+e^{-ialpha t}right)cdot e^{iomega t}right)\&=operatorname {Re} left(2cos(alpha t)cdot e^{iomega t}right)\&=2cos(alpha t)cdot operatorname {Re} left(e^{iomega t}right)\&=2cos(alpha t)cdot cos left(omega tright).end{aligned}}}$
Na física
Eletromagnetismo e engenharia elétrica
Na engenharia elétrica, a transformada de Fourier é usada para analisar tensões e correntes variáveis. O tratamento de resistores, capacitores e indutores pode então ser unificado introduzindo resistências imaginárias dependentes da frequência para os dois últimos e combinando todos os três em um único número complexo chamado impedância. Essa abordagem é chamada de cálculo fasorial.
Na engenharia elétrica, a unidade imaginária é denotada por $j$ , para evitar confusão com $I$ , que geralmente é usado para denotar corrente elétrica ou, mais particularmente, $i$ , que geralmente é usado para denotar corrente elétrica instantânea.
Como a tensão em um circuito CA é oscilante, ela pode ser representada como
${displaystyle V(t)=V_{0}e^{jomega t}=V_{0}left(cos omega t+jsin omega tright),}$
Para obter a quantidade mensurável, a parte real é tomada:
${displaystyle v(t)=operatorname {Re} (V)=operatorname {Re} left[V_{0}e^{jomega t}right]=V_{0}cos omega t.}$
O sinal de valor complexo $V (t)$ é chamado de representação analítica do valor real mensurável sinal $v (t)$ .
Dinâmica de fluidos
Na dinâmica dos fluidos, funções complexas são usadas para descrever o fluxo potencial em duas dimensões.
Mecânica quântica
O campo de número complexo é intrínseco às formulações matemáticas da mecânica quântica, onde os espaços de Hilbert complexos fornecem o contexto para uma formulação que é conveniente e talvez a mais padronizada. As fórmulas básicas originais da mecânica quântica – a equação de Schrödinger e a mecânica matricial de Heisenberg – fazem uso de números complexos.
Relatividade
Na relatividade especial e geral, algumas fórmulas para a métrica no espaço-tempo tornam-se mais simples se considerarmos que o componente de tempo do contínuo espaço-tempo é imaginário. (Essa abordagem não é mais padrão na relatividade clássica, mas é usada de maneira essencial na teoria quântica de campos.) Os números complexos são essenciais para os espinores, que são uma generalização dos tensores usados na relatividade.
Generalizações e noções relacionadas

Gráfico quaternion Cayley Q8 mostrando ciclos de multiplicação por Eu..., JJ e k
O processo de extensão do campo $mathbb {R}$ de reais a $mathbb {C}$ é conhecido como a construção Cayley–Dickson. Pode ser transportado mais para dimensões mais altas, produzindo as quaternions $mathbb {H}$ e octonions $mathbb {O}$ que (como um espaço vetorial real) são de dimensão 4 e 8, respectivamente. Neste contexto, os números complexos foram chamados de binarions.
Assim como ao aplicar a construção aos reais a propriedade de ordenação é perdida, as propriedades familiares dos números reais e complexos desaparecem com cada extensão. Os quaternions perdem comutatividade, ou seja, $x \cdot y \neq y \cdot x$ para alguns quaternions $x, y$ , e a multiplicação de octônios, além de não serem comutativos, falha em ser associativo: $(x \cdot y)\cdot z \neq x \cdot(y \cdot z)$ para alguns octônios $x, y, z$ .
Reais, números complexos, quaternions e octonions são todas álgebras de divisão normed sobre $mathbb {R}$ . Por teorema de Hurwitz eles são os únicos; as sedenions, o próximo passo na construção Cayley-Dickson, não têm essa estrutura.
A construção Cayley-Dickson está intimamente relacionada com a representação regular de ${displaystyle mathbb {C}}$ pensar de como um $mathbb {R}$ - Álgebra (an $mathbb {R}$ -Vector espaço com uma multiplicação), com respeito à base $(1 Eu...)$ . Isto significa o seguinte: $mathbb {R}$ -linear mapa
${displaystyle {begin{aligned}mathbb {C} &rightarrow mathbb {C} \z&mapsto wzend{aligned}}}$ $O quê?$ $2 \times 2$ $(1 Eu...)$ ${displaystyle {begin{pmatrix}operatorname {Re} (w)&-operatorname {Im} (w)\operatorname {Im} (w)&operatorname {Re} (w)end{pmatrix}},}$ $mathbb {C}$ ${displaystyle J={begin{pmatrix}p&q\r&-pend{pmatrix}},quad p^{2}+qr+1=0}$ $JJ 2 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = Eu...$ ${displaystyle {z=aI+bJ:a,bin mathbb {R} }}$ ${displaystyle mathbb {C}}$ ${displaystyle mathbb {R} ^{2}.}$
Os números hipercomplexos também generalizam ${displaystyle mathbb {R}}$ ${displaystyle mathbb {C}}$ ${displaystyle mathbb {H}}$ e ${displaystyle mathbb {O}.}$ Por exemplo, esta noção contém os números split-complex, que são elementos do anel ${displaystyle mathbb {R} [x]/(x^{2}-1)}$ (em oposição a ${displaystyle mathbb {R} [x]/(x^{2}+1)}$ para números complexos). Neste anel, a equação $um 2 = 1$ tem quatro soluções.
O campo $mathbb {R}$ é a conclusão de ${displaystyle mathbb {Q}}$ o campo de números racionais, com relação à métrica de valor absoluto habitual. Outras escolhas de métricas sobre $mathbb {Q}$ levar aos campos ${displaystyle mathbb {Q} _{p}}$ de números p-ádicos (para qualquer número primo $p$ ), que são, assim, análogos $mathbb {R}$ . Não há outras formas não triviais de completar $mathbb {Q}$ do que $mathbb {R}$ e ${displaystyle mathbb {Q} _{p},}$ pelo teorema de Ostrowski. Os fechamentos algébricas ${displaystyle {overline {mathbb {Q} _{p}}}}$ de ${displaystyle mathbb {Q} _{p}}$ ainda carrega uma norma, mas (não gosto $mathbb {C}$ ) não estão completos com respeito a ele. A conclusão ${mathbb {C}}_{p}$ de ${displaystyle {overline {mathbb {Q} _{p}}}}$ Parece estar algébricamente fechado. Por analogia, o campo é chamado $p$ - números complexos médicos.
Os campos ${displaystyle mathbb {R}}$ ${displaystyle mathbb {Q} _{p},}$ e suas extensões de campo finitas, incluindo ${displaystyle mathbb {C}}$ são chamados campos locais.

Contenido relacionado

Antiprisma
Em geometria, um n-gonal antiprisma ou n-antiprism é um poliedro composto de duas cópias diretas paralelas de um lado n /span> polígono, conectado por uma...
Charles Babbage
Charles Babbage KH FRS foi um polímata inglês. Um matemático, filósofo, inventor e engenheiro mecânico, Babbage originou o conceito de um computador...
Dodecaedro
Em geometria, um dodecaedro ou duodecaedro é qualquer poliedro com doze faces planas. O dodecaedro mais familiar é o dodecaedro regular com pentágonos...
Espaço euclidiano
O espaço euclidiano é o espaço fundamental da geometria, destinado a representar o espaço físico. Originalmente, isto é, nos Elementos de Euclides, era...
Absoluto Infinito
O Infinito Absoluto é uma extensão da ideia de infinito proposta pelo matemático Georg...
Más resultados...
Te puede interesar