Momento angular
Na física, o momento angular (às vezes chamado de momento do momento ou momento rotacional) é o análogo rotacional do momento linear. É uma quantidade física importante porque é uma quantidade conservada - o momento angular total de um sistema fechado permanece constante. O momento angular tem uma direção e uma magnitude, e ambas são conservadas. Bicicletas e motocicletas, discos voadores, balas espingardas e giroscópios devem suas propriedades úteis à conservação do momento angular. A conservação do momento angular também é o motivo pelo qual os furacões formam espirais e as estrelas de nêutrons têm altas taxas de rotação. Em geral, a conservação limita o possível movimento de um sistema, mas não o determina exclusivamente.
O momento angular tridimensional para uma partícula pontual é classicamente representado como um pseudovetor r × p, o produto vetorial do vetor de posição da partícula r (relativo a alguma origem) e seu vetor de momento; o último é p = mv na mecânica newtoniana. Ao contrário do momento linear, o momento angular depende de onde essa origem é escolhida, uma vez que a posição da partícula é medida a partir dela.
O momento angular é uma quantidade extensa; isto é, o momento angular total de qualquer sistema composto é a soma dos momentos angulares de suas partes constituintes. Para um corpo rígido contínuo ou um fluido, o momento angular total é o volume integral da densidade do momento angular (momento angular por unidade de volume no limite quando o volume diminui para zero) sobre todo o corpo.
Semelhante à conservação do momento linear, onde ele é conservado se não houver força externa, o momento angular é conservado se não houver torque externo. O torque pode ser definido como a taxa de variação do momento angular, análoga à força. O torque líquido externo em qualquer sistema é sempre igual ao torque total no sistema; em outras palavras, a soma de todos os torques internos de qualquer sistema é sempre 0 (este é o análogo rotacional da terceira lei do movimento de Newton). Portanto, para um sistema fechado (onde não há torque líquido externo), o torque total no sistema deve ser 0, o que significa que o momento angular total do sistema é constante. A mudança no momento angular para uma interação particular às vezes é chamada de twirl, mas isso é bastante incomum. Twirl é o análogo angular do impulso.
Definição em mecânica clássica
Assim como para a velocidade angular, existem dois tipos especiais de momento angular de um objeto: o momento angular de rotação é o momento angular em torno do centro de massa do objeto, enquanto o momento angular orbital é o momento angular em torno de um centro de rotação escolhido. A Terra tem um momento angular orbital por natureza girando em torno do Sol e um momento angular de rotação por natureza de sua rotação diária em torno do eixo polar. O momento angular total é a soma dos momentos angulares de spin e orbital. No caso da Terra, a quantidade conservada primária é o momento angular total do sistema solar porque o momento angular é trocado em uma pequena, mas importante extensão entre os planetas e o Sol. O vetor de momento angular orbital de uma partícula pontual é sempre paralelo e diretamente proporcional ao seu vetor de velocidade angular orbital ω, onde a constante de proporcionalidade depende tanto da massa da partícula quanto de sua distância da origem. O vetor de momento angular de rotação de um corpo rígido é proporcional, mas nem sempre paralelo ao vetor de velocidade angular de rotação Ω, tornando a constante de proporcionalidade um tensor de segunda ordem em vez de um escalar.
Momento angular orbital em duas dimensões
O momento angular é uma quantidade vetorial (mais precisamente, um pseudovetor) que representa o produto da inércia rotacional de um corpo e da velocidade rotacional (em radianos/s) em torno de um eixo específico. No entanto, se a trajetória da partícula estiver em um único plano, basta descartar a natureza vetorial do momento angular e tratá-lo como um escalar (mais precisamente, um pseudoescalar). O momento angular pode ser considerado um análogo rotacional do momento linear. Assim, onde o momento linear p é proporcional à massa m e velocidade linear v,
o momento angular L é proporcional ao momento de inércia I e velocidade angular ω medido em radianos por segundo.
Ao contrário da massa, que depende apenas da quantidade de matéria, o momento de inércia também depende da posição do eixo de rotação e da forma da matéria. Ao contrário da velocidade linear, que não depende da escolha da origem, a velocidade angular orbital é sempre medida em relação a uma origem fixa. Portanto, estritamente falando, L deve ser referido como o momento angular relativo a esse centro.
Porque... Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R2mNão. I=r^{2}m para uma única partícula e ω ω = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =vR{displaystyle omega ={frac Não. para movimento circular, momentum angular pode ser expandido, L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R2m)) vR,Não. L=r^{2}mcdot {frac {v}{r}},} e reduzido a,
- L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Rmv,Não. L=rmv,
o produto do raio de rotação R e o impulso linear da partícula p= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =mv- Sim., onde vNão. neste caso é a velocidade linear equivalente (tangential) no raio (= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Rω ω Não.).
Esta análise simples também pode ser aplicada a movimentos não circulares se apenas o componente do movimento que é perpendicular ao vetor raio for considerado. Nesse caso,
- L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Rmv:: ,Não. L=rmv_{perp }
Onde? v:: = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =vpecado (θ θ ){displaystyle v_{perp }=vsin(theta)} é o componente perpendicular do movimento. Expandindo, L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Rmvpecado (θ θ ),{displaystyle L=rmvsin(theta),} reorganizar, L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Rpecado (θ θ )mv,{displaystyle L=rsin(theta)mv,} e reduzindo, impulso angular também pode ser expresso,
- L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R:: mv,Não. L=r_{perp }mv,}
Onde? R:: = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Rpecado (θ θ ){displaystyle r_{perp }=rsin(theta)} é o comprimento do braço do momento, uma linha caiu perpendicularmente da origem para o caminho da partícula. É esta definição, (comprimento do braço de momento) × (momento linear) ao qual o termo momento de impulso refere-se.
Momento angular escalar da mecânica lagrangiana
Outra abordagem é definir o impulso angular como o impulso conjugado (também chamado de momentum canônico) da coordenada angular φ φ - Sim. expressa no Lagrangian do sistema mecânico. Considere um sistema mecânico com uma massa mNão. limitado a mover-se em um círculo de raio umNão. na ausência de qualquer campo de força externa. A energia cinética do sistema é
E a energia potencial é
- U= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0.- Sim.
Então o lagrangeano é
- L(φ φ ,φ φ :: )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =T- Sim. - Sim. U= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =12mum2φ φ :: 2.{displaystyle {mathcal {L}}left(phi{dot {phi }}right)=T-U={frac {1}{2}}ma^{2}{dot Sim.
O momentum generalizado "canonicamente conjugar para" a coordenada φ φ - Sim. é definido por
- pφ φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∂ ∂ L∂ ∂ φ φ :: = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =mum2φ φ :: = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...ω ω = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =L.{displaystyle p_{phi }={frac {partial {mathcal {L}}}{partial {dot {phi } }}=ma^{2} - Sim.
Momento angular orbital em três dimensões
Para definir completamente o momento angular orbital em três dimensões, é necessário conhecer a taxa na qual o vetor posição varre o ângulo, a direção perpendicular ao plano instantâneo do deslocamento angular e a massa envolvida, bem como como isso massa está distribuída no espaço. Ao manter essa natureza vetorial do momento angular, a natureza geral das equações também é mantida e pode descrever qualquer tipo de movimento tridimensional em torno do centro de rotação – circular, linear ou outro. Na notação vetorial, o momento angular orbital de uma partícula pontual em movimento em torno da origem pode ser expresso como:
- L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...ω ω ,{displaystyle mathbf {L} =I{boldsymbol {omega }}}
onde
- Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R2mNão. I=r^{2}m é o momento da inércia para uma massa de ponto,
- ω ω = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R× × vR2O que é isso? }} = {displaystyle {mathbf} times mathbf {v} }{r^{2}} é a velocidade angular orbital da partícula sobre a origem,
- R- Sim. é o vetor de posição da partícula relativa à origem, e R= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =|R|{displaystyle r=leftvert mathbf {r} rightvert },
- v(v) é a velocidade linear da partícula relativa à origem, e
- mNão. é a massa da partícula.
Isso pode ser expandido, reduzido e, pelas regras da álgebra vetorial, reorganizado:
- L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(R2m)(R× × vR2)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =m(R× × v)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R× × mv= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R× × p,{displaystyle {begin{aligned}mathbf {L} &=left(r^{2}mright)left({frac {mathbf {r} times mathbf {v} }{r^{2}}}right)&=mleft(mathbf {r} times mathbf {v} right)&=mathbf {r} times mmathbf {v} \&=mathbf {r} times mathbf {p}end{aligned}}}
que é o produto cruzado do vetor de posição R- Sim. e o impulso linear p= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =mv{displaystyle mathbf {p} =mmathbf {v} } } da partícula. Pela definição do produto cruzado, o L{displaystyle mathbf {L} } } vetor é perpendicular a ambos R- Sim. e p- Sim.. É dirigido perpendicular ao plano de deslocamento angular, conforme indicado pela regra da mão direita – de modo que a velocidade angular é vista como anti-horário da cabeça do vetor. Por outro lado, o L{displaystyle mathbf {L} } } vector define o plano em que R- Sim. e p- Sim. Mentir.
Definindo um vetor unitário u^ ^ {displaystyle mathbf {hat {u}} } perpendicular ao plano de deslocamento angular, velocidade angular escalar ω ω - Sim. resultados, onde
- ω ω u^ ^ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =ω ω ,{displaystyle omega mathbf {hat {u}} - Sim. e
- ω ω = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =v:: R,{displaystyle omega ={frac Não. }}{r}},} Onde? v:: {displaystyle v_{perp }} é o componente perpendicular do movimento, como acima.
As equações escalares bidimensionais da seção anterior podem, portanto, receber direção:
- L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...ω ω = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...ω ω u^ ^ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(R2m)ω ω u^ ^ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Rmv:: u^ ^ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R:: mvu^ ^ ,{displaystyle {begin{aligned}mathbf] Eu sou um homem. }}\&=Iomega mathbf {hat {u}} \&=left(r^{2}mright)omega mathbf {hat {u}} \&=rmv_{perp }mathbf {hat {u}} \&=r_{perp }mvmathbf {hat {u}}end{aligned}}}
e L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Rmvu^ ^ {displaystyle mathbf {L} =rmvmathbf {hat {u}} } para movimento circular, onde todo o movimento é perpendicular ao raio RNão..
No sistema de coordenadas esféricas, o vetor de momento angular é expresso como
- L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =mR× × v= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =mR2(θ θ :: φ φ ^ ^ - Sim. - Sim. φ φ :: pecado θ θ θ θ ^ ^ ).{displaystyle mathbf {L} =mmathbf {r} times mathbf {v} =mr^{2}left({dot {theta }},{hat {boldsymbol {varphi }}}-{dot {varphi }}sin theta ,mathbf {hat {boldsymbol {theta }}} right). ?
Momento angular em qualquer número de dimensões
O impulso angular pode ser definido em termos do produto cruzado apenas em três dimensões. Definindo-o como bivetor L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R∧ ∧ p{displaystyle mathbf {L} =mathbf {r}} wedge mathbf {p} }, onde ∧ ∧ - Sim. é o produto exterior, é válido em qualquer número de dimensões. Este produto exterior é equivalente a um tensor antissimétrico do grau 2, que também se aplica em qualquer número de dimensões. Nomeadamente, se xEu...Não. x_{i}} é um vetor de posição e pEu...Não. p_{i}}é o vetor de impulso linear, então podemos definir
No caso geral de momenta angular resumida de múltiplas partículas, este tensor antissimétrico tem n(n- Sim. - Sim. 1)/2(n-1)/2} componentes independentes (graus de liberdade), onde nNão. é o número de dimensões. No caso tridimensional usual tem 3 componentes independentes, o que nos permite identificá-lo com um pseudovetor dimensional M= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(Mx,MSim.,Mzangão.){displaystyle mathbf] {M} =(M_{x},M_{y},M_{z})}. Os componentes deste vetor se relacionam com os componentes do tensor de classificação 2 da seguinte forma:
Analogia ao momento linear
O momento angular pode ser descrito como o análogo rotacional do momento linear. Como o momento linear, envolve elementos de massa e deslocamento. Ao contrário do momento linear, também envolve elementos de posição e forma.
Muitos problemas em física envolvem matéria em movimento em torno de um certo ponto no espaço, seja em rotação real em torno dele, ou simplesmente passando por ele, onde se deseja saber que efeito a matéria em movimento tem sobre o ponto - pode exercer energia sobre ele ou realizar trabalho sobre ele? A energia, a capacidade de realizar trabalho, pode ser armazenada na matéria colocando-a em movimento — uma combinação de sua inércia e seu deslocamento. A inércia é medida pela sua massa e o deslocamento pela sua velocidade. O produto deles,
- (quantidade de inércia)× × (quantidade de deslocamento)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =quantidade de (inércia · Deslocamento)massa× × velocidade= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =momentom× × v= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =p{displaystyle {begin{aligned}({text{amount of inertia}})times ({text{amount of deslocamento}})&={text{amount of (inertia⋅displacement)}}\{text{mass}}times {text{velocity}}&={text{momentum}}mtimes v&=p\end{align}}}}}}
é o momentum da matéria. A referência desse momento a um ponto central apresenta uma complicação: o momento não é aplicado diretamente ao ponto. Por exemplo, uma partícula de matéria na borda externa de uma roda está, de fato, na extremidade de uma alavanca do mesmo comprimento que o raio da roda, seu momento girando a alavanca em torno do ponto central. Essa alavanca imaginária é conhecida como braço do momento. Tem o efeito de multiplicar o esforço do momento em proporção ao seu comprimento, efeito conhecido como momento. Assim, o momento da partícula refere-se a um ponto particular,
- (braço de momento)× × (quantidade de inércia)× × (quantidade de deslocamento)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =momento de (inércia⋅deslocamento)comprimento× × massa× × velocidade= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =momento de impulsoR× × m× × v= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =L{displaystyle {begin{aligned}({text{moment arm}})times ({text{amount of inertia}})times ({text{amount of deslocamento}})&={text{moment of (inertia⋅displacement)}}\{text{comprimento}}times {text{velocity}}&={textum{moment}}
é o momentum angular, às vezes chamado, como aqui, o momento de impulso da partícula versus esse ponto central particular. A equação L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =RmvNão. L=rmv combina um momento (uma massa mNão. girando o braço do momento RNão.) com uma velocidade linear (equivalente à linha estreita) vNão.. Velocidade linear referida no ponto central é simplesmente o produto da distância RNão. e a velocidade angular ω ω - Sim. contra o ponto: v= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Rω ω ,- Sim. Mais um momento. Assim, o impulso angular contém um momento duplo: L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =RmRω ω .Não. L=rmromega.} Simplificando ligeiramente, L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R2mω ω ,Não. L=r^{2}momega} a quantidade R2m- Sim. é o momento da inércia da partícula, às vezes chamado o segundo momento da massa. É uma medida de inércia rotacional.
A analogia acima do momento de translação e momento de rotação pode ser expressa na forma vetorial:
p= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =mv- Sim. para movimento linear
L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...ω ω {displaystyle mathbf {L} = I{boldsymbol) para rotação
A direção do momento está relacionada à direção da velocidade para o movimento linear. A direção do momento angular está relacionada com a velocidade angular da rotação.
Como o momento de inércia é uma parte crucial do momento angular de rotação, este último inclui necessariamente todas as complicações do primeiro, que é calculado multiplicando os bits elementares da massa pelos quadrados de suas distâncias do centro de rotação. Portanto, o momento de inércia total e o momento angular são uma função complexa da configuração da matéria sobre o centro de rotação e a orientação da rotação para os vários bits.
Para um corpo rígido, por exemplo, uma roda ou um asteroide, a orientação de rotação é simplesmente a posição do eixo de rotação versus a matéria do corpo. Pode ou não passar pelo centro de massa, ou pode ficar completamente fora do corpo. Para o mesmo corpo, o momento angular pode assumir um valor diferente para cada eixo possível em torno do qual a rotação pode ocorrer. Atinge um mínimo quando o eixo passa pelo centro de massa.
Para uma coleção de objetos que giram em torno de um centro, por exemplo, todos os corpos do Sistema Solar, as orientações podem ser um pouco organizadas, como é o Sistema Solar, com a maioria dos corpos; eixos próximos ao eixo do sistema. Suas orientações também podem ser completamente aleatórias.
Em resumo, quanto mais massa e quanto mais longe estiver do centro de rotação (mais longo o braço do momento), maior o momento de inércia e, portanto, maior o momento angular para uma determinada velocidade angular. Em muitos casos, o momento de inércia e, portanto, o momento angular, podem ser simplificados por,
- Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =k2m,Não. I=k^{2}m,}
- Onde? kNão. é o raio de giro, a distância do eixo em que toda a massa mNão. pode ser considerado como concentrado.
Da mesma forma, para uma massa de ponto mNão. o momento da inércia é definido como,
- Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R2mNão. I=r^{2}m
- Onde? RNão. é o raio da massa de ponto do centro de rotação,
e para qualquer coleção de partículas mEu...Não. m_{i}} como a soma,
- Gerenciamento Gerenciamento Eu...Eu...Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento Eu...REu...2mEu...{displaystyle sum _{i}I_{i}=sum _{i}r_{i}^{2}m_{i}}
A dependência do momento angular em relação à posição e forma é refletida em suas unidades versus momento linear: kg⋅m2/s ou N⋅m⋅s para momento angular versus kg⋅m/ s ou N⋅s para momento linear. Ao calcular o momento angular como o produto do momento de inércia vezes a velocidade angular, a velocidade angular deve ser expressa em radianos por segundo, onde o radiano assume o valor adimensional da unidade. (Ao realizar a análise dimensional, pode ser produtivo usar a análise orientacional que trata os radianos como uma unidade básica, mas isso não é feito no sistema internacional de unidades). As unidades do momento angular podem ser interpretadas como torque⋅tempo. Um objeto com momento angular de L N⋅m⋅s pode ser reduzido a velocidade angular zero por um impulso angular de L N⋅m⋅s.
O plano perpendicular ao eixo do momento angular e passando pelo centro de massa é às vezes chamado de plano invariável, porque a direção do eixo permanece fixa se apenas as interações dos corpos dentro do sistema, livre de influências externas, são considerados. Um desses planos é o plano invariável do Sistema Solar.
Momento angular e torque
A segunda lei do movimento de Newton pode ser expressa matematicamente,
- F= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =mum,{displaystyle mathbf {F} =mmathbf {a}}
ou força = massa × aceleração. O equivalente rotacional para partículas pontuais pode ser derivado da seguinte forma:
- L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...ω ω {displaystyle mathbf {L} = I{boldsymbol)
o que significa que o torque (ou seja, a derivada temporal do momento angular) é
Porque o momento da inércia é mR2{displaystyle mr^{2}}, segue-se que DEu...D)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2mRDRD)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2Rp||(dI){dt}}=2mr{frac {dr}{dt}}=2rp_{||}}e DLD)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...Dω ω D)+2Rp||ω ω ,(em inglês) (L)}{dt}}=I{frac (d{boldsymbol) Não. }}}{dt}}+2rp_{||}{boldsymbol {omega }},} que, reduz a
- ? ? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...α α +2Rp||ω ω .O que é isso? }}=I{boldsymbol }}+2rp_{||}{boldsymbol Sim.
Este é o análogo rotacional da segunda lei de Newton. Observe que o torque não é necessariamente proporcional ou paralelo à aceleração angular (como seria de se esperar). A razão para isso é que o momento de inércia de uma partícula pode mudar com o tempo, algo que não pode ocorrer para a massa comum.
Conservação do momento angular
Considerações gerais
Um análogo rotacional da terceira lei do movimento de Newton pode ser escrito, "Em um sistema fechado, nenhum torque pode ser exercido em qualquer matéria sem o esforço em alguma outra matéria de um torque igual e oposto sobre o mesmo eixo." Assim, momento angular pode ser trocado entre objetos em um sistema fechado, mas o momento angular total antes e depois de uma troca permanece constante (é conservado).
Visto de outra forma, um análogo rotacional da primeira lei do movimento de Newton pode ser escrito, "Um corpo rígido continua em um estado de rotação uniforme, a menos que seja influenciado por uma influência externa." Assim sem influência externa para atuar sobre ele, o momento angular original do sistema permanece constante.
A conservação do impulso angular é usada na análise do movimento da força central. Se a força líquida em algum corpo é direcionada sempre para algum ponto, o centro, então não há torque no corpo com respeito ao centro, pois toda a força é direcionada ao longo do vetor de raio, e nenhum é perpendicular ao raio. Matematicamente, torque ? ? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R× × F= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0,{displaystyle {boldsymbol {tau }}=mathbf {r} times mathbf {F} =mathbf {0}} porque neste caso R- Sim. e F} são vetores paralelos. Portanto, o impulso angular do corpo sobre o centro é constante. Este é o caso com atração gravitacional nas órbitas de planetas e satélites, onde a força gravitacional é sempre direcionada para o corpo primário e corpos orbitando conservam o momentum angular, trocando distância e velocidade à medida que se movem sobre o primário. O movimento da força central também é usado na análise do modelo Bohr do átomo.
Para um planeta, o momento angular é distribuído entre a rotação do planeta e sua revolução em sua órbita, e estes são frequentemente trocados por vários mecanismos. A conservação do momento angular no sistema Terra-Lua resulta na transferência do momento angular da Terra para a Lua, devido ao torque de maré que a Lua exerce sobre a Terra. Isso, por sua vez, resulta na desaceleração da taxa de rotação da Terra, em cerca de 65,7 nanossegundos por dia, e no aumento gradual do raio da órbita da Lua, em cerca de 3,82 centímetros por ano.
A conservação do momento angular explica a aceleração angular de um patinador no gelo quando ele aproxima seus braços e pernas do eixo vertical de rotação. Ao aproximar parte da massa de seu corpo do eixo, eles diminuem o momento de inércia de seu corpo. Como o momento angular é o produto do momento de inércia e da velocidade angular, se o momento angular permanecer constante (se conservar), então a velocidade angular (velocidade de rotação) do patinador deve aumentar.
O mesmo fenômeno resulta na rotação extremamente rápida de estrelas compactas (como anãs brancas, estrelas de nêutrons e buracos negros) quando são formadas a partir de estrelas muito maiores e com rotação mais lenta.
A conservação nem sempre é uma explicação completa para a dinâmica de um sistema, mas é uma restrição chave. Por exemplo, um pião está sujeito a um torque gravitacional fazendo com que ele se incline e altere o momento angular em torno do eixo de nutação, mas desprezando o atrito no ponto de contato giratório, ele tem um momento angular conservado em torno de seu eixo giratório e outro em seu eixo giratório. eixo de precessão. Além disso, em qualquer sistema planetário, os planetas, estrelas, cometas e asteróides podem se mover de várias maneiras complicadas, mas apenas para que o momento angular do sistema seja conservado.
O teorema de Noether afirma que toda lei de conservação está associada a uma simetria (invariante) da física subjacente. A simetria associada à conservação do momento angular é a invariância rotacional. O fato de a física de um sistema permanecer inalterada se ele for girado por qualquer ângulo em torno de um eixo implica que o momento angular é conservado.
Relação com a segunda lei do movimento de Newton
Embora a conservação total do momento angular possa ser entendida separadamente das leis de movimento de Newton como decorrente do teorema de Noether em sistemas simétricos sob rotações, também pode ser entendida simplesmente como um método eficiente de cálculo de resultados que também pode ser obtido diretamente da segunda lei de Newton, juntamente com as leis que regem as forças da natureza (como a terceira lei de Newton, as equações de Maxwell e a força de Lorentz). De fato, dadas as condições iniciais de posição e velocidade para cada ponto, e as forças em tal condição, pode-se usar a segunda lei de Newton para calcular a segunda derivada da posição, e resolvê-la fornece informações completas sobre o desenvolvimento de o sistema físico com o tempo. Observe, no entanto, que isso não é mais verdade na mecânica quântica, devido à existência do spin da partícula, que é o momento angular que não pode ser descrito pelo efeito cumulativo de movimentos pontuais no espaço.
Como exemplo, considere a diminuição do momento de inércia, por ex. quando um patinador artístico está puxando suas mãos, acelerando o movimento circular. Em termos de conservação do momento angular, temos, para o momento angular L, momento de inércia I e velocidade angular ω:
- 0= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =DL= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =D(Eu...)) ω ω )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =DEu...)) ω ω +Eu...)) Dω ω {displaystyle 0=dL=d(Icdot omega)=dIcdot omega +Icdot domega }
Usando isso, vemos que a mudança requer uma energia de:
- DE= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =D(12Eu...)) ω ω 2)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =12DEu...)) ω ω 2+Eu...)) ω ω )) Dω ω = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. 12DEu...)) ω ω 2{displaystyle dE=dleft({frac) {1}{2}}Icdot omega ^{2}right)={frac {1}{2}}d Icdot omega ^{2}+Icdot omega cdot domega... (em inglês) Icdot omega ^{2}}
de modo que uma diminuição no momento de inércia requer investimento de energia.
Isso pode ser comparado ao trabalho realizado conforme calculado usando as leis de Newton. Cada ponto no corpo em rotação está acelerando, em cada ponto do tempo, com aceleração radial de:
- - Sim. - Sim. R)) ω ω 2{displaystyle -rcdot omega ^{2}}
Vamos observar um ponto de massa m, cujo vetor posição em relação ao centro do movimento é perpendicular ao eixo z em um determinado ponto do tempo e está a uma distância z. A força centrípeta neste ponto, mantendo o movimento circular, é:
- - Sim. - Sim. m)) zangão.)) ω ω 2{displaystyle -mcdot zcdot omega ^{2}}
Assim, o trabalho necessário para mover este ponto para uma distância dz mais longe do centro do movimento é:
- DW= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. m)) zangão.)) ω ω 2)) Dzangão.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. m)) ω ω 2)) D(12zangão.2)Não. dW=-mcdot zcdot omega ^{2}cdot dz=-mcdot omega ^{2}cdot dleft({frac {1}{2}}z^{2}right)}
Para um corpo não pontual deve-se integrar sobre isso, com m substituído pela densidade de massa por unidade z. Isto dá:
- DW= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. 12DEu...)) ω ω 2Não. DW... (em inglês) Icdot omega ^{2}}
que é exatamente a energia necessária para manter o momento angular conservado.
Observe que o cálculo acima também pode ser realizado por massa, usando apenas cinemática. Assim, o fenômeno do patinador artístico acelerando a velocidade tangencial ao puxar suas mãos pode ser entendido da seguinte forma na linguagem do leigo: as palmas das mãos do patinador não estão se movendo em linha reta, então elas estão constantemente acelerando para dentro, mas não ganham velocidade adicional porque a aceleração é sempre feita quando seu movimento para dentro é zero. No entanto, isso é diferente ao aproximar as palmas das mãos do corpo: a aceleração devido à rotação agora aumenta a velocidade; mas por causa da rotação, o aumento da velocidade não se traduz em uma velocidade significativa para dentro, mas em um aumento da velocidade de rotação.
No formalismo lagrangiano
Na mecânica lagrangiana, o impulso angular para rotação em torno de um determinado eixo, é o impulso conjugado da coordenada generalizada do ângulo em torno do mesmo eixo. Por exemplo, Lzangão.{displaystyle L_{z}}, o impulso angular em torno do eixo z, é:
- Lzangão.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∂ ∂ L∂ ∂ θ θ :: zangão.Não. L_{z}={frac {partial {cal {L}}}{partial {dot {theta} }}
Onde? L{displaystyle {cal {L}}} é o Lagrangian e θ θ zangão.{displaystyle theta _{z}} é o ângulo em torno do eixo z.
Note que θ θ :: zangão.- Não. }}_{z}}, o derivado do tempo do ângulo, é a velocidade angular ω ω zangão.{displaystyle omega _{z}}. Ordinariamente, o Lagrangian depende da velocidade angular através da energia cinética: Este último pode ser escrito separando a velocidade à sua parte radial e tangencial, com a parte tangencial no plano x-y, em torno do eixo z, sendo igual a:
- Gerenciamento Gerenciamento Eu...12mEu...vTEu...2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento Eu...12mEu...(xEu...2+Sim.Eu...2)ω ω zangão.Eu...2{displaystyle sum _{i}{frac {1}{2}}m_{i}{v_{T}}_{i}^{2}=sum _{i){frac {1}{2}}m_{i}(x_{i}^{2}+y_{i}^{2}){{omega _{z}}_{i}}^{2}}
onde o subscrito i representa o i-ésimo corpo, e m, vT e ωz significa massa, velocidade tangencial em torno do eixo z e velocidade angular em torno desse eixo, respectivamente.
Para um corpo que não é pontual, com densidade ρ, temos:
- 12∫ ∫ ? ? (x,Sim.,zangão.)(xEu...2+Sim.Eu...2)ω ω zangão.Eu...2DxDSim.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =12Eu...zangão.Eu...ω ω zangão.Eu...2{displaystyle {frac {1}{2}}int rho (x,y,z)(x_{i}^{2}+y_{i}^{2}){{omega _{z}}_{i}}^{2},dx,dy={frac {1}{2}}{I_{z}}_{i}{{omega _{z}}_{i}}^{2}}
onde a integração percorre a área do corpo, e Iz é o momento de inércia em torno do eixo z.
Assim, assumindo que a energia potencial não depende de ωz (essa suposição pode falhar para sistemas eletromagnéticos), temos o angular Momento do iº objeto:
- Lzangão.Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∂ ∂ L∂ ∂ ω ω zangão.Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∂ ∂ Ek∂ ∂ ω ω zangão.Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...zangão.Eu...)) ω ω zangão.Eu...{displaystyle {begin{aligned}{L_{z}}_{i}&={frac - Não. {L}}} Não. _{z}}_{i}}={frac {partial E_{k}}{partial Não. _{z}}_{i}}&={I_{z}}_{i}cdot Não. _{z}}_{i}end{aligned}}}
Até agora, rotacionamos cada objeto em um ângulo separado; também podemos definir um ângulo geral θz pelo qual giramos todo o sistema, girando também cada objeto em torno do eixo z e temos o momento angular geral:
- Lzangão.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento Eu...Eu...zangão.Eu...)) ω ω zangão.Eu...Não. L_{z}=sum _{i}{I_{z}}_{i}cdot Não. _{z}}_{i}}
Das equações de Euler-Lagrange segue-se que:
- 0= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∂ ∂ L∂ ∂ θ θ zangão.Eu...- Sim. - Sim. DD)(∂ ∂ L∂ ∂ θ θ :: zangão.Eu...)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∂ ∂ L∂ ∂ θ θ zangão.Eu...- Sim. - Sim. DLzangão.Eu...D)Não. 0={frac (particular) Não. _{z}}_{i}}}}-{frac {d}{dt}}left({frac {partial {cal} {L}}}partial {{{dot {theta} }}_{z}}_{i}}right)={frac {partial {cal} {L}}} Não. _{z}}_{i}}}} -{frac {d{L_{z}}_{i}}{dt}}}
Como o lagrangeano depende dos ângulos do objeto apenas por meio do potencial, temos:
- DLzangão.Eu...D)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∂ ∂ L∂ ∂ θ θ zangão.Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. ∂ ∂ V∂ ∂ θ θ zangão.Eu...Não. {d{L_{z}}_{i}}{dt}}={frac - Não. {L}}} Não. _{z}}_{i}}=-{frac - Não. Não. _{z}}_{i}}}
que é o torque no iésimo objeto.
Suponha que o sistema é invariante para rotações, de modo que o potencial é independente de uma rotação geral pelo ângulo θzangão. (assim pode depender dos ângulos dos objetos somente através de suas diferenças, na forma V(θ θ zangão.Eu...,θ θ zangão.JJ)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =V(θ θ zangão.Eu...- Sim. - Sim. θ θ zangão.JJ)(em inglês) _{z}}_{i},{theta _{z}}_{j}=V({theta) _{z}}_{i}-{theta _{z}}_{j})}). Portanto, chegamos para o impulso angular total:
- DLzangão.D)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. ∂ ∂ V∂ ∂ θ θ zangão.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0Não. {dL_{z}}{dt}}=-{frac - Não. - Não. _{z}}=0}
E assim o momento angular em torno do eixo z é conservado.
Esta análise pode ser repetida separadamente para cada eixo, dando uma conversa sobre o vetor de momento angular. Entretanto, os ângulos em torno dos três eixos não podem ser tratados simultaneamente como coordenadas generalizadas, pois não são independentes; em particular, dois ângulos por ponto são suficientes para determinar sua posição. Embora seja verdade que, no caso de um corpo rígido, descrevê-lo completamente requer, além de três graus de liberdade de translação, também a especificação de três graus de liberdade de rotação; no entanto, estes não podem ser definidos como rotações em torno dos eixos cartesianos (ver ângulos de Euler). Esta advertência é refletida na mecânica quântica nas relações de comutação não triviais dos diferentes componentes do operador de momento angular.
No formalismo hamiltoniano
Equivalentemente, na mecânica hamiltoniana, o hamiltoniano pode ser descrito como uma função do momento angular. Como antes, a parte da energia cinética relacionada à rotação em torno do eixo z para o iésimo objeto é:
- 12Eu...zangão.Eu...ω ω zangão.Eu...2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Lzangão.Eu...22Eu...zangão.Eu...Não. {1}{2}}{I_{z}}_{i}{{omega _{z}}_{i}}^{2}={frac {{{L_{z}}_{i}}^{2}}{2{1{I_{z}}_{i}}}}}}}}_{i}}}}
que é análogo à dependência energética do impulso ao longo do eixo z, pzangão.Eu...22mEu...Não. {{{p_{z}}_{i}}^{2}}{{2m}_{i}}}}}}}}.
As equações de Hamilton relacionam o ângulo em torno do eixo z ao seu momento conjugado, o momento angular em torno do mesmo eixo:
- Dθ θ zangão.Eu...D)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∂ ∂ H. H. H.∂ ∂ Lzangão.Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Lzangão.Eu...Eu...zangão.Eu...DLzangão.Eu...D)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. ∂ ∂ H. H. H.∂ ∂ θ θ zangão.Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. ∂ ∂ V∂ ∂ θ θ zangão.Eu...Não é verdade. _{z}}_{i}}{dt}}&={frac - Não. {H}}} {L_{z}}_{i}}}={frac {{L_{z}}_{i}}{{I_{z}}_{i}}}\{frac {d{L_{z}}_{i}}{dt}}&=-{frac - Não. {H}}} - Não. _{z}}_{i}}}=-{frac - Não. - Não. _{z}}_{i}}}end{aligned}}}
A primeira equação dá
- Lzangão.Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...zangão.Eu...)) θ θ :: zangão.Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...zangão.Eu...)) ω ω zangão.Eu...Não. {L_{z}}_{i}={I_{z}}_{i}cdot Não. }}_{z}}_{i}}={I_{z}}_{i}cdot Não. _{z}}_{i}}
E assim obtemos os mesmos resultados do formalismo lagrangiano.
Observe que, para combinar todos os eixos, escrevemos a energia cinética como:
- Ek= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =12Gerenciamento Gerenciamento Eu...|pEu...|22mEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento Eu...(pREu...22mEu...+12LEu...TEu...Eu...- Sim. - Sim. 1LEu...)Não. Erro: {1}{2}}sum _{i}{frac (em inglês) {{p}_{i}|^{2}}{2m_{i}}}=sum _{i}left({frac {{{p_{r}}_{i}}^{2}}{2m_{i}}}+{frac Não. {{L}_{i}}}^{textsf {T}}{I_{i}}^{-1}{bf {{L}_{i}}}right)}
onde pr é o momento na direção radial e o momento de inércia é uma matriz tridimensional; letras em negrito representam vetores tridimensionais.
Para corpos pontuais temos:
- Ek= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento Eu...(pREu...22mEu...+|LEu...|22mEu...REu...2){displaystyle E_{k}=sum _{i}left({frac {{{p_{r}}_{i}}^{2}}{2m_{i}}}+{frac (em inglês) {{L}_{i}}}|^{2}}{2m_{i}{r_{i}}^{2}}}right)}
Esta forma da parte da energia cinética do hamiltoniano é útil na análise de problemas de potencial central e é facilmente transformada em uma estrutura de trabalho da mecânica quântica (por exemplo, no problema do átomo de hidrogênio).
Momento angular na mecânica orbital
Embora na mecânica clássica a linguagem do momento angular possa ser substituída pelas leis do movimento de Newton, ela é particularmente útil para o movimento no potencial central, como o movimento planetário no sistema solar. Assim, a órbita de um planeta no sistema solar é definida por sua energia, momento angular e ângulos do eixo principal da órbita em relação a um referencial de coordenadas.
Na astrodinâmica e na mecânica celeste, uma quantidade intimamente relacionada ao momento angular é definida como
- h= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R× × v,{displaystyle mathbf {h} - Sim. times mathbf {v}}
chamado momentum angular específico. Note que L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =mh.{displaystyle mathbf {L} =mmathbf {h}.} A massa é muitas vezes sem importância nos cálculos da mecânica orbital, porque o movimento de um corpo é determinado pela gravidade. O corpo primário do sistema é muitas vezes muito maior do que qualquer corpo em movimento sobre ele que o efeito gravitacional dos corpos menores nele pode ser negligenciado; ele mantém, de fato, velocidade constante. O movimento de todos os corpos é afetado pela sua gravidade da mesma forma, independentemente da massa, e, portanto, todos movem-se aproximadamente da mesma maneira sob as mesmas condições.
Corpos sólidos
O momento angular também é um conceito extremamente útil para descrever corpos rígidos em rotação, como um giroscópio ou um planeta rochoso. Para uma distribuição de massa contínua com função de densidade ρ(r), um elemento de volume diferencial dV com vetor de posição r dentro da massa tem um elemento de massa dm = ρ(r)dV. Portanto, o momento angular infinitesimal deste elemento é:
- DL= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R× × Dmv= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R× × ? ? (R)DVv= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =DVR× × ? ? (R)v{displaystyle dmathbf {L} =mathbf {r}} times dmmathbf {v} - Sim. times rho (mathbf {r})d Vmathbf {v} =d Vmathbf {r} times rho (mathbf {r})mathbf {v} }
e integrando este diferencial sobre o volume de toda a massa dá o seu momento angular total:
- L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ VDVR× × ? ? (R)v{displaystyle mathbf] {L} =int _{V}dVmathbf {r} times rho (mathbf {r})mathbf {v} }
Na derivação a seguir, integrais semelhantes a esta podem substituir as somas para o caso de massa contínua.
Coleção de partículas
Para uma coleção de partículas em movimento sobre uma origem arbitrária, é informativo desenvolver a equação do momento angular resolvendo seu movimento em componentes sobre seu próprio centro de massa e sobre a origem. Dado,
- mEu...Não. m_{i}} é a massa de partícula Eu...Não.,
- REu...{displaystyle mathbf {R} _{i}} é o vetor de posição de partícula Eu...Não. A origem,
- VEu...{displaystyle mathbf] {V} _{i}} é a velocidade da partícula Eu...Não. A origem,
- R{displaystyle mathbf {R} } } é o vetor de posição do centro de massa w.r.t. a origem,
- V- Sim. é a velocidade do centro da massa w.r.t. a origem,
- REu...{displaystyle mathbf {r} _{i}} é o vetor de posição de partícula Eu...Não. w.r.t. o centro da massa,
- vEu...{displaystyle mathbf {v} _{i}} é a velocidade da partícula Eu...Não. w.r.t. o centro da massa,
A massa total das partículas é simplesmente sua soma,
- M= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento Eu...mEu....Não. M = _{i}m_{i}.}
O vetor posição do centro de massa é definido por,
- MR= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento Eu...mEu...REu....Não. Mmathbf Não. _{i}m_{i}mathbf {R} _{i}.}
Por inspeção,
- REu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R+REu...{displaystyle mathbf] {R} _{i}=mathbf (R) +mathbf {r} _{i}} e VEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =V+vEu....{displaystyle mathbf] {V} _{i}=mathbf (V) +mathbf _{i}.
O momento angular total da coleção de partículas é a soma do momento angular de cada partícula,
L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento Eu...(REu...× × mEu...VEu...){displaystyle mathbf] {L} =sum _{i}left(mathbf {R} _{i}times m_{i}mathbf {V} _{i}right)} (1)
Expansão REu...{displaystyle mathbf {R} _{i}},
- L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento Eu...Não.(R+REu...)× × mEu...VEu...]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento Eu...Não.R× × mEu...VEu...+REu...× × mEu...VEu...]{displaystyle {begin{aligned}mathbf] {L} &=sum _{i}left[left(mathbf {R} +mathbf {r} _{i}right)times m_{i}mathbf {V} _{i}right]&=sum _{i}left[mathbf] {R} times m_{i}mathbf {V} _{i}+mathbf {r} _{i}times m_{i}mathbf {V} _{i}right]end{aligned}}}
Expansão VEu...{displaystyle mathbf] {V} _{i}},
- L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento Eu...Não.R× × mEu...(V+vEu...)+REu...× × mEu...(V+vEu...)]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento Eu...Não.R× × mEu...V+R× × mEu...vEu...+REu...× × mEu...V+REu...× × mEu...vEu...]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento Eu...R× × mEu...V+Gerenciamento Gerenciamento Eu...R× × mEu...vEu...+Gerenciamento Gerenciamento Eu...REu...× × mEu...V+Gerenciamento Gerenciamento Eu...REu...× × mEu...vEu...{displaystyle {begin{aligned}mathbf] {L} &=sum _{i}left[mathbf {R} times m_{i}left(mathbf {V} +mathbf {v} _{i}right)+mathbf {r} _{i}times m_{i}(mathbf) {V} +mathbf {v} _{i})right]&=sum _{i}left[mathbf] {R} times m_{i}mathbf {V} +mathbf {R} times m_{i}mathbf {v} _{i}+mathbf {r} _{i}times m_{i}mathbf (V) +mathbf {r} _{i}times m_{i}mathbf {v} _{i}right]&=sum _{i}mathbf Tempos m_{i}mathbf {V} +sum _{i}mathbf {R} times m_{i}mathbf {v} _{i}+sum _{i}mathbf {r} _{i}times m_{i}mathbf {V} +sum _{i}mathbf {r} _{i}times m_{i}mathbf {v} _{i}end{aligned}}}
Pode ser mostrado que (veja a barra lateral),
Prove que Gerenciamento Gerenciamento Eu...mEu...REu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0{displaystyle sum _{i}m_{i}mathbf {r} _{i}=mathbf Não. REu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =REu...- Sim. - Sim. RmEu...REu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =mEu...(REu...- Sim. - Sim. R)Gerenciamento Gerenciamento Eu...mEu...REu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento Eu...mEu...(REu...- Sim. - Sim. R)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento Eu...(mEu...REu...- Sim. - Sim. mEu...R)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento Eu...mEu...REu...- Sim. - Sim. Gerenciamento Gerenciamento Eu...mEu...R= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento Eu...mEu...REu...- Sim. - Sim. (Gerenciamento Gerenciamento Eu...mEu...)R= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento Eu...mEu...REu...- Sim. - Sim. MR(em inglês) _{i}&=mathbf {R} _{i}-mathbf {R} \m_{i}mathbf {r}} _{i}&=m_{i}left(mathbf {R} _{i}-mathbf {R} right)\\sum _{i}m_{i}mathbf {r} _{i}&=sum _{i}m_{i}left(mathbf {R} _{i}-mathbf {R} right)&=sum _{i}(m_{i}mathbf {R} _{i}-m_{i}mathbf {R})\&=sum _{i}m_{i}mathbf {R} _{i}-sum _{i}m_{i}mathbf {R} \&=sum _{i}m_{i}mathbf {R} _{i}-left(sum _{i}m_{i}right)mathbf {R} \&=sum _{i}m_{i}mathbf {R} _{i}-Mmathbf {R} end{aligned}}} que, pela definição do centro de massa, é 0,{displaystyle mathbf {0}} e similarmente para Gerenciamento Gerenciamento Eu...mEu...vEu....{displaystyle sum _{i}m_{i}mathbf {v} _{i}.} |
- Gerenciamento Gerenciamento Eu...mEu...REu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0{displaystyle sum _{i}m_{i}mathbf {r} _{i}=mathbf Não. e Gerenciamento Gerenciamento Eu...mEu...vEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0,{displaystyle sum _{i}m_{i}mathbf {v} _{i}=mathbf {0}
portanto, o segundo e terceiro termos desaparecem,
- L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento Eu...R× × mEu...V+Gerenciamento Gerenciamento Eu...REu...× × mEu...vEu....{displaystyle mathbf] {L} =sum _{i}mathbf {R} times m_{i}mathbf {V} +sum _{i}mathbf {r} _{i}times m_{i}mathbf {v} _{i}.}
O primeiro termo pode ser reorganizado,
- Gerenciamento Gerenciamento Eu...R× × mEu...V= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R× × Gerenciamento Gerenciamento Eu...mEu...V= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R× × MV,{displaystyle sum _{i}mathbf] {R} times m_{i}mathbf {V} =mathbf {R} times sum _{i}m_{i}mathbf {V} =mathbf {R} times Mmathbf {V}}
e o momento angular total para a coleção de partículas é, finalmente,
L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R× × MV+Gerenciamento Gerenciamento Eu...REu...× × mEu...vEu...{displaystyle mathbf] (L) Tempos Mmathbf {V} +sum _{i}mathbf {r} _{i}times m_{i}mathbf {v} _{i}} (2)
O primeiro termo é o momento angular do centro de massa em relação à origem. Semelhante a § Partícula única, abaixo, é o momento angular de uma partícula de massa M no centro de massa movendo-se com velocidade V. O segundo termo é o momento angular das partículas que se movem em relação ao centro de massa, semelhante a § Centro de massa fixo, abaixo. O resultado é geral - o movimento das partículas não está restrito à rotação ou revolução em torno da origem ou centro de massa. As partículas não precisam ser massas individuais, mas podem ser elementos de uma distribuição contínua, como um corpo sólido.
Reorganizando a equação (2) por identidades vetoriais, multiplicando ambos os termos por "um" e agrupando adequadamente,
- L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =M(R× × V)+Gerenciamento Gerenciamento Eu...Não.mEu...(REu...× × vEu...)],= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R2R2M(R× × V)+Gerenciamento Gerenciamento Eu...Não.REu...2REu...2mEu...(REu...× × vEu...)],= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R2M(R× × VR2)+Gerenciamento Gerenciamento Eu...Não.REu...2mEu...(REu...× × vEu...REu...2)],{displaystyle {begin{aligned}mathbf] (L) > {R} times mathbf {V})+sum _{i}left[m_{i}left(mathbf {r} _{i}times mathbf {v} _{i}right)right],&={frac {R^{2}}{R^{2}}}Mleft(mathbf {R} times mathbf {V} right)+sum _{i}left[{frac {r_{i}^{2}}{r_{i}^{2}}}m_{i}left(mathbf {r} _{i}times mathbf {v} _{i}right)right],&=R^{2}Mleft({frac {mathbf {R} times mathbf {V} }{R^{2}}}right)+sum _{i}left[r_{i}^{2}m_{i}left({frac Não. _{i}times mathbf {v} _{i}}{r_{i}^{2}}}right]right],\end{aligned}}}
dá o impulso angular total do sistema de partículas em termos de momento de inércia Eu...Não. Eu... e velocidade angular ω ω O que é isso?),
L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...Rω ω R+Gerenciamento Gerenciamento Eu...Eu...Eu...ω ω Eu....{displaystyle mathbf {L} =I_{R}{boldsymbol Não. }}_{R}+sum _{i}I_{i} Não. }}_{i}.} (3)
Caso de partícula única
No caso de uma única partícula se movendo em torno de uma origem arbitrária,
- REu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =vEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0,R= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R,v= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =V,m= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =M,(em inglês) _{i}&=mathbf {v} _{i}=mathbf {0}\mathbf {r} &=mathbf {R}\mathbf {v} &=mathbf {V}\m&=M,end{aligned}}}
- Gerenciamento Gerenciamento Eu...REu...× × mEu...vEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0,{displaystyle sum _{i}mathbf {r}} _{i}times m_{i}mathbf {v} _{i}=mathbf {0}
- Gerenciamento Gerenciamento Eu...Eu...Eu...ω ω Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0,{displaystyle sum _{i}I_{i} Não. }}_{i}=mathbf {0} e equações (2) e3) para a redução total do impulso angular,
- L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R× × mV= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...Rω ω R.{displaystyle mathbf {L} =mathbf {R} times mmathbf (V} = I_{R} Não. }}_{R}.}
Caso de um centro de massa fixo
Para o caso do centro de massa fixo no espaço em relação à origem,
- V= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0,{displaystyle mathbf] {V} =mathbf {0}}
- R× × MV= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0,{displaystyle mathbf {R} times Mmathbf {V} =mathbf {0}}
- Eu...Rω ω R= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0,Não. I_{R} Não. }}_{R}=mathbf {0}} e equações (2) e3) para a redução total do impulso angular,
- L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento Eu...REu...× × mEu...vEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento Eu...Eu...Eu...ω ω Eu....{displaystyle mathbf] {L} =sum _{i}mathbf {r} _{i}times m_{i}mathbf {v} _{i}=sum _{i}I_{i} Não. }}_{i}.}
Momento angular na relatividade geral
Na física teórica moderna (século 20), o momento angular (sem incluir qualquer momento angular intrínseco - veja abaixo) é descrito usando um formalismo diferente, em vez de um pseudovetor clássico. Nesse formalismo, o momento angular é a carga de Noether de 2 formas associada à invariância rotacional. Como resultado, o momento angular não é conservado para espaços-tempos curvos gerais, a menos que seja assintoticamente rotacionalmente invariante.
Na mecânica clássica, o momento angular de uma partícula pode ser reinterpretado como um elemento plano:
- L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R∧ ∧ p,{displaystyle mathbf {L} =mathbf {r} wedge mathbf {p} ,}
em que o produto externo (∧) substitui o produto vetorial (×) (esses produtos têm características semelhantes, mas não são equivalentes). Isso tem a vantagem de uma interpretação geométrica mais clara como um elemento plano, definido usando os vetores x e p, e a expressão é verdadeira em qualquer número de dimensões. Em coordenadas cartesianas:
- L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(xpSim.- Sim. - Sim. Sim.px)ex∧ ∧ eSim.+(Sim.pzangão.- Sim. - Sim. zangão.pSim.)eSim.∧ ∧ ezangão.+(zangão.px- Sim. - Sim. xpzangão.)ezangão.∧ ∧ ex= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =LxSim.ex∧ ∧ eSim.+LSim.zangão.eSim.∧ ∧ ezangão.+Lzangão.xezangão.∧ ∧ ex,{displaystyle {begin{aligned}mathbf] {L} &=left(xp_{y}-yp_{x}right)mathbf {e} _{x}wedge mathbf {e} _{y}+left (yp_{z}-zp_{y}right)mathbf {e} _{y}wedge mathbf {e} _{z}+left(zp_{x}-xp_{z}right)mathbf {e} _{z}wedge mathbf {e} _{x}\&=L_{xy}mathbf {e} _{x}wedge mathbf {e} _{y}+L_{yz}mathbf {e} _{y}wedge mathbf {e} _{z}+L_{zx}mathbf {e} _{z}wedge mathbf {e} _{x},end{aligned}}}
ou de forma mais compacta na notação de índice:
- LEu...JJ= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =xEu...pJJ- Sim. - Sim. xJJpEu....Não. L_{ij}=x_{i}p_{j}-x_{j}p_{i},.}
A velocidade angular também pode ser definida como um tensor antissimétrico de segunda ordem, com componentes ωij. A relação entre os dois tensores antissimétricos é dada pelo momento de inércia que agora deve ser um tensor de quarta ordem:
- LEu...JJ= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...Eu...JJkEu... Eu... ω ω kEu... Eu... .Não. L_{ij}=I_{ijkell }omega _{kell },.}
Novamente, esta equação em L e ω como tensores é verdadeira em qualquer número de dimensões. Essa equação também aparece no formalismo da álgebra geométrica, em que L e ω são bivetores, e o momento de inércia é um mapeamento entre eles.
Na mecânica relativística, o momento angular relativístico de uma partícula é expresso como um tensor antissimétrico de segunda ordem:
- Mα α β β = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Xα α Pβ β - Sim. - Sim. Xβ β Pα α Não. M_{alpha beta - Sim. - Sim. ?)
em termos de quatro vetores, ou seja, o X de quatro posições e o P de quatro momentos, e absorve o L acima juntos com o momento de massa, ou seja, o produto da massa relativística da partícula e seu centro de massa, que pode ser pensado como descrevendo o movimento de seu centro de massa, uma vez que massa-energia é conservada.
Em cada um dos casos acima, para um sistema de partículas, o momento angular total é apenas a soma dos momentos angulares individuais das partículas, e o centro de massa é para o sistema.
Momento angular na mecânica quântica
Na mecânica quântica, o momento angular (como outras quantidades) é expresso como um operador e suas projeções unidimensionais têm autovalores quantizados. O momento angular está sujeito ao princípio da incerteza de Heisenberg, implicando que, a qualquer momento, apenas uma projeção (também chamada de "componente") pode ser medida com precisão definida; os outros dois permanecem incertos. Por causa disso, o eixo de rotação de uma partícula quântica é indefinido. As partículas quânticas do possuem um tipo de momento angular não orbital chamado "spin", mas esse momento angular não corresponde a um movimento giratório. Na mecânica quântica relativística, a definição relativística acima torna-se um operador tensorial.
Spin, orbital e momento angular total

- Esquerda: "spin" momentum angular S é realmente orbital momento angular do objeto em cada ponto.
- Certo. momentum angular orbital extrínseco L sobre um eixo.
- Topo: o momento de inércia tensor Eu... e velocidade angular ω (L não é sempre paralelo ω).
- Parte de baixo: momento p e sua posição radial R do eixo. O impulso angular total (pin plus orbital) é JJ. Para um Quântico quântico partícula as interpretações são diferentes; o spin de partículas faz não tem a interpretação acima.
A definição clássica de impulso angular como L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R× × p{displaystyle mathbf {L} =mathbf {r}} times mathbf {p} } pode ser transportado para a mecânica quântica, por reinterpretação R como o operador de posição quântica e p como operador de momentum quântico. L é então um operador, especificamente chamado de operador de momentum angular orbital. Os componentes do operador de momentum angular satisfazem as relações de comutação da álgebra de Lie assim(3). De fato, esses operadores são precisamente a ação infinitesimal do grupo de rotação no espaço quântico Hilbert. (Ver também a discussão abaixo dos operadores de impulso angular como geradores de rotações.)
No entanto, na física quântica, existe outro tipo de momento angular, chamado momento angular de spin, representado pelo operador de spin S. O spin é frequentemente descrito como uma partícula literalmente girando em torno de um eixo, mas esta é uma imagem enganosa e imprecisa: o spin é uma propriedade intrínseca de uma partícula, não relacionada a qualquer tipo de movimento no espaço e fundamentalmente diferente do momento angular orbital. Todas as partículas elementares têm um spin característico (possivelmente zero), e quase todas as partículas elementares têm spin diferente de zero. Por exemplo, os elétrons têm "spin 1/2" (isso na verdade significa "spin ħ/2"), os fótons têm "spin 1" (isso na verdade significa "spin ħ"), e os mésons pi têm spin 0.
Finalmente, há o momento angular total J, que combina o spin e o momento angular orbital de todas as partículas e campos. (Para uma partícula, J = L + S.) Aplica-se a conservação do momento angular para J, mas não para L ou S; por exemplo, a interação spin-órbita permite que o momento angular seja transferido para frente e para trás entre L e S, com o total restante constante. Elétrons e fótons não precisam ter valores inteiros para o momento angular total, mas também podem ter valores semi-inteiros.
Em moléculas, o momento angular total F é a soma do momento angular rovibrônico (orbital) N, o momento angular de spin do elétron S, e o momento angular de spin nuclear I. Para estados singletos eletrônicos, o momento angular rovibrônico é denotado J em vez de N. Conforme explicado por Van Vleck, os componentes do momento angular rovibrônico molecular referidos aos eixos fixos na molécula têm relações de comutação diferentes daquelas para os componentes sobre eixos fixos no espaço.
Quantização
Na mecânica quântica, o momentum angular é quantificado – ou seja, não pode variar continuamente, mas apenas em "saltos quânticos" entre certos valores permitidos. Para qualquer sistema, aplicam-se as seguintes restrições aos resultados de medição, quando ? ? - Sim. é a constante de Planck reduzida e n^ ^ - Sim. é qualquer vetor euclidiano, como x, y, ou z:
| Se medires... | O resultado pode ser... |
| Ln^ ^ (n) | ...... ,- Sim. - Sim. 2? ? ,- Sim. - Sim. ? ? ,0,? ? ,2? ? ,...... {displaystyle ldots-2hbar-hbar0,hbar2hbarldots } |
| Sn^ ^ (n}}} ou JJn^ ^ (n) | ...... ,- Sim. - Sim. 32? ? ,- Sim. - Sim. ? ? ,- Sim. - Sim. 12? ? ,0,12? ? ,? ? ,32? ? ,...... {displaystyle ldots-{frac {3}{2}}hbar-hbar-{frac {1}{2}}hbar0,{frac {1}{2}hbarhbar{frac {3}{2}}hbarldots } |
| L2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Lx2+LSim.2+Lzangão.2{displaystyle {begin{aligned}&L^{2}\={}&L_{x}^{2}+L_{y}^{2}+L_{z}^{2}end{aligned}}} | Não.? ? 2n(n+1)]{displaystyle left[hbar ^{2}n(n+1)right]}, onde n= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0,1,2,...... } |
| S2{displaystyle S^{2}} ou JJ2Não. J^{2}} | Não.? ? 2n(n+1)]{displaystyle left[hbar ^{2}n(n+1)right]}, onde n= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0,12,1,32,...... {displaystyle n=0,{frac {1}{2}},1,{frac {3}{2}},ldots } |

A constante de Planck reduzida ? ? - Sim. é minúsculo por padrões diários, cerca de 10- 34. J s, e, portanto, esta quantificação não afeta notavelmente o impulso angular de objetos macroscópicos. No entanto, é muito importante no mundo microscópico. Por exemplo, a estrutura de conchas de elétrons e subvenções em química é significativamente afetada pela quantificação do impulso angular.
A quantização do momento angular foi postulada pela primeira vez por Niels Bohr em seu modelo do átomo e mais tarde foi prevista por Erwin Schrödinger em sua equação de Schrödinger.
Incerteza
Na definição L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R× × p{displaystyle mathbf {L} =mathbf {r}} times mathbf {p} }, seis operadores estão envolvidos: Os operadores de posição Rx{displaystyle r_{x}}, RSim.Não. r_{y}}, Rzangão.{displaystyle r_{z}}, e os operadores momentum px{displaystyle p_{x}}, pSim.Não. p_{y}}, pzangão.{displaystyle p_{z}}. No entanto, o princípio de incerteza de Heisenberg nos diz que não é possível que todas as seis dessas quantidades sejam conhecidas simultaneamente com precisão arbitrária. Portanto, há limites para o que pode ser conhecido ou medido sobre o impulso angular de uma partícula. Acontece que o melhor que se pode fazer é medir simultaneamente a magnitude do vetor de impulso angular e seu componente ao longo de um eixo.
A incerteza está intimamente relacionada com o fato de que diferentes componentes de um operador de momentum angular não comutam, por exemplo LxLSim.≠ ≠ LSim.LxNão. L_{x}L_{y}neq L_{y}L_{x}}. (Para as relações de comutação precisas, veja o operador de momentum angular.)
Momento angular total como gerador de rotações
Como mencionado acima, momentum angular orbital L é definido como na mecânica clássica: L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R× × p{displaystyle mathbf {L} =mathbf {r}} times mathbf {p} }, mas total momentum angular JJ é definido de uma forma diferente, mais básica: JJ é definido como o "gerador de rotações". Mais especificamente, JJ é definido para que o operador
- R(n^ ^ ,φ φ ))) exp (- Sim. - Sim. Eu...? ? φ φ JJ)) n^ ^ ){displaystyle R({hat {n}},phi)equiv exp left(-{frac {i}{hbar }}phi ,mathbf {J} cdot {hat {mathbf {n} }}right)}
é o operador de rotação que leva qualquer sistema e gira-lo por ângulo φ φ - Sim. sobre o eixo n^ ^ Não.). (O "exp" na fórmula refere-se ao operador exponencial) Para colocar isso da outra maneira ao redor, seja qual for o nosso espaço quântico Hilbert, esperamos que o grupo de rotação SO(3) aja nele. Há então uma ação associada da álgebra de Lie assim(3) de SO(3); os operadores que descrevem a ação de assim(3) em nosso espaço de Hilbert são os operadores de momentum angular (total).
A relação entre o operador de momento angular e os operadores de rotação é a mesma que a relação entre álgebras de Lie e grupos de Lie em matemática. A estreita relação entre o momento angular e as rotações é refletida no teorema de Noether, que prova que o momento angular é conservado sempre que as leis da física são rotacionalmente invariantes.
Momento angular em eletrodinâmica
Ao descrever o movimento de uma partícula carregada em um campo eletromagnético, o momento canônico P (derivado do Lagrangeano para este sistema) não é invariante de calibre. Como consequência, o momento angular canônico L = r × P também não é invariante de calibre. Em vez disso, o momento físico, o chamado momento cinético (usado ao longo deste artigo), é (em unidades do SI)
- p= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =mv= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =P- Sim. - Sim. eA{displaystyle mathbf {p} - Sim. ?
onde e é a carga elétrica da partícula e A o potencial vetorial magnético do campo eletromagnético. O momento angular invariante de calibre, ou seja, momento angular cinético, é dado por
- KK= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R× × (P- Sim. - Sim. eA){displaystyle mathbf {K} =mathbf {r} times (mathbf {P} -emathbf {A})}
A interação com a mecânica quântica é discutida mais adiante no artigo sobre relações de comutação canônica.
Momento angular em óptica
Na eletrodinâmica clássica de Maxwell, o vetor de Poynting é uma densidade de momento linear do campo eletromagnético.
- S(R,))= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =ε ε 0c2E(R,))× × B(R,)).{displaystyle mathbf] (S} (mathbf {r}t)=epsilon _{0}c^{2}mathbf {E} (mathbf {r}t)times mathbf {B} (mathbf {r}t). ?
O vetor de densidade de impulso angular L(R,)){displaystyle mathbf {L} (mathbf {r}t)} é dado por um produto vetorial como na mecânica clássica:
- Eu...(R,))= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =ε ε 0μ μ 0R× × S(R,)).{displaystyle mathbf {l} (mathbf {r}t)=epsilon _{0}mu _{0}mathbf {r} times mathbf {S} (mathbf {r}t). ?
As identidades acima são válidas localmente, ou seja, em cada ponto espacial R- Sim. em um determinado momento )Não..
Momento angular na natureza e no cosmos
Ciclones tropicais e outros fenômenos climáticos relacionados envolvem a conservação do momento angular para explicar a dinâmica. Os ventos giram lentamente em torno de sistemas de baixa pressão, principalmente devido ao efeito Coriolis. Se a baixa pressão se intensifica e o ar que circula lentamente é atraído para o centro, as moléculas devem acelerar para conservar o momento angular. Quando chegam ao centro, as velocidades tornam-se destrutivas.
Johannes Kepler determinou as leis do movimento planetário sem conhecimento da conservação do momento. No entanto, não muito depois de sua descoberta, sua derivação foi determinada a partir da conservação do momento angular. Os planetas se movem mais lentamente quanto mais longe estão em suas órbitas elípticas, o que é explicado intuitivamente pelo fato de que o momento angular orbital é proporcional ao raio da órbita. Como a massa não varia e o momento angular é conservado, a velocidade diminui.
A aceleração das marés é um efeito das forças das marés entre um satélite natural em órbita (por exemplo, a Lua) e o planeta principal que orbita (por exemplo, a Terra). O torque gravitacional entre a Lua e a protuberância de maré da Terra faz com que a Lua seja constantemente promovida a uma órbita ligeiramente mais alta e a Terra seja desacelerada em sua rotação. A Terra perde o momento angular que é transferido para a Lua de tal forma que o momento angular total é conservado.
Momento angular em engenharia e tecnologia
Exemplos de uso da conservação do momento angular para vantagens práticas são abundantes. Em motores como motores a vapor ou motores de combustão interna, um volante é necessário para converter com eficiência o movimento lateral dos pistões em movimento rotacional.
Sistemas de navegação inercial usam explicitamente o fato de que o momento angular é conservado em relação ao referencial inercial do espaço. A navegação inercial é o que permite viagens submarinas sob a calota polar, mas também é crucial para todas as formas de navegação moderna.
As balas estriadas usam a estabilidade fornecida pela conservação do momento angular para serem mais verdadeiras em sua trajetória. A invenção de armas de fogo e canhões com rifles deu aos seus usuários uma vantagem estratégica significativa na batalha e, portanto, foi um ponto de virada tecnológico na história.
História
Isaac Newton, no Principia, sugeriu o momento angular em seus exemplos da primeira lei do movimento,
Uma parte superior, cujas partes por sua coesão são perpetuamente retiradas de movimentos retilineares, não cessa sua rotação, senão como é retardada pelo ar. Os corpos maiores dos planetas e cometas, reunidos com menos resistência em espaços mais livres, preservam seus movimentos tanto progressivos quanto circulares por muito mais tempo.
Ele não investigou mais o momento angular diretamente no Principia, dizendo:
De tal tipo de reflexões também às vezes surgem os movimentos circulares de corpos sobre seus próprios centros. Mas estes são casos que eu não considero no que se segue; e seria demasiado tedioso demonstrar cada particular que se relaciona com este assunto.
No entanto, sua prova geométrica da lei das áreas é um excelente exemplo da genialidade de Newton e prova indiretamente a conservação do momento angular no caso de uma força central.
A Lei das Áreas
Derivação de Newton
Conforme um planeta orbita o Sol, a linha entre o Sol e o planeta varre áreas iguais em intervalos de tempo iguais. Isso era conhecido desde que Kepler expôs sua segunda lei do movimento planetário. Newton derivou uma prova geométrica única e passou a mostrar que a força de atração da gravidade do Sol era a causa de todas as leis de Kepler.
Durante o primeiro intervalo de tempo, um objeto está em movimento do ponto A ao ponto B. Imperturbável, continuaria a apontar c durante o segundo intervalo. Quando o objeto chega em B, ele recebe um impulso direcionado para o ponto S. O impulso dá a ele uma pequena velocidade adicional em direção a S, de modo que, se essa fosse sua única velocidade, ele se moveria de B para V durante o segundo intervalo. Pelas regras de composição de velocidade, essas duas velocidades se somam e o ponto C é encontrado pela construção do paralelogramo BcCV. Assim, o caminho do objeto é desviado pelo impulso para que ele chegue ao ponto C no final do segundo intervalo. Porque os triângulos SBc e SBC têm a mesma base SB e a mesma altura Bc ou VC, eles têm a mesma área. Por simetria, o triângulo SBc também tem a mesma área que o triângulo SAB, portanto o objeto varreu áreas iguais SAB e SBC em tempos iguais.
No ponto C, o objeto recebe outro impulso em direção a S, novamente desviando sua trajetória durante o terceiro intervalo de d para D. Assim continua para E e além, os triângulos SAB, SBc, SBC, SCd, SCD, SDe, SDE todos com a mesma área. Permitindo que os intervalos de tempo se tornem cada vez menores, o caminho ABCDE aproxima-se indefinidamente de uma curva contínua.
Observe que, como essa derivação é geométrica e nenhuma força específica é aplicada, ela prova uma lei mais geral do que a segunda lei do movimento planetário de Kepler. Mostra que a Lei das Áreas se aplica a qualquer força central, atrativa ou repulsiva, contínua ou descontínua, ou nula.
Conservação do momento angular na Lei das Áreas
A proporcionalidade do momento angular com a área varrida por um objeto em movimento pode ser entendida percebendo que as bases dos triângulos, ou seja, as linhas de S ao objeto, são equivalentes a o raio r, e que as alturas dos triângulos são proporcionais à componente perpendicular da velocidade v⊥. Portanto, se a área varrida por unidade de tempo for constante, então pela fórmula da área triangular 1/2(base)(altura), o produto (base)(height) e, portanto, o produto rv⊥ são constantes: se r e o comprimento base forem diminuídos, v⊥ e a altura devem aumentar proporcionalmente. A massa é constante, portanto o momento angular rmv⊥ é conservado por esta troca de distância e velocidade.
No caso do triângulo SBC, a área é igual a 1/2(SB)(VC). Onde quer que C seja eventualmente localizado devido ao impulso aplicado em B, o produto (SB)(VC), e, portanto, rmv⊥ permanecem constantes. Da mesma forma para cada um dos triângulos.
Depois de Newton
Leonhard Euler, Daniel Bernoulli e Patrick d'Arcy entenderam o momento angular em termos de conservação da velocidade de área, resultado de sua análise da segunda lei de Kepler do movimento planetário. É improvável que eles tenham percebido as implicações para a matéria rotativa comum.
Em 1736, Euler, como Newton, tocou em algumas das equações do momento angular em sua Mechanica sem mais desenvolvê-las.
Bernoulli escreveu em uma carta de 1744 sobre um "momento de movimento rotacional", possivelmente a primeira concepção de momento angular como o entendemos agora.
Em 1799, Pierre-Simon Laplace percebeu pela primeira vez que um plano fixo estava associado à rotação - seu plano invariável.
Louis Poinsot em 1803 começou a representar rotações como um segmento de linha perpendicular à rotação e elaborou a "conservação de momentos".
Em 1852, Léon Foucault usou um giroscópio em um experimento para exibir a rotação da Terra.
O Manual of Applied Mechanics de William J. M. Rankine de 1858 definiu o momento angular no sentido moderno pela primeira vez:
... uma linha cujo comprimento é proporcional à magnitude do impulso angular, e cuja direção é perpendicular ao plano de movimento do corpo e do ponto fixo, e tal, que quando o movimento do corpo é visto da extremidade da linha, o raio-vetor do corpo parece ter rotação de direita.
Em uma edição de 1872 do mesmo livro, Rankine afirmou que "O termo momento angular foi introduzido pelo Sr. Hayward," provavelmente referindo-se ao artigo de R.B. Hayward Sobre um método direto de estimar velocidades, acelerações e todas as quantidades semelhantes com respeito a eixos móveis de qualquer maneira no espaço com aplicações, que foi introduzido em 1856, e publicado em 1864. Rankine estava enganado, pois várias publicações apresentam o termo começando no final do século 18 e início do século 19. No entanto, o artigo de Hayward aparentemente foi o primeiro uso do termo e do conceito visto por grande parte do mundo de língua inglesa. Antes disso, o momento angular era normalmente referido como "momento de rotação" Em inglês.
Contenido relacionado
Movimento browniano
Teorema de mapeamento de Riemann
Contador Geiger


























































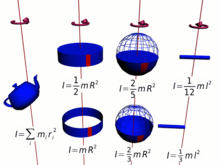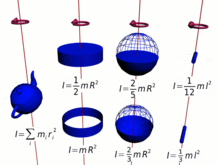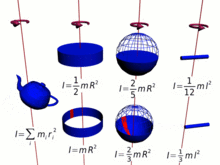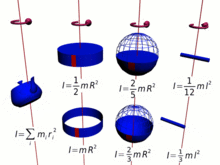



























































![{displaystyle {begin{aligned}mathbf {L} &=sum _{i}left[left(mathbf {R} +mathbf {r} _{i}right)times m_{i}mathbf {V} _{i}right]\&=sum _{i}left[mathbf {R} times m_{i}mathbf {V} _{i}+mathbf {r} _{i}times m_{i}mathbf {V} _{i}right]end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77077ef30b49ac992b78c6a4c6446709bb1720a9)
![{displaystyle {begin{aligned}mathbf {L} &=sum _{i}left[mathbf {R} times m_{i}left(mathbf {V} +mathbf {v} _{i}right)+mathbf {r} _{i}times m_{i}(mathbf {V} +mathbf {v} _{i})right]\&=sum _{i}left[mathbf {R} times m_{i}mathbf {V} +mathbf {R} times m_{i}mathbf {v} _{i}+mathbf {r} _{i}times m_{i}mathbf {V} +mathbf {r} _{i}times m_{i}mathbf {v} _{i}right]\&=sum _{i}mathbf {R} times m_{i}mathbf {V} +sum _{i}mathbf {R} times m_{i}mathbf {v} _{i}+sum _{i}mathbf {r} _{i}times m_{i}mathbf {V} +sum _{i}mathbf {r} _{i}times m_{i}mathbf {v} _{i}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4784bd78e4066783f47bd72472bfa49a0887b0bf)








![{displaystyle {begin{aligned}mathbf {L} &=M(mathbf {R} times mathbf {V})+sum _{i}left[m_{i}left(mathbf {r} _{i}times mathbf {v} _{i}right)right],\&={frac {R^{2}}{R^{2}}}Mleft(mathbf {R} times mathbf {V} right)+sum _{i}left[{frac {r_{i}^{2}}{r_{i}^{2}}}m_{i}left(mathbf {r} _{i}times mathbf {v} _{i}right)right],\&=R^{2}Mleft({frac {mathbf {R} times mathbf {V} }{R^{2}}}right)+sum _{i}left[r_{i}^{2}m_{i}left({frac {mathbf {r} _{i}times mathbf {v} _{i}}{r_{i}^{2}}}right)right],\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5324c7fa7e5e94893f678fab046c2538416bc51)


























![{displaystyle left[hbar ^{2}n(n+1)right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd720bdca13e8588818fb477347fb90c9789bb4a)