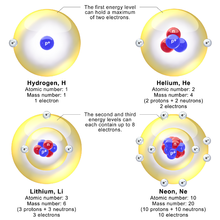
Modelo Bohr

Na física atômica, o modelo de Bohr ou modelo de Rutherford-Bohr do átomo, apresentado por Niels Bohr e Ernest Rutherford em 1913, consiste em um núcleo pequeno e denso cercado por elétrons em órbita. É análoga à estrutura do Sistema Solar, mas com atração fornecida pela força eletrostática ao invés da gravidade. Na história da física atômica, ele seguiu e finalmente substituiu vários modelos anteriores, incluindo o modelo do sistema solar de Joseph Larmor (1897), o modelo de Jean Perrin (1901), o modelo cúbico (1902), Modelo saturniano de Hantaro Nagaoka (1904), modelo do pudim de passas (1904), modelo quântico de Arthur Haas (1910), modelo de Rutherford (1911) e modelo quântico nuclear de John William Nicholson (1912). A melhoria em relação ao modelo de Rutherford de 1911 dizia respeito principalmente à nova interpretação da mecânica quântica introduzida por Haas e Nicholson, mas abandonando qualquer tentativa de explicar a radiação de acordo com a física clássica.
O principal sucesso do modelo está em explicar a fórmula de Rydberg para as linhas de emissão espectral do hidrogênio. Embora a fórmula de Rydberg fosse conhecida experimentalmente, ela não ganhou uma base teórica até que o modelo de Bohr foi introduzido. O modelo de Bohr não apenas explicou as razões para a estrutura da fórmula de Rydberg, mas também forneceu uma justificativa para as constantes físicas fundamentais que compõem os resultados empíricos da fórmula.
O modelo de Bohr é um modelo relativamente primitivo do átomo de hidrogênio, comparado ao modelo de camada de valência. Como teoria, pode ser derivada como uma aproximação de primeira ordem do átomo de hidrogênio usando a mecânica quântica mais ampla e muito mais precisa e, portanto, pode ser considerada uma teoria científica obsoleta. No entanto, por causa de sua simplicidade e seus resultados corretos para sistemas selecionados (veja abaixo para aplicação), o modelo de Bohr ainda é comumente ensinado para introduzir os alunos à mecânica quântica ou diagramas de nível de energia antes de passar para o mais preciso, mas mais complexo, átomo de camada de valência. Um modelo quântico relacionado foi proposto por Arthur Erich Haas em 1910, mas foi rejeitado até o Congresso Solvay de 1911, onde foi amplamente discutido. A teoria quântica do período entre a descoberta do quantum por Planck (1900) e o advento de uma mecânica quântica madura (1925) é frequentemente referida como a antiga teoria quântica.
Origem
No início do século 20, experimentos de Ernest Rutherford estabeleceram que os átomos consistiam em uma nuvem difusa de elétrons carregados negativamente em torno de um núcleo pequeno, denso e carregado positivamente. Dados esses dados experimentais, Rutherford naturalmente considerou um modelo planetário do átomo, o modelo de Rutherford de 1911. Este tinha elétrons orbitando um núcleo solar, mas envolvia uma dificuldade técnica: as leis da mecânica clássica (isto é, a fórmula de Larmor) predizem que o elétron liberará radiação eletromagnética enquanto orbita um núcleo. Como o elétron perderia energia, ele rapidamente espiralaria para dentro, colapsando no núcleo em uma escala de tempo de cerca de 16 picossegundos. O modelo atômico de Rutherford é desastroso porque prevê que todos os átomos são instáveis. Além disso, à medida que o elétron espirala para dentro, a emissão aumentaria rapidamente em frequência devido ao período orbital se tornar mais curto, resultando em radiação eletromagnética com um espectro contínuo. No entanto, experimentos do final do século 19 com descargas elétricas mostraram que os átomos só emitem luz (isto é, radiação eletromagnética) em certas frequências discretas. No início do século XX, esperava-se que o átomo explicasse as linhas espectrais. Em 1897, Lord Rayleigh analisou o problema. Em 1906, Rayleigh disse, “as frequências observadas no espectro podem não ser frequências de perturbação ou de oscilação no sentido comum, mas sim formar uma parte essencial da constituição original do átomo conforme determinado pelas condições de estabilidade”.
O esboço do átomo de Bohr veio durante os trabalhos da primeira Conferência Solvay em 1911 sobre o tema da Radiação e Quanta, no qual Rutherford estava presente. A palestra de Max Planck terminou com esta observação: “... átomos ou elétrons sujeitos ao vínculo molecular obedeceriam às leis da teoria quântica”. Hendrik Lorentz na discussão da palestra de Planck levantou a questão da composição do átomo com base no modelo de Thomson com uma grande parte da discussão em torno do modelo atômico desenvolvido por Arthur Erich Haas. Lorentz explicou que a constante de Planck poderia ser tomada como determinar o tamanho dos átomos, ou que o tamanho dos átomos poderia ser tomado para determinar a constante de Planck. Lorentz incluiu comentários sobre a emissão e absorção de radiação, concluindo que “Um estado estacionário será estabelecido no qual o número de elétrons que entram em suas esferas é igual ao número daqueles que os deixam.” Na discussão do que poderia regular as diferenças de energia entre átomos, Max Planck simplesmente afirmou: “Os intermediários podem ser os elétrons.” As discussões delinearam a necessidade da teoria quântica ser incluída no átomo e as dificuldades em uma teoria atômica. Planck em sua palestra disse explicitamente: “Para que um oscilador [molécula ou átomo] possa fornecer radiação de acordo com a equação, é necessário introduzir nas leis de sua operação, como já dissemos no início deste Relatório, uma hipótese física particular que é, em um ponto fundamental, em contradição com a Mecânica clássica, explicitamente ou tacitamente.” O primeiro artigo de Bohr sobre suas citações modelo atômico Planck quase palavra para palavra, dizendo: “Qualquer que seja a alteração nas leis do movimento dos elétrons, parece necessário introduzir nas leis em questão uma quantidade estrangeira à eletrodinâmica clássica, i. e. A constante de Planck, ou como muitas vezes é chamada de quântico elementar de ação.” A nota de rodapé de Bohr na parte inferior da página é para a tradução francesa do Congresso Solvay de 1911 provando que ele padronizou seu modelo diretamente no processo e princípios fundamentais estabelecidos por Planck, Lorentz, e o modelo de Arthur Haas quantificado do átomo que foi mencionado dezessete vezes. Lorentz terminou a discussão da palestra de Einstein explicando: “A suposição de que esta energia deve ser um múltiplo de leva à seguinte fórmula, onde é um inteiro: .” Rutherford poderia ter descrito estes pontos para Bohr ou dado-lhe uma cópia do processo desde que ele citou deles e usou-os como uma referência. Em uma entrevista posterior, Bohr disse que era muito interessante ouvir as observações de Rutherford sobre o Congresso Solvay. Mas Bohr disse, “Eu vi os relatórios reais” do Congresso Solvay.
Então, em 1912, Bohr encontrou a teoria de John William Nicholson do modelo atômico que quantificava o momento angular como h/2π. De acordo com uma celebração do centenário do átomo de Bohr na revista Nature, foi Nicholson quem descobriu que os elétrons irradiam as linhas espectrais à medida que descem em direção ao núcleo e sua teoria era nuclear e quântica. Niels Bohr o citou em seu artigo de 1913 sobre o modelo atômico de Bohr. A importância do trabalho do modelo atômico quântico nuclear de Nicholson no modelo de Bohr foi enfatizada por muitos historiadores.
Em seguida, Bohr foi informado por seu amigo, Hans Hansen, que a série de Balmer é calculada usando a fórmula de Balmer, uma equação empírica descoberta por Johann Balmer em 1885 que descrevia comprimentos de onda de algumas linhas espectrais de hidrogênio. Isso foi generalizado por Johannes Rydberg em 1888, resultando no que hoje é conhecido como a fórmula de Rydberg. Depois disso, declarou Bohr, “tudo ficou claro”.
Para superar os problemas do átomo de Rutherford, em 1913 Niels Bohr apresentou três postulados que resumem a maior parte de seu modelo:
- O elétron é capaz de girar em certas órbitas estáveis ao redor do núcleo sem irradiar qualquer energia, ao contrário do que o eletromagnetismo clássico sugere. Essas órbitas estáveis são chamadas de órbitas estacionárias e são alcançadas a certas distâncias discretas do núcleo. O elétron não pode ter qualquer outra órbita entre os discretos.
- As órbitas estacionárias são alcançadas a distâncias para as quais o impulso angular do elétron giratório é um inteiro múltiplo da constante Planck reduzida: , onde n = 1, 2, 3,... é chamado o número quântico principal, e ? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = h/2D. O menor valor de n é 1; isso dá o menor raio orbital possível de 0,0529 nm conhecido como o raio de Bohr. Uma vez que um elétron está nesta órbita mais baixa, ele não pode ficar mais perto do núcleo. A partir da regra quântica de momentum angular como Bohr admite é anteriormente dada por Nicholson em seu papel de 1912, Bohr foi capaz de calcular as energias das órbitas permitidas do átomo de hidrogênio e outros átomos e íons de hidrogênio. Essas órbitas estão associadas a energias definidas e também são chamadas de conchas de energia ou níveis de energia. Nestas órbitas, a aceleração do elétron não resulta em radiação e perda de energia. O modelo de Bohr de um átomo foi baseado na teoria quântica da radiação de Planck.
- Os electrões só podem ganhar e perder energia saltando de uma órbita permitida para outra, absorvendo ou emitendo radiação eletromagnética com uma frequência Processo determinada pela diferença de energia dos níveis de acordo com a relação Planck: , onde h é a constante do Planck.
Outros pontos são:
- Como a teoria de Einstein do efeito fotoelétrico, a fórmula de Bohr assume que durante um salto quântico um discreto a quantidade de energia é irradiada. No entanto, ao contrário de Einstein, Bohr preso ao clássico Teoria Maxwell do campo electromagnético. A quantidade do campo eletromagnético foi explicada pela discrição dos níveis de energia atômica; Bohr não acreditava na existência de fótons.
- De acordo com a teoria de Maxwell a frequência Processo da radiação clássica é igual à frequência de rotação ProcessoApodrecer do elétron em sua órbita, com harmônicos em múltiplos inteiros desta frequência. Este resultado é obtido a partir do modelo Bohr para saltos entre níveis de energia En e En- Sim.k quando k é muito menor do que n. Estes saltos reproduzem a frequência do k-a harmônica da órbita n. Para valores suficientemente grandes n (os chamados estados de Rydberg), as duas órbitas envolvidas no processo de emissão têm quase a mesma frequência de rotação, de modo que a frequência orbital clássica não é ambígua. Mas para pequenos n (ou grande) k), a frequência de radiação não tem interpretação clássica inequívoca. Isso marca o nascimento do princípio de correspondência, exigindo que a teoria quântica concordasse com a teoria clássica apenas no limite de grandes números quânticos.
- A teoria de Bohr-Kramers-Slater (teoria BKS) é uma tentativa fracassada de estender o modelo de Bohr, que viola a conservação da energia e do impulso em saltos quânticos, com as leis de conservação que só possuem em média.
A condição de Bohr, de que o momento angular é um múltiplo inteiro de ħ foi posteriormente reinterpretada em 1924 por de Broglie como uma condição de onda estacionária: o elétron é descrito por uma onda e uma número inteiro de comprimentos de onda deve caber ao longo da circunferência da órbita do elétron:
De acordo com a hipótese de De Broglie, as partículas de matéria, como o elétron, se comportam como ondas. O comprimento de onda de Broglie de um elétron é
o que implica que
ou
Onde? é o impulso angular do elétron orbitando. Redação para este momentum angular, a equação anterior torna-se
que é o segundo postulado de Bohr.
Bohr descreveu o momento angular da órbita do elétron como 1/2h enquanto o comprimento de onda de de Broglie de λ = h/ p descreveu h dividido pelo momento do elétron. Em 1913, no entanto, Bohr justificou sua regra apelando para o princípio da correspondência, sem fornecer qualquer tipo de interpretação de onda. Em 1913, o comportamento ondulatório de partículas de matéria, como o elétron, não era suspeito.
Em 1925, um novo tipo de mecânica foi proposto, a mecânica quântica, na qual o modelo de Bohr de elétrons viajando em órbitas quantizadas foi estendido para um modelo mais preciso de movimento de elétrons. A nova teoria foi proposta por Werner Heisenberg. Outra forma da mesma teoria, a mecânica ondulatória, foi descoberta pelo físico austríaco Erwin Schrödinger de forma independente e por raciocínios diferentes. Schrödinger empregou as ondas de matéria de De Broglie, mas buscou soluções de onda de uma equação de onda tridimensional que descreve elétrons que foram obrigados a se mover sobre o núcleo de um átomo semelhante ao hidrogênio, por serem presos pelo potencial da carga nuclear positiva..
Níveis de energia do elétron
O modelo de Bohr dá resultados quase exatos apenas para um sistema onde dois pontos carregados orbitam um ao outro a velocidades muito menores que a da luz. Isso não envolve apenas sistemas de um elétron, como o átomo de hidrogênio, hélio ionizado individualmente e lítio duplamente ionizado, mas inclui positrônio e estados de Rydberg de qualquer átomo onde um elétron está longe de todo o resto. Ele pode ser usado para cálculos de transição de raios X da linha K se outras suposições forem adicionadas (consulte a lei de Moseley abaixo). Na física de alta energia, pode ser usado para calcular as massas de mésons de quarks pesados.
O cálculo das órbitas requer duas suposições.
- Mecânica clássica
- O elétron é realizado em uma órbita circular por atração eletrostática. A força centrípeta é igual à força do Coulomb.
- Onde? me é a massa do elétron, e é a carga elementar, ke é o Coulomb constante e Z. é o número atômico do átomo. Assume-se aqui que a massa do núcleo é muito maior do que a massa de elétrons (que é uma boa suposição). Esta equação determina a velocidade do elétron em qualquer raio:
- Também determina a energia total do elétron em qualquer raio:
- A energia total é negativa e inversamente proporcional R. Isso significa que leva energia para puxar o elétron orbitando para longe do protão. Para valores infinitos de R, a energia é zero, correspondendo a um elétron sem movimento infinitamente longe do protão. A energia total é metade da energia potencial, sendo a diferença a energia cinética do elétron. Isso também é verdade para órbitas não circulares pelo teorema virial.
- Uma regra quântica
- O impulso angular L = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = mevr é um inteiro múltiplo de ?:
Derivação
Se um elétron em um átomo está se movendo em uma órbita com período T, classicamente a radiação eletromagnética se repetirá a cada período orbital. Se o acoplamento ao campo eletromagnético for fraco, de modo que a órbita não decaia muito em um ciclo, a radiação será emitida em um padrão que se repete a cada período, de modo que a transformada de Fourier terá frequências que são apenas múltiplos de 1/T. Esta é a lei da radiação clássica: as frequências emitidas são múltiplos inteiros de 1/T.
Na mecânica quântica, esta emissão deve ser em quanta de luz, de frequências que consistem em múltiplos inteiros de 1/T, de modo que a mecânica clássica é uma descrição aproximada em grandes números quânticos. Isso significa que o nível de energia correspondente a uma órbita clássica de período 1/T deve ter níveis de energia próximos que diferem em energia por h/T, e eles devem estar igualmente espaçados perto desse nível,
Bohr preocupou-se se a economia de energia 1/T deve ser melhor calculado com o período do estado de energia ou , ou alguma média - em retrospecto, este modelo é apenas a principal aproximação semiclássica.
Bohr considerou órbitas circulares. Classicamente, essas órbitas devem decair para círculos menores quando os fótons são emitidos. O espaçamento de nível entre órbitas circulares pode ser calculado com a fórmula de correspondência. Para um átomo de hidrogênio, as órbitas clássicas têm um período T determinado pela terceira lei de Kepler para escalar como r3/2. A energia escala como 1/r, então a fórmula de espaçamento de nível equivale a
É possível determinar os níveis de energia descendo recursivamente órbita por órbita, mas existe um atalho.
O impulso angular L da escala circular da órbita . A energia em termos de impulso angular é então
Assumindo, com Bohr, que os valores quantizados de L são igualmente espaçados, o espaçamento entre as energias vizinhas é
Isto é o desejado para momentos angulares igualmente espaçados. Se alguém acompanhasse as constantes, o espaçamento seria ħ, então o momento angular deveria ser um múltiplo inteiro de ħ,
Foi assim que Bohr chegou ao seu modelo.
- Substituir a expressão para a velocidade dá uma equação para R em termos de n:
- para que o raio de órbita permitido em qualquer n o
- O menor valor possível de R no átomo de hidrogênio (Z. = 1) é chamado de raio de Bohr e é igual a:
- A energia da n-o nível para qualquer átomo é determinado pelo raio e número quântico:
Um elétron no nível de energia mais baixo do hidrogênio (n = 1), portanto, tem cerca de 13,6 eV menos energia do que um elétron imóvel infinitamente distante de O núcleo. O próximo nível de energia (n = 2) é −3,4 eV. O terceiro (n = 3) é −1,51 eV e assim por diante. Para valores maiores de n, essas também são as energias de ligação de um átomo altamente excitado com um elétron em uma grande órbita circular ao redor do resto do átomo. A fórmula do hidrogênio também coincide com o produto Wallis.
A combinação de constantes naturais na fórmula de energia é chamada de energia de Rydberg (RE):
Esta expressão é esclarecida interpretando-a em combinações que formam unidades mais naturais:
- é a energia de massa restante do elétron (511 keV),
- é a estrutura fina constante,
- .
Como esta derivação é com a suposição de que o núcleo é orbitado por um elétron, podemos generalizar este resultado deixando o núcleo ter uma carga q = Ze, onde Z é o número atômico. Isso agora nos dará níveis de energia para átomos hidrogenados (semelhantes ao hidrogênio), que podem servir como uma aproximação grosseira da ordem de grandeza dos níveis de energia reais. Portanto, para núcleos com prótons Z, os níveis de energia são (aproximadamente):
Os níveis de energia reais não podem ser resolvidos analiticamente para mais de um elétron (consulte o problema de n corpos) porque os elétrons não são apenas afetados pelo núcleo, mas também interagem uns com os outros por meio da Força de Coulomb.
Quando Z = 1/α (Z ≈ 137), o movimento torna-se altamente relativístico, e Z2 cancela o α2 em R; a energia de órbita começa a ser comparável à energia de repouso. Núcleos suficientemente grandes, se fossem estáveis, reduziriam sua carga criando um elétron ligado a partir do vácuo, ejetando o pósitron ao infinito. Este é o fenômeno teórico da triagem de carga eletromagnética que prevê uma carga nuclear máxima. A emissão de tais pósitrons foi observada nas colisões de íons pesados para criar núcleos superpesados temporários.
A fórmula de Bohr usa corretamente a massa reduzida do elétron e do próton em todas as situações, em vez da massa do elétron,
No entanto, esses números são quase os mesmos, devido à massa muito maior do próton, cerca de 1836,1 vezes a massa do elétron, de modo que a massa reduzida no sistema é a massa do elétron multiplicada pela constante 1836,1/(1+1836,1) = 0,99946. Esse fato foi historicamente importante para convencer Rutherford da importância do modelo de Bohr, pois explicava o fato de que as frequências das linhas nos espectros do hélio ionizado isoladamente não diferem das do hidrogênio por um fator de exatamente 4, mas sim por 4 vezes a razão da massa reduzida para os sistemas de hidrogênio vs. os sistemas de hélio, que estava muito mais próximo da razão experimental do que exatamente 4.
Para positrônio, a fórmula usa a massa reduzida também, mas neste caso, é exatamente a massa do elétron dividida por 2. Para qualquer valor do raio, o elétron e o pósitron estão se movendo cada um com metade da velocidade em torno de seus centro de massa comum, e cada um tem apenas um quarto da energia cinética. A energia cinética total é metade do que seria para um único elétron se movendo em torno de um núcleo pesado.
- (positronium).
Fórmula de Rydberg
A fórmula de Rydberg, que era conhecida empiricamente antes da fórmula de Bohr, é vista na teoria de Bohr como descrevendo as energias de transições ou saltos quânticos entre os níveis de energia orbital. A fórmula de Bohr dá o valor numérico da já conhecida e medida constante de Rydberg, mas em termos de constantes mais fundamentais da natureza, incluindo a carga do elétron e a constante de Planck.
Quando o elétron é movido de seu nível de energia original para um nível mais alto, ele salta de volta a cada nível até chegar à posição original, o que resulta na emissão de um fóton. Usando a fórmula derivada para os diferentes níveis de energia do hidrogênio, pode-se determinar os comprimentos de onda da luz que um átomo de hidrogênio pode emitir.
A energia de um fóton emitido por um átomo de hidrogênio é dada pela diferença de dois níveis de energia do hidrogênio:
onde nf é o nível de energia final e ni é o nível de energia inicial.
Como a energia de um fóton é
o comprimento de onda do fóton emitido é dado por
Isso é conhecido como fórmula de Rydberg, e a constante de Rydberg R é RE/hc, ou RE/ 2π em unidades naturais. Esta fórmula era conhecida no século XIX por cientistas que estudavam espectroscopia, mas não havia nenhuma explicação teórica para esta forma ou uma previsão teórica para o valor de R, até Bohr. De fato, a derivação de Bohr da constante de Rydberg, bem como a concordância concomitante da fórmula de Bohr com linhas espectrais observadas experimentalmente de Lyman (nf =1), Balmer (nf =2) e Paschen (nf =3), e a previsão teórica bem-sucedida de outras linhas ainda não observadas foi uma razão pela qual seu modelo foi imediatamente aceito.
Para aplicar a átomos com mais de um elétron, a fórmula de Rydberg pode ser modificada substituindo Z por Z − b ou n com n − b onde b é uma constante representando um efeito de triagem devido para o invólucro interno e outros elétrons (consulte o invólucro do elétron e a discussão posterior do "Modelo de invólucro do átomo" abaixo). Isso foi estabelecido empiricamente antes de Bohr apresentar seu modelo.
Modelo de casca (átomos mais pesados)
Os três artigos originais de Bohr em 1913 descreviam principalmente a configuração eletrônica em elementos mais leves. Bohr chamou seus invólucros de elétrons de “anéis” em 1913. Orbitais atômicos dentro de invólucros não existiam na época de seu modelo planetário. Bohr explica na Parte 3 de seu famoso artigo de 1913 que o máximo de elétrons em uma casca é oito, escrevendo: “Nós vemos, além disso, que um anel de n elétrons não pode girar em um único anel ao redor de um núcleo de cobrança ne a menos que n < 8.” Para átomos menores, as camadas eletrônicas seriam preenchidas da seguinte forma: “anéis de elétrons só se unirão se contiverem números iguais de elétrons; e que, portanto, o número de elétrons nos anéis internos será apenas 2, 4, 8”. No entanto, em átomos maiores a camada mais interna conteria oito elétrons, “por outro lado, o sistema periódico dos elementos sugere fortemente que já no neon N = 10 ocorrerá um anel interno de oito elétrons”. Bohr escreveu "Do exposto, somos levados ao seguinte esquema possível para o arranjo dos elétrons em átomos leves:"
| Elemento | Eletrontes por concha | Elemento | Eletrontes por concha | Elemento | Eletrontes por concha |
|---|---|---|---|---|---|
| 1 | 1 | 9 | 4, 4, 1 | 17. | 8, 4, 4, 1 |
| 2 | 2 | 10. | 8, 2 | 18. | 8, 2 |
| 3 | 2, 1 | 11 | 8, 2, 1 | 19 | 8, 2, 1 |
| 4 | 2, 2 | 12 | 8, 2, 2 | 20. | 8, 2, 2 |
| 5 | 2, 3 | 13 | 8, 2, 3 | 21 | 8, 2, 3 |
| 6 | 2, 4 | 14 | 8, 2, 4 | 22 | 8, 2, 4 |
| 7 | 4, 3 | 15 | 8, 4, 3 | 23 | 8, 4, 3 |
| 8 | 4, 2, 2 | 16. | 8, 4, 2, 2 | 24. | 8, 4, 2, 2 |
No terceiro artigo de Bohr, Parte III, de 1913, chamado "Sistemas contendo vários núcleos", ele diz que dois átomos formam moléculas em um plano simétrico e ele volta a descrever o hidrogênio. O modelo de Bohr de 1913 não discutiu elementos superiores em detalhes e John William Nicholson foi um dos primeiros a provar em 1914 que não poderia funcionar para o lítio, mas era uma teoria atraente para o hidrogênio e o hélio ionizado.
Em 1921, seguindo o trabalho de químicos e outros envolvidos no trabalho da tabela periódica, Bohr estendeu o modelo do hidrogênio para fornecer um modelo aproximado para átomos mais pesados. Isso deu uma imagem física que reproduziu muitas propriedades atômicas conhecidas pela primeira vez, embora essas propriedades tenham sido propostas contemporaneamente com o trabalho idêntico do químico Charles Rugeley Bury
O parceiro de pesquisa de Bohr durante 1914 a 1916 foi Walther Kossel, que corrigiu o trabalho de Bohr para mostrar que os elétrons interagiam através dos anéis externos, e Kossel chamou os anéis de "cascas". Irving Langmuir é creditado com o primeiro arranjo viável de elétrons em camadas com apenas dois na primeira camada e subindo para oito na seguinte de acordo com a regra do octeto de 1904, embora Kossel já tivesse previsto um máximo de oito por camada em 1916. Átomos mais pesados têm mais prótons no núcleo e mais elétrons para cancelar a carga. Bohr tirou desses químicos a ideia de que cada órbita discreta só poderia conter um certo número de elétrons. Segundo Kossel, depois que a órbita estiver completa, o próximo nível teria que ser usado. Isso dá ao átomo uma estrutura de concha projetada por Kossel, Langmuir e Bury, na qual cada concha corresponde a uma órbita de Bohr.
Esse modelo é ainda mais aproximado do que o modelo do hidrogênio, porque trata os elétrons em cada camada como não interativos. Mas as repulsões dos elétrons são levadas em consideração pelo fenômeno da blindagem. Os elétrons nas órbitas externas não apenas orbitam o núcleo, mas também se movem em torno dos elétrons internos, de modo que a carga efetiva Z que eles sentem é reduzida pelo número de elétrons na órbita interna.
Por exemplo, o átomo de lítio tem dois elétrons na órbita 1s mais baixa, e estes orbitam em Z = 2. Cada um vê a carga nuclear de Z = 3 menos o efeito de blindagem do outro, que reduz grosseiramente a carga nuclear em 1 unidade. Isso significa que os elétrons mais internos orbitam em aproximadamente 1/2 do raio de Bohr. O elétron mais externo no lítio orbita aproximadamente no raio de Bohr, já que os dois elétrons internos reduzem a carga nuclear em 2. Esse elétron externo deve estar a quase um raio de Bohr do núcleo. Como os elétrons se repelem fortemente, a descrição da carga efetiva é muito aproximada; a carga efetiva Z geralmente não é um número inteiro. Mas a lei de Moseley investiga experimentalmente o par de elétrons mais interno e mostra que eles veem uma carga nuclear de aproximadamente Z − 1, enquanto o elétron mais externo em um átomo ou íon com apenas um elétron na camada mais externa orbita um núcleo com carga efetiva Z − k onde k é o número total de elétrons nas camadas internas.
O modelo da casca foi capaz de explicar qualitativamente muitas das propriedades misteriosas dos átomos que foram codificadas no final do século 19 na tabela periódica dos elementos. Uma propriedade era o tamanho dos átomos, que podia ser determinado aproximadamente medindo a viscosidade dos gases e a densidade de sólidos cristalinos puros. Os átomos tendem a ficar menores à direita na tabela periódica e se tornam muito maiores na próxima linha da tabela. Os átomos à direita da tabela tendem a ganhar elétrons, enquanto os átomos à esquerda tendem a perdê-los. Cada elemento na última coluna da tabela é quimicamente inerte (gás nobre).
No modelo de casca, esse fenômeno é explicado pelo preenchimento de casca. Átomos sucessivos tornam-se menores porque estão preenchendo órbitas do mesmo tamanho, até que a órbita esteja completa, ponto em que o próximo átomo na tabela tem um elétron externo fracamente ligado, fazendo com que ele se expanda. A primeira órbita de Bohr é preenchida quando tem dois elétrons, o que explica por que o hélio é inerte. A segunda órbita permite oito elétrons e, quando está cheia, o átomo é neon, novamente inerte. O terceiro orbital contém oito novamente, exceto que no tratamento mais correto de Sommerfeld (reproduzido na mecânica quântica moderna) há "d" elétrons. A terceira órbita pode conter 10 elétrons d extras, mas essas posições não são preenchidas até que mais alguns orbitais do próximo nível sejam preenchidos (preencher os orbitais n = 3 d produz os 10 elementos de transição). O padrão de preenchimento irregular é um efeito de interações entre elétrons, que não são levados em consideração nos modelos de Bohr ou Sommerfeld e que são difíceis de calcular mesmo no tratamento moderno.
Lei e cálculo de Moseley (linhas de emissão de raios X K-alfa)
Niels Bohr disse em 1962: "Na verdade, o trabalho de Rutherford não foi levado a sério. Não podemos entender hoje, mas não foi levado a sério. Não houve menção disso em nenhum lugar. A grande mudança veio de Moseley."
Em 1913, Henry Moseley encontrou uma relação empírica entre a linha de raios X mais forte emitida por átomos sob bombardeio de elétrons (então conhecida como linha K-alfa) e seu número atômico Z. Verificou-se que a fórmula empírica de Moseley era derivada da fórmula de Rydberg e, posteriormente, da fórmula de Bohr (Moseley, na verdade, menciona apenas Ernest Rutherford e Antonius Van den Broek em termos de modelos, pois estes foram publicados antes de Moseley& #39; e o artigo de Moseley de 1913 foi publicado no mesmo mês que o primeiro artigo modelo de Bohr). As duas suposições adicionais de que [1] esta linha de raios X veio de uma transição entre níveis de energia com números quânticos 1 e 2, e [2], que o número atômico Z quando usado na fórmula para átomos mais pesados que o hidrogênio, deve ser diminuído em 1, para ( Z − 1)2.
Moseley escreveu para Bohr, intrigado com seus resultados, mas Bohr não pôde ajudar. Naquela época, ele pensava que o postulado "K" camada de elétrons deveria ter pelo menos quatro elétrons, não os dois que teriam explicado perfeitamente o resultado. Então Moseley publicou seus resultados sem uma explicação teórica.
Foi Walther Kossel em 1914 e em 1916 quem explicou que na tabela periódica novos elementos seriam criados à medida que os elétrons fossem adicionados à camada externa. No artigo de Kossel, ele escreve: “Isso leva à conclusão de que os elétrons, que são adicionados ainda mais, devem ser colocados em anéis ou conchas concêntricas, em cada uma das quais..., oito no nosso caso - deve ser arranjado. Assim que um anel ou concha é concluído, um novo deve ser iniciado para o próximo elemento; o número de elétrons, que são mais facilmente acessíveis e estão na periferia mais externa, aumenta novamente de elemento para elemento e, portanto, na formação de cada nova camada, a periodicidade química é repetida. Mais tarde, o químico Langmuir percebeu que o efeito era causado pela triagem de carga, com uma camada interna contendo apenas 2 elétrons. Em seu artigo de 1919, Irving Langmuir postulou a existência de "células" que cada um poderia conter apenas dois elétrons cada, e estes foram arranjados em "camadas equidistantes".
No experimento de Moseley, um dos elétrons mais internos do átomo é eliminado, deixando uma vaga na órbita de Bohr mais baixa, que contém um único elétron restante. Esta vaga é então preenchida por um elétron da próxima órbita, que tem n = 2. Mas os elétrons n = 2 veem uma carga efetiva de Z − 1, que é o valor apropriado para a carga do núcleo, quando um único elétron permanece na órbita de Bohr mais baixa para proteger a carga nuclear + Z e reduza-o em -1 (devido à carga negativa do elétron protegendo a carga nuclear positiva). A energia ganha por um elétron caindo da segunda camada para a primeira fornece a lei de Moseley para linhas K-alfa,
ou
Aqui, Rv = RE/< i>h é a constante de Rydberg, em termos de frequência igual a 3,28 x 1015 Hz. Para valores de Z entre 11 e 31, esta última relação foi derivada empiricamente por Moseley, em um gráfico simples (linear) da raiz quadrada da frequência de raios X em relação ao número atômico (no entanto, para a prata, Z = 47, o obtido experimentalmente termo de triagem deve ser substituído por 0,4). Apesar de sua validade restrita, a lei de Moseley não apenas estabeleceu o significado objetivo do número atômico, mas, como observou Bohr, também fez mais do que a derivação de Rydberg para estabelecer a validade do modelo nuclear de Rutherford/Van den Broek/Bohr de o átomo, com número atômico (lugar na tabela periódica) representando unidades inteiras de carga nuclear. Van den Broek publicou seu modelo em janeiro de 1913, mostrando que a tabela periódica foi organizada de acordo com a carga, enquanto o modelo atômico de Bohr não foi publicado até julho de 1913.
A linha K-alfa do tempo de Moseley agora é conhecida como um par de linhas próximas, escritas como (Kα1 e Kα 2) na notação Siegbahn.
Deficiências
O modelo de Bohr fornece um valor incorreto L=ħ para o momento angular orbital do estado fundamental: O momento angular no verdadeiro estado fundamental é conhecido por ser zero a partir da experiência. Embora as imagens mentais falhem um pouco nesses níveis de escala, um elétron no "orbital" sem momento orbital, pode ser considerado como não girando "ao redor" o núcleo, mas apenas contorná-lo firmemente em uma elipse com área zero (isso pode ser retratado como "para frente e para trás", sem bater ou interagir com o núcleo). Isso só é reproduzido em um tratamento semiclássico mais sofisticado como o de Sommerfeld. Ainda assim, mesmo o modelo semiclássico mais sofisticado falha em explicar o fato de que o estado de menor energia é esfericamente simétrico – ele não aponta em nenhuma direção específica.
No entanto, no tratamento totalmente quântico moderno no espaço de fase, a deformação adequada (extensão completa cuidadosa) do resultado semiclássico ajusta o valor do momento angular para o efetivo correto. Como consequência, a expressão do estado fundamental físico é obtida através de um deslocamento da expressão do momento angular quântico de fuga, que corresponde à simetria esférica.
Na mecânica quântica moderna, o elétron no hidrogênio é uma nuvem esférica de probabilidade que fica mais densa perto do núcleo. A constante de taxa de decaimento de probabilidade no hidrogênio é igual ao inverso do raio de Bohr, mas como Bohr trabalhou com órbitas circulares, não com elipses de área zero, o fato de que esses dois números coincidem exatamente é considerado uma "coincidência' 34;. (No entanto, muitos desses acordos coincidentes são encontrados entre o tratamento mecânico quântico semiclássico versus completo do átomo; isso inclui níveis de energia idênticos no átomo de hidrogênio e a derivação de uma constante de estrutura fina, que surge do modelo relativístico de Bohr-Sommerfeld (veja abaixo) e que passa a ser igual a um conceito totalmente diferente, em plena mecânica quântica moderna).
O modelo de Bohr também tem dificuldade, ou falha em explicar:
- Grande parte do espectro de átomos maiores. Na melhor das hipóteses, ele pode fazer previsões sobre o K-alfa e alguns L-alfa espectros de emissão de raios X para átomos maiores, se dois. suposições adicionais ad hoc são feitas. Espectros de emissão para átomos com um único elétron externo (atomas no grupo de lítio) também podem ser aproximadamente previstos. Além disso, se os fatores de triagem empírico-nuclear para muitos átomos são conhecidos, muitas outras linhas espectrais podem ser deduzidas da informação, em átomos semelhantes de elementos diferentes, através dos princípios de combinação Ritz-Rydberg (ver fórmula Rydberg). Todas essas técnicas fazem uso essencialmente da imagem potencial-energia de Bohr Newtonian do átomo.
- as intensidades relativas de linhas espectrais; embora em alguns casos simples, a fórmula de Bohr ou modificações dele, foi capaz de fornecer estimativas razoáveis (por exemplo, cálculos de Kramers para o efeito Stark).
- A existência de estrutura fina e estrutura hiperfina em linhas espectrais, que são conhecidas por ser devido a uma variedade de efeitos relativistas e sutis, bem como complicações do spin de elétrons.
- O efeito Zeeman – mudanças nas linhas espectrais devido a campos magnéticos externos; estes também são devido a princípios quânticos mais complicados que interagem com spin elétron e campos magnéticos orbitais.
- O modelo também viola o princípio de incerteza em que considera os elétrons ter órbitas e locais conhecidos, duas coisas que não podem ser medidas simultaneamente.
- Doublets e triplets aparecem no espectro de alguns átomos como pares muito próximos de linhas. O modelo de Bohr não pode dizer por que alguns níveis de energia devem ser muito próximos juntos.
- Os átomos multieletrônicos não têm níveis de energia previstos pelo modelo. Não funciona para hélio (neutral).
Refinamentos
Foram propostas várias melhorias no modelo de Bohr, principalmente os modelos de Sommerfeld ou Bohr-Sommerfeld, que sugeriam que os elétrons viajam em órbitas elípticas ao redor de um núcleo, em vez das órbitas circulares do modelo de Bohr. Este modelo complementou a condição de momento angular quantizado do modelo de Bohr com uma condição de quantização radial adicional, a condição de quantização de Wilson-Sommerfeld
onde pr é o momento radial canonicamente conjugado à coordenada q, que é a posição radial, e T é um período orbital completo. A integral é a ação das coordenadas do ângulo de ação. Essa condição, sugerida pelo princípio da correspondência, é a única possível, pois os números quânticos são invariantes adiabáticos.
O modelo de Bohr-Sommerfeld era fundamentalmente inconsistente e levava a muitos paradoxos. O número quântico magnético media a inclinação do plano orbital em relação ao plano xy e podia levar apenas alguns valores discretos. Isso contradiz o fato óbvio de que um átomo pode ser girado para um lado e para o outro em relação às coordenadas sem restrição. A quantização de Sommerfeld pode ser executada em diferentes coordenadas canônicas e às vezes dá respostas diferentes. A incorporação de correções de radiação foi difícil, porque exigia encontrar coordenadas de ângulo de ação para um sistema combinado de radiação/átomo, o que é difícil quando a radiação pode escapar. Toda a teoria não se estendia a movimentos não integráveis, o que significava que muitos sistemas não podiam ser tratados nem mesmo em princípio. No final, o modelo foi substituído pelo moderno tratamento da mecânica quântica do átomo de hidrogênio, que foi dado pela primeira vez por Wolfgang Pauli em 1925, usando a mecânica matricial de Heisenberg. A imagem atual do átomo de hidrogênio é baseada nos orbitais atômicos da mecânica ondulatória, que Erwin Schrödinger desenvolveu em 1926.
No entanto, isso não quer dizer que o modelo de Bohr-Sommerfeld não teve sucesso. Cálculos baseados no modelo de Bohr-Sommerfeld foram capazes de explicar com precisão uma série de efeitos espectrais atômicos mais complexos. Por exemplo, até perturbações de primeira ordem, o modelo de Bohr e a mecânica quântica fazem as mesmas previsões para a divisão da linha espectral no efeito Stark. Em perturbações de ordem superior, no entanto, o modelo de Bohr e a mecânica quântica diferem, e as medições do efeito Stark sob altas intensidades de campo ajudaram a confirmar a correção da mecânica quântica sobre o modelo de Bohr. A teoria predominante por trás dessa diferença está nas formas dos orbitais dos elétrons, que variam de acordo com o estado de energia do elétron.
As condições de quantização de Bohr-Sommerfeld levam a questões na matemática moderna. A condição de quantização semiclássica consistente requer um certo tipo de estrutura no espaço de fase, o que coloca limitações topológicas nos tipos de variedades simpléticas que podem ser quantizadas. Em particular, a forma simplética deve ser a forma de curvatura de uma conexão de um feixe de linhas hermitianas, que é chamada de pré-quantização.
Bohr também atualizou seu modelo em 1922, assumindo que certos números de elétrons (por exemplo, 2, 8 e 18) correspondem a "camadas fechadas" estáveis.
Modelo da ligação química
Niels Bohr propôs um modelo do átomo e um modelo da ligação química. De acordo com seu modelo para uma molécula diatômica, os elétrons dos átomos da molécula formam um anel rotativo cujo plano é perpendicular ao eixo da molécula e equidistante dos núcleos atômicos. O equilíbrio dinâmico do sistema molecular é alcançado através do equilíbrio de forças entre as forças de atração dos núcleos ao plano do anel de elétrons e as forças de repulsão mútua dos núcleos. O modelo de Bohr da ligação química levou em consideração a repulsão de Coulomb – os elétrons do anel estão na distância máxima entre si.
Contenido relacionado
Constante física
Leonhard Euler
Alessandro volta