Matriz (estrutura de dados)
Na ciência da computação, um array é uma estrutura de dados que consiste em uma coleção de elementos (valores ou variáveis), cada um identificado por pelo menos um índice de array ou chave. Uma matriz é armazenada de forma que a posição de cada elemento possa ser calculada a partir de sua tupla de índice por uma fórmula matemática. O tipo mais simples de estrutura de dados é uma matriz linear, também chamada de matriz unidimensional.
Por exemplo, uma matriz de dez variáveis inteiras de 32 bits (4 bytes), com índices de 0 a 9, pode ser armazenada como dez palavras nos endereços de memória 2000, 2004, 2008,..., 2036, (em hexadecimal: 0x7D0, 0x7D4, 0x7D8,..., 0x7F4) para que o elemento com índice i tem o endereço 2000 + (i × 4).
O endereço de memória do primeiro elemento de uma matriz é chamado de primeiro endereço, endereço de fundação ou endereço de base.
Como o conceito matemático de uma matriz pode ser representado como uma grade bidimensional, as matrizes bidimensionais também são às vezes chamadas de "matrizes". Em alguns casos, o termo "vetor" é usado em computação para se referir a uma matriz, embora tuplas em vez de vetores sejam os equivalentes matematicamente mais corretos. As tabelas geralmente são implementadas na forma de arrays, especialmente tabelas de consulta; a palavra "mesa" às vezes é usado como sinônimo de array.
Os arrays estão entre as estruturas de dados mais antigas e importantes e são usados por quase todos os programas. Eles também são usados para implementar muitas outras estruturas de dados, como listas e strings. Eles exploram efetivamente a lógica de endereçamento dos computadores. Na maioria dos computadores modernos e em muitos dispositivos de armazenamento externo, a memória é uma matriz unidimensional de palavras, cujos índices são seus endereços. Processadores, especialmente processadores vetoriais, geralmente são otimizados para operações de matriz.
Os arrays são úteis principalmente porque os índices dos elementos podem ser calculados em tempo de execução. Entre outras coisas, esse recurso permite que uma única instrução iterativa processe arbitrariamente muitos elementos de uma matriz. Por esse motivo, os elementos de uma estrutura de dados de array devem ter o mesmo tamanho e devem usar a mesma representação de dados. O conjunto de tuplas de índice válido e os endereços dos elementos (e, portanto, a fórmula de endereçamento do elemento) são geralmente, mas nem sempre, fixos enquanto o array está em uso.
O termo "array" também pode se referir a um tipo de dados de matriz, um tipo de tipo de dados fornecido pela maioria das linguagens de programação de alto nível que consiste em uma coleção de valores ou variáveis que podem ser selecionados por um ou mais índices calculados em tempo de execução. Os tipos de matriz são geralmente implementados por estruturas de matriz; no entanto, em alguns idiomas, eles podem ser implementados por tabelas hash, listas encadeadas, árvores de pesquisa ou outras estruturas de dados.
O termo também é usado, especialmente na descrição de algoritmos, para significar matriz associativa ou "matriz abstrata", um modelo teórico de ciência da computação (um tipo de dados abstrato ou ADT) destinado a capturar as propriedades essenciais de matrizes.
História
Os primeiros computadores digitais usavam programação em linguagem de máquina para configurar e acessar estruturas de matrizes para tabelas de dados, cálculos de vetores e matrizes e para muitos outros propósitos. John von Neumann escreveu o primeiro programa de ordenação de matrizes (merge sort) em 1945, durante a construção do primeiro computador com programa armazenado.p. 159 A indexação de matriz foi originalmente feita por código auto-modificável e, posteriormente, usando registradores de índice e endereçamento indireto. Alguns mainframes projetados na década de 1960, como o Burroughs B5000 e seus sucessores, usavam a segmentação de memória para executar a verificação de limites de índice no hardware.
Linguagens de montagem geralmente não têm suporte especial para arrays, além do que a própria máquina fornece. As primeiras linguagens de programação de alto nível, incluindo FORTRAN (1957), Lisp (1958), COBOL (1960) e ALGOL 60 (1960), tinham suporte para arrays multidimensionais, assim como C (1972). Em C++ (1983), existem modelos de classe para arrays multidimensionais cuja dimensão é fixa em tempo de execução, bem como para arrays flexíveis em tempo de execução.
Aplicativos
Arrays são usados para implementar vetores e matrizes matemáticas, bem como outros tipos de tabelas retangulares. Muitos bancos de dados, pequenos e grandes, consistem em (ou incluem) matrizes unidimensionais cujos elementos são registros.
Arrays são usados para implementar outras estruturas de dados, como listas, heaps, tabelas hash, deques, filas, pilhas, strings e VLists. As implementações baseadas em array de outras estruturas de dados são frequentemente simples e eficientes em termos de espaço (estruturas de dados implícitas), exigindo pouca sobrecarga de espaço, mas podem ter baixa complexidade de espaço, particularmente quando modificadas, em comparação com estruturas de dados baseadas em árvore (compare uma matriz classificada com uma árvore de pesquisa).
Um ou mais arrays grandes às vezes são usados para emular a alocação de memória dinâmica no programa, particularmente a alocação de pool de memória. Historicamente, esta tem sido às vezes a única maneira de alocar a "memória dinâmica" portátil.
Arrays podem ser usados para determinar o fluxo de controle parcial ou completo em programas, como uma alternativa compacta para (de outra forma repetitiva) várias instruções IF. Eles são conhecidos neste contexto como tabelas de controle e são usados em conjunto com um interpretador construído especificamente cujo fluxo de controle é alterado de acordo com os valores contidos na matriz. A matriz pode conter ponteiros de sub-rotina (ou números relativos de sub-rotina que podem ser acionados por instruções SWITCH) que direcionam o caminho da execução.
Identificador de elemento e fórmulas de endereçamento
Quando os objetos de dados são armazenados em uma matriz, os objetos individuais são selecionados por um índice que geralmente é um inteiro escalar não negativo. Os índices também são chamados de subscritos. Um índice mapeia o valor da matriz para um objeto armazenado.
Existem três maneiras pelas quais os elementos de um array podem ser indexados:
- 0indexação baseada em zero)
- O primeiro elemento do array é indexado pelo subscript de 0.
- 1indexação baseada em um)
- O primeiro elemento do array é indexado por subscrição de 1.
- (indexação baseada em n)
- O índice de base de um array pode ser escolhido livremente. Normalmente linguagens de programação permitindo indexação baseada em n também permitem valores de índice negativo e outros tipos de dados escalares como enumerações, ou caracteres podem ser usados como um índice de array.
O uso da indexação baseada em zero é a escolha de design de muitas linguagens de programação influentes, incluindo C, Java e Lisp. Isso leva a uma implementação mais simples, onde o subscrito se refere a um deslocamento da posição inicial de uma matriz, de modo que o primeiro elemento tenha um deslocamento de zero.
Os arrays podem ter várias dimensões, portanto, não é incomum acessar um array usando vários índices. Por exemplo, uma matriz bidimensional A com três linhas e quatro colunas pode fornecer acesso ao elemento na 2ª linha e na 4ª coluna pela expressão A[1][3] no caso de um sistema de indexação baseado em zero. Assim, dois índices são usados para um array bidimensional, três para um array tridimensional e n para um array n dimensional.
O número de índices necessários para especificar um elemento é chamado de dimensão, dimensionalidade ou classificação do array.
Em arrays padrão, cada índice é restrito a um certo intervalo de números inteiros consecutivos (ou valores consecutivos de algum tipo enumerado) e o endereço de um elemento é calculado por um método "linear" fórmula nos índices.
Matrizes unidimensionais
Uma matriz unidimensional (ou matriz de dimensão única) é um tipo de matriz linear. Acessar seus elementos envolve um único subscrito que pode representar um índice de linha ou coluna.
Como exemplo, considere a declaração C int anArrayName[10]; que declara um array unidimensional de dez inteiros. Aqui, o array pode armazenar dez elementos do tipo int. Esta matriz tem índices começando de zero a nove. Por exemplo, as expressões anArrayName[0] e anArrayName[9] são o primeiro e o último elementos, respectivamente.
Para um vetor com endereçamento linear, o elemento com índice i está localizado no endereço B + c × i, onde B é um endereço base fixo e c uma constante fixa, às vezes chamado de incremento de endereço ou passo.
Se os índices de elementos válidos começam em 0, a constante B é simplesmente o endereço do primeiro elemento da matriz. Por esse motivo, a linguagem de programação C especifica que os índices de array sempre começam em 0; e muitos programadores chamarão esse elemento de "zeroth" em vez de "primeiro".
No entanto, pode-se escolher o índice do primeiro elemento por uma escolha apropriada do endereço base B. Por exemplo, se a matriz tiver cinco elementos, indexados de 1 a 5, e o endereço base B for substituído por B + 30c, então os índices desses mesmos elementos serão de 31 a 35. Se a numeração não começar em 0, a constante B pode não ser o endereço de nenhum elemento.
Matrizes multidimensionais
Para um array multidimensional, o elemento com índices i,j teria endereço B + c · i + d · j, onde os coeficientes c e d são os linha e incrementos de endereço de coluna, respectivamente.
De forma mais geral, em uma matriz kdimensional, o endereço de um elemento com índices i1, i2,..., ik é
- B + c1 · Eu...1 + c2 · Eu...2 + ck · Eu...k.
Por exemplo: int a[2][3];
Isso significa que o array a tem 2 linhas e 3 colunas, e o array é do tipo inteiro. Aqui podemos armazenar 6 elementos, eles serão armazenados linearmente, mas começando na primeira linha linear e continuando com a segunda linha. A matriz acima será armazenada como a11, a12, a13, a21, a22, a23.
Esta fórmula requer apenas k multiplicações e k adições, para qualquer matriz que caiba na memória. Além disso, se qualquer coeficiente for uma potência fixa de 2, a multiplicação pode ser substituída por deslocamento de bits.
Os coeficientes ck devem ser escolhidos de forma que cada tupla de índice válida seja mapeada para o endereço de um elemento distinto.
Se o valor legal mínimo para cada índice for 0, então B é o endereço do elemento cujos índices são todos zero. Como no caso unidimensional, os índices dos elementos podem ser alterados alterando o endereço base B. Assim, se uma matriz bidimensional tiver linhas e colunas indexadas de 1 a 10 e 1 a 20, respectivamente, substitua B por B + c1 − 3c2 fará com que sejam renumerados de 0 a 9 e 4 a 23, respectivamente. Aproveitando esse recurso, algumas linguagens (como FORTRAN 77) especificam que os índices de array começam em 1, como na tradição matemática, enquanto outras linguagens (como Fortran 90, Pascal e Algol) permitem que o usuário escolha o valor mínimo para cada índice.
Vetores de drogas
A fórmula de endereçamento é completamente definida pela dimensão d, o endereço base B e os incrementos c1, c2,..., ck. Muitas vezes é útil empacotar esses parâmetros em um registro chamado descritor ou vetor de passo ou vetor dope do array. O tamanho de cada elemento e os valores mínimo e máximo permitidos para cada índice também podem ser incluídos no vetor dope. O vetor dope é um manipulador completo para o array e é uma maneira conveniente de passar arrays como argumentos para procedimentos. Muitas operações úteis de fatiamento de array (como selecionar um sub-array, trocar índices ou inverter a direção dos índices) podem ser executadas com muita eficiência pela manipulação do vetor dope.
Layouts compactos
Muitas vezes os coeficientes são escolhidos de forma que os elementos ocupem uma área contígua de memória. No entanto, isso não é necessário. Mesmo que os arrays sejam sempre criados com elementos contíguos, algumas operações de fatiamento do array podem criar sub-arrays não contíguos a partir deles.
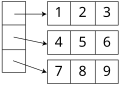
Existem dois layouts compactos sistemáticos para uma matriz bidimensional. Por exemplo, considere a matriz
- A= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Não.123456789].Não. A={begin{bmatrix}1&2&3\4&5&67&8&9end{bmatrix}}.}
No layout de ordem principal da linha (adotado por C para matrizes declaradas estaticamente), os elementos em cada linha são armazenados em posições consecutivas e todos os elementos de uma linha têm um endereço mais baixo do que qualquer um dos elementos de um consecutivo linha:
1 2 3 4 5 6 7 8 9
Na ordem da coluna principal (tradicionalmente usada pelo Fortran), os elementos em cada coluna são consecutivos na memória e todos os elementos de uma coluna têm um endereço menor do que qualquer um dos elementos de uma coluna consecutiva:
1 4 7 2 5 8 3 6 9
Para matrizes com três ou mais índices, "ordem principal da linha" coloca em posições consecutivas quaisquer dois elementos cujas tuplas de índice diferem apenas por um no último índice. "Ordem principal da coluna" é análogo em relação ao índice primeiro.
Em sistemas que usam cache do processador ou memória virtual, a varredura de uma matriz é muito mais rápida se os elementos sucessivos forem armazenados em posições consecutivas na memória, em vez de espalhados esparsamente. Muitos algoritmos que usam arrays multidimensionais irão escaneá-los em uma ordem previsível. Um programador (ou um compilador sofisticado) pode usar essas informações para escolher entre o layout principal de linha ou coluna para cada array. Por exemplo, ao calcular o produto A·B de duas matrizes, seria melhor ter A armazenado na ordem da linha principal e B na ordem da coluna principal.
Redimensionando
Os arrays estáticos têm um tamanho fixo quando são criados e consequentemente não permitem a inserção ou remoção de elementos. No entanto, ao alocar um novo array e copiar o conteúdo do array antigo para ele, é possível implementar efetivamente uma versão dinâmica de um array; veja matriz dinâmica. Se esta operação for feita com pouca frequência, as inserções no final da matriz exigirão apenas o tempo constante amortizado.
Algumas estruturas de dados de array não realocam o armazenamento, mas armazenam uma contagem do número de elementos do array em uso, chamada de contagem ou tamanho. Isso efetivamente torna a matriz uma matriz dinâmica com um tamanho ou capacidade máxima fixa; Strings Pascal são exemplos disso.
Fórmulas não lineares
Fórmulas mais complicadas (não lineares) são usadas ocasionalmente. Para uma matriz triangular bidimensional compacta, por exemplo, a fórmula de endereçamento é um polinômio de grau 2.
Eficiência
Ambos armazenar e selecionar levam (pior caso determinístico) tempo constante. As matrizes ocupam espaço linear (O(n)) no número de elementos n que contêm.
Em uma matriz com tamanho de elemento k e em uma máquina com tamanho de linha de cache de B bytes, iterar em uma matriz de n elementos requer o mínimo de teto (nk/B) falha no cache, porque seus elementos ocupam locais de memória contíguos. Isso é aproximadamente um fator de B/k melhor do que o número de faltas de cache necessárias para acessar n elementos em locais de memória aleatórios. Como consequência, a iteração sequencial sobre um array é visivelmente mais rápida na prática do que a iteração sobre muitas outras estruturas de dados, uma propriedade chamada localidade de referência (isso não significa, no entanto, que usar um hash perfeito ou um hash trivial dentro do mesmo array (local), não será ainda mais rápido - e alcançável em tempo constante). As bibliotecas fornecem recursos otimizados de baixo nível para copiar intervalos de memória (como memcpy) que podem ser usados para mover blocos contíguos de elementos de matriz significativamente mais rápido do que pode ser obtido por meio do acesso a elementos individuais. A aceleração dessas rotinas otimizadas varia de acordo com o tamanho do elemento da matriz, arquitetura e implementação.
Em termos de memória, os arrays são estruturas de dados compactas sem overhead por elemento. Pode haver uma sobrecarga por array (por exemplo, para armazenar limites de índice), mas isso depende do idioma. Também pode acontecer que os elementos armazenados em um array requeiram menos memória do que os mesmos elementos armazenados em variáveis individuais, porque vários elementos do array podem ser armazenados em uma única palavra; tais arrays são geralmente chamados de arrays empacotados. Um caso extremo (mas comumente usado) é o array de bits, onde cada bit representa um único elemento. Um único octeto pode conter até 256 combinações diferentes de até 8 condições diferentes, na forma mais compacta.
Acessos de array com padrões de acesso estaticamente previsíveis são uma fonte importante de paralelismo de dados.
Comparação com outras estruturas de dados
| Peek. (index) | Mutato (inserir ou excluir) em... | Espaço excessivo, média | |||
|---|---|---|---|---|---|
| Início | Fim | Meio ambiente | |||
| Lista vinculada | Θ (n) | Θ(1) | Θ(1), elemento final conhecido; Θ (n), elemento final desconhecido | Tempo de espreita + Θ(1) | Θ (n) |
| Array | Θ(1) | — | — | — | 0 |
| array dinâmico | Θ(1) | Θ (n) | Θ(1) amortizado | Θ (n) | Θ (n) |
| Árvore equilibrada | Θ(log n) | Θ(log n) | Θ (em inglês) n) | Θ (em inglês) n) | Θ (n) |
| Random...lista de acesso | Θ(log n) | Θ(1) | — | — | Θ (n) |
| Árvore da matriz de Hashed | Θ(1) | Θ (n) | Θ(1) amortizado | Θ (n) | Θ(√)n) |
Arrays dinâmicos ou arrays expansíveis são semelhantes aos arrays, mas adicionam a capacidade de inserir e excluir elementos; adicionar e excluir no final é particularmente eficiente. No entanto, eles reservam armazenamento adicional linear (Θ(n)), enquanto os arrays não reservam armazenamento adicional.
Arrays associativos fornecem um mecanismo para funcionalidade semelhante a array sem grandes sobrecargas de armazenamento quando os valores de índice são esparsos. Por exemplo, uma matriz que contém valores apenas nos índices 1 e 2 bilhões pode se beneficiar do uso dessa estrutura. Matrizes associativas especializadas com chaves inteiras incluem tentativas Patricia, matrizes Judy e árvores van Emde Boas.
Árvores balanceadas requerem tempo O(log n) para acesso indexado, mas também permitem inserir ou deletar elementos em tempo O(log n), enquanto arrays expansíveis requerem linear (Θ(n)) tempo para inserir ou excluir elementos em uma posição arbitrária.
Listas encadeadas permitem remoção e inserção de tempo constante no meio, mas levam tempo linear para acesso indexado. Seu uso de memória é tipicamente pior do que arrays, mas ainda é linear.
Um vetor Iliffe é uma alternativa para uma estrutura de matriz multidimensional. Ele usa uma matriz unidimensional de referências a matrizes de uma dimensão a menos. Para duas dimensões, em particular, esta estrutura alternativa seria um vetor de ponteiros para vetores, um para cada linha (ponteiro em c ou c++). Assim, um elemento na linha i e na coluna j de um array A seria acessado por indexação dupla (A[ i][j] em notação típica). Essa estrutura alternativa permite matrizes irregulares, onde cada linha pode ter um tamanho diferente — ou, em geral, onde o intervalo válido de cada índice depende dos valores de todos os índices anteriores. Ele também economiza uma multiplicação (pelo incremento do endereço da coluna) substituindo-a por um deslocamento de bit (para indexar o vetor de ponteiros de linha) e um acesso extra à memória (buscando o endereço da linha), o que pode valer a pena em algumas arquiteturas.
Dimensão
A dimensão de um array é o número de índices necessários para selecionar um elemento. Assim, se o array é visto como uma função em um conjunto de possíveis combinações de índices, ele é a dimensão do espaço do qual seu domínio é um subconjunto discreto. Assim, um array unidimensional é uma lista de dados, um array bidimensional é um retângulo de dados, um array tridimensional um bloco de dados, etc.
Isso não deve ser confundido com a dimensão do conjunto de todas as matrizes com um determinado domínio, ou seja, o número de elementos do array. Por exemplo, uma matriz com 5 linhas e 4 colunas é bidimensional, mas essas matrizes formam um espaço de 20 dimensões. Da mesma forma, um vetor tridimensional pode ser representado por uma matriz unidimensional de tamanho três.
Contenido relacionado
Herança múltipla
Protocolo de Configuração de Host Dinâmico
Computação distribuída