Mapa logístico

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

O mapa logístico é um mapeamento polinomial (equivalentemente, relação de recorrência) de grau 2, muitas vezes referido como um exemplo arquetípico de como o comportamento caótico e complexo pode surgir de equações dinâmicas não lineares muito simples. O mapa foi popularizado em um artigo de 1976 pelo biólogo Robert May, em parte como um modelo demográfico de tempo discreto análogo à equação logística escrita por Pierre François Verhulst. Matematicamente, o mapa logístico é escrito

Não. x_{n+1}=rx_{n}(1-x_{n}),}

(1)

onde $x n$ é um número entre zero e um, que representa a proporção de população para a população máxima possível. Esta equação de diferença não linear destina-se a capturar dois efeitos:

reprodução, onde a população vai aumentar a uma taxa proporcional à população atual quando o tamanho da população é pequeno,
fome (mortalidade dependente da densidade), onde a taxa de crescimento diminuirá a uma taxa proporcional ao valor obtido tomando a "capacidade de transporte" teórica do ambiente menos a população atual.

Os valores usuais de interesse para o parâmetro $r$ são aqueles no intervalo $[0, 4]$ , de modo que $x n$ permaneça limitado em $[0, 1]$ . O caso $r = 4$ do mapa logístico é uma transformação não linear tanto do mapa de deslocamento de bits quanto do $< i>μ = 2$ caso do mapa da tenda. Se $r > 4$ , isso leva a tamanhos populacionais negativos. (Este problema não aparece no modelo Ricker mais antigo, que também exibe dinâmica caótica.) Pode-se também considerar valores de $r$ em o intervalo $[-2, 0]$ , de modo que $x n$ permanece limitado em $[-0.5, 1.5]$ .

Características do mapa

Comportamento dependente de r

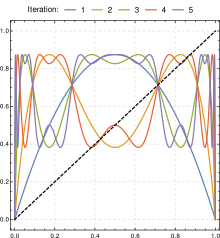
A imagem abaixo mostra o conteúdo de amplitude e frequência de algumas iterações de mapas logísticos para valores de parâmetros que variam de 2 a 4.

Ao variar o parâmetro $r$ , observa-se o seguinte comportamento:

Evolução de diferentes condições iniciais como função de

R

Com $R$ entre 0 e 1, a população acabará por morrer, independente da população inicial.
Com $R$ entre 1 e 2, a população abordará rapidamente o valor $R - 1 / R$ , independente da população inicial.
Evolução de diferentes condições iniciais como função de $R$ com viés
Com $R$ entre 2 e 3, a população também eventualmente abordará o mesmo valor $R - 1 / R$ , mas primeiro flutuará em torno desse valor por algum tempo. A taxa de convergência é linear, exceto para $R = 3$ , quando é dramaticamente lento, menos do que linear (ver memória Bifurcation).
Com $R$ entre 3 e 1 +√6 ≈ 3.449 a população abordará oscilações permanentes entre dois valores. Estes dois valores dependem de $R$ e dado por ${displaystyle x_{pm }={frac {1}{2r}}left(r+1pm {sqrt {(r-3)(r+1)}}right)}$ .
Com $R$ entre 3.44949 e 3.54409 (aproximadamente), de quase todas as condições iniciais a população abordará oscilações permanentes entre quatro valores. O último número é uma raiz de um polinomial de 12o grau (sequência A086181 no OEIS).
Com $R$ aumentando além de 3.54409, de quase todas as condições iniciais, a população abordará oscilações entre 8 valores, então 16, 32, etc. Os comprimentos dos intervalos de parâmetros que produzem oscilações de um determinado comprimento diminuem rapidamente; a relação entre os comprimentos de dois intervalos sucessivos de bifurcação aproxima-se da constante de Feigenbaum $δ \approx 4.66920$ . Este comportamento é um exemplo de uma cascata de duplicação de período.
Em $R \approx 3.56995$ (sequência) A098587 no OEIS) é o início do caos, no final da cascata de duplicação do período. De quase todas as condições iniciais, já não vemos oscilações de período finito. Pequenas variações na população inicial produzem resultados dramaticamente diferentes ao longo do tempo, uma característica primordial do caos.
A maioria dos valores $R$ além de 3.56995 apresentam comportamento caótico, mas ainda existem certas gamas isoladas de $R$ que mostram comportamento não caótico; estas são às vezes chamadas ilhas de estabilidade. Por exemplo, começando em 1 +√8 (aproximadamente 3.82843) há uma gama de parâmetros $R$ que mostram oscilação entre três valores, e para valores ligeiramente maiores $R$ oscilação entre 6 valores, então 12 etc.
Em ${displaystyle r=1+{sqrt {8}}=3.8284...}$ , o ciclo de período-3 estável emerge.
O desenvolvimento do comportamento caótico da sequência logística como parâmetro $R$ varia de aproximadamente 3,56995 a aproximadamente 3.82843 é às vezes chamado de cenário Pomeau-Manneville, caracterizado por uma fase periódica (laminar) interrompida por explosões de comportamento aperiódico. Tal cenário tem uma aplicação em dispositivos semicondutores. Existem outras gamas que produzem oscilação entre 5 valores etc; todos os períodos de oscilação ocorrem para alguns valores de $R$ . A janela de duplicação de período com parâmetro $c$ é uma gama de $R$ -valores que consistem em uma sucessão de sub-ranges. O $k$ th subrange contém os valores de $R$ para o qual há um ciclo estável (um ciclo que atrai um conjunto de pontos iniciais da medida unitária) do período $2 k c$ . Esta sequência de sub-ranges é chamada de cascata de harmônicos. Em um sub-range com um ciclo estável do período $2 k * c$ , há ciclos instáveis do período $2 k c$ para todos $k < k *$ . O $R$ valor no final da sequência infinita de sub-ranges é chamado o ponto de acumulação da cascata de harmônicos. Como $R$ sobe há uma sucessão de novas janelas com diferentes $c$ valores. O primeiro é para $c = 1$ ; todas as janelas subseqüentes envolvendo ímpar $c$ ocorrer em ordem decrescente de $c$ começando com arbitrariamente grande $c$ .
Além disso. $R = 4$ , quase todos os valores iniciais eventualmente deixam o intervalo $[0,1]$ e divergir. O conjunto de condições iniciais que permanecem no interior $[0,1]$ formar um conjunto Cantor e a dinâmica restrita a este conjunto Cantor é caótico.

Para qualquer valor de $r$ existe no máximo um ciclo estável. Se existe um ciclo estável, ele é globalmente estável, atraindo quase todos os pontos. Alguns valores de $r$ com um ciclo estável de algum período têm infinitos ciclos instáveis de vários períodos.

O diagrama de bifurcação à direita resume isso. O eixo horizontal mostra os possíveis valores do parâmetro $r$ enquanto o eixo vertical mostra o conjunto de valores de $x$ visitado assintoticamente de quase todas as condições iniciais pelos iterados da equação logística com aquele $valor$ .

Diagrama de bifurcação para o mapa logístico. O atrator para qualquer valor do parâmetro

R

é mostrado na linha vertical em que

R

O diagrama de bifurcação é autossimilar: se ampliarmos o valor acima mencionado $r \approx 3,82843$ e focarmos em um braço de os três, a situação próxima parece uma versão reduzida e ligeiramente distorcida de todo o diagrama. O mesmo é verdade para todos os outros pontos não caóticos. Este é um exemplo da conexão profunda e onipresente entre o caos e os fractais.

Magnificação da região caótica do mapa.

Regiões estáveis dentro da região caótica, onde ocorre uma bifurcação tangente na fronteira entre o atrator caótico e periódico, dando trajetórias intermitentes como descrito no cenário Pomeau-Manneville.

Também podemos considerar valores negativos de $r$ :

Para $R$ entre -2 e -1 a sequência logística também apresenta comportamento caótico.
Com $R$ entre -1 e 1 -√6 e para $x$ ₀ entre 1 e 1 $R$ e 1-1/ $R$ , a população abordará oscilações permanentes entre dois valores, como no caso de $R$ entre 3 e 1 +√6, e dada pela mesma fórmula.

O caos e o mapa logístico

Um diagrama de cobweb do mapa logístico, mostrando comportamento caótico para a maioria dos valores de

R > 3.5.7

Função logística

f

(azul) e suas versões iteradas

f 2

f 3

f 4

f 5

para

R = 3.5

. Por exemplo, para qualquer valor inicial no eixo horizontal,

f 4

dá o valor das quatro iterações iteradas mais tarde.

A relativa simplicidade do mapa logístico torna-o um ponto de entrada amplamente utilizado na consideração do conceito de caos. Uma descrição aproximada do caos é que os sistemas caóticos exibem uma grande sensibilidade às condições iniciais - uma propriedade do mapa logístico para a maioria dos valores de $r$ entre cerca de 3,57 e 4 (conforme observado acima). Uma fonte comum de tal sensibilidade às condições iniciais é que o mapa representa uma dobra repetida e um alongamento do espaço no qual é definido. No caso do mapa logístico, a equação de diferença quadrática que o descreve pode ser pensada como uma operação de alongamento e dobra no intervalo $(0,1)$ .

A figura a seguir ilustra o alongamento e dobramento de uma sequência de iterações do mapa. A Figura (a), à esquerda, mostra um gráfico de Poincaré bidimensional do espaço de estado do mapa logístico para $r = 4$ , e claramente mostra a curva quadrática da equação de diferenças (1). No entanto, podemos incorporar a mesma sequência em um espaço de estado tridimensional, a fim de investigar a estrutura mais profunda do mapa. A Figura (b), à direita, demonstra isso, mostrando como pontos inicialmente próximos começam a divergir, particularmente nas regiões de $x t$ correspondente às seções mais íngremes do gráfico.

Esse alongamento e dobramento não produz apenas uma divergência gradual das sequências de iterados, mas uma divergência exponencial (ver expoentes de Lyapunov), evidenciada também pela complexidade e imprevisibilidade do mapa logístico caótico. De facto, a divergência exponencial de sequências de iterados explica a ligação entre caos e imprevisibilidade: um pequeno erro no suposto estado inicial do sistema tenderá a corresponder a um grande erro mais tarde na sua evolução. Portanto, as previsões sobre estados futuros tornam-se progressivamente (de fato, exponencialmente) piores quando há erros ainda muito pequenos em nosso conhecimento do estado inicial. Essa qualidade de imprevisibilidade e aparente aleatoriedade levou a equação do mapa logístico a ser usada como um gerador de números pseudo-aleatórios nos primeiros computadores.

Em r = 2, a função ${displaystyle rx(1-x)}$ intersetos $- Sim.$ precisamente no ponto máximo, assim a convergência ao ponto de equilíbrio está na ordem de ${displaystyle delta ^{2^{n}}}$ . Consequentemente, o ponto de equilíbrio é chamado de "superstável". Seu expoente de Lyapunov é $- Sim.$ . Um argumento semelhante mostra que há uma superestável $Não.$ valor dentro de cada intervalo onde o sistema dinâmico tem um ciclo estável. Isso pode ser visto no enredo expoente de Lyapunov como mergulhos afiados.

Como o mapa está confinado a um intervalo na reta numérica real, sua dimensão é menor ou igual à unidade. As estimativas numéricas geram uma dimensão de correlação de 0,500±0,005 (Grassberger, 1983), uma dimensão Hausdorff de cerca de 0,538 (Grassberger 1981) e uma dimensão de informação de aproximadamente 0,5170976 (Grassberger 1983) para $r \approx 3,5699456$ (início do caos). Nota: Pode-se mostrar que a dimensão da correlação certamente está entre 0,4926 e 0,5024.

Muitas vezes é possível, no entanto, fazer declarações precisas e precisas sobre a probabilidade de um estado futuro em um sistema caótico. Se um sistema dinâmico (possivelmente caótico) tem um atrator, então existe uma medida de probabilidade que dá a proporção de longo prazo do tempo gasto pelo sistema nas várias regiões do atrator. No caso do mapa logístico com parâmetro $r = 4$ e estado inicial em $(0,1)< /span>, o atrator também é o intervalo (0,1) e a medida de probabilidade corresponde à distribuição beta com parâmetros a = 0,5 e b = 0,5 . Especificamente, a medida invariante é$

{displaystyle {frac {1}{pi {sqrt {x(1-x)}}}}}

A imprevisibilidade não é aleatoriedade, mas em algumas circunstâncias parece muito com isso. Portanto, e felizmente, mesmo que saibamos muito pouco sobre o estado inicial do mapa logístico (ou algum outro sistema caótico), ainda podemos dizer algo sobre a distribuição de estados arbitrariamente distantes no futuro e usar esse conhecimento para informar as decisões. com base no estado do sistema.

Mapa logístico com função exponente lyapunov.

Representação gráfica

O diagrama de bifurcação para o mapa logístico pode ser visualizado com o seguinte código Python:

importação - Sim. como nimportação Gerenciamento de contas como Não.intervalo = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = (2., 4) # start, endprecisão = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 0,01reps = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 600 # número de repetiçõesTemporada = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 200Lims = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = n.zeros(reps)Figueira, Biaxial = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = Não..Subplots()Figueira.set_size_inches(16., 9)LimsNão.0] = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = n.aleatório.rand()para R em n.uma variedade(intervaloNão.0] intervaloNão.1] precisão: para Eu... em gama(reps- Não.1: LimsNão.Eu...+1] = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = R*LimsNão.Eu...]*(1- Não.LimsNão.Eu...] Biaxial.enredo(R]*Temporada, LimsNão.reps- Não.Temporada: B. ', marcadores de tamanho= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =.02)Biaxial.conjunto(xlabel= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =' ', - Sim.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = ="x" ', título= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Mapa logístico ')Não..mostrar()

Casos especiais do mapa

Limite superior quando 0 ≤ r ≤ 1

Embora soluções exatas para a relação de recorrência estejam disponíveis apenas em um pequeno número de casos, um limite superior de forma fechada no mapa logístico é conhecido quando $0 \leq r \leq 1$ . Existem dois aspectos do comportamento do mapa logístico que devem ser capturados por um limite superior neste regime: o decaimento geométrico assintótico com constante $r< /span>, e o rápido declínio inicial quando x 0 está próximo de 1, impulsionado pelo (1 - x n) termo na relação de recorrência. O limite a seguir captura esses dois efeitos:$

{displaystyle forall nin {0,1,ldots }quad {text{and}}quad x_{0},rin [0,1],quad x_{n}leq {frac {x_{0}}{r^{-n}+x_{0}n}}.}

Solução quando r = 4

O caso especial de $r = 4$ pode de fato ser resolvido exatamente, assim como o caso com $< i>r = 2$ ; no entanto, o caso geral só pode ser previsto estatisticamente. A solução quando $r = 4$ é,

{displaystyle x_{n}=sin ^{2}left(2^{n}theta pi right),}

onde o parâmetro de condição inicial $θ$ é dado por

{displaystyle theta ={tfrac Não. }}sin ^{-1}left({sqrt {x_{0}}}right).}

Para $θ$ racional, após um número finito de iterações $x n$ mapeia em uma sequência periódica. Mas quase todos os $θ$ são irracionais e, para irracionais $θ$ , $x n$ nunca se repete – é não periódico. Esta equação de solução demonstra claramente as duas principais características do caos – alongamento e dobra: o fator $2 n$ mostra o crescimento exponencial de alongamento, o que resulta em dependência sensível das condições iniciais, enquanto a função seno ao quadrado mantém $x n$ dobrado dentro do intervalo $[0,1]$ .

Para $r = 4$ , uma solução equivalente em termos de números complexos em vez de funções trigonométricas é

Não. x_{n}={frac {-alpha ^{2^{n}}-alpha ^{-2^{n}}+2}{4}}}

onde $α$ é um dos números complexos

{displaystyle alfa =1-2x_{0}pm {sqrt {left(1-2x_{0}right)^{2}-1}}}

com módulo igual a 1. Assim como a função seno ao quadrado na solução trigonométrica não leva nem ao encolhimento nem à expansão do conjunto de pontos visitados, na última solução esse efeito é obtido pelo módulo unitário de $α$ .

Por outro lado, a solução quando $r = 2$ é

Não. x_{n] {1}{2}}. {1}{2}}left(1-2x_{0}right)^{2^{n}}}

para $x 0 \in [0,1)$ . Desde $(1 - 2 x 0) \in (-1,1)$ para qualquer valor de $x 0$ além do ponto fixo instável 0, o termo $(1 - 2 x 0) 2 n$ vai para 0 como $n$ vai para o infinito, então $x n$ vai para o ponto fixo estável 1/2.

Encontrar ciclos de qualquer comprimento quando r = 4

Para o caso $r = 4$ , de quase todas as condições iniciais, a sequência iterada é caótica. No entanto, existe um número infinito de condições iniciais que levam a ciclos e, de fato, existem ciclos de comprimento $k$ para todos inteiros $k > 0$ . Podemos explorar a relação do mapa logístico com a transformação diádica (também conhecida como mapa de deslocamento de bits) para encontrar ciclos de qualquer comprimento. Se $x$ seguir o mapa logístico $x n + 1 = 4 x n (1 - x n)$ e $y$ segue a transformação diádica

Não. y_{n+1}={begin{cases}2y_{n}&0leq - Sim. {1}{2}}\2y_{n}-1&{tfrac {1}{2}}leq y_{n}<1,end{cases}}}

então os dois estão relacionados por um homeomorfismo

{displaystyle x_{n}=sin ^{2}left(2pi y_{n}right).}

A razão pela qual a transformação dídica também é chamada de mapa de bit-shift é que quando $Sim.$ é escrito em notação binária, o mapa move o ponto binário um lugar para a direita (e se o bit para a esquerda do ponto binário se tornou um "1", este "1" é alterado para um "0"). Um ciclo de comprimento 3, por exemplo, ocorre se um iterado tem uma sequência de repetição de 3 bits em sua expansão binária (que não é também uma sequência de repetição de um bit): 001, 010, 100, 110, 101, ou 011. O iterado 001001... mapas em 010010010..., que mapeia em 100100100..., que, por sua vez, mapeia no original 001001001...; assim, este é um 3-ciclo do mapa da mudança de bits. E as outras três sequências de repetição de expansão binária dão o triciclo 110110110... → 101101101... → 011011011... → 110110110.... Qualquer um destes 3 ciclos pode ser convertido em forma de fração: por exemplo, o primeiro triciclo dado pode ser escrito como 1/7 → 2/7 → 4/7 → 1/7. Usando a tradução acima do mapa bit-shift para o $- Sim.$ mapa logístico dá o ciclo logístico correspondente 0.611260467... → 0.950484434... → 0.188255099... → 0.611260467.... Nós poderíamos igualmente traduzir o outro bit-shift 3-ciclo em seu ciclo logístico correspondente. Da mesma forma, ciclos de qualquer comprimento $k$ pode ser encontrado no mapa bit-shift e depois traduzido para os ciclos logísticos correspondentes.

No entanto, como quase todos os números em $[0,1)$ são irracionais, quase todas as condições iniciais do mapa de deslocamento de bits levam à não periodicidade do caos. Esta é uma maneira de ver que o mapa logístico $r = 4$ é caótico para quase todas as condições iniciais.

O número de ciclos de comprimento (mínimo) $k = 1, 2, 3,\dots$ para o mapa logístico com $r = 4$ (mapa de tenda com $μ = 2$ ) é uma sequência inteira conhecida (sequência A001037 no OEIS): 2, 1, 2, 3, 6, 9, 18, 30, 56, 99, 186, 335, 630, 1161.... Isso nos diz que o mapa logístico com $r = 4$ tem 2 pontos fixos, 1 ciclo de comprimento 2, 2 ciclos de comprimento 3 e assim por diante. Esta sequência assume uma forma particularmente simples para primo $k$ : $2 \cdot 2 k - 1 - 1 / k$ . Por exemplo: 2 ⋅ 2^{13 − 1} − 1/13 = 630 é o número de ciclos de comprimento 13. Como este caso do mapa logístico é caótico para quase todos os ciclos iniciais condições, todos esses ciclos de comprimento finito são instáveis.

Conceitos relacionados

Universalidade de Feigenbaum de mapas 1-D

Universalidade de mapas unidimensionais com maxima parabólico e constantes de Feigenbaum ${displaystyle delta =4.669201...}$ , ${displaystyle alpha =2.502907...}$ é bem visível com mapa proposto como um brinquedo modelo para dinâmica laser discreta: ${displaystyle xrightarrow Gx(1-tanh(x)}$ , Onde? $Não.$ significa amplitude de campo elétrico, $Não. G.$ é ganho a laser como parâmetro de bifurcação.

O aumento gradual de $Não. G.$ em intervalo $[0,infty]}$ mudanças dinâmicas de regular para caótico com qualitativamente o mesmo diagrama de bifurcação como aqueles para mapa logístico.

Contenido relacionado

Más resultados...