Mapa linear

ImprimirCitar

Função matemática, em álgebra linear

Em matemática, e mais especificamente em álgebra linear, mapa linear (também chamado de mapeamento linear, transformação linear, homomorfismo do espaço vetorial, ou em alguns contextos função linear) é um mapeamento $Vto W$ entre dois espaços vetoriais que preservam as operações de adição vetorial e multiplicação escalar. Os mesmos nomes e a mesma definição também são usados para o caso mais geral de módulos sobre um anel; veja o homomorfismo do Módulo.

Se um mapa linear é uma bijeção, então é chamado de isomorfismo linear. No caso em que ${displaystyle V=W}$ , um mapa linear é chamado de endomorfismo linear. Às vezes o termo operador linear refere-se a este caso, mas o termo "operador linear" pode ter diferentes significados para diferentes convenções: por exemplo, pode ser usado para enfatizar que $V$ e $W$ são espaços vetoriais reais (não necessariamente com ${displaystyle V=W}$ ), ou pode ser usado para enfatizar que $V$ é um espaço de função, que é uma convenção comum em análise funcional. Às vezes o termo função linear tem o mesmo significado que mapa linear, enquanto em análise não faz.

Um mapa linear de V para W sempre mapeia a origem de V para a origem de W. Além disso, mapeia subespaços lineares em V em subespaços lineares em W (possivelmente de dimensão inferior); por exemplo, mapeia um plano passando pela origem em V para um plano passando pela origem em W, uma linha passando pela origem em W, ou apenas a origem em W. Mapas lineares geralmente podem ser representados como matrizes, e exemplos simples incluem transformações lineares de rotação e reflexão.

Na linguagem da teoria das categorias, os mapas lineares são os morfismos dos espaços vetoriais.

Definição e primeiras consequências

Vamos. $V$ e $W$ ser espaços vetoriais sobre o mesmo campo $K$ . Uma função $f:Vto W$ é dito ser um mapa linear se para qualquer dois vetores ${textstyle mathbf {u}mathbf {v} in V}$ e qualquer escalar ${displaystyle cin K}$ as seguintes duas condições estão satisfeitas:

Aditividade / operação de adição ${displaystyle f(mathbf {u} +mathbf {v})=f(mathbf {u})+f(mathbf {v})}$
Homogeneidade do grau 1 / operação da multiplicação escalar ${displaystyle f(cmathbf {u})=cf(mathbf {u})}$

Assim, diz-se que um mapa linear preserva a operação. Em outras palavras, não importa se o mapa linear é aplicado antes (lado direito dos exemplos acima) ou depois (lado esquerdo dos exemplos) das operações de adição e multiplicação escalar.

Pela associatividade da operação de adição denotada como +, para qualquer vetor ${textstyle mathbf {u} _{1},ldotsmathbf {u} _{n}in V}$ e escalares ${textstyle c_{1},ldotsc_{n}in K,}$ a seguinte igualdade:

{displaystyle f(c_{1}mathbf {u} _{1}+cdots +c_{n}mathbf {u} _{n})=c_{1}f(mathbf {u} _{1})+cdots +c_{n}f(mathbf {u} _{n}).}

Denotando os elementos zero dos espaços vetoriais $V$ e $W$ por ${textstyle mathbf {0} _{V}}$ e ${textstyle mathbf {0} _{W}}$ respetivamente, segue-se que ${textstyle f(mathbf {0} _{V})=mathbf {0} _{W}.}$ Vamos. $c=0$ e ${textstyle mathbf {v} in V}$ na equação para homogeneidade do grau 1:

{displaystyle f(mathbf {0} _{V})=f(0mathbf {v})=0f(mathbf {v})=mathbf {0} _{W}.}

Um mapa linear ${displaystyle Vto K}$ com $K$ visto como um espaço vetorial unidimensional sobre si mesmo é chamado de funcional linear.

Estas declarações generalizam-se em qualquer módulo esquerdo ${textstyle {}_{R}M}$ sobre um anel $R$ sem modificação, e para qualquer direito-módulo após a reverso da multiplicação escalar.

Exemplos

Um exemplo prototípico que dá mapas lineares seu nome é uma função ${displaystyle f:mathbb {R} to mathbb {R}:xmapsto cx}$ , do qual o grafo é uma linha através da origem.
Mais geralmente, qualquer homothety ${textstyle mathbf {v} mapsto cmathbf {v} }$ Onde? $c$ centrado na origem de um espaço vetorial é um mapa linear.
O mapa zero ${textstyle mathbf {x} mapsto mathbf {0} }$ entre dois espaços vetoriais (sobre o mesmo campo) é linear.
O mapa de identidade em qualquer módulo é um operador linear.
Para números reais, o mapa ${textstyle xmapsto x^{2}}$ não é linear.
Para números reais, o mapa ${textstyle xmapsto x+1}$ não é linear (mas é uma transformação affine).
Se $A$ é um $mtimes n$ matriz real, então $A$ define um mapa linear de $mathbb {R} ^{n}$ para $mathbb{R} ^{m}$ enviando um vetor de coluna ${displaystyle mathbf {x} in mathbb {R} ^{n}}$ para o vetor de coluna ${displaystyle Amathbf {x} in mathbb {R} ^{m}}$ . Por outro lado, qualquer mapa linear entre espaços vetoriais finito-dimensionais pode ser representado desta forma; veja o § Matrices, abaixo.
Se ${textstyle f:Vto W}$ é uma isometria entre espaços reais e normed tais que ${textstyle f(0)=0}$ então $f$ é um mapa linear. Este resultado não é necessariamente verdadeiro para o espaço complexo e não normalizado.
A diferenciação define um mapa linear do espaço de todas as funções diferenciadas para o espaço de todas as funções. Ele também define um operador linear no espaço de todas as funções lisas (um operador linear é um operador linear endomorfismo, isto é, um mapa linear com o mesmo domínio e codomínio). Um exemplo é ${displaystyle {frac {d}{dx}}left(c_{1}f_{1}(x)+c_{2}f_{2}(x)+cdots +c_{n}f_{n}(x)right)=c_{1}{frac {df_{1}(x)}{dx}}+c_{2}{frac {df_{2}(x)}{dx}}+cdots +c_{n}{frac {df_{n}(x)}{dx}}.}$
Uma integral definida em algum intervalo $Eu...$ é um mapa linear do espaço de todas as funções integrais reais em $Eu...$ para $mathbb {R}$ . Por exemplo, ${displaystyle int _{a}^{b}left[c_{1}f_{1}(x)+c_{2}f_{2}(x)+dots +c_{n}f_{n}(x)right],dx={c_{1}int _{a}^{b}f_{1}(x),dx}+c_{2}int _{a}^{b}f_{2}(x),dx+cdots +c_{n}int _{a}^{b}f_{n}(x),dx.}$
Uma integral indefinida (ou antiderivativa) com um ponto de partida de integração fixa define um mapa linear do espaço de todas as funções integrais de valor real em $mathbb {R}$ para o espaço de todas as funções reais e diferenciadas em $mathbb {R}$ . Sem um ponto de partida fixo, os mapas antiderivativos para o espaço quociente das funções diferenciadas pelo espaço linear de funções constantes.
Se $V$ e $W$ são espaços vetoriais de dimensão finita sobre um campo $F$ das respectivas dimensões $m$ e $n$ , então a função que mapeia mapas lineares ${textstyle f:Vto W}$ para $n \times m$ matrizes na forma descrita em matrizes (abaixo) é um mapa linear, e até mesmo um isomorfismo linear.
O valor esperado de uma variável aleatória (que é de fato uma função, e como tal elemento de um espaço vetorial) é linear, como para variáveis aleatórias $X$ e $Y$ nós temos ${displaystyle E[X+Y]=E[X]+E[Y]}$ e ${displaystyle E[aX]=aE[X]}$ , mas a variância de uma variável aleatória não é linear.

A função ${textstyle f:mathbb {R} ^{2}to mathbb {R} ^{2}}$ com ${textstyle f(x,y)=(2x,y)}$ é um mapa linear. Esta função escala o ${textstyle x}$ componente de um vetor pelo fator ${textstyle 2}$ .
A função ${textstyle f(x,y)=(2x,y)}$ é aditivo: Não importa se os vetores são adicionados pela primeira vez e depois mapeados ou se são mapeados e finalmente adicionados: ${textstyle f(mathbf {a} +mathbf {b})=f(mathbf {a})+f(mathbf {b})}$
A função ${textstyle f(x,y)=(2x,y)}$ é homogêneo: Não importa se um vetor é escalado pela primeira vez e depois mapeado ou primeiro mapeado e depois dimensionado: ${textstyle f(lambda mathbf {a})=lambda f(mathbf {a})}$

Extensões lineares

Muitas vezes, um mapa linear é construído definindo-o em um subconjunto de um espaço vetorial e, em seguida, estendendo-se pela linearidade para a extensão linear do domínio. Suponha $X$ e $Y$ são espaços vetoriais e ${displaystyle f:Sto Y}$ é uma função definida em algum subconjunto ${displaystyle Ssubseteq X.}$ Então... extensão linear de $f$ para $X,$ se existir, é um mapa linear ${displaystyle F:Xto Y}$ definido em $X$ que se estende $f$ (que significa que ${displaystyle F(s)=f(s)}$ para todos $sin S$ ) e toma os seus valores do codomínio $f.$ Quando o subconjunto $S$ é um subespaço vetorial de $X$ então um ( $Y$ -valorizado) extensão linear de $f$ a todos $X$ é garantido existir se (e somente se) ${displaystyle f:Sto Y}$ é um mapa linear. Em particular, se $f$ tem uma extensão linear para ${displaystyle operatorname {span} S,}$ então tem uma extensão linear para todos $X.$

O mapa ${displaystyle f:Sto Y}$ pode ser estendido para um mapa linear ${displaystyle F:operatorname {span} Sto Y}$ se e somente se sempre $0}" xmlns="http://www.w3.org/1998/Math/MathML">n>0- Sim. 0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/27a6a5d982d54202a14f111cb8a49210501b2c96" style="vertical-align: -0.338ex; width:5.656ex; height:2.176ex;"/>$ é um inteiro, $c_{1},ldotsc_{n}$ são escalares, e ${displaystyle s_{1},ldotss_{n}in S}$ são vetores tais que ${displaystyle 0=c_{1}s_{1}+cdots +c_{n}s_{n},}$ então, necessariamente ${displaystyle 0=c_{1}fleft(s_{1}right)+cdots +c_{n}fleft(s_{n}right).}$ Se uma extensão linear de ${displaystyle f:Sto Y}$ existe então a extensão linear ${displaystyle F:operatorname {span} Sto Y}$ é único e

{displaystyle Fleft(c_{1}s_{1}+cdots c_{n}s_{n}right)=c_{1}fleft(s_{1}right)+cdots +c_{n}fleft(s_{n}right)}

{displaystyle n,c_{1},ldotsc_{n},}

{displaystyle s_{1},ldotss_{n}}

S

{displaystyle f:Sto Y}

{displaystyle ;operatorname {span} Sto Y}

Por exemplo, se ${displaystyle X=mathbb {R} ^{2}}$ e ${displaystyle Y=mathbb {R} }$ então a atribuição ${displaystyle (1,0)to -1}$ e ${displaystyle (0,1)to 2}$ pode ser linearmente estendido do conjunto linearmente independente de vetores ${displaystyle S:={(1,0),(0,1)}}$ para um mapa linear em ${displaystyle operatorname {span} {(1,0),(0,1)}=mathbb {R} ^{2}.}$ A extensão linear única ${displaystyle F:mathbb {R} ^{2}to mathbb {R} }$ é o mapa que envia ${displaystyle (x,y)=x(1,0)+y(0,1)in mathbb {R} ^{2}}$ para

{displaystyle F(x,y)=x(-1)+y(2)=-x+2y.}

Cada (scalar-valorizado) funcional linear $f$ definido em um subespaço vetorial de um espaço vetorial real ou complexo $X$ tem uma extensão linear para todos $X.$ De fato, o teorema de extensão dominado por Hahn-Banach garante mesmo que quando este funcional linear $f$ é dominado por algum seminorm dado ${displaystyle p:Xto mathbb {R} }$ (que significa que ${displaystyle |f(m)|leq p(m)}$ para todos $m$ no domínio de $f$ ) então existe uma extensão linear para $X$ que também é dominado por $p.$

Matrizes

Se $V$ e $W$ são espaços vetoriais de dimensão finita e uma base é definida para cada espaço vetorial, então cada mapa linear de $V$ para $W$ pode ser representado por uma matriz. Isso é útil porque permite cálculos concretos. As matrizes produzem exemplos de mapas lineares: se $A$ é um verdadeiro $mtimes n$ matriz, então ${displaystyle f(mathbf {x})=Amathbf {x} }$ descreve um mapa linear ${displaystyle mathbb {R} ^{n}to mathbb {R} ^{m}}$ (ver espaço euclidiano).

Vamos. ${displaystyle {mathbf {v} _{1},ldotsmathbf {v} _{n}}}$ ser uma base para $V$ . Então, cada vector ${displaystyle mathbf {v} in V}$ é exclusivamente determinado pelos coeficientes ${displaystyle c_{1},ldotsc_{n}}$ no campo $mathbb {R}$ :

{displaystyle mathbf {v} =c_{1}mathbf {v} _{1}+cdots +c_{n}mathbf {v} _{n}.}

Se ${textstyle f:Vto W}$ é um mapa linear,

{displaystyle f(mathbf {v})=f(c_{1}mathbf {v} _{1}+cdots +c_{n}mathbf {v} _{n})=c_{1}f(mathbf {v} _{1})+cdots +c_{n}fleft(mathbf {v} _{n}right),}

que implica que a função f é inteiramente determinado pelos vetores ${displaystyle f(mathbf {v} _{1}),ldotsf(mathbf {v} _{n})}$ . Agora deixa-me. ${displaystyle {mathbf {w} _{1},ldotsmathbf {w} _{m}}}$ ser uma base para $W$ . Então podemos representar cada vector ${displaystyle f(mathbf {v} _{j})}$ como

{displaystyle fleft(mathbf {v} _{j}right)=a_{1j}mathbf {w} _{1}+cdots +a_{mj}mathbf {w} _{m}.}

Assim, a função $f$ é inteiramente determinado pelos valores de $a_{ij}$ . Se colocarmos esses valores em um $mtimes n$ matriz de matriz $M$ , então podemos usá-lo convenientemente para calcular a saída vetorial de $f$ para qualquer vetor em $V$ . Para começar $M$ , cada coluna $j$ de $M$ is a vector

{displaystyle {begin{pmatrix}a_{1j}\vdots \a_{mj}end{pmatrix}}}

{displaystyle f(mathbf {v} _{j})}

j

{displaystyle f(mathbf {v} _{j})}

{displaystyle mathbf {M} ={begin{pmatrix} cdots &a_{1j}&cdots \&vdots &\&a_{mj}&end{pmatrix}}}

M

f

j=1,ldotsn

{displaystyle f(mathbf {v} _{j})}

{displaystyle a_{1j},cdotsa_{mj}}

j

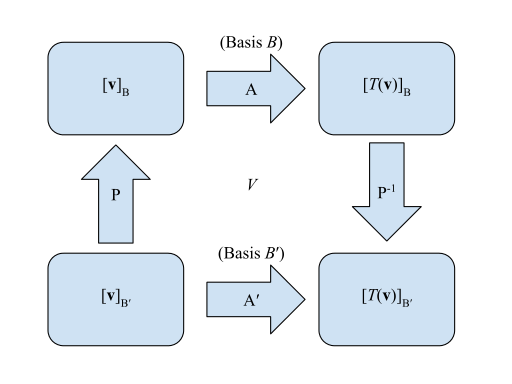
As matrizes de uma transformação linear podem ser representadas visualmente:

Matriz para ${textstyle T}$ em relação a ${textstyle B}$ : ${textstyle A}$
Matriz para ${textstyle T}$ em relação a ${textstyle B'}$ : ${textstyle A'}$
Matriz de transição ${textstyle B'}$ para ${textstyle B}$ : ${textstyle P}$
Matriz de transição ${textstyle B}$ para ${textstyle B'}$ : ${textstyle P^{-1}}$

A relação entre matrizes em uma transformação linear

Tal que começando no canto inferior esquerdo ${textstyle left[mathbf {v} right]_{B'}}$ e procurando o canto inferior direito ${textstyle left[Tleft(mathbf {v} right)right]_{B'}}$ , um de esquerda-múltipla - isto é, ${textstyle A'left[mathbf {v} right]_{B'}=left[Tleft(mathbf {v} right)right]_{B'}}$ . O método equivalente seria o método "mais longo" indo no sentido horário a partir do mesmo ponto tal que ${textstyle left[mathbf {v} right]_{B'}}$ é multiplicado pela esquerda ${textstyle P^{-1}AP}$ ou ${textstyle P^{-1}APleft[mathbf {v} right]_{B'}=left[Tleft(mathbf {v} right)right]_{B'}}$ .

Exemplos em duas dimensões

No espaço bidimensional R² mapas lineares são descritos por matrizes 2 × 2. Estes são alguns exemplos:

rotação
- por 90 graus no sentido contrário: ${displaystyle mathbf {A} ={begin{pmatrix}0&-1\1&0end{pmatrix}}}$
- por um ângulo θ no sentido horário: ${displaystyle mathbf {A} ={begin{pmatrix}cos theta &-sin theta \sin theta &cos theta end{pmatrix}}}$
reflexão
- através do x eixo: ${displaystyle mathbf {A} ={begin{pmatrix}1&0\0&-1end{pmatrix}}}$
- através do Sim. eixo: ${displaystyle mathbf {A} ={begin{pmatrix}-1&0\0&1end{pmatrix}}}$
- através de uma linha fazendo um ângulo θ com a origem: ${displaystyle mathbf {A} ={begin{pmatrix}cos 2theta &sin 2theta \sin 2theta &-cos 2theta end{pmatrix}}}$
escalar por 2 em todas as direções: ${displaystyle mathbf {A} ={begin{pmatrix}2&0\0&2end{pmatrix}}=2mathbf {I} }$
mapeamento horizontal do cisalhamento: ${displaystyle mathbf {A} ={begin{pmatrix}1&m\0&1end{pmatrix}}}$
apertar mapeamento: ${displaystyle mathbf {A} ={begin{pmatrix}k&0\0&{frac {1}{k}}end{pmatrix}}}$
projeção na Sim. eixo: ${displaystyle mathbf {A} ={begin{pmatrix}0&0\0&1end{pmatrix}}.}$

Espaço vetorial de mapas lineares

A composição dos mapas lineares é linear: se $f:Vto W$ e ${textstyle g:Wto Z}$ são lineares, então a sua composição ${textstyle gcirc f:Vto Z}$ . Resulta disto que a classe de todos os espaços vetoriais sobre um determinado campo KK, juntamente com KK- mapas lineares como morfismos, forma uma categoria.

O inverso de um mapa linear, quando definido, é novamente um mapa linear.

Se ${textstyle f_{1}:Vto W}$ e ${textstyle f_{2}:Vto W}$ são lineares, então a sua soma pontual $f_1 + f_2$ , que é definido por ${displaystyle (f_{1}+f_{2})(mathbf {x})=f_{1}(mathbf {x})+f_{2}(mathbf {x})}$ .

Se ${textstyle f:Vto W}$ é linear e ${textstyle alpha }$ é um elemento do campo terrestre ${textstyle K}$ , então o mapa ${textstyle alpha f}$ , definido por ${textstyle (alpha f)(mathbf {x})=alpha (f(mathbf {x}))}$ , também é linear.

Assim, o conjunto ${textstyle {mathcal {L}}(V,W)}$ de mapas lineares de ${textstyle V}$ para ${textstyle W}$ em si forma um espaço vetorial sobre ${textstyle K}$ , às vezes denotado ${textstyle operatorname {Hom} (V,W)}$ . Além disso, no caso de ${textstyle V=W}$ , este espaço vetorial, denotado ${textstyle operatorname {End} (V)}$ , é uma álgebra associativa sob a composição de mapas, uma vez que a composição de dois mapas lineares é novamente um mapa linear, e a composição dos mapas é sempre associativa. Este caso é discutido em mais detalhes abaixo.

Dado novamente o caso de dimensão finita, se as bases foram escolhidas, então a composição de mapas lineares corresponde à multiplicação de matrizes, a adição de mapas lineares corresponde à adição de matrizes e a multiplicação de mapas lineares com escalares corresponde a a multiplicação de matrizes com escalares.

Endomorfismos e automorfismos

Uma transformação linear ${textstyle f:Vto V}$ é um endomorfismo de ${textstyle V}$ ; o conjunto de todos esses endomorfismos ${textstyle operatorname {End} (V)}$ em conjunto com a adição, composição e multiplicação escalar conforme definido acima forma uma álgebra associativa com elemento de identidade sobre o campo ${textstyle K}$ (e em particular um anel). O elemento de identidade multiplicador desta álgebra é o mapa de identidade ${textstyle operatorname {id}:Vto V}$ .

Um endomorfismo ${textstyle V}$ que também é um isomorfismo é chamado de automorfismo ${textstyle V}$ . A composição de dois automorfismos é novamente um automorfismo, e o conjunto de todos os automorfismos de ${textstyle V}$ forma um grupo, o grupo de automorfismo ${textstyle V}$ que é denotado por ${textstyle operatorname {Aut} (V)}$ ou ${textstyle operatorname {GL} (V)}$ . Como os automorfismos são precisamente aqueles endomorfismos que possuem inversos sob a composição, ${textstyle operatorname {Aut} (V)}$ é o grupo de unidades no anel ${textstyle operatorname {End} (V)}$ .

Se ${textstyle V}$ tem dimensão finita ${textstyle n}$ , então ${textstyle operatorname {End} (V)}$ isomorfo para a álgebra associativa de todos ${textstyle ntimes n}$ matrizes com entradas em ${textstyle K}$ . O grupo de automorfismo ${textstyle V}$ isomorfo para o grupo linear geral ${textstyle operatorname {GL} (n,K)}$ de todos ${textstyle ntimes n}$ matrizes invertíveis com entradas em ${textstyle K}$ .

Núcleo, imagem e o teorema da nulidade de classificação

Se ${textstyle f:Vto W}$ é linear, nós definemos o kernel e a imagem ou o intervalo de ${textstyle f}$ por

{displaystyle {begin{aligned}ker(f)&={,mathbf {x} in V:f(mathbf {x})=mathbf {0} ,}\operatorname {im} (f)&={,mathbf {w} in W:mathbf {w} =f(mathbf {x}),mathbf {x} in V,}end{aligned}}}

${textstyle ker(f)}$ é um subespaço de ${textstyle V}$ e ${textstyle operatorname {im} (f)}$ é um subespaço de ${textstyle W}$ . A seguinte fórmula de dimensão é conhecida como teorema de classificação-nulidade:

{displaystyle dim(ker(f))+dim(operatorname {im} (f))=dim(V).}

O número ${textstyle dim(operatorname {im} (f))}$ é também chamado de classificação ${textstyle f}$ e escrito como ${textstyle operatorname {rank} (f)}$ , ou às vezes, ${textstyle rho (f)}$ ; o número ${textstyle dim(ker(f))}$ é chamado de nulidade de ${textstyle f}$ e escrito como ${textstyle operatorname {null} (f)}$ ou ${textstyle nu (f)}$ . Se ${textstyle V}$ e ${textstyle W}$ são finito-dimensional, bases foram escolhidas e ${textstyle f}$ é representado pela matriz ${textstyle A}$ , então a classificação e nulidade de ${textstyle f}$ são iguais à classificação e nulidade da matriz ${textstyle A}$ , respectivamente.

Cokernel

Uma invariante mais sutil de uma transformação linear ${textstyle f:Vto W}$ é o coquetel, que é definido como

{displaystyle operatorname {coker} (f):=W/f(V)=W/operatorname {im} (f).}

Esta é a noção dual para o kernel: assim como o kernel é um subespaço do domínio, o co-kernel é um espaço quociente do alvo. Formalmente, tem-se a sequência exata

{displaystyle 0to ker(f)to Vto Wto operatorname {coker} (f)to 0.}

Eles podem ser interpretados assim: dada uma equação linear f(v) = w para resolver,

o kernel é o espaço de soluções ao homogêneo Equação f(v) = 0, e sua dimensão é o número de graus de liberdade no espaço de soluções, se não estiver vazio;
o co-kernel é o espaço de restrições que as soluções devem satisfazer, e sua dimensão é o número máximo de restrições independentes.

A dimensão do co-kernel e a dimensão da imagem (a classificação) somam a dimensão do espaço de destino. Para dimensões finitas, isso significa que a dimensão do espaço quociente W/f(V) é a dimensão do espaço alvo menos a dimensão da imagem.

Como um exemplo simples, considere o mapa f: R² → R², dado por f(x, Sim.) = (0, Sim.). Então para uma equação f(x, Sim.) = (um, b)) ter uma solução, devemos ter um = 0 (uma restrição), e nesse caso o espaço de solução é (x, b)) ou declarada equivalente, (0, b)) + (x, 0), (um grau de liberdade). O kernel pode ser expresso como subespaço (x, 0) < V: o valor de x é a liberdade em uma solução – enquanto o coquetel pode ser expresso através do mapa W → R, ${textstyle (a,b)mapsto (a)}$ : dado um vetor (um, b)), o valor de um é o obstrução para lá ser uma solução.

Um exemplo ilustrando o caso infinita-dimensional é concedido pelo mapa f: R^∞ → R^∞, ${textstyle left{a_{n}right}mapsto left{b_{n}right}}$ com b)₁ = 0 e b)_{n + 1} = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = um_n para n > 0. Sua imagem consiste em todas as sequências com o primeiro elemento 0, e assim seu coquetel consiste nas classes de sequências com o primeiro elemento idêntico. Assim, enquanto seu kernel tem dimensão 0 (ele mapeia apenas a sequência zero para a sequência zero), seu co-kernel tem dimensão 1. Uma vez que o domínio e o espaço de destino são os mesmos, a classificação e a dimensão do kernel adicionam até a mesma soma que a classificação e a dimensão do co-kernel ( ${textstyle aleph _{0}+0=aleph _{0}+1}$ ), mas no caso infinita-dimensional não pode ser inferido que o kernel e o co-kernel de um endomorfismo têm a mesma dimensão (0 ≠ 1). A situação inversa obtém-se para o mapa h: R^∞ → R^∞, ${textstyle left{a_{n}right}mapsto left{c_{n}right}}$ com c_n = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = um_{n + 1}. Sua imagem é todo o espaço-alvo, e daí seu co-kernel tem dimensão 0, mas como mapeia todas as sequências em que apenas o primeiro elemento é não-zero para a sequência zero, seu kernel tem dimensão 1.

Índice

Para um operador linear com kernel e co-kernel de dimensão finita, pode-se definir índice como:

{displaystyle operatorname {ind} (f):=dim(ker(f))-dim(operatorname {coker} (f)),}

Para uma transformação entre espaços vetoriais de dimensão finita, isso é apenas a diferença dim(V) − dim(W), por posto–nulidade. Isso dá uma indicação de quantas soluções ou quantas restrições se tem: se mapear de um espaço maior para um menor, o mapa pode estar sobre e, portanto, terá graus de liberdade mesmo sem restrições. Por outro lado, se mapear de um espaço menor para um maior, o mapa não pode ser inserido e, portanto, haverá restrições mesmo sem graus de liberdade.

O índice de um operador é precisamente a característica de Euler do complexo de 2 termos 0 → V → W → 0. Na teoria dos operadores, o índice dos operadores de Fredholm é um objeto de estudo, com um resultado importante sendo o teorema do índice de Atiyah-Singer.

Classificações algébricas de transformações lineares

Nenhuma classificação de mapas lineares pode ser exaustiva. A lista incompleta a seguir enumera algumas classificações importantes que não requerem nenhuma estrutura adicional no espaço vetorial.

Deixe $V$ e $W$ denotam espaços vetoriais sobre um campo $F$ e permitem $T : V \to W$ seja um mapa linear.

Monomorfismo

$T$ é dito ser injetivo ou um monomorfismo se qualquer uma das seguintes condições equivalentes for verdadeira:

$T$ é um a um como um mapa de conjuntos.
$ker T ? V ?$
$(em inglês) T) = 0$
$T$ é monic ou cancelável à esquerda, ou seja, para qualquer espaço vetorial $U$ e qualquer par de mapas lineares $R : U \to V$ e $S : U \to V$ , a equação $TRIBUNAL = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = TS$ implica $R = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = S$ .
$T$ é irreversível, o que é dizer que existe um mapa linear $S : W \to V$ tal que $ST$ é o mapa de identidade sobre $V$ .

Epimorfismo

$T$ é dito ser sobrejetivo ou um epimorfismo se qualquer uma das seguintes condições equivalentes for verdadeira:

$T$ é como um mapa de conjuntos.
$Coquete T ? W ?$
$T$ é épico ou direito-cancelável, ou seja, para qualquer espaço vetorial $U$ e qualquer par de mapas lineares $R : W \to U$ e $S : W \to U$ , a equação $RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT RT = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = ST$ implica $R = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = S$ .
$T$ é invertível, o que é dizer que existe um mapa linear $S : W \to V$ tal que $TS$ é o mapa de identidade sobre $W$ .

Isomorfismo

$T$ é considerado um isomorfismo se for invertível à esquerda e à direita. Isso é equivalente a $T$ sendo um-para-um e sobre (uma bijeção de conjuntos) ou também $T$ sendo tanto épico quanto mônico, sendo assim um bimorfismo.

Se $T : V \to V$ é um endomorfismo, então:

Se, para algum inteiro positivo $n$ , o $n$ - o iterado de $T$ , $T n$ , é idêntico zero, então $T$ é dito ser nilpotent.
Se $T 2 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = T$ , então $T$ é dito para ser idempotent
Se $T = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = KI$ , onde $k$ é algum escalar, então $T$ é dito ser uma transformação escalonante ou mapa de multiplicação escalar; ver matriz escalar.

Mudança de base

Dado um mapa linear que é um endomorfismo cuja matriz é A, na base B do espaço ele transforma as coordenadas vetoriais [u] como [v] = A[u]. Como os vetores mudam com o inverso de B (os vetores são contravariantes), sua transformação inversa é [v] = B[v'].

Substituindo isso na primeira expressão

{displaystyle Bleft[v'right]=ABleft[u'right]}

{displaystyle left[v'right]=B^{-1}ABleft[u'right]=A'left[u'right].}

Portanto, a matriz na nova base é A′ = B⁻¹AB, sendo B a matriz da base dada.

Portanto, mapas lineares são considerados objetos 1-co- 1-contra-variantes, ou tensores do tipo (1, 1).

Continuidade

Uma transformação linear entre espaços vetoriais topológicos, por exemplo espaços normados, pode ser contínua. Se seu domínio e contradomínio forem iguais, ele será um operador linear contínuo. Um operador linear em um espaço linear normado é contínuo se e somente se for limitado, por exemplo, quando o domínio for de dimensão finita. Um domínio de dimensão infinita pode ter operadores lineares descontínuos.

Um exemplo de uma transformação linear ilimitada, portanto descontínua, é a diferenciação no espaço de funções suaves equipadas com a norma suprema (uma função com valores pequenos pode ter uma derivada com valores grandes, enquanto a derivada de 0 é 0). Para um exemplo específico, $sin(nx)/ n$ converge para 0, mas sua derivada $cos(nx)$ não, então a diferenciação não é contínua em 0 (e por uma variação deste argumento, não é contínua em qualquer lugar).

Aplicativos

Uma aplicação específica de mapas lineares é para transformações geométricas, como as realizadas em computação gráfica, onde a translação, rotação e dimensionamento de objetos 2D ou 3D é realizada pelo uso de uma matriz de transformação. Mapeamentos lineares também são usados como um mecanismo para descrever mudanças: por exemplo, em cálculo, correspondem a derivadas; ou na relatividade, usado como um dispositivo para acompanhar as transformações locais dos referenciais.

Outra aplicação dessas transformações é em otimizações de compilador de código de loop aninhado e em paralelizar técnicas de compilador.

Contenido relacionado

Más resultados...