Johnson sólido

Girobicupola quadrada alongada (JJ₃₇), um sólido Johnson

Este exemplo de triângulo equilátero 24 não é um sólido Johnson porque não é convexo.

Este exemplo de 24 quadrados não é um sólido Johnson porque não é estritamente convexo (tem ângulos dihedrais de 180°.)

Em geometria, um sólido de Johnson é um poliedro estritamente convexo em que cada face é um polígono regular. Não há exigência de que cada face seja o mesmo polígono ou que os mesmos polígonos se unam em torno de cada vértice. Um exemplo de sólido de Johnson é a pirâmide de base quadrada com lados equiláteros (J1); tem 1 face quadrada e 4 faces triangulares. Alguns autores exigem que o sólido não seja uniforme (ou seja, não sólido platônico, sólido arquimediano, prisma uniforme ou antiprisma uniforme) antes de se referirem a ele como um "sólido de Johnson".

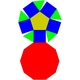
Como em qualquer sólido estritamente convexo, pelo menos três faces se encontram em cada vértice e o total de seus ângulos é inferior a 360 graus. Como um polígono regular tem ângulos de pelo menos 60 graus, segue-se que no máximo cinco faces se encontram em qualquer vértice. A pirâmide pentagonal (J₂) é um exemplo que tem um vértice de grau 5.

Embora não haja nenhuma restrição óbvia de que qualquer polígono regular dado não possa ser uma face de um sólido de Johnson, verifica-se que as faces de sólidos de Johnson que não são uniformes (ou seja, não são sólidos platônicos, sólidos arquimedianos, prismas uniformes, ou antiprisma uniforme) sempre têm 3, 4, 5, 6, 8 ou 10 lados.

Em 1966, Norman Johnson publicou uma lista que incluía todos os 92 sólidos de Johnson (excluindo os 5 sólidos platônicos, os 13 sólidos arquimedianos, os infinitos prismas uniformes e os infinitos antiprismas uniformes) e deu a eles seus nomes e números. Ele não provou que havia apenas 92, mas conjecturou que não havia outros. Victor Zalgaller em 1969 provou que a lista de Johnson estava completa.

Dos sólidos de Johnson, a girobicúpula quadrada alongada (J₃₇), também chamada de pseudorrombicuboctaedro, é única por serem localmente uniformes nos vértices: há 4 faces em cada vértice, e sua disposição é sempre a mesma: 3 quadrados e 1 triângulo. No entanto, não é um vértice transitivo, pois tem diferentes isometrias em diferentes vértices, tornando-o um sólido de Johnson em vez de um sólido de Arquimedes.

Nomes

A nomenclatura dos sólidos de Johnson segue uma fórmula descritiva flexível e precisa, de modo que muitos sólidos podem ser nomeados de maneiras diferentes sem comprometer sua precisão como descrição. A maioria dos sólidos de Johnson pode ser construída a partir dos primeiros (pirâmides, cúpulas e rotundas), juntamente com os sólidos platônicos e arquimedianos, prismas e antiprismas; o centro do nome de um determinado sólido refletirá esses ingredientes. A partir daí, uma série de prefixos são anexados à palavra para indicar acréscimos, rotações e transformações:

• Bi-[] indica que duas cópias do sólido em questão são unidas base para base. Para cupolae e rotundas, os sólidos podem ser unidos para que tanto como rostos (orto...) ou ao contrário dos rostos (Gyro...) conhecer. Usando esta nomenclatura, um octahedron pode ser descrito como um bipirâmida quadrada[4], um cuboctahedron como um gyrobicupola triangular[3cc*]e um icosidodecaedro como um gyrobirotunda pentagonal[5rr*].
• Elongado [=] indica um prisma é unido à base do sólido em questão, ou entre as bases no caso de Bi- sólidos. Um rhombicuboctahedron pode assim ser descrito como um ortobicupola quadrada alongada.
• Gyroelongated[z] indica que um antiprisma é unido à base do sólido em questão ou entre as bases no caso de Bi- sólidos. Um icosaedro pode assim ser descrito como um bipiramida pentagonal alongada.
• Aumentada [+] indica outro poliedro, ou seja, uma pirâmide ou cúpula, é unido a uma ou mais faces do sólido em questão.
• Diminuição. indica uma pirâmide ou cúpula é removida de uma ou mais faces do sólido em questão.
• Gyrate [*] indica uma cúpula montada em ou destaque no sólido em questão é girada de tal forma que diferentes bordas correspondem, como na diferença entre orto- e girobóbicaupolae.

As últimas três operações—aumento, diminuição e giração—podem ser executadas várias vezes para determinados sólidos grandes. Bi- & Tri- indicam uma operação dupla e tripla, respectivamente. Por exemplo, um sólido bigirato tem duas cúpulas rotacionadas e um sólido tridiminuto tem três pirâmides ou cúpulas removidas.

Em certos sólidos grandes, é feita uma distinção entre sólidos onde as faces alteradas são paralelas e sólidos onde as faces alteradas são oblíquas. Para- indica o primeiro, que o sólido em questão tem faces paralelas alteradas, e meta- o último, faces oblíquas alteradas. Por exemplo, um sólido parabiaaumentado teve duas faces paralelas aumentadas e um sólido metabigirato teve 2 faces oblíquas giradas.

Os últimos sólidos de Johnson têm nomes baseados em certos complexos de polígonos a partir dos quais são montados. Esses nomes são definidos por Johnson com a seguinte nomenclatura:

• A Lune é um complexo de dois triângulos ligados a lados opostos de um quadrado.
• Spheno- indica um complexo semelhante à cunha formado por duas lunas adjacentes. Dispheno... indica dois desses complexos.
• Hebespheno- indica um complexo de dois tons separados por uma terceira faixa.
• Corona é um complexo de oito triângulos.
• Megacorona é um complexo maior tipo coroa de 12 triângulos.
• O sufixo...Cangulum indica um cinto de 12 triângulos.

Enumeração

Pirâmides, cúpulas e rotundas

Os primeiros 6 sólidos de Johnson são pirâmides, cúpulas ou rotundas com no máximo 5 faces laterais. Pirâmides e cúpulas com 6 ou mais faces laterais são coplanares e, portanto, não são sólidos de Johnson.

Pirâmides

Os dois primeiros sólidos de Johnson, J1 e J2, são pirâmides. A pirâmide triangular é o tetraedro regular, portanto não é um sólido de Johnson. Eles representam seções de poliedros regulares.

Regular 3> T	J1 4	J2 5>
Pirâmide triangular (Tetraedro)	pirâmide quadrada	Pirâmide Pentágono
Poliedros regulares relacionados
Tetraedro	Octaedron	Icosahedron

Cúpulas e rotundas

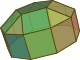
Os próximos quatro sólidos de Johnson são três cúpulas e uma rotunda. Eles representam seções de poliedros uniformes.

Cupola				Rotunda
Uniforme	J3 3c aC...	J4 4c	J5 5c	J6 5r aD...
Rápido (Digonal cupola) (Triangular prisma)	Taça triangular	cúpula quadrada	Cupola Pentagonal	rotunda Pentágona
Poliedros uniformes relacionados
	Anúncio grátis para sua empresa	Anúncio grátis para sua empresa	O que é isso?	Icosido descaído

Pirâmides modificadas

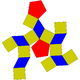
Os sólidos de Johnson 7 a 17 são derivados de pirâmides.

Pirâmides alongadas e giro-alongadas

Na pirâmide triangular girolongada, três pares de triângulos adjacentes são coplanares e formam losangos não quadrados, portanto não é um sólido de Johnson.

Pirâmides alongados			Pirâmides alongados de giro
J7 3=>	J8 4=>	J9 5=>	Coplanar	J10 4z>	J11 5z> Eu...
pirâmide triangular alongada	pirâmide quadrada alongada	Pirâmide pentagonal alongada	pirâmide triangular alongada (diminuído trapezohedron trigonal)	pirâmide quadrada alongada	Pirâmide pentagonal alongada de giro
Aumentado de poliedros
Tetrahedron prisma triangular	pirâmide quadrada Cubo	pirâmide pentagonal pentagonal prisma	Tetrahedron octahedron	pirâmide quadrada antiprisma quadrado	pirâmide pentagonal antiprisma pentagonal

Bipirâmides

A bipirâmide quadrada é o octaedro regular, enquanto a bipirâmide pentagonal giro-alongada é o icosaedro regular, portanto não são sólidos de Johnson. Na bipirâmide triangular girolongada, seis pares de triângulos adjacentes são coplanares e formam losangos não quadrados, portanto também não é um sólido de Johnson.

Bipiramidas			Bipiramidas alongadas			Bipiramidas alongadas
J12 3	Regular	J13 5	J14 3	J15 4	J16 5	Coplanar	J17 4	Regular
Bipiramida triangular	Bipiramida quadrada (octahedron)	Bipiramida Pentagonal	Bipiramida triangular alongada	Bipiramida quadrada alongada	Bipiramida pentagonal alongada	Bipiramida triangular alongada (armadilha trigonal)	Bipiramida quadrada alongada	Bipiramida pentagonal alongada de giro - Não.
Aumentado de poliedros
Tetrahedron	pirâmide quadrada	pirâmide pentagonal	Tetrahedron prisma triangular	pirâmide quadrada Cubo	pirâmide pentagonal pentagonal prisma	Tetrahedron Octaedron	pirâmide quadrada antiprisma quadrado	pirâmide pentagonal antiprisma pentagonal

Cúpulas e rotundas modificadas

Os sólidos de Johnson 18 a 48 são derivados de cúpulas e rotundas.

Cúpulas e rotundas alongadas e giro-alongadas

Copola alongada				rotunda alongada	Copola alongada de giro				rotunda alongada de giro
Coplanar	J18 3c...	J19 4c = eC	J20 5c...	J21 5r.	Concave	J22 3cz	J23 4cz	J24 5cz	J25 5rz
Fastigium alongado	Copola triangular alongada	cúpula quadrada alongada	Cupola pentagonal alongada	rotunda pentagonal alongada	Gyroelongated fastigium	cúpula triangular alongada	cúpula quadrada alongada	Cupola pentagonal alongada de giro	rotunda pentagonal alongada de giro
Aumentado de poliedros
Praça prisma Prisma triangular	Prisma hexagonal Taça triangular	Prisma octogonal cúpula quadrada	Prisma Decagonal Cupola Pentagonal	Prisma Decagonal rotunda Pentágona	antiprisma quadrado Prisma triangular	Antiprisma hexagonal Taça triangular	Antiprisma octogonal cúpula quadrada	Antiprisma Decagonal Cupola Pentagonal	Antiprisma Decagonal rotunda Pentágona

Bicúpulas

A girobicúpula triangular é um sólido arquimediano (neste caso, o cuboctaedro), portanto não é um sólido de Johnson.

Ortopedia				Anúncio grátis para sua empresa
Coplanar	J27 3	J28 4cc	J30 5cc	J26 2cc	Semiregular	J29 4cc	J31 5cc
Ortodoxo	Ortopedia Triangular	Ortopedia quadrada	Ortopedia Pentagonal	Girobigénio	Giróbicas triangulares (cuboctahedron)	Girobicupola quadrada	Girobicupola Pentagonal
Aumentado de poliedro
Prisma triangular	Taça triangular	cúpula quadrada	Cupola Pentagonal	Prisma triangular	Taça triangular	cúpula quadrada	Cupola Pentagonal

Cupola-rotundas e birotundas

O girobirotunda pentagonal é um sólido de Arquimedes (neste caso, o icosidodecaedro), portanto não é um sólido de Johnson.

Copo-rotunda		Birotunda
J32 5cr	J33 5cr	J34 5rr aD	Semiregular
Ortopedia Pentagonal	Girocupolarotunda Pentagonal	Ortopedia Pentágona	Girobirotunda Pentagonal (esidodecaedro)
Aumentado de poliedros
Cupola Pentagonal rotunda Pentágona		rotunda Pentágona

Bicúpulas alongadas

A ortobicúpula quadrada alongada é um sólido de Arquimedes (neste caso, o rombicuboctaedro), portanto não é um sólido de Johnson.

Ortobicupola alongada				Girobicupola alongada
Coplanar	J35 3c	Semiregular	J38 5c	Coplanar	J36 3c = c	J37 4c = c)	J39 5c = c
Ortobifastigium alongado	Ortobicupola triangular alongada	Ortobicupola quadrada alongada (rhombicuboctahedron)	Ortobicupola pentagonal alongada	Girobifastigium alongado	Girobicupola triangular alongada	Girobicupola quadrada alongada	Girobicupola pentagonal alongada
Aumentado de poliedros
Praça prisma Prisma triangular	Prisma hexagonal Taça triangular	Prisma octogonal cúpula quadrada	Prisma Decagonal Cupola Pentagonal	Praça prisma Prisma triangular	Prisma hexagonal Taça triangular	Prisma octogonal cúpula quadrada	Prisma Decagonal Cupola Pentagonal

Cúpula-rotundas e birotundas alongadas

Copola alongada-rotunda		Birotunda alongada
J40 5c =	J41 5c =	J42 5r.	J43 5r.
Ortopedia pentagonal alongada	Girocupolarotunda pentagonal alongada	Ortobirotunda pentagonal alongada	Girobirotunda pentagonal alongada
Aumentado de poliedros
Prisma Decagonal Cupola Pentagonal rotunda Pentágona		Prisma Decagonal rotunda Pentágona

Bicúpulas girolongadas, cúpula-rotundas e birotundas

Esses sólidos de Johnson têm 2 formas quirais.

Bicupola alongada de giro				Copo-rotunda alongada de giro	Birotunda alongada de giro
Concave	J44 3czc	J45 4c	J46 5czc	J47 5czr	J48 5rzr
Bifastigium alongado de giro	Bicupola triangular alongada	Bicupola quadrada alongada	Bicupola pentagonal alongada de giro	Cupolarotunda pentagonal alongada de giro	Birotunda pentagonal alongada de giro
Aumentado de poliedros
Prisma triangular Antiprisma quadrado	Taça triangular Antiprisma hexagonal	cúpula quadrada Antiprisma octogonal	Cupola Pentagonal Antiprisma Decagonal	Cupola Pentagonal rotunda Pentágona Antiprisma Decagonal	rotunda Pentágona Antiprisma Decagonal

Prismas aumentados

Os sólidos de Johnson 49 a 57 são construídos aumentando os lados dos prismas com pirâmides quadradas.

Prismas triangulares aumentados			Prismas pentagonais aumentados		Prismas hexagonais aumentados
J49 3+	J50 3+	J51 3+	J52 5+	J53 5 = ++	J54 6+	J55 6 ++	J56 6+x	J57 6+
Prisma triangular aumentada	Prisma triangular hidratado	Prisma triangular reforçado	Prisma pentagonal aumentada	Prisma pentagonal aumentada	Prisma hexagonal aumentada	Prisma hexagonal parabiaugnado	Prisma hexagonal metabida	Prisma hexagonal aumentada
Aumentado de poliedros
Prisma triangular pirâmide quadrada			Prisma Pentágono pirâmide quadrada		Prisma hexagonal pirâmide quadrada

J8 e J15 também caberiam aqui, como um prisma quadrado aumentado e um prisma quadrado biaumentado.

Sólidos platônicos modificados

Os sólidos de Johnson 58 a 64 são construídos aumentando ou diminuindo os sólidos platônicos.

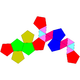
Dodecaedro aumentado

J58 D+	J59 D++	J60 D+x	J61 D+++
Dodecaedro aumentado	Dodecaedron parabiaugmente	Dodecaedro metabólico	Dodecaedrons de Triaugmente
Aumentado de poliedros
Dodecaedro e pirâmide pentagonal

Icosaedro diminuído e aumentado

Diminuindo icosahedron				icosahedron tridiminished aumentada
J11 (Repetido)	Uniforme	J62 I-	J63...	J64 I...+
Diminuindo icosahedron (Gyroelongated pentagonal pirâmide)	Parabidiminiedron (Pentagonal antiprisma)	Metabidiminiedron	Tridiminiedron	icosahedron tridiminished aumentada

Sólidos arquimedianos modificados

Os sólidos de Johnson 65 a 83 são construídos aumentando, diminuindo ou girando sólidos arquimedianos.

Sólidos arquimedianos aumentados

Tetraedro truncado aumentado	Cubos truncados aumentados		Dodecahedra truncado aumentada
J65 tT+	J66 tC+	J67 tC++	J68 tD+	J69 tD++	J70 tD+x	J71 tD+++
Tetraedro truncado aumentado	Cubo truncado aumentado	Biaugmented truncado cubo	Dodecaedro truncado aumentado	Dodecaedro truncado parabiaugmente	Dodecaedro truncado metabiçado	Triaugmente truncado dodecaedron
Aumentado de poliedros
tetraedro truncado cúpula triangular	cubo truncado cúpula quadrada		dodecaedro truncado cúpula pentagonal

Rombicosidodecaedros girados e diminuídos

Produtos de plástico
J72 eD	J73 eD	J74 eD '	J75 eD
Linha de montagem automática	Parabigyrate rhombicosidodecahedron	Medidores de água	Categoria de produtos
Diminuição de rótulos
J76 eD...	J80 eD...	J81 eD...	J83 eD...
Diminuição de rótulo	Parabidiminiedrosidodecahedron	Metabidiminuição de rótulo	Tridiminuição de rótulo
Gyrate diminuiu rhombicosidodecahedra
J77...	J78... '	J79...	J82...
Paragyrate diminuiu rhombicosidodecahedron	Metagyrate diminuiu rhombicosidodecahedron	Bigyrate diminuiu rhombicosidodecahedron	Gyrate bidiminiedor de rinoceronte

J37 também apareceria aqui como uma duplicata (é um rombicuboctaedro giratório).

Outros sólidos arquimedianos girados e diminuídos

Outros sólidos arquimedianos podem ser girados e diminuídos, mas todos resultam em sólidos previamente contados.

J27	J3	J34	J6	J37	J19	Uniforme
Cúboctahedron Gyrate (triangular ortobicupola)	Diminuiu o cuboctahedron (copola triangular)	Linha de produção (ortobirotunda pentagonal)	Diminuindo icosidodecahedron (podrina pentagonal)	Gyrate rhombicuboctahedron (Girobicupola quadrada alongada)	Rhombicuboctahedron diminuído (copola quadrada alongada)	Rhombicuboctahedron bidimini (prisma octogonal)
Girado ou diminuído de polihedra
Anúncio grátis para sua empresa		Icosido descaído		Anúncio grátis para sua empresa

Sólidos elementares

Sólidos de Johnson 84 a 92 não são derivados de "cortar e colar" manipulações de sólidos uniformes.

Snob antiprismas

Os antiprismas snub podem ser construídos como uma alternância de um antiprisma truncado. Os gyrobianticupolae são outra construção para os antiprismas arrebitados. Apenas antiprismas arrebitados com no máximo 4 lados podem ser construídos a partir de polígonos regulares. O antiprisma triangular achatado é o icosaedro regular, portanto não é um sólido de Johnson.

J84	Regular	J85
Snub disphenoid - Sim.	Icosahedron - Sim.	Snub antiprisma quadrado Ss{2,8}
Girobianticupola	Girobianticupola Triangular	Girobianticupola quadrada

Outros

J86	J87	J88
Sphenocorona	Esquenocorona aumentada	Sphenomegacorona
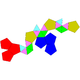
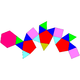
J89	J90	J91	J92
Hebesphenomegacorona	Disciplina	Anúncio grátis para sua empresa	Hebesfeno de Triangular

Classificação por tipos de faces

Sólidos de Johnson com faces triangulares

Cinco sólidos de Johnson são deltaedros, com todas as faces de triângulos equiláteros:

Sólidos de Johnson triangulares e de face quadrada

Vinte e quatro sólidos de Johnson têm apenas faces triangulares ou quadradas:

Sólidos de Johnson com faces triangulares e pentágonos

Eleven Johnson sólidos têm apenas faces triangulares e pentágonos:

Sólidos de Johnson triangulares, quadrados e pentágonos

Sólidos de vinte Johnson têm apenas faces triangulares, quadradas e pentágonos:

Sólidos de Johnson com faces triangulares, quadradas e hexagonais

Oito sólidos de Johnson têm apenas faces triangulares, quadradas e hexagonais:

Sólidos de Johnson com faces triangulares, quadradas e octogonais

Cinco sólidos de Johnson têm apenas faces triangulares, quadradas e octogonais:

Sólidos de Johnson com faces de triângulo, pentágono e decágono

Dois sólidos de Johnson têm apenas faces de triângulo, pentágono e decágono:

Sólidos de Johnson triangulares, quadrados, pentágonos e hexagonais

Apenas um sólido de Johnson tem faces triangulares, quadradas, pentágonos e hexagonais:

Sólidos de Johnson com faces triangulares, quadradas, pentágono e decágono

Dezesseis sólidos de Johnson têm apenas faces triangulares, quadradas, pentágonos e decágonos:

Sólidos de Johnson circunscritíveis

25 dos sólidos de Johnson têm vértices que existem na superfície de uma esfera: 1–6,11,19,27,34,37,62,63,72–83. Todos eles podem ser vistos como relacionados a um poliedro regular ou uniforme por giro, diminuição ou dissecação.

Octaedron	Anúncio grátis para sua empresa		Anúncio grátis para sua empresa
J1	J3	J27	J4	J19	J37

Icosahedron				Icosido descaído
J2	J11	J62	J63	J6	J34

O que é isso?
J5	J72	J73	J74	J75	J76	J77
	J78	J79	J80	J81	J82	J83