Integral elíptica

ImprimirCitar

Função especial definida por uma integral

No cálculo integral, uma integral elíptica é uma das várias funções relacionadas definidas como o valor de certas integrais, que foram estudadas pela primeira vez por Giulio Fagnano e Leonhard Euler (c. 1750). Seu nome se origina de sua origem em conexão com o problema de encontrar o comprimento do arco de uma elipse.

A matemática moderna define uma "integral elíptica" como qualquer função $f$ que pode ser expressa na forma

{displaystyle f(x)=int _{c}^{x}Rleft(t,{sqrt {P(t)}}right),dt,}

onde $R$ é uma função racional de seus dois argumentos, $P$ é um polinômio de grau 3 ou 4 sem raízes repetidas e $c$ é uma constante.

Em geral, integrais nesta forma não podem ser expressas em termos de funções elementares. Exceções a esta regra geral são quando $P$ tem raízes repetidas ou quando $R (x, y)$ não contém potências ímpares de $y$ ou se o a integral é pseudo-elíptica. No entanto, com a fórmula de redução apropriada, toda integral elíptica pode ser trazida para uma forma que envolva integrais sobre funções racionais e as três formas canônicas de Legendre (ou seja, as integrais elípticas do primeiro, segundo e terceiro tipo).

Além da forma de Legendre fornecida abaixo, as integrais elípticas também podem ser expressas na forma simétrica de Carlson. Informações adicionais sobre a teoria da integral elíptica podem ser obtidas por meio do estudo do mapeamento de Schwarz–Christoffel. Historicamente, as funções elípticas foram descobertas como funções inversas de integrais elípticas.

Notação de argumento

Integrais elípticos incompletos são funções de dois argumentos; integrais elípticas completas são funções de um único argumento. Esses argumentos são expressos de várias maneiras diferentes, mas equivalentes (eles fornecem a mesma integral elíptica). A maioria dos textos segue um esquema de nomenclatura canônico, usando as seguintes convenções de nomenclatura.

Para expressar um argumento:

$α$ , o ângulo modular
$k = pecado α$ , o módulo elíptico ou excentricidade
$m = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = k 2 = pecado 2 α$ , o parâmetro

Cada uma das três quantidades acima é completamente determinada por qualquer uma das outras (dado que são não negativas). Assim, eles podem ser usados de forma intercambiável.

O outro argumento também pode ser expresso como $φ$ , a amplitude ou como $x$ ou $u$ , onde $x = sin φ = sn u$ e $sn$ é uma das funções elípticas jacobianas.

A especificação do valor de qualquer uma dessas quantidades determina as outras. Observe que $u$ também depende de $m$ . Alguns relacionamentos adicionais envolvendo $u$ incluem

{displaystyle cos varphi =operatorname {cn} u,quad {textrm {and}}quad {sqrt {1-msin ^{2}varphi }}=operatorname {dn} u.}

O último é às vezes chamado de amplitude delta e escrito como $Δ(φ) = dn u$ . Às vezes, a literatura também se refere ao parâmetro complementar, ao módulo complementar ou ao ângulo modular complementar. Estes são definidos mais detalhadamente no artigo sobre períodos trimestrais.

Nesta notação, o uso de uma barra vertical como delimitador indica que o argumento seguinte é o "parâmetro" (conforme definido acima), enquanto a barra invertida indica que é o ângulo modular. O uso de um ponto e vírgula implica que o argumento que o precede é o seno da amplitude:

{displaystyle F(varphisin alpha)=Fleft(varphi mid sin ^{2}alpha right)=F(varphi setminus alpha)=F(sin varphi;sin alpha).}

Existem ainda outras convenções para a notação de integrais elípticas empregadas na literatura. A notação com argumentos trocados, $F (k, φ)$ , é frequentemente encontrada; e similarmente $E (k, φ)$ para a integral de segundo tipo. Abramowitz e Stegun substituem a integral do primeiro tipo, $F (φ, k)$ , para o argumento $φ$ em sua definição das integrais do segundo e terceiro tipos, a menos que este argumento seja seguido por uma barra vertical: ou seja, $E (F (φ, k) | k 2)$ para $E (φ | k 2)$ . Além disso, suas integrais completas empregam o parâmetro $k 2$ como argumento no lugar do módulo $k$ , ou seja, $K (k 2)$ em vez de $K (k)$ . E a integral do terceiro tipo definida por Gradshteyn e Ryzhik, $Π(φ, n, k)$ , coloca a amplitude $φ$ primeiro e não a "característica" $n$ .

Assim, deve-se ter cuidado com a notação ao usar essas funções, porque várias referências respeitáveis e pacotes de software usam diferentes convenções nas definições das funções elípticas. Por exemplo, o software Mathematica da Wolfram e o Wolfram Alpha definem a integral elíptica completa de primeiro tipo em termos do parâmetro $m$ , em vez de o módulo elíptico $k$ .

Integral elíptica incompleta de primeiro tipo

A integral elíptica incompleta de primeiro tipo $F$ é definida como

{displaystyle F(varphik)=Fleft(varphi mid k^{2}right)=F(sin varphi;k)=int _{0}^{varphi }{frac {dtheta }{sqrt {1-k^{2}sin ^{2}theta }}}.}

Esta é a forma trigonométrica da integral; substituindo $t = sin θ$ e $x = sin φ$ , obtém-se a forma normal de Legendre:

{displaystyle F(x;k)=int _{0}^{x}{frac {dt}{sqrt {left(1-t^{2}right)left(1-k^{2}t^{2}right)}}}.}

Equivalentemente, em termos de amplitude e ângulo modular tem-se:

{displaystyle F(varphi setminus alpha)=F(varphisin alpha)=int _{0}^{varphi }{frac {dtheta }{sqrt {1-left(sin theta sin alpha right)^{2}}}}.}

Com $x = sn(u, k)$ tem-se:

{displaystyle F(x;k)=u;}

A integral elíptica incompleta do primeiro tipo tem o seguinte teorema de adição:

{displaystyle F{bigl [}arctan(x),k{bigr ]}+F{bigl [}arctan(y),k{bigr ]}=Fleft[arctan left({frac {x{sqrt {k'^{2}y^{2}+1}}}{sqrt {y^{2}+1}}}right)+arctan left({frac {y{sqrt {k'^{2}x^{2}+1}}}{sqrt {x^{2}+1}}}right),kright]}

O módulo elíptico pode ser transformado dessa forma:

{displaystyle F{bigl [}arcsin(x),k{bigr ]}={frac {2}{1+{sqrt {1-k^{2}}}}}Fleft[arcsin left({frac {left(1+{sqrt {1-k^{2}}}right)x}{1+{sqrt {1-k^{2}x^{2}}}}}right),{frac {1-{sqrt {1-k^{2}}}}{1+{sqrt {1-k^{2}}}}}right]}

Integral elíptica incompleta de segundo tipo

A integral elíptica incompleta de segundo tipo $E$ na forma trigonométrica é

{displaystyle E(varphik)=Eleft(varphi ,|,k^{2}right)=E(sin varphi;k)=int _{0}^{varphi }{sqrt {1-k^{2}sin ^{2}theta }},dtheta.}

Substituindo $t = sin θ$ e $x = sin φ$ , obtém-se a forma normal de Legendre:

{displaystyle E(x;k)=int _{0}^{x}{frac {sqrt {1-k^{2}t^{2}}}{sqrt {1-t^{2}}}},dt.}

Equivalentemente, em termos de amplitude e ângulo modular:

{displaystyle E(varphi setminus alpha)=E(varphisin alpha)=int _{0}^{varphi }{sqrt {1-left(sin theta sin alpha right)^{2}}},dtheta.}

As relações com as funções elípticas de Jacobi incluem

{displaystyle {begin{aligned}E{bigl (}operatorname {sn} (u;k);k{bigr)}&=int _{0}^{u}operatorname {dn} ^{2}(w;k),dw\&=u-k^{2}int _{0}^{u}operatorname {sn} ^{2}(w;k),dw\&=left(1-k^{2}right)u+k^{2}int _{0}^{u}operatorname {cn} ^{2}(w;k),dw.end{aligned}}}

O comprimento do arco meridiano do equador à latitude $φ$ é escrito em termos de $E$ :

{displaystyle m(varphi)=aleft(E(varphie)+{frac {d^{2}}{dvarphi ^{2}}}E(varphie)right),}

um

e

A integral elíptica incompleta de segundo tipo tem o seguinte teorema de adição:

{displaystyle E{bigl [}arctan(x),k{bigr ]}+E{bigl [}arctan(y),k{bigr ]}=Eleft[arctan left({frac {x{sqrt {k'^{2}y^{2}+1}}}{sqrt {y^{2}+1}}}right)+arctan left({frac {y{sqrt {k'^{2}x^{2}+1}}}{sqrt {x^{2}+1}}}right),kright]+{frac {k^{2}xy}{k'^{2}x^{2}y^{2}+x^{2}+y^{2}+1}}left({frac {x{sqrt {k'^{2}y^{2}+1}}}{sqrt {y^{2}+1}}}+{frac {y{sqrt {k'^{2}x^{2}+1}}}{sqrt {x^{2}+1}}}right)}

O módulo elíptico pode ser transformado dessa forma:

{displaystyle E{bigl [}arcsin(x),k{bigr ]}=left(1+{sqrt {1-k^{2}}}right)Eleft[arcsin left({frac {left(1+{sqrt {1-k^{2}}}right)x}{1+{sqrt {1-k^{2}x^{2}}}}}right),{frac {1-{sqrt {1-k^{2}}}}{1+{sqrt {1-k^{2}}}}}right]-{sqrt {1-k^{2}}}F{bigl [}arcsin(x),k{bigr ]}+{frac {k^{2}x{sqrt {1-x^{2}}}}{1+{sqrt {1-k^{2}x^{2}}}}}}

Integral elíptica incompleta de terceiro tipo

A integral elíptica incompleta de terceiro tipo $Π$ é

{displaystyle Pi (n;varphi setminus alpha)=int _{0}^{varphi }{frac {1}{1-nsin ^{2}theta }}{frac {dtheta }{sqrt {1-left(sin theta sin alpha right)^{2}}}}}

{displaystyle Pi (n;varphi ,|,m)=int _{0}^{sin varphi }{frac {1}{1-nt^{2}}}{frac {dt}{sqrt {left(1-mt^{2}right)left(1-t^{2}right)}}}.}

O número $n$ é chamado de característica e pode assumir qualquer valor, independentemente dos outros argumentos. Observe, porém, que o valor $Π(1; π / 2 | m)$ é infinito, para qualquer $m$ .

Uma relação com as funções elípticas jacobianas é

{displaystyle Pi {bigl (}n;,operatorname {am} (u;k);,k{bigr)}=int _{0}^{u}{frac {dw}{1-n,operatorname {sn} ^{2}(w;k)}}.}

O comprimento do arco meridiano do equador à latitude $φ$ também está relacionado a um caso especial de $Π$ :

{displaystyle m(varphi)=aleft(1-e^{2}right)Pi left(e^{2};varphi ,|,e^{2}right).}

Integral elíptico completo de primeiro tipo

Lote da integral elíptica completa do primeiro tipo

KK (k)

As integrais elípticas são consideradas 'completas' quando a amplitude $φ = π / 2$ e, portanto, $x = 1$ . A integral elíptica completa de primeiro tipo $K$ pode assim ser definida como

{displaystyle K(k)=int _{0}^{tfrac {pi }{2}}{frac {dtheta }{sqrt {1-k^{2}sin ^{2}theta }}}=int _{0}^{1}{frac {dt}{sqrt {left(1-t^{2}right)left(1-k^{2}t^{2}right)}}},}

{displaystyle K(k)=Fleft({tfrac {pi }{2}},kright)=Fleft({tfrac {pi }{2}},|,k^{2}right)=F(1;k).}

Pode ser expresso como uma série de potências

{displaystyle K(k)={frac {pi }{2}}sum _{n=0}^{infty }left({frac {(2n)!}{2^{2n}(n!)^{2}}}right)^{2}k^{2n}={frac {pi }{2}}sum _{n=0}^{infty }{bigl (}P_{2n}(0){bigr)}^{2}k^{2n},}

onde $P n$ é o polinômio de Legendre, que é equivalente a

{displaystyle K(k)={frac {pi }{2}}left(1+left({frac {1}{2}}right)^{2}k^{2}+left({frac {1cdot 3}{2cdot 4}}right)^{2}k^{4}+cdots +left({frac {left(2n-1right)!!}{left(2nright)!!}}right)^{2}k^{2n}+cdots right),}

onde $n!!$ denota o fatorial duplo. Em termos da função hipergeométrica de Gauss, a integral elíptica completa do primeiro tipo pode ser expressa como

{displaystyle K(k)={tfrac {pi }{2}},{}_{2}F_{1}left({tfrac {1}{2}},{tfrac {1}{2}};1;k^{2}right).}

A integral elíptica completa do primeiro tipo é algumas vezes chamada de período trimestral. Pode ser calculado de forma muito eficiente em termos da média aritmética-geométrica:

{displaystyle K(k)={frac {pi }{2operatorname {agm} left(1,{sqrt {1-k^{2}}}right)}}.}

Portanto, o módulo pode ser transformado dessa maneira:

{displaystyle {begin{aligned}K(k)&={frac {pi }{2operatorname {agm} left(1,{sqrt {1-k^{2}}}right)}}\[4pt]&={frac {pi }{2operatorname {agm} left({frac {1}{2}}+{frac {sqrt {1-k^{2}}}{2}},{sqrt[{4}]{1-k^{2}}}right)}}\[4pt]&={frac {pi }{left(1+{sqrt {1-k^{2}}}right)operatorname {agm} left(1,{frac {2{sqrt[{4}]{1-k^{2}}}}{left(1+{sqrt {1-k^{2}}}right)}}right)}}\[4pt]&={frac {2}{1+{sqrt {1-k^{2}}}}}Kleft({frac {1-{sqrt {1-k^{2}}}}{1+{sqrt {1-k^{2}}}}}right)end{aligned}}}

Esta expressão é válida para todos ${displaystyle nin mathbb {N} }$ e $0 \leq k \leq 1$ :

{displaystyle K(k)=nleft[sum _{a=1}^{n}operatorname {dn} left({frac {2a}{n}}K(k);kright)right]^{-1}Kleft[k^{n}prod _{a=1}^{n}operatorname {sn} left({frac {2a-1}{n}}K(k);kright)^{2}right]}

Relação com a função gama

Se $k 2 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = λ (Eu... \sqrt R)$ e ${displaystyle rin mathbb {Q} ^{+}}$ (onde) $λ$ é a função lambda modular), então $KK (k)$ é expressível em forma fechada em termos da função gama. Por exemplo, $R = 2$ e $R = 7$ dar, respectivamente,

{displaystyle Kleft({sqrt {2}}-1right)={frac {Gamma left({frac {1}{8}}right)Gamma left({frac {3}{8}}right){sqrt {{sqrt {2}}+1}}}{8{sqrt[{4}]{2}}{sqrt {pi }}}},}

{displaystyle Kleft({frac {3-{sqrt {7}}}{4{sqrt {2}}}}right)={frac {Gamma left({frac {1}{7}}right)Gamma left({frac {2}{7}}right)Gamma left({frac {4}{7}}right)}{4{sqrt[{4}]{7}}pi }}.}

Em geral, a condição que

{displaystyle {frac {iK'}{K}}={frac {iKleft({sqrt {1-k^{2}}}right)}{K(k)}}}

k = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = e 5 πi /6

IK ? / KK = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = e 2 πi /3

{displaystyle Kleft(e^{5pi i/6}right)={frac {e^{-pi i/12}Gamma ^{3}left({frac {1}{3}}right){sqrt[{4}]{3}}}{4{sqrt[{3}]{2}}pi }}.}

Relação com a função teta de Jacobi

A relação com a função theta de Jacobi é dada por

{displaystyle K(k)={frac {pi }{2}}theta _{3}^{2}(q),}

q

{displaystyle q(k)=exp left(-pi {frac {Kleft({sqrt {1-k^{2}}}right)}{K(k)}}right).}

Expressões assintóticas

{displaystyle Kleft(kright)approx {frac {pi }{2}}+{frac {pi }{8}}{frac {k^{2}}{1-k^{2}}}-{frac {pi }{16}}{frac {k^{4}}{1-k^{2}}}}

3×10.^-4

k < 1 / 2

k < 1 / 2

Equação diferencial

A equação diferencial para a integral elíptica de primeiro tipo é

{displaystyle {frac {d}{dk}}left(kleft(1-k^{2}right){frac {dK(k)}{dk}}right)=k,K(k)}

Uma segunda solução para esta equação é $K (\sqrt 1 - k 2)$ . Esta solução satisfaz a relação

{displaystyle {frac {d}{dk}}K(k)={frac {E(k)}{kleft(1-k^{2}right)}}-{frac {K(k)}{k}}.}

Fração contínua

Uma expansão de fração contínua é:

{displaystyle {frac {K(k)}{2pi }}=-{frac {1}{4}}+sum _{n=0}^{infty }{frac {q^{n}}{1+q^{2n}}}=-{frac {1}{4}}+{cfrac {1}{1-q+{cfrac {left(1-qright)^{2}}{1-q^{3}+{cfrac {qleft(1-q^{2}right)^{2}}{1-q^{5}+{cfrac {q^{2}left(1-q^{3}right)^{2}}{1-q^{7}+{cfrac {q^{3}left(1-q^{4}right)^{2}}{1-q^{9}+cdots }}}}}}}}}},}

q = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = q (k)

Integral elíptico completo de segundo tipo

Lote da integral elíptica completa do segundo tipo

E (k)

A integral elíptica completa de segundo tipo $E$ é definida como

{displaystyle E(k)=int _{0}^{tfrac {pi }{2}}{sqrt {1-k^{2}sin ^{2}theta }},dtheta =int _{0}^{1}{frac {sqrt {1-k^{2}t^{2}}}{sqrt {1-t^{2}}}},dt,}

ou mais compactamente em termos da integral incompleta de segundo tipo $E (φ, k)$ como

{displaystyle E(k)=Eleft({tfrac {pi }{2}},kright)=E(1;k).}

Para uma elipse com semi-eixo maior $a$ e semi-eixo menor $b$ e excentricidade $e = \sqrt 1 - b 2 / a 2$ , a integral elíptica completa de segundo tipo $E (e)$ é igual a um quarto da circunferência $C$ da elipse medido em unidades do semi-eixo maior $a$ . Em outras palavras:

{displaystyle C=4aE(e).}

A integral elíptica completa do segundo tipo pode ser expressa como uma série de potências

{displaystyle E(k)={frac {pi }{2}}sum _{n=0}^{infty }left({frac {(2n)!}{2^{2n}left(n!right)^{2}}}right)^{2}{frac {k^{2n}}{1-2n}},}

que é equivalente a

{displaystyle E(k)={frac {pi }{2}}left(1-left({frac {1}{2}}right)^{2}{frac {k^{2}}{1}}-left({frac {1cdot 3}{2cdot 4}}right)^{2}{frac {k^{4}}{3}}-cdots -left({frac {(2n-1)!!}{(2n)!!}}right)^{2}{frac {k^{2n}}{2n-1}}-cdots right).}

Em termos da função hipergeométrica de Gauss, a integral elíptica completa de segundo tipo pode ser expressa como

{displaystyle E(k)={tfrac {pi }{2}},{}_{2}F_{1}left({tfrac {1}{2}},-{tfrac {1}{2}};1;k^{2}right).}

O módulo pode ser transformado dessa forma:

{displaystyle E(k)=left(1+{sqrt {1-k^{2}}}right),Eleft({frac {1-{sqrt {1-k^{2}}}}{1+{sqrt {1-k^{2}}}}}right)-{sqrt {1-k^{2}}},K(k)}

Computação

Assim como a integral do primeiro tipo, a integral elíptica completa do segundo tipo pode ser calculada de forma muito eficiente usando a média aritmética-geométrica.

Defina as sequências $a n$ e $g n$ , onde $a 0 = 1$ , $g 0 = \sqrt 1 - k 2 = estilo k'$ e as relações de recorrência $a n + 1 = a n + g n / 2$ , $g n + 1 = \sqrt a n g n$ espera. Além disso, defina

{displaystyle c_{n}={sqrt {left|a_{n}^{2}-g_{n}^{2}right|}}.}

Por definição,

{displaystyle a_{infty }=lim _{nto infty }a_{n}=lim _{nto infty }g_{n}=operatorname {agm} left(1,{sqrt {1-k^{2}}}right).}

Também

{displaystyle lim _{nto infty }c_{n}=0.}

Então

{displaystyle E(k)={frac {pi }{2a_{infty }}}left(1-sum _{n=0}^{infty }2^{n-1}c_{n}^{2}right).}

Na prática, a média aritmética-geométrica seria simplesmente calculada até algum limite. Esta fórmula converge quadraticamente para todos os $| k | \leq 1$ . Para acelerar ainda mais a computação, a relação $c n + 1 = c n 2 / 4 a n + 1$ pode ser usado.

Além disso, se $k 2 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = λ (Eu... \sqrt R)$ e ${displaystyle rin mathbb {Q} ^{+}}$ (onde) $λ$ é a função lambda modular), então $E (k)$ é exprimível em forma fechada em termos de

{displaystyle K(k)={frac {pi }{2operatorname {agm} left(1,{sqrt {1-k^{2}}}right)}}}

R = 1

R = 7

{displaystyle Eleft({frac {1}{sqrt {2}}}right)=Kleft({frac {1}{sqrt {2}}}right)+{frac {pi }{4Kleft({frac {1}{sqrt {2}}}right)}},}

{displaystyle Eleft({frac {3-{sqrt {7}}}{4{sqrt {2}}}}right)={frac {7+2{sqrt {7}}}{14}}Kleft({frac {3-{sqrt {7}}}{4{sqrt {2}}}}right)+{frac {pi {sqrt {7}}}{28Kleft({frac {3-{sqrt {7}}}{4{sqrt {2}}}}right)}}.}

Equação derivada e diferencial

{displaystyle {frac {dE(k)}{dk}}={frac {E(k)-K(k)}{k}}}

{displaystyle left(k^{2}-1right){frac {d}{dk}}left(k;{frac {dE(k)}{dk}}right)=kE(k)}

Uma segunda solução para esta equação é $E (\sqrt 1 - k 2) - K (\sqrt 1 - k 2)$ .

Integral elíptica completa de terceiro tipo

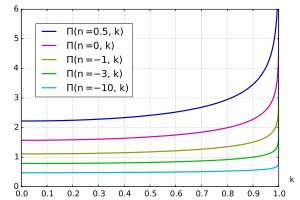
Lote da integral elíptica completa do terceiro tipo

D. n, k)

com vários valores fixos de

n

A integral elíptica completa de terceiro tipo $Π$ pode ser definida como

{displaystyle Pi (n,k)=int _{0}^{frac {pi }{2}}{frac {dtheta }{left(1-nsin ^{2}theta right){sqrt {1-k^{2}sin ^{2}theta }}}}.}

Observe que às vezes a integral elíptica do terceiro tipo é definida com um sinal inverso para a característica $n$ ,

{displaystyle Pi '(n,k)=int _{0}^{frac {pi }{2}}{frac {dtheta }{left(1+nsin ^{2}theta right){sqrt {1-k^{2}sin ^{2}theta }}}}.}

Assim como as integrais elípticas completas do primeiro e segundo tipo, a integral elíptica completa do terceiro tipo pode ser calculada de forma muito eficiente usando a média aritmética-geométrica.

Derivadas parciais

{displaystyle {begin{aligned}{frac {partial Pi (n,k)}{partial n}}&={frac {1}{2left(k^{2}-nright)(n-1)}}left(E(k)+{frac {1}{n}}left(k^{2}-nright)K(k)+{frac {1}{n}}left(n^{2}-k^{2}right)Pi (n,k)right)\[8pt]{frac {partial Pi (n,k)}{partial k}}&={frac {k}{n-k^{2}}}left({frac {E(k)}{k^{2}-1}}+Pi (n,k)right)end{aligned}}}

Relações funcionais

Relação do Legendre:

{displaystyle K(k)Eleft({sqrt {1-k^{2}}}right)+E(k)Kleft({sqrt {1-k^{2}}}right)-K(k)Kleft({sqrt {1-k^{2}}}right)={frac {pi }{2}}.}

Contenido relacionado

Más resultados...