Icosaedro truncado
Em geometria, o icosaedro truncado é um sólido de Arquimedes, um dos 13 sólidos convexos isogonais não prismáticos cujas 32 faces são dois ou mais tipos de polígonos regulares. É a única dessas formas que não contém triângulos ou quadrados. No uso geral, o grau de truncamento é considerado uniforme, a menos que seja especificado.
Possui 12 faces pentagonais regulares, 20 faces hexagonais regulares, 60 vértices e 90 arestas.
É o poliedro GPV(1,1) ou {5+,3}1,1 de Goldberg, contendo faces pentagonais e hexagonais.
Esta geometria está associada a bolas de futebol, tipicamente padronizadas com hexágonos brancos e pentágonos pretos. Cúpulas geodésicas, como aquelas cuja arquitetura foi pioneira em Buckminster Fuller, são frequentemente baseadas nesta estrutura. Também corresponde à geometria da molécula de fulereno C60 ("buckyball").
É usado no mosaico hiperbólico de preenchimento de espaço transitivo celular, o favo de mel dodecaédrico de ordem 5 bitruncado.
Construção

Este poliedro pode ser construído a partir de um icosaedro truncando ou cortando cada um dos 12 vértices na marca de um terço de cada aresta, criando 12 faces pentagonais e transformando as 20 faces originais do triângulo em hexágonos regulares.
Características
Na geometria e na teoria dos grafos, existem algumas características padrão dos poliedros.
Coordenadas cartesianas
As coordenadas cartesianas para os vértices de um icosaedro truncado centrado na origem são todas permutações pares de:
- (0, ±1, ±3φ)
- (±1, ± 2 +φ), ±2φ)
- (φ, ±2, ±2φ+ 1))
onde φ = 1 + √5/2 é o meio-termo. O circunraio é √9φ + 10 ≈ 4,956 e as arestas têm comprimento 2.
Projeções ortogonais
O icosaedro truncado possui cinco projeções ortogonais especiais, centradas, em um vértice, em dois tipos de arestas e dois tipos de faces: hexagonal e pentagonal. Os dois últimos correspondem aos planos A2 e H2 Coxeter.
| Centro por | Verbos | Borda 5-6 | Borda 6-6 | Cara Hexagonal | Cara Pentágono |
|---|---|---|---|---|---|
| Sólido |  |  |  | ||
| Estrutura de fio |  | 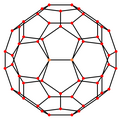 |  |  |  |
| Projeto simetria | [2] | [2] | [2] | [6] | [10] |
| Dual | 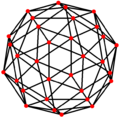 | 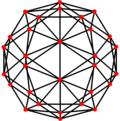 |  |  |  |
Ladrilhos esféricos
O icosaedro truncado também pode ser representado como um ladrilho esférico e projetado no plano por meio de uma projeção estereográfica. Esta projeção é conforme, preservando ângulos, mas não áreas ou comprimentos. As linhas retas na esfera são projetadas como arcos circulares no plano.
 |  Pentágono centrado |  hexágono centrado |
| Projeção ortográfico | Projeções estereográficas | |
|---|---|---|
Dimensões
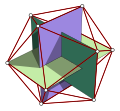
Se o comprimento da aresta de um icosaedro truncado for a, o raio de uma esfera circunscrita (aquela que toca o icosaedro truncado em todos os vértices) é:
- Ru= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =um21+9φ φ 2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =um458+18.5? ? 2.47801866umNão é verdade. {a}{2}}{sqrt {1+9varphi ^{2}}}={frac {a}{4}}{sqrt {58+18{sqrt {5}}approx 2.478,018,66a}
onde φ é a proporção áurea.
Esse resultado é fácil de obter usando um dos três retângulos dourados ortogonais desenhados no icosaedro original (antes do corte) como ponto de partida para nossas considerações. O ângulo entre os segmentos que unem o centro e os vértices conectados por aresta compartilhada (calculado com base nesta construção) é de aproximadamente 23,281446°.
Área e volume
A área A e o volume V do icosaedro truncado de comprimento de aresta a são:
- A= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(20.)) 323+12)) 541+25)um2? ? 72.607253um2V= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =125+4354um3? ? 55.2877308um3.{displaystyle {begin{aligned}A&=left(20cdot {frac {3}{2}}{sqrt {3}}+12cdot {frac {5}{4}}{sqrt {1+{frac {2}{sqrt {5}}}right)a^{2}&approx 72.607,253a^{2}\V&={frac {125+43{sqrt {5}}}{4}}a^{3}&&approx 55.287,7308a^{3}.end{aligned}}}
Com arestas unitárias, a área da superfície é (arredondada) 21 para os pentágonos e 52 para os hexágonos, juntos 73 (ver áreas de polígonos regulares). O icosaedro truncado demonstra facilmente a característica de Euler:
- 32 + 60 − 90 = 2.
Aplicativos
As bolas usadas no futebol e no handebol coletivo são talvez o exemplo mais conhecido de um poliedro esférico análogo ao icosaedro truncado, encontrado na vida cotidiana. A bola tem o mesmo padrão de pentágonos regulares e hexágonos regulares, mas é mais esférica devido à pressão do ar em seu interior e à elasticidade da bola. Este tipo de bola foi introduzido na Copa do Mundo em 1970 (a partir de 2006, esse design icônico foi substituído por padrões alternativos).
Os sinais de trânsito britânicos que indicam campos de futebol usam uma seção hexagonal de cores uniformes para representar uma bola de futebol, em vez de um icosaedro truncado. Isso irritou o matemático e comediante Matt Parker, que iniciou uma petição ao governo do Reino Unido para que esses sinais fossem alterados para serem geometricamente precisos. A petição foi finalmente recusada.
As cúpulas geodésicas são normalmente baseadas em facetas triangulares desta geometria com exemplos de estruturas encontradas em todo o mundo, popularizadas por Buckminster Fuller.
Uma variação do icosaedro foi usada como base das rodas em favo de mel (feitas de material polifundido) usadas pela Pontiac Motor Division entre 1971 e 1976 em seu Trans Am e Grand Prix.
Esse formato também era a configuração das lentes usadas para focar as ondas de choque explosivas dos detonadores tanto no gadget quanto nas bombas atômicas Fat Man.
O icosaedro truncado também pode ser descrito como um modelo da molécula Buckminsterfulereno (fulereno) (C60), ou "buckyball" – um alótropo de carbono elementar, descoberto em 1985. O diâmetro da bola de futebol e da molécula de fulereno é de 22 cm e cerca de 0,71 nm, respectivamente, portanto, a proporção de tamanho é de ≈31.000.000:1.
Na cultura artesanal popular, grandes bolas brilhantes podem ser feitas usando um padrão icosaedro e copos de plástico, isopor ou papel.
Nas artes
- Galeria
O icosahedron truncado (à esquerda) comparado com um futebol de associação.
Fullerene C60 molécula
Truncated icosahedral radome em uma estação meteorológica
Truncated icosahedron usinado de 6061-T6 alumínio
Uma arte de madeira truncada icosahedron por George W. Hart.
Poliedros relacionados
These uniform star-polyhedra, and one icosahedron stellation have nonuniform truncated icosahedron convex hulls:
Este poliedro é semelhante ao dodecaedro chanfrado uniforme que possui 12 pentágonos, mas 30 hexágonos.
Did you mean:Truncated icosahedron graph
No campo matemático da teoria dos grafos, um grafo icosaédrico truncado é o gráfico dos vértices e arestas do icosaedro truncado, um dos sólidos de Arquimedes. Possui 60 vértices e 90 arestas e é um grafo cúbico de Arquimedes.
 Simetria de 5 vezes | 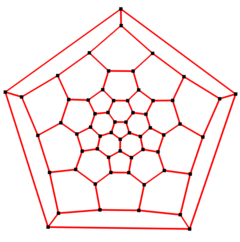 diagrama de Schlegel de 5 vezes |
Histórico

O icosaedro truncado era conhecido por Arquimedes, que classificou os 13 sólidos de Arquimedes em uma obra perdida. Tudo o que sabemos sobre o seu trabalho sobre estas formas vem de Pappus de Alexandria, que apenas lista o número de faces de cada uma: 12 pentágonos e 20 hexágonos, no caso do icosaedro truncado. A primeira imagem conhecida e descrição completa de um icosaedro truncado vem de uma redescoberta por Piero della Francesca, em seu livro do século XV De quinque corporibus regularibus, que incluía cinco dos sólidos de Arquimedes (os cinco truncamentos de os poliedros regulares). A mesma forma foi retratada por Leonardo da Vinci, em suas ilustrações para o plágio de Luca Pacioli do livro de della Francesca em 1509. Embora Albrecht Dürer tenha omitido esta forma dos outros sólidos de Arquimedes listados em seu livro de 1525 sobre poliedros, Underweysung der Messung, uma descrição dele foi encontrada em seus artigos póstumos, publicados em 1538. Johannes Kepler mais tarde redescobriu a lista completa dos 13 sólidos de Arquimedes, incluindo o icosaedro truncado, e os incluiu em seu Livro de 1609, Harmonices Mundi.
Contenido relacionado
Antiprisma
4-politopo
Esfera
Tesserato
Quadrângulo