Gradiente
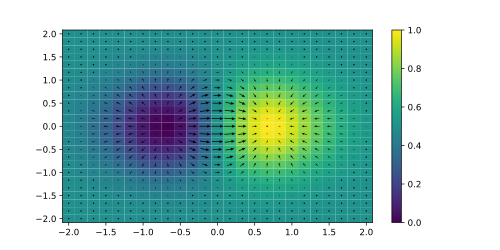
No cálculo vetorial, o Gradient de uma função diferencial de valor escalar fNão. de várias variáveis é o campo vetorial (ou função de valor vetorial) ? ? f- Sim. cujo valor em um ponto pNão. é a "direção e taxa de aumento mais rápido". Se o gradiente de uma função é non-zero em um ponto pNão., a direção do gradiente é a direção em que a função aumenta mais rapidamente de pNão., e a magnitude do gradiente é a taxa de aumento nessa direção, o maior derivado direcional absoluto. Além disso, um ponto onde o gradiente é o vetor zero é conhecido como um ponto estacionário. O gradiente desempenha assim um papel fundamental na teoria da otimização, onde é usado para maximizar uma função por subida gradiente. Em termos sem coordenadas, o gradiente de uma função f(R)(mathbf {r})} pode ser definido por:
- Df= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =? ? f)) DR{displaystyle df=nabla fcdot d{bf {r}}}
Onde? DfNão. é a mudança infinitasimal total em fNão. para um deslocamento infinitesimal DR{displaystyle d{bf {r}}}, e é visto como máximo quando DR{displaystyle d{bf {r}}} está na direção do gradiente ? ? f- Sim.. O símbolo da nabla ? ? - Sim., escrito como um triângulo de cabeça para baixo e pronunciado "del", denota o operador diferencial vetorial.
Quando um sistema de coordenadas é usado em que os vetores de base não são funções de posição, o gradiente é dado pelo vetor cujos componentes são os derivados parciais de fNão. em pNão.. Isso é, para f:: Rn→ → R{displaystyle fcolon mathbb {R} ^{n}to mathbb Não., seu gradiente ? ? f:: Rn→ → Rn{displaystyle nabla fcolon mathbb {R} ^{n}to mathbb Não. é definido no ponto p= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(x1,...... ,xn)(x_{1},ldotsx_{n})} em Não.espaço dimensional como o vetor
- ? ? f(p)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Não.∂ ∂ f∂ ∂ x1(p)FORMAÇÃO FORMAÇÃO ∂ ∂ f∂ ∂ xn(p)].{displaystyle nabla f(p)={begin{bmatrix}{frac {partial f}{partial x_{1}}}(p)vdots \{frac {partial f}{partial x_{n}}}(p)end{bmatrix}}}.}
O gradiente é dual ao derivado total DfNão.: o valor do gradiente em um ponto é um vetor tangente – um vetor em cada ponto; enquanto o valor do derivado em um ponto é um vetor cotangente – um funcional linear em vetores. Eles estão relacionados em que o produto do ponto do gradiente do fNão. em um ponto pNão. com outro vetor tangente v(v) igual ao derivado direcional de fNão. em pNão. da função ao longo v(v); isto é, ? ? f(p))) v= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∂ ∂ f∂ ∂ v(p)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Dfp(v){textstyle nabla f(p)cdot mathbf {v} ={frac {partial f}{partial mathbf {v} }}(p)=df_{p}(mathbf {v})}. O gradiente admite múltiplas generalizações para funções mais gerais em coletores; ver § Generalizações.
Motivação
Considere uma sala onde a temperatura é dada por um campo escalar, T, então em cada ponto (x, y, z) a temperatura é T (x, y, z), independente do tempo. Em cada ponto da sala, o gradiente de T naquele ponto mostrará a direção na qual a temperatura sobe mais rapidamente, afastando-se de (x, y, z). A magnitude do gradiente determinará a rapidez com que a temperatura sobe nessa direção.
Considere uma superfície cuja altura acima do nível do mar no ponto (x, y) é H(x, y). O gradiente de H em um ponto é um vetor plano apontando na direção do declive ou inclinação mais íngreme naquele ponto. A inclinação da inclinação naquele ponto é dada pela magnitude do vetor gradiente.
O gradiente também pode ser usado para medir como um campo escalar muda em outras direções, em vez de apenas na direção de maior mudança, tomando um produto escalar. Suponha que a maior inclinação em uma colina seja de 40%. Uma estrada subindo diretamente a colina tem inclinação de 40%, mas uma estrada que contorna a colina em ângulo terá uma inclinação menor. Por exemplo, se a estrada estiver em um ângulo de 60° da direção ascendente (quando ambas as direções são projetadas no plano horizontal), a inclinação ao longo da estrada será o produto escalar entre o vetor gradiente e um vetor unitário ao longo da estrada, ou seja, 40% vezes o cosseno de 60°, ou 20%.
De forma mais geral, se a função de altura da colina H for diferenciável, então o gradiente de H pontilhado com um vetor unitário dá a inclinação da colina na direção do vetor, a derivada direcional de H ao longo do vetor unitário.
Notação
O gradiente de uma função fNão. ponto umNão. é geralmente escrito como ? ? f(um)(a)}. Também pode ser denotado por qualquer um dos seguintes:
- ? ? → → f(um)(A)}: enfatizar a natureza vetorial do resultado.
- Grad f
- ∂ ∂ Eu...f{displaystyle partial _{i}f} e fEu...Não. f_{i}}: Notação de Einstein.
Definição
O gradiente (ou campo vetorial gradiente) de uma função escalar f(x1, x2, x3, …, xn) é denotado ∇f ou ∇→f onde ∇ (nabla) denota o operador diferencial vetorial, del. A notação grad f também é comumente usada para representar o gradiente. O gradiente de f é definido como o campo vetorial único cujo produto escalar com qualquer vetor v em cada ponto x é a derivada direcional de f ao longo de v. Aquilo é,
- (? ? f(x)))) v= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Dvf(x)(}nabla f(x){big)}cdot mathbf {v} =D_{mathbf {v} }f(x)}
onde a mão do lado direito é a derivada direcional e há muitas maneiras de representá-la. Formalmente, a derivada é dual ao gradiente; ver relação com derivada.
Quando uma função também depende de um parâmetro como o tempo, o gradiente geralmente se refere apenas ao vetor de suas derivadas espaciais (consulte Gradiente espacial).
A magnitude e a direção do vetor de gradiente são independentes da representação de coordenadas específica.
Coordenadas cartesianas
No sistema de coordenadas cartesianas tridimensionais com uma métrica euclidiana, o gradiente, se existir, é dado por:
- ? ? f= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∂ ∂ f∂ ∂ xEu...+∂ ∂ f∂ ∂ Sim.JJ+∂ ∂ f∂ ∂ zangão.k,{displaystyle nabla f={frac {partial f}{partial x}}mathbf {i} +{frac {partial f}{partial y}}mathbf {j} +{frac {partial f}{partial z}}mathbf {k}}
onde i, j, k são os vetores unitários padrão nas direções de x, y e z, respectivamente. Por exemplo, o gradiente da função
- f(x,Sim.,zangão.)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2x+3Sim.2- Sim. - Sim. pecado (zangão.)(x,y,z)=2x+3y^{2}-sin(z)}
é
- ? ? f= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2Eu...+6Sim.JJ- Sim. - Sim. e (zangão.)k.{displaystyle nabla f=2mathbf {i} +6ymathbf {j} -cos(z)mathbf {k}.}
Em algumas aplicações é comum representar o gradiente como um vetor linha ou vetor coluna de seus componentes em um sistema de coordenadas retangulares; este artigo segue a convenção do gradiente sendo um vetor coluna, enquanto a derivada é um vetor linha.
Coordenadas cilíndricas e esféricas
Em coordenadas cilíndricas com métrica euclidiana, o gradiente é dado por:
- ? ? f(? ? ,φ φ ,zangão.)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∂ ∂ f∂ ∂ ? ? e? ? +1? ? ∂ ∂ f∂ ∂ φ φ eφ φ +∂ ∂ f∂ ∂ zangão.ezangão.,{displaystyle nabla f(rhovarphiz)={frac {partial f}{partial rho }}mathbf {e} _{rho }+{frac {1}{rho }}{frac {partial f}{partial varphi }}mathbf {e} _{varphi }+{frac {partial f}{partial z}}mathbf {e} _{z},}
onde ρ é a distância axial, φ é o ângulo azimutal ou azimutal, z é a coordenada axial e eρ, eφ e ez são vetores unitários apontando ao longo das direções das coordenadas.
Em coordenadas esféricas, o gradiente é dado por:
- ? ? f(R,θ θ ,φ φ )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∂ ∂ f∂ ∂ ReR+1R∂ ∂ f∂ ∂ θ θ eθ θ +1Rpecado θ θ ∂ ∂ f∂ ∂ φ φ eφ φ ,{displaystyle nabla f(r,thetavarphi)={frac {partial f}{partial r}}mathbf {e} _{r}+{frac {1}{r}}{frac {partial f}{partial theta }}mathbf {e} _{theta }+{frac {1}{rsin theta }}{frac {partial f}{partial varphi }}mathbf {e} _{varphi },}
onde r é a distância radial, φ é o ângulo azimutal e θ é o ângulo polar, e er, eθ e eφ são novamente vetores unitários locais apontando nas direções das coordenadas (isto é, a base covariante normalizada).
Para o gradiente em outros sistemas de coordenadas ortogonais, consulte Coordenadas ortogonais (operadores diferenciais em três dimensões).
Coordenadas gerais
Consideramos as coordenadas gerais, que escrevemos como x1, …, x i, …, xn, onde n é o número de dimensões do domínio. Aqui, o índice superior refere-se à posição na lista da coordenada ou componente, então x2 refere-se ao segundo componente—não a quantidade x ao quadrado. A variável de índice i refere-se a um elemento arbitrário x i. Usando a notação de Einstein, o gradiente pode ser escrito como:
Onde? eEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∂ ∂ x/∂ ∂ xEu...(e) _{i}=partial mathbf {x} /partial x^{i}} e eEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =DxEu...{displaystyle mathbf {e} ^{i}=mathrm {d} x^{i}} referem-se às bases covariantes e contravariantes locais não normalizadas, respectivamente, gEu...JJ{displaystyle g^{ij}} é o tensor métrico inverso, e a convenção de soma de Einstein implica a soma sobre Eu... e JJ.
Se as coordenadas são ortogonais podemos facilmente expressar o gradiente (e o diferencial) em termos de bases normalizadas, que nos referimos como e^ ^ Eu...Não. }}_{i}} e e^ ^ Eu...{displaystyle {mathbf {e} }}^{i}}}}, usando os fatores de escala (também conhecidos como coeficientes Lamé) hEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =‖ ‖ eEu...‖ ‖ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =gEu...Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1/‖ ‖ eEu...‖ ‖ Não. H_{i}=l Ver também _{i}r Vert ={sqrt {g_{ii}}}=1,/l Vert mathbf {e} ^{i}r Vert:
onde não podemos usar a notação de Einstein, uma vez que é impossível evitar a repetição de mais de dois índices. Apesar do uso de índices superiores e inferiores, e^ ^ Eu...{displaystyle mathbf {hat {e}}} _{i}}, e^ ^ Eu...{displaystyle mathbf {hat {e}} ^{i}}}e hEu...Não. h_{i}} não são contravariantes nem covariantes.
A última expressão avalia as expressões dadas acima para coordenadas cilíndricas e esféricas.
Relação com derivada
Relação com a derivada total
O gradiente está intimamente relacionado com o derivado total (diferenciamento total) DfNão.: eles são transpose (dual) uns aos outros. Usando a convenção que vetores em Rn{displaystyle mathbb {R} ^{n}} são representados por vetores de coluna, e que covectores (Mapas lineares Rn→ → R{displaystyle mathbb {R} ^{n}to mathbb Não.) são representados por vetores de linha, o gradiente ? ? f- Sim. e o derivado DfNão. são expressos como uma coluna e vetor de linha, respectivamente, com os mesmos componentes, mas transpose uns dos outros:
- ? ? f(p)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Não.∂ ∂ f∂ ∂ x1(p)FORMAÇÃO FORMAÇÃO ∂ ∂ f∂ ∂ xn(p)];{displaystyle nabla f(p)={begin{bmatrix}{frac {partial f}{partial x_{1}}}(p)vdots \{frac {partial f}{partial x_{n}}}(p)end{bmatrix}};}
- Dfp= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Não.∂ ∂ f∂ ∂ x1(p)⋯ ⋯ ∂ ∂ f∂ ∂ xn(p)].Não. df_{p}={begin{bmatrix}{frac {partial f}{partial x_{1}}}(p)&cdots &{frac {partial f}{partial x_{n}}}(p)end{bmatrix}}}
Embora ambos tenham os mesmos componentes, eles diferem em que tipo de objeto matemático eles representam: em cada ponto, o derivado é um vetor cotangente, uma forma linear (covetor) que expressa quanto a saída (scalar) muda para uma determinada mudança infinitesimal na entrada (vetor), enquanto em cada ponto, o gradiente é um vetor tangente, que representa uma mudança infinitasimal na entrada (vector). Em símbolos, o gradiente é um elemento do espaço tangente em um ponto, ? ? f(p)∈ ∈ TpRn{displaystyle nabla f(p)in T_{p}mathbb Não., enquanto o derivado é um mapa do espaço tangente para os números reais, Dfp:: TpRn→ → RNão. df_{p}colon T_{p}mathbb {R} ^{n}to mathbb Não.. Os espaços tangentes em cada ponto de Rn{displaystyle mathbb {R} ^{n}} pode ser "naturalmente" identificado com o espaço vetorial Rn{displaystyle mathbb {R} ^{n}} em si, e similarmente o espaço cotangente em cada ponto pode ser naturalmente identificado com o espaço vetorial duplo (Rn)∗ ∗ (mathbb {R} ^{n})^{*}} de covetores; assim, o valor do gradiente em um ponto pode ser pensado de um vetor no original Rn{displaystyle mathbb {R} ^{n}}, não apenas como um vetor tangente.
Computacionalmente, dado um vetor tangente, o vetor pode ser multiplicado pela derivada (como matrizes), que é igual a tomar o produto escalar com o gradiente:
- (Dfp)(v)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Não.∂ ∂ f∂ ∂ x1(p)⋯ ⋯ ∂ ∂ f∂ ∂ xn(p)]Não.v1FORMAÇÃO FORMAÇÃO vn]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1n∂ ∂ f∂ ∂ xEu...(p)vEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Não.∂ ∂ f∂ ∂ x1(p)FORMAÇÃO FORMAÇÃO ∂ ∂ f∂ ∂ xn(p)])) Não.v1FORMAÇÃO FORMAÇÃO vn]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =? ? f(p))) v(df_{p})(v)={begin{bmatrix}{frac {partial f}{partial x_{1}}}(p)&cdots &{frac {partial f}{partial x_{n}}}(p)end{bmatrix}}{begin{bmatrix}v_{1}\vdots \v_{n}end{bmatrix}}=sum _{i=1}^{n}{frac - Não. x_{i}}}(p)v_{i}={begin{bmatrix}{frac - Não. x_{1}}}(p)\vdots \{frac {partial f}{partial x_{n}}}(p)end{bmatrix}}cdot {begin{bmatrix}v_{1}\vdots \v_{n}end{bmatrix}}=nabla f(p)cdot v}
Diferencial ou derivada (exterior)
A melhor aproximação linear para uma função diferenciável
- f:Rn→ → R{displaystyle f:mathbb] {R} ^{n}to mathbb Não.
em um ponto xNão. em Rn{displaystyle mathbb {R} ^{n}} é um mapa linear de Rn{displaystyle mathbb {R} ^{n}} para R{displaystyle mathbb {R} } } que é frequentemente denotado por Dfx{displaystyle df_{x}} ou Df(x)(x)} e chamado de derivado diferencial ou total de fNão. em xNão.. A função DfNão., que mapas xNão. para Dfx{displaystyle df_{x}}, é chamado de diferencial total ou derivado exterior de fNão. e é um exemplo de uma forma diferencial 1.
Assim como a derivada de uma função de uma única variável representa a inclinação da tangente ao gráfico da função, a derivada direcional de uma função em várias variáveis representa a inclinação do hiperplano tangente na direção do vetor.
O gradiente está relacionado ao diferencial pela fórmula
- (? ? f)x)) v= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Dfx(v)(nabla f)_{x}cdot v=df_{x}(v)}
para qualquer v∈ ∈ Rn{displaystyle vin mathbb Não., onde )) - Sim. é o produto do ponto: tomar o produto do ponto de um vetor com o gradiente é o mesmo que tomar o derivado direcional ao longo do vetor.
Se Rn{displaystyle mathbb {R} ^{n}} é visto como o espaço de (dimensão nNão.) vetores de colunas (de números reais), então pode-se considerar DfNão. como o vetor de linha com componentes
- (∂ ∂ f∂ ∂ x1,...... ,∂ ∂ f∂ ∂ xn),{displaystyle left({frac {partial f}{partial x_{1}}},dots{frac {partial f}{partial x_{n}}}right),}
assim Dfx(v)(v)} é dado pela multiplicação da matriz. Assumindo a métrica euclidiana padrão Rn{displaystyle mathbb {R} ^{n}}, o gradiente é então o vetor de coluna correspondente, ou seja,
- (? ? f)Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =DfEu...T.(nabla f)_{i}=df_{i}^{mathsf {T}}.}
Aproximação linear de uma função
A melhor aproximação linear a uma função pode ser expressa em termos do gradiente, em vez do derivado. O gradiente de uma função fNão. do espaço euclidiano Rn{displaystyle mathbb {R} ^{n}} para R{displaystyle mathbb {R} } } a qualquer ponto particular x0{displaystyle x_{0}} em Rn{displaystyle mathbb {R} ^{n}} caracteriza a melhor aproximação linear para fNão. em x0{displaystyle x_{0}}. A aproximação é a seguinte:
- f(x)? ? f(x0)+(? ? f)x0)) (x- Sim. - Sim. x0){displaystyle f(x)approx f(x_{0})+(nabla f)_{x_{0}}cdot (x-x_{0})}
para xNão. perto de x0{displaystyle x_{0}}, onde (? ? f)x0(nabla f)_{x_{0}}} é o gradiente de fNão. computado em x0{displaystyle x_{0}}, e o ponto denota o produto do ponto em Rn{displaystyle mathbb {R} ^{n}}. Esta equação é equivalente aos dois primeiros termos na expansão multivariável da série Taylor fNão. em x0{displaystyle x_{0}}.
Relação com derivado de Fréchet
Seja U um conjunto aberto em Rn. Se a função f: U → R for diferenciável, então a diferencial de f é a derivada Fréchet de f. Assim, ∇f é uma função de U para o espaço Rn tal que
Como consequência, as propriedades usuais da derivada valem para o gradiente, embora o gradiente não seja uma derivada em si, mas sim dual à derivada:
- Linearidade
- O gradiente é linear no sentido de que se f e g são duas funções reais diferenciadas no ponto um ∈ Rne α e β são duas constantes, então α + β é diferente em um, e mais além ? ? (α α f+β β g)(um)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =α α ? ? f(um)+β β ? ? g(um).{displaystyle nabla left(alpha f+beta gright)(a)=alpha nabla f(a)+beta nabla g(a).}
- Regra de produto
- Se f e g são funções reais diferenciadas em um ponto um ∈ Rn, então a regra do produto afirma que o produto fg é diferente em ume ? ? (fg)(um)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =f(um)? ? g(um)+g(um)? ? f(um).{displaystyle nabla (fg)(a)=f(a)nabla g(a)+g(a)nabla f(a). ?
- Regra de cadeia
- Suponha que f: A → R é uma função de valor real definida em um subconjunto A de Rne isso f é diferente em um ponto um. Existem duas formas da regra da cadeia que se aplicam ao gradiente. Primeiro, suponha que a função g é uma curva paramétrica; isto é, uma função g: Eu... → Rn mapeia um subconjunto Eu... ? R para dentro Rn. Se g é diferente em um ponto c ∈ Eu... tal que g(c) = um, então onde: é o operador de composição: (f∘g)x) = f(g(x).(f∘ ∘ g)?(c)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =? ? f(um))) g?(c),(fcirc g)'(c)=nabla f(a)cdot g'(c),}
Mais geralmente, se I ⊂ Rk, então vale o seguinte:
Para a segunda forma da regra da cadeia, suponha que h: I → R é uma função de valor real em um subconjunto I de R, e que h é diferenciável no ponto f(a ) ∈ Eu. Então
Outras propriedades e aplicações
Conjuntos de níveis
Uma superfície nivelada, ou isosuperfície, é o conjunto de todos os pontos onde alguma função tem um determinado valor.
Se f for diferenciável, então o produto escalar (∇f ) x ⋅ v do gradiente em um ponto x com um vetor v fornece a derivada direcional de f em x na direção v. Segue-se que, neste caso, o gradiente de f é ortogonal aos conjuntos de nível de f. Por exemplo, uma superfície nivelada no espaço tridimensional é definida por uma equação da forma F(x, y, z) = c. O gradiente de F é então normal à superfície.
De forma mais geral, qualquer hipersuperfície embutida em uma variedade Riemanniana pode ser cortada por uma equação da forma F(P) = 0 tal que dF não é zero. O gradiente de F é então normal à hipersuperfície.
Da mesma forma, uma hipersuperfície algébrica afim pode ser definida por uma equação F(x1,..., xn) = 0, onde F é um polinômio. O gradiente de F é zero em um ponto singular da hipersuperfície (esta é a definição de um ponto singular). Em um ponto não singular, é um vetor normal diferente de zero.
Campos vetoriais conservativos e o teorema do gradiente
O gradiente de uma função é chamado de campo de gradiente. Um campo gradiente (contínuo) é sempre um campo vetorial conservativo: sua integral de linha ao longo de qualquer caminho depende apenas das extremidades do caminho e pode ser avaliada pelo teorema do gradiente (o teorema fundamental do cálculo para integrais de linha). Por outro lado, um campo vetorial conservativo (contínuo) é sempre o gradiente de uma função.
Generalizações
Jacobiano
A matriz jacobiana é a generalização do gradiente para funções vetoriais de várias variáveis e aplicações diferenciáveis entre espaços euclidianos ou, mais geralmente, variedades. Uma generalização adicional para uma função entre espaços de Banach é a derivada de Fréchet.
Suponha f: Rn → Rm é uma função tal que cada um de seus derivados parciais de primeira ordem existem em Rn. Então a matriz jacobina f é definido como um m×n matriz, denotado por JJf(x)(J} _{mathbb {f} }(mathbb {x})} ou simplesmente JJ- Sim.. O (Eu...,JJ)a entrada é JJEu...JJ= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∂ ∂ fEu...∂ ∂ xJJ{displaystyle mathbf {J} _{ij}={frac {partial f_{i}}{partial x_{j}}. Explicitativamente
Gradiente de um campo vetorial
Como a derivada total de um campo vetorial é um mapeamento linear de vetores para vetores, é uma quantidade tensorial.
Em coordenadas retangulares, o gradiente de um campo vetorial f = ( f1, f2, f3) é definido por:
- ? ? f= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =gJJk∂ ∂ fEu...∂ ∂ xJJeEu...⭐ ⭐ ek,{displaystyle nabla mathbf {f} =g^{jk}{frac {partial f^{i}}{partial x^{j}}}mathbf {e} _{i}otimes mathbf {e} _{k},}
(onde a notação de somatório de Einstein é usada e o produto tensorial dos vetores ei e ek é um tensor diádico do tipo (2,0)). No geral, esta expressão é igual à transposta da matriz jacobiana:
- ∂ ∂ fEu...∂ ∂ xJJ= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∂ ∂ (f1,f2,f3)∂ ∂ (x1,x2,x3).{displaystyle } f^{i}} x^{j}}}={frac {partial (f^{1},f^{2},f^{3})}{partial (x^{1},x^{2},x^{3})}}}.}
Em coordenadas curvilíneas, ou mais geralmente em uma variedade curva, o gradiente envolve símbolos de Christoffel:
- ? ? f= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =gJJk(∂ ∂ fEu...∂ ∂ xJJ+)) Eu...JJEu...fEu...)eEu...⭐ ⭐ ek,{displaystyle nabla mathbf {f} =g^{jk}left({frac {partial} f^{i}} x^{j}}}+ Gamma ^{i}}_{jl}f^{l}right)mathbf {e} _{i}otimes mathbf {e} _{k},}
onde gjk são os componentes do tensor métrico inverso e o ei são os vetores de base de coordenadas.
Expresso de forma mais invariável, o gradiente de um campo vetorial f pode ser definido pela conexão Levi-Civita e pelo tensor métrico:
- ? ? umfb)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =gumc? ? cfb),{displaystyle nabla ^{a}f^{b}=g^{ac}nabla _{c}f^{b},}
onde ∇c é a conexão.
Variedades Riemannianas
Para qualquer função suave f em uma variedade Riemanniana (M, g), o gradiente de f é o campo vetorial ∇f tal que para qualquer campo vetorial X,
- g(? ? f,X)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∂ ∂ Xf,{displaystyle g(nabla f,X)=partial _{X}f,}
ou seja,
- gx((? ? f)x,Xx)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(∂ ∂ Xf)(x),(}(nabla f)_{x},X_{x}{big)}=(partial _{X}f)(x),}
onde gx() denota o produto interno de vetores tangentes em x definido pela métrica g e ∂X f é a função que toma qualquer ponto x ∈ M para a derivada direcional de f na direção X, avaliado em x. Em outras palavras, em um gráfico de coordenadas φ de um subconjunto aberto de M para um subconjunto aberto de Rn, (∂X f )(x) é dado por:
- Gerenciamento Gerenciamento JJ= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1nXJJ(φ φ (x))∂ ∂ ∂ ∂ xJJ(f∘ ∘ φ φ - Sim. - Sim. 1)|φ φ (x),{displaystyle sum _{j=1}^{n}X^{j}{big (}varphi (x){big)}{frac {partial }{partial x_{j}}}(fcirc varphi ^{-1}){Bigg |}_{varphi (x)},}
onde Xj denota o jº componente de X neste gráfico de coordenadas.
Assim, a forma local do gradiente assume a forma:
- ? ? f= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =gEu...k∂ ∂ f∂ ∂ xkeEu....{displaystyle nabla f=g^{ik}{frac {partial f}{partial x^{k}}} {e}}_{i}.}
Generalizando o caso M = Rn, o gradiente de uma função está relacionado com sua derivada externa, pois
- (∂ ∂ Xf)(x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(Df)x(Xx).(partial _{X}f)(x)=(df)_{x}(X_{x}). ?
Mais precisamente, o gradiente ∇f é o campo vetorial associado à 1-forma diferencial df usando o isomorfismo musical
- ♯ ♯ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =♯ ♯ g:: T∗ ∗ M→ → TM{displaystyle sharp =sharp ^{g}colon T^{*}Mto TM}
(chamado "sharp") definido pela métrica g. A relação entre a derivada externa e o gradiente de uma função em Rn é uma caso especial disso em que a métrica é a métrica plana dada pelo produto escalar.
Contenido relacionado
Prueba original del teorema de completitud de Gödel
Modulación de frecuencia
Lista de ecuaciones en mecánica clásica