Funtor

Em matemática, especificamente a teoria da categoria, a functor é um mapeamento entre as categorias. Os funções foram considerados pela primeira vez na topologia algébrica, onde objetos algébricos (como o grupo fundamental) estão associados a espaços topológicos, e os mapas entre esses objetos algébricos estão associados a mapas contínuos entre os espaços. Atualmente, os funções são usados em toda a matemática moderna para relacionar várias categorias. Assim, os funções são importantes em todas as áreas da matemática à qual a teoria da categoria é aplicada.

As palavras categoria e functor foram emprestadas por matemáticos dos filósofos Aristóteles e Rudolf Carnap, respectivamente. O último usou functor em um contexto linguístico; Veja a palavra da função.

Definição

Funcionários FNão. deve preservar a composição dos morfismos gNão. e fNão.

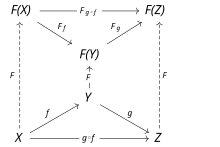
Seja C e D categorias. Um functor F de C a D é um mapeamento que

• associa cada objeto X- Sim. em C a um objeto F(X)(X)} em D,
• associa cada morfismo f:: X→ → Y{displaystyle fcolon Xto Y} em C para um morfismo F(f):: F(X)→ → F(Y){displaystyle F(f)colon F(X)to F(Y)} em D tal que as seguintes duas condições deter:
  • F(Eu...DX)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...DF(X){displaystyle F(mathrm {id} _{X})=mathrm {id} _{F(X)},!} para cada objeto X- Sim. em C,
  • F(g∘ ∘ f)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =F(g)∘ ∘ F(f){displaystyle F(gcirc f)=F(g)circ F(f)} para todos os morfismos f:: X→ → Y{displaystyle fcolon Xto Y,! e g:: Y→ → Z.{displaystyle gcolon Sim. em C.

Ou seja, functores devem preservar morfismos de identidade e composição de morfismos.

Covariância e contravariância

Existem muitas construções em matemática que seriam funtores, mas pelo fato de "inverter morfismos" e "composição reversa". Em seguida, definimos um functor contravariante F de C a D como um mapeamento que

• associa cada objeto X- Sim. em C com um objeto F(X)(X)} em D,
• associa cada morfismo f:: X→ → Y{displaystyle fcolon Xto Y} em C com um morfismo F(f):: F(Y)→ → F(X){displaystyle F(f)colon F(Y)to F(X)} em D tal que as seguintes duas condições deter:
  • F(Eu...DX)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...DF(X){displaystyle F(mathrm {id} _{X})=mathrm {id} _{F(X)},!} para cada objeto X- Sim. em C,
  • F(g∘ ∘ f)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =F(f)∘ ∘ F(g){displaystyle F(gcirc f)=F(f)circ F(g)} para todos os morfismos f:: X→ → Y{displaystyle fcolon Xto Y} e g:: Y→ → Z.{displaystyle gcolon Sim. em C.

Observe que os funções contravariantes revertem a direção da composição.

Os funtores comuns também são chamados funtores covariantes para distingui-los dos contravariantes. Note que também se pode definir um funtor contravariante como um covariante funtor na categoria oposta CopNão. C^{mathrm {op} }}. Alguns autores preferem escrever todas as expressões de forma covariante. Isso é, em vez de dizer F:: C→ → DNão. Fcolon Cto D} é um funtor contravariante, eles simplesmente escrevem F:: Cop→ → D{displaystyle Fcolon C^{mathrm {op} }to D} (ou às vezes) F:: C→ → DopNão. Fcolon Cto D^{mathrm {op} }}) e chamá-lo de funtor.

Funtores contravariantes também são ocasionalmente chamados de cofuntores.

Há uma convenção que se refere a "vetores" - isto é, campos vetoriais, elementos do espaço de seções )) (TM)(TM)} de um pacote tangente TMNão.— como "contravariante" e "covetores" — isto é, 1 formas, elementos do espaço de seções )) (T∗ ∗ M){displaystyle Gamma {mathord {left(T^{*}Mright)}}} de um pacote cotangent T∗ ∗ MNão. T^{*}M}— como "covariante". Esta terminologia se origina na física, e sua racionalidade tem a ver com a posição dos índices ("upstairs" e "downstairs") em expressões como x?Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =:: JJEu...xJJ{displaystyle {x'}^{,i}=Lambda _{j}^{i}x^{j}} para x?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =:: x{displaystyle mathbf {x}={boldsymbol Não. ou ω ω Eu...?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =:: Eu...JJω ω JJ{displaystyle omega "Serviço" _{i}^{j}omega _{j}} para ω ω ?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =ω ω :: T.O que é isso? Sim. Não.) (Lambda }}^{textsf {T}}.} Neste formalismo observa-se que o símbolo de transformação da coordenada :: Eu...JJNão. Lambda _{i}^{j}} (representando a matriz :: T- Não. Não. }}^{textsf (T)) atua sobre os vetores de base "da mesma forma" como nas "coordenadas do covector": eEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =:: Eu...JJeJJ(e) _{i}=Lambda _{i}^{j}mathbf {e} _{j}}— enquanto actua "no sentido oposto" nas "coordenadas de actor" (mas "no mesmo modo" como na base covectores: eEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =:: JJEu...eJJ{displaystyle mathbf {e} ^{i}=Lambda _{j}^{i}mathbf {e} ^{j}}). Esta terminologia é contrária ao usado na teoria da categoria porque é os covetores que têm retrocessos em geral e são assim contravariante, enquanto os vetores em geral são covariante porque eles podem ser em frente. Veja também Covariância e contravariância de vetores.

Funtor oposto

Cada funtor F:: C→ → DNão. Fcolon Cto D} induz o funtor oposto Fop:: Cop→ → DopNão. F^{mathrm {op} }colon C^{mathrm {op} }to D^{mathrm {op} }}, onde CopNão. C^{mathrm {op} }} e DopNão. D^{mathrm {op} }} são as categorias opostas a CNão. C. e DNão.. Por definição, FopNão. F^{mathrm {op} }} mapeia objetos e morfismos da forma idêntica FNão.. Desde então CopNão. C^{mathrm {op} }} não coincide com CNão. C. como uma categoria, e similarmente para DNão., FopNão. F^{mathrm {op} }} distingue-se de FNão.. Por exemplo, ao compor F:: C0→ → C1{displaystyle Fcolon C_{0}to C_{1}} com G:: C1op→ → C2{displaystyle Gcolon C_{1}^{mathrm {op} }to C_{2}}, um deve usar qualquer G∘ ∘ FopNão. Gcirc F^{mathrm {op} }} ou Gop∘ ∘ FNão. G^{mathrm {op} }circ F}. Note que, seguindo a propriedade da categoria oposta, (Fop)op= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =F{displaystyle left(F^{mathrm {op} }right)^{mathrm {op} }=F}.

Bifuntores e multifuncionais

Um bifuntor (também conhecido como funtor binário) é um funtor cujo domínio é uma categoria de produto. Por exemplo, o functor Hom é do tipo C^op × C → Set. Pode ser visto como um functor em dois argumentos. O functor Hom é um exemplo natural; é contravariante em um argumento, covariante no outro.

Um multifuntor é uma generalização do conceito de funtor para n variáveis. Então, por exemplo, um bifuntor é um multifuncional com n = 2.

Propriedades

Duas consequências importantes dos axiomas do funtor são:

• F transforma cada diagrama comutativo em C em um diagrama comutativo em D;
• se f é um isomorfismo em C, então F(f) é um isomorfismo em D.

Pode-se compor functores, ou seja, se F é um functor de A a B e G é um functor de B para C então pode-se formar o functor composto G ∘ F de A a C. A composição dos functores é associativa quando definida. A identidade da composição dos functores é o functor identidade. Isso mostra que os functores podem ser considerados como morfismos em categorias de categorias, por exemplo, na categoria de pequenas categorias.

Uma pequena categoria com um único objeto é a mesma coisa que um monóide: os morfismos de uma categoria de um objeto podem ser pensados como elementos do monóide, e a composição na categoria é pensada como a operação monóide. Functors entre categorias de um objeto correspondem a homomorfismos monóides. Então, de certa forma, functores entre categorias arbitrárias são um tipo de generalização de homomorfismos monóides para categorias com mais de um objeto.

Exemplos

Diagram

For categories C and J, a diagram of type J in C is a covariant functor D : J → C {displaystyle Dcolon Jto C} .

(Category theoretical) presheaf

For categories C and J, a J-presheaf on C is a contravariant functor D : C → J {displaystyle Dcolon Cto J} .

In the special case when J is Set, the category of sets and functions, D is called a presheaf on C.

Presheaves (over a topological space)

If X is a topological space, then the open sets in X form a partially ordered set Open(X) under inclusion. Like every partially ordered set, Open(X) forms a small category by adding a single arrow U → V if and only if U ⊆ V {displaystyle Usubseteq V} . Contravariant functors on Open(X) are called presheaves on X. For instance, by assigning to every open set U the associative algebra of real-valued continuous functions on U, one obtains a presheaf of algebras on X.

Constant functor

The functor C → D which maps every object of C to a fixed object X in D and every morphism in C to the identity morphism on X. Such a functor is called a constant or selection functor.

Endofunctor

A functor that maps a category to that same category; e.g., polynomial functor.

Identity functor

In category C, written 1_C or id_C, maps an object to itself and a morphism to itself. The identity functor is an endofunctor.

Diagonal functor

The diagonal functor is defined as the functor from D to the functor category D^C which sends each object in D to the constant functor at that object.

Limit functor

For a fixed index category J, if every functor J → C has a limit (for instance if C is complete), then the limit functor C^J → C assigns to each functor its limit. The existence of this functor can be proved by realizing that it is the right-adjoint to the diagonal functor and invoking the Freyd adjoint functor theorem. This requires a suitable version of the axiom of choice. Similar remarks apply to the colimit functor (which assigns to every functor its colimit, and is covariant).

Power sets functor

The power set functor P: Set → Set maps each set to its power set and each function f : X → Y {displaystyle fcolon Xto Y} to the map which sends U ∈ P ( X ) {displaystyle Uin {mathcal {P}}(X)} to its image f ( U ) ∈ P ( Y ) {displaystyle f(U)in {mathcal {P}}(Y)} . One can also consider the contravariant power set functor which sends f : X → Y {displaystyle fcolon Xto Y} to the map which sends V ⊆ Y {displaystyle Vsubseteq Y} to its inverse image f − 1 ( V ) ⊆ X . {displaystyle f^{-1}(V)subseteq X.}

For example, if X = { 0 , 1 } {displaystyle X={0,1}} then F ( X ) = P ( X ) = { { } , { 0 } , { 1 } , X } {displaystyle F(X)={mathcal {P}}(X)={{},{0},{1},X}} . Suppose f ( 0 ) = { } {displaystyle f(0)={}} and f ( 1 ) = X {displaystyle f(1)=X} . Then F ( f ) {displaystyle F(f)} is the function which sends any subset U {displaystyle U} of X {displaystyle X} to its image f ( U ) {displaystyle f(U)} , which in this case means { } ↦ f ( { } ) = { } {displaystyle {}mapsto f({})={}} , where ↦ {displaystyle mapsto } denotes the mapping under F ( f ) {displaystyle F(f)} , so this could also be written as ( F ( f ) ) ( { } ) = { } {displaystyle (F(f))({})={}} . For the other values, { 0 } ↦ f ( { 0 } ) = { f ( 0 ) } = { { } } , {displaystyle {0}mapsto f({0})={f(0)}={{}}, } { 1 } ↦ f ( { 1 } ) = { f ( 1 ) } = { X } , {displaystyle {1}mapsto f({1})={f(1)}={X}, } { 0 , 1 } ↦ f ( { 0 , 1 } ) = { f ( 0 ) , f ( 1 ) } = { { } , X } . {displaystyle {0,1}mapsto f({0,1})={f(0),f(1)}={{},X}.} Note that f ( { 0 , 1 } ) {displaystyle f({0,1})} consequently generates the trivial topology on X {displaystyle X} . Also note that although the function f {displaystyle f} in this example mapped to the power set of X {displaystyle X} , that need not be the case in general.

Dual vector space

The map which assigns to every vector space its dual space and to every linear map its dual or transpose is a contravariant functor from the category of all vector spaces over a fixed field to itself.

Fundamental group

Consider the category of pointed topological spaces, i.e. topological spaces with distinguished points. The objects are pairs (X, x₀), where X is a topological space and x₀ is a point in X. A morphism from (X, x₀) to (Y, y₀) is given by a continuous map f: X → Y with f(x₀) = y₀.

To every topological space X with distinguished point x₀, one can define the fundamental group based at x₀, denoted π₁(X, x₀). This is the group of homotopy classes of loops based at x₀, with the group operation of concatenation. If f: X → Y is a morphism of pointed spaces, then every loop in X with base point x₀ can be composed with f to yield a loop in Y with base point y₀. This operation is compatible with the homotopy equivalence relation and the composition of loops, and we get a group homomorphism from π(X, x₀) to π(Y, y₀). We thus obtain a functor from the category of pointed topological spaces to the category of groups.

In the category of topological spaces (without distinguished point), one considers homotopy classes of generic curves, but they cannot be composed unless they share an endpoint. Thus one has the fundamental groupoid instead of the fundamental group, and this construction is functorial.

Algebra of continuous functions

A contravariant functor from the category of topological spaces (with continuous maps as morphisms) to the category of real associative algebras is given by assigning to every topological space X the algebra C(X) of all real-valued continuous functions on that space. Every continuous map f: X → Y induces an algebra homomorphism C(f): C(Y) → C(X) by the rule C(f)(φ) = φ ∘ f for every φ in C(Y).

Tangent and cotangent bundles

The map which sends every differentiable manifold to its tangent bundle and every smooth map to its derivative is a covariant functor from the category of differentiable manifolds to the category of vector bundles.

Doing this constructions pointwise gives the tangent space, a covariant functor from the category of pointed differentiable manifolds to the category of real vector spaces. Likewise, cotangent space is a contravariant functor, essentially the composition of the tangent space with the dual space above.

Group actions/representations

Every group G can be considered as a category with a single object whose morphisms are the elements of G. A functor from G to Set is then nothing but a group action of G on a particular set, i.e. a G-set. Likewise, a functor from G to the category of vector spaces, Vect_K, is a linear representation of G. In general, a functor G → C can be considered as an "action" of G on an object in the category C. If C is a group, then this action is a group homomorphism.

Lie algebras

Assigning to every real (complex) Lie group its real (complex) Lie algebra defines a functor.

Tensor products

If C denotes the category of vector spaces over a fixed field, with linear maps as morphisms, then the tensor product V ⊗ W {displaystyle Votimes W} defines a functor C × C → C which is covariant in both arguments.

Forgetful functors

The functor U: Grp → Set which maps a group to its underlying set and a group homomorphism to its underlying function of sets is a functor. Functors like these, which "forget" some structure, are termed forgetful functors. Another example is the functor Rng → Ab which maps a ring to its underlying additive abelian group. Morphisms in Rng (ring homomorphisms) become morphisms in Ab (abelian group homomorphisms).

Free functors

Going in the opposite direction of forgetful functors are free functors. The free functor F: Set → Grp sends every set X to the free group generated by X. Functions get mapped to group homomorphisms between free groups. Free constructions exist for many categories based on structured sets. See free object.

Homomorphism groups

To every pair A, B of abelian groups one can assign the abelian group Hom(A, B) consisting of all group homomorphisms from A to B. This is a functor which is contravariant in the first and covariant in the second argument, i.e. it is a functor Ab^op × Ab → Ab (where Ab denotes the category of abelian groups with group homomorphisms). If f: A₁ → A₂ and g: B₁ → B₂ are morphisms in Ab, then the group homomorphism Hom(f, g): Hom(A₂, B₁) → Hom(A₁, B₂) is given by φ ↦ g ∘ φ ∘ f. See Hom functor.

Representable functors

We can generalize the previous example to any category C. To every pair X, Y of objects in C one can assign the set Hom(X, Y) of morphisms from X to Y. This defines a functor to Set which is contravariant in the first argument and covariant in the second, i.e. it is a functor C^op × C → Set. If f: X₁ → X₂ and g: Y₁ → Y₂ are morphisms in C, then the map Hom(f, g): Hom(X₂, Y₁) → Hom(X₁, Y₂) is given by φ ↦ g ∘ φ ∘ f.

Functors like these are called representable functors. An important goal in many settings is to determine whether a given functor is representable.

Relação com outros conceitos categóricos

Seja C e D categorias. A coleção de todos os functores de C a D forma os objetos de uma categoria: a categoria de functor. Morfismos nesta categoria são transformações naturais entre functores.

Functores são geralmente definidos por propriedades universais; exemplos são o produto tensorial, a soma direta e o produto direto de grupos ou espaços vetoriais, construção de grupos e módulos livres, limites diretos e inversos. Os conceitos de limite e colimite generalizam vários dos anteriores.

Construções universais geralmente dão origem a pares de funtores adjuntos.

Implementações de computador

Às vezes, os functores aparecem na programação funcional. Por exemplo, a linguagem de programação Haskell possui uma classe Functor onde fmap é uma função politípica usada para mapear funções (morfismos em Hask, a categoria de tipos Haskell) entre tipos existentes para funções entre alguns novos tipos.