Força centrípeta

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Força dirigida ao centro de rotação

Uma partícula é perturbada de seu movimento linear uniforme por uma série de chutes curtos (1, 2,...), dando à sua trajetória uma forma quase circular. A força é chamada de força centrípeta no limite de uma força de ação contínua direcionada para o centro da curvatura do caminho.

Uma força centrípeta (do latim centrum, "centro" e petere, "buscar&# 34;) é uma força que faz um corpo seguir uma trajetória curva. A direção da força centrípeta é sempre ortogonal ao movimento do corpo e em direção ao ponto fixo do centro instantâneo de curvatura da trajetória. Isaac Newton a descreveu como "uma força pela qual os corpos são atraídos ou impelidos, ou de alguma forma tendem, em direção a um ponto como um centro". Na teoria da mecânica newtoniana, a gravidade fornece a força centrípeta que causa as órbitas astronômicas.

Um exemplo comum envolvendo força centrípeta é o caso em que um corpo se move com velocidade uniforme ao longo de uma trajetória circular. A força centrípeta é direcionada perpendicularmente ao movimento e também ao longo do raio em direção ao centro do caminho circular. A descrição matemática foi derivada em 1659 pelo físico holandês Christiaan Huygens.

Fórmula

Da cinemática do movimento curvo, sabe-se que um objeto que se move com velocidade tangencial v ao longo de uma trajetória com raio de curvatura r acelera em direção ao centro de curvatura a uma avaliar

{displaystyle {textbf {a}}_{c}=lim _{Delta tto 0}{frac {|Delta {textbf {v}}|}{Delta t}},quad a_{c}={frac {v^{2}}{r}}}

a_c

{displaystyle Delta {textbf {v}}}

{displaystyle t+Delta {t}}

t

Pela segunda lei de Newton, a causa da aceleração é uma força resultante agindo sobre o objeto, que é proporcional à sua massa m e à sua aceleração. A força, geralmente referida como uma força centrípeta, tem uma magnitude

{displaystyle F_{c}=ma_{c}=m{frac {v^{2}}{r}}}

Derivação

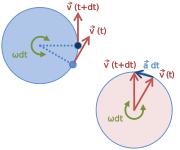
A aceleração centrípeta pode ser inferida a partir do diagrama dos vetores de velocidade em duas instâncias. No caso de movimento circular uniforme as velocidades têm magnitude constante. Como cada um é perpendicular ao seu respectivo vetor de posição, a subtração vetorial simples implica dois triângulos isosceles semelhantes com ângulos congruentes – um que compreende uma base de ${displaystyle Delta {textbf {v}}}$ e um comprimento da perna $v$ e o outro uma base de ${displaystyle Delta {textbf {r}}}$ (diferença do vetor de posição) e um comprimento da perna $r$ :

{displaystyle {frac {|Delta {textbf {v}}|}{v}}={frac {|Delta {textbf {r}}|}{r}}}

{displaystyle |Delta {textbf {v}}|={frac {v}{r}}|Delta {textbf {r}}|}

{displaystyle |Delta {textbf {v}}|}

{displaystyle {frac {v}{r}}|Delta {textbf {r}}|}

{displaystyle a_{c}=lim _{Delta tto 0}{frac {|Delta {textbf {v}}|}{Delta t}}={frac {v}{r}}lim _{Delta tto 0}{frac {|Delta {textbf {r}}|}{Delta t}}=omega lim _{Delta tto 0}{frac {|Delta {textbf {r}}|}{Delta t}}=vomega ={frac {v^{2}}{r}}}

Esta força também é às vezes escrita em termos da velocidade angular ω do objeto sobre o centro do círculo, relacionada à velocidade tangencial pela fórmula

{displaystyle v=omega r}

{displaystyle F_{c}=mromega ^{2},.}

Expresso usando o período orbital T para uma revolução do círculo,

{displaystyle omega ={frac {2pi }{T}}}

{displaystyle F_{c}=mrleft({frac {2pi }{T}}right)^{2}.}

Em aceleradores de partículas, a velocidade pode ser muito alta (próxima da velocidade da luz no vácuo), então a mesma massa de repouso agora exerce maior inércia (massa relativística), exigindo assim maior força para a mesma aceleração centrípeta, então a equação se torna:

{displaystyle F_{c}={frac {gamma mv^{2}}{r}}}

{displaystyle gamma ={frac {1}{sqrt {1-{frac {v^{2}}{c^{2}}}}}}}

Assim, a força centrípeta é dada por:

{displaystyle F_{c}=gamma mvomega }

{displaystyle gamma mv}

Análise de vários casos

Abaixo estão três exemplos de complexidade crescente, com derivações das fórmulas que governam a velocidade e a aceleração.

Notas e referências

^ Craig, John (1849). Um novo dicionário etimológico, tecnológico e pronuncio universal da língua inglesa: abraçando todos os termos usados na arte, ciência e literatura, Volume 1. Universidade de Harvard. p. 291. Extrato da página 291
^ Newton, Isaac (2010). O principia: princípios matemáticos da filosofia natural. [S.l.]: Snowball Pub. p. 10. ISBN 978-1-60796-240-3.
^ Russelkl C Hibbeler (2009). «Equations of Motion: Normal and tangential coordinates» (em inglês). Mecânica de Engenharia: Dinâmica (12 ed.). Prentice Hall. p. 131. ISBN 978-0-13-607791-6.
^ Paul Allen Tipler; Gene Mosca (2003). Física para cientistas e engenheiros (5a ed.). Macmillan. p. 129. ISBN 978-0-7167-8339-8.
^ P. Germain; M. Piau; D. Caillerie, eds. (2012). Mecânica Teórica e Aplicada. Elsevier. ISBN 9780444600202.
^ Chris Carter (2001). Fatos e Prática para A-Level: Física. S.2.: Oxford University Press. p. 30. ISBN 978-0-19-914768-7.{{cite book}}: CS1: localização (link)
↑ a b «Uniform Circular Motion» (em inglês).
^ Eugene Lommel; George William Myers (1900). Física experimental. K. Paul, Trench, Trübner & Co. p. 63.
^ Colwell, Catharine H. «A Derivation of the Formulas for Centripetal Acceleration» (em inglês). Física. Arquivado do original em 15 de agosto de 2011. Retrieved 31 de Julho 2011.
^ Conte, Mario; Mackay, William W (1991). Uma introdução à física dos aceleradores de partículas. World Scientific. p. 8. ISBN 978-981-4518-00-0. Extrato da página 8
^ Theo Koupelis (2010). In Quest of the Universe (em inglês). Jones & Bartlett Learning. p. 83. ISBN 978-0-7637-6858-4.
^ A. V. Durrant (1996). Vetores em física e engenharia. CRC Press. p. 103. ISBN 978-0-412-62710-1.
^ Lawrence S. Lerner (1997). Física para cientistas e engenheiros. Boston: Jones & Bartlett Publishers. p. 128. ISBN 978-0-86720-479-7.
^ Arthur Beiser (2004). O esboço de física aplicada de Schaum. New York: McGraw-Hill Professional. p. 103. ISBN 978-0-07-142611-4.
^ Alan Darbyshire (2003). Engenharia Mecânica: Unidades de Opção Nacional BTEC. Oxford: Newnes. p. 56. ISBN 978-0-7506-5761-7.
^ Federal Aviation Administration (2007). Encyclopedia of Aeronautical Knowledge (em inglês). Cidade de Oklahoma OK: Skyhorse Publishing Inc. Figura 3–21. ISBN 978-1-60239-034-8.
^ Nota: ao contrário dos vetores da unidade cartesiana ${displaystyle {hat {mathbf {i} }}}$ e ${displaystyle {hat {mathbf {j} }}}$ , que são constantes, em coordenadas polares a direção dos vetores unitários u_R e u_θ depender θ, e assim em geral têm derivados de tempo não zero.
^ Embora o sistema de coordenadas polares se mova com a partícula, o observador não. A descrição do movimento de partículas permanece uma descrição do ponto de vista do observador estacionário.
^ Observe que este sistema de coordenadas local não é autônomo; por exemplo, sua rotação no tempo é ditada pela trajetória traçada pela partícula. O vetor radial R()) não representa o raio da curvatura do caminho.
^ John Robert Taylor (2005). Mecânica clássica. Sausa! CA: University Science Books. pp. 28–29. ISBN 978-1-891389-22-1.
^ Cornelius Lanczos (1986). Os Princípios Variacionais da Mecânica. Nova Iorque: Courier Dover Publications. p. 103. ISBN 978-0-486-65067-8.
^ Veja, por exemplo, Howard D. Curtis (2005). Mecânica Orbital para Estudantes de Engenharia. Butterworth-Heinemann. p. 5. ISBN 978-0-7506-6169-0.
^ S. Y. Lee (2004). Física aceleradora (2a ed.). Hackensack NJ: World Scientific. p. 37. ISBN 978-981-256-182-4.
^ O observador do movimento ao longo da curva está usando essas coordenadas locais para descrever o movimento do observador quadro de referência, isto é, de um ponto de vista estacionário. Em outras palavras, embora o sistema de coordenadas local se mova com a partícula, o observador não. Uma mudança no sistema de coordenadas utilizado pelo observador é apenas uma mudança no seu descrição de observações, e não significa que o observador mudou seu estado de movimento, e vice-versa.
^ Zhilin Li; Kazufumi Ito (2006). O método de interface imerso: soluções numéricas de PDEs envolvendo interfaces e domínios irregulares. Filadélfia: Sociedade de Matemática Industrial e Aplicada. p. 16. ISBN 978-0-89871-609-2.
^ K L Kumar (2003). Mecânica de Engenharia. Nova Deli: Tata McGraw-Hill. p. 339. ISBN 978-0-07-049473-2.
^ Lakshmana C. Rao; J. Lakshminarasimhan; Raju Sethuraman; SM Sivakuma (2004). Dinâmica de Engenharia: Estática e Dinâmica. Prentice Hall of Índia. p. 133. ISBN 978-81-203-2189-2.
^ Shigeyuki Morita (2001). Geometria de formas diferenciais. American Mathematical Society. p. 1. ISBN 978-0-8218-1045-3. coordenadas locais.
^ O círculo oscilante em um determinado ponto P em uma curva é o círculo limitante de uma sequência de círculos que passam P e dois outros pontos na curva, Q e R, em cada lado de P, como Q e R abordagem P. Veja o texto online de Lamb: Horace Lamb (1897). Um Curso Elementar de Calculus Infinitosimal. University Press. p. 406. ISBN 978-1-108-00534-0. círculo oscilante.
↑ a b Guang Chen; Fook Fah Yap (2003). Uma Introdução à Dinâmica Planar (3a ed.). Central Learning Ásia/Thomson Learning Ásia. p. 34. ISBN 978-981-243-568-2.
^ R. Douglas Gregory (2006). Classical Mechanics: An Undergraduate Text. Cambridge University Press. p. 20. ISBN 978-0-521-82678-5.
^ Edmund Taylor Whittaker; William McCrea (1988). Um tratado sobre a dinâmica analítica de partículas e corpos rígidos: com uma introdução ao problema de três corpos (4a ed.). Cambridge University Press. p. 20. ISBN 978-0-521-35883-5.
^ Jerry H. Ginsberg (2007). Dinâmica de Engenharia. Cambridge University Press. p. 33. ISBN 978-0-521-88303-0.
^ Joseph F. Shelley (1990). 800 problemas resolvidos na mecânica vetorial para engenheiros: Dinâmica. McGraw-Hill Professional. p. 47. ISBN 978-0-07-056687-3.
^ Larry C. Andrews; Ronald L. Phillips (2003). Técnicas Matemáticas para Engenheiros e Cientistas. SPIE Press. p. 164. ISBN 978-0-8194-4506-3.
^ Ch V Ramana Murthy; NC Srinivas (2001). Matemática Aplicada. New Delhi: S. Chand & Co. p. 337. ISBN 978-81-219-2082-7.
^ O artigo sobre curvatura trata um caso mais geral onde a curva é parametrizada por uma variável arbitrária (denotada )), em vez de pelo comprimento do arco S.
^ Ahmed A. Shabana; Khaled E. Zaazaa; Hiroyuki Sugiyama (2007). Dinâmica do veículo ferroviário: uma abordagem computacional. CRC Press. p. 91. ISBN 978-1-4200-4581-9.

Contenido relacionado

Más resultados...