Força

AjustarCompartirImprimirCitar

InfluÃancia que pode causar movimento de um objeto

Na física, uma força é uma influência que faz com que o movimento de um objeto com massa mude sua velocidade (por exemplo, movendo-se de um estado de repouso), ou seja, para acelerar. Pode ser um empurrão ou um puxão, sempre com magnitude e direção, tornando-se uma grandeza vetorial. É medido na unidade SI de newton (N) e representado pelo símbolo $F$ (anteriormente $P$ ).

A forma original da segunda lei de Newton afirma que a força resultante agindo sobre um objeto é igual à taxa na qual seu momento varia com o tempo. Se a massa do objeto for constante, esta lei implica que a aceleração de um objeto é diretamente proporcional à força resultante que atua sobre o objeto, está na direção da força resultante e é inversamente proporcional à massa do objeto.

Conceitos relacionados à força incluem: impulso, que aumenta a velocidade de um objeto; arrasto, que diminui a velocidade de um objeto; e torque, que produz mudanças na velocidade de rotação de um objeto. Em um corpo estendido, cada parte geralmente aplica forças nas partes adjacentes; a distribuição de tais forças através do corpo é o estresse mecânico interno. Essas tensões mecânicas internas não causam aceleração desse corpo, pois as forças se equilibram. A pressão, a distribuição de muitas pequenas forças aplicadas sobre uma área de um corpo, é um tipo simples de tensão que, se desequilibrada, pode fazer com que o corpo acelere. O estresse geralmente causa deformação de materiais sólidos ou fluxo em fluidos.

Desenvolvimento do conceito

Os filósofos da antiguidade usaram o conceito de força no estudo de objetos estacionários e em movimento e máquinas simples, mas pensadores como Aristóteles e Arquimedes retiveram erros fundamentais na compreensão da força. Em parte, isso se deveu a um entendimento incompleto da força de atrito às vezes não óbvia e, conseqüentemente, a uma visão inadequada da natureza do movimento natural. Um erro fundamental foi a crença de que uma força é necessária para manter o movimento, mesmo a uma velocidade constante. A maioria dos mal-entendidos anteriores sobre movimento e força acabou sendo corrigida por Galileu Galilei e Sir Isaac Newton. Com sua visão matemática, Sir Isaac Newton formulou leis de movimento que não foram melhoradas por quase trezentos anos. No início do século 20, Einstein desenvolveu uma teoria da relatividade que previu corretamente a ação de forças em objetos com momentos crescentes próximos à velocidade da luz e também forneceu informações sobre as forças produzidas pela gravitação e inércia.

Com insights modernos sobre mecânica quântica e tecnologia que podem acelerar partículas próximas à velocidade da luz, a física de partículas desenvolveu um Modelo Padrão para descrever forças entre partículas menores que átomos. O Modelo Padrão prevê que as partículas trocadas chamadas bósons de calibre são os meios fundamentais pelos quais as forças são emitidas e absorvidas. Apenas quatro interações principais são conhecidas: em ordem decrescente de força, são elas: forte, eletromagnética, fraca e gravitacional. As observações da física de partículas de alta energia feitas durante as décadas de 1970 e 1980 confirmaram que as forças fracas e eletromagnéticas são expressões de uma interação eletrofraca mais fundamental.

Conceitos pré-newtonianos

Aristóteles descreveu famosamente uma força como qualquer coisa que faz com que um objeto passasse por "movimento não natural"

Desde a antiguidade, o conceito de força é reconhecido como parte integrante do funcionamento de cada uma das máquinas simples. A vantagem mecânica dada por uma máquina simples permitia que menos força fosse usada em troca dessa força atuando em uma distância maior para a mesma quantidade de trabalho. A análise das características das forças culminou no trabalho de Arquimedes, que ficou especialmente famoso por formular um tratamento das forças de empuxo inerentes aos fluidos.

Aristóteles forneceu uma discussão filosófica do conceito de força como parte integrante da cosmologia aristotélica. Na visão de Aristóteles, a esfera terrestre continha quatro elementos que paravam em diferentes "lugares naturais" lá no. Aristóteles acreditava que os objetos imóveis na Terra, aqueles compostos principalmente pelos elementos terra e água, estavam em seu lugar natural no solo e que permaneceriam assim se deixados sozinhos. Ele distinguiu entre a tendência inata dos objetos de encontrar seu "lugar natural" (por exemplo, para a queda de corpos pesados), o que levou ao "movimento natural" e ao movimento não natural ou forçado, que exigia a aplicação contínua de uma força. Essa teoria, baseada na experiência cotidiana de como os objetos se movem, como a aplicação constante de uma força necessária para manter um carrinho em movimento, apresentava problemas conceituais para explicar o comportamento de projéteis, como o vôo de flechas. O local onde o arqueiro move o projétil foi no início do vôo e, enquanto o projétil navegava no ar, nenhuma causa eficiente discernível atuava sobre ele. Aristóteles estava ciente desse problema e propôs que o ar deslocado pelo caminho do projétil leva o projétil ao seu alvo. Essa explicação exige um continuum como o ar para a mudança de lugar em geral.

A física aristotélica começou a enfrentar críticas na ciência medieval, primeiro por John Philoponus no século VI.

As deficiências da física aristotélica não seriam totalmente corrigidas até o trabalho do século 17 de Galileu Galilei, que foi influenciado pela ideia medieval tardia de que objetos em movimento forçado carregavam uma força inata de ímpeto. Galileu construiu um experimento no qual pedras e balas de canhão foram lançadas em uma inclinação para refutar a teoria aristotélica do movimento. Ele mostrou que os corpos eram acelerados pela gravidade de uma forma independente de sua massa e argumentou que os objetos retêm sua velocidade a menos que sejam influenciados por uma força, por exemplo, o atrito.

No início do século XVII, antes dos Principia de Newton, o termo "força" (latim: vis) foi aplicado a muitos fenômenos físicos e não físicos, por exemplo, para uma aceleração de um ponto. O produto de uma massa pontual e o quadrado de sua velocidade foi denominado vis viva (força viva) por Leibniz. O conceito moderno de força corresponde ao vis motrix de Newton (força aceleradora).

Mecânica newtoniana

Sir Isaac Newton descreveu o movimento de todos os objetos usando os conceitos de inércia e força e, ao fazê-lo, descobriu que eles obedecem a certas leis de conservação. Em 1687, Newton publicou sua tese Philosophiæ Naturalis Principia Mathematica. Nesta obra, Newton estabeleceu três leis de movimento que até hoje são a forma como as forças são descritas na física.

Primeira lei

A primeira lei do movimento de Newton afirma que os objetos continuam a se mover em um estado de velocidade constante, a menos que sejam influenciados por uma força líquida externa (força resultante). Essa lei é uma extensão da percepção de Galileu de que a velocidade constante estava associada à falta de força resultante (veja uma descrição mais detalhada disso abaixo). Newton propôs que todo objeto com massa tem uma inércia inata que funciona como o equilíbrio fundamental "estado natural" no lugar da ideia aristotélica do "estado natural de repouso". Ou seja, a primeira lei empírica de Newton contradiz a crença intuitiva aristotélica de que uma força líquida é necessária para manter um objeto em movimento com velocidade constante. Ao tornar o repouso fisicamente indistinguível da velocidade constante diferente de zero, a primeira lei de Newton conecta diretamente a inércia com o conceito de velocidades relativas. Especificamente, em sistemas onde os objetos se movem com velocidades diferentes, é impossível determinar qual objeto está "em movimento" e qual objeto está "em repouso". As leis da física são as mesmas em todos os referenciais inerciais, ou seja, em todos os referenciais relacionados por uma transformação galileana.

Por exemplo, ao viajar em um veículo em movimento a uma velocidade constante, as leis da física não mudam como resultado de seu movimento. Se uma pessoa dentro do veículo jogar uma bola para cima, essa pessoa a observará subir e cair verticalmente e não terá que aplicar uma força na direção em que o veículo está se movendo. Outra pessoa, observando a passagem do veículo em movimento, observaria a bola seguir uma trajetória parabólica curva na mesma direção do movimento do veículo. É a inércia da bola associada à sua velocidade constante na direção do movimento do veículo que garante que a bola continue avançando mesmo quando é lançada para cima e cai de volta. Do ponto de vista da pessoa no carro, o veículo e tudo dentro dele está em repouso: É o mundo exterior que se move com velocidade constante na direção oposta do veículo. Como não há experimento que possa distinguir se é o veículo que está em repouso ou o mundo exterior que está em repouso, as duas situações são consideradas fisicamente indistinguíveis. A inércia, portanto, aplica-se igualmente bem ao movimento de velocidade constante e ao repouso.

Embora a equação mais famosa de Sir Isaac Newton seja

{vec {F}}=m{vec {a}}

, ele realmente escreveu uma forma diferente para sua segunda lei de movimento que não usou cálculo diferencial

Segunda lei

Uma declaração moderna da segunda lei de Newton é uma equação vetorial:

{displaystyle {vec {F}}={frac {mathrm {d} {vec {p}}}{mathrm {d} t}},}

vec{p}

{displaystyle {vec {F}}}

Rede líquidadesequilibrado

Pela definição de momento,

{displaystyle {vec {F}}={frac {mathrm {d} {vec {p}}}{mathrm {d} t}}={frac {mathrm {d} left(m{vec {v}}right)}{mathrm {d} t}},}

{displaystyle {vec {v}}}

Se a segunda lei de Newton for aplicada a um sistema de massa constante, m pode ser movido para fora do operador de derivada. A equação então fica

{displaystyle {vec {F}}=m{frac {mathrm {d} {vec {v}}}{mathrm {d} t}}.}

{displaystyle {vec {F}}=m{vec {a}}.}

A segunda lei de Newton afirma a proporcionalidade direta da aceleração à força e a proporcionalidade inversa da aceleração à massa. As acelerações podem ser definidas por meio de medições cinemáticas, que são bem descritas por meio da análise do quadro de referência em física avançada. A relatividade geral oferece uma equivalência entre espaço-tempo e massa, mas sem uma teoria coerente da gravidade quântica, não está claro como ou se essa conexão é relevante em microescalas. Com alguma justificativa, a segunda lei de Newton pode ser tomada como uma definição quantitativa de massa escrevendo a lei como uma igualdade; as unidades relativas de força e massa são então fixas.

Alguns livros usam a segunda lei de Newton como uma definição de força, mas isso foi menosprezado em outros livros. Físicos, filósofos e matemáticos notáveis que buscaram uma definição mais explícita do conceito de força incluem Ernst Mach e Walter Noll.

A segunda lei de Newton pode ser usada para medir a intensidade das forças. Por exemplo, o conhecimento das massas dos planetas junto com as acelerações de suas órbitas permite aos cientistas calcular as forças gravitacionais nos planetas.

Terceira lei

Sempre que um corpo exerce uma força sobre outro, o último simultaneamente exerce uma força igual e oposta no primeiro. Em forma vetorial, se ${displaystyle {vec {F}}_{1,2}}$ é a força do corpo 1 no corpo 2 e ${displaystyle {vec {F}}_{2,1}}$ o do corpo 2 no corpo 1, então

{displaystyle {vec {F}}_{1,2}=-{vec {F}}_{2,1}.}

lei de ação-reação

{displaystyle {vec {F}}_{1,2}}

Acção

{displaystyle -{vec {F}}_{2,1}}

reacção

A Terceira Lei de Newton é o resultado da aplicação de simetria a situações em que as forças podem ser atribuídas à presença de diferentes objetos. A terceira lei significa que todas as forças são interações entre corpos diferentes e, portanto, não existe uma força unidirecional ou uma força que atue em apenas um corpo.

Em um sistema composto de objeto 1 e objeto 2, a força resultante no sistema devido a suas interações mútuas é zero:

{displaystyle {vec {F}}_{1,2}+{vec {F}}_{2,1}=0.}

Combinando as Segundas e Terceiras Leis de Newton, é possível mostrar que o impulso linear de um sistema é conservado. Em um sistema de duas partículas, se ${displaystyle {vec {p}}_{1}}$ é o momento do objeto 1 e ${displaystyle {vec {p}}_{2}}$ o momento do objeto 2, então

{displaystyle {frac {mathrm {d} {vec {p}}_{1}}{mathrm {d} t}}+{frac {mathrm {d} {vec {p}}_{2}}{mathrm {d} t}}={vec {F}}_{1,2}+{vec {F}}_{2,1}=0.}

Teoria especial da relatividade

Na teoria especial da relatividade, massa e energia são equivalentes (como pode ser visto calculando o trabalho necessário para acelerar um objeto). Quando a velocidade de um objeto aumenta, também aumenta sua energia e, portanto, sua massa equivalente (inércia). Portanto, requer mais força para acelerá-lo na mesma quantidade do que em uma velocidade menor. Segunda Lei de Newton,

{displaystyle {vec {F}}={frac {mathrm {d} {vec {p}}}{mathrm {d} t}},}

{displaystyle {vec {p}}={frac {m_{0}{vec {v}}}{sqrt {1-v^{2}/c^{2}}}},}

m_{0}

c

A expressão relativista relacionando força e aceleração para uma partícula com massa de descanso constante não zero $m$ em movimento $x$ direção é:

{displaystyle {vec {F}}=left(gamma ^{3}ma_{x},gamma ma_{y},gamma ma_{z}right),}

{displaystyle gamma ={frac {1}{sqrt {1-v^{2}/c^{2}}}}.}

No início da história da relatividade, as expressões $gamma ^{3}m$ e $gamma m$ foram chamadas de massa longitudinal e transversal. A força relacional não produz uma aceleração constante, mas uma aceleração crescente à medida que o objeto aproxima a velocidade da luz. Note que $gamma$ aproxima-se assintoticamente um valor infinito e é indefinido para um objeto com uma massa de repouso não-zero enquanto se aproxima da velocidade da luz, e a teoria não produz nenhuma previsão a essa velocidade.

Se $v$ é muito pequeno em comparação com $c$ , então $gamma$ é muito perto de 1 e

{displaystyle F=ma}

{displaystyle F^{mu }=mA^{mu }}

F^{mu }

m

A^{mu }

Descrições

Diagramas corpo livre de um bloco em uma superfície plana e um plano inclinado. As forças são resolvidas e adicionadas em conjunto para determinar suas magnitudes e a força líquida.

Como as forças são percebidas como empurrões ou puxões, isso pode fornecer uma compreensão intuitiva para descrever as forças. Tal como acontece com outros conceitos físicos (por exemplo, temperatura), a compreensão intuitiva das forças é quantificada usando definições operacionais precisas que são consistentes com observações diretas e comparadas a uma escala de medição padrão. Por meio da experimentação, determina-se que as medições de forças em laboratório são totalmente consistentes com a definição conceitual de força oferecida pela mecânica newtoniana.

As forças agem em uma direção particular e têm tamanhos dependentes de quão forte é o empurrão ou puxão. Devido a essas características, as forças são classificadas como "quantidades vetoriais". Isso significa que as forças seguem um conjunto diferente de regras matemáticas do que as quantidades físicas que não têm direção (denominadas quantidades escalares). Por exemplo, ao determinar o que acontece quando duas forças atuam sobre o mesmo objeto, é necessário conhecer tanto a magnitude quanto a direção de ambas as forças para calcular o resultado. Se essas duas informações não forem conhecidas para cada força, a situação é ambígua. Por exemplo, se você sabe que duas pessoas estão puxando a mesma corda com magnitudes de força conhecidas, mas não sabe em que direção cada pessoa está puxando, é impossível determinar qual será a aceleração da corda. As duas pessoas podem estar puxando uma contra a outra como em um cabo de guerra ou as duas pessoas podem estar puxando na mesma direção. Neste exemplo unidimensional simples, sem conhecer a direção das forças, é impossível decidir se a força resultante é o resultado da soma das duas magnitudes de força ou da subtração de uma da outra. A associação de forças com vetores evita tais problemas.

Historicamente, as forças foram primeiro investigadas quantitativamente em condições de equilíbrio estático, onde várias forças se anulavam. Tais experimentos demonstram as propriedades cruciais de que as forças são quantidades vetoriais aditivas: elas têm magnitude e direção. Quando duas forças atuam sobre uma partícula pontual, a força resultante, a resultante (também chamada de força resultante), pode ser determinada seguindo a regra do paralelogramo da adição de vetores: o a adição de dois vetores representados pelos lados de um paralelogramo dá um vetor resultante equivalente que é igual em módulo e direção à transversal do paralelogramo. A magnitude da resultante varia da diferença das magnitudes das duas forças à sua soma, dependendo do ângulo entre suas linhas de ação. Se atuando sobre um corpo estendido, suas respectivas linhas de aplicação também devem ser especificadas para dar conta de seus efeitos sobre o movimento do corpo.

Os diagramas de corpo livre podem ser usados como uma maneira conveniente de acompanhar as forças que atuam em um sistema. Idealmente, esses diagramas são desenhados com os ângulos e magnitudes relativas dos vetores de força preservados para que a adição gráfica de vetores possa ser feita para determinar a força resultante.

Além de serem adicionadas, as forças também podem ser decompostas em componentes independentes em ângulos retos entre si. Uma força horizontal apontando para o nordeste pode, portanto, ser dividida em duas forças, uma apontando para o norte e outra apontando para o leste. A soma dessas forças componentes usando a adição de vetores produz a força original. Resolver vetores de força em componentes de um conjunto de vetores de base costuma ser uma maneira matematicamente mais limpa de descrever forças do que usar magnitudes e direções. Isso ocorre porque, para componentes ortogonais, os componentes da soma vetorial são determinados exclusivamente pela adição escalar dos componentes dos vetores individuais. Os componentes ortogonais são independentes uns dos outros porque as forças que atuam a noventa graus uma da outra não têm efeito sobre a magnitude ou direção uma da outra. A escolha de um conjunto de vetores de base ortogonais geralmente é feita considerando qual conjunto de vetores de base tornará a matemática mais conveniente. A escolha de um vetor de base que esteja na mesma direção de uma das forças é desejável, pois essa força teria apenas um componente diferente de zero. Os vetores de força ortogonais podem ser tridimensionais com o terceiro componente sendo perpendicular aos outros dois.

Equilíbrio

Quando todas as forças que agem sobre um objeto estão equilibradas, diz-se que o objeto está em estado de equilíbrio. Portanto, o equilíbrio ocorre quando a força resultante que age sobre uma partícula pontual é zero (isto é, a soma vetorial de todas as forças é zero). Ao se tratar de um corpo estendido, também é necessário que o torque líquido seja zero.

Existem dois tipos de equilíbrio: equilíbrio estático e equilíbrio dinâmico.

Estático

O equilíbrio estático era compreendido bem antes da invenção da mecânica clássica. Objetos que estão em repouso têm força resultante nula atuando sobre eles.

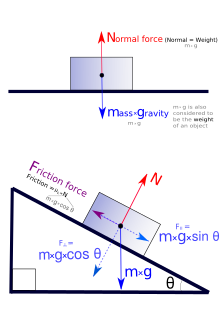
O caso mais simples de equilíbrio estático ocorre quando duas forças são iguais em magnitude, mas opostas em direção. Por exemplo, um objeto em uma superfície plana é puxado (atraído) para baixo em direção ao centro da Terra pela força da gravidade. Ao mesmo tempo, uma força é aplicada pela superfície que resiste à força para baixo com igual força para cima (chamada de força normal). A situação produz força líquida zero e, portanto, nenhuma aceleração.

Empurrar um objeto que repousa sobre uma superfície de atrito pode resultar em uma situação em que o objeto não se move porque a força aplicada se opõe ao atrito estático, gerado entre o objeto e a superfície da mesa. Para uma situação sem movimento, a força de atrito estático exatamente equilibra a força aplicada, resultando em nenhuma aceleração. O atrito estático aumenta ou diminui em resposta à força aplicada até um limite superior determinado pelas características do contato entre a superfície e o objeto.

Um equilíbrio estático entre duas forças é a forma mais usual de medir forças, usando dispositivos simples como balanças e balanças de mola. Por exemplo, um objeto suspenso em uma balança de mola vertical experimenta a força da gravidade agindo sobre o objeto equilibrado por uma força aplicada pela "força de reação da mola", que é igual ao peso do objeto. Usando tais ferramentas, algumas leis quantitativas de força foram descobertas: que a força da gravidade é proporcional ao volume para objetos de densidade constante (amplamente explorada por milênios para definir pesos padrão); Arquimedes' princípio de flutuabilidade; Arquimedes' análise da alavanca; Lei de Boyle para pressão de gás; e a lei de Hooke para molas. Tudo isso foi formulado e verificado experimentalmente antes de Isaac Newton expor suas Três Leis do Movimento.

Dinâmico

Galileu Galilei foi o primeiro a apontar as contradições inerentes contidas na descrição de Aristóteles de forças.

O equilíbrio dinâmico foi descrito pela primeira vez por Galileu, que percebeu que certas suposições da física aristotélica eram contrariadas por observações e lógica. Galileu percebeu que a simples adição de velocidade exige que o conceito de um "recurso de repouso absoluto" não existe. Galileu concluiu que o movimento em velocidade constante era completamente equivalente ao repouso. Isso era contrário à noção de Aristóteles de um "estado natural" de repouso que os objetos com massa se aproximaram naturalmente. Experimentos simples mostraram que o entendimento de Galileu sobre a equivalência entre velocidade constante e repouso estava correto. Por exemplo, se um marinheiro jogasse uma bala de canhão do ninho de um navio movendo-se a uma velocidade constante, a física aristotélica faria a bala de canhão cair enquanto o navio se movia abaixo dela. Assim, em um universo aristotélico, a bala de canhão cairia atrás do pé do mastro de um navio em movimento. Quando esse experimento é realmente realizado, a bala sempre cai ao pé do mastro, como se a bala soubesse viajar com o navio apesar de estar separada dele. Como não há força horizontal para frente sendo aplicada à bala de canhão enquanto ela cai, a única conclusão que resta é que a bala de canhão continua a se mover com a mesma velocidade do barco ao cair. Portanto, nenhuma força é necessária para manter a bala de canhão em movimento com velocidade constante.

Além disso, qualquer objeto viajando a uma velocidade constante deve estar sujeito a força líquida zero (força resultante). Esta é a definição de equilíbrio dinâmico: quando todas as forças em um objeto se equilibram, mas ele ainda se move a uma velocidade constante.

Um caso simples de equilíbrio dinâmico ocorre em movimento de velocidade constante através de uma superfície com atrito cinético. Em tal situação, uma força é aplicada na direção do movimento enquanto a força de atrito cinético se opõe exatamente à força aplicada. Isso resulta em força líquida zero, mas como o objeto começou com uma velocidade diferente de zero, ele continua a se mover com uma velocidade diferente de zero. Aristóteles interpretou mal este movimento como sendo causado pela força aplicada. Quando o atrito cinético é levado em consideração, fica claro que não há força resultante causando movimento de velocidade constante.

Mecânica quântica

A noção "força" mantém seu significado na mecânica quântica, embora agora esteja lidando com operadores em vez de variáveis clássicas e embora a física seja agora descrita pela equação de Schrödinger em vez de equações de Newton. Isso tem a consequência de que os resultados de uma medição são agora às vezes "quantizados", ou seja, eles aparecem em porções discretas. Isto é, naturalmente, difícil de imaginar no contexto das "forças". Os potenciais $V (x, Sim., zangão.)$ ou campos, dos quais as forças geralmente podem ser derivadas, são tratados de forma semelhante às variáveis de posição clássica, ou seja, $V(x,y,z)to {hat {V}}({hat {x}},{hat {y}},{hat {z}})$ .

Isso se torna diferente apenas na estrutura da teoria quântica de campos, onde esses campos também são quantizados.

A mecânica quântica tem uma ressalva; as partículas que atuam umas sobre as outras não possuem apenas a variável espacial, mas também uma variável discreta intrínseca semelhante ao momento angular chamada "spin", e existe o princípio de exclusão de Pauli relacionando o espaço e as variáveis de spin. Dependendo do valor do spin, partículas idênticas se dividem em duas classes diferentes, férmions e bósons. Se dois férmions idênticos (por exemplo, elétrons) têm uma função de spin simétrico (por exemplo, spins paralelos), as variáveis espaciais devem ser antisimétricas (ou seja, elas se excluem mutuamente de seus lugares, como se havia uma força repulsiva), e vice-versa, ou seja, para spins antiparalelos, as variáveis de posição devem ser simétricas (ou seja, a força aparente deve ser atrativa). Assim, no caso de dois férmions, há uma correlação estritamente negativa entre variáveis espaciais e de spin, enquanto que para dois bósons (por exemplo, quanta de ondas eletromagnéticas, fótons) a correlação é estritamente positiva.

Assim, a noção de "força" já perde parte do seu significado.

Diagramas de Feynman

Diagrama de Feynman para a decadência de um nêutron em um protão. O bóson W está entre dois vértices indicando uma repulsão.

Na física de partículas moderna, as forças e a aceleração das partículas são explicadas como um subproduto matemático da troca de bósons de medida portadores de momento. Com o desenvolvimento da teoria quântica de campos e da relatividade geral, percebeu-se que a força é um conceito redundante decorrente da conservação do momento (momento 4 na relatividade e momento das partículas virtuais na eletrodinâmica quântica). A conservação do momento pode ser derivada diretamente da homogeneidade ou simetria do espaço e, portanto, é geralmente considerada mais fundamental do que o conceito de força. Assim, as forças fundamentais atualmente conhecidas são consideradas com mais precisão como "interações fundamentais". Quando a partícula A emite (cria) ou absorve (aniquila) a partícula virtual B, uma conservação do momento resulta no recuo da partícula A, causando impressão de repulsão ou atração entre as partículas A A' troca por B. Esta descrição se aplica a todas as forças decorrentes de interações fundamentais. Embora descrições matemáticas sofisticadas sejam necessárias para prever, em todos os detalhes, o resultado preciso de tais interações, existe uma maneira conceitualmente simples de descrever tais interações por meio do uso de diagramas de Feynman. Em um diagrama de Feynman, cada partícula de matéria é representada como uma linha reta (ver linha do mundo) viajando no tempo, que normalmente aumenta para cima ou para a direita no diagrama. Partículas de matéria e antimatéria são idênticas, exceto por sua direção de propagação através do diagrama de Feynman. Linhas mundiais de partículas se cruzam em vértices de interação, e o diagrama de Feynman representa qualquer força decorrente de uma interação ocorrendo no vértice com uma mudança instantânea associada na direção das linhas mundiais de partículas. Os bósons de calibre são emitidos para longe do vértice como linhas onduladas e, no caso de troca virtual de partículas, são absorvidos em um vértice adjacente.

A utilidade dos diagramas de Feynman é que outros tipos de fenômenos físicos que fazem parte do quadro geral das interações fundamentais, mas são conceitualmente separados das forças, também podem ser descritos usando as mesmas regras. Por exemplo, um diagrama de Feynman pode descrever em detalhes sucintos como um nêutron decai em um elétron, próton e neutrino, uma interação mediada pelo mesmo bóson de calibre que é responsável pela força nuclear fraca.

Interações fundamentais

Todas as forças conhecidas do universo são classificadas em quatro interações fundamentais. As forças forte e fraca atuam apenas em distâncias muito curtas e são responsáveis pelas interações entre partículas subatômicas, incluindo núcleons e núcleos compostos. A força eletromagnética atua entre cargas elétricas, e a força gravitacional atua entre massas. Todas as outras forças da natureza derivam dessas quatro interações fundamentais. Por exemplo, o atrito é uma manifestação da força eletromagnética que atua entre os átomos de duas superfícies e o princípio de exclusão de Pauli, que não permite que os átomos passem um pelo outro. Da mesma forma, as forças nas molas, modeladas pela lei de Hooke, são o resultado das forças eletromagnéticas e do princípio de exclusão de Pauli agindo em conjunto para retornar um objeto à sua posição de equilíbrio. Forças centrífugas são forças de aceleração que surgem simplesmente da aceleração de referenciais rotativos.

As teorias fundamentais para as forças desenvolveram-se a partir da unificação de diferentes ideias. Por exemplo, Sir Isaac Newton unificou, com sua teoria universal da gravitação, a força responsável pela queda de objetos próximos à superfície da Terra com a força responsável pela queda dos corpos celestes em torno da Terra (a Lua) e ao redor do Sol (o planetas). Michael Faraday e James Clerk Maxwell demonstraram que as forças elétricas e magnéticas foram unificadas através de uma teoria do eletromagnetismo. No século 20, o desenvolvimento da mecânica quântica levou a um entendimento moderno de que as três primeiras forças fundamentais (todas exceto a gravidade) são manifestações da matéria (férmions) interagindo por meio da troca de partículas virtuais chamadas bósons de calibre. Este Modelo Padrão da física de partículas assume uma semelhança entre as forças e levou os cientistas a prever a unificação das forças fraca e eletromagnética na teoria eletrofraca, o que foi posteriormente confirmado pela observação. A formulação completa do Modelo Padrão prevê um mecanismo de Higgs ainda não observado, mas observações como oscilações de neutrinos sugerem que o Modelo Padrão está incompleto. Uma Grande Teoria Unificada que permite a combinação da interação eletrofraca com a força forte é apresentada como uma possibilidade com teorias candidatas, como a supersimetria proposta para acomodar alguns dos problemas pendentes não resolvidos da física. Os físicos ainda estão tentando desenvolver modelos de unificação autoconsistentes que combinariam todas as quatro interações fundamentais em uma teoria de tudo. Einstein tentou e falhou nessa empreitada, mas atualmente a abordagem mais popular para responder a essa pergunta é a teoria das cordas.

**As quatro forças fundamentais da natureza**
Propriedade/Interação	Gravitação	Fraca	Eletromagnética	Forte
Propriedade/Interação	Gravitação	(Electroweak)		Fundamental	Resíduos
Atos sobre:	Massa - Energia	Sabor	Carga elétrica	Carga de cor	Núcleos atômicos
Experiência de partículas:	Todos	Quarks, leptons	Carga elétrica	Quarks, Gluons	Hadrons
Partículas mediando:	Graviton (ainda não observado)	W⁺ W^{- Sim.} Z.⁰	γ	Gluons	Mesons
Força na escala de quarks:	10.^{- Não.}	10.^-4	1	60	Não aplicável para quarks
Força na escala de prótons/neutrons:	10.^{- 36.}	10.^-7	1	Não aplicável para os hadrons	20.

Gravitacional

Imagens de um basquete que cai livremente com um estroboscópio em 20 flashes por segundo. As unidades de distância à direita são múltiplos de cerca de 12 milímetros. O basquetebol começa em repouso. No momento do primeiro flash (distância zero) é liberado, após o qual o número de unidades caídas é igual ao quadrado do número de flashes.

O que agora chamamos de gravidade não foi identificado como uma força universal até a obra de Isaac Newton. Antes de Newton, a tendência para os objetos cairem em direção à Terra não era entendida como relacionada com os movimentos de objetos celestiais. Galileu foi fundamental para descrever as características dos objetos caindo, determinando que a aceleração de cada objeto em queda livre era constante e independente da massa do objeto. Hoje, essa aceleração devido à gravidade para a superfície da Terra é geralmente designada como ${displaystyle {vec {g}}}$ e tem uma magnitude de cerca de 9,81 metros por segundo quadrado (esta medição é tomada do nível do mar e pode variar dependendo da localização), e pontos para o centro da Terra. Esta observação significa que a força da gravidade em um objeto na superfície da Terra é diretamente proporcional à massa do objeto. Assim, um objeto que tem uma massa de $m$ vai experimentar uma força:

{displaystyle {vec {F}}=m{vec {g}}.}

Para um objeto em queda livre, esta força não tem oposição e a força resultante sobre o objeto é o seu peso. Para objetos que não estão em queda livre, a força da gravidade se opõe às forças de reação aplicadas por seus suportes. Por exemplo, uma pessoa em pé no solo experimenta força líquida nula, pois uma força normal (uma força de reação) é exercida pelo solo para cima na pessoa que contrabalança seu peso direcionado para baixo.

A contribuição de Newton para a teoria gravitacional foi unificar os movimentos dos corpos celestes, que Aristóteles assumiu estarem em um estado natural de movimento constante, com o movimento de queda observado na Terra. Ele propôs uma lei da gravidade que poderia explicar os movimentos celestes descritos anteriormente usando as leis de movimento planetário de Kepler.

Newton chegou a perceber que os efeitos da gravidade podem ser observados de maneiras diferentes a distâncias maiores. Em particular, Newton determinou que a aceleração da Lua ao redor da Terra poderia ser atribuída à mesma força de gravidade se a aceleração devido à gravidade diminuísse como uma lei quadrada inversa. Além disso, Newton percebeu que a aceleração de um corpo devido à gravidade é proporcional à massa do outro corpo que atrai. Combinar essas ideias dá uma fórmula que relaciona a massa ( ${displaystyle m_{oplus }}$ ) e o raio ( ${displaystyle R_{oplus }}$ ) da Terra à aceleração gravitacional:

{displaystyle {vec {g}}=-{frac {Gm_{oplus }}{{R_{oplus }}^{2}}}{hat {r}},}

onde a direção do vetor é dada por ${hat {r}}$ , é o vetor unitário dirigido para fora do centro da Terra.

Nesta equação, uma constante dimensional $G$ é usado para descrever a força relativa da gravidade. Esta constante veio a ser conhecida como a constante Newtoniana da gravitação, embora seu valor fosse desconhecido na vida de Newton. Não até 1798 foi Henry Cavendish capaz de fazer a primeira medição de $G$ usando um equilíbrio de torção; isso foi amplamente relatado na imprensa como uma medida da massa da Terra desde saber $G$ poderia permitir que se resolvesse para a massa da Terra dada a equação acima. Newton percebeu que, uma vez que todos os corpos celestes seguiam as mesmas leis de movimento, sua lei de gravidade tinha de ser universal. Succinctly afirmou, Lei de Gravitação de Newton afirma que a força em um objeto esférico de massa $m_{1}$ devido à atração gravitacional de massa $m_{2}$ o

{displaystyle {vec {F}}=-{frac {Gm_{1}m_{2}}{r^{2}}}{hat {r}},}

r

{hat {r}}

Esta fórmula foi poderosa o suficiente para servir de base para todas as descrições subsequentes de movimento dentro do sistema solar até o século XX. Durante esse tempo, métodos sofisticados de análise de perturbação foram inventados para calcular os desvios de órbitas devido à influência de múltiplos corpos em um planeta, lua, cometa ou asteroide. O formalismo era exato o suficiente para permitir que os matemáticos previssem a existência do planeta Netuno antes que ele fosse observado.

Instrumentos como GRAVITY fornecem uma poderosa sonda para detecção de força de gravidade.

A órbita de Mercúrio não correspondia à prevista pela Lei da Gravitação de Newton. Alguns astrofísicos previram a existência de um planeta não descoberto (Vulcano) que poderia explicar as discrepâncias. Quando Albert Einstein formulou sua teoria da relatividade geral (GR), ele se concentrou na órbita problemática de Mercúrio e descobriu que sua teoria acrescentava uma correção, que poderia explicar a discrepância. Esta foi a primeira vez que a Teoria da Gravidade de Newton se mostrou inexata.

Desde então, a relatividade geral tem sido reconhecida como a teoria que melhor explica a gravidade. Na GR, a gravitação não é vista como uma força, mas sim, objetos que se movem livremente em campos gravitacionais viajam sob sua própria inércia em linhas retas através do espaço-tempo curvo – definido como o caminho mais curto do espaço-tempo entre dois eventos espaço-temporais. Da perspectiva do objeto, todo movimento ocorre como se não houvesse nenhuma gravidade. É somente ao observar o movimento em um sentido global que a curvatura do espaço-tempo pode ser observada e a força é inferida a partir do caminho curvo do objeto. Assim, o caminho em linha reta no espaço-tempo é visto como uma linha curva no espaço, e é chamado de trajetória balística do objeto. Por exemplo, uma bola de basquete lançada do solo se move em uma parábola, pois está em um campo gravitacional uniforme. Sua trajetória espaço-temporal é quase uma linha reta, levemente curva (com raio de curvatura da ordem de alguns anos-luz). A derivada temporal da variação do momento do objeto é o que rotulamos como "força gravitacional".

Eletromagnético

A força eletrostática foi descrita pela primeira vez em 1784 por Coulomb como uma força que existia intrinsecamente entre duas cargas. As propriedades da força eletrostática eram que ela variava como uma lei do inverso do quadrado direcionada na direção radial, era atrativa e repulsiva (havia polaridade intrínseca), era independente da massa dos objetos carregados e seguia o princípio da superposição. A lei de Coulomb unifica todas essas observações em uma afirmação sucinta.

Matemáticos e físicos subsequentes descobriram que a construção do campo elétrico era útil para determinar a força eletrostática em uma carga elétrica em qualquer ponto do espaço. O campo elétrico foi baseado no uso de uma hipotética "carga de teste" em qualquer lugar no espaço e, em seguida, usando a Lei de Coulomb para determinar a força eletrostática. Assim, o campo elétrico em qualquer lugar no espaço é definido como

{displaystyle {vec {E}}={{vec {F}} over {q}},}

q

Enquanto isso, descobriu-se que a força de Lorentz do magnetismo existe entre duas correntes elétricas. Tem o mesmo caráter matemático da Lei de Coulomb, com a condição de que correntes iguais se atraem e correntes diferentes se repelem. Semelhante ao campo elétrico, o campo magnético pode ser usado para determinar a força magnética sobre uma corrente elétrica em qualquer ponto do espaço. Neste caso, a magnitude do campo magnético foi determinada como sendo

{displaystyle B={F over {Iell }},}

I

ell

Através da combinação da definição de corrente elétrica como a taxa de variação da carga elétrica no tempo, uma regra de multiplicação vetorial chamada Lei de Lorentz descreve a força sobre uma carga que se move em um campo magnético. A conexão entre eletricidade e magnetismo permite a descrição de uma força eletromagnética unificada que atua sobre uma carga. Essa força pode ser escrita como a soma da força eletrostática (devido ao campo elétrico) e da força magnética (devido ao campo magnético). Totalmente declarada, esta é a lei:

{displaystyle {vec {F}}=qleft({vec {E}}+{vec {v}}times {vec {B}}right),}

{displaystyle {vec {F}}}

q

{displaystyle {vec {E}}}

{displaystyle {vec {v}}}

{displaystyle {vec {B}}}

A origem dos campos elétrico e magnético não seria totalmente explicada até 1864, quando James Clerk Maxwell unificou várias teorias anteriores em um conjunto de 20 equações escalares, que foram posteriormente reformuladas em 4 equações vetoriais por Oliver Heaviside e Josiah Willard Gibbs. Estas "Equações de Maxwell" descreveu completamente as fontes dos campos como sendo cargas estacionárias e móveis, e as interações dos próprios campos. Isso levou Maxwell a descobrir que campos elétricos e magnéticos poderiam ser "autogerados" através de uma onda que viajou a uma velocidade que ele calculou ser a velocidade da luz. Esse insight uniu os campos nascentes da teoria eletromagnética com a ótica e levou diretamente a uma descrição completa do espectro eletromagnético.

As tentativas de reconciliar a teoria eletromagnética com duas observações, o efeito fotoelétrico e a inexistência da catástrofe ultravioleta, mostraram-se problemáticas. Através do trabalho dos principais físicos teóricos, uma nova teoria do eletromagnetismo foi desenvolvida usando a mecânica quântica. Essa modificação final na teoria eletromagnética levou à eletrodinâmica quântica (ou QED), que descreve completamente todos os fenômenos eletromagnéticos como sendo mediados por partículas de onda conhecidas como fótons. Na QED, os fótons são a partícula de troca fundamental, que descreve todas as interações relacionadas ao eletromagnetismo, incluindo a força eletromagnética.

Nuclear forte

Existem duas "forças nucleares", que hoje são geralmente descritas como interações que ocorrem nas teorias quânticas da física de partículas. A força nuclear forte é a força responsável pela integridade estrutural dos núcleos atômicos, enquanto a força nuclear fraca é responsável pelo decaimento de certos núcleons em léptons e outros tipos de hádrons.

A força forte é hoje entendida como representando as interações entre quarks e glúons conforme detalhado pela teoria da cromodinâmica quântica (QCD). A força forte é a força fundamental mediada pelos glúons, atuando sobre quarks, antiquarks e os próprios glúons. A interação forte (apropriadamente chamada) é a interação "mais forte" das quatro forças fundamentais.

A força forte só age diretamente sobre as partículas elementares. Um resíduo é observado entre os hádrons (notavelmente, os nucleons em núcleos atômicos), conhecido como força nuclear. Aqui a força forte atua indiretamente, transmitida como glúons que fazem parte dos mésons pi e rho virtuais, os transmissores clássicos da força nuclear. O fracasso de muitas buscas por quarks livres mostrou que as partículas elementares afetadas não são diretamente observáveis. Este fenômeno é chamado de confinamento de cor.

Nuclear fraco

A força fraca é devida à troca dos bósons pesados W e Z. Como a força fraca é mediada por dois tipos de bósons, ela pode ser dividida em dois tipos de interação ou "vértices" — corrente carregada, envolvendo os bósons W⁺ e W^- eletricamente carregados, e corrente neutra, envolvendo bósons Z⁰ eletricamente neutros. O efeito mais conhecido da interação fraca é o decaimento beta (de nêutrons em núcleos atômicos) e a radioatividade associada. Este é um tipo de interação de corrente carregada. A palavra "fraco" deriva do fato de que a intensidade do campo é cerca de 10¹³ vezes menor que a da força forte. Ainda assim, é mais forte que a gravidade em distâncias curtas. Uma teoria eletrofraca consistente também foi desenvolvida, o que mostra que as forças eletromagnéticas e a força fraca são indistinguíveis em temperaturas acima de aproximadamente 10¹⁵ kelvins. Essas temperaturas foram sondadas em modernos aceleradores de partículas e mostram as condições do universo nos primeiros momentos do Big Bang.

Tipos não fundamentais

Algumas forças são consequências das fundamentais. Em tais situações, modelos idealizados podem ser usados para obter insight físico.

Normal

F_N representa a força normal exercida sobre o objeto.

A força normal é devida a forças repulsivas de interação entre átomos em contato próximo. Quando suas nuvens de elétrons se sobrepõem, segue-se a repulsão de Pauli (devido à natureza fermiônica dos elétrons), resultando na força que age em uma direção normal à interface da superfície entre dois objetos. A força normal, por exemplo, é responsável pela integridade estrutural de mesas e pisos, além de ser a força que responde sempre que uma força externa empurra um objeto sólido. Um exemplo da força normal em ação é a força de impacto em um objeto colidindo com uma superfície imóvel.

Atrito

A fricção é uma força de superfície que se opõe ao movimento relativo. A força de atrito está diretamente relacionada à força normal que atua para manter dois objetos sólidos separados no ponto de contato. Existem duas classificações amplas de forças de atrito: atrito estático e atrito cinético.

A força de atrito estática ( $F_{mathrm {sf} }$ ) opor-se-á exatamente às forças aplicadas a um objeto paralelo a um contato superficial até o limite especificado pelo coeficiente de atrito estático ( $mu _{mathrm {sf} }$ ) multiplicado pela força normal ( $F_{N}$ ). Em outras palavras, a magnitude da força de atrito estático satisfaz a desigualdade:

{displaystyle 0leq F_{mathrm {sf} }leq mu _{mathrm {sf} }F_{mathrm {N} }.}

A força de atrito cinético ( $F_{mathrm {kf} }$ ) é independente das forças aplicadas e do movimento do objeto. Assim, a magnitude da força é igual:

{displaystyle F_{mathrm {kf} }=mu _{mathrm {kf} }F_{mathrm {N} },}

Onde? $mu _{mathrm {kf} }$ é o coeficiente de atrito cinético. Para a maioria das interfaces de superfície, o coeficiente de atrito cinético é menor do que o coeficiente de atrito estático.

Tensão

As forças de tensão podem ser modeladas usando cordas ideais que são sem massa, sem atrito, inquebráveis e inextensíveis. Eles podem ser combinados com polias ideais, que permitem que as cordas ideais mudem a direção física. Cordas ideais transmitem forças de tensão instantaneamente em pares ação-reação de modo que, se dois objetos são conectados por uma corda ideal, qualquer força direcionada ao longo da corda pelo primeiro objeto é acompanhada por uma força direcionada ao longo da corda na direção oposta pelo segundo objeto. Ao conectar a mesma corda várias vezes ao mesmo objeto por meio do uso de uma configuração que usa polias móveis, a força de tensão em uma carga pode ser multiplicada. Para cada corda que atua sobre uma carga, outro fator da força de tração na corda atua sobre a carga. Tais máquinas permitem uma vantagem mecânica para um aumento correspondente no comprimento da coluna deslocada necessária para mover a carga. Esses efeitos tandem resultam, em última instância, na conservação da energia mecânica, uma vez que o trabalho realizado na carga é o mesmo, não importa quão complicada seja a máquina.

Elasticidade

F_k é a força que responde à carga na mola

Uma força elástica age para retornar uma mola ao seu comprimento natural. Uma mola ideal é tomada para ser sem massa, sem atrito, inquebrável e infinitamente extensível. Tais molas exercem forças que empurram quando contratadas, ou puxam quando estendida, em proporção ao deslocamento da mola de sua posição de equilíbrio. Esta relação linear foi descrita por Robert Hooke em 1676, para quem a lei de Hooke é nomeada. Se $Delta x$ é o deslocamento, a força exercida por uma mola ideal é igual:

{displaystyle {vec {F}}=-kDelta {vec {x}},}

k

Mecânica contínua

Quando a força de arrasto (

F_{d}

) associado à resistência do ar torna-se igual em magnitude à força da gravidade em um objeto que cai (

F_{g}

), o objeto atinge um estado de equilíbrio dinâmico na velocidade terminal.

As leis de Newton e a mecânica newtoniana em geral foram desenvolvidas pela primeira vez para descrever como as forças afetam partículas pontuais idealizadas em vez de objetos tridimensionais. Na vida real, a matéria tem uma estrutura estendida e as forças que agem em uma parte de um objeto podem afetar outras partes de um objeto. Para situações em que a rede que mantém os átomos unidos em um objeto é capaz de fluir, contrair, expandir ou mudar de forma, as teorias da mecânica do contínuo descrevem a maneira como as forças afetam o material. Por exemplo, em fluidos estendidos, as diferenças de pressão resultam em forças sendo direcionadas ao longo dos gradientes de pressão como segue:

{displaystyle {frac {vec {F}}{V}}=-{vec {nabla }}P,}

Onde? $V$ é o volume do objeto no fluido e $P$ é a função escalar que descreve a pressão em todos os locais no espaço. Os gradientes e diferenciais de pressão resultam na força buoyant para fluidos suspensos em campos gravitacionais, ventos em ciência atmosférica e o elevador associado com aerodinâmica e voo.

Uma instância específica de tal força associada à pressão dinâmica é a resistência do fluido: uma força corporal que resiste ao movimento de um objeto através de um fluido devido à viscosidade. Para os chamados "Stokes' arraste" a força é aproximadamente proporcional à velocidade, mas oposta na direção:

{displaystyle {vec {F}}_{mathrm {d} }=-b{vec {v}},}

$b$ é uma constante que depende das propriedades do fluido e das dimensões do objeto (geralmente da área transversal), e
${displaystyle {vec {v}}}$ é a velocidade do objeto.

Mais formalmente, as forças na mecânica do contínuo são totalmente descritas por um tensor de tensão com termos que são aproximadamente definidos como

{displaystyle sigma ={frac {F}{A}},}

Onde? $A$ é a área transversal relevante para o volume para o qual o tensor de estresse está sendo calculado. Este formalismo inclui termos de pressão associados a forças que agem normais para a área transversal (as diagonais matrizes do tensor) bem como termos de cisalhamento associados a forças que agem paralelas à área transversal (os elementos fora-diagonais). O tensor de estresse responde por forças que causam todas as tensões (deformações) incluindo também tensões de tração e compressões.

Fictício

Existem forças dependentes do referencial, ou seja, surgem devido à adoção de referenciais não newtonianos (ou seja, não inerciais). Tais forças incluem a força centrífuga e a força de Coriolis. Essas forças são consideradas fictícias porque não existem em referenciais que não estão acelerando. Como essas forças não são genuínas, elas também são chamadas de "pseudo forças".

Na relatividade geral, a gravidade se torna uma força fictícia que surge em situações onde o espaço-tempo se desvia de uma geometria plana. Como extensão, a teoria de Kaluza-Klein e a teoria das cordas atribuem o eletromagnetismo e as outras forças fundamentais, respectivamente, à curvatura de dimensões de escala diferente, o que implicaria, em última análise, que todas as forças são fictícias.

Rotação e torque

Relação entre força (F), torque (τ), e vetores de impulso (p e L) em um sistema rotativo.

As forças que causam objetos estendidos para girar estão associadas a torques. Matematicamente, o torque de uma força ${displaystyle {vec {F}}}$ é definido em relação a um ponto de referência arbitrário como o produto cruzado:

{displaystyle {vec {tau }}={vec {r}}times {vec {F}},}

{displaystyle {vec {r}}}

O torque é o equivalente de rotação da força da mesma forma que o ângulo é o equivalente de rotação para a posição, a velocidade angular para a velocidade e o momento angular para o momento. Como consequência da Primeira Lei do Movimento de Newton, existe inércia rotacional que garante que todos os corpos mantenham seu momento angular, a menos que sejam influenciados por um torque desequilibrado. Da mesma forma, a Segunda Lei do Movimento de Newton pode ser usada para derivar uma equação análoga para a aceleração angular instantânea do corpo rígido:

{displaystyle {vec {tau }}=I{vec {alpha }},}

onde

$I$ é o momento da inércia do corpo
${displaystyle {vec {alpha }}}$ é a aceleração angular do corpo.

Isso fornece uma definição para o momento de inércia, que é o equivalente rotacional da massa. Em tratamentos de mecânica mais avançados, onde é descrita a rotação em um intervalo de tempo, o momento de inércia deve ser substituído pelo tensor que, quando devidamente analisado, determina plenamente as características das rotações incluindo precessão e nutação.

Equivalentemente, a forma diferencial da Segunda Lei de Newton fornece uma definição alternativa de torque:

{displaystyle {vec {tau }}={frac {mathrm {d} {vec {L}}}{mathrm {dt} }},}

{displaystyle {vec {L}}}

A Terceira Lei do Movimento de Newton exige que todos os objetos que exercem torques experimentem torques iguais e opostos e, portanto, também implica diretamente na conservação do momento angular para sistemas fechados que experimentam rotações e revoluções por meio da ação de torques internos.

Centripetalidade

Para um objeto acelerando em movimento circular, a força desequilibrada que age sobre o objeto é igual a:

{displaystyle {vec {F}}=-{frac {mv^{2}{hat {r}}}{r}},}

Onde? $m$ é a massa do objeto, $v$ é a velocidade do objeto e $r$ é a distância para o centro do caminho circular e ${displaystyle {hat {r}}}$ é o vetor unitário apontando na direção radial para fora do centro. Isso significa que a força centrípeta desequilibrada sentida por qualquer objeto é sempre direcionada para o centro do caminho de curva. Tais forças atuam perpendicularmente ao vetor de velocidade associado ao movimento de um objeto, e, portanto, não mudam a velocidade do objeto (magnitude da velocidade), mas apenas a direção do vetor de velocidade. A força desequilibrada que acelera um objeto pode ser resolvida em um componente que é perpendicular ao caminho, e que é tangencial ao caminho. Isso produz tanto a força tangencial, que acelera o objeto, diminuindo-o ou acelerando-o, e a força radial (centripetal), que muda sua direção.

Integrais cinemáticos

As forças podem ser usadas para definir vários conceitos físicos integrando com relação a variáveis cinemáticas. Por exemplo, integrando em relação ao tempo dá a definição de impulso:

{displaystyle {vec {J}}=int _{t_{1}}^{t_{2}}{{vec {F}},mathrm {d} t},}

Da mesma forma, a integração em relação à posição fornece uma definição para o trabalho realizado por uma força:

{displaystyle W=int _{{vec {x}}_{1}}^{{vec {x}}_{2}}{{vec {F}}cdot {mathrm {d} {vec {x}}}},}

que é equivalente a mudanças na energia cinética (produzindo o teorema da energia do trabalho).

Poder P é a taxa de mudança dW/D) do trabalho W, como a trajetória é estendida por uma mudança de posição ${displaystyle d{vec {x}}}$ em um intervalo de tempo d):

{displaystyle mathrm {d} W={frac {mathrm {d} W}{mathrm {d} {vec {x}}}}cdot mathrm {d} {vec {x}}={vec {F}}cdot mathrm {d} {vec {x}},}

{displaystyle P={frac {mathrm {d} W}{mathrm {d} t}}={frac {mathrm {d} W}{mathrm {d} {vec {x}}}}cdot {frac {mathrm {d} {vec {x}}}{mathrm {d} t}}={vec {F}}cdot {vec {v}},}

{displaystyle {vec {v}}=mathrm {d} {vec {x}}/mathrm {d} t}

Energia potencial

Em vez de uma força, muitas vezes o conceito matematicamente relacionado de um campo de energia potencial pode ser usado para conveniência. Por exemplo, a força gravitacional agindo sobre um objeto pode ser vista como a ação do campo gravitacional que está presente na localização do objeto. Repondo matematicamente a definição de energia (através da definição de trabalho), um campo escalar potencial ${displaystyle U({vec {r}})}$ é definido como aquele campo cujo gradiente é igual e oposto à força produzida em cada ponto:

{displaystyle {vec {F}}=-{vec {nabla }}U.}

As forças podem ser classificadas como conservativas ou não conservativas. As forças conservativas são equivalentes ao gradiente de um potencial, enquanto as forças não conservativas não são.

Conservação

Uma força conservativa que atua em um sistema fechado tem um trabalho mecânico associado que permite que a energia seja convertida apenas entre formas cinéticas ou potenciais. Isso significa que, para um sistema fechado, a energia mecânica líquida é conservada sempre que uma força conservativa atua sobre o sistema. A força, portanto, está diretamente relacionada à diferença de energia potencial entre dois locais diferentes no espaço e pode ser considerada um artefato do campo potencial da mesma forma que a direção e a quantidade de um fluxo de água podem ser consideradas. ser um artefato do mapa de contorno da elevação de uma área.

As forças conservadoras incluem a gravidade, a força eletromagnética e a força da mola. Cada uma dessas forças tem modelos que dependem de uma posição muitas vezes dada como um vetor radial ${displaystyle {vec {r}}}$ emanando de potenciais esféricos simétricos. Exemplos deste seguimento:

Para gravidade:

{displaystyle {vec {F}}_{g}=-{frac {Gm_{1}m_{2}}{r^{2}}}{hat {r}},}

G

m_{n}

Para forças eletrostáticas:

{displaystyle {vec {F}}_{e}={frac {q_{1}q_{2}}{4pi varepsilon _{0}r^{2}}}{hat {r}},}

varepsilon_{0}

q_{n}

Para forças de mola:

{displaystyle {vec {F}}_{s}=-kr{hat {r}},}

k

Para certos cenários físicos, é impossível modelar as forças como sendo devidas ao gradiente de potenciais. Isso geralmente se deve a considerações macrofísicas que produzem forças como decorrentes de uma média estatística macroscópica de microestados. Por exemplo, o atrito é causado pelos gradientes de numerosos potenciais eletrostáticos entre os átomos, mas se manifesta como um modelo de força independente de qualquer vetor de posição em macroescala. As forças não conservativas além do atrito incluem outras forças de contato, tensão, compressão e arrasto. Para qualquer descrição suficientemente detalhada, todas essas forças são resultados de forças conservativas, uma vez que cada uma dessas forças macroscópicas é o resultado líquido dos gradientes de potenciais microscópicos.

A conexão entre forças não conservativas macroscópicas e forças conservativas microscópicas é descrita por tratamento detalhado com mecânica estatística. Em sistemas fechados macroscópicos, as forças não conservativas agem para alterar as energias internas do sistema e estão frequentemente associadas à transferência de calor. De acordo com a Segunda Lei da Termodinâmica, as forças não conservativas resultam necessariamente em transformações de energia dentro de sistemas fechados de condições ordenadas para mais aleatórias à medida que a entropia aumenta.

Unidades de medida

A unidade SI de força é o newton (símbolo N), que é a força necessária para acelerar uma massa de um quilograma a uma taxa de um metro por segundo ao quadrado, ou kg·m·s⁻². A unidade CGS correspondente é o dina, a força necessária para acelerar uma massa de um grama em um centímetro por segundo ao quadrado, ou g·cm·s⁻². Um newton é, portanto, igual a 100.000 dinas.

A unidade de força gravitacional pé-libra-segundo é a libra-força (lbf), definida como a força exercida pela gravidade sobre uma libra-massa no campo gravitacional padrão de 9,80665 m·s⁻². A libra-força fornece uma unidade alternativa de massa: um slug é a massa que acelerará em um pé por segundo ao quadrado quando acionada por uma libra-força.

Uma unidade alternativa de força em um sistema diferente de pé-libra-segundo, o sistema fps absoluto, é o poundal, definido como a força necessária para acelerar uma massa de uma libra a uma taxa de um pé por segundo ao quadrado. As unidades de slug e poundal são projetadas para evitar uma constante de proporcionalidade na Segunda Lei de Newton.

A libra-força tem uma contraparte métrica, menos comumente usada que o newton: o quilograma-força (kgf) (às vezes kilopond), é a força exercida pela gravidade padrão em um quilograma de massa. O quilograma-força leva a uma unidade de massa alternativa, mas raramente usada: o slug métrico (às vezes mug ou hyl) é aquela massa que acelera a 1 m·s⁻² quando submetida a uma força de 1 kgf. O quilograma-força não faz parte do sistema SI moderno e é geralmente obsoleto, às vezes usado para expressar o peso da aeronave, o impulso do jato, a tensão do raio da bicicleta, as configurações da chave de torque e o torque de saída do motor. Outras unidades arcanas incluem o sthène, que é equivalente a 1000 N, e o kip, que é equivalente a 1000 lbf.

Unidades de força
v ) e	novato	dyne	quilograma-força, quilopond	força de libra	libra
1 N	≡ 1kg/s²	= 10⁵Dyn.	≈ 0,10197- Sim.	≈ 0,22481Ib.	≈ 7.2330Pdl
1Dyn.	= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =10.^-5N	)1g⋅cm/s²	?1.0197×10.^-6- Sim.	?2.248.×10.^-6Ib.	?7.2330×10.^-5Pdl
1- Sim.	= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =9.80665N	= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =980665Dyn.	)g_n×1kg	?2.2046Ib.	?70.932Pdl
1 lbf	?4.4482N	?444822Dyn.	?0- Sim.	)g_n×1Ib.	?32.174Pdl
1Pdl	?0.138255N	?13825Dyn.	?0,001.98- Sim.	?0,031081Ib.	)1Lb⋅ft/s²
O valor do gn como usado na definição oficial da força do quilograma (9.80665 m/s²) é usado aqui para todas as unidades gravitacionais.

Veja também Ton-força.

Medição de força

Consulte medidor de força, balança de mola, célula de carga

Contenido relacionado

Más resultados...