Favo de mel uniforme convexo
Em geometria, um favo de mel uniforme convexo é um mosaico uniforme que preenche o espaço euclidiano tridimensional com células poliédricas uniformes convexas não sobrepostas.
Vinte e oito desses favos de mel são conhecidos:
- o favo de mel cúbico familiar e 7 truncas dele;
- o favo de mel cúbico alternado e 4 truncas dele;
- 10 formas prismáticas baseadas nos tilings planos uniformes (11 se incluindo o favo de mel cúbico);
- 5 modificações de alguns dos acima por alongamento e / ou giro.
Eles podem ser considerados o análogo tridimensional dos ladrilhos uniformes do plano.
O diagrama de Voronoi de qualquer rede forma um favo de mel convexo uniforme no qual as células são zonoedros.
História
- 1900: Thorold Gosset enumera a lista de politopos convexos semiregulares com células regulares (sólidos platônicos) em sua publicação Nas Figuras Regulares e Semi-Regulares no Espaço de n Dimensões, incluindo um favo de mel cúbico regular, e duas formas semiregulares com tetrahedra e octahedra.
- 1905: Alfredo Andreini enumera 25 dessas tessellations.
- 1991: manuscrito de Norman Johnson Politopos uniformes identificou a lista de 28.
- 1994: Branko Grünbaum, em seu artigo Nível uniforme de 3 espaços, também enumerados independentemente todos os 28, depois de descobrir erros na publicação de Andreini. Ele encontrou o papel de 1905, que listava 25, tinha 1 errado, e 4 desaparecidos. Grünbaum afirma neste artigo que Norman Johnson merece prioridade para alcançar a mesma enumeração em 1991. Ele também menciona que eu. Alexeyev da Rússia tinha contactado ele sobre uma enumeração putativa dessas formas, mas que Grünbaum foi incapaz de verificar isso na época.
- 2006: George Olshevsky, em seu manuscrito Panoploide uniforme Produtos químicos, juntamente com a repetição da lista derivada de 11 tilings uniformes convexos, e 28 favos uniformes convexos, expande uma lista mais derivada de 143 tetracombs uniformes convexos (combos de mel de 4 politopos uniformes em 4 espaço).
Apenas 14 dos poliedros uniformes convexos aparecem nestes padrões:
- três dos cinco sólidos platônicos (o tetraedro, cubo e octahedron),
- seis dos treze sólidos arqueicos (os com simetria tetraedral reflexiva ou octahedral), e
- cinco da família infinita de prismas (os 3-, 4-, 6-, 8- e 12-gonais; o prisma 4-gonal duplica o cubo).
O icosaedro, o cubo achatado e o antiprisma quadrado aparecem em algumas alternâncias, mas esses favos de mel não podem ser realizados com todas as arestas de comprimento unitário.
Nomes
Este conjunto pode ser chamado de favo de mel regular e semirregular. Foi chamado de favo de mel de Arquimedes por analogia com os poliedros uniformes convexos (não regulares), comumente chamados de sólidos de Arquimedes. Recentemente, Conway sugeriu nomear o conjunto como Pavimentações arquitetônicas e os favos de mel duplos como Tesselações catóptricas.
Os favos de mel individuais são listados com nomes dados a eles por Norman Johnson. (Alguns dos termos usados abaixo são definidos em Uniform 4-polytope#Geometric derivations for 46 nonprismatic Wythoffian uniform 4-polytopes)
Para referência cruzada, eles são fornecidos com índices de lista de Andreini (1-22), Williams(1-2,9-19), Johnson (11-19, 21–25, 31–34, 41–49, 51–52, 61–65) e Grünbaum(1-28). Coxeter usa δ4 para um favo de mel cúbico, hδ4 para um favo de mel cúbico alternado, qδ4 para um quarto de mel cúbico, com subscritos para outros formas baseadas nos padrões de anéis do diagrama de Coxeter.
Tesselações uniformes euclidianas compactas (por suas infinitas famílias de grupos de Coxeter)
Os grupos de Coxeter infinitos fundamentais para o espaço tridimensional são:
- O C~ ~ 3{displaystyle {tilde {C}}_{3}}[4,3,4], cúbico,






 (8 formas únicas mais uma alternância)
(8 formas únicas mais uma alternância) - O B~ ~ 3{displaystyle {tilde {B}}_{3}}[4,3]1.1], alternado cúbico,




 (11 formas, 3 novas)
(11 formas, 3 novas) - O A~ ~ 3{displaystyle {tilde {A}}_{3}} grupo cíclico, [3,3,3,3)] ou [3[4]]


 (5 formas, um novo)
(5 formas, um novo)
Há uma correspondência entre as três famílias. Removendo um espelho de C~ ~ 3{displaystyle {tilde {C}}_{3}} produz B~ ~ 3{displaystyle {tilde {B}}_{3}}e removendo um espelho de B~ ~ 3{displaystyle {tilde {B}}_{3}} produz A~ ~ 3{displaystyle {tilde {A}}_{3}}. Isso permite várias construções das mesmas favos. Se as células são coloridas com base em posições únicas dentro de cada construção Wythoff, essas simetrias diferentes podem ser mostradas.
Além disso, existem 5 favos de mel especiais que não possuem simetria reflexiva pura e são construídos a partir de formas reflexivas com operações de alongamento e giração.
O total de favos de mel únicos acima é 18.
As pilhas prismáticas de grupos Coxeter infinitos para 3 espaços são:
- O C~ ~ 2Não. (C}}_{2}}×Eu...~ ~ 1{displaystyle {tilde {I}}_{1}}, [4,2,∞] grupo prismático,








 (2 novas formas)
(2 novas formas) - O G~ ~ 2Não. (G}}_{2}}×Eu...~ ~ 1{displaystyle {tilde {I}}_{1}}, [6,3,2,∞] grupo prismático,








 (7 formas únicas)
(7 formas únicas) - O A~ ~ 2{displaystyle {tilde {A}}_{2}}×Eu...~ ~ 1{displaystyle {tilde {I}}_{1}}, [(3,3,3),2,∞] grupo prismático,






 (Sem novas formas)
(Sem novas formas) - O Eu...~ ~ 1{displaystyle {tilde {I}}_{1}}×Eu...~ ~ 1{displaystyle {tilde {I}}_{1}}×Eu...~ ~ 1{displaystyle {tilde {I}}_{1}}, [∞,2,∞,2,∞] grupo prismático,










 (Estes todos se tornam um favo de mel cúbico)
(Estes todos se tornam um favo de mel cúbico)
Além disso, há uma forma alongada especial do favo de mel prismático triangular.
O total de favos de mel prismáticos únicos acima (excluindo o cúbico contado anteriormente) é 10.
Combinando essas contagens, 18 e 10 nos dá o total de 28 favos de mel uniformes.
O grupo C̃3, [4,3,4] (cúbico)
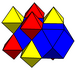
O favo de mel cúbico regular, representado pelo símbolo Schläfli {4,3,4}, oferece sete favos de mel uniformes derivados exclusivos por meio de operações de truncamento. (Uma forma redundante, o favo de mel cúbico runcinado, é incluída para completar, embora seja idêntica ao favo de mel cúbico.) A simetria reflexiva é o grupo afim de Coxeter [4,3,4]. Existem quatro subgrupos de índice 2 que geram alternâncias: [1+,4,3,4], [(4,3,4,2+)], [4,3+,4] e [4,3,4]+, com as duas primeiras formas repetidas geradas e as duas últimas não uniformes.
| C3 melão | |||||
|---|---|---|---|---|---|
| Grupo de espaço | Fibrilação | Estendidometria | Estendido diagrama | Ordem | Flores de mel |
| Pm3m (221) | 4- Sim.: | [4,3] | × | ||
| F m3m (225) | 2- Sim.: | [2]+,4,3,4] Legislação1.1] | ↔ | Metade | |
| Eu...43 m (217) | 4o: | [(4,3,4,2+) | Meia × 2 | ||
| FED3m (227) | 2+: | [[1]+,4,3,4,1+] ↔ [3][4]] | ↔ | Bairro × 2 | |
| Eu...3m (229) | 8o: | [4,3,4]] | × |
| |
B̃3, [4,31,1] grupo
O B~ ~ 3{displaystyle {tilde {B}}_{3}}, [4,3] grupo oferece 11 formas derivadas através de operações de truncação, quatro sendo únicos favos uniformes. Existem 3 subgrupos índice 2 que geram alternações: [2]+,4,31.1[4]1.1)+E...1.1]+. O primeiro gera favo de mel repetido, e os dois últimos são não uniformes, mas incluídos para a plenitude.
Os favos de mel deste grupo são chamados cúbicos alternados porque a primeira forma pode ser vista como um favo de mel cúbico com vértices alternados removidos, reduzindo células cúbicas a tetraedros e criando octaedros células nas lacunas.
Os nós são indexados da esquerda para a direita como 0,1,0',3 com 0' estando abaixo e intercambiável com 0. Os nomes cúbicos alternativos fornecidos são baseados nesta ordem.
| B3 melões | |||||
|---|---|---|---|---|---|
| Grupo de espaço | Fibrilação | Estendidometria | Estendido diagrama | Ordem | Flores de mel |
| F m3m (225) | 2- Sim.: | [4]1.1] Legislação [4,3,4,1+] | ↔ | × | |
| F m3m (225) | 2- Sim.: | <+,4,31.1- Sim. <[3][4]- Sim. | ↔ | × | |
| Pm3m (221) | 4- Sim.: | <[4]1.1- Sim. | × |
| |
Ã3, [3[4]] grupo
Há 5 formas construídas a partir do A~ ~ 3{displaystyle {tilde {A}}_{3}}[3][4]] Grupo Coxeter, dos quais apenas o favo de mel cúbico é único. Há um subgrupo índice 2 [3[4]]+ que gera a forma snub, que não é uniforme, mas incluído para a plenitude.
Formas não wythoffianas (giradas e alongadas)
Três favos de mel mais uniformes são gerados quebrando um ou outro dos favos de mel acima onde suas faces formam um plano contínuo, então girando camadas alternadas em 60 ou 90 graus (giração) e/ou inserindo um camada de prismas (alongamento).
Os ladrilhos cúbicos alternados alongados e giro-alongados têm a mesma figura de vértice, mas não são iguais. Na forma alongada, cada prisma encontra um tetraedro em uma extremidade triangular e um octaedro na outra. Na forma giroalongada, prismas que encontram tetraedros em ambas as extremidades se alternam com prismas que encontram octaedros em ambas as extremidades.
O ladrilho prismático triangular giro-alongado tem a mesma figura de vértice que um dos ladrilhos prismáticos planos; os dois podem ser derivados das telhas prismáticas triangulares giradas e planas, respectivamente, inserindo camadas de cubos.
Pilhas prismáticas
Onze ladrilhos prismáticos são obtidos empilhando-se os onze ladrilhos planos uniformes, mostrados abaixo, em camadas paralelas. (Um desses favos de mel é o cúbico, mostrado acima.) A figura do vértice de cada um é uma bipirâmide irregular cujas faces são triângulos isósceles.
O C̃2×Ĩ1(∞), [4,4,2,∞], grupo prismático
Existem apenas 3 favos de mel exclusivos do ladrilho quadrado, mas todos os 6 truncamentos de ladrilhos estão listados abaixo para serem completos, e as imagens de ladrilhos são mostradas por cores correspondentes a cada forma.
O grupo prismático G̃2xĨ1(∞), [6,3,2,∞]
Enumeração de formulários Wythoff
Todas as construções não prismáticas de Wythoff por grupos de Coxeter são dadas abaixo, junto com suas alternâncias. Soluções uniformes são indexadas com a listagem de Branko Grünbaum. Fundos verdes são mostrados em favos de mel repetidos, com as relações expressas nos diagramas de simetria estendidos.
| Grupo Coxeador | Estendidometria | Flores de mel | Chiral alargada simetria | Comprimidos de mel alternativos | ||
|---|---|---|---|---|---|---|
| [4,3] | [4,3] | 6 | [2]+,4,3+4,1+] | (2) | ||
| [2]+[4,3,4]] | (1) | [2]+[4.3]+4,2+) | (1) | |||
| [2]+[4,3,4]] | 1 | [2]+[4.3]+4,2+) | (1) | |||
| [2]+[4,3,4]] | 2 | [2]+[4,3,4]]+ | (1) | |||
| [4]1.1] | [4]1.1] | 4 | ||||
| [14]1.1[4,3] | 7) | [1[1]+,4,31.1]+ | (2) | |||
| [14]1.1]+ [4,3]+ | (1) | |||||
| [3][4]] | [3][4]] | (não) | ||||
| [2]+[3][4]] | 1 | |||||
| [1[3][4][4.3]1.1] | (2) | |||||
| [2][4][4,3] | (1) | |||||
| [2]+,4)[3][4]O quê?+[4,3,4]] | (1) | [2]+,4)[3][4]]+ [2]+[4,3,4]]+ | (1) | |||
Exemplos
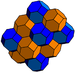
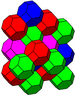
Todas as 28 dessas tesselações são encontradas em arranjos de cristal.
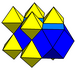
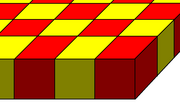
O favo de mel cúbico alternado é de especial importância, pois seus vértices formam um empacotamento cúbico de esferas. A treliça de preenchimento espacial de octaedros e tetraedros compactados foi aparentemente descoberta pela primeira vez por Alexander Graham Bell e redescoberta independentemente por Buckminster Fuller (que a chamou de treliça do octeto e a patenteou na década de 1940). [3] [4] [5] [6]. As treliças octetos estão agora entre os tipos mais comuns de treliças usadas na construção.
Frizar formulários
Se for permitido que as células sejam ladrilhos uniformes, mais favos de mel uniformes podem ser definidos:
Famílias:
- C~ ~ 2Não. (C}}_{2}}×A1Não. A_{1}}: [4,2]






 Mel de laje cubículo (3 formas)
Mel de laje cubículo (3 formas) - G~ ~ 2Não. (G}}_{2}}×A1Não. A_{1}}: [6,3,2]






 Mel de laje tri-hexagonal (8 formas)
Mel de laje tri-hexagonal (8 formas) - A~ ~ 2{displaystyle {tilde {A}}_{2}}×A1Não. A_{1}}: [3,3,3),2]




 Mel de laje triangular (Sem novas formas)
Mel de laje triangular (Sem novas formas) - Eu...~ ~ 1{displaystyle {tilde {I}}_{1}}×A1Não. A_{1}}×A1Não. A_{1}}: [∞,2,2]






 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =
= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 





 Coluna cúbica (1 formulário)
Coluna cúbica (1 formulário) - Eu...2(p)(p)}×Eu...~ ~ 1{displaystyle {tilde {I}}_{1}}: [p,2,∞]






 Coluna poligonal de mel (análogos aos duoprismos: estes parecem uma única torre infinita de prismas p-gonais, com o espaço restante cheio de prismas apeirogonais)
Coluna poligonal de mel (análogos aos duoprismos: estes parecem uma única torre infinita de prismas p-gonais, com o espaço restante cheio de prismas apeirogonais) - Eu...~ ~ 1{displaystyle {tilde {I}}_{1}}×Eu...~ ~ 1{displaystyle {tilde {I}}_{1}}×A1Não. A_{1}}: [∞,2,∞,2] = [4,2] -








 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =
= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 





 (Mesmo como família de favo de mel de laje cúbica)
(Mesmo como família de favo de mel de laje cúbica)
As duas primeiras formas mostradas acima são semirregulares (uniformes com apenas facetas regulares) e foram listadas por Thorold Gosset em 1900, respectivamente, como semi-cheque 3-ico e semi-cheque tetraédrico verifique.
Favo de mel escaliforme
Um favo de mel escaliforme é transitivo de vértice, como um favo de mel uniforme, com faces poligonais regulares, enquanto células e elementos superiores só precisam ser orbiformes, equiláteros, com seus vértices sobre hiperesferas. Para favos de mel 3D, isso permite um subconjunto de sólidos de Johnson junto com os poliedros uniformes. Alguns escaliformes podem ser gerados por um processo de alternância, deixando, por exemplo, lacunas de pirâmides e cúpulas.
Formas hiperbólicas
Existem 9 famílias de grupos de Coxeter de favos de mel uniformes compactos em 3 espaços hiperbólicos, gerados como construções de Wythoff e representados por permutações de anéis dos diagramas de Coxeter-Dynkin para cada família.
Destas 9 famílias, há um total de 76 favos de mel únicos gerados:
- [3,5,3]:






 - 9 formulários
- 9 formulários - [5,3,4]:






 - 15 formas
- 15 formas - [5,3,5]:






 - 9 formulários
- 9 formulários - [5]1.1?




 - 11 formas (7 sobreposição com [5,3,4] família, 4 são únicos)
- 11 formas (7 sobreposição com [5,3,4] família, 4 são únicos) - [(4,3,3,3)]



 - 9 formulários
- 9 formulários - [(4,3,4,3)]




 - 6 formas
- 6 formas - [(5,3,3,3)]:



 - 9 formulários
- 9 formulários - [(5,3,4,3)]




 - 9 formulários
- 9 formulários - [(5,3,5,3)]:




 - 6 formas
- 6 formas
Várias formas não Wythoffianas fora da lista de 76 são conhecidas; não se sabe quantos são.
Formas hiperbólicas paracompactas
Existem também 23 grupos Coxeter paracompactos de nível 4. Essas famílias podem produzir favos de mel uniformes com facetas ilimitadas ou figura de vértice, incluindo vértices ideais no infinito:
| Tipo | Grupos de Coxeador | Contagem única de favo de mel |
|---|---|---|
| Gráficos lineares | 4×15+6+8+8 = 82 | |
| Gráficos tridentais | 4+4+0 = 8 | |
| Gráficos cíclicos | 4×9+5+1+4+1+0 = 47 | |
| Gráficos de cauda | 4+4+4+2+2 = 14 |
Contenido relacionado
Cromodinâmica quântica
Teoria dos conjuntos ingênuos (livro)
Teoria ingênua dos conjuntos