Espaço-tempo
Na física, espaço-tempo é qualquer modelo matemático que funde as três dimensões do espaço e a dimensão única do tempo em um único continuum quadridimensional. Os diagramas de espaço-tempo são úteis na visualização e compreensão dos efeitos relativísticos, como a forma como diferentes observadores percebem onde e quando os eventos ocorrem.
Até a virada do século 20, a suposição era que a geometria tridimensional do universo (sua descrição em termos de locais, formas, distâncias e direções) era distinta do tempo (a medição de quando os eventos ocorrem dentro do universo). No entanto, o espaço e o tempo adquiriram novos significados com a transformação de Lorentz e a teoria da relatividade especial.
Em 1908, Hermann Minkowski apresentou uma interpretação geométrica da relatividade especial que fundia o tempo e as três dimensões espaciais do espaço num único continuum quadridimensional agora conhecido como espaço de Minkowski. Esta interpretação revelou-se vital para a teoria geral da relatividade, em que o espaço-tempo é curvado pela massa e pela energia.
Fundamentos
Definições
A mecânica clássica não relativística trata o tempo como uma quantidade universal de medida que é uniforme em todo o espaço e separada do espaço. A mecânica clássica assume que o tempo tem uma taxa de passagem constante, independente do estado de movimento do observador ou de qualquer coisa externa. Além disso, assume que o espaço é euclidiano: assume que o espaço segue a geometria do bom senso.
No contexto da relatividade especial, o tempo não pode ser separado das três dimensões do espaço, porque a taxa observada na qual o tempo passa para um objeto depende da velocidade do objeto em relação ao observador. A relatividade geral também fornece uma explicação de como os campos gravitacionais podem retardar a passagem do tempo para um objeto visto por um observador fora do campo.
No espaço comum, uma posição é especificada por três números, conhecidos como dimensões. No sistema de coordenadas cartesianas, elas são chamadas de x, y e z. Uma posição no espaço-tempo é chamada de evento e requer a especificação de quatro números: a localização tridimensional no espaço, mais a posição no tempo (Fig. 1). Um evento é representado por um conjunto de coordenadas x, y, z e t. O espaço-tempo é, portanto, quadridimensional.
Ao contrário das analogias usadas em escritos populares para explicar eventos, como fogos de artifício ou faíscas, os eventos matemáticos têm duração zero e representam um único ponto no espaço-tempo. Embora seja possível estar em movimento em relação ao estouro de um fogo de artifício ou de uma faísca, não é possível que um observador esteja em movimento em relação a um evento.
O caminho de uma partícula através do espaço-tempo pode ser considerado uma sucessão de eventos. A série de eventos pode ser ligada entre si para formar uma linha que representa o progresso de uma partícula através do espaço-tempo. Essa linha é chamada de linha do mundo da partícula.
Matematicamente, espaço-tempo é um colector, ou seja, parece localmente "flat" perto de cada ponto da mesma forma que, em pequenas escalas suficientes, um globo parece plano. Um fator de escala, (convencionalmente chamado de velocidade de luz) relaciona distâncias medidas no espaço com distâncias medidas no tempo. A magnitude deste fator de escala (cerca de 300.000 quilômetros ou 190.000 milhas no espaço sendo equivalente a um segundo no tempo), juntamente com o fato de que o espaço-tempo é um colector, implica que a velocidades comuns, não-relativistas e a distâncias comuns, em escala humana, há pouco que os seres humanos possam observar que é visivelmente diferente do que eles poderiam observar se o mundo fosse Euclidiano. Foi apenas com o advento de medidas científicas sensíveis em meados da década de 1800, como a experiência Fizeau e a experiência Michelson-Morley, que as discrepâncias intrigantes começaram a ser observadas entre a observação versus as previsões baseadas na suposição implícita do espaço euclidiano.

Na relatividade especial, um observador significará, na maioria dos casos, um quadro de referência a partir do qual um conjunto de objetos ou eventos está sendo medido. Este uso difere significativamente do significado comum do termo em inglês. Os referenciais são construções inerentemente não locais e, de acordo com este uso do termo, não faz sentido falar de um observador como tendo uma localização. Na Figura 1-1, imagine que o quadro em consideração esteja equipado com uma rede densa de relógios, sincronizados dentro deste quadro de referência, que se estende indefinidamente pelas três dimensões do espaço. Qualquer localização específica dentro da rede não é importante. A rede de relógios é usada para determinar a hora e a posição dos eventos que ocorrem em todo o quadro. O termo observador refere-se a todo o conjunto de relógios associados a um referencial inercial. Neste caso idealizado, cada ponto do espaço tem um relógio associado e, assim, os relógios registam cada evento instantaneamente, sem qualquer atraso entre um evento e a sua gravação. Um observador real, entretanto, verá um atraso entre a emissão de um sinal e sua detecção devido à velocidade da luz. Para sincronizar os relógios, na redução de dados após um experimento, o horário em que um sinal é recebido será corrigido para refletir seu horário real caso tivesse sido registrado por uma rede idealizada de relógios.
Em muitos livros sobre relatividade especial, especialmente nos mais antigos, a palavra "observador" é usado no sentido mais comum da palavra. Geralmente fica claro no contexto qual significado foi adotado.
Os físicos distinguem entre o que se mede ou observa (depois de fatorar os atrasos de propagação do sinal) e o que se vê visualmente sem tais correções. A falha em compreender a diferença entre o que se mede/observa e o que se vê é a fonte de muitos erros entre os estudantes iniciantes da relatividade.
Histórico
Em meados de 1800, vários experimentos, como a observação da mancha de Arago e medições diferenciais da velocidade da luz no ar versus na água, foram considerados como tendo provado a natureza ondulatória da luz, em oposição a uma teoria corpuscular. Supôs-se então que a propagação das ondas exigia a existência de um meio ondulante; no caso das ondas de luz, este foi considerado um hipotético éter luminífero. No entanto, as várias tentativas para estabelecer as propriedades deste meio hipotético produziram resultados contraditórios. Por exemplo, o experimento Fizeau de 1851, conduzido pelo físico francês Hippolyte Fizeau, demonstrou que a velocidade da luz na água corrente era menor que a soma da velocidade da luz no ar mais a velocidade da água em uma quantidade dependente da água. #39;índice de refração. Entre outras questões, a dependência do arrasto parcial do éter implícito neste experimento no índice de refração (que depende do comprimento de onda) levou à conclusão desagradável de que o éter simultaneamente flui em velocidades diferentes para cores diferentes. de luz. O famoso experimento de Michelson-Morley de 1887 (Fig. 1-2) não mostrou nenhuma influência diferencial dos movimentos da Terra através do éter hipotético na velocidade da luz, e a explicação mais provável, o arrasto completo do éter, estava em conflito com a observação da aberração estelar.
George Francis FitzGerald em 1889, e Hendrik Lorentz em 1892, propuseram independentemente que os corpos materiais que viajavam através do éter fixo eram fisicamente afetados por sua passagem, contraindo-se na direção do movimento em uma quantidade que era exatamente o necessário para explicar o resultados negativos do experimento Michelson-Morley. (Não ocorrem alterações de comprimento nas direções transversais à direção do movimento.)
Em 1904, Lorentz expandiu sua teoria de tal forma que chegou a equações formalmente idênticas àquelas que Einstein derivaria mais tarde (ou seja, a transformação de Lorentz). Como uma teoria da dinâmica (o estudo das forças e torques e seus efeitos no movimento), sua teoria pressupunha deformações físicas reais dos constituintes físicos da matéria. As equações de Lorentz previram uma quantidade que ele chamou de hora local, com a qual ele poderia explicar a aberração da luz, o experimento Fizeau e outros fenômenos.
Henri Poincaré foi o primeiro a combinar espaço e tempo em espaço-tempo. Ele argumentou em 1898 que a simultaneidade de dois eventos é uma questão de convenção. Em 1900, ele reconheceu que a "hora local" é na verdade o que é indicado pelo movimento dos relógios, aplicando uma definição operacional explícita de sincronização do relógio, assumindo uma velocidade de luz constante. Em 1900 e 1904, ele sugeriu a inerente indetectabilidade do éter, enfatizando a validade do que chamou de princípio da relatividade, e em 1905/1906 aperfeiçoou matematicamente a teoria dos elétrons de Lorentz, a fim de trazê-la de acordo com o postulado da relatividade. Ao discutir várias hipóteses sobre a gravitação invariante de Lorentz, ele introduziu o conceito inovador de um espaço-tempo quadridimensional definindo vários quatro vetores, nomeadamente quatro posições, quatro velocidades e quatro forças. Ele não seguiu o formalismo quadridimensional em artigos subsequentes, entretanto, afirmando que esta linha de pesquisa parecia “implicar grande dor para lucro limitado”, concluindo em última análise “que a linguagem tridimensional parece o mais adequado à descrição do nosso mundo". Além disso, ainda em 1909, Poincaré continuou a descrever a interpretação dinâmica da transformada de Lorentz.
Em 1905, Albert Einstein analisou a relatividade especial em termos de cinemática (o estudo de corpos em movimento sem referência a forças) em vez de dinâmica. Seus resultados foram matematicamente equivalentes aos de Lorentz e Poincaré. Ele os obteve reconhecendo que toda a teoria pode ser construída sobre dois postulados: o princípio da relatividade e o princípio da constância da velocidade da luz. Seu trabalho estava repleto de imagens vívidas envolvendo a troca de sinais luminosos entre relógios em movimento, medições cuidadosas do comprimento das hastes em movimento e outros exemplos.
Além disso, Einstein em 1905 substituiu tentativas anteriores de uma relação massa-energia eletromagnética, introduzindo a equivalência geral de massa e energia, que foi fundamental para sua formulação subsequente do princípio de equivalência em 1907, que declara a equivalência de inercial e massa gravitacional. Ao utilizar a equivalência massa-energia, Einstein mostrou, além disso, que a massa gravitacional de um corpo é proporcional ao seu conteúdo energético, o que foi um dos primeiros resultados do desenvolvimento da relatividade geral. Embora pareça que a princípio ele não pensou geometricamente sobre o espaço-tempo, no desenvolvimento posterior da relatividade geral Einstein incorporou totalmente o formalismo do espaço-tempo.
Quando Einstein publicou em 1905, outro dos seus concorrentes, o seu antigo professor de matemática Hermann Minkowski, também tinha chegado à maior parte dos elementos básicos da relatividade especial. Max Born relatou um encontro que teve com Minkowski, buscando ser aluno/colaborador de Minkowski:
Fui a Colônia, conheci Minkowski e ouvi sua célebre palestra "Espaço e Tempo" entregue em 2 de setembro de 1908. [...] Ele me disse mais tarde que ele veio a ele como um grande choque quando Einstein publicou seu artigo em que a equivalência dos diferentes tempos locais de observadores que se movem em relação uns aos outros foi pronunciado; porque ele tinha alcançado as mesmas conclusões independentemente, mas não as publicou porque ele queria primeiro trabalhar a estrutura matemática em todo o seu esplendor. Ele nunca fez uma reivindicação prioritária e sempre deu a Einstein toda a sua parte na grande descoberta.
Minkowski estava preocupado com o estado da eletrodinâmica após os experimentos disruptivos de Michelson, pelo menos desde o verão de 1905, quando Minkowski e David Hilbert lideraram um seminário avançado com a presença de físicos notáveis da época para estudar os artigos de Lorentz., Poincaré et al. Minkowski via o trabalho de Einstein como uma extensão do de Lorentz e foi influenciado mais diretamente por Poincaré.
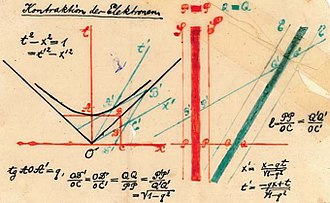
Em 5 de novembro de 1907 (pouco mais de um ano antes de sua morte), Minkowski apresentou sua interpretação geométrica do espaço-tempo em uma palestra para a Sociedade Matemática de Göttingen com o título, O Princípio da Relatividade (< i>Das Relativitätsprinzip). Em 21 de setembro de 1908, Minkowski apresentou sua famosa palestra, Espaço e Tempo (Raum und Zeit), à Sociedade Alemã de Cientistas e Médicos. As palavras iniciais de Espaço e Tempo incluem a famosa afirmação de Minkowski de que “Doravante, o espaço para si e o tempo para si serão completamente reduzidos a uma mera sombra, e apenas a algum tipo de sombra”. a união dos dois preservará a independência. Espaço e Tempo incluiu a primeira apresentação pública de diagramas de espaço-tempo (Fig. 1-4) e incluiu uma demonstração notável de que o conceito de intervalo invariante (discutido abaixo), junto com a observação empírica de que a velocidade da luz é finita, permite derivar a totalidade da relatividade especial.
O conceito de espaço-tempo e o grupo de Lorentz estão intimamente ligados a certos tipos de geometrias esféricas, hiperbólicas ou conformes e seus grupos de transformação já desenvolvidos no século XIX, nos quais são utilizados intervalos invariantes análogos ao intervalo de espaço-tempo.
Einstein, por sua vez, inicialmente rejeitou a interpretação geométrica da relatividade especial de Minkowski, considerando-a como überflüssige Gelehrsamkeit (aprendizagem supérflua). No entanto, para completar a sua busca pela relatividade geral, iniciada em 1907, a interpretação geométrica da relatividade revelou-se vital e, em 1916, Einstein reconheceu plenamente a sua dívida para com Minkowski, cuja interpretação facilitou enormemente a transição para a relatividade geral. Como existem outros tipos de espaço-tempo, como o espaço-tempo curvo da relatividade geral, o espaço-tempo da relatividade especial é hoje conhecido como espaço-tempo de Minkowski.
Espaço-tempo na relatividade especial
Intervalo de espaço-tempo
Em três dimensões, o distância entre dois pontos pode ser definido usando o teorema de Pitágora:
Embora dois visualizadores possam medir a posição x, y e z dos dois pontos usando sistemas de coordenadas diferentes, a distância entre os pontos os pontos serão iguais para ambos (assumindo que eles estão medindo usando as mesmas unidades). A distância é "invariante".
Na relatividade especial, porém, a distância entre dois pontos não é mais a mesma se medida por dois observadores diferentes quando um dos observadores está em movimento, devido à contração de Lorentz. A situação é ainda mais complicada se os dois pontos estiverem separados no tempo e também no espaço. Por exemplo, se um observador vê dois eventos ocorrendo no mesmo local, mas em momentos diferentes, uma pessoa que se move em relação ao primeiro observador verá os dois eventos ocorrendo em locais diferentes, porque (do seu ponto de vista) eles são estacionários., e a posição do evento está recuando ou se aproximando. Assim, uma medida diferente deve ser utilizada para medir a "distância" entre dois eventos.
Em espaço-tempo de quatro dimensões, o analógico à distância é o intervalo. Embora o tempo entre como uma quarta dimensão, é tratado de forma diferente das dimensões espaciais. O espaço de Minkowski, portanto, difere em aspectos importantes do espaço euclidiano de quatro dimensões. A razão fundamental para fundir espaço e tempo em espaço-tempo é que espaço e tempo não são separadamente invariantes, o que é dizer que, sob as condições adequadas, diferentes observadores irão discordar no tempo entre dois eventos (por causa da dilatação do tempo) ou a distância entre os dois eventos (por causa da contração do comprimento). Mas a relatividade especial fornece um novo invariante, chamado o intervalo espaço-tempo, que combina distâncias no espaço e no tempo. Todos os observadores que medem o tempo e a distância entre os dois eventos terminarão computando o mesmo intervalo espaço-tempo. Suponha que um observador mede dois eventos como sendo separado no tempo por e uma distância espacial Então o intervalo espaço-tempo entre os dois eventos que são separados por uma distância no espaço e por no - Coordenar é:
ou para três dimensões espaciais,
A constante a velocidade da luz, converte unidades de tempo (como segundos) em unidades espaciais (como metros). O intervalo quadrado é uma medida de separação entre eventos A e B que são tempo separado e, além disso, espaço separado, quer porque há dois objetos separados submetidos a eventos, ou porque um único objeto no espaço está se movendo inercialmente entre seus eventos. O intervalo de separação é derivado por squaring a distância espacial separando evento B do evento A e subtraindo-o do quadrado da distância espacial percorrida por um sinal de luz nesse mesmo intervalo de tempo . Se a separação do evento é devido a um sinal de luz, então esta diferença desaparece e .
Quando o evento considerado é infinitamente próximo um do outro, então podemos escrever
Em um quadro inercial diferente, diga com coordenadas , o intervalo espaço-tempo pode ser escrito em uma mesma forma como acima. Por causa da constância da velocidade da luz, os eventos de luz em todos os quadros inerciais pertencem a intervalo zero, . Para qualquer outro evento infinitesimal onde , um pode provar que que, por sua vez, conduz à integração . A invariância do intervalo de qualquer evento entre todos os quadros interciais de referência é um dos resultados fundamentais da teoria especial da relatividade.
Embora para a brevidade, muitas vezes se vê expressões de intervalo expressas sem deltas, incluindo na maioria das discussões a seguir, deve-se entender que, em geral, significa , etc. Estamos sempre preocupados com diferenças de valores de coordenadas espaciais ou temporais pertencentes a dois eventos, e como não há origem preferida, valores de coordenadas únicas não têm significado essencial.

A equação acima é semelhante ao teorema de Pythagorean, exceto com um sinal de menos entre o e o termos. O intervalo espaço-tempo é a quantidade não em si. A razão é que, ao contrário das distâncias na geometria euclidiana, intervalos no espaço de Minkowski podem ser negativos. Em vez de lidar com raízes quadradas de números negativos, os físicos costumam considerar como um símbolo distinto em si mesmo, em vez do quadrado de algo.
Em geral pode assumir qualquer valor de número real. Se é positivo, o intervalo espaço-tempo é referido como Tempo. Uma vez que a distância espacial atravessada por qualquer objeto maciço é sempre menos do que a distância percorrida pela luz para o mesmo intervalo de tempo, intervalos reais são sempre semelhantes ao tempo. Se é negativo, diz-se que o intervalo de espaço espaço, onde o intervalo espaço-tempo é imaginário. Os intervalos espaciais são iguais a zero quando Em outras palavras, o intervalo espaço-tempo entre dois eventos na linha mundial de algo que se move na velocidade da luz é zero. Tal intervalo é denominado luz ou Null. Um fóton que chega ao nosso olho de uma estrela distante não envelhecerá, apesar de ter (de nossa perspectiva) passado anos em sua passagem.
Um diagrama de espaço-tempo é tipicamente desenhado com apenas um espaço e uma única coordenada de tempo. Fig. 2-1 apresenta um diagrama espaço-tempo ilustrando as linhas mundiais (isto é, caminhos no espaço-tempo) de dois fótons, A e B, originários do mesmo evento e indo em direções opostas. Além disso, C ilustra a linha mundial de um objeto de velocidade mais lenta do que a luz. A coordenada de tempo vertical é dimensionada para que tenha as mesmas unidades (metros) que a coordenada horizontal do espaço. Como os fótons viajam à velocidade da luz, suas linhas mundiais têm uma inclinação de ±1. Em outras palavras, cada metro que um fóton viaja para a esquerda ou direita requer aproximadamente 3,3 nanossegundos de tempo.
Existem duas convenções de sinais em uso na literatura da relatividade:
e
Essas convenções de sinais estão associadas às assinaturas métricas (+−−−) e (−+++). Uma pequena variação é colocar a coordenada de tempo por último e não primeiro. Ambas as convenções são amplamente utilizadas no campo de estudo.
Quadros de referência


Para obter informações sobre como as coordenadas do espaço-tempo medidas por observadores em diferentes referenciais se comparam entre si, é útil trabalhar com uma configuração simplificada com quadros em uma configuração padrão. Com cuidado, isso permite simplificação da matemática sem perda de generalidade nas conclusões a que se chega. Na Figura 2-2, dois referenciais galileanos (isto é, quadros convencionais de 3 espaços) são exibidos em movimento relativo. O quadro S pertence a um primeiro observador O, e o quadro S′ (pronuncia-se "S prime") pertence a um segundo observador O′.
- O x, Sim., zangão. eixos de quadro S são orientados paralelamente aos respectivos eixos primod do quadro S′.
- Quadro S′ move-se no x-direção do quadro S com velocidade constante v como medida no quadro S.
- As origens de quadros S e S são coincidentes quando o tempo ) = 0 para quadro S e )′ = 0 para quadro S′.
Fig. 2-3a redesenha a Fig. 2-2 em uma orientação diferente. A Fig. 2-3b ilustra um diagrama de espaço-tempo do ponto de vista do observador O. Como S e S′ estão na configuração padrão, suas origens coincidem nos tempos t = 0 no quadro S e t′ = 0 no quadro S′. O eixo ct′ passa pelos eventos no quadro S′ que têm x′ = 0. Mas os pontos com x′ = 0 estão se movendo na direção x do quadro S com velocidade v, de modo que eles não coincidam com o eixo ct em nenhum momento diferente de zero. Portanto, o eixo ct′ é inclinado em relação ao eixo ct por um ângulo θ dado por
O eixo x′ também é inclinado em relação ao eixo x. Para determinar o ângulo dessa inclinação, lembramos que a inclinação da linha mundial de um pulso de luz é sempre ±1. A Figura 2-3c apresenta um diagrama de espaço-tempo do ponto de vista do observador O′. O evento P representa a emissão de um pulso de luz em x′ = 0, ct′ = −a. O pulso é refletido em um espelho situado a uma distância a da fonte de luz (evento Q) e retorna à fonte de luz em x′ = 0, ct ′ = a (evento R).
Os mesmos eventos P, Q, R são plotados na Fig. 2-3b no referencial do observador O. Os caminhos da luz têm inclinações = 1 e −1, de modo que △PQR forma um triângulo retângulo com PQ e QR ambos a 45 graus em relação aos eixos x e ct. Como OP = OQ = OR, o ângulo entre x′ e x também deve ser θ.
Enquanto o quadro restante possui eixos de espaço e tempo que se encontram em ângulos retos, o quadro móvel é desenhado com eixos que se encontram em um ângulo agudo. Os quadros são realmente equivalentes. A assimetria se deve a distorções inevitáveis na forma como as coordenadas do espaço-tempo podem ser mapeadas em um plano cartesiano, e não deve ser considerada mais estranha do que a maneira pela qual, em uma projeção da Terra de Mercator, os tamanhos relativos das massas de terra próximas aos pólos (Groenlândia e Antártica) são altamente exageradas em relação às massas de terra próximas ao Equador.
Cone de luz

Na Figura 2–4, o evento O está na origem de um diagrama de espaço-tempo, e as duas linhas diagonais representam todos os eventos que têm intervalo de espaço-tempo zero em relação ao evento de origem. Essas duas linhas formam o que é chamado de cone de luz do evento O, já que a adição de uma segunda dimensão espacial (Fig. 2-5) dá a aparência de dois cones circulares retos encontrando-se com seus vértices em O Um cone se estende para o futuro (t>0), o outro para o passado (t<0).

Um cone de luz (duplo) divide o espaço-tempo em regiões separadas em relação ao seu ápice. O interior do futuro cone de luz consiste em todos os eventos que estão separados do ápice por mais tempo (distância temporal) do que o necessário para cruzar sua distância espacial na velocidade da luz; esses eventos compreendem o futuro temporal do evento O. Da mesma forma, o passado temporal compreende os eventos interiores do cone de luz passado. Portanto, em intervalos semelhantes ao tempo Δct é maior que Δx, tornando os intervalos semelhantes ao tempo positivos. A região externa ao cone de luz consiste em eventos que são separados do evento O por mais espaço do que pode ser atravessado à velocidade da luz em um tempo determinado. Esses eventos compreendem a chamada região espacial do evento O, denotada como "Outro lugar" na Figura 2-4. Diz-se que os eventos no próprio cone de luz são semelhantes à luz (ou separados por nulos) de O. Devido à invariância do intervalo de espaço-tempo, todos os observadores atribuirão o mesmo cone de luz a qualquer evento e, portanto, concordarão com esta divisão do espaço-tempo.
O cone de luz tem um papel essencial dentro do conceito de causalidade. É possível que um sinal não mais rápido que a velocidade da luz viaje da posição e tempo de O para a posição e tempo de D (Fig. 2-4). Portanto, é possível que o evento O tenha uma influência causal no evento D. O cone de luz futuro contém todos os eventos que poderiam ser influenciados causalmente por O. Da mesma forma, é possível que um sinal não mais rápido que a velocidade da luz seja viajam da posição e tempo de A até a posição e tempo de O. O cone de luz passado contém todos os eventos que poderiam ter uma influência causal em O. Em contraste, assumindo que os sinais não podem viajar mais rápido que a velocidade da luz, qualquer evento, como por ex. B ou C, na região semelhante a um espaço (em outro lugar), não podem afetar o evento O, nem podem ser afetados pelo evento O que emprega tal sinalização. Sob esta suposição, qualquer relação causal entre o evento O e quaisquer eventos na região espacial de um cone de luz é excluída.
Relatividade da simultaneidade

Todos os observadores concordarão que, para qualquer evento, um evento dentro do cone de luz futuro do evento ocorre após o evento em questão. Da mesma forma, para qualquer evento, um evento dentro do cone de luz passado do evento ocorre antes do evento em questão. A relação antes-depois observada para eventos separados no tempo permanece inalterada, não importa qual seja o referencial do observador, ou seja, não importa como o observador possa estar se movendo. A situação é bem diferente para eventos separados pelo espaço. A Figura 2-4 foi desenhada a partir do referencial de um observador movendo-se em v = 0. A partir deste referencial, observa-se que o evento C ocorre após o evento O, e observa-se que o evento B ocorre antes do evento O. A partir de um quadro de referência diferente, as ordenações desses eventos não relacionados causalmente podem ser invertidas. Em particular, observa-se que se dois eventos são simultâneos em um determinado referencial, eles são necessariamente separados por um intervalo semelhante a um espaço e, portanto, estão relacionados de forma não causal. A observação de que a simultaneidade não é absoluta, mas depende do referencial do observador, é chamada de relatividade da simultaneidade.
Fig. 2-6 ilustra o uso de diagramas de espaço-tempo na análise da relatividade da simultaneidade. Os eventos no espaço-tempo são invariantes, mas os referenciais de coordenadas se transformam conforme discutido acima na Figura 2-3. Os três eventos (A, B, C) são simultâneos a partir do referencial de um observador movendo-se em v = 0. A partir do referencial de um observador movendo-se em v = 0,3c, os eventos parecem ocorrem na ordem C, B, A. Do referencial de um observador movendo-se a v = −0,5 c, os eventos parecem ocorrer na ordem A, B, C. A linha branca representa um plano de simultaneidade sendo movido do passado do observador para o futuro do observador, destacando os eventos que nele residem. A área cinza é o cone de luz do observador, que permanece invariante.
Um intervalo espaço-tempo dá a mesma distância que um observador mediria se os eventos que estavam sendo medidos fossem simultâneos ao observador. Um intervalo espaço-tempo assim fornece uma medida de distância adequada, ou seja, a verdadeira distância = Da mesma forma, um intervalo espaço-tempo do tempo dá a mesma medida do tempo que seria apresentado pelo cócerego cumulativo de um relógio que se move ao longo de uma determinada linha mundial. Um intervalo espaço-tempo, portanto, proporciona uma medida do tempo adequado = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =
Hírbole invariante

No espaço euclidiano (tendo apenas dimensões espaciais), o conjunto de pontos equidistantes (usando a métrica euclidiana) de algum ponto forma um círculo (em duas dimensões) ou uma esfera (em três dimensões). No espaço-tempo Minkowski (1+1)-dimensional (tendo uma dimensão temporal e uma dimensão espacial), os pontos em algum intervalo constante do espaço-tempo longe da origem (usando a métrica de Minkowski) formam curvas dadas pelas duas equações
com alguma constante real positiva. Estas equações descrevem duas famílias de hiperbolae em uma x–ct diagrama espaço-tempo, que são denominados hiperbola invariável.
Na Figura 2-7a, cada hipérbole magenta conecta todos os eventos que têm alguma separação espacial fixa da origem, enquanto as hipérboles verdes conectam eventos de separação temporal igual.
A magenta hiperbolae, que atravessa a x eixo, são curvas tipo tempo, o que é dizer que essas hiperbolas representam caminhos reais que podem ser atravessadas por partículas (constantemente acelerando) no espaço-tempo: Entre dois eventos em um hiperbola é possível uma relação de causalidade, porque o inverso da inclinação - representando a velocidade necessária - para todos os secantes é menor do que . Por outro lado, a hiperbola verde, que cruza a ct eixo, são curvas espaciais porque todos os intervalos por aí. estas hiperbolas são intervalos espaciais: Nenhuma causalidade é possível entre dois pontos em uma dessas hiperbolas, porque todas as secantes representam velocidades maiores do que as de secantes. .
Fig. 2-7b reflete a situação no espaço-tempo Minkowski (1+2)-dimensional (uma dimensão temporal e duas dimensões espaciais) com os hiperbolóides correspondentes. As hipérboles invariantes deslocadas por intervalos espaciais da origem geram hiperbolóides de uma folha, enquanto as hipérboles invariantes deslocadas por intervalos semelhantes ao tempo da origem geram hiperbolóides de duas folhas.
A fronteira dimensional (1+2) entre hiperbolóides semelhantes ao espaço e ao tempo, estabelecida pelos eventos que formam um intervalo zero do espaço-tempo até a origem, é composta pela degeneração dos hiperbolóides no cone de luz. Nas dimensões (1+1), as hipérboles degeneram para as duas linhas cinzas de 45° representadas na Fig. 2-7a.
Dilatação do tempo e contração do comprimento
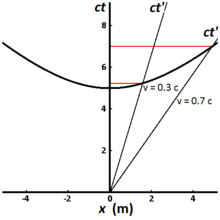
Fig. 2-8 ilustra a hipérbole invariante para todos os eventos que podem ser alcançados a partir da origem em um tempo adequado de 5 metros (aproximadamente 1,67×10−8 s). Diferentes linhas mundiais representam relógios movendo-se em velocidades diferentes. Um relógio estacionário em relação ao observador tem uma linha mundial vertical e o tempo decorrido medido pelo observador é igual ao tempo próprio. Para um relógio viajando a 0,3 c, o tempo decorrido medido pelo observador é de 5,24 metros (1,75×10−8 s), enquanto para um relógio viajando a 0,7 c, o tempo decorrido medido pelo observador é de 7,00 metros (2,34×10−8 s). Isso ilustra o fenômeno conhecido como dilatação do tempo. Relógios que viajam mais rápido demoram mais (no referencial do observador) para marcar a mesma quantidade de tempo adequado e viajam mais ao longo do eixo x dentro desse tempo adequado do que viajariam sem a dilatação do tempo. A medição da dilatação do tempo por dois observadores em diferentes referenciais inerciais é mútua. Se o observador O mede os relógios do observador O′ como sendo mais lentos em seu referencial, o observador O′, por sua vez, medirá os relógios do observador O como sendo mais lentos.

A contração do comprimento, assim como a dilatação do tempo, é uma manifestação da relatividade da simultaneidade. A medição do comprimento requer a medição do intervalo de espaço-tempo entre dois eventos que são simultâneos no referencial de alguém. Mas os acontecimentos que são simultâneos num referencial não são, em geral, simultâneos noutros referenciais.
Fig. 2-9 ilustra os movimentos de uma haste de 1 m que se desloca a 0,5 c ao longo do eixo x. As bordas da faixa azul representam as linhas mundiais dos dois pontos finais da haste. A hipérbole invariante ilustra eventos separados da origem por um intervalo espacial de 1 m. Os pontos finais O e B medidos quando t′ = 0 são eventos simultâneos no quadro S′. Mas para um observador no referencial S, os eventos O e B não são simultâneos. Para medir o comprimento, o observador no quadro S mede as extremidades da haste projetadas no eixo x ao longo de suas linhas mundiais. A projeção da folha do mundo da haste no eixo x produz o comprimento encurtado OC.
(não ilustrado) Desenhar uma linha vertical através de A de modo que cruze o eixo x′ demonstra que, mesmo que OB seja encurtado do ponto de vista do observador O, OA também é encurtado de o ponto de vista do observador O′. Da mesma forma que cada observador mede os relógios do outro como lentos, cada observador mede os governantes do outro como contraídos.
Em relação à contração mútua do comprimento, a Fig. 2-9 ilustra que os quadros preparados e não preparados são girados mutuamente por um ângulo hiperbólico (análogo aos ângulos comuns na geometria euclidiana). Por causa dessa rotação, a projeção de uma régua métrica preparada no eixo x não preparada é encurtada, enquanto a projeção de uma régua métrica não preparada no eixo x′ preparada é igualmente encurtada.
Dilatação mútua do tempo e o paradoxo dos gêmeos
Dilatação mútua do tempo
A dilatação mútua do tempo e a contração do comprimento tendem a parecer aos iniciantes conceitos inerentemente contraditórios. Se um observador no referencial S mede um relógio, em repouso no referencial S', correndo mais devagar que o seu', enquanto S' está se movendo com velocidade v em S, então o princípio da relatividade exige que um observador no referencial S' da mesma forma, mede um relógio no quadro S, movendo-se na velocidade −v em S', correndo mais devagar que o dela. Como dois relógios podem funcionar ambos mais devagar que o outro é uma questão importante que “vai ao cerne da compreensão da relatividade especial”.
Essa aparente contradição decorre da não consideração correta das diferentes configurações das medições necessárias e relacionadas. Essas configurações permitem uma explicação consistente da contradição única aparente. Não se trata do tique-taque abstrato de dois relógios idênticos, mas de como medir em um quadro a distância temporal de dois tique-taques de um relógio em movimento. Acontece que na observação mútua da duração entre os tiques dos relógios, cada um se movendo no respectivo quadro, diferentes conjuntos de relógios devem estar envolvidos. Para medir no quadro S a duração do tick de um relógio em movimento W′ (em repouso em S′), são usados dois relógios sincronizados adicionais W1 e W< sub>2 em repouso em dois pontos fixos arbitrariamente em S com a distância espacial d.
- Dois eventos podem ser definidos pela condição "dois relógios estão simultaneamente em um lugar", ou seja, quando W′ passa cada W1 e W2. Para ambos os eventos as duas leituras dos relógios colocated são gravadas. A diferença das duas leituras de W1 e W2 é a distância temporal dos dois eventos em S, e sua distância espacial é D. A diferença das duas leituras de W′ é a distância temporal dos dois eventos em S′. Em S′ estes eventos são apenas separados no tempo, eles acontecem no mesmo lugar em S′. Por causa da invariância do intervalo espaço-tempo spanned por estes dois eventos, e a separação espacial nonzero D em S, a distância temporal em S′ deve ser menor do que a em S: o menor distância temporal entre os dois eventos, resultante das leituras do relógio em movimento W′, pertence ao mais devagar relógio de corrida W′.
Por outro lado, para julgar no quadro S′ a distância temporal de dois eventos em um relógio em movimento W (em repouso em S), são necessários dois relógios em repouso em S′.
- Nesta comparação o relógio W está se movendo com velocidade −v. Gravar novamente as quatro leituras para os eventos, definidas por "dois relógios simultaneamente em um só lugar", resulta nas distâncias temporais análogas dos dois eventos, agora temporal e espacialmente separados em S", e apenas temporalmente separados, mas colocados em S. Para manter o intervalo espaço-tempo invariante, a distância temporal em S deve ser menor do que em S′, por causa da separação espacial dos eventos em S′: agora o relógio W é observado para correr mais lento.
As gravações necessárias para os dois julgamentos, com "um relógio em movimento" e "dois relógios em repouso" em respectivamente S ou S′, envolve dois conjuntos diferentes, cada um com três relógios. Como existem diferentes conjuntos de relógios envolvidos nas medições, não há necessidade inerente de que as medições sejam reciprocamente “consistentes”; de tal forma que, se um observador mede que o relógio em movimento está lento, o outro observador mede que o relógio dele está rápido.
Fig. 2.10 ilustra a discussão anterior sobre dilatação mútua do tempo com diagramas de Minkowski. A imagem superior reflete as medições vistas do quadro S "em repouso" com eixos retangulares não preparados e quadro S′ "movendo-se com v > 0", coordenado por eixos oblíquos, inclinados para a direita; a imagem inferior mostra o quadro S′ "em repouso" com coordenadas retangulares preparadas e quadro S "movendo-se com −v < 0", com eixos oblíquos, sem escorvamento, inclinados para a esquerda.
Cada linha desenhada paralelamente a um eixo espacial (x, x′) representa uma linha de simultaneidade. Todos os eventos nessa linha têm o mesmo valor de tempo (ct, ct′). Da mesma forma, cada linha desenhada paralelamente a um eixo temporal (ct, ct′) representa uma linha de valores de coordenadas espaciais iguais (x, x′).
- Pode-se designar em ambas as imagens a origem O Não. O?) como evento, onde o respectivo "relógio móvel" é colocado com o "primeiro relógio em repouso" em ambas as comparações. Obviamente, para este evento as leituras em ambos os relógios em ambas as comparações são zero. Como consequência, as mundanas dos relógios em movimento são os inclinados para a direita ct′-axis (imagens superiores, relógio W′) e o inclinado para a esquerda ct-axes (Imagens mais baixas, relógio W). As mundanas de W1 e W1 são os eixos de tempo vertical correspondentes (ct nas imagens superiores, e ct′ nas imagens inferiores).
- Na imagem superior o lugar para W2 é levado a ser Ax > 0, e assim a linha do mundo (não mostrada nas imagens) deste relógio interseta a linha do mundo do relógio em movimento (o relógio em movimento) ct′-axis) no evento rotulado A, onde "dois relógios estão simultaneamente em um lugar". Na imagem inferior o lugar para W′2 é levado a ser Cx?< 0, e assim nesta medição o relógio móvel W passa W′2 no evento C.
- Na imagem superior o ct- coordenada A) do evento A (a leitura de W2) é rotulada B, dando assim o tempo decorrido entre os dois eventos, medidos com W1 e W2, como OB. Para uma comparação, o comprimento do intervalo de tempo OA, medido com W′, deve ser transformado à escala da ct-axis. Isto é feito pela hiperbola invariante (ver também Fig. 2-8) através A, conectando todos os eventos com o mesmo intervalo espaço-tempo da origem como A. Isso produz o evento C sobre o ct-axis, e obviamente: OC<OB, o relógio "moving" W′ corre mais devagar.
Para mostrar a dilatação mútua do tempo imediatamente na imagem superior, o evento D pode ser construído como o evento em x′ = 0 (a localização do relógio W′ em S′), que é simultâneo a C (OC tem intervalo de espaço-tempo igual a OA) em S′. Isso mostra que o intervalo de tempo OD é maior que OA, mostrando que o "movimento" o relógio funciona mais devagar.
Na imagem inferior, o referencial S está se movendo com velocidade −v no referencial S′ em repouso. A linha do mundo do relógio W é o eixo ct (inclinado para a esquerda), a linha do mundo de W′1 é o ct′- eixo, e a linha mundial de W′2 é a vertical através do evento C, com coordenada ct′ D. A hipérbole invariante através do evento C dimensiona o intervalo de tempo OC para OA, que é menor que OD; além disso, B é construído (semelhante a D nas imagens superiores) como simultâneo a A em S, em x = 0. O resultado OB > OC corresponde novamente ao acima.
A palavra "medida" é importante. Na física clássica, um observador não pode afetar um objeto observado, mas o estado de movimento do objeto pode afetar as observações do objeto pelo observador.
Paradoxo dos gêmeos
Muitas introduções à relatividade especial ilustram as diferenças entre a relatividade galileana e a relatividade especial, apresentando uma série de "paradoxos". Estes paradoxos são, na verdade, problemas mal colocados, resultantes da nossa falta de familiaridade com velocidades comparáveis à velocidade da luz. A solução é resolver muitos problemas da relatividade especial e familiarizar-se com as suas chamadas previsões contra-intuitivas. A abordagem geométrica para estudar o espaço-tempo é considerada um dos melhores métodos para desenvolver uma intuição moderna.
O paradoxo dos gêmeos é um experimento mental que envolve gêmeos idênticos, um dos quais faz uma viagem ao espaço em um foguete de alta velocidade, voltando para casa e descobrindo que o gêmeo que permaneceu na Terra envelheceu mais. Este resultado parece intrigante porque cada gémeo observa o outro gémeo em movimento e, portanto, à primeira vista, pareceria que cada um deveria descobrir que o outro envelheceu menos. O paradoxo dos gêmeos contorna a justificativa para a dilatação mútua do tempo apresentada acima, evitando a exigência de um terceiro relógio. No entanto, o paradoxo dos gémeos não é um verdadeiro paradoxo porque é facilmente compreendido no contexto da relatividade especial.
A impressão de que existe um paradoxo decorre de um mal-entendido sobre o que a relatividade especial afirma. A relatividade especial não declara que todos os referenciais são equivalentes, apenas referenciais inerciais. A estrutura da gêmea viajante não é inercial durante os períodos em que ela está acelerando. Além disso, a diferença entre os gêmeos é detectável pela observação: o gêmeo viajante precisa disparar seus foguetes para poder voltar para casa, enquanto o gêmeo que fica em casa não.
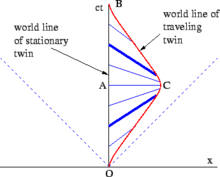
Essas distinções devem resultar em uma diferença no comportamento dos gêmeos. idades. O diagrama de espaço-tempo da Figura 2-11 apresenta o caso simples de um gêmeo indo direto ao longo do eixo x e imediatamente voltando. Do ponto de vista do gêmeo que fica em casa, não há nada de intrigante no paradoxo dos gêmeos. O tempo adequado medido ao longo da linha mundial do gêmeo viajante de O a C, mais o tempo adequado medido de C a B, é menor que o tempo adequado do gêmeo que fica em casa medido de O a A para B. Trajetórias mais complexas requerem a integração do tempo adequado entre os respectivos eventos ao longo da curva (ou seja, a integral do caminho) para calcular a quantidade total de tempo adequado experimentado pelo gêmeo viajante.
As complicações surgem se o paradoxo dos gêmeos for analisado do ponto de vista do gêmeo viajante.
A nomenclatura de Weiss, designando o gêmeo que fica em casa como Terence e o gêmeo viajante como Stella, é usada a seguir.
Stella não está em um referencial inercial. Dado este facto, por vezes é afirmado incorrectamente que a resolução completa do paradoxo dos gémeos requer a relatividade geral:
Uma análise SR pura seria a seguinte: Analisada na moldura de descanso de Stella, ela é imóvel para toda a viagem. Quando ela dispara seus foguetes para a volta, ela experimenta uma força pseudo que se assemelha a uma força gravitacional. Fig. 2-6 e 2-11 ilustram o conceito de linhas (planos) de simultaneidade: Linhas paralelas ao observador x-axis (Xy!-plane) representam conjuntos de eventos que são simultâneos no quadro do observador. Na Fig. 2-11, as linhas azuis conectam eventos na linha do mundo de Terence que, do ponto de vista de Stella, são simultâneas com eventos em sua linha mundial. (Terence, por sua vez, observaria um conjunto de linhas horizontais de simultaneidade.) Ao longo da saída e das pernas inbound da jornada de Stella, ela mede os relógios de Terence tão lentos quanto seus. Mas durante a volta (isto é, entre as linhas azuis arrojadas na figura), uma mudança ocorre no ângulo de suas linhas de simultaneidade, correspondendo a um salto rápido dos eventos na linha do mundo de Terence que Stella considera ser simultânea com sua própria. Portanto, no final de sua viagem, Stella descobre que Terence envelheceu mais do que ela.
Embora a relatividade geral não seja necessária para analisar o paradoxo dos gêmeos, a aplicação do Princípio de Equivalência da relatividade geral fornece alguns insights adicionais sobre o assunto. Stella não está estacionária em um referencial inercial. Analisada no quadro de repouso de Stella, ela fica imóvel durante toda a viagem. Quando ela está desacelerando, seu repouso é inercial e o relógio de Terence parece estar lento. Mas quando ela dispara seus foguetes para dar a volta, seu referencial de repouso é um referencial acelerado e ela experimenta uma força que a empurra como se ela estivesse em um campo gravitacional. Terence parecerá estar no alto desse campo e por causa da dilatação do tempo gravitacional, seu relógio parecerá andar rápido, tanto que o resultado líquido será que Terence envelheceu mais do que Stella quando eles voltarem a ficar juntos. Os argumentos teóricos que prevêem a dilatação do tempo gravitacional não são exclusivos da relatividade geral. Qualquer teoria da gravidade irá prever a dilatação do tempo gravitacional se respeitar o princípio da equivalência, incluindo a teoria de Newton.
Gravitação
Esta seção introdutória enfocou o espaço-tempo da relatividade especial, por ser o mais fácil de descrever. O espaço-tempo de Minkowski é plano, não leva em conta a gravidade, é totalmente uniforme e serve apenas como um pano de fundo estático para os eventos que nele ocorrem. A presença da gravidade complica muito a descrição do espaço-tempo. Na relatividade geral, o espaço-tempo não é mais um fundo estático, mas interage ativamente com os sistemas físicos que contém. As curvas do espaço-tempo na presença de matéria podem propagar ondas, desviar a luz e exibir uma série de outros fenômenos. Alguns desses fenômenos são descritos nas seções posteriores deste artigo.
Matemática básica do espaço-tempo
Transformações galileanas
Um objetivo básico é ser capaz de comparar medições feitas por observadores em movimento relativo. Se houver um observador O no quadro S que mediu as coordenadas de tempo e espaço de um evento, atribuindo a este evento três coordenadas cartesianas e o tempo medido em sua rede de relógios sincronizados ( x, y, z, t) (veja Fig. 1-1). Um segundo observador O′ em um referencial diferente S′ mede o mesmo evento em seu sistema de coordenadas e sua rede de relógios sincronizados (x′, y′, z′, t′). Com referenciais inerciais, nenhum dos observadores está sob aceleração, e um simples conjunto de equações nos permite relacionar as coordenadas (x, y, z, t) para (x′, y′, z ′, t′). Dado que os dois sistemas de coordenadas estão na configuração padrão, o que significa que eles estão alinhados com (x, y, z) coordenadas e que t = 0 quando t ′ = 0, a transformação de coordenadas é a seguinte:
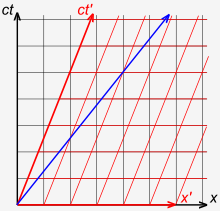
Fig. 3-1 ilustra que na teoria de Newton, o tempo é universal, não a velocidade da luz. Considere o seguinte experimento de pensamento: A seta vermelha ilustra um trem que se move em 0,4 c em relação à plataforma. Dentro do trem, um passageiro dispara uma bala com uma velocidade de 0,4 c no quadro do trem. A flecha azul ilustra que uma pessoa em pé nas faixas do trem mede a bala como viajando a 0.8 c. Isso está de acordo com nossas expectativas ingênuas.
Mais geralmente, assumindo que o referencial S′ está se movendo com velocidade v em relação ao referencial S, então dentro do referencial S′, o observador O′ mede um objeto se movendo com velocidade u′. Velocidade u em relação ao quadro S, já que x = ut, x′ = x − vt e t = t′, pode ser escrito como x′ = ut − vt = (u − < i>v)t = (u − v)t′. Isso leva a u′ = x′/t′ e, finalmente,
- ou
que é o senso comum Direito Galileu para a adição de velocidades.
Composição relativística de velocidades

A composição das velocidades é bastante diferente no espaço-tempo relativístico. Para reduzir ligeiramente a complexidade das equações, introduzimos uma abreviação comum para a razão entre a velocidade de um objeto em relação à luz,
Fig. 3-2a ilustra um trem vermelho que avança a uma velocidade dada por v/c = β = s/a. Da estrutura preparada do trem, um passageiro atira uma bala com uma velocidade dada por u′/c = β′ = n/m, onde a distância é medida ao longo de uma linha paralela ao x′ eixo em vez de paralelo ao eixo preto x. Qual é a velocidade composta u da bala em relação à plataforma, representada pela seta azul? Referindo-se à Figura 3-2b:
- Da plataforma, a velocidade composta da bala é dada por u = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = c(S + R)um + b)).
- Os dois triângulos amarelos são semelhantes porque são triângulos certos que compartilham um ângulo comum α. No triângulo amarelo grande, a razão S/um = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = v/c = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = β.
- As razões dos lados correspondentes dos dois triângulos amarelos são constantes, de modo que R/um = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = b)/S = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = n/m = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = β?. Então... b) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = u?S/c e R = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = u?um/c.
- Substitua as expressões para b) e R na expressão para u na etapa 1 para produzir a fórmula de Einstein para a adição de velocidades:
A fórmula relativística para adição de velocidades apresentada acima apresenta várias características importantes:
- Se u? e v são ambos muito pequenos em comparação com a velocidade da luz, então o produto V.?/c2 torna-se extremamente pequeno, e o resultado geral torna-se indistinguível da fórmula Galileia (fórmula de Newton) para a adição de velocidades: u= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =u?+v. A fórmula Galileia é um caso especial da fórmula relativista aplicável a baixas velocidades.
- Se u? é definido como c, então a fórmula produz u= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =c independentemente do valor inicial de v. A velocidade da luz é a mesma para todos os observadores, independentemente de seus movimentos relativos à fonte emissora.
Dilatação do tempo e contração do comprimento revisitadas

É simples obter expressões quantitativas para dilatação do tempo e contração do comprimento. A Fig. 3-3 é uma imagem composta contendo quadros individuais retirados de duas animações anteriores, simplificados e renomeados para os fins desta seção.
Para reduzir um pouco a complexidade das equações, há uma variedade de diferentes notações abreviadas para ct:
- e são comuns.
- Também se vê muito frequentemente o uso da convenção

Na Fig. 3-3a, segmentos OA e Está bem. representam intervalos espaciais iguais. A dilatação do tempo é representada pela razão OB/Está bem.. A hiperbola invariante tem a equação O quê? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = √x2 + k2 Onde? k= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Está bem., e a linha vermelha que representa a linha mundial de uma partícula em movimento tem a equação O quê?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =x/β= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =xc/v. Um pouco de manipulação algébrica produz
A expressão que envolve o símbolo da raiz quadrada aparece muito frequentemente na relatividade, e uma sobre a expressão é chamada fator Lorentz, denotado pela letra grega gamma :
Se v é maior ou igual a c, a expressão para torna-se fisicamente sem sentido, implicando que c é a velocidade máxima possível na natureza. Para qualquer v maior que zero, o fator Lorentz será maior que um, embora a forma da curva seja tal que para velocidades baixas, o fator Lorentz é extremamente próximo de um.
Na Figura 3-3b, os segmentos OA e OK representam intervalos de espaço-tempo iguais. A contração do comprimento é representada pela razão OB/OK. A hipérbole invariante tem a equação x = √w2 + k2, onde k = OK, e as bordas da faixa azul que representa as linhas mundiais das extremidades de uma haste em movimento têm inclinação 1/β = c/v. O Evento A tem coordenadas (x, w) = (γk, γβk). Como a reta tangente que passa por A e B tem a equação w = (x − OB)/β, temos tem γβk = (γk − OB)/β e
Transformações de Lorentz
As transformações galileanas e sua consequente lei de adição de velocidades funcionam bem em nosso mundo comum de baixa velocidade de aviões, carros e bolas. No entanto, a partir de meados de 1800, instrumentos científicos sensíveis começaram a encontrar anomalias que não se adaptavam bem à adição normal de velocidades.
As transformações de Lorentz são usadas para transformar as coordenadas de um evento de um referencial para outro na relatividade especial.
O fator de Lorentz aparece nas transformações de Lorentz:
As transformações inversas de Lorentz são:
Quando v ≪ c e x são pequenos o suficiente, o v2/c2 e vx/c2 se aproximam de zero, e o As transformações de Lorentz aproximam-se das transformações galileanas.
etc., na maioria das vezes realmente significa etc. Embora para a brevidade as equações de transformação de Lorentz sejam escritas sem deltas, x significa Δx, etc. Estamos, em geral, sempre preocupados com o espaço e o tempo diferenças entre eventos.
Chamar um conjunto de transformações de transformações normais de Lorentz e o outro de transformações inversas é enganoso, uma vez que não há diferença intrínseca entre os quadros. Diferentes autores chamam um ou outro conjunto de transformações de "inverso" definir. As transformações direta e inversa são trivialmente relacionadas entre si, uma vez que o quadro S só pode se mover para frente ou para trás em relação a S′. Portanto, inverter as equações envolve simplesmente trocar as variáveis primárias e não primárias e substituir v por −v.
Exemplo: Terence e Stella estão em uma corrida espacial Earth-to-Mars. Terence é oficial na linha de partida, enquanto Stella é participante. À hora ) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = )? = 0, nave espacial de Stella acelera instantaneamente a uma velocidade de 0,5c. A distância da Terra para Marte é de 300 segundos-luz (sobre 90.0×10.6km). Terence observa Stella cruzando o relógio de linha de chegada em )= 600.00 s. Mas Stella observa o tempo em seu cronômetro de navio para ser como ela passa a linha de chegada, e ela calcula a distância entre as linhas de início e acabamento, como medida em seu quadro, para ser 259.81 segundos-luz (sobre 77.9×10.6km).1).
Derivar as transformações de Lorentz
Houve muitas dezenas de derivações das transformações de Lorentz desde o trabalho original de Einstein em 1905, cada uma com seu foco particular. Embora a derivação de Einstein tenha sido baseada na invariância da velocidade da luz, existem outros princípios físicos que podem servir como pontos de partida. Em última análise, estes pontos de partida alternativos podem ser considerados diferentes expressões do princípio subjacente da localidade, que afirma que a influência que uma partícula exerce sobre outra não pode ser transmitida instantaneamente.
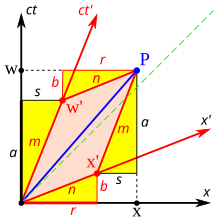
A derivação dada aqui e ilustrada na Fig. 3-5 é baseada em uma apresentada por Bais e faz uso de resultados anteriores das seções Composição Relativística de Velocidades, Dilatação do Tempo e Contração de Comprimento. O evento P tem coordenadas (w, x) no "sistema de descanso" e coordenadas (w′, x′) no quadro vermelho que está se movendo com o parâmetro de velocidade < i>β = v/c. Para determinar w′ e x′ em termos de w e x (ou vice-versa) é mais fácil no início derivar a transformação inversa de Lorentz.
- Não pode haver tal coisa como a expansão/contração do comprimento nas direções transversais. Sim.' deve ser igual Sim. e zangão.? deve ser igual zangão., caso contrário, se uma bola de 1 m de movimento rápido poderia caber através de um buraco circular de 1 m dependeria do observador. O primeiro postulado da relatividade afirma que todos os quadros inerciais são equivalentes, e a expansão/contração transversal violaria esta lei.
- Do desenho, O quê? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = um + b) e x= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R+S
- De resultados anteriores usando triângulos semelhantes, sabemos que S/um= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =b)/R = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = v/c= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =β.
- Por causa da dilatação do tempo, um= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =γ?
- Equação de substitução (4) em S/um= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =β produção S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =γ?β.
- Contração de comprimento e triângulos semelhantes nos dão R= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =γx? e b)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =β = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = βγx?
- Substituir as expressões para S, um, R e b) nas equações no Passo 2 imediatamente rende
As equações acima são expressões alternativas para as equações t e x da transformação inversa de Lorentz, como pode ser visto substituindo ct por w, ct′ para w′ e v/c para β. A partir da transformação inversa, as equações da transformação direta podem ser derivadas resolvendo para t′ e x′.
Linearidade das transformações de Lorentz
As transformações de Lorentz possuem uma propriedade matemática chamada linearidade, pois x′ e t′ são obtidos como combinações lineares de x e t, sem poderes superiores envolvidos. A linearidade da transformação reflete uma propriedade fundamental do espaço-tempo que foi tacitamente assumida na derivação, a saber, que as propriedades dos referenciais inerciais são independentes da localização e do tempo. Na ausência de gravidade, o espaço-tempo parece igual em todos os lugares. Todos os observadores inerciais concordarão sobre o que constitui movimento acelerado e não acelerado. Qualquer observador pode usar suas próprias medidas de espaço e tempo, mas não há nada de absoluto nelas. As convenções de outro observador servirão igualmente bem.
Um resultado da linearidade é que se duas transformações de Lorentz forem aplicadas sequencialmente, o resultado também será uma transformação de Lorentz.
Exemplo: Terence observa Stella se afastando dele a 0,500 c e ele pode usar as transformações de Lorentz com < i>β = 0,500 para relacionar as medidas de Stella com as dele. Stella, em seu enquadramento, observa Ursula se afastando dela a 0,250 c, e ela pode usar as transformações de Lorentz com β = 0,250< /span> para relacionar as medidas de Ursula com as dela. Devido à linearidade das transformações e à composição relativística das velocidades, Terence pode usar as transformações de Lorentz com β = 0,666 para relacionar as transformações de Ursula medições com as suas próprias.
Efeito Doppler
O efeito Doppler é a mudança na frequência ou comprimento de onda de uma onda para um receptor e uma fonte em movimento relativo. Para simplificar, consideramos aqui dois cenários básicos: (1) os movimentos da fonte e/ou receptor ocorrem exatamente ao longo da linha que os conecta (efeito Doppler longitudinal), e (2) os movimentos são perpendiculares à referida linha (efeito Doppler transversal). Estamos ignorando cenários onde eles se movem em ângulos intermediários.
Efeito Doppler longitudinal
A análise Doppler clássica lida com ondas que se propagam em um meio, como ondas sonoras ou ondulações na água, e que são transmitidas entre fontes e receptores que se aproximam ou se afastam um do outro. A análise de tais ondas depende se a fonte, o receptor ou ambos estão se movendo em relação ao meio. Dado o cenário onde o receptor está estacionário em relação ao meio, e a fonte está se movendo diretamente para longe do receptor a uma velocidade de vs para um parâmetro de velocidade de < i>βs, o comprimento de onda é aumentado e a frequência observada f é dada por
Por outro lado, dado o cenário em que a fonte está estacionária e o receptor está se movendo diretamente para longe da fonte a uma velocidade de vr para um parâmetro de velocidade de βr, o comprimento de onda não é alterado, mas a velocidade de transmissão das ondas em relação ao receptor é diminuída e a frequência observada < i>f é dado por
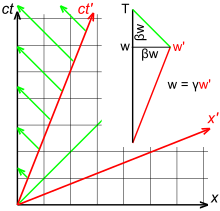
A luz, ao contrário de ondas sonoras ou de água, não se propaga através de um meio, e não há distinção entre uma fonte que se afasta do receptor ou um receptor que se afasta da fonte. Fig. 3-6 ilustra um diagrama espacial relativista que mostra uma fonte que separa do receptor com um parâmetro de velocidade β, para que a separação entre fonte e receptor no tempo O quê? o β. Por causa da dilatação do tempo, . Desde a inclinação do raio de luz verde é −1, . Assim, o efeito Doppler relativista é dado por
Efeito Doppler transversal
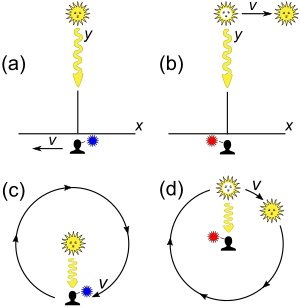
Suponha que uma fonte e um receptor, ambos aproximando-se um do outro em movimento inercial uniforme ao longo de linhas que não se cruzam, estejam mais próximos um do outro. Parece que a análise clássica prevê que o receptor não detecta desvio Doppler. Devido às sutilezas da análise, essa expectativa não é necessariamente verdadeira. No entanto, quando adequadamente definido, o desvio Doppler transversal é um efeito relativístico que não possui análogo clássico. As sutilezas são estas:
- Fig. 3-7a. Qual é a medição de frequência quando o receptor está geometricamente em sua aproximação mais próxima à fonte? Este cenário é mais facilmente analisado a partir do quadro S' da fonte.
- Fig. 3-7b. Qual é a medição de frequência quando o receptor ver a fonte como sendo mais próxima dela? Este cenário é mais facilmente analisado a partir do quadro S do receptor.
Dois outros cenários são comumente examinados em discussões de transversal Doppler turno:
- Fig. 3-7c. Se o receptor estiver se movendo em um círculo ao redor da fonte, que frequência o receptor mede?
- Fig. 3-7d. Se a fonte está se movendo em um círculo ao redor do receptor, que frequência o receptor mede?
No cenário (a), o ponto de maior aproximação é independente do quadro e representa o momento em que não há mudança na distância versus tempo (ou seja, dr/dt = 0 onde r é a distância entre o receptor e a fonte) e, portanto, nenhum desvio Doppler longitudinal. A fonte observa o receptor iluminado por luz de frequência f′, mas também observa o receptor como tendo um relógio dilatado no tempo. No quadro S, o receptor é, portanto, iluminado por luz com desvio azul de frequência
No cenário (b), a ilustração mostra o receptor sendo iluminado pela luz de quando a fonte estava mais próxima do receptor, mesmo que a fonte tenha se movido. Como os relógios da fonte estão dilatados no tempo conforme medido no quadro S, e como dr/dt era igual a zero neste ponto, a luz da fonte, emitida deste ponto mais próximo, é desviada para o vermelho com frequência
Cenários (c) e (d) podem ser analisados por argumentos de dilatação de tempo simples. Em (c), o receptor observa a luz da fonte como sendo blueshifted por um fator de , e em (d), a luz é redshifted. A única complicação aparente é que os objetos orbitando estão em movimento acelerado. No entanto, se um observador inercial olhar para um relógio acelerado, apenas a velocidade instantânea do relógio é importante quando a dilatação do tempo de computação. (O inverso, no entanto, não é verdade.) A maioria dos relatos da mudança transversa do Doppler referem-se ao efeito como um redshift e analisam o efeito em termos de cenários (b) ou (d).
Energia e impulso
Estendendo o impulso para quatro dimensões

Na mecânica clássica, o estado de movimento de uma partícula é caracterizado por sua massa e sua velocidade. O momento linear, o produto da massa e da velocidade de uma partícula, é uma grandeza vetorial, possuindo a mesma direção que a velocidade: p = mv. É uma quantidade conservada, o que significa que se um sistema fechado não for afetado por forças externas, o seu momento linear total não pode mudar.
Na mecânica relativista, o vetor momentum é estendido para quatro dimensões. Adicionado ao vetor momentum é um componente de tempo que permite que o vetor momentum espaçotime para transformar como o vetor de posição espaçotime . Ao explorar as propriedades do momentum espaço-tempo, começamos, na Fig. 3-8a, examinando como uma partícula parece em repouso. No resto do quadro, o componente espacial do impulso é zero, ou seja, p= 0, mas o componente do tempo é igual Mc.
Podemos obter os componentes transformados deste vetor no quadro móvel usando as transformações de Lorentz, ou podemos lê-lo diretamente da figura porque sabemos que e , uma vez que os eixos vermelhos são redimensionados por gamma. Fig. 3-8b ilustra a situação como aparece no quadro móvel. É evidente que os componentes do espaço e do tempo do quatro-momento vão para o infinito como a velocidade do quadro móvel se aproxima c.
Usaremos esta informação em breve para obter uma expressão para o quatro momento.
Momento da luz
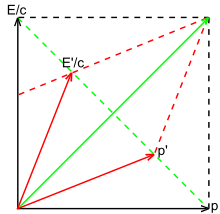
Partículas de luz, ou fótons, viajam à velocidade de c, a constante convencionalmente conhecida como velocidade da luz. Esta afirmação não é uma tautologia, uma vez que muitas formulações modernas da relatividade não partem da velocidade constante da luz como postulado. Os fótons, portanto, propagam-se ao longo de uma linha de mundo semelhante à luz e, em unidades apropriadas, têm componentes de espaço e tempo iguais para cada observador.
Uma consequência da teoria de Maxwell do eletromagnetismo é que a luz carrega energia e impulso, e que sua relação é uma constante: . Reorganizar, , e desde para fótons, os componentes do espaço e do tempo são iguais, E/c deve, portanto, ser equiparado com o componente de tempo do vetor momentum espaço-tempo.
Os fótons viajam à velocidade da luz, mas têm momento e energia finitos. Para que isso aconteça, o termo de massa em γmc deve ser zero, o que significa que os fótons são partículas sem massa. Infinito vezes zero é uma quantidade mal definida, mas E/c está bem definida.
Por esta análise, se a energia de um fóton é igual E no quadro de descanso, é igual em um quadro móvel. Este resultado pode ser derivado pela inspeção da Fig. 3-9 ou pela aplicação das transformações de Lorentz, e é consistente com a análise do efeito Doppler dado anteriormente.
Relação massa-energia
A consideração das inter-relações entre os vários componentes do vetor momento relativístico levou Einstein a várias conclusões famosas.
- No limite de baixa velocidade como β = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = v/c aproxima-se de zero, γ aproxima-se 1, então o componente espacial do momentum relativista abordagens MV, o termo clássico para momentum. Seguindo esta perspectiva, γm pode ser interpretado como uma generalização relativista de m. Einstein propôs que o massa relativista de um objeto aumenta com a velocidade de acordo com a fórmula .
- Da mesma forma, comparando o componente temporal do impulso relativista com o do fóton, , de modo que Einstein chegou ao relacionamento . Simplificado para o caso da velocidade zero, esta é a famosa equação de Einstein relativa à energia e massa.
Outra maneira de observar a relação entre massa e energia é considerar uma expansão em série de γmc2 em baixa velocidade:
O segundo termo é apenas uma expressão para a energia cinética da partícula. A massa realmente parece ser outra forma de energia.
O conceito de massa relativística que Einstein introduziu em 1905, mrel, embora amplamente validado todos os dias em aceleradores de partículas em todo o mundo (ou mesmo em qualquer instrumentação cujo uso depende de partículas de alta velocidade, como microscópios eletrônicos, televisores coloridos antiquados, etc.), não provou ser um conceito frutífero em física, no sentido de que não é um conceito que serviu de base para outros desenvolvimentos teóricos. A massa relativística, por exemplo, não desempenha nenhum papel na relatividade geral.
Por esta razão, bem como por preocupações pedagógicas, a maioria dos físicos prefere actualmente uma terminologia diferente quando se referem à relação entre massa e energia. "Massa relativística" é um termo obsoleto. O termo "massa" por si só refere-se à massa de repouso ou massa invariante e é igual ao comprimento invariante do vetor momento relativístico. Expresso como uma fórmula,
Esta fórmula aplica-se a todas as partículas, massivas e massivas. Para fótons onde mdescansar. igual a zero, produz, .
Quatro momentos
Por causa da estreita relação entre massa e energia, o quatro momento (também chamado de 4-momento) também é chamado de vetor 4 energia-momento. Usando um P maiúsculo para representar o quatro-momento e um p minúsculo para denotar o momento espacial, o quatro-momento pode ser escrito como
- ou alternativamente,
- usando a convenção que
Leis de conservação
Na física, as leis de conservação estabelecem que certas propriedades mensuráveis específicas de um sistema físico isolado não mudam à medida que o sistema evolui ao longo do tempo. Em 1915, Emmy Noether descobriu que subjacente a cada lei de conservação está uma simetria fundamental da natureza. O fato de que os processos físicos não se importam com onde no espaço eles ocorrem (simetria de translação espacial) produz a conservação do momento, o fato de que tais processos não se importam com quando eles ocorrem (simetria de translação temporal), produz conservação de energia e assim por diante. Nesta seção, examinamos as visões newtonianas da conservação de massa, momento e energia a partir de uma perspectiva relativística.
Momentum total
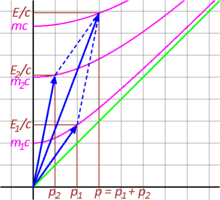
Para compreender como a visão newtoniana da conservação do momento precisa ser modificada num contexto relativístico, examinamos o problema da colisão de dois corpos limitados a uma única dimensão.
Na mecânica newtoniana, dois casos extremos deste problema podem ser distinguidos, resultando em matemática de complexidade mínima:
- (1) Os dois corpos recuam um do outro em uma colisão completamente elástica.
- (2) Os dois corpos ficam juntos e continuam se movendo como uma única partícula. Este segundo caso é o caso de colisão completamente inelástica.
Para ambos os casos (1) e (2), o momento, a massa e a energia total são conservados. No entanto, a energia cinética não é conservada em casos de colisão inelástica. Uma certa fração da energia cinética inicial é convertida em calor.
No caso (2), duas massas com impulsos e colide para produzir uma única partícula de massa conservada viajando no centro da velocidade de massa do sistema original, . O impulso total é conservado.
Fig. 3-10 ilustra a colisão inelástica de duas partículas de uma perspectiva relativista. Os componentes do tempo e adicionar até ao total E/c do vetor resultante, o que significa que a energia é conservada. Da mesma forma, os componentes do espaço e Adicionar ao formulário p do vetor resultante. O quatro-momento é, como esperado, uma quantidade conservada. No entanto, a massa invariante da partícula fundida, dada pelo ponto em que a hiperbola invariante do impulso total intersecta o eixo de energia, não é igual à soma das massas invariantes das partículas individuais que colidiram. De fato, é maior do que a soma das massas individuais: .
Olhando para os acontecimentos deste cenário na sequência inversa, vemos que a não conservação da massa é uma ocorrência comum: quando uma partícula elementar instável decai espontaneamente em duas partículas mais leves, a energia total é conservada, mas a massa não. Parte da massa é convertida em energia cinética.
Escolha dos referenciais
A liberdade de escolher qualquer quadro no qual realizar uma análise permite-nos escolher aquele que pode ser particularmente conveniente. Para análise de problemas de momento e energia, o referencial mais conveniente é geralmente o "referencial do centro do momento" (também chamado de quadro de momento zero ou quadro COM). Este é o referencial no qual a componente espacial do momento total do sistema é zero. A Fig. 3-11 ilustra a divisão de uma partícula de alta velocidade em duas partículas filhas. No quadro do laboratório, as partículas filhas são emitidas preferencialmente em uma direção orientada ao longo da trajetória da partícula original. No referencial COM, entretanto, as duas partículas filhas são emitidas em direções opostas, embora suas massas e a magnitude de suas velocidades geralmente não sejam as mesmas.
Conservação de energia e momento
Em uma análise Newtoniana de partículas interagindo, a transformação entre quadros é simples porque tudo o que é necessário é aplicar a transformação Galileia a todas as velocidades. Desde então , o impulso . Se o impulso total de um sistema interagindo de partículas é observado para ser conservado em um quadro, ele também será observado para ser conservado em qualquer outro quadro.
A conservação do ímpeto no quadro COM equivale à exigência de p= 0 antes e depois da colisão. Na análise Newtoniana, a conservação da massa dita que . Nos cenários simplificados e unidimensionais que temos pensado, apenas uma restrição adicional é necessária antes que o momento de saída das partículas possa ser determinado - uma condição de energia. No caso unidimensional de uma colisão completamente elástica sem perda de energia cinética, as velocidades de saída das partículas de rebote no quadro COM serão precisamente iguais e opostas às suas velocidades de entrada. No caso de uma colisão completamente inelástica com perda total de energia cinética, as velocidades de saída das partículas de rebote serão zero.
momenta newtoniana, calculada como , não se comportar corretamente sob a transformação Lorentzian. A transformação linear das velocidades é substituído pelo altamente não linear para que um cálculo que demonstra a conservação do impulso em um quadro será inválido em outros quadros. Einstein foi confrontado com ter que abandonar a conservação do ímpeto, ou mudar a definição de impulso. Esta segunda opção foi o que ele escolheu.
A lei relativística de conservação de energia e momento substitui as três leis clássicas de conservação de energia, momento e massa. A massa não é mais conservada de forma independente, porque foi incluída na energia relativística total. Isto torna a conservação relativística da energia um conceito mais simples do que na mecânica não relativística, porque a energia total é conservada sem quaisquer qualificações. A energia cinética convertida em calor ou energia potencial interna aparece como um aumento na massa.
D- Sim.
→ μ− + Proc?
Fig. 3-12a ilustra o diagrama de energia-momentum para esta reação de decadência no resto do quadro do pion. Por causa de sua massa negligível, um neutrino viaja em quase a velocidade da luz. A expressão relativista de sua energia, como a do fóton, é que é também o valor do componente espacial do seu impulso. Para conservar o impulso, o muon tem o mesmo valor do componente espacial do impulso do neutrino, mas na direção oposta.
Análises algébricas das enérgicas desta reação de decaimento estão disponíveis on-line, assim Fig. 3-12b apresenta em vez uma solução de calculadora de grafos. A energia do neutrino é 29.79 MeV, e a energia do muon é 33.91 MeV − 29.79 MeV = 4.12 MeV. A maior parte da energia é transportada pelo neutrino quase zero-massa.Além do básico
Os tópicos desta seção são de dificuldade técnica significativamente maior do que os das seções anteriores e não são essenciais para a compreensão da Introdução ao espaço-tempo curvo.
Rapidez
As transformações de Lorentz relacionam as coordenadas dos eventos em um referencial com as de outro referencial. A composição relativística de velocidades é usada para somar duas velocidades. As fórmulas para realizar estes últimos cálculos não são lineares, tornando-as mais complexas do que as fórmulas galileanas correspondentes.
Essa não linearidade é um artefato da nossa escolha de parâmetros. Observamos anteriormente que em um diagrama de espaço-tempo x–ct, os pontos em algum intervalo constante de espaço-tempo a partir da origem formam uma hipérbole invariante. Observamos também que os sistemas de coordenadas de dois referenciais do espaço-tempo na configuração padrão são girados hiperbolicamente um em relação ao outro.
As funções naturais para expressar essas relações são os análogos hiperbólicos das funções trigonométricas. A Fig. 4-1a mostra um círculo unitário com sen(a) e cos(a), a única diferença entre este diagrama e o círculo unitário familiar da trigonometria elementar é que a é interpretado, não como o ângulo entre o raio e o x-eixo, mas como o dobro da área do setor varrido pelo raio do xeixo. (Numericamente, as medidas de ângulo e 2 × área para o círculo unitário são idênticas.) A Fig. 4-1b mostra uma hipérbole unitária com sinh(a) e cosh(a), onde a também é interpretado como o dobro da área colorida. A Figura 4-2 apresenta gráficos das funções sinh, cosh e tanh.
Para o círculo unitário, a inclinação do raio é dada por
No plano cartesiano, rotação do ponto (x, y) no ponto (x, y) no ponto (x', y') pelo ângulo θ é dado por
Em um diagrama de espaço-tempo, o parâmetro de velocidade é o analógico de inclinação. O rapidez, φ, é definido por
onde
A rapidez definida acima é muito útil na relatividade especial, porque muitas expressões assumem uma forma consideravelmente mais simples quando expressas em termos dela. Por exemplo, a rapidez é simplesmente aditiva na fórmula de adição de velocidade colinear;
ou em outras palavras,
As transformações de Lorentz assumem uma forma simples quando expressas em termos de rapidez. O fator γ pode ser escrito como
As transformações que descrevem o movimento relativo com velocidade uniforme e sem rotação dos eixos de coordenadas espaciais são chamadas de impulsos.
Substituindo γ e γβ nas transformações apresentadas anteriormente e reescrevendo em forma de matriz, o impulso de Lorentz no x -direção pode ser escrito como
e o aumento inverso de Lorentz na direção x pode ser escrito como
Em outras palavras, os impulsos de Lorentz representam rotações hiperbólicas no espaço-tempo de Minkowski.
As vantagens do uso de funções hiperbólicas são tantas que alguns livros didáticos, como os clássicos de Taylor e Wheeler, introduzem seu uso desde muito cedo.
4 vetores
Quatro vetores foram mencionados acima no contexto do 4-vetor de energia-momentum, mas sem grande ênfase. Na verdade, nenhuma das derivações elementares da relatividade especial as exige. Mas, uma vez compreendidos, os 4 vetores e, de forma mais geral, os tensores, simplificam enormemente a matemática e a compreensão conceitual da relatividade especial. Trabalhar exclusivamente com tais objetos leva a fórmulas que são manifestamente relativisticamente invariantes, o que é uma vantagem considerável em contextos não triviais. Por exemplo, demonstrar a invariância relativística das equações de Maxwell em sua forma usual não é trivial, embora seja apenas um cálculo de rotina (na verdade, não mais do que uma observação) usando a formulação do tensor de intensidade de campo. Por outro lado, a relatividade geral, desde o início, depende fortemente de 4 vetores e, mais geralmente, de tensores, representando entidades fisicamente relevantes. Relacioná-los por meio de equações que não dependem de coordenadas específicas requer tensores, capazes de conectar tais 4‑vetores mesmo dentro de um espaço-tempo curvo, e não apenas dentro de um espaço-tempo curvo. um plano como na relatividade especial. O estudo de tensores está fora do escopo deste artigo, que fornece apenas uma discussão básica do espaço-tempo.
Definição de 4 vetores
Um 4-tuple, é um "4-vector" se seu componente AEu... transformar entre quadros de acordo com a transformação de Lorentz.
Se usar coordenadas, A é um 4 vencedor se ele se transformar (no x-direção) segundo
que vem simplesmente substituindo ct por A0 e x por A1 na apresentação anterior da transformação de Lorentz.
Como sempre, quando escrevemos x, t, etc. geralmente queremos dizer Δx, Δt etc..
Os últimos três componentes de um 4 vencedor deve ser um vetor padrão no espaço tridimensional. Portanto, um 4 vencedor deve transformar-se como sob transformações de Lorentz, bem como rotações.
Propriedades de 4 vetores
- Encerramento sob combinação linear: Se A e B são 4-vectores, então é também um 4-vector.
- Invariância de produto interno: Se A e B são 4-vectores, então seu produto interno (produto escalar) é invariante, ou seja, seu produto interno é independente do quadro em que é calculado. Note como o cálculo do produto interno difere do cálculo do produto interno de um 3-vector. No seguinte, e são 3-vectores:
- Além de ser invariante sob a transformação de Lorentz, o produto interno acima também é invariante sob rotação em 3-espaço.
- Dizem que dois vetores são ortogonal se Ao contrário do caso com 3 vencedores, ortogonal 4-vectores não estão necessariamente em ângulos certos uns com os outros. A regra é que dois 4-vectores são ortogonais se são compensados por ângulos iguais e opostos da linha de 45 ° que é a linha mundial de um raio leve. Isso implica que um leve 4-vector é ortogonal com em si mesmo.
- Invariância da magnitude de um vetor: A magnitude de um vetor é o produto interno de um 4-vector com si mesmo, e é uma propriedade independente de quadro. Como em intervalos, a magnitude pode ser positiva, negativa ou zero, de modo que os vetores são referidos como tempo, espaço ou nulo (leveira). Note que um vetor nulo não é o mesmo que um vetor zero. Um vetor nulo é um para o qual enquanto um vetor zero é um cujos componentes são todos zero. Casos especiais que ilustram a invariância da norma incluem o intervalo invariante e o comprimento invariante do vetor dinâmica relativista
Exemplos de 4 vetores
- Deslocamento 4-vector: Caso contrário conhecido como o separação espaço-tempoIsto é... (Δt, Δx, Δy, Δz), ou para separações infinitesimais, (Dt, dx, dy, dz).
- Velocity 4-vector: Isso resulta quando o deslocamento 4-vector é dividido por , onde é o momento adequado entre os dois eventos que produzem Dt, dx, dye D..
- O 4-velocidade é tangente à linha mundial de uma partícula, e tem um comprimento igual a uma unidade de tempo no quadro da partícula.
- Uma partícula acelerada não tem um quadro inercial no qual está sempre em repouso. No entanto, um quadro inercial sempre pode ser encontrado que é momentaneamente comoving com a partícula. Este quadro, o momentaneamente comoving frame de referência (MCRF), permite a aplicação da relatividade especial à análise de partículas aceleradas.
- Desde que os fótons se movem em linhas nulas, para um fóton, e um 4-velocidade não pode ser definido. Não há nenhum quadro em que um fóton está em repouso, e nenhum MCRF pode ser estabelecido ao longo do caminho de um fóton.
- Energia-momento 4-vector:
- Como indicado anteriormente, existem diferentes tratamentos para o movimento de energia 4-vector para que se veja também expresso como ou O primeiro componente é a energia total (incluindo massa) da partícula (ou sistema de partículas) em um dado quadro, enquanto os componentes restantes são o seu impulso espacial. A energia-momento 4-vector é uma quantidade conservada.
- Aceleração 4-vetor: Isso resulta de tomar o derivado da velocidade 4-vector com respeito a
- Força 4-vector: Este é o derivado do momentum 4-vector com respeito a
Como esperado, os componentes finais dos 4 vetores acima são todos 3 vetores correspondentes ao 3-momento, 3-força etc.
4-vetores e leis físicas
O primeiro postulado da relatividade especial declara a equivalência de todos os referenciais inerciais. Uma lei física válida em um referencial deve ser aplicada em todos os referenciais, caso contrário seria possível diferenciar os referenciais. Os momentos newtonianos não se comportam adequadamente sob a transformação Lorentziana, e Einstein preferiu mudar a definição de momento para uma que envolva 4 vetores em vez de desistir da conservação do momento.
As leis físicas devem ser baseadas em construções independentes de estrutura. Isso significa que as leis físicas podem assumir a forma de equações que conectam escalares, que são sempre independentes de referencial. No entanto, equações envolvendo 4 vetores requerem o uso de tensores com classificação apropriada, que podem ser considerados como sendo construídos a partir de 4 vetores .
Aceleração
É um equívoco comum pensar que a relatividade especial é aplicável apenas a referenciais inerciais e que é incapaz de lidar com objetos em aceleração ou referenciais em aceleração. Na verdade, objetos em aceleração geralmente podem ser analisados sem a necessidade de lidar com quadros acelerados. Somente quando a gravitação é significativa é que a relatividade geral é necessária.
No entanto, o manuseio adequado de quadros de aceleração requer alguns cuidados. A diferença entre a relatividade especial e a geral é que (1) Na relatividade especial, todas as velocidades são relativas, mas a aceleração é absoluta. (2) Na relatividade geral, todo movimento é relativo, seja inercial, acelerado ou giratório. Para acomodar esta diferença, a relatividade geral utiliza o espaço-tempo curvo.
Nesta seção, analisamos diversos cenários envolvendo referenciais acelerados.
Paradoxo da nave espacial Dewan–Beran–Bell
O paradoxo da nave espacial Dewan-Beran-Bell (paradoxo da nave espacial de Bell) é um bom exemplo de um problema em que o raciocínio intuitivo sem a ajuda da visão geométrica da abordagem do espaço-tempo pode levar a problemas.

Na Figura 4-4, duas naves espaciais idênticas flutuam no espaço e estão em repouso uma em relação à outra. Eles são conectados por uma corda que é capaz de esticar apenas uma quantidade limitada antes de quebrar. Num dado instante no nosso referencial, o referencial do observador, ambas as naves espaciais aceleram na mesma direção ao longo da linha entre elas com a mesma aceleração constante própria. A corda vai quebrar?
Quando o paradoxo era novo e relativamente desconhecido, até mesmo os físicos profissionais tiveram dificuldade em encontrar a solução. Duas linhas de raciocínio levam a conclusões opostas. Ambos os argumentos, apresentados a seguir, são falhos, embora um deles produza a resposta correta.
- Para os observadores no resto do quadro, as naves espaciais começam uma distância L separados e permanecer a mesma distância distante durante a aceleração. Durante a aceleração, L é uma distância contraída de comprimento da distância L' γL no quadro das naves espaciais acelerantes. Depois de um tempo suficientemente longo, γ aumentará para um fator suficientemente grande que a cadeia deve quebrar.
- Vamos. A e B ser as naves traseiras e frontais. No quadro das naves espaciais, cada nave espacial vê a outra nave espacial fazendo a mesma coisa que está fazendo. A diz que B tem a mesma aceleração que ele tem, e B vê que A combina com ela cada movimento. Assim, as naves espaciais permanecem a mesma distância separada, e a cadeia não quebra.
O problema com o primeiro argumento é que não existe uma "estrutura das naves espaciais." Não pode haver, porque as duas naves espaciais medem uma distância crescente entre as duas. Como não existe uma estrutura comum das naves espaciais, o comprimento da corda é mal definido. No entanto, a conclusão está correta e o argumento está principalmente correto. O segundo argumento, contudo, ignora completamente a relatividade da simultaneidade.
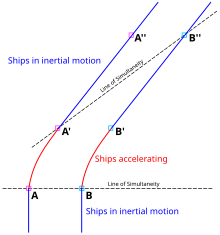
Um diagrama espacial (Fig. 4-5) torna a solução correta para este paradoxo quase imediatamente evidente. Dois observadores no espaço-tempo de Minkowski aceleram com magnitude constante aceleração para o tempo adequado (aceleração e tempo decorrido medido pelos próprios observadores, não algum observador inercial). São comoventes e inerciais antes e depois desta fase. Na geometria de Minkowski, o comprimento ao longo da linha de simultaneidade resulta ser maior do que o comprimento ao longo da linha de simultaneidade .
O aumento de comprimento pode ser calculado com a ajuda da transformação de Lorentz. Se, como ilustrado na Fig. 4-5, a aceleração for concluída, os navios permanecerão em um deslocamento constante em algum quadro Se e são as posições dos navios as posições no quadro são:
O "paradoxo", como era, vem da maneira que Bell construiu seu exemplo. Na discussão habitual da contração de Lorentz, o comprimento do resto é fixo e o comprimento de movimento encurta como medido no quadro . Como mostrado na Fig. 4-5, o exemplo de Bell afirma os comprimentos em movimento e medido em quadro para ser fixado, forçando assim o comprimento do quadro de descanso em moldura para aumentar.
Observador acelerado com horizonte
Certas configurações de problemas da relatividade especial podem levar a insights sobre fenômenos normalmente associados à relatividade geral, como horizontes de eventos. No texto que acompanha a Figura 2-7, as hipérboles magenta representavam caminhos reais que são rastreados por um viajante em constante aceleração no espaço-tempo. Durante períodos de aceleração positiva, a velocidade do viajante apenas se aproxima da velocidade da luz, enquanto, medida no nosso referencial, a aceleração do viajante diminui constantemente.
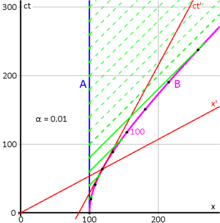
Fig. 4-6 detalhes várias características do movimento do viajante com mais especificidade. Em qualquer momento, seu eixo espacial é formado por uma linha que passa pela origem e sua posição atual na hiperbola, enquanto seu eixo do tempo é o tangente para a hiperbola em sua posição. O parâmetro velocidade aproxima um limite de um como aumentos. Igualmente. aproxima-se do infinito.
A forma da hipérbole invariante corresponde a um caminho de aceleração própria constante. Isto é demonstrável da seguinte forma:
- Lembramos que
- Desde então nós concluímos que
- Da lei relativa da força,
- Substituto da etapa 2 e da expressão para da etapa 3 rendimentos que é uma expressão constante.
Fig. 4-6 ilustra um cenário calculado específico. Terence (A) e Stella (B) inicialmente ficam juntos a 100 horas-luz da origem. Stella decola no tempo 0, sua espaçonave acelerando a 0,01 c por hora. A cada vinte horas, Terence transmite atualizações por rádio para Stella sobre a situação em casa (linhas verdes contínuas). Stella recebe essas transmissões regulares, mas a distância crescente (compensada em parte pela dilatação do tempo) faz com que ela receba as comunicações de Terence cada vez mais tarde, conforme medido em seu relógio, e ela nunca recebe nenhuma comunicação. de Terence após 100 horas em seu relógio (linhas verdes tracejadas).
Depois de 100 horas de acordo com o relógio de Terence, Stella entra em uma região escura. Ela viajou para fora do futuro temporal de Terence. Por outro lado, Terence pode continuar a receber mensagens de Stella para ele indefinidamente. Ele só tem que esperar o suficiente. O espaço-tempo foi dividido em regiões distintas separadas por um horizonte de eventos aparente. Enquanto Stella continuar a acelerar, ela nunca poderá saber o que acontece por trás desse horizonte.
Introdução ao espaço-tempo curvo
Proposições básicas
As teorias de Newton presumiam que o movimento ocorre contra o pano de fundo de um quadro de referência euclidiano rígido que se estende por todo o espaço e por todo o tempo. A gravidade é mediada por uma força misteriosa, agindo instantaneamente à distância, cujas ações são independentes do espaço intermediário. Em contraste, Einstein negou que existisse qualquer referencial euclidiano de fundo que se estendesse por todo o espaço. Nem existe força gravitacional, apenas a própria estrutura do espaço-tempo.
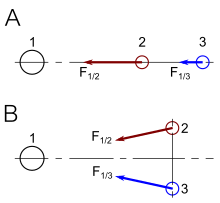
Em termos de espaço-tempo, a trajetória de um satélite que orbita a Terra não é ditada pelas influências distantes da Terra, da Lua e do Sol. Em vez disso, o satélite move-se através do espaço apenas em resposta às condições locais. Como o espaço-tempo é localmente plano em todos os lugares quando considerado em uma escala suficientemente pequena, o satélite segue sempre uma linha reta em seu referencial inercial local. Dizemos que o satélite segue sempre a trajetória de uma geodésica. Nenhuma evidência de gravitação pode ser descoberta acompanhando os movimentos de uma única partícula.
Em qualquer análise do espaço-tempo, a evidência da gravitação requer que se observem as acelerações relativas de dois corpos ou duas partículas separadas. Na Fig. 5-1, duas partículas separadas, em queda livre no campo gravitacional da Terra, exibem acelerações de maré devido a heterogeneidades locais no campo gravitacional, de modo que cada partícula segue um caminho diferente através do espaço-tempo. As acelerações das marés que estas partículas exibem umas em relação às outras não requerem forças para serem explicadas. Em vez disso, Einstein os descreveu em termos da geometria do espaço-tempo, ou seja, da curvatura do espaço-tempo. Estas acelerações das marés são estritamente locais. É o efeito cumulativo total de muitas manifestações locais de curvatura que resultam no aparecimento de uma força gravitacional agindo a uma longa distância da Terra.
Duas proposições centrais fundamentam a relatividade geral.
- O primeiro conceito crucial é coordenar a independência: As leis da física não podem depender do sistema de coordenadas que se usa. Esta é uma grande extensão do princípio da relatividade da versão usada em relatividade especial, que afirma que as leis da física devem ser as mesmas para cada observador que se move em quadros de referência não acelerados (inerciais). Na relatividade geral, para usar as próprias palavras de Einstein, "as leis da física devem ser de tal natureza que se aplicam a sistemas de referência em qualquer tipo de movimento". Isso leva a uma questão imediata: Em quadros acelerados, sentimos forças que aparentemente permitiriam avaliar o estado de aceleração em um sentido absoluto. Einstein resolveu este problema através do princípio da equivalência.

- O princípio da equivalência afirma que em qualquer região suficientemente pequena do espaço, os efeitos da gravitação são os mesmos que os da aceleração.
- Na Fig. 5-2, pessoa A está em uma nave espacial, longe de qualquer objeto maciço, que sofre uma aceleração uniforme de g. Pessoa B está numa caixa a descansar na Terra. Desde que a nave espacial seja suficientemente pequena para que os efeitos de maré não sejam mensuráveis (dadada a sensibilidade da instrumentação de medição de gravidade atual, A e B devem ser presumivelmente Lilliputians), não há experimentos que A e B podem executar que lhes permitirão contar em que configuração estão.
- Uma expressão alternativa do princípio da equivalência é observar que na lei universal de Newton da gravitação, F = GMmg/2 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = mgg e na segunda lei de Newton, F = mEu...um, não há a priori razão pela qual a massa gravitacional mg deve ser igual à massa inercial mEu.... O princípio da equivalência afirma que essas duas massas são idênticas.
Para ir da descrição elementar acima do espaço-tempo curvo até uma descrição completa da gravitação, é necessário cálculo tensorial e geometria diferencial, tópicos que requerem um estudo considerável. Sem estas ferramentas matemáticas, é possível escrever sobre a relatividade geral, mas não é possível demonstrar quaisquer derivações não triviais.
Curvatura do tempo
Na discussão da relatividade especial, as forças desempenharam apenas um papel secundário. A relatividade especial pressupõe a capacidade de definir referenciais inerciais que preenchem todo o espaço-tempo, cujos relógios funcionam na mesma velocidade que o relógio na origem. Isso é realmente possível? Num campo gravitacional não uniforme, a experiência determina que a resposta é não. Os campos gravitacionais tornam impossível a construção de um referencial inercial global. Em regiões suficientemente pequenas do espaço-tempo, referenciais inerciais locais ainda são possíveis. A relatividade geral envolve a união sistemática desses quadros locais em uma imagem mais geral do espaço-tempo.
Anos antes da publicação da teoria geral em 1916, Einstein usou o princípio de equivalência para prever a existência de redshift gravitacional no seguinte experimento de pensamento: (i) Assumir que uma torre de altura h (Fig. 5-3) foi construído. (ii) Solte uma partícula de massa de repouso m do topo da torre. Cai livremente com aceleração g, atingindo o chão com velocidade v (2Não.)1/2-2001, para que a sua energia total E, como medida por um observador no terreno, é (iii) Um conversor de energia em massa transforma a energia total da partícula em um único fóton de alta energia, que direciona para cima. (iv) No topo da torre, um conversor de massa energética transforma a energia do fóton E' voltar para uma partícula de massa de descanso m'.
Deve ser que m = m', pois caso contrário seria possível construir um dispositivo de movimento perpétuo. Portanto, prevemos que E' = m, de modo que
Um fóton subindo no campo gravitacional da Terra perde energia e sofre desvio para o vermelho. As primeiras tentativas de medir esse desvio para o vermelho através de observações astronômicas foram um tanto inconclusivas, mas observações laboratoriais definitivas foram realizadas por Pound & Rebka (1959) e mais tarde por Pound & Snider (1964).
A luz tem uma frequência associada, e essa frequência pode ser usada para controlar o funcionamento de um relógio. O desvio para o vermelho gravitacional leva a uma conclusão importante sobre o próprio tempo: a gravidade faz o tempo correr mais devagar. Suponha que construímos dois relógios idênticos cujas taxas são controladas por alguma transição atômica estável. Coloque um relógio no topo da torre, enquanto o outro permanece no chão. Um experimentador no topo da torre observa que os sinais do relógio de solo têm frequência mais baixa do que os do relógio próximo a ela na torre. A luz que sobe na torre é apenas uma onda, e é impossível que as cristas das ondas desapareçam durante a subida. Exatamente tantas oscilações de luz chegam ao topo da torre quantas foram emitidas na parte inferior. O experimentador conclui que o relógio de solo está lento e pode confirmar isso abaixando o relógio da torre para compará-lo lado a lado com o relógio de solo. Para uma torre de 1 km, a discrepância seria de cerca de 9,4 nanossegundos por dia, facilmente mensurável com instrumentação moderna.
Nem todos os relógios em um campo gravitacional funcionam na mesma velocidade. Experimentos como o experimento Pound-Rebka estabeleceram firmemente a curvatura do componente temporal do espaço-tempo. O experimento Pound-Rebka não diz nada sobre a curvatura do componente espaço do espaço-tempo. Mas os argumentos teóricos que prevêem a dilatação do tempo gravitacional não dependem de forma alguma dos detalhes da relatividade geral. Qualquer teoria da gravidade irá prever a dilatação do tempo gravitacional se respeitar o princípio da equivalência. Isso inclui a gravitação newtoniana. Uma demonstração padrão na relatividade geral é mostrar como, no "limite newtoniano" (ou seja, as partículas estão se movendo lentamente, o campo gravitacional é fraco e o campo é estático), a curvatura do tempo por si só é suficiente para derivar a lei da gravidade de Newton.
A gravitação newtoniana é uma teoria do tempo curvo. A relatividade geral é uma teoria do tempo curvo e do espaço curvo. Dado G como a constante gravitacional, M como a massa de uma estrela newtoniana, e orbitando corpos de massa insignificante a uma distância r da estrela, o intervalo de espaço-tempo para a gravitação newtoniana é aquele para o qual apenas o coeficiente de tempo é variável:
Curvatura do espaço
O coeficiente na frente de descreve a curvatura do tempo na gravitação Newtoniana, e esta curvatura responde completamente por todos os efeitos gravitacionais Newtonianos. Como esperado, este fator de correção é diretamente proporcional ao e e por causa do no denominador, o fator de correção aumenta à medida que se aproxima do corpo gravitante, o que significa que o tempo é curvado.
Mas a relatividade geral é uma teoria do espaço curvo e do tempo curvo, portanto, se existem termos que modificam os componentes espaciais do intervalo de espaço-tempo apresentado acima, seus efeitos não deveriam ser vistos em, digamos, órbitas planetárias e de satélite devido a fatores de correção de curvatura aplicados aos termos espaciais?
A resposta é que eles são visto, mas os efeitos são minúsculos. A razão é que as velocidades planetárias são extremamente pequenas em comparação com a velocidade da luz, de modo que para planetas e satélites do sistema solar, o termo anões os termos espaciais.
Apesar da minúcia dos termos espaciais, os primeiros indícios de que algo estava errado com a gravitação newtoniana foram descobertos há mais de um século e meio. Em 1859, Urbain Le Verrier, numa análise das observações cronometradas disponíveis dos trânsitos de Mercúrio sobre o disco solar de 1697 a 1848, relatou que a física conhecida não poderia explicar a órbita de Mercúrio, a menos que existisse possivelmente um planeta ou cinturão de asteróides dentro da órbita de Mercúrio. O periélio da órbita de Mercúrio exibiu uma taxa de precessão excessiva acima daquela que poderia ser explicada pelos puxões dos outros planetas. A capacidade de detectar e medir com precisão o valor minuto desta precessão anômala (apenas 43 segundos de arco por século tropical) é um testemunho da sofisticação da astrometria do século XIX.

Como o famoso astrônomo que já havia descoberto a existência de Netuno "na ponta da caneta" ao analisar oscilações na órbita de Urano, o anúncio de Le Verrier desencadeou um longo período de duas décadas de “mania vulcana”, enquanto astrónomos profissionais e amadores procuravam o hipotético novo planeta. Esta busca incluiu vários avistamentos falsos de Vulcano. Em última análise, foi estabelecido que tal planeta ou cinturão de asteróides não existia.
Em 1916, Einstein iria mostrar que esta precessão anómala de Mercúrio é explicada pelos termos espaciais da curvatura do espaço-tempo. A curvatura no termo temporal, sendo simplesmente uma expressão da gravitação newtoniana, não tem nenhum papel na explicação desta precessão anômala. O sucesso do seu cálculo foi uma indicação poderosa para os pares de Einstein de que a teoria geral da relatividade poderia estar correta.
A mais espectacular das previsões de Einstein foi o seu cálculo de que os termos de curvatura nas componentes espaciais do intervalo de espaço-tempo poderiam ser medidos na curvatura da luz em torno de um corpo massivo. A luz tem uma inclinação de ±1 em um diagrama de espaço-tempo. Seu movimento no espaço é igual ao seu movimento no tempo. Para a expressão de campo fraco do intervalo invariante, Einstein calculou uma curvatura de sinal exatamente igual, mas oposta, em seus componentes espaciais.
Na gravitação de Newton, o coeficiente na frente de prediz a flexão da luz em torno de uma estrela. Na relatividade geral, a coeficiente na frente de prevê um duplicar da curvatura total.
A história da expedição do eclipse de Eddington em 1919 e da ascensão de Einstein à fama é bem contada em outros lugares.
Fontes da curvatura do espaço-tempo

Na teoria da gravitação de Newton, a única fonte de força gravitacional é a massa.
Em contraste, a relatividade geral identifica várias fontes de curvatura espaço-tempo além da massa. Nas equações de campo de Einstein, as fontes de gravidade são apresentadas no lado direito em o tensor stress-energia.
Fig. 5-5 classifica as várias fontes de gravidade no tensor tensão-energia:
- (vermelho): A densidade de massa-energia total, incluindo quaisquer contribuições para a energia potencial de forças entre as partículas, bem como a energia cinética de movimentos térmicos aleatórios.
- e (laranja) São termos de densidade dinâmica. Mesmo que não haja movimento em massa, a energia pode ser transmitida por condução térmica, e a energia conduzida carregará impulso.
- são as taxas de fluxo do Eu...- Componente de momentum por unidade de área JJ-direção. Mesmo que não haja movimento a granel, movimentos térmicos aleatórios das partículas darão origem ao fluxo de ímpeto, então o Eu... = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = JJ termos (verde) representam pressão isotrópica, e o Eu... ≠ JJ termos (azul) representam tensão de cisalhamento.
Uma conclusão importante a ser derivada das equações é que, coloquialmente falando, gravidade em si cria gravidade. A energia tem massa. Mesmo em gravidade newtoniana, o campo gravitacional está associado a uma energia, chamada de energia potencial gravitacional. Na relatividade geral, a energia do campo gravitacional se alimenta de volta à criação do campo gravitacional. Isso torna as equações não lineares e difíceis de resolver em qualquer outra coisa além de casos de campo fracos. A relatividade numérica é um ramo da relatividade geral usando métodos numéricos para resolver e analisar problemas, muitas vezes empregando supercomputadores para estudar buracos negros, ondas gravitacionais, estrelas de nêutrons e outros fenômenos no forte regime de campo.
Momento energético
Na relatividade especial, a energia da massa está intimamente ligada ao momento. Assim como o espaço e o tempo são aspectos diferentes de uma entidade mais abrangente chamada espaço-tempo, a massa-energia e o momento são apenas aspectos diferentes de uma quantidade unificada e quadridimensional chamada de quatro momentos. Consequentemente, se massa-energia é uma fonte de gravidade, o momento também deve ser uma fonte. A inclusão do momento como fonte de gravidade leva à previsão de que massas em movimento ou rotação podem gerar campos análogos aos campos magnéticos gerados por cargas em movimento, um fenômeno conhecido como gravitomagnetismo.

Sabe-se bem que a força do magnetismo pode ser deduzida aplicando as regras da relatividade especial às cargas em movimento. (Uma demonstração eloquente disto foi apresentada por Feynman no volume II, capítulo 13–6 de seu Palestras sobre Física, disponível online.) A lógica análoga pode ser usada para demonstrar a origem do gravitomagnetismo. Na Fig. 5-7a, dois fluxos paralelos e infinitamente longos de partículas maciças têm velocidades iguais e opostas -v e +v relativa a uma partícula de teste em repouso e centrada entre os dois. Por causa da simetria da configuração, a força líquida na A partícula central é zero. Assumir para que as velocidades sejam simplesmente aditivas. Fig. 5-7b mostra exatamente a mesma configuração, mas no quadro do fluxo superior. A partícula de teste tem uma velocidade de +v, e o fluxo inferior tem uma velocidade de +2v. Uma vez que a situação física não mudou, apenas o quadro em que as coisas são observadas, a partícula de teste não deve ser atraída para qualquer fluxo. Mas não é absolutamente claro que as forças exercidas na partícula de teste são iguais. (1) Uma vez que o fluxo inferior está se movendo mais rápido do que o topo, cada partícula no fluxo inferior tem uma maior energia em massa do que uma partícula no topo. (2) Por causa da contração de Lorentz, há mais partículas por comprimento da unidade no fluxo inferior do que no fluxo superior. (3) Outra contribuição para a massa gravitacional ativa do fluxo inferior vem de um termo de pressão adicional que, neste momento, não temos formação suficiente para discutir. Todos esses efeitos juntos aparentemente exigiriam que a partícula de teste fosse desenhada para o fluxo inferior.
A partícula de teste não é atraída para a corrente de fundo por causa de uma força dependente da velocidade que serve para repelir uma partícula que está se movendo na mesma direção da corrente de fundo. Essa força gravitacional dependente da velocidade efeito é o gravitomagnetismo.
A matéria em movimento através de um campo gravitomagnético está, portanto, sujeita aos chamados efeitos de arrastamento de quadro, análogos à indução eletromagnética. Foi proposto que tais forças gravitomagnéticas estão subjacentes à geração dos jatos relativísticos (Fig. 5-8) ejetados por alguns buracos negros supermassivos em rotação.
Pressão e estresse
Quantidades que estão diretamente relacionadas à energia e ao momento também devem ser fontes de gravidade, ou seja, pressão interna e estresse. Juntos, massa-energia, momento, pressão e tensão servem como fontes de gravidade: coletivamente, são o que diz ao espaço-tempo como se curvar.
A relatividade geral prevê que a pressão atua como uma fonte gravitacional com exatamente a mesma força que a densidade massa-energia. A inclusão da pressão como fonte de gravidade leva a diferenças dramáticas entre as previsões da relatividade geral e as da gravitação newtoniana. Por exemplo, o termo pressão estabelece um limite máximo para a massa de uma estrela de nêutrons. Quanto mais massiva for uma estrela de nêutrons, maior será a pressão necessária para suportar seu peso contra a gravidade. O aumento da pressão, no entanto, aumenta a acção da gravidade sobre a massa da estrela. Acima de uma certa massa determinada pelo limite de Tolman-Oppenheimer-Volkoff, o processo torna-se descontrolado e a estrela de nêutrons colapsa formando um buraco negro.
Os termos de tensão tornam-se altamente significativos ao realizar cálculos como simulações hidrodinâmicas de supernovas com colapso do núcleo.
Essas previsões para os papéis da pressão, do momento e do estresse como fontes da curvatura do espaço-tempo são elegantes e desempenham um papel importante na teoria. No que diz respeito à pressão, o universo primitivo era dominado pela radiação, e é altamente improvável que qualquer um dos dados cosmológicos relevantes (por exemplo, abundâncias de nucleossíntese, etc.) pudesse ser reproduzido se a pressão não contribuísse para a gravidade, ou se não tivesse o mesma força que uma fonte de gravidade que massa-energia. Da mesma forma, a consistência matemática das equações de campo de Einstein seria quebrada se os termos de tensão não contribuíssem como fonte de gravidade.
Teste experimental das fontes da curvatura do espaço-tempo
Definições: massa ativa, passiva e inercial
Bondi distingue entre diferentes tipos possíveis de massa: (1) massa ativa () é a massa que age como o fonte de um campo gravitacional; (2)massa passiva () é a massa que reage a um campo gravitacional; (3) massa inercial () é a massa que reage à aceleração.
- é o mesmo que massa gravitacional () na discussão do princípio da equivalência.
Na teoria newtoniana,
- A terceira lei de ação e reação dita que e deve ser o mesmo.
- Por outro lado, se e são iguais é um resultado empírico.
Na relatividade geral,
- A igualdade de oportunidades e é ditado pelo princípio da equivalência.
- Não há princípio de "ação e reação" ditando qualquer relação necessária entre e .
Pressão como fonte gravitacional
O experimento clássico para medir a força de uma fonte gravitacional (ou seja, sua massa ativa) foi conduzido pela primeira vez em 1797 por Henry Cavendish (Fig. 5-9a). Duas bolas pequenas, mas densas, estão suspensas em um fio fino, formando um equilíbrio de torção. Aproximar duas grandes massas de teste das esferas introduz um torque detectável. Dadas as dimensões do aparelho e a constante mensurável da mola do fio de torção, a constante gravitacional G pode ser determinada.
Estudar os efeitos da pressão comprimindo as massas de teste é inútil, porque as pressões laboratoriais atingíveis são insignificantes em comparação com a energia-massa de uma bola de metal.
No entanto, as pressões eletromagnéticas repulsivas resultantes dos prótons fortemente comprimidos dentro dos núcleos atômicos são normalmente da ordem de 1028 atm ≈ 1033 Pa ≈ 10 33 kg·s−2m−1. Isso equivale a cerca de 1% da densidade de massa nuclear de aproximadamente 1018kg/m3 (após fatoração em c2 ≈ 9×10 16m2s−2).
Se a pressão não agir como fonte gravitacional, então a razão deve ser menor para núcleos com maior número atômico Z., em que as pressões eletrostáticas são maiores. L. B. Kreuzer (1968) fez um experimento Cavendish usando uma massa de Teflon suspenso em uma mistura do tricloroetileno líquido e dibromoetano tendo a mesma densidade buoyant que o Teflon (Fig. 5-9b). Fluorina tem número atômico Z. = 9, enquanto bromine tem Z. = 35. Kreuzer descobriu que reposicionar a massa Teflon não causou deflexão diferencial da barra de torção, portanto, estabelecendo massa ativa e massa passiva para ser equivalente a uma precisão de 5×10-5.
Embora Kreuzer tenha originalmente considerado este experimento apenas como um teste da razão entre massa ativa e massa passiva, Clifford Will (1976) reinterpretou o experimento como um teste fundamental do acoplamento de fontes a campos gravitacionais.
Em 1986, Bartlett e Van Buren notaram que o laser lunar detectou um deslocamento de 2 km entre o centro da figura da Lua e seu centro de massa. Isto indica uma assimetria na distribuição de Fe (abundante no núcleo da Lua) e Al (abundante em sua crosta e manto). Se a pressão não contribuísse igualmente para a curvatura do espaço-tempo como acontece com a massa-energia, a lua não estaria na órbita prevista pela mecânica clássica. Eles usaram suas medições para restringir os limites de quaisquer discrepâncias entre massa ativa e passiva para cerca de 10−12.
Gravitomagnetismo

A existência do gravitomagnetismo foi comprovada pela Gravity Probe B (GP-B), uma missão baseada em satélite lançada em 20 de abril de 2004. A fase do voo espacial durou até
Os resultados iniciais confirmaram o efeito geodésico relativamente grande (que se deve à simples curvatura do espaço-tempo e também é conhecido como precessão de Sitter) com uma precisão de cerca de 1%. O efeito de arrasto de quadro muito menor (que é devido ao gravitomagnetismo, e também é conhecido como precessão de Lense-Thirring) foi difícil de medir devido a efeitos de carga inesperados que causam desvio variável nos giroscópios. No entanto, em , o efeito de arrasto de quadros foi confirmado em 15% do resultado esperado, enquanto o efeito geodésico foi confirmado em melhor que 0,5%.
Medições subsequentes de arrastamento de quadros por observações de laser dos satélites LARES, LAGEOS-1 e LAGEOS-2 melhorou na medição GP-B, com resultados (a partir de 2016) demonstrando o efeito dentro de 5% de seu valor teórico, embora tenha havido alguma discordância sobre a precisão desta resultado.
Outro esforço, o experimento Giroscópios na Relatividade Geral (GINGER), busca usar três anéis de laser de 6 m montados em ângulos retos entre si, 1.400 m abaixo da superfície da Terra, para medir esse efeito.
Tópicos técnicos
O espaço-tempo é realmente curvo?
Na visão convencionalista de Poincaré, os critérios essenciais segundo os quais se deveria selecionar uma geometria euclidiana versus uma geometria não-euclidiana seriam a economia e a simplicidade. Um realista diria que Einstein descobriu que o espaço-tempo é não-euclidiano. Um convencionalista diria que Einstein simplesmente achou mais conveniente usar a geometria não-euclidiana. O convencionalista sustentaria que a análise de Einstein nada dizia sobre o que a geometria do espaço-tempo realmente é.
Dito isto,
- 1. É possível representar a relatividade geral em termos de espaço-tempo plano?
- 2. Existem situações em que uma interpretação plana do espaço-tempo da relatividade geral pode ser mais conveniente do que a interpretação de espaço-tempo curva habitual?
Em resposta à primeira pergunta, vários autores, incluindo Deser, Grishchuk, Rosen, Weinberg, etc., forneceram várias formulações da gravitação como um campo em uma variedade plana. Essas teorias são chamadas de “gravidade bimétrica”, a “abordagem teórica de campo da relatividade geral” e assim por diante. Kip Thorne forneceu uma revisão popular dessas teorias.
O paradigma do espaço-tempo plano postula que a matéria cria um campo gravitacional que faz com que as réguas encolham quando são viradas da orientação circunferencial para a radial, e isso faz com que a velocidade dos relógios se dilate. O paradigma do espaço-tempo plano é totalmente equivalente ao paradigma do espaço-tempo curvo, pois ambos representam os mesmos fenômenos físicos. No entanto, suas formulações matemáticas são totalmente diferentes. Os físicos em atividade alternam rotineiramente entre o uso de técnicas de espaço-tempo curvo e plano, dependendo dos requisitos do problema. O paradigma do espaço-tempo plano é conveniente ao realizar cálculos aproximados em campos fracos. Conseqüentemente, técnicas de espaço-tempo plano tendem a ser usadas na resolução de problemas de ondas gravitacionais, enquanto técnicas de espaço-tempo curvo tendem a ser usadas na análise de buracos negros.
Simetrias assintóticas
O grupo de simetria do espaço-tempo para a Relatividade Especial é o grupo de Poincaré, que é um grupo de dez dimensões de três impulsos de Lorentz, três rotações e quatro translações do espaço-tempo. É lógico perguntar quais simetrias, se houver alguma, podem ser aplicadas na Relatividade Geral. Um caso tratável poderia ser considerar as simetrias do espaço-tempo conforme visto por observadores localizados longe de todas as fontes do campo gravitacional. A expectativa ingênua de simetrias assintoticamente planas do espaço-tempo poderia ser simplesmente estender e reproduzir as simetrias do espaço-tempo plano da relatividade especial, viz., o grupo de Poincaré.
Em 1962, Hermann Bondi, M. G. van der Burg, A. W. Metzner e Rainer K. Sachs abordaram este problema de simetria assintótica para investigar o fluxo de energia no infinito devido à propagação de ondas gravitacionais. O primeiro passo foi decidir sobre algumas condições de contorno fisicamente sensíveis para colocar no campo gravitacional no infinito semelhante à luz para caracterizar o que significa dizer que uma métrica é assintoticamente plana, sem fazer suposições a priori sobre a natureza da métrica. o grupo de simetria assintótica – nem mesmo a suposição de que tal grupo exista. Então, depois de projetar o que consideraram ser as condições de contorno mais sensíveis, eles investigaram a natureza das transformações de simetria assintóticas resultantes que deixam invariante a forma das condições de contorno apropriadas para campos gravitacionais assintoticamente planos. O que eles descobriram foi que as transformações de simetria assintóticas realmente formam um grupo e a estrutura deste grupo não depende do campo gravitacional particular que esteja presente. Isto significa que, como esperado, pode-se separar a cinemática do espaço-tempo da dinâmica do campo gravitacional pelo menos no infinito espacial. A surpresa intrigante em 1962 foi a descoberta de um grupo rico de dimensão infinita (o chamado grupo BMS) como o grupo de simetria assintótica, em vez do grupo Poincaré de dimensão finita, que é um subgrupo do grupo BMS. As transformações de Lorentz não são apenas transformações de simetria assintóticas, mas também há transformações adicionais que não são transformações de Lorentz, mas são transformações de simetria assintóticas. Na verdade, eles encontraram uma infinidade adicional de geradores de transformação conhecidos como supertraduções. Isto implica a conclusão de que a Relatividade Geral (RG) não se reduz à relatividade especial no caso de campos fracos a longas distâncias.
Geometria Riemanniana
A geometria riemanniana é o ramo da geometria diferencial que estuda os coletores Riemannianos, definidos como coletores lisos com um métrica de Riemann (um produto interno no espaço tangente em cada ponto que varia suavemente de ponto a ponto). Isso dá, em particular, noções locais de ângulo, comprimento de curvas, área de superfície e volume. A partir desses, algumas outras quantidades globais podem ser derivadas através da integração de contribuições locais.
A geometria riemanniana originou-se com a visão de Bernhard Riemann expressa em sua palestra inaugural "Ueber die Hypothesen, welche der Geometrie zu Grunde liegen" ("Sobre as hipóteses em que a geometria é baseada"). É uma generalização muito ampla e abstrata da geometria diferencial de superfícies em R3. O desenvolvimento da geometria riemanniana resultou na síntese de diversos resultados relativos à geometria das superfícies e ao comportamento da geodésica sobre elas, com técnicas que podem ser aplicadas ao estudo de diferentes variedades de dimensões mais altas. Ele permitiu a formulação da teoria geral da relatividade de Einstein, fez um profundo impacto na teoria dos grupos e na teoria da representação, bem como a análise, e estimulou o desenvolvimento da topologia algébrica e diferencial.
Variedades curvas
Por razões físicas, um continuum espaço-tempo é matematicamente definido como um coletor de quatro dimensões, suave e conectado Lorentzian . Isto significa a métrica suave Lorentz tem assinatura . A métrica determina o geometria do espaço-tempo, bem como determinar a geodésica de partículas e feixes de luz. Sobre cada ponto (evento) neste coletor, tabelas de coordenadas são usadas para representar observadores em quadros de referência. Normalmente, as coordenadas cartesianas são usados. Além disso, para a simplicidade, as unidades de medição são geralmente escolhidas de modo que a velocidade da luz é igual a 1.
Um quadro de referência (observador) pode ser identificado com um desses gráficos de coordenadas; qualquer observador pode descrever qualquer evento . Outro quadro de referência pode ser identificado por um segundo gráfico de coordenadas sobre . Dois observadores (um em cada quadro de referência) podem descrever o mesmo evento mas obter descrições diferentes.
Normalmente, muitos gráficos de coordenadas sobrepostas são necessários para cobrir um coletor. Dado dois gráficos de coordenadas, um contendo (representando um observador) e outro contendo (representando outro observador), a interseção dos gráficos representa a região do espaço-tempo em que ambos os observadores podem medir quantidades físicas e, portanto, comparar resultados. A relação entre os dois conjuntos de medidas é dada por uma transformação não-singular coordenada nesta interseção. A ideia de coordenar gráficos como observadores locais que podem realizar medições em suas proximidades também faz bom senso físico, pois é assim que se coleta dados físicos – localmente.
Por exemplo, dois observadores, um dos quais está na Terra, mas o outro que está em um foguete rápido para Júpiter, pode observar um cometa caindo em Júpiter (este é o evento ). Em geral, eles vão discordar sobre a localização exata e o timing deste impacto, ou seja, eles terão diferentes 4-tuples (como eles estão usando diferentes sistemas de coordenadas). Embora suas descrições cinemáticas diferirem, leis dinâmicas (físicas), tais como a conservação do ímpeto e a primeira lei da termodinâmica, ainda serão mantidas. Na verdade, a teoria da relatividade requer mais do que isso no sentido de que estipula essas leis (e todas as outras físicas) devem tomar a mesma forma em todos os sistemas de coordenadas. Isso introduz tensores na relatividade, pela qual todas as quantidades físicas são representadas.
Diz-se que as geodésicas são semelhantes ao tempo, nulas ou semelhantes ao espaço se o vetor tangente a um ponto da geodésica for desta natureza. Os caminhos das partículas e dos feixes de luz no espaço-tempo são representados por geodésicas semelhantes ao tempo e nulas (semelhantes à luz), respectivamente.
Caráter privilegiado do espaço-tempo 3+1
Existem dois tipos de dimensões: espacial (bidirecional) e temporal (unidirecional). Deixe o número de dimensões espaciais ser N e o número de dimensões temporais ser T. Isso. N = 3 T = 1, pondo de lado as dimensões compactadas invocadas pela teoria das cordas e indetectáveis até à data, podem ser explicadas recorrendo às consequências físicas de deixar N diferem de 3 e T diferem de 1. O argumento é muitas vezes de um caráter antrópico e possivelmente o primeiro de seu tipo, embora antes do conceito completo veio em voga.
A noção implícita de que a dimensão do universo é especial é atribuída primeiramente a Gottfried Wilhelm Leibniz, que no Discurso sobre Metafísica sugeriu que o mundo é "o que é ao mesmo tempo o mais simples em hipótese e o mais rico em fenômenos". Immanuel Kant argumentou que o espaço tridimensional era uma consequência da lei quadrada inversa da gravitação universal. Enquanto o argumento de Kant é historicamente importante, John D. Barrow disse que ele "devolve a linha de soco para a frente: é a tridimensionalidade do espaço que explica por que vemos leis de força quadrada inversa na Natureza, não vice-versa" (Barrow 2002:204).
Em 1920, Paul Ehrenfest mostrou que se houver apenas uma dimensão de tempo e mais de três dimensões espaciais, a órbita de um planeta sobre o seu O sol não pode permanecer estável. O mesmo é verdade da órbita de uma estrela em torno do centro de sua galáxia. Ehrenfest também mostrou que se houver um número uniforme de dimensões espaciais, então as diferentes partes de um impulso de onda viajarão a diferentes velocidades. Se houver dimensões espaciais, onde k é um número inteiro positivo, então impulsos de onda se tornam distorcidos. Em 1922, Hermann Weyl afirmou que a teoria do eletromagnetismo de Maxwell pode ser expressa em termos de uma ação apenas para um coletor de quatro dimensões. Finalmente, Tangherlini mostrou em 1963 que quando há mais de três dimensões espaciais, os orbitais dos elétrons em torno dos núcleos não podem ser estáveis; os elétrons cairiam no núcleo ou dispersariam.
Max Tegmark expande-se sobre o argumento anterior da seguinte forma antrópica. Se T difere de 1, o comportamento de sistemas físicos não poderia ser previsto de forma confiável do conhecimento das equações diferenciais parciais relevantes. Em tal universo, a vida inteligente capaz de manipular a tecnologia não poderia surgir. Além disso, se T > 1, Tegmark sustenta que os prótons e elétrons seriam instáveis e poderiam decair em partículas com maior massa do que eles mesmos. (Este não é um problema se as partículas têm uma temperatura suficientemente baixa.) Por último, se N < 3, a gravitação de qualquer tipo se torna problemática, e o universo provavelmente seria muito simples para conter observadores. Por exemplo, quando N < 3, os nervos não podem atravessar sem intersecção. Daí os argumentos antrópicos e outros descartam todos os casos exceto N = 3 T = 1, que descreve o mundo ao nosso redor.
Por outro lado, em vista da criação de buracos negros de um gás monatômico ideal sob sua auto-gravidade, Wei-Xiang Feng mostrou que (3+1) espaço-dimensional é a dimensão marginal. Além disso, é a dimensão única que pode permitir uma esfera de gás "estável" com uma constante cosmológica "positiva". No entanto, um gás auto-gravitação não pode ser esteticamente ligado se a esfera de massa é maior do que ~1021 massas solares, devido à pequena positividade da constante cosmológica observada.
Em 2019, James Scargill argumentou que a vida complexa pode ser possível com duas dimensões espaciais. De acordo com Scargill, uma teoria puramente escalar da gravidade pode permitir uma força gravitacional local, e as redes 2D podem ser suficientes para redes neurais complexas.Detalhes adicionais
- ^ Diferentes repórteres vendo os cenários apresentados nesta figura interpretam os cenários de forma diferente dependendo de seu conhecimento da situação. (i) Um primeiro repórter, no centro de massa de partículas 2 e 3 mas sem saber da grande massa1, conclui que uma força de repulsão existe entre as partículas no cenárioA enquanto uma força de atração existe entre as partículas no cenárioB. (ii) Um segundo repórter, consciente da grande massa1Sorri para o primeiro repórter. Este segundo repórter sabe que na realidade, as forças aparentes entre partículas 2 e 3 realmente representam efeitos de maré resultantes de sua atração diferencial por massa1(iii) Um terceiro repórter, treinado em relatividade geral, sabe que não há, de fato, nenhuma força agindo entre os três objetos. Ao contrário, todos os três objetos se movem ao longo da geodésica no espaço-tempo.
Contenido relacionado
Alcino
Dispersão
Atómica








































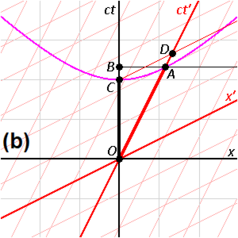



























































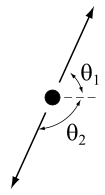







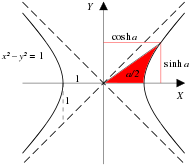


































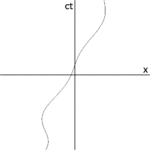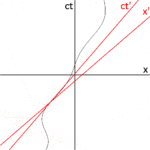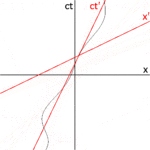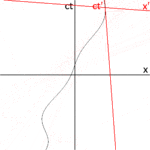









































![{displaystyle -,left(1+{frac {2GM}{c^{2}r}}right)left[(Delta x)^{2}+(Delta y)^{2}+(Delta z)^{2}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e004b8eb220d5cc0f0e835a4f9a584ebfdc3ef02)

![{displaystyle left[(Delta x)^{2}+(Delta y)^{2}+(Delta z)^{2}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b88b386b994cad15b04251eedd908b3828db4d66)






















