Espaço Banach
Na matemática, mais especificamente na análise funcional, um espaço de Banach (pronuncia-se [ˈbanax]) é um espaço vetorial normado completo. Assim, um espaço de Banach é um espaço vetorial com uma métrica que permite o cálculo do comprimento vetorial e da distância entre vetores e é completo no sentido de que uma sequência de vetores de Cauchy sempre converge para um limite bem definido que está dentro do espaço.
Os espaços de Banach recebem o nome do matemático polonês Stefan Banach, que introduziu esse conceito e o estudou sistematicamente em 1920–1922 junto com Hans Hahn e Eduard Helly. Maurice René Fréchet foi o primeiro a usar o termo "espaço de Banach" e Banach, por sua vez, cunhou o termo "Fréchet space." Os espaços de Banach surgiram originalmente do estudo dos espaços funcionais de Hilbert, Fréchet e Riesz no início do século. Os espaços de Banach desempenham um papel central na análise funcional. Em outras áreas de análise, os espaços em estudo são frequentemente espaços de Banach.
Definição
A Espaço de Banach é um espaço completo e normalizado (X,‖ ‖ )) ‖ ‖ ).(X,|cdot |).} Um espaço normal é um par (X,‖ ‖ )) ‖ ‖ )(X,|cdot |)} consistindo de um espaço vetorial X- Sim. sobre um campo escalar KK{displaystyle mathbb {K} } (onde) KK{displaystyle mathbb {K} } é comumente R{displaystyle mathbb {R} } } ou C{displaystyle mathbb {C} } }) em conjunto com uma distinção normas ‖ ‖ )) ‖ ‖ :X→ → R.{displaystyle |cdot |:Xto mathbb {R}.} Como todas as normas, esta norma induz uma tradução invariante função de distância, chamado de canônico ou (norm) métrica induzida, definida por
Por definição, o espaço normal (X,‖ ‖ )) ‖ ‖ )(X,|cdot |)} é um Espaço de Banach se a norma induzida métrica DNão. é uma métrica completa, ou disse de forma diferente, se (X,D)(X,d)} é um espaço métrico completo. A norma ‖ ‖ )) ‖ ‖ {displaystyle |cdot |} de um espaço normalizado (X,‖ ‖ )) ‖ ‖ )(X,|cdot |)} é chamado de norma completa se (X,‖ ‖ )) ‖ ‖ )(X,|cdot |)} é um espaço Banach.
Produto L-semi-interno
Para qualquer espaço normalizado (X,‖ ‖ )) ‖ ‖ ),(X,|cdot |),} existe um produto L-semi-inner ⟨ ⟨ )) ,)) )) {displaystyle langle cdotcdot rangle } sobre X- Sim. tal que ‖ ‖ x‖ ‖ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =⟨ ⟨ x,x)) {textstyle |x|={sqrt {langle x,xrangle }}} para todos x∈ ∈ X{displaystyle xin X}; em geral, pode haver infinitamente muitos produtos L-semi-inner que satisfazem esta condição. Os produtos L-semi-inner são uma generalização de produtos internos, que são o que distingue fundamentalmente os espaços de Hilbert de todos os outros espaços de Banach. Isso mostra que todos os espaços normáticos (e, portanto, todos os espaços de Banach) podem ser considerados como generalizações de espaços (pré-)Hilbert.
Caracterização em termos de séries
A estrutura do espaço vetorial permite relacionar o comportamento de seqüências de Cauchy com a de converging série de vetores. Um espaço normal X- Sim. é um espaço Banach se e somente se cada série absolutamente convergente em X- Sim. converge em X,Não. X,
Topologia
A métrica canônica DNão. de um espaço normalizado (X,‖ ‖ )) ‖ ‖ )(X,|cdot |)} induz a topologia métrica usual ? ? D{displaystyle tau _{d}} sobre X,Não. X, que é referido como o canônico ou topologia induzida por norma. Cada espaço normal é automaticamente assumido para transportar esta topologia Hausdorff, a menos que indicado de outra forma. Com esta topologia, cada espaço de Banach é um espaço de Baire, embora existam espaços normáticos que são Baire, mas não Banach. A norma ‖ ‖ )) ‖ ‖ :(X,? ? D)→ → R{displaystyle |,cdot ,|:left(X,tau _{d}right)to mathbb Não. é sempre uma função contínua em relação à topologia que induz.
As bolas abertas e fechadas do raio 0}" xmlns="http://www.w3.org/1998/Math/MathML">R>0- Sim. 0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/23cbbcd53bd13620bc53490e3eec42790850b452" style="vertical-align: -0.338ex; width:5.31ex; height:2.176ex;"/> centrado em um ponto x∈ ∈ X{displaystyle xin X} são, respectivamente, os conjuntos
Subconjuntos compactos e convexos
Há um subconjunto compacto SNão. S. de Eu... Eu... 2(N){displaystyle ell ^{2}(mathbb {N})} cujo casco convexo co (S){displaystyle operatorname {co} (S)} o não fechado e assim também não compacto (veja esta nota de rodapé por exemplo). No entanto, como em todos os espaços de Banach, o casco convexo fechado co? ? S{displaystyle {overline {operatorname {co} }}S} deste (e cada outro) subconjunto compacto será compacto. Mas se um espaço normed não está completo, então é em geral não garantido co? ? S{displaystyle {overline {operatorname {co} }}S} será compacto sempre SNão. S. é; um exemplo pode até ser encontrado em um (não-completo) pré-Hilbert subespaço vetorial de Eu... Eu... 2(N).{displaystyle ell ^{2}(mathbb {N}).}
Como espaços vetoriais topológicos
Esta topologia induzida por norma também faz (X,? ? D){displaystyle left(X,tau _{d}right)} para o que é conhecido como um espaço vetorial topológico (TVS), que por definição é um espaço vetorial dotado de uma topologia tornando as operações de adição e multiplicação escalar contínua. É enfatizado que o TVS (X,? ? D){displaystyle left(X,tau _{d}right)} o apenas um espaço vetorial junto com um certo tipo de topologia; isto é, quando considerado como TVS, é não associado com qualquer um norma particular ou métrica (ambos são "forgotten"). Este Hausdorff TVS (X,? ? D){displaystyle left(X,tau _{d}right)} é mesmo localmente convexo porque o conjunto de todas as bolas abertas centradas na origem forma uma base de vizinhança na origem que consiste em conjuntos abertos equilibrados convexo. Este TVS também é Norma, que por definição refere-se a qualquer TVS cuja topologia é induzida por alguns (possivelmente desconhecido) norma. Normable TVSs são caracterizados por ser Hausdorff e ter um bairro convexo limitado da origem.
Comparação de topologias vetoriais metrizáveis completas
O teorema de mapeamento aberto implica que se ? ? e? ? 2{displaystyle tau {text{ e }}tau _{2}} são topologias em X- Sim. que fazem os dois (X,? ? )(X,tau)} e (X,? ? 2){displaystyle left(X,tau _{2}right)} em TVS metrizable completo (por exemplo, Banach ou Fréchet espaços) e se uma topologia é mais fina ou mais grosseira do que a outra, então eles devem ser iguais (ou seja, se ? ? ⊆ ⊆ ? ? 2ou? ? 2⊆ ⊆ ? ? então? ? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =? ? 2{displaystyle tau subseteq tau _{2}{text{ ou }}tau _{2}subseteq tau {text{ então }}tau =tau _{2}}). Por exemplo, se (X,p)e(X,q)(X,p){text{ e }}(X,q)} são espaços de Banach com topologia ? ? pe? ? q{displaystyle tau _{p}{text{ e }}tau _{q}} e se um desses espaços tem alguma bola aberta que também é um subconjunto aberto do outro espaço (ou equivalentemente, se um de p:(X,? ? q)→ → R{displaystyle p:left(X,tau _{q}right)to mathbb Não. ou q:(X,? ? p)→ → R{displaystyle q:left(X,tau _{p}right)to mathbb Não. é contínuo) então suas topologias são idênticas e suas normas são equivalentes.
Integridade
Normas completas e normas equivalentes
Duas normas, pNão. e q,Não. em um espaço vetorial dizem ser equivalente se eles induzirem a mesma topologia, isso acontece se e somente se houver números reais positivos 0}" xmlns="http://www.w3.org/1998/Math/MathML">c,C>0{displaystyle c,C>0}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/162c3821972f14a29ea8156f42fda96fac3822d7" style="vertical-align: -0.671ex; width:8.068ex; height:2.509ex;"/> tal que cq(x)≤ ≤ p(x)≤ ≤ Cq(x){textstyle cq(x)leq p(x)leq Cq(x)} para todos x∈ ∈ X.{displaystyle xin X.} Se pNão. e qNão. são duas normas equivalentes em um espaço vetorial X- Sim. então (X,p)(X,p)} é um espaço Banach se e somente se (X,q)(X,q)} é um espaço Banach.
Veja esta nota de rodapé para um exemplo de uma norma contínua em um espaço Banach que é não equivalente à norma do espaço Banach.
Todas as normas em um espaço vetorial finito-dimensional são equivalentes e cada espaço normático de dimensão finita é um espaço Banach.
Normas completas x métricas completas
Uma métrica DNão. em um espaço vetorial X- Sim. é induzida por uma norma X- Sim. se e somente se DNão. é a tradução invariante e absolutamente homogêneo, o que significa que D(Sx,SSim.)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =|S|D(x,Sim.){displaystyle D(sx,sy)=|D(x,y)} para todos os escalares SNão. e todos x,Sim.∈ ∈ X,{displaystyle x,yin X,} em que caso a função ‖ ‖ x‖ ‖ ?D(x,0){displaystyle |x|=D(x,0)} define uma norma X- Sim. e a métrica canônica induzida por ‖ ‖ )) ‖ ‖ {displaystyle |cdot |} é igual a D.Não. D.
Suponha que (X,‖ ‖ )) ‖ ‖ )(X,|cdot |)} é um espaço normal e isso ? ? - Sim. é a topologia norma induzida em X.Sim. Suponha que DNão. o qualquer um métrica em X- Sim. tal que a topologia que DNão. induz em X- Sim. é igual a ? ? .- Sim. Se DNão. é a tradução invariante então (X,‖ ‖ )) ‖ ‖ )(X,|cdot |)} é um espaço Banach se e somente se (X,D)(X,D)} é um espaço métrico completo. Se DNão. o não tradução invariante, então pode ser possível para (X,‖ ‖ )) ‖ ‖ )(X,|cdot |)} para ser um espaço Banach, mas para (X,D)(X,D)} para não ser um espaço métrico completo (veja esta nota de rodapé por exemplo). Em contraste, um teorema de Klee, que também se aplica a todos os espaços vetoriais topológicos metrizáveis, implica que se existe qualquer um métrica completa DNão. sobre X- Sim. que induz a topologia norma ? ? - Sim. sobre X,Não. X, então (X,‖ ‖ )) ‖ ‖ )(X,|cdot |)} é um espaço Banach.
Um espaço Fréchet é um espaço vetorial topológico localmente convexo, cuja topologia é induzida por alguma métrica completa invariante de tradução. Cada espaço Banach é um espaço Fréchet, mas não inversamente; de fato, existem mesmo espaços Fréchet em que nenhuma norma é uma função contínua (como o espaço de sequências reais) RN= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =? ? Eu...∈ ∈ NR- Sim. (R) {N} }=prod _{iin mathbb {N} }mathbb {R} } com a topologia do produto). No entanto, a topologia de cada espaço Fréchet é induzida por alguma família contável de mapas reais (necessariamente contínuos) chamados seminormas, que são generalizações de normas. É mesmo possível para um espaço Fréchet ter uma topologia que é induzida por uma família contável de normas (as normas seriam necessariamente contínuas) mas não ser um espaço Banach/normável porque sua topologia não pode ser definida por qualquer único Norm. Um exemplo desse espaço é o espaço Fréchet C∞ ∞ (KK),(K),} cuja definição pode ser encontrada no artigo sobre espaços de funções de teste e distribuições.
Normas completas vs espaços vetoriais topológicos completos
Há outra noção de plenitude além da completa métrica e essa é a noção de um espaço vetorial topológico completo (TVS) ou TVS-completude, que usa a teoria dos espaços uniformes. Especificamente, a noção de TVS-completude usa uma uniformidade invariante de tradução única, chamada de uniformidade canônica, que depende apenas na subtração vetorial e na topologia ? ? - Sim. que o espaço vetorial é dotado com, e assim, em particular, esta noção de plenitude TVS é independente de qualquer norma induzida a topologia ? ? - Sim. (e mesmo se aplica a TVSs que são não mesmo metrizável). Cada espaço Banach é um TVS completo. Além disso, um espaço normático é um espaço Banach (ou seja, sua métrica induzida por norma é completa) se e somente se estiver completo como um espaço vetorial topológico. Se (X,? ? )(X,tau)} é um espaço de vetor topológico metrizável (como qualquer topologia induzida por norma, por exemplo), então (X,? ? )(X,tau)} é um TVS completo se e somente se for um sequencialmente TVS completo, o que significa que é o suficiente para verificar que cada Cauda sequência em (X,? ? )(X,tau)} converge em (X,? ? )(X,tau)} a algum ponto de X- Sim. (ou seja, não há necessidade de considerar a noção mais geral de redes de Cauchy arbitrárias).
Se (X,? ? )(X,tau)} é um espaço vetorial topológico cuja topologia é induzida por alguns (possivelmente desconhecido) norma (tais espaços são chamados Norma), então (X,? ? )(X,tau)} é um espaço de vetor topológico completo se e somente se X- Sim. pode ser atribuído uma norma ‖ ‖ )) ‖ ‖ {displaystyle |cdot |} que induz em X- Sim. a topologia ? ? - Sim. e também faz (X,‖ ‖ )) ‖ ‖ )(X,|cdot |)} num espaço de Banach. A Hausdorff localmente convex topological vector space X- Sim. é normativo se e somente se seu espaço dual forte Xb)? ? Não. X_{b}^{prime }} é normativo, em que caso Xb)? ? Não. X_{b}^{prime }} é um espaço Banach (Xb)? ? Não. X_{b}^{prime }} denota o forte espaço dual de X,Não. X, cuja topologia é uma generalização da topologia induzida por norma dupla no espaço duplo contínuo X? ? Não. X^{prime }}; veja esta nota de rodapé para mais detalhes). Se X- Sim. é um TVS convexo local metrizável, então X- Sim. é normativo se e somente se Xb)? ? Não. X_{b}^{prime }} é um espaço Fréchet-Urysohn. Isso mostra que na categoria de TVSs convexas localmente, os espaços Banach são exatamente aqueles espaços completos que são metrizáveis e têm espaços duplos fortes metrizáveis.
Conclusões
Todo espaço normado pode ser isometricamente embutido em um subespaço vetorial denso de algum espaço de Banach, onde esse espaço de Banach é chamado de completação do espaço normado. Esta conclusão de Hausdorff é única até o isomorfismo isométrico.
Mais precisamente, para cada espaço normalizado X,Não. X, existe um espaço de Banach YNão. Sim. e um mapeamento T:X→ → YNão. T:Xto Y} tal que TNão. T. é um mapeamento isométrico e T(X)T(X)} é densa em Y.Não. Sim. Se Z.Não. é outro espaço de Banach tal que há um isomorfismo isométrico de X- Sim. em um subconjunto denso de Z.,Não. Z, então Z.Não. isometicamente isomorfo Y.Não. Sim.Este espaço de Banach YNão. Sim. é a conclusão Hausdorff do espaço normal X.Sim. O espaço métrico subjacente para YNão. Sim. é o mesmo que a conclusão métrica de X,Não. X, com as operações de espaço vetorial estendidas X- Sim. para Y.Não. Sim. A conclusão X- Sim. é por vezes denotado por X^ ^ .{displaystyle {widehat {X}}}
Teoria geral
Operadores lineares, isomorfismos
Se X- Sim. e YNão. Sim. são espaços normáticos sobre o mesmo campo terrestre KK,{displaystyle mathbb {K}} o conjunto de todos os contínuos KK{displaystyle mathbb {K} }- mapas lineares T:X→ → YNão. T:Xto Y} é denotado por B(X,Y).{displaystyle B(X,Y).} Em espaços de dimensão infinita, nem todos os mapas lineares são contínuos. Um mapeamento linear de um espaço normalizado X- Sim. para outro espaço normalizado é contínuo se e somente se for limitado na esfera de unidade fechada de X.Sim. Assim, o espaço vetorial B(X,Y)(X,Y)} pode ser dada a norma do operador
Para YNão. Sim. um espaço Banach, o espaço B(X,Y)(X,Y)} é um espaço Banach com respeito a esta norma. Em contextos categógicos, às vezes é conveniente restringir o espaço de função entre dois espaços Banach para apenas os mapas curtos; nesse caso, o espaço B(X,Y)(X,Y)} reaparece como um bifuntor natural.
Se X- Sim. é um espaço Banach, o espaço B(X)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =B(X,X){displaystyle B(X)=B(X,X)} forma uma álgebra Banach unital; a operação de multiplicação é dada pela composição de mapas lineares.
Se X- Sim. e YNão. Sim. são espaços normáticos, eles são espaços normáticos isomorfos se existe uma bijeção linear T:X→ → YNão. T:Xto Y} tal que TNão. T. e seu inverso T- Sim. - Sim. 1Não. T^{-1}} são contínuos. Se um dos dois espaços X- Sim. ou YNão. Sim. é completo (ou reflexivo, separável, etc) então assim é o outro espaço. Dois espaços normáticos X- Sim. e YNão. Sim. são isomorfose se além disso, TNão. T. é uma isometria, ou seja, ‖ ‖ T(x)‖ ‖ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =‖ ‖ x‖ ‖ {displaystyle |T(x)|=|x|} para todos xNão. em X.Sim. A distância de Banach–Mazur D(X,Y)(X,Y)} entre dois espaços isomorfo mas não isométricos X- Sim. e YNão. Sim. dá uma medida de quanto os dois espaços X- Sim. e YNão. Sim. diferem.
Funções lineares contínuas e limitadas e seminormas
Cada operador linear contínuo é um operador linear limitado e se lidar apenas com espaços normáticos, então o converso também é verdadeiro. Ou seja, um operador linear entre dois espaços normalizados é limitado se e somente se for uma função contínua. Então, em particular, porque o campo escalar (que é R{displaystyle mathbb {R} } } ou C{displaystyle mathbb {C} } }) é um espaço normático, um funcional linear em um espaço normático é um funcional linear limitado se e somente se for um funcional linear contínuo. Isso permite que os resultados relacionados à continuidade (como os abaixo) sejam aplicados aos espaços Banach. Embora o limite seja o mesmo que a continuidade de mapas lineares entre espaços normed, o termo "bounded" é mais comumente usado quando se trata principalmente de espaços Banach.
Se f:X→ → R{displaystyle f:Xto mathbb Não. é uma função subadditiva (como uma norma, uma função sublinear ou funcional linear real), então fNão. é contínua na origem se e somente se fNão. é uniformemente contínuo em todos os X- Sim.; e se em adição f(0)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0(0)=0} então fNão. é contínuo se e somente se seu valor absoluto |f|:X→ → Não.0,∞ ∞ )|f|:Xto [0,infty)} é contínuo, o que acontece se e somente se <math alttext="{displaystyle {xin X:|f(x)|(x∈ ∈ X:|f(x)|<1?{displaystyle {xin X:|f(x)|<1}}<img alt="{displaystyle {xin X:|f(x)| é um subconjunto aberto de X.Sim. E muito importante para aplicar o teorema de Hahn-Banach, um funcional linear fNão. é contínuo se e somente se isso for verdade de sua parte real Repito f{displaystyle operatorname {Re} f} e além disso, ‖ ‖ Repito f‖ ‖ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =‖ ‖ f‖ ‖ {displaystyle |operatorname {Re} f|=|f|} e a parte real Repito f{displaystyle operatorname {Re} f} determina completamente f,Não. é por isso que o teorema de Hahn-Banach é frequentemente declarado apenas para funcionais reais lineares. Além disso, um funcional linear fNão. sobre X- Sim. é contínuo se e somente se o seminorm |f||f|} é contínuo, o que acontece se e somente se houver um seminormado contínuo p:X→ → R{displaystyle p:Xto mathbb Não. tal que |f|≤ ≤ p|f|leq p}; esta última declaração envolvendo o funcional linear fNão. e seminorm pNão. é encontrado em muitas versões do teorema de Hahn-Banach.
Noções básicas
O produto cartesiano X× × YNão. Xtimes Y} de dois espaços normáticos não é canonicamente equipado com uma norma. No entanto, várias normas equivalentes são comumente usadas, como
Se MNão. é um subespaço linear fechado de um espaço normal X,Não. X, há uma norma natural no espaço quociente X/M,{displaystyle X/M,}
O quociente X/M- Sim. é um espaço de Banach quando X- Sim. está completo. O mapa de citações a partir de X- Sim. sobre X/M,{displaystyle X/M,} envio x∈ ∈ X{displaystyle xin X} à sua classe x+M,{displaystyle x+M,} é linear, sobre e tem norma 1,- Sim. excepto quando M= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =X,- Sim. em que caso o quociente é o espaço nulo.
O subespaço linear fechado MNão. de X- Sim. é dito ser um subespaço complementado de X- Sim. se MNão. é a gama de uma projeção linear limitada surjetiva P:X→ → M.{displaystyle P:Xto M.} Neste caso, o espaço X- Sim. isomorfo para a soma direta de MNão. e ker P,{displaystyle ker P,} o kernel da projeção P.Não. P.
Suponha que X- Sim. e YNão. Sim. são espaços de Banach e que T∈ ∈ B(X,Y).{displaystyle Tin B(X,Y).} Existe uma fatoração canônica de TNão. T. como
Espaços clássicos
Exemplos básicos de espaços de Banach incluem: os espaços Lp LpNão. L^{p}} e seus casos especiais, os espaços de sequência Eu... Eu... p{displaystyle ell ^{p}} que consistem em sequências escalares indexadas por números naturais N{displaystyle mathbb {N} } }; entre eles, o espaço Eu... Eu... 1{displaystyle ell ^{1}} de sequências absolutamente sumamáveis e o espaço Eu... Eu... 2{displaystyle ell ^{2}} de sequências sonoras quadradas; o espaço c0{displaystyle c_{0}} de sequências tendendo a zero e o espaço Eu... Eu... ∞ ∞ {displaystyle ell ^{infty }} de sequências limitadas; o espaço C(KK)(K)} de funções escalares contínuas em um espaço compacto Hausdorff KK,- Sim. equipado com a norma máxima,
De acordo com o teorema de Banach-Mazur, cada espaço de Banach é isometicamente isomorfo para um subespaço de alguns C(KK).{displaystyle C(K).} Para cada espaço de Banach separável X,Não. X, há um subespaço fechado MNão. de Eu... Eu... 1{displaystyle ell ^{1}} tal que X?Eu... Eu... 1/M.{displaystyle X:=ell ^{1}/M.}
Qualquer espaço de Hilbert serve como um exemplo de um espaço de Banach. Um espaço de Hilbert H. H. H.Não. H. sobre KK= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R,C{displaystyle mathbb - Não. (R}mathbb) Não. é completo para uma norma da forma
Por exemplo, o espaço L2Não. L^{2}} é um espaço de Hilbert.
Os espaços Hardy, os espaços Sobolev são exemplos de espaços Banach que estão relacionados com LpNão. L^{p}} espaços e têm estrutura adicional. Eles são importantes em diferentes ramos de análise, análise harmônica e equações diferenciais parciais entre outros.
Álgebras de Banach
A Álgebra de Banach é um espaço de Banach ANão. A. sobre KK= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R{displaystyle mathbb - Não. Não. ou C,{displaystyle mathbb {C}} em conjunto com uma estrutura de álgebra sobre KK{displaystyle mathbb {K} }, tal que o mapa do produto A× × A∋ ∋ (um,b))↦ ↦ umb)∈ ∈ ANão. Atimes Ani (a,b)mapsto abin A} é contínuo. Uma norma equivalente sobre ANão. A. pode ser encontrado para ‖ ‖ umb)‖ ‖ ≤ ≤ ‖ ‖ um‖ ‖ ‖ ‖ b)‖ ‖ {displaystyle |ab|leq |a||b|} para todos um,b)∈ ∈ A.- Sim.
Exemplos
- O espaço de Banach C(KK)(K)} com o produto pontual, é uma álgebra de Banach.
- A álgebra de disco A(D)A(mathbf {D})} consiste em funções holomorphic no disco da unidade aberta D⊆ ⊆ CNão. Dsubseq mathbb Não. e contínuo em seu fechamento: D? ? .{displaystyle {overline {mathbf {D} }}} Equipado com a norma máx. D? ? ,{displaystyle {overline {mathbf {D} }}} a álgebra de disco A(D)A(mathbf {D})} é uma subalgebra fechada de C(D? ? ).{displaystyle Cleft({overline {mathbf {D} }}right). ?
- A álgebra de Wiener A(T){displaystyle A(mathbf {T})} é a álgebra das funções no círculo da unidade T{displaystyle mathbf {T} } } com série absolutamente convergente Fourier. Através do mapa associando uma função em T{displaystyle mathbf {T} } } para a sequência de seus coeficientes Fourier, esta álgebra é isomorfo para a álgebra de Banach Eu... Eu... 1(Z.),(Z),} onde o produto é a convolução de sequências.
- Para cada espaço de Banach X,Não. X, o espaço B(X)(X)} de operadores lineares limitados em X,Não. X, com a composição de mapas como produto, é uma álgebra de Banach.
- A C*-algebra é uma álgebra complexa de Banach ANão. A. com uma involução antilinear um↦ ↦ um∗ ∗ {displaystyle amapsto a^{*}} tal que ‖um∗ ∗ um‖= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =‖ ‖ um‖ ‖ 2.{displaystyle left|a^{*}aright|=|a|^{2}.} O espaço B(H. H. H.)(H)} de operadores lineares limitados em um espaço de Hilbert H. H. H.Não. H. é um exemplo fundamental da C*-algebra. O teorema de Gelfand-Naimark afirma que cada C*-algebra é isometicamente isomorfo para uma C*-subalgebra de alguns B(H. H. H.).{displaystyle B(H).} O espaço C(KK)(K)} de funções contínuas complexas em um espaço compacto Hausdorff KKNão. é um exemplo de C*-algebra comutativa, onde a involução associa a cada função fNão. sua conjugação complexa f? ? .{displaystyle {overline {f}}}
Espaço duplo
Se X- Sim. é um espaço normal e KK{displaystyle mathbb {K} } o campo subjacente (sendo os números reais ou complexos), o espaço dual contínuo é o espaço de mapas lineares contínuos de X- Sim. para dentro KK,{displaystyle mathbb {K}} ou funcionais lineares contínuas. A notação para a dupla contínua é X? ? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =B(X,KK){displaystyle X^{prime }=B(X,mathbb {K})} neste artigo. Desde então KK{displaystyle mathbb {K} } é um espaço Banach (usando o valor absoluto como norma), o dual X? ? Não. X^{prime }} é um espaço Banach, para cada espaço normalizado X.Sim.
A principal ferramenta para provar a existência de funcionais lineares contínuos é o teorema de Hahn–Banach.
Teorema de Hahn–Banach—Vamos. X- Sim. ser um espaço vetorial sobre o campo KK= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R,C.{displaystyle mathbb - Não. (R}mathbb) Não. Deixe mais
- Y⊆ ⊆ XNão. Ysubseteq X} ser um subespaço linear,
- p:X→ → R{displaystyle p:Xto mathbb Não. ser uma função sublinear e
- f:Y→ → KK{displaystyle f:Yto mathbb Não. ser um funcional linear para que Repito (f(Sim.))≤ ≤ p(Sim.){displaystyle operatorname {Re} (f(y))leq p(y)} para todos Sim.∈ ∈ Y.{displaystyle yin Y.}
Então, existe um funcional linear F:X→ → KK{displaystyle F:Xto mathbb Não. assim
Em particular, cada funcional linear contínuo em um subespaço de um espaço normático pode ser continuamente estendido para todo o espaço, sem aumentar a norma do funcional. Um caso especial importante é o seguinte: para cada vetor xNão. em um espaço normalizado X,Não. X, existe um funcional linear contínuo fNão. sobre X- Sim. tal que
Quando xNão. não é igual ao 0{displaystyle mathbf {0} } } vector, o funcional fNão. deve ter uma norma, e é chamado de norming funcional para x.Sim.
O teorema da separação de Hahn-Banach afirma que dois conjuntos convexos não vazios disjuntos em um espaço de Banach real, um deles aberto, podem ser separados por um hiperplano afim fechado. O conjunto convexo aberto fica estritamente em um lado do hiperplano, o segundo conjunto convexo fica do outro lado, mas pode tocar o hiperplano.
Um subconjunto SNão. S. em um espaço de Banach X- Sim. o total se a extensão linear de SNão. S. é densa em X.Sim. O subconjunto SNão. S. é total em X- Sim. se e somente se o único funcional linear contínuo que desaparece SNão. S. é o 0{displaystyle mathbf {0} } } funcional: esta equivalência segue do teorema de Hahn-Banach.
Se X- Sim. é a soma direta de dois subespaços lineares fechados MNão. e N,Não. Não. então o dual X? ? Não. X^{prime }} de X- Sim. é isomorfo para a soma direta das duplas MNão. e N.Não. Não. Se MNão. é um subespaço linear fechado em X,Não. X, um pode associar o ortogonal de MNão. no dual,
O ortogonal M:: {displaystyle M^{bot }} é um subespaço linear fechado da dupla. A dupla de MNão. isometicamente isomorfo X?/M:: .Não. X'/M^{bot } A dupla de X/M- Sim. isometicamente isomorfo M:: .{displaystyle M^{bot }.}
O dual de um espaço de Banach separável não precisa ser separável, mas:
Teorem—Vamos. X- Sim. ser um espaço normal. Se X?Não. X's é separável, então X- Sim. é separável.
Quando X?Não. X's é separável, o critério acima para a totalidade pode ser usado para provar a existência de um subconjunto total contável em X.Sim.
Topologias fracas
O topologia fraca em um espaço de Banach X- Sim. é a topologia mais grosseira em X- Sim. para o qual todos os elementos x? ? {displaystyle x^{prime }} no espaço duplo contínuo X? ? Não. X^{prime }} são contínuos. A topologia da norma é, portanto, mais fina do que a topologia fraca. Ele segue do teorema de separação Hahn-Banach que a topologia fraca é Hausdorff, e que um subconjunto convexo fechado de norma de um espaço Banach também é fracamente fechado. Um mapa linear contínuo de normas entre dois espaços Banach X- Sim. e YNão. Sim. também fracamente contínuo, isto é, contínuo da topologia fraca de X- Sim. para o de Y.Não. Sim.
Se X- Sim. é infinita-dimensional, existem mapas lineares que não são contínuos. O espaço X∗ ∗ Não. X^{*}} de todos os mapas lineares de X- Sim. para o campo subjacente KK{displaystyle mathbb {K} } (este espaço X∗ ∗ Não. X^{*}} é chamado de espaço duplo algébrica, para distingui-lo X? ? Não. X^{prime }} também induz uma topologia em X- Sim. que é mais fino do que a topologia fraca, e muito menos usado na análise funcional.
Em um espaço duplo X? ? ,{displaystyle X^{prime },} há uma topologia mais fraca do que a topologia fraca de X? ? ,{displaystyle X^{prime },} chamada topologia fraca*. É a topologia mais grosseira em X? ? Não. X^{prime }} para o qual todos os mapas de avaliação x? ? ∈ ∈ X? ? ↦ ↦ x? ? (x),{displaystyle x^{prime }in X^{prime }mapsto x^{prime }(x),} Onde? xNão. escalas sobre X,Não. X, são contínuos. Sua importância vem do teorema de Banach-Alaoglu.
Banach–Alaoglu teorema—Vamos. X- Sim. ser um espaço vetorial normal. Então a bola de unidade fechada B= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(x∈ ∈ X:‖ ‖ x‖ ‖ ≤ ≤ 1?{displaystyle B=left{xin X:|x|leq 1right}} do espaço duplo é compacto na topologia fraca*.
O teorema de Banach-Alaoglu pode ser provado usando o teorema de Tychonoff sobre produtos infinitos de espaços Hausdorff compactos. Quando X- Sim. é separável, a bola da unidade B? ? Não. B^{prime }} do dual é um compacto metrizável na topologia fraca*.
Exemplos de espaços duplos
A dupla de c0{displaystyle c_{0}} isometicamente isomorfo Eu... Eu... 1{displaystyle ell ^{1}}: para cada funcional linear limitado fNão. sobre c0,Não. há um elemento único Sim.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(Sim.n?∈ ∈ Eu... Eu... 1{displaystyle y=left{y_{n}right}in ell ^{1}} tal que
A dupla de Eu... Eu... 1{displaystyle ell ^{1}} isometicamente isomorfo Eu... Eu... ∞ ∞ {displaystyle ell ^{infty }}. O dual de espaço de Lebesgue Lp(Não.0,1])([0,1])} isometicamente isomorfo Lq(Não.0,1])([0,1])} quando <math alttext="{displaystyle 1leq p1≤ ≤ p<∞ ∞ {displaystyle 1leq p<infty }<img alt="1 leq p e 1p+1q= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1.{displaystyle {frac {1}{p}}+{frac Não.
Para cada vetor Sim.- Sim. em um espaço de Hilbert H. H. H.,Não. H, o mapeamento
define um funcional linear contínuo fSim.{displaystyle f_{y}} sobre H. H. H..Não. H.O teorema da representação de Riesz afirma que todo funcional linear contínuo em H. H. H.Não. H. é da forma fSim.{displaystyle f_{y}} para um vetor único definido Sim.- Sim. em H. H. H..Não. H.O mapeamento Sim.∈ ∈ H. H. H.→ → fSim.{displaystyle yin Hto f_{y}} é uma bijeção isométrica antilinear de H. H. H.Não. H. para a sua dupla H. H. H.?.Não. H'. Quando os escalares são reais, este mapa é um isomorfismo isométrico.
Quando KKNão. é um espaço topológico Hausdorff compacto, o dual M(KK)(K)} de C(KK)(K)} é o espaço de medidas Radon no sentido de Bourbaki. O subconjunto P(KK)(K)} de M(KK)(K)} consistindo em medidas não negativas de massa 1 (medidas de probabilidade) é um subconjunto de convexo w*-fechado da esfera unitária de M(KK).{displaystyle M(K).} Os pontos extremos de P(KK)(K)} são as medidas de Dirac KK.Não. K. O conjunto de medidas de Dirac KK,- Sim. equipado com w*-topologia, é homeomorphic a KK.Não. K.
Banach–Stone Teorem—Se KKNão. e LNão. L. são espaços Hausdorff compactos e se C(KK)(K)} e C(L)(L)} são isometralmente isomorfos, então os espaços topológicos KKNão. e LNão. L. são homeomorfos.
O resultado foi estendido por Amir e Cambern para o caso quando a distância multiplicativa de Banach-Mazur entre C(KK)(K)} e C(L)(L)} o <math alttext="{displaystyle <2.Não. <2.<img alt="{displaystyle O teorema não é mais verdadeiro quando a distância é = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2.Não. -2.
Na álgebra de Banach comutativa C(KK),{displaystyle C(K),} os ideais máximos são precisamente núcleos de medidas de Dirac sobre KK,- Sim.
Mais geralmente, pelo teorema de Gelfand-Mazur, os ideais máximos de uma álgebra de Banach comutativa unitária podem ser identificados com seus personagens - não apenas como conjuntos, mas como espaços topológicos: o primeiro com a topologia do casco e o último com a topologia w*. Nesta identificação, o espaço ideal máximo pode ser visto como um subconjunto W*-compact da bola unitária na dupla A?.- Sim.
Teorem—Se KKNão. é um espaço Hausdorff compacto, então o espaço ideal máximo ? ? - Sim. da álgebra de Banach C(KK)(K)} é homeomorfo para KK.Não. K.
Nem toda álgebra de Banach comutativa unitária é da forma C(KK)(K)} para algum espaço Hausdorff compacto KK.Não. K. No entanto, esta declaração afirma se um lugar C(KK)(K)} na categoria menor de C*-algebras comutativas. O teorema de representação de Gelfand para C*-algebras comutativas afirma que cada unidade comutativa C*-algebra ANão. A. isometicamente isomorfose para um C(KK)(K)} espaço. O espaço compacto Hausdorff KKNão. aqui é novamente o espaço ideal máximo, também chamado de espectro de ANão. A. no contexto C*-algebra.
Bidual
Se X- Sim. é um espaço normal, o (contínuo) dual X"- Sim. da dupla X?Não. X's é chamado lanceou segunda dupla de X.Sim. Para cada espaço normalizado X,Não. X, há um mapa natural,
Isso define FX(x)(x)} como um funcional linear contínuo X? ? ,{displaystyle X^{prime },} isto é, um elemento de X? ? ? ? .Não. X^{prime prime }.} O mapa FX:x→ → FX(x)Não. F_{X}:xto F_{X}(x)} é um mapa linear de X- Sim. para X? ? ? ? .Não. X^{prime prime }.} Como consequência da existência de uma norma funcional fNão. para todos x∈ ∈ X,{displaystyle xin X,} este mapa FXNão. F_{X}} isométrico, assim injetável.
Por exemplo, o dual de X= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =c0Não. X=c_{0}} é identificado com Eu... Eu... 1,{displaystyle ell ^{1},} e o dual de Eu... Eu... 1{displaystyle ell ^{1}} é identificado com Eu... Eu... ∞ ∞ ,} o espaço de sequências escalares limitadas. Sob estas identificações, FXNão. F_{X}} é o mapa de inclusão de c0{displaystyle c_{0}} para Eu... Eu... ∞ ∞ .- Sim. É de fato isométrico, mas não sobre.
Se FXNão. F_{X}} é surjetivo, então o espaço normed X- Sim. é chamado reflexivo (veja abaixo). Sendo o dual de um espaço normático, o lance X"- Sim. é completo, portanto, cada espaço reflexivo e normático é um espaço Banach.
Usando a incorporação isométrica FX,Não. F_{X},} é habitual considerar um espaço normal X- Sim. como um subconjunto do seu lance. Quando X- Sim. é um espaço Banach, é visto como um subespaço linear fechado X? ? ? ? .Não. X^{prime prime }.} Se X- Sim. não é reflexivo, a bola unitária de X- Sim. é um subconjunto adequado da bola da unidade X? ? ? ? .Não. X^{prime prime }.} O teorema de Goldstine afirma que a esfera unitária de um espaço normático é fracamente*-dense na esfera unitária do bidual. Em outras palavras, para cada x"Não. no bidual, existe uma rede (xEu...)Eu...∈ ∈ Eu...{displaystyle left(x_{i}right)_{iin I. em X- Sim. assim
A rede pode ser substituída por uma sequência fracamente*-convergente quando a dupla X?Não. X's é separável. Por outro lado, elementos do lance de Eu... Eu... 1{displaystyle ell ^{1}} que não estão dentro Eu... Eu... 1{displaystyle ell ^{1}} não pode ser fraco*-limite de sequências em Eu... Eu... 1,{displaystyle ell ^{1},} desde então Eu... Eu... 1{displaystyle ell ^{1}} é fracamente sequencialmente completo.
Teoremas de Banach
Aqui estão os principais resultados gerais sobre os espaços de Banach que remontam à época do livro de Banach (Banach (1932)) e estão relacionados ao teorema da categoria de Baire. De acordo com este teorema, um espaço métrico completo (como um espaço de Banach, um espaço de Fréchet ou um espaço F) não pode ser igual a uma união de muitos subconjuntos contáveis fechados com interiores vazios. Portanto, um espaço de Banach não pode ser a união de muitos subespaços fechados contáveis, a menos que já seja igual a um deles; um espaço de Banach com uma base de Hamel contável é de dimensão finita.
Banach–Steinhaus Teorem—Vamos. X- Sim. ser um espaço Banach e YNão. Sim. ser um espaço vetorial normal. Suponha que FNão. é uma coleção de operadores lineares contínuos de X- Sim. para Y.Não. Sim. O princípio uniforme de amarração afirma que, se para todos xNão. em X- Sim. nós temos <math alttext="{displaystyle sup _{Tin F}|T(x)|_{Y}Vamos.T∈ ∈ F‖ ‖ T(x)‖ ‖ Y<∞ ∞ ,{displaystyle sup _{Tin F}|T(x)|_{Y}<infty}<img alt="{displaystyle sup _{Tin F}|T(x)|_{Y} então <math alttext="{displaystyle sup _{Tin F}|T|_{Y}Vamos.T∈ ∈ F‖ ‖ T‖ ‖ Y<∞ ∞ .{displaystyle sup _{Tin F}|T|_{Y}<infty.}<img alt="{displaystyle sup _{Tin F}|T|_{Y}
O teorema de Banach–Steinhaus não se limita aos espaços de Banach. Pode ser alargado, por exemplo, ao caso em que X- Sim. é um espaço Fréchet, desde que a conclusão seja modificada da seguinte forma: sob a mesma hipótese, existe um bairro UNão. de 0{displaystyle mathbf {0} } } em X- Sim. tal que tudo TNão. T. em FNão. estão uniformemente ligados U,Não. U,
O Teorema de Mapeamento Aberto—Vamos. X- Sim. e YNão. Sim. ser espaços de Banach e T:X→ → YNão. T:Xto Y} ser um operador linear contínuo subjetivo, então TNão. T. é um mapa aberto.
Colocação—Cada operador linear unidirecionado de um espaço Banach em um espaço Banach é um isomorfismo.
O primeiro teorema do Isomorfismo para espaços de Banach—Suponha que X- Sim. e YNão. Sim. são espaços de Banach e que T∈ ∈ B(X,Y).{displaystyle Tin B(X,Y).} Suponha mais que o intervalo de TNão. T. está fechado Y.Não. Sim. Então... X/ker T{displaystyle X/ker T} isomorfo para T(X).{displaystyle T(X).}
Este resultado é uma consequência direta do teorema do isomorfismo de Banach anterior e da fatoração canônica de mapas lineares limitados.
Colocação—Se um espaço de Banach X- Sim. é a soma direta interna de subespaços fechados M1,...... ,Mn,{displaystyle M_{1},ldots M_{n}, então X- Sim. isomorfo para M1⊕ ⊕ ⋯ ⋯ ⊕ ⊕ Mn.{displaystyle M_{1}oplus cdots oplus M_{n}
Esta é outra consequência do teorema do isomorfismo de Banach, aplicado à bijeção contínua de M1⊕ ⊕ ⋯ ⋯ ⊕ ⊕ Mn{displaystyle M_{1}oplus cdots oplus M_{n}} sobre X- Sim. envio m1,⋯ ⋯ ,mn{displaystyle m_{1},cdotsm_{n}} para a soma m1+⋯ ⋯ +mn.Não. m_{1}+cdots +m_{n}.
O teorema do gráfico fechado—Vamos. T:X→ → YNão. T:Xto Y} ser um mapeamento linear entre espaços Banach. O gráfico de TNão. T. está fechado X× × YNão. Xtimes Y} se e somente se TNão. T. é contínuo.
Reflexividade
O espaço normal X- Sim. é chamado reflexivo quando o mapa natural
Teorem—Se X- Sim. é um espaço de Banach reflexivo, cada subespaço fechado de X- Sim. e cada espaço quociente X- Sim. são reflexivos.
Esta é uma consequência do teorema de Hahn-Banach. Além disso, pelo teorema de mapeamento aberto, se houver um operador linear limitado do espaço Banach X- Sim. para o espaço de Banach Y,Não. Sim. então YNão. Sim. é reflexivo.
Teorem—Se X- Sim. é um espaço Banach, então X- Sim. é reflexivo se e somente se X? ? Não. X^{prime }} é reflexivo.
Colocação—Vamos. X- Sim. ser um espaço de Banach reflexivo. Então... X- Sim. é separável se e somente se X? ? Não. X^{prime }} é separável.
De facto, se a dupla Y? ? Não. Y^{prime }} de um espaço de Banach YNão. Sim. é separável, então YNão. Sim. é separável. Se X- Sim. é reflexivo e separável, então o dual de X? ? Não. X^{prime }} é separável, assim X? ? Não. X^{prime }} é separável.
Teorem—Suponha que X1,...... ,Xn{displaystyle X_{1},ldots X_{n}} são espaços normalizados e que X= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =X1⊕ ⊕ ⋯ ⋯ ⊕ ⊕ Xn.{displaystyle X=X_{1}oplus cdots oplus X_{n}.} Então... X- Sim. é reflexivo se e somente se cada XJJNão. X_{j}} é reflexivo.
Os espaços de Hilbert são reflexivos. O LpNão. L^{p}} espaços são reflexivos quando <math alttext="{displaystyle 1<p1<p<∞ ∞ .{displaystyle 1<p<infty.}<img alt="{displaystyle 1<p Mais geralmente, espaços convexos uniformemente são reflexivos, pelo teorema de Milman–Pettis. Os espaços c0,Eu... Eu... 1,L1(Não.0,1]),C(Não.0,1]){displaystyle c_{0},ell ^{1},L^{1}([0,1]),C([0,1])} não são reflexivos. Nestes exemplos de espaços não-reflexivos X,Não. X, o lance X"- Sim. é "muito maior" do que X.Sim. Nomeadamente, sob a incorporação isométrica natural de X- Sim. para dentro X"- Sim. dada pelo teorema de Hahn-Banach, o quociente X? ? ? ? /XNão. X^{prime prime }/X} é infinita-dimensional, e até mesmo não separável. No entanto, Robert C. James construiu um exemplo de um espaço não-reflexivo, geralmente chamado de "o espaço de James" e denotado por JJ,- Sim. tal que o quociente JJ? ? ? ? /JJNão. J^{prime prime }/J} é unidimensional. Além disso, este espaço JJNão. isometicamente isomorfo para o seu lance.
Teorem—Um espaço de Banach X- Sim. é reflexivo se e somente se sua bola unitária é compacta na topologia fraca.
Quando X- Sim. é reflexivo, segue-se que todos os subconjuntos convexos fechados e limitados de X- Sim. são fracamente compactos. Em um espaço de Hilbert H. H. H.,Não. H, a compactação fraca da bola da unidade é muito frequentemente usada da seguinte maneira: cada sequência limitada em H. H. H.Não. H. tem subsequências fracamente convergentes.
A compactação fraca da bola unitária fornece uma ferramenta para encontrar soluções em espaços reflexivos para certos problemas de otimização. Por exemplo, cada função contínua convexa na bola da unidade BNão. de um espaço reflexivo atinge seu mínimo em algum ponto em B.Não. B.
Como um caso especial do resultado precedente, quando X- Sim. é um espaço reflexivo sobre R,{displaystyle mathbb {R}} cada funcional linear contínuo fNão. em X? ? Não. X^{prime }} atinge seu máximo ‖ ‖ f‖ ‖ {displaystyle |f|}} na bola da unidade X.Sim. O seguinte teorema de Robert C. James fornece uma declaração conversa.
James Theorem—Para um espaço Banach as duas propriedades seguintes são equivalentes:
- X- Sim. é reflexivo.
- para todos fNão. em X? ? Não. X^{prime }} existe x∈ ∈ X{displaystyle xin X} com ‖ ‖ x‖ ‖ ≤ ≤ 1,{displaystyle |x|leq 1,} assim f(x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =‖ ‖ f‖ ‖ .{displaystyle f(x)=|f|.}
O teorema pode ser estendido para dar uma caracterização de conjuntos convexos fracamente compactos.
Em cada espaço de Banach não-reflexivo X,Não. X, existem funcionais lineares contínuas que não são manutenção da norma. No entanto, o teorema Bishop-Phelps afirma que os funcionais de manutenção da norma são densos na dupla X? ? Não. X^{prime }} de X.Sim.
Fraca convergência de sequências
Uma sequência (xn?{displaystyle left{x_{n}right}} em um espaço de Banach X- Sim. o fracamente convergente para um vetor x∈ ∈ X{displaystyle xin X} se (f(xn)?{displaystyle left{fleft(x_{n}rightright)right}} converge para f(x)(x)} para cada funcional linear contínuo fNão. na dupla X? ? .Não. X^{prime } A sequência (xn?{displaystyle left{x_{n}right}} é um sequência fracamente Cauchy se (f(xn)?{displaystyle left{fleft(x_{n}rightright)right}} converge para um limite escalar L(f),,{displaystyle L(f),} para todos fNão. em X? ? .Não. X^{prime } Uma sequência (fn?{displaystyle left{f_{n}right}} na dupla X? ? Não. X^{prime }} o fraco* convergente a um funcional f∈ ∈ X? ? {displaystyle fin X^{prime }} se fn(x)(x)} converge para f(x)(x)} para todos xNão. em X.Sim. Fracamente seqüências de Cauchy, fracamente convergentes e fracamente* seqüências convergentes são normas limitadas, como consequência do teorema de Banach–Steinhaus.
Quando a sequência (xn?{displaystyle left{x_{n}right}} em X- Sim. é uma sequência fracamente Cauchy, o limite LNão. L. acima define um funcional linear limitado no dual X? ? ,{displaystyle X^{prime },} isto é, um elemento LNão. L. do lance de X,Não. X, e LNão. L. é o limite de (xn?{displaystyle left{x_{n}right}} no fraco*-topologia do lance. O espaço de Banach X- Sim. o fracamente sequencialmente completo se cada sequência fracamente Cauchy é fracamente convergente em X.Sim. Resulta da discussão anterior que os espaços reflexivos são fracamente sequencialmente completos.
Teorem —Para cada medida μ μ ,- Sim. o espaço L1(μ μ )(mu)} é fracamente sequencialmente completo.
Uma sequência ortonormal em um espaço de Hilbert é um exemplo simples de uma sequência fracamente convergente, com limite igual ao 0{displaystyle mathbf {0} } } vector. A base vetorial da unidade Eu... Eu... p{displaystyle ell ^{p}} para <math alttext="{displaystyle 1<p1<p<∞ ∞ ,{displaystyle 1<p<infty}<img alt="{displaystyle 1<p ou de c0,Não. é outro exemplo de um sequência fracamente nula, isto é, uma sequência que converge fracamente para 0.{displaystyle mathbf {0}.} Para cada sequência fracamente nula em um espaço de Banach, existe uma sequência de combinações convexas de vetores da dada sequência que é norma-convergente para 0.{displaystyle mathbf {0}.}
A base vetorial da unidade Eu... Eu... 1{displaystyle ell ^{1}} não é fracamente Cauchy. Fracamente seqüências de Cauchy em Eu... Eu... 1{displaystyle ell ^{1}} são fracamente convergentes, uma vez que L1Não. L^{1}}- Os espaços são fracamente sequencialmente completos. Na verdade, seqüências fracamente convergentes em Eu... Eu... 1{displaystyle ell ^{1}} são normas convergentes. Isso significa que Eu... Eu... 1{displaystyle ell ^{1}} satisfaz a propriedade de Schur.
Resultados envolvendo o ℓ 1 {displaystyle ell ^{1}} base
Fracamente seqüências Cauchy e o Eu... Eu... 1{displaystyle ell ^{1}} base são os casos opostos da dicotomia estabelecida no seguinte resultado profundo de H. P. Rosenthal.
Teorem—Vamos. (xn?n∈ ∈ N{displaystyle left{x_{n}right}_{nin - Sim. ser uma sequência limitada em um espaço Banach. Ou (xn?n∈ ∈ N{displaystyle left{x_{n}right}_{nin - Sim. tem uma subsequência fracamente Cauchy, ou admite uma subseqüência equivalente à base vetorial unitária padrão Eu... Eu... 1.- Sim.
Um complemento a esse resultado se deve a Odell e Rosenthal (1975).
Teorem—Vamos. X- Sim. ser um espaço Banach separável. Os seguintes são equivalentes:
- O espaço X- Sim. não contém uma isomorfose subespacial fechada a Eu... Eu... 1.- Sim.
- Cada elemento do lance X"- Sim. é o limite fraco* de uma sequência (xn?{displaystyle left{x_{n}right}} em X.Sim.
Pelo teorema Goldstine, cada elemento da bola unitária B? ? ? ? Não. B^{prime prime }} de X? ? ? ? Não. X^{prime prime }} é fraco*-limite de uma rede na bola unitária de X.Sim. Quando X- Sim. não contém Eu... Eu... 1,{displaystyle ell ^{1},} cada elemento de B? ? ? ? Não. B^{prime prime }} é fraco*-limite de um sequência na bola da unidade X.Sim.
Quando o espaço de Banach X- Sim. é separável, a bola da unidade da dupla X? ? ,{displaystyle X^{prime },} equipado com o fraco*-topologia, é um espaço compacto metrizável KK,- Sim. e cada elemento x? ? ? ? {displaystyle x^{prime prime }} no lance X? ? ? ? Não. X^{prime prime }} define uma função limitada em KKNão.:
Esta função é contínua para a topologia compacta de KKNão. se e somente se x? ? ? ? {displaystyle x^{prime prime }} na verdade X,Não. X, considerado como subconjunto de X? ? ? ? .Não. X^{prime prime }.} Assuma além do resto do parágrafo que X- Sim. não contém Eu... Eu... 1.- Sim. Pelo resultado anterior de Odell e Rosenthal, a função x? ? ? ? {displaystyle x^{prime prime }} é o limite pontual em KKNão. de uma sequência (xn?⊆ ⊆ XNão. left{x_{n}right}subseq X. de funções contínuas em KK,- Sim. é, portanto, uma primeira função de classe Baire em KK.Não. K. A bola unitária do bidual é um subconjunto compacto pontual da primeira classe Baire em KK.Não. K.
Sequências, compactação fraca e fraca*
Quando X- Sim. é separável, a bola unitária do dual é fraca*-compacto pelo teorema de Banach-Alaoglu e metrizável para a topologia fraca*, daí que cada sequência limitada no dual tem subsequências convergentes fracamente*. Isso se aplica a espaços reflexivos separáveis, mas mais é verdade neste caso, como indicado abaixo.
A topologia fraca de um espaço de Banach X- Sim. é metrizável se e somente se X- Sim. é finito-dimensional. Se o dual X?Não. X's é separável, a topologia fraca da bola unitária de X- Sim. é metrizável. Isto aplica-se em particular aos espaços de Banach reflexivos separáveis. Embora a topologia fraca da bola unitária não seja metrizável em geral, pode-se caracterizar a compactação fraca usando sequências.
Teorema de Eberlein–Šmulian—Um conjunto ANão. A. em um espaço Banach é relativamente fracamente compacto se e somente se cada sequência (umn?{displaystyle left{a_{n}right}} em ANão. A. tem uma subsequência fracamente convergente.
Um espaço de Banach X- Sim. é reflexivo se e somente se cada sequência limitada em X- Sim. tem uma subsequência fracamente convergente.
Um subconjunto fracamente compacto ANão. A. em Eu... Eu... 1{displaystyle ell ^{1}} é normal. Na verdade, cada sequência em ANão. A. tem subsequências fracamente convergentes por Eberlein–Šmulian, que são norma convergente pela propriedade Schur de Eu... Eu... 1.- Sim.
Bases de Schauder
A Base de Schauder em um espaço de Banach X- Sim. é uma sequência (en?n≥ ≥ 0{displaystyle left{e_{n}right}_{ngeq 0) de vetores em X- Sim. com a propriedade que para cada vetor x∈ ∈ X,{displaystyle xin X,} existe únicamente escalares definidos (xn?n≥ ≥ 0{displaystyle left{x_{n}right}_{ngeq 0) dependendo x,- Sim. tal que
Espaços de Banach com uma base de Schauder são necessariamente separáveis, porque o conjunto contável de combinações lineares finitas com coeficientes racionais (digamos) é denso.
Segue do teorema de Banach-Steinhaus que os mapeamentos lineares (Pn?{displaystyle left{P_{n}right}} são uniformemente limitados por alguma constante C.Não. C. Vamos. (en∗ ∗ ?{displaystyle left{e_{n}^{*}right}} denote as funções de coordenadas que atribuem a cada xNão. em X- Sim. a coordenada xnNão. x_{n}} de xNão. na expansão acima. Eles são chamados funcionais biorthogonais. Quando os vetores de base têm norma 1,- Sim. as funções de coordenadas (en∗ ∗ ?{displaystyle left{e_{n}^{*}right}} tem norma ≤ ≤ 2C{displaystyle ,leq 2C} na dupla de X.Sim.
A maioria dos espaços separáveis clássicos têm bases explícitas. O sistema Haar (hn?{displaystyle left{h_{n}right}} é uma base para <math alttext="{displaystyle L^{p}([0,1]),1leq pLp(Não.0,1]),1≤ ≤ p<∞ ∞ .([0,1]),1leq p<infty.}<img alt="{displaystyle L^{p}([0,1]),1leq p O sistema trigonométrico é uma base em Lp(T)(mathbf {T})} quando <math alttext="{displaystyle 1<p1<p<∞ ∞ .{displaystyle 1<p<infty.}<img alt="{displaystyle 1<p O sistema Schauder é uma base no espaço C(Não.0,1]).([0,1]).} A questão de se a álgebra de disco A(D)A(mathbf {D})} tem uma base permaneceu aberta por mais de quarenta anos, até Bočkarev mostrou em 1974 que A(D)A(mathbf {D})} admite uma base construída a partir do sistema Franklin.
Desde cada vector xNão. em um espaço de Banach X- Sim. com uma base é o limite de Pn(x),(x),} com PnNão. P_{n}} de posição finita e uniformemente limitado, o espaço X- Sim. satisfaz a propriedade de aproximação limitada. O primeiro exemplo de Enflo de um espaço que falha na propriedade de aproximação foi ao mesmo tempo o primeiro exemplo de um espaço Banach separável sem uma base Schauder.
Robert C. James caracterizou a reflexividade em espaços de Banach com uma base: o espaço X- Sim. com uma base de Schauder é reflexiva se e somente se a base estiver encolher e limitadomente completo. Neste caso, as funções biorthogonais formam uma base do dual de X.Sim.
Produto tensor
Vamos. X- Sim. e YNão. Sim. ser dois KK{displaystyle mathbb {K} }- Espaços de vencedores. O produto tensor X⭐ ⭐ YNão. Xotimes Y} de X- Sim. e YNão. Sim. é um KK{displaystyle mathbb {K} }- Espaço de receptor Z.Não. com um mapeamento bilinear T:X× × Y→ → Z.{displaystyle T:Xtimes Yto Z} que tem a seguinte propriedade universal:
- Se T1:X× × Y→ → Z.1Não. T_{1}:Xtimes Yto Z_{1}} é qualquer mapeamento bilinear em um KK{displaystyle mathbb {K} }- Espaço de receptor Z.1,- Sim. então existe um mapeamento linear único f:Z.→ → Z.1{displaystyle f:Zto Z_{1}} tal que T1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =f∘ ∘ T.Não. T_{1}=fcirc T.
A imagem abaixo TNão. T. de um casal (x,Sim.)(x,y)} em X× × YNão. Xtimes Y} é denotado por x⭐ ⭐ Sim.,{displaystyle xotimes y,} e chamado de Tensor simples. Cada elemento zangão.Não. em X⭐ ⭐ YNão. Xotimes Y} é uma soma finita de tais tensores simples.
Existem várias normas que podem ser colocadas no produto tensorial dos espaços vetoriais subjacentes, entre outras a norma cruzada projetiva e a norma cruzada injetiva introduzidas por A. Grothendieck em 1955.
Em geral, o produto tensor de espaços completos não está completo novamente. Ao trabalhar com espaços Banach, é costume dizer que o produto tensor projetivo de dois espaços de Banach X- Sim. e YNão. Sim. é o conclusão X⭐ ⭐ ^ ^ D D YNão. X{widehat Sim. do produto tensor algébrica X⭐ ⭐ YNão. Xotimes Y} equipado com a norma tensor projetiva, e igualmente para o produto tensor injetável X⭐ ⭐ ^ ^ ε ε Y.Não. X{widehat }}_ * Sim. Grothendieck provou em particular que
Produtos tensoriais e a propriedade de aproximação
Vamos. X- Sim. ser um espaço Banach. O produto tensor X?⭐ ⭐ ^ ^ ε ε XNão. X'{widehat * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * é identificado isometricamente com o fechamento em B(X)(X)} do conjunto de operadores de classificação finitas. Quando X- Sim. tem a propriedade de aproximação, este fechamento coincide com o espaço de operadores compactos em X.Sim.
Para cada espaço de Banach Y,Não. Sim. há uma norma natural 1Não. 1 mapa linear
Grothendieck conjecturou que X⭐ ⭐ ^ ^ D D YNão. X{widehat Sim. e X⭐ ⭐ ^ ^ ε ε YNão. X{widehat - Sim. deve ser diferente sempre que X- Sim. e YNão. Sim. são espaços Banach de dimensão infinita. Isso foi reprovado por Gilles Pisier em 1983. Pisier construiu um espaço Banach de dimensão infinita X- Sim. tal que X⭐ ⭐ ^ ^ D D XNão. X{widehat - Sim. e X⭐ ⭐ ^ ^ ε ε XNão. X{widehat * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * são iguais. Além disso, assim como o exemplo de Enflo, este espaço X- Sim. é um espaço "hand-made" que não tem a propriedade de aproximação. Por outro lado, Szankowski provou que o espaço clássico B(Eu... Eu... 2){displaystyle Bleft(ell ^{2}right)} não tem a propriedade de aproximação.
Alguns resultados da classificação
Caracterizações do espaço de Hilbert entre os espaços de Banach
Uma condição necessária e suficiente para a norma de um espaço de Banach X- Sim. estar associado a um produto interno é a identidade do paralelograma:
Identificação do paralelograma—para todos x,Sim.∈ ∈ X:‖ ‖ x+Sim.‖ ‖ 2+‖ ‖ x- Sim. - Sim. Sim.‖ ‖ 2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2(‖ ‖ x‖ ‖ 2+‖ ‖ Sim.‖ ‖ 2).{displaystyle x,yin X:qquad |x+y|^{2}+|x-y|^{2}=2left(|x|^{2}+|y|^{2}right).}
Segue-se, por exemplo, que o espaço Lebesgue Lp(Não.0,1])([0,1])} é um espaço de Hilbert apenas quando p= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2.Não. Se esta identidade estiver satisfeita, o produto interno associado é dado pela identidade de polarização. No caso de escalares reais, isso dá:
Para escalares complexos, definindo o produto interno para ser C{displaystyle mathbb {C} } }-linear em x,- Sim. anti-linear em Sim.,Sim. a identidade de polarização dá:
Para ver que a lei do paralelograma é suficiente, observa-se no caso real que ⟨ ⟨ x,Sim.)) {displaystyle langle x,yrangle } é simétrico, e no caso complexo, que satisfaz a propriedade da simetria hermitiana e ⟨ ⟨ Eu...x,Sim.)) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...⟨ ⟨ x,Sim.)) .{displaystyle langle ix,yrangle =ilangle x,yrangle.} A lei do paralelograma implica que ⟨ ⟨ x,Sim.)) {displaystyle langle x,yrangle } é aditivo em x.Sim. Segue-se que é linear sobre as racionais, assim linear por continuidade.
Existem várias caracterizações de espaços isomorfos (em vez de isométricos) para os espaços de Hilbert. A lei do paralelograma pode ser estendida para mais de dois vetores, e enfraquecida pela introdução de uma desigualdade de dois lados com uma constante c≥ ≥ 1{displaystyle cgeq 1}: Kwapień provou que se
Lindenstrauss e Tzafriri provaram que um espaço de Banach em que cada subespaço linear fechado é complementado (isto é, é a gama de uma projeção linear limitada) é isomorfo para um espaço de Hilbert. A prova repousa sobre o teorema de Dvoretzky sobre seções euclidianas de corpos convexos simétricos centralmente de alta dimensão. Em outras palavras, o teorema de Dvoretzky afirma que para cada inteiro n,Não. qualquer espaço normal finito-dimensional, com dimensão suficientemente grande em comparação com n,Não. contém subespaços quase isométricos para o nNão.-dimensional Espaço euclidiano.
O próximo resultado dá a solução do chamado problema de espaço homogêneo. Um espaço Banach de dimensão infinita X- Sim. é dito para ser homogêneo se for isomorfo para todos os seus subespaços fechados de dimensão infinita. Um espaço de Banach isomorfo para Eu... Eu... 2{displaystyle ell ^{2}} é homogêneo, e Banach pediu o converso.
Teorem—Um espaço de Banach isomorfo para todos os seus subespaços fechados de dimensão infinita é isomorfo para um espaço de Hilbert separável.
Um espaço Banach de dimensão infinita é indecomponível hereditária quando nenhum subespaço dele pode ser isomorfo para a soma direta de dois espaços de Banach infinita-dimensional. O teorema da dicotomia de Gowers afirma que todo espaço de Banach infinita-dimensional X- Sim. contém, ou um subespaço YNão. Sim. com base incondicional, ou um subespaço hereditário indecomponível Z.,Não. Z, e em particular, Z.Não. não é isomorfo para seus hiperplanes fechados. Se X- Sim. é homogênea, portanto, deve ter uma base incondicional. Segue-se então a partir da solução parcial obtida por Komorowski e Tomczak-Jaegermann, para espaços com base incondicional, que X- Sim. isomorfo para Eu... Eu... 2.{displaystyle ell ^{2}.}
Classificação de métricas
Se T:X→ → YNão. T:Xto Y} é uma isometria do espaço Banach X- Sim. para o espaço de Banach YNão. Sim. (onde ambos X- Sim. e YNão. Sim. são espaços vetoriais R{displaystyle mathbb {R} } }), então o teorema Mazur–Ulam afirma que TNão. T. deve ser uma transformação affine. Em particular, se T(0X)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0Y,{displaystyle T(0_{X})=0_{Y},} Isto é... TNão. T. mapeia o zero de X- Sim. para o zero de Y,Não. Sim. então TNão. T. deve ser linear. Este resultado implica que a métrica em espaços de Banach, e mais geralmente em espaços normáticos, capta completamente sua estrutura linear.
Classificação topológica
Os espaços de Banach de dimensão finita são homeomorfos como espaços topológicos, se e somente se tiverem a mesma dimensão que os espaços vetoriais reais.
O teorema de Anderson–Kadec (1965–66) prova que quaisquer dois espaços de Banach separáveis de dimensão infinita são homeomorfos como espaços topológicos. O teorema de Kadec foi estendido por Torunczyk, que provou que quaisquer dois espaços de Banach são homeomorfos se e somente se eles tiverem o mesmo caráter de densidade, a cardinalidade mínima de um subconjunto denso.
Espaços de funções contínuas
Quando dois espaços Hausdorff compactos KK1Não. K_{1}} e KK2{displaystyle K_{2}} são homeomorfos, os espaços de Banach C(KK1)(K_{1}right)} e C(KK2)Não. Cleft(K_{2}right)} são isométricos. Por outro lado, quando KK1Não. K_{1}} não é homeomorfo para KK2,Não. K_{2}, a distância (multiplicativa) Banach–Mazur entre C(KK1)(K_{1}right)} e C(KK2)Não. Cleft(K_{2}right)} deve ser maior ou igual a 2,- Sim. ver acima os resultados de Amir e Cambern. Embora espaços métricos compactos incontáveis possam ter diferentes tipos de homeomorfos, um tem o seguinte resultado devido a Milutin:
Teorem—Vamos. KKNão. ser um espaço métrico compacto incontável. Então... C(KK)(K)} isomorfo para C(Não.0,1]).([0,1]).}
A situação é diferente para espaços Hausdorff compactos contáveis. Cada compacto contavelmente infinito KKNão. é homeomorfo para algum intervalo fechado de números ordinais
Exemplos
Glossário de símbolos da tabela abaixo:
- F{displaystyle mathbb {F} } } denota o campo dos números reais R{displaystyle mathbb {R} } } ou números complexos C.{displaystyle mathbb {C}.}
- KKNão. é um espaço Hausdorff compacto.
- p,q∈ ∈ R{displaystyle p,qin mathbb Não. são números reais com <math alttext="{displaystyle 1<p,q1<p,q<∞ ∞ {displaystyle 1<p,q<infty }<img alt="{displaystyle 1<p,q que são Hölder conjuga, o que significa que eles satisfazem 1q+1p= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1{displaystyle {frac {1}{q}}+{frac Não. e assim também q= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =pp- Sim. - Sim. 1.- Sim. {p}{p-1}}.}
- Σ Σ Não. Sim. é um σ σ - Sim.- Álcool de conjuntos.
- ? ? - Sim. é uma álgebra de conjuntos (para espaços que exigem apenas aditividade finita, como o espaço ba).
- μ μ - Sim. é uma medida com variação |μ μ |.|mu |.} Uma medida positiva é uma função definida positiva de valor real definida em uma σ σ - Sim.- álgebra que é contável aditivo.
| Classical Banach spaces | ||||||
| Dual space | Reflexive | weakly sequentially complete | Norm | Notes | ||
|---|---|---|---|---|---|---|
| F n {displaystyle mathbb {F} ^{n}} | F n {displaystyle mathbb {F} ^{n}} | Yes | Yes | ‖ x ‖ 2 {displaystyle |x|_{2}} | = ( ∑ i = 1 n | x i | 2 ) 1 / 2 {displaystyle =left(sum _{i=1}^{n}|x_{i}|^{2}right)^{1/2}} | Euclidean space |
| ℓ p n {displaystyle ell _{p}^{n}} | ℓ q n {displaystyle ell _{q}^{n}} | Yes | Yes | ‖ x ‖ p {displaystyle |x|_{p}} | = ( ∑ i = 1 n | x i | p ) 1 p {displaystyle =left(sum _{i=1}^{n}|x_{i}|^{p}right)^{frac {1}{p}}} | |
| ℓ ∞ n {displaystyle ell _{infty }^{n}} | ℓ 1 n {displaystyle ell _{1}^{n}} | Yes | Yes | ‖ x ‖ ∞ {displaystyle |x|_{infty }} | = max 1 ≤ i ≤ n | x i | {displaystyle =max nolimits _{1leq ileq n}|x_{i}|} | |
| ℓ p {displaystyle ell ^{p}} | ℓ q {displaystyle ell ^{q}} | Yes | Yes | ‖ x ‖ p {displaystyle |x|_{p}} | = ( ∑ i = 1 ∞ | x i | p ) 1 p {displaystyle =left(sum _{i=1}^{infty }|x_{i}|^{p}right)^{frac {1}{p}}} | |
| ℓ 1 {displaystyle ell ^{1}} | ℓ ∞ {displaystyle ell ^{infty }} | No | Yes | ‖ x ‖ 1 {displaystyle |x|_{1}} | = ∑ i = 1 ∞ | x i | {displaystyle =sum _{i=1}^{infty }left|x_{i}right|} | |
| ℓ ∞ {displaystyle ell ^{infty }} | ba {displaystyle operatorname {ba} } | No | No | ‖ x ‖ ∞ {displaystyle |x|_{infty }} | = sup i | x i | {displaystyle =sup nolimits _{i}left|x_{i}right|} | |
| c {displaystyle operatorname {c} } | ℓ 1 {displaystyle ell ^{1}} | No | No | ‖ x ‖ ∞ {displaystyle |x|_{infty }} | = sup i | x i | {displaystyle =sup nolimits _{i}left|x_{i}right|} | |
| c 0 {displaystyle c_{0}} | ℓ 1 {displaystyle ell ^{1}} | No | No | ‖ x ‖ ∞ {displaystyle |x|_{infty }} | = sup i | x i | {displaystyle =sup nolimits _{i}left|x_{i}right|} | Isomorphic but not isometric to c . {displaystyle c.} |
| bv {displaystyle operatorname {bv} } | ℓ ∞ {displaystyle ell ^{infty }} | No | Yes | ‖ x ‖ b v {displaystyle |x|_{bv}} | = | x 1 | + ∑ i = 1 ∞ | x i + 1 − x i | {displaystyle =left|x_{1}right|+sum _{i=1}^{infty }left|x_{i+1}-x_{i}right|} | Isometrically isomorphic to ℓ 1 . {displaystyle ell ^{1}.} |
| bv 0 {displaystyle operatorname {bv} _{0}} | ℓ ∞ {displaystyle ell ^{infty }} | No | Yes | ‖ x ‖ b v 0 {displaystyle |x|_{bv_{0}}} | = ∑ i = 1 ∞ | x i + 1 − x i | {displaystyle =sum _{i=1}^{infty }left|x_{i+1}-x_{i}right|} | Isometrically isomorphic to ℓ 1 . {displaystyle ell ^{1}.} |
| bs {displaystyle operatorname {bs} } | ba {displaystyle operatorname {ba} } | No | No | ‖ x ‖ b s {displaystyle |x|_{bs}} | = sup n | ∑ i = 1 n x i | {displaystyle =sup nolimits _{n}left|sum _{i=1}^{n}x_{i}right|} | Isometrically isomorphic to ℓ ∞ . {displaystyle ell ^{infty }.} |
| cs {displaystyle operatorname {cs} } | ℓ 1 {displaystyle ell ^{1}} | No | No | ‖ x ‖ b s {displaystyle |x|_{bs}} | = sup n | ∑ i = 1 n x i | {displaystyle =sup nolimits _{n}left|sum _{i=1}^{n}x_{i}right|} | Isometrically isomorphic to c . {displaystyle c.} |
| B ( K , Ξ ) {displaystyle B(K,Xi)} | ba ( Ξ ) {displaystyle operatorname {ba} (Xi)} | No | No | ‖ f ‖ B {displaystyle |f|_{B}} | = sup k ∈ K | f ( k ) | {displaystyle =sup nolimits _{kin K}|f(k)|} | |
| C ( K ) {displaystyle C(K)} | rca ( K ) {displaystyle operatorname {rca} (K)} | No | No | ‖ x ‖ C ( K ) {displaystyle |x|_{C(K)}} | = max k ∈ K | f ( k ) | {displaystyle =max nolimits _{kin K}|f(k)|} | |
| ba ( Ξ ) {displaystyle operatorname {ba} (Xi)} | ? | No | Yes | ‖ μ ‖ b a {displaystyle |mu |_{ba}} | = sup S ∈ Σ | μ | ( S ) {displaystyle =sup nolimits _{Sin Sigma }|mu |(S)} | |
| ca ( Σ ) {displaystyle operatorname {ca} (Sigma)} | ? | No | Yes | ‖ μ ‖ b a {displaystyle |mu |_{ba}} | = sup S ∈ Σ | μ | ( S ) {displaystyle =sup nolimits _{Sin Sigma }|mu |(S)} | A closed subspace of ba ( Σ ) . {displaystyle operatorname {ba} (Sigma).} |
| rca ( Σ ) {displaystyle operatorname {rca} (Sigma)} | ? | No | Yes | ‖ μ ‖ b a {displaystyle |mu |_{ba}} | = sup S ∈ Σ | μ | ( S ) {displaystyle =sup nolimits _{Sin Sigma }|mu |(S)} | A closed subspace of ca ( Σ ) . {displaystyle operatorname {ca} (Sigma).} |
| L p ( μ ) {displaystyle L^{p}(mu)} | L q ( μ ) {displaystyle L^{q}(mu)} | Yes | Yes | ‖ f ‖ p {displaystyle |f|_{p}} | = ( ∫ | f | p d μ ) 1 p {displaystyle =left(int |f|^{p},dmu right)^{frac {1}{p}}} | |
| L 1 ( μ ) {displaystyle L^{1}(mu)} | L ∞ ( μ ) {displaystyle L^{infty }(mu)} | No | Yes | ‖ f ‖ 1 {displaystyle |f|_{1}} | = ∫ | f | d μ {displaystyle =int |f|,dmu } | The dual is L ∞ ( μ ) {displaystyle L^{infty }(mu)} if μ {displaystyle mu } is σ {displaystyle sigma } -finite. |
| BV ( [ a , b ] ) {displaystyle operatorname {BV} ([a,b])} | ? | No | Yes | ‖ f ‖ B V {displaystyle |f|_{BV}} | = V f ( [ a , b ] ) + lim x → a + f ( x ) {displaystyle =V_{f}([a,b])+lim nolimits _{xto a^{+}}f(x)} | V f ( [ a , b ] ) . {displaystyle V_{f}([a,b]).} is the total variation of f {displaystyle f} |
| NBV ( [ a , b ] ) {displaystyle operatorname {NBV} ([a,b])} | ? | No | Yes | ‖ f ‖ B V {displaystyle |f|_{BV}} | = V f ( [ a , b ] ) {displaystyle =V_{f}([a,b])} | NBV ( [ a , b ] ) {displaystyle operatorname {NBV} ([a,b])} consists of BV ( [ a , b ] ) {displaystyle operatorname {BV} ([a,b])} functions such that lim x → a + f ( x ) = 0 {displaystyle lim nolimits _{xto a^{+}}f(x)=0} |
| AC ( [ a , b ] ) {displaystyle operatorname {AC} ([a,b])} | F + L ∞ ( [ a , b ] ) {displaystyle mathbb {F} +L^{infty }([a,b])} | No | Yes | ‖ f ‖ B V {displaystyle |f|_{BV}} | = V f ( [ a , b ] ) + lim x → a + f ( x ) {displaystyle =V_{f}([a,b])+lim nolimits _{xto a^{+}}f(x)} | Isomorphic to the Sobolev space W 1 , 1 ( [ a , b ] ) . {displaystyle W^{1,1}([a,b]).} |
| C n ( [ a , b ] ) {displaystyle C^{n}([a,b])} | rca ( [ a , b ] ) {displaystyle operatorname {rca} ([a,b])} | No | No | ‖ f ‖ {displaystyle |f|} | = ∑ i = 0 n sup x ∈ [ a , b ] | f ( i ) ( x ) | {displaystyle =sum _{i=0}^{n}sup nolimits _{xin [a,b]}left|f^{(i)}(x)right|} | Isomorphic to R n ⊕ C ( [ a , b ] ) , {displaystyle mathbb {R} ^{n}oplus C([a,b]),} essentially by Taylor's theorem. |
Derivados
Vários conceitos de uma derivada podem ser definidos em um espaço de Banach. Consulte os artigos sobre a derivada de Fréchet e a derivada de Gateaux para obter detalhes. A derivada de Fréchet permite uma extensão do conceito de derivada total para espaços de Banach. A derivada Gateaux permite uma extensão de uma derivada direcional para espaços vetoriais topológicos localmente convexos. A diferenciabilidade de Fréchet é uma condição mais forte do que a diferenciabilidade de Gateaux. A quase-derivada é outra generalização da derivada direcional que implica uma condição mais forte que a diferenciabilidade de Gateaux, mas uma condição mais fraca que a diferenciabilidade de Fréchet.
Generalizações
Vários espaços importantes na análise funcional, por exemplo, o espaço de todas as funções infinitamente muitas vezes diferenciadas R→ → R,{displaystyle mathbb {R} to mathbb (R) ou o espaço de todas as distribuições em R,{displaystyle mathbb {R}} são completos, mas não são espaços vetoriais normalizados e, portanto, não espaços de Banach. Nos espaços Fréchet ainda há uma métrica completa, enquanto os espaços LF são espaços vetoriais uniformes completos que surgem como limites dos espaços Fréchet.
Contenido relacionado
Círculo
Exponenciação ao quadrado
Aritmética






































































































































































































![{displaystyle L^{p}([0,1])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d53d55ccc06ce5cc9ec3bede2be3e7933c206ee3)
![{displaystyle L^{q}([0,1])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a03e8e5b19ee520920c0f1415e1ddb4c59b58d0d)















































![{displaystyle c_{0},ell ^{1},L^{1}([0,1]),C([0,1])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e865f393700c33f7fed51aa7c595261b480f309c)









































![{displaystyle C([0,1]).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48046f59cbf686554839918953b0000a1d9ac39b)


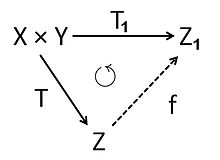











![{displaystyle {begin{aligned}C(K){widehat {otimes }}_{varepsilon }Y&simeq C(K,Y),\L^{1}([0,1]){widehat {otimes }}_{pi }Y&simeq L^{1}([0,1],Y),end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fdda0e4532c785e0ccddd2743db91e009ace27bb)

![{displaystyle L^{1}([0,1],Y)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/260abf31df513876af3c866808034d0d771cf448)
![[0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)































































































![{displaystyle operatorname {BV} ([a,b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f6474e123b8d06d5989e779c17b9084f2ba8314)

![{displaystyle =V_{f}([a,b])+lim nolimits _{xto a^{+}}f(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25115dbc151a6a6ca22cd714e3c0a588ae8c97ab)
![{displaystyle V_{f}([a,b]).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/905358a6da56a9c1e75a7c8722635a2fd65e47c6)
![{displaystyle operatorname {NBV} ([a,b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97eacd1b77125924adb034d279f23ccb1aae4cfc)
![{displaystyle =V_{f}([a,b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3978b950e1c45a40b89de47e166dff3e3f640f90)

![{displaystyle operatorname {AC} ([a,b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1215f6bb4f5dcce36b275a1038200a2da63ffc8)
![{displaystyle mathbb {F} +L^{infty }([a,b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ef63fd9a8ef0c7df601ba2aa141815ea86073da)
![{displaystyle W^{1,1}([a,b]).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a982993a7010fe121285b640c096068e79e74874)
![{displaystyle C^{n}([a,b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e5f2c81e52a668fa74a30946eac00229b1d642f)
![{displaystyle operatorname {rca} ([a,b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8788ca02e303b567e9d47a44b0fd48a574ddbfb)
![{displaystyle =sum _{i=0}^{n}sup nolimits _{xin [a,b]}left|f^{(i)}(x)right|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cc9f7a9abc638e6fe431d6f36760dbd074b3019)
![{displaystyle mathbb {R} ^{n}oplus C([a,b]),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e48ac47f9406ef46b3c762f19d0d246b54425aa5)
