Empurrão (física)
Na física, jerk ou salto é a taxa na qual a aceleração de um objeto muda em relação ao tempo. É uma quantidade vetorial (tendo módulo e direção). Jerk é mais comumente indicado pelo símbolo j e expresso em m/s3 (unidades SI) ou gravidades padrão por segundo (g0/s).
Expressões
Como um vetor, jerk j pode ser expresso como a primeira derivada temporal da aceleração, a segunda derivada temporal da velocidade e a terceira derivada temporal da posição:
Onde:
- um é aceleração
- v é velocidade
- R posição
- ) é tempo
Equações diferenciais de terceira ordem da forma
Efeitos fisiológicos e percepção humana
A posição do corpo humano é controlada pelo equilíbrio das forças dos músculos antagonistas. Ao equilibrar uma determinada força, como segurar um peso, o giro pós-central estabelece um circuito de controle para alcançar o equilíbrio desejado. Se a força mudar muito rapidamente, os músculos não podem relaxar ou ficar tensos rápido o suficiente e disparar em qualquer direção, causando uma perda temporária de controle. O tempo de reação para responder às mudanças de força depende das limitações fisiológicas e do nível de atenção do cérebro: uma mudança esperada será estabilizada mais rapidamente do que uma diminuição ou aumento súbito da carga.
Para evitar que os passageiros do veículo percam o controle sobre o movimento do corpo e se machuquem, é necessário limitar a exposição tanto à força máxima (aceleração) quanto ao solavanco máximo, pois é necessário tempo para ajustar a tensão muscular e adaptar-se até mesmo a mudanças limitadas de estresse. Mudanças repentinas na aceleração podem causar ferimentos como chicotada. O solavanco excessivo também pode resultar em uma condução desconfortável, mesmo em níveis que não causem ferimentos. Os engenheiros gastam um esforço considerável de projeto minimizando o "movimento brusco" em elevadores, bondes e outros meios de transporte.
Por exemplo, considere os efeitos da aceleração e solavancos ao andar de carro:
- Drivers qualificados e experientes podem acelerar suavemente, mas iniciantes muitas vezes fornecem um Idiota. montar. Ao mudar as engrenagens em um carro com uma embreagem operada a pé, a força acelerante é limitada pela potência do motor, mas um motorista inexperiente pode causar um embuste grave por causa do fechamento de força intermitente sobre a embreagem.
- A sensação de ser pressionado para os assentos em um carro esportivo de alta potência é devido à aceleração. À medida que o carro lança do resto, há um grande idiota positivo à medida que sua aceleração aumenta rapidamente. Após o lançamento, há um pequeno e sustentado idiota negativo à medida que a força da resistência ao ar aumenta com a velocidade do carro, diminuindo gradualmente a aceleração e reduzindo a força pressionando o passageiro para o assento. Quando o carro atinge sua velocidade máxima, a aceleração atingiu 0 e permanece constante, após o qual não há nenhum idiota até que o motorista desacelere ou mude a direção.
- Ao travar repentinamente ou durante colisões, os passageiros apalpam com uma aceleração inicial que é maior do que durante o resto do processo de travagem porque a tensão muscular recupera o controle do corpo rapidamente após o início da travagem ou impacto. Estes efeitos não são modelados em testes de veículos porque cadáveres e manequins teste de acidente não têm controle muscular ativo.
- Para minimizar os efeitos de um idiota, as curvas ao longo das estradas são projetadas para ser panoides como são curvas de estrada de ferro e costas de montanha-russa.
Força, aceleração e solavanco
Para uma massa constante m, aceleração a é diretamente proporcional à força F de acordo com a segunda lei do movimento de Newton:
Na mecânica clássica dos corpos rígidos, não existem forças associadas às derivadas da aceleração; no entanto, os sistemas físicos experimentam oscilações e deformações como resultado do solavanco. Ao projetar o Telescópio Espacial Hubble, a NASA estabeleceu limites tanto para o solavanco quanto para o solavanco.
A força de Abraham-Lorentz é a força de recuo em uma partícula carregada em aceleração que emite radiação. Essa força é proporcional ao solavanco da partícula e ao quadrado de sua carga. A teoria do absorvedor de Wheeler-Feynman é uma teoria mais avançada, aplicável em um ambiente relativístico e quântico e responsável pela auto-energia.
Em um ambiente idealizado
Descontinuidades na aceleração não ocorrem em ambientes do mundo real devido à deformação, efeitos da mecânica quântica e outras causas. No entanto, uma descontinuidade de salto na aceleração e, conseqüentemente, um solavanco ilimitado são viáveis em um cenário idealizado, como uma massa pontual idealizada movendo-se ao longo de um caminho totalmente contínuo e suave por partes. A descontinuidade de salto ocorre em pontos onde o caminho não é suave. Extrapolando a partir dessas configurações idealizadas, pode-se descrever, explicar e prever qualitativamente os efeitos do idiota em situações reais.
A descontinuidade do salto na aceleração pode ser modelada usando uma função delta de Dirac no jerk, dimensionada para a altura do salto. A integração do jerk ao longo do tempo através do delta de Dirac produz a descontinuidade do salto.
Por exemplo, considere um caminho ao longo de um arco de raio r, que se conecta tangencialmente a uma linha reta. Todo o caminho é contínuo e suas partes são lisas. Agora, suponha que uma partícula pontual se mova com velocidade constante ao longo desse caminho, de modo que sua aceleração tangencial seja zero. A aceleração centrípeta dada por v2/r é normal para o arco e para dentro. Quando a partícula passa pela conexão das peças, ela experimenta um salto-descontinuidade na aceleração dada por v2/r , e sofre um solavanco que pode ser modelado por um delta de Dirac, dimensionado para a descontinuidade de salto.
Para um exemplo mais tangível de aceleração descontínua, considere um sistema massa-mola ideal com a massa oscilando em uma superfície idealizada com atrito. A força sobre a massa é igual à soma vetorial da força da mola e da força de atrito cinético. Quando a velocidade muda de sinal (nos deslocamentos máximo e mínimo), o módulo da força sobre a massa muda duas vezes o módulo da força de atrito, porque a força da mola é contínua e a força de atrito inverte a direção com a velocidade. O salto na aceleração é igual à força sobre a massa dividida pela massa. Ou seja, cada vez que a massa passa por um deslocamento mínimo ou máximo, a massa experimenta uma aceleração descontínua e o solavanco contém um delta de Dirac até que a massa pare. A força de atrito estático se adapta à força residual da mola, estabelecendo equilíbrio com força líquida zero e velocidade zero.
Considere o exemplo de um carro freando e desacelerando. As pastilhas de freio geram forças de atrito cinético e torques de frenagem constantes nos discos (ou tambores) das rodas. A velocidade rotacional diminui linearmente até zero com desaceleração angular constante. A força de atrito, o torque e a desaceleração do carro atingem repentinamente zero, o que indica um delta de Dirac em solavanco físico. O delta de Dirac é suavizado pelo ambiente real, cujos efeitos cumulativos são análogos ao amortecimento do solavanco percebido fisiologicamente. Este exemplo negligencia os efeitos do deslizamento do pneu, mergulho da suspensão, deflexão real de todos os mecanismos idealmente rígidos, etc.
Outro exemplo de solavanco significativo, análogo ao primeiro exemplo, é o corte de uma corda com uma partícula em sua extremidade. Suponha que a partícula esteja oscilando em uma trajetória circular com aceleração centrípeta diferente de zero. Quando a corda é cortada, o caminho da partícula muda abruptamente para um caminho reto e a força na direção interna muda repentinamente para zero. Imagine uma fibra monomolecular cortada por um laser; a partícula experimentaria taxas muito altas de jerk por causa do tempo de corte extremamente curto.
Em rotação
Considere um corpo rígido girando em torno de um eixo fixo em um referencial inercial. Se sua posição angular em função do tempo for θ(t), a velocidade angular, a aceleração e o solavanco podem ser expresso da seguinte forma:
- Velocidade angular, ω ω ())= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =θ θ :: ())= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Dθ θ ())D){displaystyle omega (t)={dot {theta }}(t)={frac {mathrm {d} theta (t)}{mathrm {d} - Sim., é o tempo derivado de θ()).
- Aceleração angular, α α ())= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =ω ω :: ())= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Dω ω ())D){displaystyle alpha (t)={dot {omega }}(t)={frac {mathrm {d} omega (t)}{mathrm {d} - Sim., é o tempo derivado de ω()).
- Idiota angular, ζ ζ ())= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =α α :: ())= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =ω ω " " ())= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =θ θ ...()){displaystyle zeta (t)={dot {alpha }}(t)={ddot {omega }}(t)={overset {...}{theta }}(t)}, é o tempo derivado de α()).
A aceleração angular é igual ao torque que atua no corpo, dividido pelo momento de inércia do corpo em relação ao eixo momentâneo de rotação. Uma mudança no torque resulta em solavanco angular.
O caso geral de um corpo rígido em rotação pode ser modelado usando a teoria do parafuso cinemático, que inclui um vetor axial, velocidade angular Ω(t), e um vetor polar, velocidade linear v(t). A partir disso, a aceleração angular é definida como
e o solavanco angular é dado por
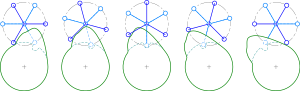
Por exemplo, considere uma unidade de Genebra, um dispositivo usado para criar rotação intermitente de uma roda motriz (a roda azul na animação) por rotação contínua de uma roda motriz (a roda vermelha na animação). Durante um ciclo da roda motriz, a posição angular da roda motriz θ muda em 90 graus e depois permanece constante. Devido à espessura finita do garfo da roda motriz (a ranhura do pino motriz), esse dispositivo gera uma descontinuidade na aceleração angular α, e um solavanco angular ilimitado ζ na roda motriz.
O Jerk não impede que a unidade Geneva seja usada em aplicativos como projetores de filmes e câmeras. Em projetores de cinema, o filme avança quadro a quadro, mas a operação do projetor tem baixo ruído e é altamente confiável devido à baixa carga de filme (apenas uma pequena seção de filme pesando alguns gramas é conduzida), a velocidade moderada (2,4 m/s) e o baixo atrito.
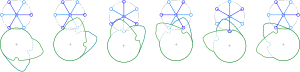
Com sistemas de acionamento de came, o uso de um came duplo pode evitar o solavanco de um único came; no entanto, a câmera dupla é mais volumosa e mais cara. O sistema de came duplo tem dois cames em um eixo que desloca um segundo eixo em uma fração de revolução. O gráfico mostra acionamentos escalonados de um sexto e um terço de rotação por uma revolução do eixo motriz. Não há folga radial porque dois braços da roda escalonada estão sempre em contato com o came duplo. Geralmente, contatos combinados podem ser usados para evitar solavancos (e desgaste e ruído) associados a um único seguidor (como um único seguidor deslizando ao longo de um slot e mudando seu ponto de contato de um lado do slot para o outro pode ser evitado por usando dois seguidores deslizando ao longo do mesmo slot, um lado cada).
Em matéria elasticamente deformável
Uma massa elasticamente deformável se deforma sob uma força aplicada (ou aceleração); a deformação é uma função de sua rigidez e da magnitude da força. Se a mudança na força for lenta, o solavanco é pequeno e a propagação da deformação é considerada instantânea em comparação com a mudança na aceleração. O corpo distorcido age como se estivesse em regime quase-estático, e somente uma força variável (solavanco diferente de zero) pode causar a propagação de ondas mecânicas (ou ondas eletromagnéticas para uma partícula carregada); portanto, para solavancos diferentes de zero a alto, uma onda de choque e sua propagação pelo corpo devem ser consideradas.
A propagação da deformação é mostrada no gráfico "Padrões de onda de compressão" como uma onda plana de compressão através de um material elasticamente deformável. Também são mostradas, para solavancos angulares, as ondas de deformação que se propagam em um padrão circular, o que causa tensão de cisalhamento e possivelmente outros modos de vibração. A reflexão das ondas ao longo dos limites causa padrões de interferência construtiva (não ilustrados), produzindo tensões que podem ultrapassar os limites do material. As ondas de deformação podem causar vibrações, que podem levar a ruídos, desgastes e falhas, principalmente em casos de ressonância.
O gráfico com a legenda "Poste com topo maciço" mostra um bloco conectado a um poste elástico e um topo maciço. O poste dobra quando o bloco acelera, e quando a aceleração para, o topo oscilará (amortecido) sob o regime de rigidez do poste. Pode-se argumentar que um solavanco (periódico) maior pode excitar uma amplitude maior de oscilação porque pequenas oscilações são amortecidas antes do reforço por uma onda de choque. Pode-se também argumentar que um solavanco maior pode aumentar a probabilidade de excitar um modo ressonante porque os componentes de onda maiores da onda de choque têm frequências e coeficientes de Fourier mais altos.
Para reduzir a amplitude das ondas de tensão e vibrações excitadas, pode-se limitar o solavanco moldando o movimento e tornando a aceleração contínua com inclinações tão planas quanto possível. Devido às limitações dos modelos abstratos, os algoritmos para redução de vibrações incluem derivadas superiores, como jounce, ou sugerem regimes contínuos tanto para aceleração quanto para jerk. Um conceito para limitar o solavanco é moldar a aceleração e a desaceleração senoidalmente com aceleração zero no meio (consulte o gráfico com a legenda "Perfil de aceleração senoidal"), fazendo com que a velocidade pareça senoidal com velocidade máxima constante. O solavanco, no entanto, permanecerá descontínuo nos pontos onde a aceleração entra e sai das fases zero.
No desenho geométrico de estradas e trilhos
Estradas e trilhas são projetadas para limitar o solavanco causado por mudanças em sua curvatura. Nas ferrovias, os projetistas usam 0,35 m/s3 como meta de projeto e 0,5 m/s3 como máximo. As curvas de transição de pista limitam o solavanco ao fazer a transição de uma linha reta para uma curva ou vice-versa. Lembre-se de que no movimento de velocidade constante ao longo de um arco, o jerk é zero na direção tangencial e diferente de zero na direção normal interna. As curvas de transição aumentam gradativamente a curvatura e, consequentemente, a aceleração centrípeta.
Uma espiral de Euler, a curva de transição teoricamente ideal, aumenta linearmente a aceleração centrípeta e resulta em solavancos constantes (ver gráfico). Em aplicações do mundo real, o plano da via é inclinado (cant) ao longo das seções curvas. A inclinação causa aceleração vertical, que é uma consideração de projeto para desgaste na via e no aterro. A Wiener Kurve (Curva Vienense) é uma curva patenteada projetada para minimizar esse desgaste.
As montanhas-russas também são projetadas com transições de pista para limitar o solavanco. Ao entrar em um loop, os valores de aceleração podem chegar a cerca de 4g (40 m/s2), e pilotar neste ambiente de alta aceleração só é possível com transições de pista. Curvas em forma de S, como oitos, também usam transições de pista para passeios suaves.
No controle de movimento
No controle de movimento, o foco do projeto está no movimento reto e linear, com a necessidade de mover um sistema de uma posição estável para outra (movimento ponto a ponto). A preocupação do projeto de uma perspectiva de empurrão é empurrão vertical; o solavanco da aceleração tangencial é efetivamente zero, pois o movimento linear não é rotacional.
Aplicações de controle de movimento incluem elevadores de passageiros e ferramentas de usinagem. Limitar o solavanco vertical é considerado essencial para a conveniência de andar no elevador. A ISO 18738 especifica métodos de medição para a qualidade da viagem do elevador com relação a solavancos, aceleração, vibração e ruído; no entanto, o padrão especifica níveis de qualidade de condução aceitável ou inaceitável. É relatado que a maioria dos passageiros classifica um solavanco vertical de 2 m/s3 como aceitável e 6 m/s3 como intolerável. Para hospitais, 0,7 m/s3 é o limite recomendado.
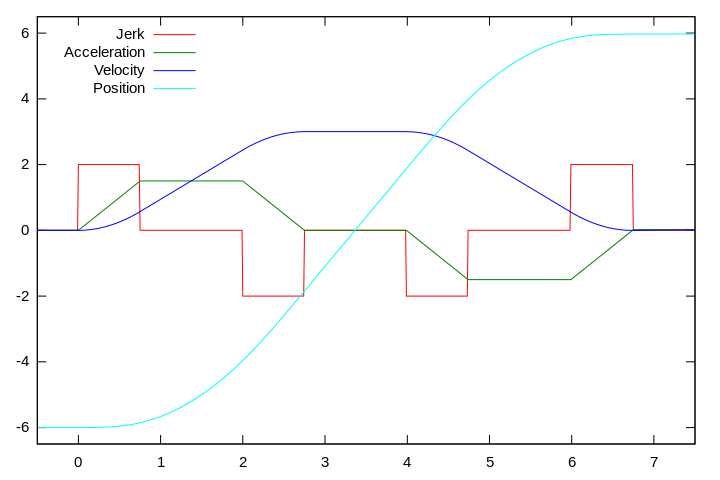
Um objetivo principal do projeto para controle de movimento é minimizar o tempo de transição sem exceder os limites de velocidade, aceleração ou solavanco. Considere um perfil de controle de movimento de terceira ordem com rampa quadrática e fases deramping em velocidade (veja a figura).
Este perfil de movimento consiste nos seguintes sete segmentos:
- Acceleration build up — limite de empurrão positivo; aumento linear na aceleração ao limite de aceleração positiva; aumento quadrático da velocidade
- Limite de aceleração superior — zero idiota; aumento linear da velocidade
- Rampa de aceleração para baixo — limite de golpe negativo; diminuição linear na aceleração; (negativo) aumento quadrático na velocidade, aproximando-se do limite de velocidade desejado
- Limite de velocidade — zero idiota; zero aceleração
- Aumento de desaceleração — limite de golpe negativo; diminuição linear na aceleração ao limite de aceleração negativa; (negativa) diminuição quadrática na velocidade
- Limite de desaceleração inferior — zero idiota; diminuição linear da velocidade
- Rampa de desaceleração para baixo — limite de idiota positivo; aumento linear na aceleração a zero; diminuição quadrática na velocidade; aproximação da posição desejada à velocidade zero e aceleração zero
O período de tempo do segmento quatro (velocidade constante) varia com a distância entre as duas posições. Se esta distância for tão pequena que omitir o segmento quatro não seria suficiente, então os segmentos dois e seis (aceleração constante) poderiam ser igualmente reduzidos e o limite de velocidade constante não seria atingido. Se essa modificação não reduzir suficientemente a distância percorrida, os segmentos um, três, cinco e sete podem ser encurtados em uma quantidade igual e os limites de aceleração constante não serão alcançados.
Outras estratégias de perfil de movimento são usadas, como minimizar o quadrado do solavanco para um determinado tempo de transição e, conforme discutido acima, perfis de aceleração em formato senoidal. Os perfis de movimento são adaptados para aplicações específicas, incluindo máquinas, transportadores de pessoas, talhas de corrente, automóveis e robótica.
Na fabricação
O Jerk é uma consideração importante nos processos de fabricação. Mudanças rápidas na aceleração de uma ferramenta de corte podem levar ao desgaste prematuro da ferramenta e resultar em cortes irregulares; conseqüentemente, os controladores de movimento modernos incluem recursos de limitação de solavancos. Na engenharia mecânica, o solavanco, além da velocidade e aceleração, é considerado no desenvolvimento de perfis de came devido às implicações tribológicas e à capacidade do corpo acionado de seguir o perfil do came sem trepidação. O empurrão é frequentemente considerado quando a vibração é uma preocupação. Um dispositivo que mede jerk é chamado de "jerkmeter".
Mais derivados
Outros derivados de tempo também foram nomeados, como snap ou jounce (quarta derivada), crackle (quinta derivada) e pop (sexta derivada). No entanto, derivadas temporais de posição de ordem superior a quatro aparecem raramente.
Os termos snap, crackle e pop—para a quarta, quinta e sexta derivadas de posição—foram inspirados no mascotes publicitários Snap, Crackle e Pop.