Efeito Doppler

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Mudança de frequência de uma onda para o observador em relação à sua fonte

Mudança de comprimento de onda causada pelo movimento da fonte.

Uma animação ilustrando como o efeito Doppler faz com que um motor de carro ou sirene soe mais alto no campo quando se aproxima do que quando está retroceder. Os círculos vermelhos representam ondas sonoras.

Passando chifre de carro

O efeito Doppler ou deslocamento Doppler (ou simplesmente Doppler, quando no contexto) é a mudança aparente na frequência de uma onda em relação para um observador que está se movendo em relação à fonte de onda. É nomeado após o físico austríaco Christian Doppler, que descreveu o fenômeno em 1842.

Um exemplo comum de deslocamento Doppler é a mudança de tom ouvida quando um veículo soando uma buzina se aproxima e se afasta de um observador. Em comparação com a frequência emitida, a frequência recebida é maior durante a aproximação, idêntica no instante da passagem e menor durante a recessão.

A razão para o efeito Doppler é que quando a fonte das ondas está se movendo em direção ao observador, cada crista de onda sucessiva é emitida de uma posição mais próxima do observador do que a crista da onda anterior. Portanto, cada onda leva um pouco menos de tempo para chegar ao observador do que a onda anterior. Assim, o tempo entre as chegadas de sucessivas cristas de onda ao observador é reduzido, causando um aumento na frequência. Enquanto viajam, a distância entre as frentes de onda sucessivas é reduzida, de modo que as ondas "se agrupam". Por outro lado, se a fonte das ondas estiver se afastando do observador, cada onda é emitida de uma posição mais distante do observador do que a onda anterior, de modo que o tempo de chegada entre as ondas sucessivas é aumentado, reduzindo a frequência. A distância entre frentes de onda sucessivas é então aumentada, de modo que as ondas "se espalham".

Para ondas que se propagam em um meio, como ondas sonoras, a velocidade do observador e da fonte são relativas ao meio no qual as ondas são transmitidas. O efeito Doppler total pode, portanto, resultar do movimento da fonte, do movimento do observador ou do movimento do meio. Cada um desses efeitos é analisado separadamente. Para ondas que não requerem um meio, como ondas eletromagnéticas ou ondas gravitacionais, apenas a diferença relativa de velocidade entre o observador e a fonte precisa ser considerada. Quando esta velocidade relativa não é desprezível em comparação com a velocidade da luz, surge um efeito Doppler relativístico mais complicado.

História

Experimento por Buys Ballot (1845) retratado em uma parede em Utrecht (2019)

Doppler propôs esse efeito pela primeira vez em 1842 em seu tratado "Über das farbige Licht der Doppelsterne und einiger anderer Gestirne des Himmels" (Sobre a luz colorida das estrelas binárias e algumas outras estrelas dos céus). A hipótese foi testada para ondas sonoras por Buys Ballot em 1845. Ele confirmou que o tom do som era maior que a frequência emitida quando a fonte sonora se aproximava dele e menor que a frequência emitida quando a fonte sonora se afastava dele. Hippolyte Fizeau descobriu independentemente o mesmo fenômeno em ondas eletromagnéticas em 1848 (na França, o efeito às vezes é chamado de "effet Doppler-Fizeau", mas esse nome não foi adotado pelo resto do mundo como Fizeau's descoberta foi seis anos após a proposta de Doppler). Na Grã-Bretanha, John Scott Russell fez um estudo experimental do efeito Doppler (1848).

Geral

Na física clássica, onde as velocidades da fonte e o receptor relativo ao meio são menores do que a velocidade das ondas no meio, a relação entre a frequência observada $f$ e frequência emitida $f_{{text{0}}}$ é dado por:

{displaystyle f=left({frac {cpm v_{text{r}}}{cpm v_{text{s}}}}right)f_{0}}

$c$ é a velocidade de propagação de ondas no meio;
${displaystyle v_{text{r}}}$ é a velocidade do receptor em relação ao meio, adicionado ao $c$ se o receptor estiver se movendo para a fonte, subtraído se o receptor estiver se afastando da fonte;
${displaystyle v_{text{s}}}$ é a velocidade da fonte relativa ao meio, adicionado a $c$ se a fonte estiver se afastando do receptor, subtraído se a fonte estiver se movendo para o receptor.

Observe que esta relação prevê que a frequência diminuirá se a fonte ou o receptor estiver se afastando um do outro.

Equivalentemente, assumindo que a fonte está se aproximando ou se afastando diretamente do observador:

{displaystyle {frac {f}{v_{wr}}}={frac {f_{0}}{v_{ws}}}={frac {1}{lambda }}}

${displaystyle v_{wr}}$ é a velocidade da onda em relação ao receptor;
${displaystyle v_{ws}}$ é a velocidade da onda em relação à fonte;
$lambda$ é o comprimento de onda.

Se a fonte se aproxima do observador em um ângulo (mas ainda com uma velocidade constante), a frequência observada que é ouvida pela primeira vez é maior do que a frequência emitida pelo objeto. A partir daí, há um decréscimo monotônico na frequência observada à medida que se aproxima do observador, por igualdade quando vem de uma direção perpendicular ao movimento relativo (e foi emitida no ponto de maior aproximação; mas quando a onda é recebida, a fonte e o observador não estarão mais próximos) e uma diminuição monotônica contínua à medida que se afasta do observador. Quando o observador está muito próximo da trajetória do objeto, a transição de alta para baixa frequência é muito abrupta. Quando o observador está longe do caminho do objeto, a transição de alta para baixa frequência é gradual.

Se as velocidades ${displaystyle v_{text{s}}}$ e $v_{{text{r}}},$ são pequenos em comparação com a velocidade da onda, a relação entre a frequência observada $f$ e frequência emitida $f_{{text{0}}}$ é aproximadamente

Frequência observada	Mudança de frequência
${displaystyle f=left(1+{frac {Delta v}{c}}right)f_{0}}$	${displaystyle Delta f={frac {Delta v}{c}}f_{0}}$

onde

${displaystyle Delta f=f-f_{0}}$
${displaystyle Delta v=-(v_{text{r}}-v_{text{s}})}$ é o oposto da velocidade relativa do receptor com respeito à fonte: é positivo quando a fonte e o receptor estão se movendo para o outro.

Prova

Conduzido ${displaystyle f=left({frac {c+v_{text{r}}}{c+v_{text{s}}}}right)f_{0}}$

nós dividimos para $c$

{displaystyle f=left({frac {1+{frac {v_{text{r}}}{c}}}{1+{frac {v_{text{s}}}{c}}}}right)f_{0}=left(1+{frac {v_{text{r}}}{c}}right)left({frac {1}{1+{frac {v_{text{s}}}{c}}}}right)f_{0}}

Desde então ${frac {v_{{text{s}}}}{c}}ll 1$ podemos substituir a expansão geométrica:

{displaystyle {frac {1}{1+{frac {v_{text{s}}}{c}}}}approx 1-{frac {v_{text{s}}}{c}}}

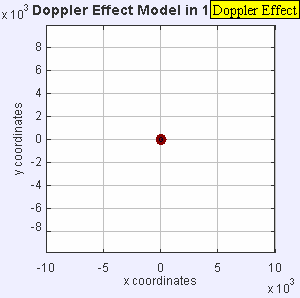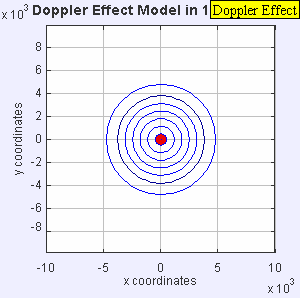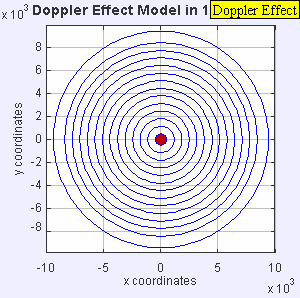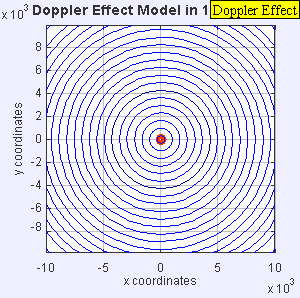
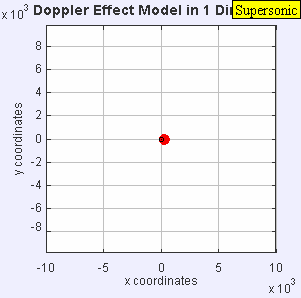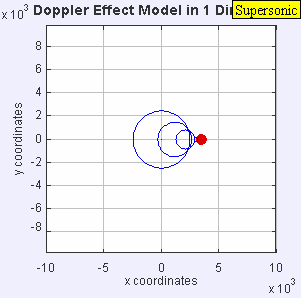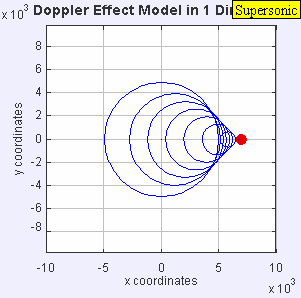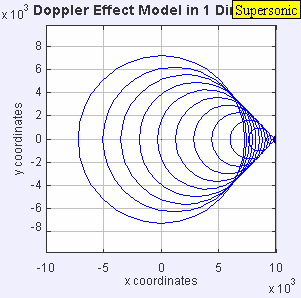
Fonte de som estacionária produz ondas sonoras a uma frequência constante $f$ , e as margens de onda se propagam simetricamente longe da fonte a uma velocidade constante c. A distância entre as margens de onda é o comprimento de onda. Todos os observadores ouvirão a mesma frequência, que será igual à frequência real da fonte $f = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = f 0$ .
A mesma fonte de som é irradiando ondas sonoras a uma frequência constante no mesmo meio. No entanto, agora a fonte de som está se movendo com uma velocidade $Tu S = 0,7 c$ . Uma vez que a fonte está se movendo, o centro de cada nova margem de onda agora está ligeiramente deslocado para a direita. Como resultado, as frentes de onda começam a se juntar no lado direito (na frente de) e se espalhar mais para o lado esquerdo (abaixo) da fonte. Um observador na frente da fonte vai ouvir uma frequência maior $f = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = c + 0 / c - 0,7 c f 0 = 3.33 f 0$ e um observador por trás da fonte vai ouvir uma frequência menor $f = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = c - 0 / c + 0,7 c f 0 = 0,59 f 0$ .
Agora a fonte está se movendo na velocidade do som no meio ( $Tu S = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = c$ ). As frentes de onda na frente da fonte estão agora todos agrupados no mesmo ponto. Como resultado, um observador na frente da fonte não detectará nada até que a fonte chegue e um observador por trás da fonte ouvirá uma frequência inferior $f = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = c - 0 / c + c f 0 = 0,5 f 0$ .
A fonte de som agora superou a velocidade do som no meio, e está viajando em 1.4 c. Uma vez que a fonte está se movendo mais rápido do que as ondas sonoras que cria, ele realmente leva a frente de onda avançando. A fonte sonora passará por um observador estacionário antes que o observador ouça o som. Como resultado, um observador na frente da fonte não detectará nada e um observador por trás da fonte ouvirá uma frequência menor $f = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = c - 0 / c + 1.4 c f 0 = 0,42 f 0$ .

Consequências

Com um observador estacionário em relação ao meio, se uma fonte em movimento está emitindo ondas com uma frequência real $f_{0}$ (neste caso, o comprimento de onda é alterado, a velocidade de transmissão da onda mantém constante; note que velocidade de transmissão da onda não depende da velocidade da fonte), então o observador detecta ondas com uma frequência $f$ por

{displaystyle f=left({frac {c}{cpm v_{text{s}}}}right)f_{0}}

Uma análise semelhante para um observador em movimento e uma fonte estacionária (neste caso, o comprimento de onda se mantém constante, mas devido ao movimento, a taxa na qual o observador recebe ondas e, portanto, velocidade de transmissão da onda [em relação ao observador] é alterada) produz a frequência observada:

{displaystyle f=left({frac {cpm v_{text{r}}}{c}}right)f_{0}}

Assumindo um observador estacionário e uma fonte se movendo na velocidade do som, a equação Doppler prevê uma frequência infinita momentânea percebida por um observador na frente de uma fonte que está viajando na velocidade do som. Todos os picos estão no mesmo lugar, então o comprimento de onda é zero e a frequência é infinita. Essa sobreposição de todas as ondas produz uma onda de choque que, no caso das ondas sonoras, é conhecida como explosão sônica.

Quando a fonte se move mais rápido que a velocidade da onda, a fonte ultrapassa a onda. A equação dá valores de frequência negativa, que não têm sentido físico neste contexto (nenhum som será ouvido pelo observador até que a fonte passe por eles).

Lord Rayleigh previu o seguinte efeito em seu livro clássico sobre som: se o observador se afastasse da fonte (estacionária) com o dobro da velocidade do som, uma peça musical anteriormente emitida por essa fonte seria ser ouvido no andamento e tom corretos, mas como se fosse tocado ao contrário.

Aplicativos

Perfil de corrente Doppler acústico

Um perfilador de corrente Doppler acústico (ADCP) é um medidor de corrente hidroacústico semelhante a um sonar, usado para medir as velocidades das correntes de água em uma faixa de profundidade usando o efeito Doppler das ondas sonoras espalhadas pelas partículas dentro da coluna de água. O termo ADCP é um termo genérico para todos os perfis acústicos de corrente, embora a abreviatura se origine de uma série de instrumentos introduzida pela RD Instruments na década de 1980. A faixa de frequências de trabalho dos ADCPs varia de 38 kHz a vários Megahertz. O dispositivo usado no ar para perfis de velocidade do vento usando som é conhecido como SODAR e funciona com os mesmos princípios subjacentes.

Robótica

O planejamento de caminho dinâmico em tempo real em robótica para auxiliar o movimento de robôs em um ambiente sofisticado com obstáculos em movimento geralmente recebe a ajuda do efeito Doppler. Tais aplicativos são usados especialmente para robótica competitiva onde o ambiente está em constante mudança, como robosoccer.

Sirenes

Sirenes a passar veículos de emergência.

Uma sirene em um veículo de emergência que passa começa mais alto do que seu tom estacionário, desliza para baixo ao passar e continua abaixo de seu tom estacionário conforme se afasta do observador. O astrônomo John Dobson explicou o efeito assim:

A razão pela qual a sirene desliza é porque não lhe bate.

Em outras palavras, se a sirene se aproximasse diretamente do observador, o tom permaneceria constante, em um tom mais alto que o estacionário, até que o veículo o atingisse, para então imediatamente pular para um novo tom mais baixo. Como o veículo passa pelo observador, a velocidade radial não permanece constante, mas varia em função do ângulo entre sua linha de visão e a velocidade da sirene:

{displaystyle v_{text{radial}}=v_{text{s}}cos(theta)}

theta

Astronomia

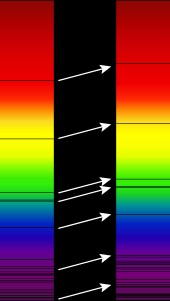
Redshift de linhas espectrais no espectro óptico de um supercluster de galáxias distantes (direita), em comparação com a do Sol (esquerda)

O efeito Doppler para ondas eletromagnéticas, como a luz, é amplamente utilizado na astronomia para medir a velocidade com que estrelas e galáxias se aproximam ou se afastam de nós, resultando no chamado desvio para o azul ou desvio para o vermelho, respectivamente. Isso pode ser usado para detectar se uma estrela aparentemente única é, na realidade, um binário próximo, para medir a velocidade de rotação de estrelas e galáxias ou para detectar exoplanetas. Esse efeito geralmente ocorre em uma escala muito pequena; não haveria uma diferença perceptível na luz visível a olho nu. O uso do efeito Doppler na astronomia depende do conhecimento de frequências precisas de linhas discretas no espectro das estrelas.

Entre as estrelas próximas, as maiores velocidades radiais em relação ao Sol são +308 km/s (BD-15°4041, também conhecida como LHS 52, a 81,7 anos-luz de distância) e −260 km/s (Woolley 9722, também conhecido como Wolf 1106 e LHS 64, a 78,2 anos-luz de distância). Velocidade radial positiva significa que a estrela está se afastando do Sol, negativa que está se aproximando.

O redshift também é usado para medir a expansão do espaço, mas não é realmente um efeito Doppler. Em vez disso, o redshifting devido à expansão do espaço é conhecido como redshift cosmológico, que pode ser derivado puramente da métrica de Robertson-Walker sob o formalismo da relatividade geral. Dito isto, também acontece que existem efeitos Doppler detectáveis em escalas cosmológicas, que, se interpretados incorretamente como origem cosmológica, levam à observação de distorções do espaço para o vermelho.

Radar

Soldado do Exército dos EUA usando uma arma de radar, uma aplicação de radar Doppler, para apanhar violadores em velocidade.

O efeito Doppler é usado em alguns tipos de radar, para medir a velocidade dos objetos detectados. Um feixe de radar é disparado em um alvo em movimento - por exemplo, um automóvel, pois a polícia usa o radar para detectar motoristas em alta velocidade - conforme ele se aproxima ou se afasta da fonte do radar. Cada onda de radar sucessiva tem que viajar mais longe para alcançar o carro, antes de ser refletida e detectada novamente perto da fonte. Como cada onda tem que se mover mais longe, o intervalo entre cada onda aumenta, aumentando o comprimento de onda. Em algumas situações, o feixe do radar é disparado no carro em movimento conforme ele se aproxima, caso em que cada onda sucessiva percorre uma distância menor, diminuindo o comprimento de onda. Em qualquer situação, os cálculos do efeito Doppler determinam com precisão a velocidade do carro. Além disso, a espoleta de proximidade, desenvolvida durante a Segunda Guerra Mundial, depende do radar Doppler para detonar explosivos no tempo, altura, distância etc. corretos.

Como a mudança de Doppler afeta o incidente de onda no alvo, bem como a onda refletiu de volta ao radar, a mudança de frequência observada por um radar devido a um alvo que se move em velocidade relativa $Delta v$ é o dobro do mesmo alvo emitindo uma onda:

{displaystyle Delta f={frac {2Delta v}{c}}f_{0}.}

Médico

Ultrassonografia de fluxo de cor (Doppler) de uma artéria carotídea – scanner e tela

Um ecocardiograma pode, dentro de certos limites, produzir uma avaliação precisa da direção do fluxo sanguíneo e da velocidade do sangue e do tecido cardíaco em qualquer ponto arbitrário usando o efeito Doppler. Uma das limitações é que o feixe de ultrassom deve ser o mais paralelo possível ao fluxo sanguíneo. As medições de velocidade permitem a avaliação das áreas e funções das válvulas cardíacas, comunicações anormais entre os lados esquerdo e direito do coração, vazamento de sangue pelas válvulas (regurgitação valvular) e cálculo do débito cardíaco. O ultrassom com contraste aprimorado usando meios de contraste de microbolhas preenchidos com gás pode ser usado para melhorar a velocidade ou outras medições médicas relacionadas ao fluxo.

Embora "Doppler" tornou-se sinônimo de "medição de velocidade" em imagens médicas, em muitos casos não é a mudança de frequência (desvio Doppler) do sinal recebido que é medida, mas a mudança de fase (quando o sinal recebido chega).

As medições de velocidade do fluxo sanguíneo também são usadas em outros campos da ultrassonografia médica, como a ultrassonografia obstétrica e a neurologia. A medição da velocidade do fluxo sanguíneo nas artérias e veias com base no efeito Doppler é uma ferramenta eficaz para o diagnóstico de problemas vasculares como a estenose.

Medição de vazão

Instrumentos como o velocímetro laser Doppler (LDV) e o velocímetro acústico Doppler (ADV) foram desenvolvidos para medir velocidades em um fluxo de fluido. O LDV emite um feixe de luz e o ADV emite uma explosão acústica ultrassônica e mede a mudança Doppler nos comprimentos de onda das reflexões das partículas que se movem com o fluxo. O fluxo real é calculado em função da velocidade e da fase da água. Essa técnica permite medições de vazão não intrusivas, com alta precisão e alta frequência.

Medição do perfil de velocidade

Desenvolvido originalmente para medições de velocidade em aplicações médicas (fluxo sanguíneo), a Velocimetria Doppler Ultrassônica (UDV) pode medir em tempo real o perfil de velocidade completo em quase todos os líquidos que contenham partículas em suspensão, como poeira, bolhas de gás, emulsões. Os fluxos podem ser pulsantes, oscilantes, laminares ou turbulentos, estacionários ou transitórios. Esta técnica é totalmente não invasiva.

Satélites

Possíveis Doppler desloca na dependência do ângulo de elevação (LEO: altitude da órbita

h

= 750 km). Estação fixa.

Geometria para efeitos de Doppler. Variáveis:

{displaystyle v_{text{mob}}}

é a velocidade da estação móvel,

{displaystyle v_{text{Sat}}}

é a velocidade do satélite,

{displaystyle v_{text{rel,sat}}}

é a velocidade relativa do satélite,

phi

é o ângulo de elevação do satélite e

theta

é a direção com respeito ao satélite.

Efeito doppler no canal móvel. Variáveis:

{displaystyle f_{c}={frac {c}{lambda _{rm {c}}}}}

é a frequência do transportador,

{displaystyle f_{rm {D,max}}={frac {v_{rm {mob}}}{lambda _{rm {c}}}}}

é o máximo Deslocamento do Doppler devido ao movimento da estação móvel (ver Doppler Spread) e

{displaystyle f_{rm {D,Sat}}}

é a mudança adicional Doppler devido ao movimento por satélite.

Navegação por satélite

O deslocamento Doppler pode ser explorado para navegação por satélite, como no Transit e DORIS.

Comunicação por satélite

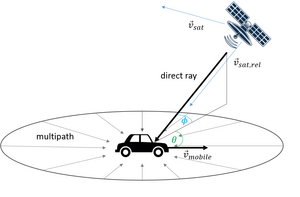
O Doppler também precisa ser compensado na comunicação via satélite. Satélites em movimento rápido podem ter um deslocamento Doppler de dezenas de quilohertz em relação a uma estação terrestre. A velocidade, portanto, a magnitude do efeito Doppler, muda devido à curvatura da Terra. A compensação Doppler dinâmica, onde a frequência de um sinal é alterada progressivamente durante a transmissão, é usada para que o satélite receba um sinal de frequência constante. Depois de perceber que o deslocamento Doppler não havia sido considerado antes do lançamento da sonda Huygens da missão Cassini-Huygens de 2005, a trajetória da sonda foi alterada para se aproximar de Titã de tal forma que suas transmissões viajaram perpendicularmente à sua direção de movimento em relação à Cassini. reduzindo bastante o desvio Doppler.

O deslocamento Doppler do caminho direto pode ser estimado pela seguinte fórmula:

{displaystyle f_{rm {D,dir}}={frac {v_{rm {mob}}}{lambda _{rm {c}}}}cos phi cos theta }

{displaystyle v_{text{mob}}}

{displaystyle lambda _{rm {c}}}

phi

theta

O deslocamento Doppler adicional devido ao movimento do satélite pode ser descrito como:

{displaystyle f_{rm {D,sat}}={frac {v_{rm {rel,sat}}}{lambda _{rm {c}}}}}

{displaystyle v_{rm {rel,sat}}}

Áudio

O alto-falante Leslie, mais comumente associado e usado predominantemente com o famoso órgão Hammond, aproveita o efeito Doppler usando um motor elétrico para girar uma corneta acústica em torno de um alto-falante, enviando seu som em um círculo. Isso resulta no ouvido do ouvinte em frequências de rápida flutuação de uma nota do teclado.

Medição de vibração

Um vibrômetro laser Doppler (LDV) é um instrumento sem contato para medir a vibração. O feixe de laser do LDV é direcionado para a superfície de interesse, e a amplitude e a frequência da vibração são extraídas do deslocamento Doppler da frequência do feixe de laser devido ao movimento da superfície.

Biologia do desenvolvimento

Durante a segmentação de embriões de vertebrados, ondas de expressão gênica varrem o mesoderma pré-somítico, o tecido a partir do qual os precursores das vértebras (somitos) são formados. Um novo somito é formado com a chegada de uma onda na extremidade anterior do mesoderma pré-somítico. No peixe-zebra, foi demonstrado que o encurtamento do mesoderma pré-somítico durante a segmentação leva a um efeito semelhante ao Doppler à medida que a extremidade anterior do tecido se move nas ondas. Este efeito contribui para o período de segmentação.

Efeito Doppler inverso

Desde 1968, cientistas como Victor Veselago especulam sobre a possibilidade de um efeito Doppler inverso. O tamanho do deslocamento Doppler depende do índice de refração do meio pelo qual uma onda está se propagando. Mas alguns materiais são capazes de refração negativa, o que deve levar a um deslocamento Doppler que funciona na direção oposta à de um deslocamento Doppler convencional. O primeiro experimento que detectou esse efeito foi conduzido por Nigel Seddon e Trevor Bearpark em Bristol, Reino Unido, em 2003. Posteriormente, o efeito Doppler inverso foi observado em alguns materiais não homogêneos e previsto dentro de um cone Vavilov-Cherenkov.

Fontes primárias

^ Buys Ballot (1845). «Akustische Versuche auf der Niederländischen Eisenbahn, nebst gelegentlichen Bemerkungen zur Theorie des Hrn. Prof. Doppler (em alemão)». Annalen der Physik und Chemie. 142 (11): 321–351. Bibcode:1845AnP...142..321B. doi:10.1002/andp.18451421102.
^ Fizeau: "Acoustique et optique". Palestra, Société Philomathique de Paris, 29 de Dezembro de 1848. De acordo com Becker(pg. 109), isso nunca foi publicado, mas contado por M. Moigno(1850): "Répertoire d'optique moderne" (em francês), vol 3. pp 1165–1203 e, mais tarde, completo por Fizeau, "Des effets du mouvement sur le ton des vibrações sonores et sur la longeur d'onde des rayons 1870; Annales de Chimie et de Physique, 19, 211-221.
^ Scott Russell, John (1848). «Sobre certos efeitos produzidos no som pelo movimento rápido do observador». Relatório do XVIII Encontro da Associação Britânica para o Avanço da Ciência. 18. (7): 37–38. Retrieved 2008-07-08.
^ Petrescu, Florian Ion T (2015). «Improving Medical Imaging and Blood Flow Measurement by using a New Doppler Effect Relations» (em inglês). American Journal of Engineering and Applied Sciences. 8 (4): 582–588. doi:10.3844/ajeassp.2015.582.588 – via Proquest.
^ Soroldoni, D.; Jörg, D. J.; Morelli, L. G.; Richmond, D. L.; Schindelin, J.; Jülicher, F.; Oates, A. C. (2014). «A Doppler Effect in Embryonic Pattern Formation» (em inglês). Ciência. 345 (6193): 222-225. Bibcode:2014Sci...345..222S. doi:10.1126/science.1253089. PMC7611034PMID 25013078. S2CID 206556621.
^ Kozyrev, Alexander B.; van der Weide, Daniel W. (2005). «Explanation of the Inverse Doppler Effect Observed in Nonlinear Transmission Lines» (em inglês). Cartas de Revisão Física. 94 (20): 203902. Bibcode:2005PhRvL..94t3902K. doi:10.1103/PhysRevLett.94.203902. PMID 16090248.

Contenido relacionado

Más resultados...