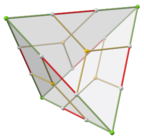
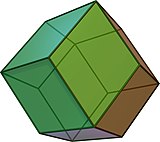
Dodecaedro
Em geometria, um dodecaedro (grego δωδεκάεδρον, de δώδεκα dōdeka "doze" + ἕδρα hédra "base", "assento" ou "face") ou duodecaedro é qualquer poliedro com doze faces planas. O dodecaedro mais familiar é o dodecaedro regular com pentágonos regulares como faces, que é um sólido platônico. Existem também três dodecaedros de estrelas regulares, que são construídos como estrelas da forma convexa. Todos estes têm simetria icosaédrica, ordem 120.
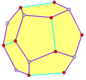
Alguns dodecaedros têm a mesma estrutura combinatória do dodecaedro regular (em termos do grafo formado por seus vértices e arestas), mas suas faces pentagonais não são regulares: O piritoedro, uma forma cristalina comum na pirita, tem simetria piritoédrica, enquanto o tetraédrico tem simetria tetraédrica.
O dodecaedro rômbico pode ser visto como um caso limite do piritoedro, e tem simetria octaédrica. As variações do dodecaedro alongado e do dodecaedro trapezorômbico, juntamente com o dodecaedro rômbico, preenchem o espaço. Existem numerosos outros dodecaedros.
Embora o dodecaedro regular compartilhe muitas características com outros sólidos platônicos, uma propriedade única dele é que se pode começar em um canto da superfície e desenhar um número infinito de linhas retas na figura que retornam ao ponto original sem cruzar sobre qualquer outro canto.
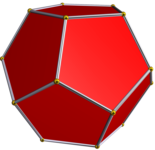
Dodecaedro regular
O dodecaedro regular convexo é um dos cinco sólidos regulares platônicos e pode ser representado por seu símbolo Schläfli {5, 3}.
O poliedro dual é o icosaedro regular {3, 5}, com cinco triângulos equiláteros em torno de cada vértice.
 Convexo regular dodecahedron |  Dodecaedro estelar pequeno |  Grande dodecaedron |  Grande dodecaedro estelar |
O dodecaedro regular convexo também tem três estrelas, todas elas dodecaedros regulares. Eles formam três dos quatro poliedros Kepler-Poinsot. Eles são o pequeno dodecaedro estrelado {5/2, 5}, o grande dodecaedro {5, 5/2} e o grande dodecaedro estrelado {5/2, 3}. O pequeno dodecaedro estrelado e o grande dodecaedro são duais entre si; o grande dodecaedro estrelado é dual ao grande icosaedro {3, 5/2}. Todos esses dodecaedros de estrelas regulares têm faces pentagonais ou pentagrâmicas regulares. O dodecaedro regular convexo e o grande dodecaedro estrelado são diferentes realizações do mesmo poliedro regular abstrato; o pequeno dodecaedro estrelado e o grande dodecaedro são diferentes realizações de outro poliedro regular abstrato.
Outro dodecaedro pentagonal
Na cristalografia, dois dodecaedros importantes podem ocorrer como formas cristalinas em algumas classes de simetria do sistema cristalino cúbico que são topologicamente equivalentes ao dodecaedro regular, mas menos simétricos: o piritoedro com simetria piritoédrica e o tetartoide com simetria tetraédrica:
Piritoedro
Um piritoedro é um dodecaedro com simetria piritoédrica (Th). Como o dodecaedro regular, ele tem doze faces pentagonais idênticas, com três se encontrando em cada um dos 20 vértices (veja a figura). No entanto, os pentágonos não são constrangidos a serem regulares, e o arranjo atômico subjacente não possui um verdadeiro eixo de simetria quíntupla. Suas 30 arestas são divididas em dois conjuntos – contendo 24 e 6 arestas de mesmo comprimento. Os únicos eixos de simetria rotacional são três eixos duplos mutuamente perpendiculares e quatro eixos triplos.
Embora os dodecaedros regulares não existam nos cristais, a forma piritoedro ocorre nos cristais do mineral pirita, e pode ser uma inspiração para a descoberta da forma sólida regular platônica. O verdadeiro dodecaedro regular pode ocorrer como uma forma de quasicristais (como hólmio-magnésio-zinco quasicristal) com simetria icosaédrica, que inclui verdadeiros eixos de rotação quíntupla.
Cristal pirita
O nome cristal pirita vem de um dos dois hábitos cristalinos comuns mostrados pela pirita (o outro é o cubo). Na pirita piritoédrica, as faces têm um índice de Miller de (210), o que significa que o ângulo diedro é 2·arctan(2) ≈ 126,87° e cada face pentagonal tem um ângulo de aproximadamente 121,6° entre dois ângulos de aproximadamente 106,6° e dois ângulos opostos de aproximadamente 102,6°. As fórmulas a seguir mostram as medidas da face de um cristal perfeito (que raramente é encontrado na natureza).
Altura= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =52)) Longo lado{displaystyle {text{Height}}={frac {sqrt {5}}{2}}cdot {text{Long side}}}
Largura= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =43)) Longo lado{displaystyle {text{Width}}={frac {4}{3}}cdot {text{Long side}}}
Lados curtos= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =712)) Longo lado{displaystyle {text{Short sides}}={sqrt {frac {7}{12}}}cdot {text{Long side}}}}}
Pirita natural (com ângulos de face na direita) |
Coordenadas cartesianas
Os oito vértices de um cubo têm as coordenadas (±1, ±1, ±1).
As coordenadas dos 12 vértices adicionais são (0, ±(1 + h), ±(1 − h2)), (±(1 + h), ±(1 − h2), 0) e (±(1 − h2), 0, ±(1 + h)).
h é a altura do "teto" acima das faces desse cubo com comprimento de aresta 2.
Um caso importante é h = 1/2 (um quarto do comprimento da borda do cubo) para pirita natural perfeita (também o piritoedro na estrutura Weaire-Phelan).
Outro é h = 1/φ = 0,618... para o dodecaedro regular. Consulte a seção Liberdade geométrica para outros casos.
Dois piritoedros com coordenadas diferentes de zero trocadas estão em posições duais entre si, como o dodecaedro no composto de dois dodecaedros.
Projeções ortográficos do piritoedro com h = 1/2 | Alturas 1/2 e 1/φ |
| Animações | |
|---|---|
 |  |
| Comboio de convexo alternado e piritohedra côncavo com alturas entre ±1/φ | Alturas entre 0 (cube) e 1 (dodecaedro rômbico) |
Liberdade geométrica
O piritoedro tem um grau de liberdade geométrico com casos limites de uma casca cúbica convexa em um limite de arestas colineares, e um dodecaedro rômbico como o outro limite, pois 6 arestas são degeneradas para comprimento zero. O dodecaedro regular representa um caso intermediário especial onde todas as arestas e ângulos são iguais.
É possível ultrapassar estes casos limites, criando piritoedros côncavos ou não convexos. O endododecaedro é côncavo e equilátero; pode pavimentar o espaço com o dodecaedro regular convexo. Continuando a partir daí nessa direção, passamos por um caso degenerado onde doze vértices coincidem no centro, e para o grande dodecaedro estrelado regular onde todas as arestas e ângulos são iguais novamente, e as faces foram distorcidas em pentagramas regulares. Do outro lado, além do dodecaedro rômbico, obtemos um dodecaedro equilátero não convexo com faces pentagonais equiláteras auto-intersectivas em forma de peixe.
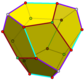
Tetartóide
Um tetartóide (também dodecaedro pentagonal tetragonal, pentágono-tritetraedro e dodecaedro pentágono tetraédrico) é um dodecaedro com simetria tetraédrica quiral (T). Como o dodecaedro regular, ele tem doze faces pentagonais idênticas, com três se encontrando em cada um dos 20 vértices. No entanto, os pentágonos não são regulares e a figura não tem eixos de simetria quíntupla.
Embora os dodecaedros regulares não existam nos cristais, a forma tetartoide existe. O nome tetartóide vem da raiz grega para um quarto porque tem um quarto de simetria octaédrica completa e metade de simetria piritoédrica. O mineral cobaltita pode ter esta forma de simetria.
As abstrações que compartilham a topologia e a simetria do sólido podem ser criadas a partir do cubo e do tetraedro. No cubo, cada face é cortada ao meio por uma aresta inclinada. No tetraedro, cada aresta é trissectada e cada um dos novos vértices é conectado a um centro de face. (Na notação de poliedro de Conway, este é um tetraedro giroscópico.)
Projeções ortográficos de eixos 2 e 3 vezes | Forma cúbica e tetraedral |
| Relação ao dyakis dodecahedron | ||
|---|---|---|
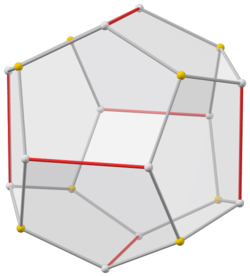
Um tetartoide pode ser criado ampliando 12 das 24 faces de um dyakis dodecahedron. (O tetartoide mostrado aqui é baseado em um que é criado por si mesmo, ampliando 24 das 48 faces do desdyakis dodecahedron.)
O modelo de cristal à direita mostra um tetartoide criado ampliando as faces azuis do núcleo dyakis dodecaedral. Portanto, as bordas entre as faces azuis são cobertas pelas bordas vermelhas do esqueleto. |
Coordenadas cartesianas
Os seguintes pontos são vértices de um pentágono tetraédrico sob simetria tetraédrica:
- (um, b), c);um,b), c);n/D1,n/D1, n/D1);c,um, b));n/D2, n/D2, n/D2),
nas seguintes condições:
- 0 ≤ um ≤ b) ≤ c,
- n = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = um2c - Sim. b)2,
- D1 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = um2 - Sim. A + b)2 + ACÇÃO - 2b),
- D2 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = um2 + A + b)2 - Sim. ACÇÃO - 2b),
- n1D2 ≠ 0.
Liberdade geométrica
O dodecaedro regular é um tetratóide com mais do que a simetria necessária. O tetraedro triakis é um caso degenerado com 12 arestas de comprimento zero. (Em termos das cores usadas acima, isso significa que os vértices brancos e as bordas verdes são absorvidos pelos vértices verdes.)
| Variações de tetartoide de dodecaedro regular a triakis tetrahedron | |||||||
|---|---|---|---|---|---|---|---|
 |  |  |  |  |  |  |  |
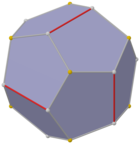
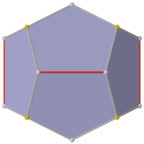
Dual de girobianticupola triangular
Uma forma de simetria inferior do dodecaedro regular pode ser construída como o dual de um poliedro construído a partir de duas anticúpulas triangulares conectadas base a base, chamada de girobianticupola triangular. Tem D Simetria 3d, ordem 12. Tem 2 conjuntos de 3 pentágonos idênticos na parte superior e inferior, conectados 6 pentágonos em torno dos lados que se alternam para cima e para baixo. Este formulário tem uma seção transversal hexagonal e cópias idênticas podem ser conectadas como um favo de mel hexagonal parcial, mas todos os vértices não serão correspondentes.
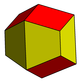
Dodecaedro rômbico
O dodecaedro rômbico é um zonoedro com doze faces rômbicas e simetria octaédrica. É dual ao cuboctaedro quasiregular (um sólido arquimediano) e ocorre na natureza como uma forma de cristal. O dodecaedro rômbico se agrupa para preencher o espaço.
O dodecaedro rômbico pode ser visto como um piritoedro degenerado onde as 6 arestas especiais foram reduzidas a comprimento zero, reduzindo os pentágonos a faces rômbicas.
O dodecaedro rômbico tem várias estrelas, a primeira das quais também é um espaço paralelo-édrico.
Outro importante dodecaedro rômbico, o dodecaedro de Bilinski, tem doze faces congruentes com as do triacontaedro rômbico, ou seja, as diagonais estão na proporção da proporção áurea. É também um zonoedro e foi descrito por Bilinski em 1960. Esta figura é outro preenchedor de espaço, e também pode ocorrer em preenchimentos de espaço não periódicos junto com o triacontaedro rômbico, o icosaedro rômbico e o hexaedro rômbico.
Outro dodecaedro
Existem 6.384.634 dodecaedros convexos topologicamente distintos, excluindo imagens espelhadas - o número de vértices varia de 8 a 20. (Dois poliedros são "topologicamente distintos" se tiverem intrinsecamente diferentes arranjos de faces e vértices, de modo que seja impossível distorcer um no outro simplesmente alterando o comprimento das arestas ou os ângulos entre arestas ou faces.)
Dodecaedros topologicamente distintos (excluindo formas pentagonais e rômbicas)
- Poliedros uniformes:
- Prisma Decagonal – 10 quadrados, 2 decagonais, simetria D10h, ordem 40.
- Antiprisma Pentagonal – 10 triângulos equiláteros, 2 pentágonos, simetria D5d, ordem 20
- Johnson solids (frente regular):
- Cupola Pentagonal – 5 triângulos, 5 quadrados, 1 pentágono, 1 decagono, simetria C5v, ordem 10
- Snub disphenoid – 12 triângulos, D2d, ordem 8
- dipyramida quadrada alongada – 8 triângulos e 4 quadrados, simetria D4h, ordem 16
- Metabidiminished icosahedron – 10 triângulos e 2 pentágonos, simetria C2v, ordem 4
- Congruente de face irregular: (face-transitivo)
- Bipiramida hexagonal – 12 triângulos isosceles, dual de prisma hexagonal, simetria D6h, ordem 24
- Armadilha hexagonal – 12 kites, duplo de antiprisma hexagonal, simetria D6d, ordem 24
- Triakis tetrahedron – 12 triângulos isosceles, duplo de tetraedro truncado, simetria de TD, ordem 24
- Outros menos regulares enfrentados:
- Pirâmide hendecagonal – 11 triângulos isosceles e 1 hendecagon regular, C11v, ordem 11
- Trapezo-rhombic dodecahedron – 6 rhombi, 6 trapezoidais – dual de ortobicupola triangular, simetria D3h, ordem 12
- Dodecaedro de Rhombo-hexagonal ou alongado Dodecahedron – 8 rhombi e 4 hexágonos equiláteros, simetria D4h, ordem 16
- Truncated pentagonal trapezohedron, D5d, ordem 20, topologicamente equivalente ao dodecahedron regular
Uso prático
Armand Spitz usou um dodecaedro como o "globo" equivalente para seu projetor de planetário Digital Dome, baseado em uma sugestão de Albert Einstein.
Contenido relacionado
Antiprisma
Charles Babbage
Espaço euclidiano