Dipolo
Na física, um dipolo (do grego δίς (dis) 'duas vezes' e πόλος (polos) 'eixo') é um fenômeno eletromagnético que ocorre de duas maneiras:
- Um dipolo elétrico lida com a separação das cargas elétricas positivas e negativas encontradas em qualquer sistema eletromagnético. Um exemplo simples deste sistema é um par de cargas de magnitude igual, mas sinal oposto separado por alguma distância tipicamente pequena. (Um dipolo elétrico permanente é chamado de electret.)
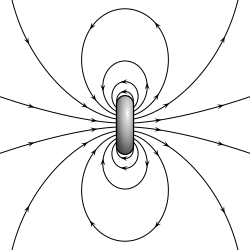
- Um dipolo magnético é a circulação fechada de um sistema de corrente elétrica. Um exemplo simples é um único loop de fio com corrente constante através dele. Um íman de bar é um exemplo de um ímã com um momento dipole magnético permanente.
Os dipolos, sejam elétricos ou magnéticos, podem ser caracterizados por seu momento de dipolo, uma grandeza vetorial. Para o dipolo elétrico simples, o momento do dipolo elétrico aponta da carga negativa para a carga positiva e tem uma magnitude igual à força de cada carga vezes a separação entre as cargas. (Para ser preciso: para a definição do momento de dipolo, deve-se sempre considerar o "limite de dipolo", onde, por exemplo, a distância das cargas geradoras deve convergir para 0 enquanto simultaneamente, a força da carga deve divergir para o infinito de tal forma que o produto permaneça uma constante positiva.)
Para o loop de corrente magnética (dipolo), o momento do dipolo magnético aponta através do loop (de acordo com a regra da mão direita), com uma magnitude igual à corrente no loop vezes a área do loop.
Semelhante aos loops de corrente magnética, a partícula de elétron e algumas outras partículas fundamentais têm momentos de dipolo magnético, pois um elétron gera um campo magnético idêntico ao gerado por um loop de corrente muito pequeno. No entanto, o momento de dipolo magnético de um elétron não é devido a um loop de corrente, mas a uma propriedade intrínseca do elétron. O elétron também pode ter um momento de dipolo elétrico, embora isso ainda não tenha sido observado (ver momento de dipolo elétrico do elétron).
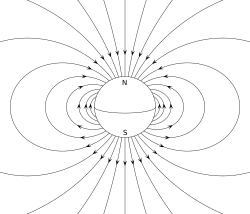
Um imã permanente, como um imã em barra, deve seu magnetismo ao momento de dipolo magnético intrínseco do elétron. As duas extremidades de uma barra magnética são referidas como pólos - não confundir com monopolos, consulte a classificação abaixo) - e podem ser rotuladas como "norte" e "sul". Em termos do campo magnético da Terra, eles são, respectivamente, "buscando o norte" e "em busca do sul" pólos: se o ímã fosse livremente suspenso no campo magnético da Terra, o pólo norte apontaria para o norte e o pólo sul apontaria para o sul. O momento de dipolo da barra magnética aponta de seu sul magnético para seu pólo norte magnético. Em uma bússola magnética, o pólo norte de uma barra magnética aponta para o norte. No entanto, isso significa que o polo norte geomagnético da Terra é o polo sul (polo que busca o sul) de seu momento de dipolo e vice-versa.
Os únicos mecanismos conhecidos para a criação de dipolos magnéticos são por loops de corrente ou rotação quântica, uma vez que a existência de monopolos magnéticos nunca foi demonstrada experimentalmente.
Classificação
Um dipolo físico consiste em duas cargas pontuais iguais e opostas: no sentido literal, dois polos. Seu campo a grandes distâncias (ou seja, distâncias grandes em comparação com a separação dos pólos) depende quase inteiramente do momento de dipolo conforme definido acima. Um dipolo (elétrico) pontual é o limite obtido deixando a separação tender a 0 enquanto mantém o momento de dipolo fixo. O campo de um dipolo pontual tem uma forma particularmente simples, e o termo de ordem 1 na expansão multipolar é precisamente o campo dipolo pontual.
Embora não existam monopolos magnéticos conhecidos na natureza, existem dipolos magnéticos na forma de spin da mecânica quântica associados a partículas como elétrons (embora a descrição precisa de tais efeitos caia fora do eletromagnetismo clássico). Um dipolo de ponto magnético teórico tem um campo magnético exatamente da mesma forma que o campo elétrico de um dipolo de ponto elétrico. Um loop de transporte de corrente muito pequeno é aproximadamente um dipolo de ponto magnético; o momento de dipolo magnético de tal loop é o produto da corrente que flui no loop e a área (vetorial) do loop.
Qualquer configuração de cargas ou correntes tem um 'momento de dipolo', que descreve o dipolo cujo campo é a melhor aproximação, em grandes distâncias, daquele da configuração dada. Este é simplesmente um termo na expansão multipolo quando a carga total ("momento monopolo") é 0 - como sempre é para o caso magnético, já que não há monopolos magnéticos. O termo dipolo é o dominante em grandes distâncias: seu campo cai proporcionalmente a 1/r3, em comparação com 1/r 4 para o próximo termo (quadrupolo) e potências superiores de 1/r para termos superiores, ou 1/r2 para o termo monopolo.
Dipolos moleculares
Muitas moléculas têm esses momentos de dipolo devido a distribuições não uniformes de cargas positivas e negativas nos vários átomos. Tal é o caso de compostos polares como o fluoreto de hidrogênio (HF), onde a densidade de elétrons é compartilhada de forma desigual entre os átomos. Portanto, o dipolo de uma molécula é um dipolo elétrico com um campo elétrico inerente que não deve ser confundido com um dipolo magnético, que gera um campo magnético.
O físico-químico Peter J. W. Debye foi o primeiro cientista a estudar extensivamente os dipolos moleculares e, como consequência, os momentos de dipolo são medidos na unidade não SI chamada debye em sua homenagem.
Para moléculas, existem três tipos de dipolos:
- Dipolos permanentes
- Estes ocorrem quando dois átomos em uma molécula têm elétronegatividade substancialmente diferente: Um átomo atrai elétrons mais do que outro, tornando-se mais negativo, enquanto o outro átomo se torna mais positivo. Uma molécula com um momento dipolo permanente é chamada de polarização molécula. Veja atrações dipole–dipole.
- Dipolos instantâneos
- Estes ocorrem devido ao acaso quando os elétrons acontecem ser mais concentrados em um lugar do que outro em uma molécula, criando um dipolo temporário. Estes dipolos são menores em magnitude do que os dipolos permanentes, mas ainda desempenham um grande papel na química e bioquímica devido à sua prevalência. Veja dipolo instantâneo.
- Dipolos induzidos
- Estes podem ocorrer quando uma molécula com um dipolo permanente repele os elétrons de outra molécula, indução Um momento dipolo nessa molécula. Uma molécula é polarização quando carrega um dipolo induzido. Veja atração induzida por dipolos.
Em geral, um dipolo induzido de qualquer distribuição de carga polarizável ρ (lembre-se de que uma molécula tem uma distribuição de carga) é causado por um campo elétrico externo a ρ. Este campo pode, por exemplo, originar-se de um íon ou molécula polar nas proximidades de ρ ou pode ser macroscópico (por exemplo, uma molécula entre as placas de um capacitor carregado). O tamanho do momento de dipolo induzido é igual ao produto da intensidade do campo externo e a polarizabilidade do dipolo de ρ.
Os valores do momento dipolar podem ser obtidos a partir da medição da constante dielétrica. Alguns valores típicos de fase gasosa em unidades de bye são:
- dióxido de carbono: 0
- monóxido de carbono: 0,112 D
- ozônio: 0,53 D
- fosgene: 1.17 D
- NH3 tem um momento dipolo de 1.42 D
- vapor de água: 1.85 D
- cianeto de hidrogênio: 2.98 D
- cianamida: 4.27 D
- brometo de potássio: 10.41 D
O brometo de potássio (KBr) tem um dos maiores momentos dipolares porque é um composto iônico que existe como uma molécula na fase gasosa.
O momento de dipolo geral de uma molécula pode ser aproximado como uma soma vetorial dos momentos de dipolo da ligação. Como uma soma vetorial, depende da orientação relativa das ligações, de modo que a partir do momento dipolar pode-se deduzir informações sobre a geometria molecular.
Por exemplo, o dipolo zero de CO2 implica que os dois momentos dipolares da ligação C=O se cancelam, de modo que a molécula deve ser linear. Para H2O, os momentos de ligação O-H não se cancelam porque a molécula é dobrada. Para o ozônio (O3), que também é uma molécula dobrada, os momentos de dipolo da ligação não são zero, embora as ligações O-O sejam entre átomos semelhantes. Isso está de acordo com as estruturas de Lewis para as formas de ressonância do ozônio que mostram uma carga positiva no átomo de oxigênio central.
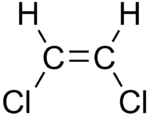
Um exemplo em química orgânica do papel da geometria na determinação do momento dipolar são os isômeros cis e trans do 1,2-dicloroeteno. No isômero cis, as duas ligações polares C−Cl estão do mesmo lado da ligação dupla C=C e o momento de dipolo molecular é 1,90 D. No isômero trans, o momento de dipolo é zero porque as duas ligações C−Cl estão em lados opostos do C=C e cancelam (e os dois momentos de ligação para as ligações C−H muito menos polares também se cancelam).
Outro exemplo do papel da geometria molecular é o trifluoreto de boro, que possui três ligações polares com uma diferença de eletronegatividade maior que o limite tradicionalmente citado de 1,7 para ligação iônica. No entanto, devido à distribuição triangular equilátera dos íons de flúor centrados e no mesmo plano que o cátion boro, a simetria da molécula resulta em seu momento de dipolo ser zero.
Operador dipolo mecânico quântico
Considere uma coleção de N partículas com cargas qi e vetores de posição re. Por exemplo, esta coleção pode ser uma molécula composta por elétrons, todos com carga −e, e núcleos com carga eZi, onde Zi é o número atômico do i ésimo núcleo. O dipolo observável (quantidade física) tem o operador dipolo da mecânica quântica:
- p= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1NqEu...REu....{displaystyle {mathfrak {p}}=sum _{i=1}^{N},q_{i},mathbf {r} _{i},.}
Observe que esta definição é válida apenas para átomos ou moléculas neutras, ou seja, carga total igual a zero. No caso ionizado, temos
- p= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1NqEu...(REu...- Sim. - Sim. Rc),{displaystyle {mathfrak {p}}=sum _{i=1}^{N},q_{i},(mathbf {r} _{i}-mathbf {r} _{c}),}
Onde? Rc{displaystyle mathbf {r}} _{c}} é o centro de massa da molécula / grupo de partículas.
Dipolos atômicos
Um átomo não degenerado (estado S) pode ter apenas um dipolo permanente zero. Este fato decorre da mecânica quântica da simetria de inversão dos átomos. Todos os 3 componentes do operador dipolo são antisimétricos sob inversão em relação ao núcleo,
- Eu...pEu...- Sim. - Sim. 1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. p,{displaystyle {mathfrak {I}};{mathfrak {p}};{mathfrak {I}}^{-1}=-{mathfrak {p}},}
Onde? p{displaystyle {mathfrak {p}}} é o operador de dipolo e Eu...{displaystyle {mathfrak {I}}} é o operador de inversão.
O momento dipolar permanente de um átomo em um estado não degenerado (ver nível de energia degenerado) é dado como o valor esperado (médio) do operador dipolo,
- ⟨p)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =⟨S|p|S),{displaystyle leftlangle {mathfrak} {p}}rightrangle =leftlangle ,S,|{mathfrak {p}}|,S,rightrangle}
Onde? |S)) Não. |,S,rangle } é um S- estado, não degenerado, função de onda, que é simétrica ou antissimétrica sob inversão: Eu...|S)) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =± ± |S)) {displaystyle {mathfrak {I}},|,S,rangle =pm |,S,rangle }. Desde que o produto da função de onda (no ket) e seu complexo conjugado (no sutiã) é sempre simétrico sob inversão e seu inverso,
- ⟨p)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =⟨Eu...- Sim. - Sim. 1S|p|Eu...- Sim. - Sim. 1S)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =⟨S|Eu...pEu...- Sim. - Sim. 1|S)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. ⟨p){displaystyle leftlangle {mathfrak} {p}}rightrangle =leftlangle ,{mathfrak {I}}^{-1},S,|{mathfrak {p}}|,{mathfrak {I}}^{-1}, S,rightrangle =leftlangle ,S,|{mathfrak {I}},{mathfrak {p}},{mathfrak {I}}^{-1}|, S,rightrangle =-leftlangle {mathfrak {p}}rightrangle }
segue que o valor de expectativa muda de sinal sob inversão. Nós usamos aqui o fato de que Eu...{displaystyle {mathfrak {I}}}, sendo um operador de simetria, é unitário: Eu...- Sim. - Sim. 1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...∗ ∗ {displaystyle {mathfrak {I}}^{-1}={mathfrak {I}}^{*},} e por definição o adjunto hermitiano Eu...∗ ∗ {displaystyle {mathfrak {I}}^{*},} pode ser movido de sutiã para ket e, em seguida, torna-se Eu...∗ ∗ ∗ ∗ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...{displaystyle {mathfrak {I}}^{**}={mathfrak {I}},}. Uma vez que a única quantidade que é igual a menos em si é o zero, o valor de expectativa desaparece,
- ⟨p)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0.{displaystyle leftlangle {mathfrak} {p}}rightrangle - Sim.
No caso de átomos de camada aberta com níveis de energia degenerados, pode-se definir um momento de dipolo com a ajuda do efeito Stark de primeira ordem. Isso dá um dipolo não nulo (por definição proporcional a um deslocamento Stark de primeira ordem não nulo) apenas se algumas das funções de onda pertencentes às energias degeneradas tiverem paridade oposta; ou seja, têm comportamento diferente sob inversão. Esta é uma ocorrência rara, mas acontece para o átomo H excitado, onde os estados 2s e 2p são "acidentalmente" degenerado (veja o artigo vetor Laplace–Runge–Lenz para a origem desta degenerescência) e tem paridade oposta (2s é par e 2p é ímpar).
Campo de um dipolo magnético estático
Magnitude
A força de campo distante, B, de um campo magnético dipolo é dada por
- B(m,R,λ λ )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =μ μ 04D D mR31+3pecado2 (λ λ ),{displaystyle B(m,r,lambda)={frac {mu _{0}}{4pi }}{frac {m}{r^{3}}}{sqrt {1+3sin ^{2}(lambda)}},}
onde
- B é a força do campo, medida em teslas
- R é a distância do centro, medida em metros
- λ é a latitude magnética (igual a 90° −θ) onde θ é a colatitude magnética, medida em radianos ou graus do eixo dipolo
- m é o momento dipolo, medido em metros ampere-quadrado ou joules por tesla
- μ0 é a permeabilidade do espaço livre, medida em henries por metro.
A conversão para coordenadas cilíndricas é obtida usando r2 = z2 + ρ2 e
- λ λ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Produtos de plástico (zangão.zangão.2+? ? 2){displaystyle lambda =arcsin left({frac) {z}{sqrt {z^{2}+rho ^{2}}right)}
onde ρ é a distância perpendicular do eixo z. Então,
- B(? ? ,zangão.)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =μ μ 0m4D D (zangão.2+? ? 2)321+3zangão.2zangão.2+? ? 2{displaystyle B(rhoz)={frac {mu _{0}m}{4pi left(z^{2}+rho ^{2}right)^{frac {3}{2}}} (em inglês) {3z^{2}}{z^{2}+rho ^{2}}}}}}}}
Forma vetorial
O próprio campo é uma quantidade vetorial:
- B(m,R)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =μ μ 04D D 3(m)) R^ ^ )R^ ^ - Sim. - Sim. mR3{displaystyle mathbf {B} (mathbf {m}mathbf {r})={frac {mu _{0}}{4pi }} {frac {3(mathbf {m} cdot {hat {mathbf {r} }}{hat {mathbf {r} } }}-mathbf {m} }{r^{3}}
onde
- B é o campo
- R é o vetor da posição do dipolo para a posição onde o campo está sendo medido
- R é o valor absoluto de R: a distância do dipolo
- ̂ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = R/R é o vetor de unidade paralelo a R;
- m é o momento dipolo (vetor)
- μ0 é a permeabilidade do espaço livre
Este é exatamente o campo de um dipolo pontual, exatamente o termo dipolo na expansão multipolar de um campo arbitrário e aproximadamente o campo de qualquer configuração tipo dipolo em grandes distâncias.
Potencial vetorial magnético
O potencial vetorial A de um dipolo magnético é
- A(R)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =μ μ 04D D m× × R^ ^ R2{displaystyle mathbf {A} (mathbf {r})={frac {mu _{0}}{4pi }}{frac {mathbf {m} times {hat {mathbf {r}} }}}{r^{2}}
com as mesmas definições acima.
Campo de um dipolo elétrico
O potencial eletrostático na posição r devido a um dipolo elétrico na origem é dado por:
- Φ Φ (R)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =14D D ε ε 0p)) R^ ^ R2Não. Phi (mathbf {r})={frac {1}{4pi epsilon _{0}}},{frac {mathbf {p} Não. }}}{r^{2}}
onde p é o momento dipolar (vetorial) e є0 é a permissividade do espaço livre.
Este termo aparece como o segundo termo na expansão multipolar de um potencial eletrostático arbitrário Φ(r). Se a fonte de Φ(r) for um dipolo, como é assumido aqui, este termo é o único termo não nulo na expansão multipolar de Φ(r). O campo elétrico de um dipolo pode ser encontrado a partir do gradiente desse potencial:
- E= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. ? ? Φ Φ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =14D D ε ε 03(p)) R^ ^ )R^ ^ - Sim. - Sim. pR3- Sim. - Sim. δ δ 3(R)p3ε ε 0.{displaystyle mathbf] Não. Phi ={frac {1}{4pi epsilon _{0}}} {frac {3(mathbf {p} cdot {hat {mathbf {r} }}{hat {mathbf {r} } }}-mathbf {p} }{r^{3}}}-delta ^{3}(mathbf {r}){frac {mathbf {p} ¿3epsilon _{0}}}.}
Esta é a mesma forma da expressão para o campo magnético de um dipolo magnético pontual, ignorando a função delta. Em um dipolo elétrico real, no entanto, as cargas estão fisicamente separadas e o campo elétrico diverge ou converge nas cargas pontuais. Isso é diferente do campo magnético de um dipolo magnético real que é contínuo em todos os lugares. A função delta representa o campo forte apontando na direção oposta entre as cargas puntiformes, o que é frequentemente omitido, pois raramente se está interessado no campo na posição do dipolo. Para maiores discussões sobre o campo interno dos dipolos, veja Momento magnético#Campo magnético interno de um dipolo.
Torque em um dipolo
Como a direção de um campo elétrico é definida como a direção da força em uma carga positiva, as linhas do campo elétrico apontam para longe de uma carga positiva e em direção a uma carga negativa.
Quando colocado em um campo elétrico ou magnético homogêneo, forças iguais, mas opostas, surgem em cada lado do dipolo, criando um torque τ}:
- ? ? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =p× × E{displaystyle {boldsymbol {tau }}=mathbf {p} times mathbf Não.
para um momento de dipolo elétrico p (em coulomb-metros), ou
- ? ? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =m× × B{displaystyle {boldsymbol {tau }}=mathbf {m} times mathbf Não.
para um momento de dipolo magnético m (em ampères-metros quadrados).
O torque resultante tenderá a alinhar o dipolo com o campo aplicado, que no caso de um dipolo elétrico, produz uma energia potencial de
- U= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. p)) E{displaystyle U=-mathbf {p} cdot mathbf Não..
A energia de um dipolo magnético é similarmente
- U= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. m)) B{displaystyle U=-mathbf {m} cdot mathbf Não..
Radiação dipolo
Além dos dipolos em eletrostática, também é comum considerar um dipolo elétrico ou magnético que oscila no tempo. É uma extensão, ou um próximo passo mais físico, para a radiação de ondas esféricas.
Em particular, considere um dipolo elétrico oscilando harmonicamente, com frequência angular ω e um momento dipolar p0 ao longo do ẑ direção do formulário
- p(R,))= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =p(R)e- Sim. - Sim. Eu...ω ω )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =p0zangão.^ ^ e- Sim. - Sim. Eu...ω ω ).{displaystyle mathbf {p} (mathbf {r}t)=mathbf {p} (mathbf {r})e^{-iomega T=p_{0} }}e^{-iomega Não.
No vácuo, o campo exato produzido por este dipolo oscilante pode ser derivado usando a formulação de potencial retardado como:
- E= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =14D D ε ε 0(ω ω 2c2R(R^ ^ × × p)× × R^ ^ +(1R3- Sim. - Sim. Eu...ω ω cR2)(3R^ ^ Não.R^ ^ )) p]- Sim. - Sim. p)?eEu...ω ω Rce- Sim. - Sim. Eu...ω ω )B= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =ω ω 24D D ε ε 0c3(R^ ^ × × p)(1- Sim. - Sim. cEu...ω ω R)eEu...ω ω R/cRe- Sim. - Sim. Eu...ω ω ).{displaystyle {begin{aligned}mathbf] Não. Não. - Sim. _{0}}}left{{frac {omega ^{2}}{c^{2}r}}left({hat {mathbf {r} }}times mathbf {p} right)times {hat {mathbf {r} }}+left({frac {1}{r^{3}}}-{frac {iomega }{cr^{2}}}right)left(3{hat {mathbf {r} }}left[{hat {mathbf {r} }}cdot mathbf {p}right]-mathbf {p} rightrightright}eega {B} &={frac {omega ^{2}}{4pi varepsilon _{0}c^{3}}}({hat {mathbf {r}}} }}times mathbf {p})left(1-{frac {c}{iomega r}}right){frac {e^{iomega r/c}}{r}}e^{-iomega t}.end{aligned}}}
Para rω/c ≫ 1, o campo distante assume a forma mais simples de uma radiação "esférica" onda, mas com dependência angular embutida no produto vetorial:
- B= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =ω ω 24D D ε ε 0c3(R^ ^ × × p)eEu...ω ω (R/c- Sim. - Sim. ))R= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =ω ω 2μ μ 0p04D D c(R^ ^ × × zangão.^ ^ )eEu...ω ω (R/c- Sim. - Sim. ))R= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. ω ω 2μ μ 0p04D D cpecado (θ θ )eEu...ω ω (R/c- Sim. - Sim. ))Rφ φ ^ ^ E= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =cB× × R^ ^ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. ω ω 2μ μ 0p04D D pecado (θ θ )(φ φ ^ ^ × × R^ ^ )eEu...ω ω (R/c- Sim. - Sim. ))R= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. ω ω 2μ μ 0p04D D pecado (θ θ )eEu...ω ω (R/c- Sim. - Sim. ))Rθ θ ^ ^ .{displaystyle {begin{aligned}mathbf] {B} &={frac {omega ^{2}}{4pi varepsilon _{0}c^{3}}}({hat {mathbf {r} }}times mathbf {p}){frac {e^{iomega (r/c-t)}}{r}}={frac {omega ^{2}mu _{0}p_{0}}{4pi c}}({hat {mathbf {r} }}times {hat {mathbf {z} }}){frac {e^{iomega (r/c-t)}}{r}}=-{frac {omega ^{2}mu _{0}p_{0}}{4pi c}}sin(theta){frac {e^{iomega (r/c-t)}}{r}}mathbf {hat {phi }} \mathbf {E} &=cmathbf {B} Tempos }}=-{frac {omega ^{2}mu _{0}p_{0}}{4pi }}sin(theta)left({hat {phi }}times mathbf {hat {r}} right){frac {e^{iomega (r/c-t)}}{r}}=-{frac {omega ^{2}mu _{0}p_{0}}{4pi }}sin(theta){frac {e^{iomega (r/c-t)}}{r}}{hat {theta }}end{aligned}}}
O vetor Poynting de tempo médio
- ⟨ ⟨ S)) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(μ μ 0p02ω ω 432D D 2c)pecado2 (θ θ )R2R^ ^ {displaystyle langle mathbf] {S} rangle =left({frac {mu _{0}p_{0}^{2}omega ^{4}}{32pi ^{2}c}}right){frac {sin ^{2}(theta)}{r^{2}}}mathbf {hat {r}} }
não é distribuído isotropicamente, mas concentrado em torno das direções perpendiculares ao momento dipolar, como resultado das ondas elétricas e magnéticas não esféricas. De fato, a função harmônica esférica (sin θ) responsável por tal distribuição angular toroidal é justamente a função l = 1 "p" aceno.
A potência média total irradiada pelo campo pode então ser derivada do vetor de Poynting como
- P= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =μ μ 0ω ω 4p0212D D c.- Sim. _{0}omega ^{4}p_{0}^{2}}{12pi C}}.
Observe que a dependência da potência na quarta potência da frequência da radiação está de acordo com a dispersão de Rayleigh e os efeitos subjacentes por que o céu consiste principalmente na cor azul.
Um dipolo polarizado circular é descrito como uma superposição de dois dipolos lineares.
Contenido relacionado
Decaimento alfa
Densidade
Ampère


































![{displaystyle {begin{aligned}mathbf {E} &={frac {1}{4pi varepsilon _{0}}}left{{frac {omega ^{2}}{c^{2}r}}left({hat {mathbf {r} }}times mathbf {p} right)times {hat {mathbf {r} }}+left({frac {1}{r^{3}}}-{frac {iomega }{cr^{2}}}right)left(3{hat {mathbf {r} }}left[{hat {mathbf {r} }}cdot mathbf {p} right]-mathbf {p} right)right}e^{frac {iomega r}{c}}e^{-iomega t}\mathbf {B} &={frac {omega ^{2}}{4pi varepsilon _{0}c^{3}}}({hat {mathbf {r} }}times mathbf {p})left(1-{frac {c}{iomega r}}right){frac {e^{iomega r/c}}{r}}e^{-iomega t}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a84ead8e373689b51cea6ced6348616d2201bd6)


